
Color Beaver: Bounding Illumination Estimations for Higher Accuracy
Karlo Ko
ˇ
s
ˇ
cevi
´
c, Nikola Bani
´
c and Sven Lon
ˇ
cari
´
c
Image Processing Group, Department of Electronic Systems and Information Processing,
Faculty of Electrical Engineering and Computing, University of Zagreb, 10000 Zagreb, Croatia
Keywords:
Chromaticity, Color Constancy, Genetic Algorithm, Illumination Estimation, Image Enhancement, White
Balancing.
Abstract:
The image processing pipeline of most contemporary digital cameras performs illumination estimation in
order to remove the influence of illumination on image scene colors. In this paper an experiment is described
that examines some of the basic properties of illumination estimation methods for several Canon’s camera
models. Based on the obtained observations, an extension to any illumination estimation method is proposed
that under certain conditions alters the results of the underlying method. It is shown that with statistics-based
methods as underlying methods the proposed extension can outperform camera’s illumination estimation in
terms of accuracy. This effectively demonstrates that statistics-based methods can still be successfully used for
illumination estimation in digital cameras. The experimental results are presented and discussed. The source
code is available at https://ipg.fer.hr/ipg/resources/color
constancy.
1 INTRODUCTION
Among many abilities human visual system (HVS)
can recognize colors of objects regardless of scene
illumination. This ability is known as color con-
stancy (Ebner, 2007). Achieving computational co-
lor constancy is an important pre-processing step in
image processing pipeline as different scene illumina-
tions may cause the image colors to differ as shown in
figure 1. In order to remove the influence of illumina-
tion color, accurate illumination estimation followed
by chromatic adaptation must be preformed. For both
tasks the following image f formation model, which
includes Lambertian assumption, is most often used:
f
c
(x) =
Z
ω
I(λ, x)R(x, λ)ρ
c
(λ)dλ (1)
where c is a color channel, x is a given image
pixel, λ is the wavelength of the light, ω is the vi-
sible spectrum, I(λ, x) is the spectral distribution of
the light source, R(x, λ) is the surface reflectance, and
ρ
c
(λ) is the camera sensitivity of c-th color channel.
With the assumption of uniform illumination the pro-
blem can be simplified, as now x is removed from
I(λ, x) and the observed light source color is given
as:
e =
e
R
e
G
e
B
=
Z
ω
I(λ)ρ(λ)dλ (2)
(a) (b)
Figure 1: The same scene (a) with and (b) without illumi-
nation color cast.
For a successful chromatic adaptation, what is
required is only the direction of e (Barnard et al.,
2002). Since it is very common that only image pixel
values f are given and both I(λ) and ρ(λ) remain
unknown, calculating e is an ill-posed problem. To
solve this problem, additional assumptions must be
made, which leads to many color constancy methods
that are divided into two major groups. First group
of methods are low-level statistic-based methods like
White-patch (Land, 1977; Funt and Shi, 2010), its
improvements (Bani
´
c and Lon
ˇ
cari
´
c, 2013; Bani
´
c and
Lon
ˇ
cari
´
c, 2014a; Bani
´
c and Lon
ˇ
cari
´
c, 2014b), Gray-
world (Buchsbaum, 1980), Shades-of-Gray (Finlay-
son and Trezzi, 2004), Gray-Edge (1st and 2nd or-
der) (Van De Weijer et al., 2007a), using bright and
dark colors (Cheng et al., 2014). The second group
is formed of learning-based methods like gamut map-
ping (pixel, edge, and intersection based) (Finlayson
Koš
ˇ
cevi
´
c, K., Bani
´
c, N. and Lon
ˇ
cari
´
c, S.
Color Beaver: Bounding Illumination Estimations for Higher Accuracy.
DOI: 10.5220/0007393701830190
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 183-190
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
183

(a) (b) (c) (d) (e) (f) (g) (h)
Figure 2: Color checker cast with projector light of various colors.
et al., 2006), using high-level visual information (Van
De Weijer et al., 2007b), natural image statistics (Gi-
jsenij and Gevers, 2007), Bayesian learning (Gehler
et al., 2008), spatio-spectral learning (maximum li-
kelihood estimate, and with gen. prior) (Chakra-
barti et al., 2012), simplifying the illumination so-
lution space (Bani
´
c and Lon
ˇ
cari
´
c, 2015a; Bani
´
c and
Lon
ˇ
cari
´
c, 2015b; Bani
´
c and Lon
ˇ
cari
´
c, 2015b), using
color/edge moments (Finlayson, 2013), using regres-
sion trees with simple features from color distribu-
tion statistics (Cheng et al., 2015), performing vari-
ous kinds of spatial localizations (Barron, 2015; Bar-
ron and Tsai, 2017), using convolutional neural net-
works (Bianco et al., 2015; Shi et al., 2016; Hu et al.,
2017; Qiu et al., 2018).
While learning-based method have a much higher
accuracy, it are low-level statistics-based methods that
are still being widely used among digital camera ma-
nufacturers since they are much faster and often more
hardware-friendly than learning-based methods. This
is also one of the reasons why statistics-based met-
hods are still important for research. Nevertheless,
since cameras are commercial systems, the fact that
they still widely use statistics-based methods is not
publicly stated. In this paper an experiment is des-
cribed that examines some of the basic properties of
illumination estimation methods for several Canon’s
camera models. Based on the obtained observations,
an extension to any illumination estimation method is
proposed that under certain conditions alters the re-
sults of the underlying method by bounding them to
a previously learned region in the chromaticity plane.
The bounding procedure is simple and does not add
any significant cost to the overall computation. It is
shown that with statistics-based methods as under-
lying methods the proposed extension can outperform
camera’s built-in illumination estimation in terms of
accuracy. This effectively demonstrates that statistics-
based methods can still be successfully used for illu-
mination estimation in digital cameras’ pipelines.
The paper is structured as follows: Section 2 lays
out the motivation for the paper, in Section 3 the pro-
posed method is described, Section 4 shows the expe-
rimental results, and Section 5 concludes the paper.
2 MOTIVATION
2.1 Do statistics-based Methods
Matter?
Digital cameras are being used ever more widely, es-
pecially with the growing number of smartphones.
This definitely means that the results of the rese-
arch on computational color constancy now also have
a higher impact so the importance of this research
grows, especially when considering that it is an ill-
posed problem. In literature and in the reviews of
papers it is sometimes claimed that there is little pur-
pose in researching low-level statistics-based methods
since there are now much more accurate learning-
based methods that significantly outperform them in
accuracy. In contrast to that many experts with ex-
perience in the industry claim that many commercial
white balancing systems are still based on low-level
statistics-based methods. The main reason for that
is their simplicity, low cost of implementation, and
hardware-friendliness. If this is indeed so, then the
research on such methods is definitely still important
and should be further conducted and supported.
To check to what degree all these claims are true, it
should be enough to examine some of the white balan-
cing systems widely used in commercial cameras. In
the world of professional cameras Canon has been the
market leader for 15 years (Canon, 2018) and in 2018
it held an estimated 49% of the market share (Pho-
toRumors, 2018). Since practically every digital ca-
mera performs white balancing in its image proces-
sing pipeline, it can be claimed that Canon’s white
balancing system is one of the most widely spread
ones. However, since Canon is a commercial com-
pany, full details of the white balancing system used
in its digital cameras are not publicly known.
2.2 Learning from Existing Systems
One approach to gain more information on Canon’s
white balancing system is to look at the results of il-
lumination estimation for various images taken under
illumination of numerous colors. The following three
camera models have been used to perform this expe-
riment: EOS 550D, EOS 6D, and EOS 750D.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
184

Figure 3: Comparison of chromaticities of projector light color, color of the second achromatic color checker patch, and
camera’s illumination estimation for Canon EOS 550D in the rb-chromaticity plane. The red chromaticity is shown on the x
axis, while the blue chromaticity is shown on the y axis.
The experiment was conducted in a dark room
where only a projector has been used as a light source.
The projector was used to cast illumination of vari-
ous colors, with chromaticities evenly spread in the
chromaticity plane, on a color checker as shown in Fi-
gure 2. These images of the color checker were taken
with every of the three previously mentioned cameras.
Although the illumination color was supposed to
be computationally determined by projecting specifi-
cally created content, due to the projector and camera
sensor characteristics the effective illumination color
is altered. Its value as perceived by the camera can be
read from the achromatic patches in the last row of the
color checker and it serves as the ground-truth illumi-
nation for the given image. Ideally, it is this color that
an illumination estimation method should predict.
Finally, the last step of the experiment was to
check the results of illumination estimation perfor-
med by each of the cameras. The results of a ca-
mera’s illumination estimation for a taken image can
be reconstructed from the Exif metadata stored in the
image file. The fields needed for this are Red Balance
and Blue Balance, which have the values of channel
gains i.e. the factors by which the red and blue chan-
nels have to be multiplied to perform chromatic adap-
tation. For practical reasons in cameras the green gain
is fixed to 1. The combined inverse values of these
gains give the illumination estimation vector. When
this vector is normalized, it represents the chromati-
city of camera’s illumination estimation, which can
be directly used to calculate the estimation accuracy
by comparing it to the ground-truth illumination.
A comparison between the chromaticities for pro-
jected illumination color, achromatic patch color,
and camera illumination estimations for Canon EOS
550D camera is given in Figure 3. The values read
from achromatic white patches are squeezed with re-
spect to the ones sent by the projector, but a more in-
teresting observation is that none of the camera’s il-
lumination estimation are outside of a surface that re-
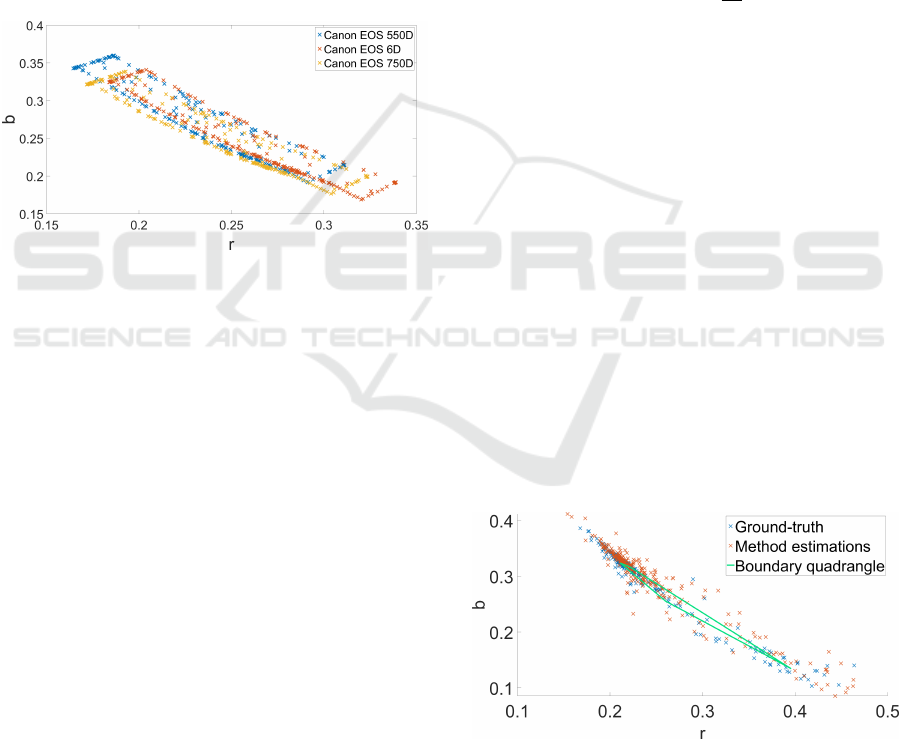
sembles a parallelogram. As shown in Figure 4, simi-
lar results are obtained for other used camera models
as well. Although there are some differences between
the parallelograms mostly visible on two opposite si-
des, the parallelograms otherwise mostly cover a si-
milar space in the chromaticity plane.
2.3 Observations
Based on these observations it can be concluded that
one of the core properties of Canon’s white balancing
system is limiting its illumination estimation so that
they do not appear outside of a polygon very similar
to a parallelogram. Such limitation can be justified by
the goal of avoiding unlikely illuminations and thus
minimizing the occurrence of too high errors. This
can be useful if it can be assumed that the expected
illuminations are similar to black body radiation, but
Color Beaver: Bounding Illumination Estimations for Higher Accuracy
185
sometimes it can be an disadvantage if artificially co-
lored illumination sources are present like in Figure 2.
On the other hand, there is little that can be said
about the white balancing system’s behavior inside of
the parallelogram. Nevertheless, the limitation obser-
vation is already useful because of its potential to li-
mit maximum errors for illumination estimations. As
for the behavior of illumination estimation inside the
parallelogram, a possible solution is to use some of
the already existing methods. Additionally, it can be
immediately remarked that a parallelogram is a rela-
tively regular quadrangle and polygon in general.
At least two questions can be raised here: first, is
there a better quadrangle i.e. polygon for bounding
the illuminations, and second, which method to use
as the baseline underlying method that gets bounded?
Figure 4: Comparison of cameras’ illumination estimation
for Canon EOS 550D, Canon EOS 6D, and Canon EOS
750D. The red chromaticity is shown on the x axis, while
the blue chromaticity is shown on the y axis.
3 PROPOSED METHOD
Inspired by the bounds used by Canon cameras ob-
served in Figure 4 and in order to give an answer to
the two questions from the previous section, in this
paper a new method i.e. extension to any chosen un-
derlying illumination estimation method is proposed.
The extension learns a bounding polygon with an ar-
bitrary number of vertices that is used to restrict the
illumination estimations of the initially chosen under-
lying method to the chromaticity region specified by
the bounding polygon. As explained in the previous
section, the motivation for this are the observations
of boundaries used by Canon cameras and it can be
applied to any illumination estimation method.
A genetic algorithm is used to learn the bounda-
ries. First, the illumination estimations for the ini-
tially chosen underlying method are calculated on a
given set of images. The boundary polygon popula-
tion of size s is initialized by taking randomly chosen
ground-truth illumination chromaticities as polygon
vertices. Empirically, it has been shown that the four-
point polygons i.e. quadrangles are generally a good
fit for illumination restriction and there is no signifi-
cant gain when the number of points is increased. The
fitness function calculation for a given quadrangle is
based on the ground-truth illuminations and the re-
stricted illuminations that are the result of applying
the boundary polygon to the underlying method’s il-
lumination estimations. Empirically, it has been con-
cluded that the negative sum of the median angular
error and a tenth of the maximum angular error is ge-
nerally a good fitness function; angular error is ex-
plained in more detail in Section 4.1. More formally,
if A = {a
1
, . . . , a
n
} is the set of angular errors on n
images, then the chosen fitness function is given as
f(A) = −
med(A) +
1
10
max(A)
. (3)
The maximum error was also included in the fit-
ness function in order to discourage quadrangles that
perform very well on the majority of the images, but
have poor performance of several outliers. As the se-
lection method the 3-way tournament selection (Mit-
chell, 1998) with random sampling is used. Avera-
ging crossover function of the two of the best indi-
viduals produces a new child which is randomly mu-
tated. The quadrangle with the lowest fitness value
among the three ones chosen in the selection proce-
dure is replaced in the current population by the ne-
wly created child quadrangle. The mutation is done
by translating each vertex of a bounding polygon by
the value from the normal distribution with µ = 0
and σ = 0.2. Mutation rate, which states whether the
whole individual should me mutated, is set to 0.3. Af-
ter all training iterations have finished, the boundary
quadrangle with the highest fitness value is chosen as
the final result. Figure 5 shows an example of a lear-
ned quadrangle.
Figure 5: Example of a learned boundary quadrangle for
the Canon1 dataset (Cheng et al., 2014) in the chromaticity
plane. The red chromaticity is shown on the x axis, while
the blue chromaticity is shown on the y axis.
Since the proposed extension bounds illumination
estimations and beavers are known to bound water
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
186

flows by building dams, the proposed extension was
named Color Beaver. In the rest of the paper exten-
ding a method M by the Color Beaver extension will
be denoted as Color Beaver + M. The training proce-
dure for Color Beaver is summarized in Algorithm 2.
Algorithm 1: Color Beaver Training.
Input: training images I, ground truth G, met-
hod M, iterations number N, population size s, fitness
function f
Output: boundary polygon P
1: E = estimateIllumination(I, M)
2: P = initializePolygonPopulation(s)
3: for i ∈ {1, ..N} do
4: t
1
, t
2
, t
3
= tournamentSelection(P, 3, f)
5: t
0
= crossover(t
1
, t
2
)
6: t
0
.mutateMaybe(0.3)d
7: R = restrictIllumination(E, t
0
)
8: P.ReplaceExistingWith(t
3
, t
0
)
9: end for
10: P = P.GetFittest(f)
Algorithm 2: Color Beaver Application.
Input: image I, method M, boundary polygon P
Output: illumination estimation e
1: e
M
= estimateIllumination(I, M)
2: e = restrictIllumination(e
M
, P)
4 EXPERIMENTAL RESULTS
4.1 Experimental Setup
Eight linear NUS datasets (Cheng et al., 2014) and the
Cube dataset (Bani
´
c and Lon
ˇ
cari
´
c, 2017) have been
used to test the proposed extension and compare its
performance to the one of other methods. All these
datasets have linear images, which is also expected
by the model described by Eq. (3). The ColorChecker
dataset (Gehler et al., 2008; Shi and Funt, 2018) has
not been used because of much confusion that is still
present in many papers due to of its misuses in the
past (Lynch et al., 2013; Finlayson et al., 2017).
The most commonly used accuracy measure
among many proposed (Gijsenij et al., 2009; Finlay-
son and Zakizadeh, 2014; Bani
´
c and Lon
ˇ
cari
´
c, 2015a)
is the angular error. It is the angle between the vectors
of illumination estimation and the ground-truth illu-
mination. When the angular errors obtained on each
individual image of a given benchmark dataset need
to be summarized, one of the most important statistics
is the median angular error (Hordley and Finlayson,
Table 1: Performance of different color constancy methods
on the Cube dataset (Bani
´
c and Lon
ˇ
cari
´
c, 2017) in terms
of angular error statistics (lower Avg. is better). The used
format is the same as in (Barron and Tsai, 2017).
Algorithm MeanMed. Tri.
Best
25%
Worst
25%
Avg.
White-Patch (Funt and Shi,
2010)
6.58 4.48 5.27 1.18 15.23 4.88
Gray-world (Buchsbaum, 1980) 3.75 2.91 3.15 0.69 8.18 2.87
Camera built-in 2.96 2.56 2.64 0.82 5.79 2.49
Color Tiger (Bani
´
c and Lon
ˇ
cari
´
c,
2017)
2.94 2.59 2.66 0.61 5.88 2.35
Shades-of-Gray (Finlayson and
Trezzi, 2004)
2.58 1.79 1.95 0.38 6.19 1.84
2nd-order Gray-Edge (Van
De Weijer et al., 2007a)
2.49 1.60 1.80 0.49 6.00 1.84
1st-order Gray-Edge (Van
De Weijer et al., 2007a)
2.45 1.58 1.81 0.48 5.89 1.81
General Gray-World (Barnard
et al., 2002)
2.50 1.61 1.79 0.37 6.23 1.76
Color Beaver Camera +
built-in (proposed)
1.70 0.96 1.15 0.31 4.38 1.20
Color Beaver + WP (proposed) 1.59 0.87 1.04 0.25 4.15 1.08
Restricted Color Tiger (Bani
´
c
and Lon
ˇ
cari
´
c, 2017)
1.64 0.82 1.05 0.24 4.37 1.08
Color Dog (Bani
´
c and Lon
ˇ
cari
´
c,
2015b)
1.50 0.81 0.99 0.27 3.86 1.05
Smart Color Cat (Bani
´
c and
Lon
ˇ
cari
´
c, 2015b)
1.49 0.88 1.06 0.24 3.75 1.04
Color Beaver + SoG (proposed) 1.51 0.81 1.00 0.22 3.97 1.01
Color Beaver + GW (proposed) 1.48 0.76 0.98 0.21 3.90 0.98
2004). Despite that fact, the geometric mean of se-
veral statistics including the median angular error has
increasingly been gaining popularity in recent publi-
cations (Barron and Tsai, 2017) and the same format
as there is also used in this paper.
For both the NUS datasets and the Cube data-
set a three-fold cross-validation with folds of equal
size was used like in previous publications. The
source code for recreating the results reported later
in the paper is publicly available at https://ipg.fer.hr/
ipg/resources/color constancy.
(a) (b)
Figure 6: A failure case for Color Beaver + SoG with chro-
matic adaptation results based on a) the restricted illumi-
nation estimation with angular error of 10.74
◦
and b) the
ground-truth illumination.
Color Beaver: Bounding Illumination Estimations for Higher Accuracy
187

Table 2: Combined performance of different color con-
stancy methods on eight NUS dataset in terms of angular
error statisrics (lower Avg. is better). The used format is
the same as in (Barron and Tsai, 2017).
Algorithm MeanMed. Tri.
Best
25%
Worst
25%
Avg.
White-Patch (Funt and Shi,
2010)
9.91 7.44 8.78 1.44 21.27 7.24
Pixels-based Gamut (Gijsenij
et al., 2010)
5.27 4.26 4.45 1.28 11.16 4.27
Grey-world (Buchsbaum, 1980) 4.59 3.46 3.81 1.16 9.85 3.70
Edge-based Gamut (Gijsenij
et al., 2010)
4.40 3.30 3.45 0.99 9.83 3.45
Color Beaver + WP (proposed) 5.40 2.12 2.75 0.58 16.08 3.12
Shades-of-Gray (Finlayson and
Trezzi, 2004)
3.67 2.94 3.03 0.98 7.75 3.01
Color Beaver + GW (proposed) 3.73 2.65 2.90 0.72 8.55 2.82
Natural Image Statistics (Gijsenij
and Gevers, 2011)
3.45 2.88 2.95 0.83 7.18 2.81
Local Surface Reflectance
Statistics (Gao et al., 2014)
3.45 2.51 2.70 0.98 7.32 2.79
2nd-order Gray-Edge (Van
De Weijer et al., 2007a)
3.36 2.70 2.80 0.89 7.14 2.76
1st-order Gray-Edge (Van
De Weijer et al., 2007a)
3.35 2.58 2.76 0.79 7.18 2.67
Bayesian (Gehler et al., 2008) 3.50 2.36 2.57 0.78 8.02 2.66
General Gray-World (Barnard
et al., 2002)
3.20 2.56 2.68 0.85 6.68 2.63
Spatio-spectral
Statistics (Chakrabarti et al.,
2012)
3.06 2.58 2.74 0.87 6.17 2.59
Bright-and-dark Colors
PCA (Cheng et al., 2014)
2.93 2.33 2.42 0.78 6.13 2.40
Corrected-Moment (Finlayson,
2013)
2.95 2.05 2.16 0.59 6.89 2.21
Color Beaver + SoG (proposed) 2.86 1.99 2.21 0.59 6.62 2.17
Color Tiger (Bani
´
c and Lon
ˇ
cari
´
c,
2017)
2.96 1.70 1.97 0.53 7.50 2.09
Color Dog (Bani
´
c and Lon
ˇ
cari
´
c,
2015b)
2.83 1.77 2.03 0.48 7.04 2.03
Shi et al. 2016 (Shi et al., 2016) 2.24 1.46 1.68 0.48 6.08 1.74
CCC (Barron, 2015) 2.38 1.48 1.69 0.45 5.85 1.74
Cheng 2015 (Cheng et al., 2015) 2.18 1.48 1.64 0.46 5.03 1.65
FFCC (Barron and Tsai, 2017) 1.99 1.31 1.43 0.35 4.75 1.44
4.2 Accuracy
Tables 1 and 2 show the comparisons between the
accuracies of methods extended by the proposed ex-
tension and other illumination estimation methods. It
can be seen that all of the extended methods outper-
form their initial non-extended versions. As a mat-
ter of fact, the extended version of the Shades-of-
Gray method outperforms the camera built-in method.
Additionally, the extended versions also outperform
many learning-based methods. All these results de-
monstrate the usability of the proposed extension. An
example of a failure case for the proposed extension
of Shades-of-Gray is shown in Figure 6.
While other methods such as Gray-edge could
also have been tested and shown in the Tables,
Shades-of-Gray was already good enough to outper-
form camera’s built-in methods. Extending Gray-
edge also increases its accuracy, but Gray-edge is slo-
wer than Shades-of-Gray (Cheng et al., 2014), more
complex, and it requires additional memory. Hence
it was left out of the testing procedures since Shades-
of-Gray is already sufficient to successfully answer
the questions that were raised in this paper.
4.3 Discussion
The fact that statistics-based methods extended by the
proposed method outperform camera built-in illumi-
nation estimation methods is significant for drawing
further conclusions about the nature of camera’s il-
lumination estimation methods. Namely, if extended
statistics-based methods outperform them, it can be
freely stated that statistics-based are good enough to
be used in digital cameras. Additionally, it may be
that the extended method managed to outperform the
camera’s built-in methods because that they are also
statistics-based, which in turn confirms that cameras
do indeed use such method. In any of these two cases
it can be concluded that research on statistics-based
methods still has a large field of applications and the
obtained results only further prove its importance.
5 CONCLUSIONS
An experiment was conducted to examine some of the
details of built-in illumination estimation methods for
several Canon camera models. Inspired by the ob-
served results, an extension to any underlying illumi-
nation estimation method has been proposed. It li-
mits the values of the illumination estimations of the
underlying method by forcing it to stay inside a pre-
viously learned region in the chromaticity plane wit-
hout adding any significant computation cost. By li-
miting some of the best-known statistics-based met-
hods, the obtained accuracy outperforms the one of
cameras’ built-in methods. This effectively demon-
strates that by only using slightly modified statistics-
based methods it is possible to be more accurate than
contemporary cameras. It also proves the claim that
statistics-based methods can and probably are used
for illumination estimation in digital cameras. Future
research will include looking for new method modifi-
cations that result in even higher estimation accuracy.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
188

ACKNOWLEDGEMENTS
This work has been supported by the Croatian Science
Foundation under Project IP-06-2016-2092.
REFERENCES
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2015a). Color Cat: Remembe-
ring Colors for Illumination Estimation. Signal Pro-
cessing Letters, IEEE, 22(6):651–655.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2015b). Using the red chroma-
ticity for illumination estimation. In Image and Signal
Processing and Analysis (ISPA), 2015 9th Internatio-
nal Symposium on, pages 131–136. IEEE.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2017). Unsupervised
Learning for Color Constancy. arXiv preprint
arXiv:1712.00436.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2013). Using the Random
Sprays Retinex Algorithm for Global Illumination Es-
timation. In Proceedings of The Second Croatian
Computer Vision Workshopn (CCVW 2013), pages 3–
7. University of Zagreb Faculty of Electrical Engi-
neering and Computing.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2014a). Color Rabbit: Gui-
ding the Distance of Local Maximums in Illumina-
tion Estimation. In Digital Signal Processing (DSP),
2014 19th International Conference on, pages 345–
350. IEEE.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2014b). Improving the White
patch method by subsampling. In Image Processing
(ICIP), 2014 21st IEEE International Conference on,
pages 605–609. IEEE.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2015a). A Perceptual Measure
of Illumination Estimation Error. In VISAPP, pages
136–143.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2015b). Color Dog: Guiding the
Global Illumination Estimation to Better Accuracy. In
VISAPP, pages 129–135.
Barnard, K., Cardei, V., and Funt, B. (2002). A compa-
rison of computational color constancy algorithms. i:
Methodology and experiments with synthesized data.
Image Processing, IEEE Transactions on, 11(9):972–
984.
Barron, J. T. (2015). Convolutional Color Constancy. In
Proceedings of the IEEE International Conference on
Computer Vision, pages 379–387.
Barron, J. T. and Tsai, Y.-T. (2017). Fast Fourier Color
Constancy. In Computer Vision and Pattern Recogni-
tion, 2017. CVPR 2017. IEEE Computer Society Con-
ference on, volume 1. IEEE.
Bianco, S., Cusano, C., and Schettini, R. (2015). Color
Constancy Using CNNs. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion Workshops, pages 81–89.
Buchsbaum, G. (1980). A spatial processor model for object
colour perception. Journal of The Franklin Institute,
310(1):1–26.
Canon (2018). Canon celebrates 15th consecutive year of
No.1 share of global interchangeable-lens digital ca-
mera market.
Chakrabarti, A., Hirakawa, K., and Zickler, T. (2012). Color
constancy with spatio-spectral statistics. Pattern Ana-
lysis and Machine Intelligence, IEEE Transactions on,
34(8):1509–1519.
Cheng, D., Prasad, D. K., and Brown, M. S. (2014). Illu-
minant estimation for color constancy: why spatial-
domain methods work and the role of the color distri-
bution. JOSA A, 31(5):1049–1058.
Cheng, D., Price, B., Cohen, S., and Brown, M. S. (2015).
Effective learning-based illuminant estimation using
simple features. In Proceedings of the IEEE Confe-
rence on Computer Vision and Pattern Recognition,
pages 1000–1008.
Ebner, M. (2007). Color Constancy. The Wiley-IS&T Se-
ries in Imaging Science and Technology. Wiley.
Finlayson, G. D. (2013). Corrected-moment illuminant es-
timation. In Proceedings of the IEEE International
Conference on Computer Vision, pages 1904–1911.
Finlayson, G. D., Hemrit, G., Gijsenij, A., and Gehler, P.
(2017). A Curious Problem with Using the Colour
Checker Dataset for Illuminant Estimation. In Color
and Imaging Conference, volume 2017, pages 64–69.
Society for Imaging Science and Technology.
Finlayson, G. D., Hordley, S. D., and Tastl, I. (2006). Ga-
mut constrained illuminant estimation. International
Journal of Computer Vision, 67(1):93–109.
Finlayson, G. D. and Trezzi, E. (2004). Shades of gray
and colour constancy. In Color and Imaging Confe-
rence, volume 2004, pages 37–41. Society for Ima-
ging Science and Technology.
Finlayson, G. D. and Zakizadeh, R. (2014). Reproduction
angular error: An improved performance metric for
illuminant estimation. perception, 310(1):1–26.
Funt, B. and Shi, L. (2010). The rehabilitation of MaxRGB.
In Color and Imaging Conference, volume 2010,
pages 256–259. Society for Imaging Science and
Technology.
Gao, S., Han, W., Yang, K., Li, C., and Li, Y. (2014). Ef-
ficient color constancy with local surface reflectance
statistics. In European Conference on Computer Vi-
sion, pages 158–173. Springer.
Gehler, P. V., Rother, C., Blake, A., Minka, T., and Sharp, T.
(2008). Bayesian color constancy revisited. In Com-
puter Vision and Pattern Recognition, 2008. CVPR
2008. IEEE Conference on, pages 1–8. IEEE.
Gijsenij, A. and Gevers, T. (2007). Color Constancy using
Natural Image Statistics. In CVPR, pages 1–8.
Gijsenij, A. and Gevers, T. (2011). Color constancy using
natural image statistics and scene semantics. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 33(4):687–698.
Gijsenij, A., Gevers, T., and Lucassen, M. P. (2009). Per-
ceptual analysis of distance measures for color con-
stancy algorithms. JOSA A, 26(10):2243–2256.
Gijsenij, A., Gevers, T., and Van De Weijer, J. (2010).
Generalized gamut mapping using image derivative
Color Beaver: Bounding Illumination Estimations for Higher Accuracy
189

structures for color constancy. International Journal
of Computer Vision, 86(2):127–139.
Hordley, S. D. and Finlayson, G. D. (2004). Re-evaluating
colour constancy algorithms. In Pattern Recognition,
2004. ICPR 2004. Proceedings of the 17th Internatio-
nal Conference on, volume 1, pages 76–79. IEEE.
Hu, Y., Wang, B., and Lin, S. (2017). Fully Convolutional
Color Constancy with Confidence-weighted Pooling.
In Computer Vision and Pattern Recognition, 2017.
CVPR 2017. IEEE Conference on, pages 4085–4094.
IEEE.
Land, E. H. (1977). The retinex theory of color vision.
Scientific America.
Lynch, S. E., Drew, M. S., and Finlayson, k. G. D. (2013).
Colour Constancy from Both Sides of the Shadow
Edge. In Color and Photometry in Computer Vision
Workshop at the International Conference on Compu-
ter Vision. IEEE.
Mitchell, M. (1998). An introduction to genetic algorithms.
MIT press.
PhotoRumors (2018). 2018 Canon, Nikon and Sony market
share (latest Nikkei, BCN and CIPA reports).
Qiu, J., Xu, H., Ma, Y., and Ye, Z. (2018). PILOT:
A Pixel Intensity Driven Illuminant Color Estima-
tion Framework for Color Constancy. arXiv preprint
arXiv:1806.09248.
Shi, L. and Funt, B. (2018). Re-processed Version of the
Gehler Color Constancy Dataset of 568 Images.
Shi, W., Loy, C. C., and Tang, X. (2016). Deep Specialized
Network for Illuminant Estimation. In European Con-
ference on Computer Vision, pages 371–387. Springer.
Van De Weijer, J., Gevers, T., and Gijsenij, A. (2007a).
Edge-based color constancy. Image Processing, IEEE
Transactions on, 16(9):2207–2214.
Van De Weijer, J., Schmid, C., and Verbeek, J. (2007b).
Using high-level visual information for color con-
stancy. In Computer Vision, 2007. ICCV 2007. IEEE
11th International Conference on, pages 1–8. IEEE.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
190
