Bio-inspired Event-based Motion Analysis with Spiking Neural Networks

ıs Oudjail and Jean Martinet

Univ. Lille, CNRS, Centrale Lille, UMR 9189 – CRIStAL, France

Keywords:

Video Analysis, Spiking Neural Networks, Motion Analysis, Address-event Representation.

Abstract:

This paper presents an original approach to analyze the motion of a moving pattern with a Spiking Neural

Network, using visual data encoded in the Address-Event Representation. Our objective is to identify a mini-

mal network structure able to recognize the motion direction of a simple binary pattern. For this purpose, we

generated synthetic data of 3 different patterns moving in 4 directions, and we designed several variants of a

one-layer fully-connected feed-forward spiking neural network with varying number of neurons in the output

layer. The networks are trained in an unsupervised manner by presenting the synthetic temporal data to the

network for a few seconds. The experimental results show that such networks quickly converged to a state

where input classes can be successfully distinguished for 2 of the considered patterns, no network conﬁgura-

tion did converge for the third pattern. In the convergence cases, the network proved a remarkable stability for

several output layer sizes. We also show that the sequential order of presentation of classes impacts the ability

of the network to learn the input.

1 INTRODUCTION

Video analysis is a widespread task in the computer

vision community that traditionally requires either the

extraction and processing of key-frames, or the deﬁ-

nition of motion descriptors such as optical ﬂow. De-

termining the optical ﬂow is useful to estimate the

elementary displacements of key-points in a video

stream.

In this paper, we investigate temporal data ana-

lysis with Spiking Neural Networks (SNN) for vi-

deo. The visual input needs to be converted into spi-

kes. We consider the Address-Event Representation

(AER) of a video, namely used by Dynamic Vision

Sensors (Lichtsteiner et al., 2008). In this represen-

tation, each pixel individually encodes positive and

negative intensity variations – every change triggers

an event that is transmitted asynchronously. There

are two types of event: ON events for positive vari-

ations, and OFF events for negative variations. Such

a representation is well adapted to SNN, because the

events resemble spikes, and therefore they can be used

to feed the network in a straightforward manner.

This increases the processing efﬁciency while re-

ducing potential sensor/compression noise. The big-

term objective of this work is the development of

an end-to-end bio-inspired vision approach. Our

objective is to exhibit a minimal network structure

able to identify a basic stimulus coming from a

reduced window. We successfully trained simple

one-layer fully-connected feed-forward spiking neu-

ral networks to recognize the motion orientation of a

binary pattern in a 5 × 5 window, in an unsupervised

manner.

The remainder of the paper is organized as fol-

lows: Section 2 discusses the use of SNN in vision,

namely for image and video classiﬁcation, Section 3

describes the core of our work, by giving details re-

garding the dataset, the network structure, and the ex-

perimental protocol, Section 4 shows and discusses

the ﬁndings of our study, and Section 5 concludes the

paper and discusses future work.

2 RELATED WORK

Spiking Neural Networks represent a special class of

artiﬁcial neural networks (Maass, 1997), where neu-

rons communicate by sequences of spikes (Ponulak

and Kasinski, 2011). Contrary to widely-used deep

convolutional neural networks, spiking neurons do

not ﬁre at each propagation cycle, but rather ﬁre only

when their activation level (or membrane potential, an

intrinsic quality of the neuron related to its membrane

electrical charge) reaches a speciﬁc threshold value.

Therefore, the network is asynchronous and allege-

Oudjail, V. and Martinet, J.

Bio-inspired Event-based Motion Analysis with Spiking Neural Networks.

DOI: 10.5220/0007397303890394

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 389-394

ISBN: 978-989-758-354-4

389

dly likely to handle well temporal data such as vi-

deo. SNNs do not rely on stochastic gradient descent

and backpropagation. Instead, neurons are connected

through synapses, that implement a learning mecha-

nism inspired from biology: it rests upon the Spike-

Timing-Dependent Plasticity, a rule that updates syn-

aptic weights according to the spike timings, and in-

creases the weight when a presynaptic spike occurs

just before a postsynaptic spike (within a few millise-

conds). Therefore, the learning process is intrinsically

not supervised, and SNN can be successfully used to

detect patterns in data in an unsupervised manner (Bi-

chler et al., 2012; Hopkins et al., 2018). In parallel,

several studies have attempted to reproduce and ap-

ply to SNN several mechanisms that contribute to the

success of deep networks, such as the stochastic gra-

dient descent (Lee et al., 2016) or deep convolutional

architectures (Cao et al., 2015; Tavanaei and Maida,

2017). SNN have long been used in the neuroscience

community as a reliable model to precisely simulate

biology and understand brain mechanisms (Paugam-

Moisy and Bohte, 2012).

In addition, SNN are increasingly used in data

processing because of their implementability on low-

energy hardware such as neuromorphic circuits (Me-

rolla et al., 2014; Sourikopoulos et al., 2017; Kreiser

et al., 2017). SNN have been used in vision-related

tasks (Masquelier and Thorpe, 2007), and some re-

searchers are keen to attack standard vision data-

sets with SNN and AER, e.g. converting a visual

input into AER, such as Poker-DVS, MNIST-DVS

(Serrano-Gotarredona and Linares-Barranco, 2015),

N-MNIST (Orchard et al., 2015), CIFAR-DVS (Li

et al., 2017).

More speciﬁcally in video analysis, several at-

tempts to apply SNN for video classiﬁcation or for

more speciﬁc tasks on the same type of data exist.

Bichler et al. (Bichler et al., 2012) have used a feed-

forward SNN capable of recognizing the movement of

a ball among 8 discretized directions from AER data.

They also show in another experiment that SNN can

be used to count cars passing on a highway lane. The

data is captured by an artiﬁcial sensor (TMPDIFF128

DVS by iniLabs) which generate events if a local tem-

poral change in contrast (over a threshold) occurs in

its ﬁeld of view and is transmitted in AER format.

Orchard et al. (Orchard et al., 2013) developed a

system to extract the optical ﬂow from an AER video

sequence. Their architecture imposes constraints si-

milar to Lucas-Kanade algorithm. In their approach,

they use neurons with a 5x5 receptive ﬁeld size, all

of which are sensitive to movement with a certain di-

rection and speed (8 directions and 8 speeds), with the

assumption that the speed is constant. In the model,

they integrate, among other things, synaptic delays in

order to be sensitive to spatio-temporal patterns. All

parameters are set at the begining, so there is no lear-

ning phase.

Zhao et al. (Zhao et al., 2015) combine an HMAX

and SNN feed-forward architecture to recognize the

following 3 human actions: bending, walking and

standing/sitting, where the type of movement can be

simpliﬁed by a diagonal, horizontal and vertical mo-

tion. The data is encoded into AER format. Amir et

al. (Amir et al., 2017) have designed a tool that is

able to recognize more than 10 hand gestures in real

time with a low-energy consumption, by exploiting a

neuromorphic processor with a capacity of one mil-

lion neurons, on which authors use an SNN coupled

to a pre-trained CNN. Such a system reached a 96.5%

success rate.

All previously mentioned work use both ON and

OFF event types. With this rich information, if we

assume a constant intensity for objects and back-

grounds, the object motion can be inferred in short

temporal windows. Let us take the example of a white

ball moving towards the right before a darker back-

ground. The right edge of the ball will generate a set

of ON events and the opposite edge (left) will simul-

taneously generate a set of OFF events. In this setting,

the motion recognition problem boils down to a static

pattern recognition problem, because the very motion

is encoded in a static way. Moreover, if the object is

either large or close to the sensor, then ON events and

OFF events will be much separated in space, or even

separated in time (i.e. they will not occur simultane-

ously) if the object is larger than the sensor’s ﬁeld of

view, making it almost impossible for such static ap-

proaches to infer a motion.

Our objective is to study the use of feed-forward

SNN for learning the dynamic object motions. The-

refore, we deliberately ignore the event types, and we

use a single event type, indicating both types of in-

tensity variation. The purpose is to train detectors

that are sensitive to certain directions of motion. To

achieve this, we aim to identify the structure of a mi-

nimal network whose output layer is capable of lear-

ning the direction of a given binary texture in motion

at the input.

3 METHODOLOGY

We wish to investigate the ability of a simple feed-

forward network to learn the motion direction of a bi-

nary texture pattern. This section relates how the data

was generated, gives details of the network structure

and parameters, and describes the experimental pro-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

390

tocol.

3.1 Synthetic AER-like Data

Standard AER encodes positive and negative pixel-

wise luminosity variation in the form of ON- and

OFF-events. In our model, we used a simpliﬁed re-

presentation considering only a single type of event.

We generated synthetic simpliﬁed-AER data mi-

micking the displacement of simple texture patterns

in four directions (NORTH, SOUTH, WEST, EAST)

inside a 5 × 5 window. We selected 3 types of pat-

terns corresponding to a vertical line, a diagonal line,

and a square pattern. Figure 1 shows an example of

our synthetic data. Note that in the ﬁrst 2 patterns

(vertical and diagonal lines), only 2 directions can be

distinguished because of the aperture problem. For

instance, NORTH and SOUTH directions are not vi-

sible for the vertical line (yet the corresponding events

are kept in the input data), and therefore only WEST

and EAST can be distinguished. Also, for the diago-

nal line, NORTH and WEST as well as SOUTH and

EAST directions are not distinguishable. Also note

that because of the symmetry of both the network and

the data, horizontal and vertical lines are equivalent

and so are both diagonals. For each direction, the pat-

tern is sequentially shifted as illustrated in Figure 2.

Figure 1: Three input patterns used in our experiments.

Figure 2: Illustration of the square pattern motion in the

EAST direction.

Therefore, we have four classes for each pattern.

The speed is set to 480 pixels/s as in the experiments

described in (Bichler et al., 2012), and one sample in-

put corresponds to a 200-ms duration of stimulation.

3.2 Network Details

Our network is a simple one-layer fully-connected

feed-forward SNN, that takes the AER data as a 5 × 5

continuous input (as illustrated in the Figure 3), and

whose output layer is a vector encoding the motion

class.

Among several neuron models, we use the Leaky-

Integrate-and-Fire (LIF) model (Ponulak and Kasin-

Figure 3: Topological overview of the network.

ski, 2011), and a simpliﬁed STDP learning rule – see

(Bichler et al., 2012) for details:

∆t = t

post

− t

pre

std p(∆t) =



∆w

if 0 ≤ ∆t ≤ T

LTP

∆w

−

otherwise

(1)

where t

pre

(resp. t

post

) represents the presynaptic

(resp. postsynaptic) spike time-stamp, and T

LTP

the

width of the potentiation window. If the postsyn-

aptic spike occurs within T

LTP

ms after the presyn-

aptic spike, the synapse is potentiated by ∆w

(Long Term Potentiation). Otherwise the synapse is

depressed by ∆w

−

mV (Long Term Depression). In

our experiments, parameters are set individually for

each synapse in the following way: a minimum and

a maximum bound are set randomly, and the initial

value of the synapse is chosen randomly inside the

bounds. Moreover, ∆w

−

and ∆w

are also set rand-

omly for each synapse, with the only constraint that

∆w

−

< ∆w

. M Moreover, our model includes 3 bio-

inspired mechanisms:

• a competition constraint that prevents all output

units to learn the same pattern: neurons are equip-

ped with lateral inhibition capability, where an

active neuron prevents its neighbors to spike;

• refractory periods to prevent a single output unit

to continuously burst without giving other units a

chance;

• synaptic delays to avoid that all incoming spikes

occur simultaneously.

We implemented this network using Brian2 SNN si-

mulator (Goodman and Brette, 2009) with parameters

inpired from (Bichler et al., 2012).

3.3 Protocol

We study our model by exploring its behavior accor-

ding to the type of input pattern among the three con-

sidered patterns. We expect that the model should

be able to differentiate between WEST and EAST

directions for the vertical line (two distinguisha-

ble classes), between NORTH/WEST directions and

SOUTH/EAST directions for the diagonal pattern

Bio-inspired Event-based Motion Analysis with Spiking Neural Networks

391

(two distinguishable classes), and between NORTH,

SOUTH, WEST, EAST directions for the square pat-

tern (four distinguishable classes).

We also investigate a possible impact of the stimu-

lation sequence strategy. Indeed, different simulation

orders are likely to inﬂuence the way synaptic weig-

hts are updated. For a given pattern, the stimulus is

presented to the network using the 3 following strate-

gies: (1) ordered sequence e.g. NNNSSSWWWEEE,

(2) sequences of quadruplets where classes are per-

muted so that they appear in a random sequence e.g

NSWE-ESWN-WNES- etc. – this guarantees a uni-

form class distribution, and (3) random sequence (e.g.

NSSESWN etc.). We stimulated the network using

these 3 strategies, and each run consists in presenting

40 samples to the network (i.e. 8 s).

Finally, we try several sizes for the output layer,

ranging from 2 to 6:

• 4 output neurons is the natural size for four clas-

ses;

• 2 output neurons is the minimal number for two

classes (vertical and diagonal lines);

• 6 output neurons increases the chance to get a spe-

cialized output neuron for each class;

• we also tried values in between: 3 and 5.

We describe the experimental results varying these

settings and parameters in the next section.

4 EXPERIMENTAL RESULTS

The aim of the unsupervised training step is to reach a

network state where the outputs precisely distinguish

between input classes. This means that some output

layer neurons would become specialized in detecting

a particular input class. A necessary situation of spe-

cialization is when some synaptic weights have con-

verged to values close to 0 or 1, indicating that the

corresponding output neuron has become either in-

sensitive or sensitive to the corresponding input neu-

ron, therefore proving a specialization of the network

toward a particular stimulus.

4.1 Evolution of Weights

For each simulation, we observe the evolution of syn-

aptic weights, that are initially given random values.

Figure 4 shows an illustration of synaptic weights spe-

cialization for a network with a 6-neuron output layer.

Each cell in this 6 × 25 matrix represents the normali-

zed synaptic weight between one of the 25 input neu-

rons and one of the 6 output neurons. The matrix on

the left shows the weights after a random initializa-

tion, before the training, and the matrix on the right

shows the same weights after 8s of stimulation. We

observe that a number of weights have changed to-

ward a lower or higher value, indicating a specializa-

tion of synaptic connections.

Figure 4: Evolution of weights – LEFT: random initializa-

tion before training. RIGHT: after training, light/dark zones

indicate weight variations towards specialized outputs.

4.2 Results and Discussion

Because of the random initializations, we ran a num-

ber of simulations for each situation in order to eva-

luate the stability of the results. We successfully trai-

ned several network conﬁgurations able to recognize

the motion direction for the vertical and diagonal li-

nes. However, the simulations with the square pattern

mainly resulted in an oscillating network state, where

no convergence allowed for the correct classiﬁcation

of input classes, as illustrated in the Figure 6. The net-

work reaches an inﬁnite oscillation state that does not

converge. This resembles situations of too large le-

arning rate in stochastic gradient descent, that causes

the gradient to diverge.

A plausible clue to explain this situation lies in the

amount of active input neurons: 5 for the vertical and

diagonal lines, and 9 for the square pattern. There-

fore, the overall expected input voltage is higher for

this pattern. In other words, each spike train stimula-

tes a larger number of neurons. With a given set of

neuronal and synaptic parameters, it is likely that the

network is able to reach a stable state only if the input

spike volume lies inside speciﬁc bounds. This would

indicate an unwanted sensitivity that would require to

ﬁne tune parameters according to the input – see fu-

ture work.

Figure 5 shows in the top row the activity of the

output neurons for several network conﬁgurations and

sequence order strategies, and in the bottom row the

evolution of the standard deviation of the synaptic

weights during the simulation.

In Figure 5 the top-left plot corresponds to the di-

agonal line pattern, with random sequence order of

presentation, where the network has 6 output neurons.

After 1000 ms, we see that the neuron at index 3 spe-

cializes for the SOUTH/EAST class (Blue and Yel-

low) and the neuron at index 2 becomes selective to

the NORTH/WEST class (Red and Violet). We obser-

ved that only 3 output neurons are sufﬁcient to distin-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

392

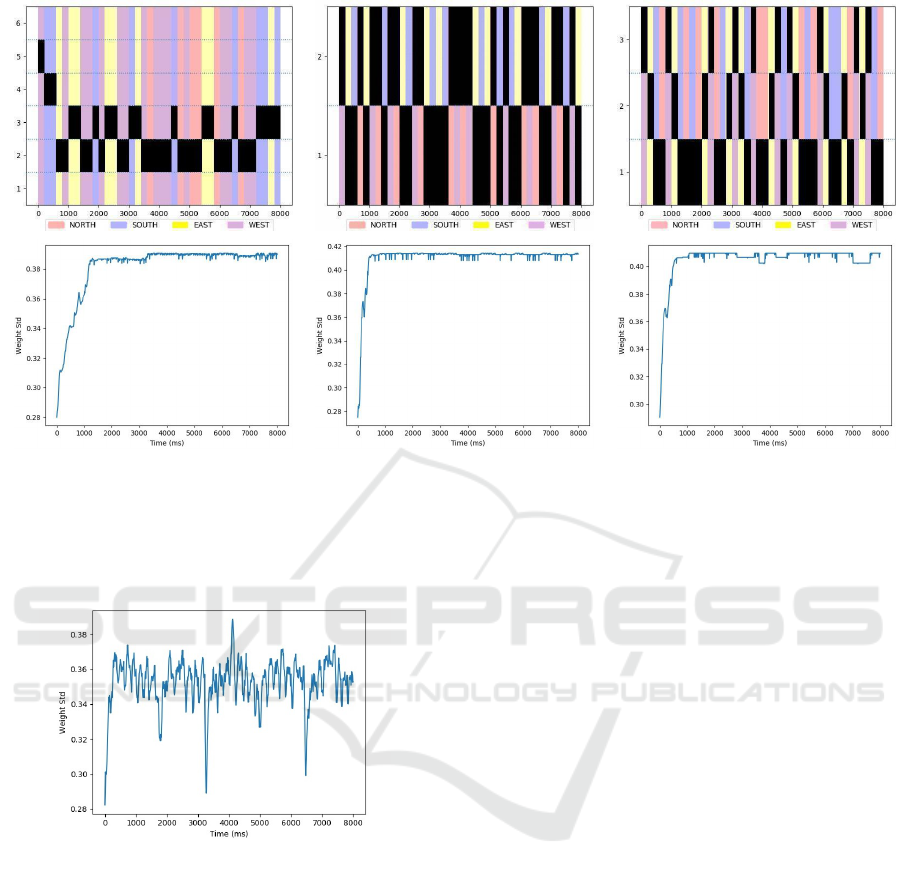
Figure 5: Best seen in color. Top row: The ordinate axis corresponds to the output neuron indices and the abscissa is the

simulation time in ms. The black markers indicate the pulses from the corresponding output neuron. The color patches

displayed in the background are associated with the input class. When the network is trained, we target a situation where

certain neurons react to a particular class. Bottom row: Evolution of the standard deviation of the synaptic weights during

the simulation. We observe a large increase early in the simulation, and then a plateau indicating a stable state (homeostasis)

of the network.

Figure 6: Evolution of the standard deviation of the synaptic

weights during the simulation for the square pattern. We

observed no stability, and therefore no convergence of the

network weights.

guish the 3 following different input classes: WEST,

EAST, and NORTH/SOUTH. For this last class, in-

cluding NORTH and SOUTH directions, even though

there is no visible motion, input neurons are active

and the network is able to detect this activity, That is

different from having no input.

The top-central plot corresponds to a diagonal

pattern, with a random quadruplet strategy, with a

network composed of 2 output neurons – the raster

shows a specialization of both neurons. We notice

that only 2 output neurons are sufﬁcient to classify

NORTH/WEST and SOUTH/EAST classes.

Finally, the top-right plot shows the result for the

vertical line with a random sequence order, where the

network has 3 output neurons. In this conﬁguration, 3

input classes WEST, EAST, and NORTH/SOUTH are

recognized by output neurons with indices 3, 2, and 1

respectively.

In all experiments, we found that the selected

number of output neurons (between 2 and 6) is not

signiﬁcant for the ability of the networks to correctly

classify the inputs. More importantly, we noticed that

the stimulation sequence strategy did not play an im-

portant role for the training. Indeed, among the 3 pre-

sentation strategies, we generally observed the same

ability to correctly classify input classes.

5 CONCLUSION

The objective of this study was to train a spiking neu-

ral network to recognize the motion direction of pat-

terns, where the data is expressed in AER. Our main

ﬁndings are as follows: (1) we achieved a conver-

gence for 2 out of 3 patterns after unsupervised trai-

ning, where the motion direction is successfully re-

cognized by the network, (2) in successful situati-

ons, the network weights quickly converge to a stable

state, (3) we observed that the sequence of presenta-

tion has no impact on the training of the network.

Bio-inspired Event-based Motion Analysis with Spiking Neural Networks

393

In future work, we will naturally address the pro-

blem of convergence for the square input. Also, we

wish to target invariance regarding motion speed, pos-

sibly by further exploiting synaptic delays so that se-

veral speeds will trigger the same network output.

Other directions will be investigated. One of them

will be the estimation of a classiﬁcation score, e.g.

based on the number of distinguishable classes. We

will also work towards establishing a theoretical link

between the network parameters and the convergence

conditions. For example, it would be interesting to

automatically update neuronal parameters depending

on recent activity of the input layer, in order to dy-

namically adapt its sensitivity. Then, we will try to

validate the proposed parameters on random patterns

containing a varying number of pixels and appearing

on windows of various sizes.

Once such a minimal motion analysis architecture

is identiﬁed, the long-term objective of our work is to

use them as elementary units whose input is a limited

receptive ﬁeld, to be laid out in layers or other archi-

tectures to enable analysis of more complex motion

patterns.

ACKNOWLEDGEMENTS

This work has been partly funded by IRCICA (Univ.

Lille, CNRS, USR 3380 IRCICA, Lille, France).

REFERENCES

Amir, A., Taba, B., Berg, D. J., Melano, T., McKinstry,

J. L., Di Nolfo, C., Nayak, T. K., Andreopoulos, A.,

Garreau, G., Mendoza, M., et al. (2017). A low po-

wer, fully event-based gesture recognition system. In

CVPR, pages 7388–7397.

Bichler, O., Querlioz, D., Thorpe, S. J., Bourgoin, J.-P.,

and Gamrat, C. (2012). Extraction of temporally

correlated features from dynamic vision sensors with

spike-timing-dependent plasticity. Neural Networks,

32:339–348.

Cao, Y., Chen, Y., and Khosla, D. (2015). Spiking deep

convolutional neural networks for energy-efﬁcient ob-

ject recognition. International Journal of Computer

Vision, 113(1):54–66.

Goodman, D. F. and Brette, R. (2009). The brian simulator.

Frontiers in neuroscience, 3:26.

Hopkins, M., Pineda-Garc

ıa, G., Bogdan, P. A., and Furber,

S. B. (2018). Spiking neural networks for computer

vision. Interface Focus, 8(4):20180007.

Kreiser, R., Moraitis, T., Sandamirskaya, Y., and Indiveri,

G. (2017). On-chip unsupervised learning in winner-

take-all networks of spiking neurons. In Biomedi-

cal Circuits and Systems Conference (BioCAS), 2017

IEEE, pages 1–4. IEEE.

Lee, J. H., Delbruck, T., and Pfeiffer, M. (2016). Training

deep spiking neural networks using backpropagation.

Frontiers in neuroscience, 10:508.

Li, H., Liu, H., Ji, X., Li, G., and Shi, L. (2017). Cifar10-

dvs: an event-stream dataset for object classiﬁcation.

Frontiers in neuroscience, 11:309.

Lichtsteiner, P., Posch, C., and Delbruck, T. (2008). A

128×128 120 db 15µ s latency asynchronous tempo-

ral contrast vision sensor. IEEE journal of solid-state

circuits, 43(2):566–576.

Maass, W. (1997). Networks of spiking neurons: the third

generation of neural network models. Neural net-

works, 10(9):1659–1671.

Masquelier, T. and Thorpe, S. J. (2007). Unsupervised lear-

ning of visual features through spike timing dependent

plasticity. PLoS comput. bio., 3(2):e31.

Merolla, P. A., Arthur, J. V., Alvarez-Icaza, R., Cassidy,

A. S., Sawada, J., Akopyan, F., Jackson, B. L., Imam,

N., Guo, C., Nakamura, Y., et al. (2014). A mil-

lion spiking-neuron integrated circuit with a scala-

ble communication network and interface. Science,

345(6197):668–673.

Orchard, G., Benosman, R., Etienne-Cummings, R., and

Thakor, N. V. (2013). A spiking neural network ar-

chitecture for visual motion estimation. In Biomedi-

cal Circuits and Systems Conference (BioCAS), 2013

IEEE, pages 298–301. IEEE.

Orchard, G., Jayawant, A., Cohen, G. K., and Thakor, N.

(2015). Converting static image datasets to spiking

neuromorphic datasets using saccades. Frontiers in

neuroscience, 9:437.

Paugam-Moisy, H. and Bohte, S. (2012). Computing with

spiking neuron networks. In Handbook of natural

computing, pages 335–376. Springer.

Ponulak, F. and Kasinski, A. (2011). Introduction to spi-

king neural networks: Information processing, lear-

ning and applications. Acta neurobiologiae experi-

mentalis, 71(4):409–433.

Serrano-Gotarredona, T. and Linares-Barranco, B. (2015).

Poker-dvs and mnist-dvs. their history, how they were

made, and other details. Frontiers in neuroscience,

9:481.

Sourikopoulos, I., Hedayat, S., Loyez, C., Danneville, F.,

Hoel, V., Mercier, E., and Cappy, A. (2017). A 4-

fj/spike artiﬁcial neuron in 65 nm cmos technology.

Frontiers in neuroscience, 11:123.

Tavanaei, A. and Maida, A. S. (2017). Multi-layer unsuper-

vised learning in a spiking convolutional neural net-

work. In Neural Networks (IJCNN), 2017 Internatio-

nal Joint Conference on, pages 2023–2030. IEEE.

Zhao, B., Ding, R., Chen, S., Linares-Barranco, B., and

Tang, H. (2015). Feedforward categorization on aer

motion events using cortex-like features in a spiking

neural network. IEEE Trans. Neural Netw. Learning

Syst., 26(9):1963–1978.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

394