Detection and Certification of Faint Streaks in Astronomical Images
Vojtˇech Cvrˇcek and Radim
ˇ
S´ara
a
Department of Cybernetics, Czech Technical University in Prague, Czech Republic
Keywords:
Space Debris, Object Detection, Bayesian Model Selection, Image Analysis and Understanding.
Abstract:
Fast-moving celestial objects, like near-Earth objects (NEOs), orbiting space debris, or meteors, appear as st-
reaks superimposed over the star background in images taken by an optical telescope at long exposures. As the
apparent magnitude of the object increases (the object becomes fainter), its detection becomes progressively
harder. We discuss a statistical procedure that makes a binary decision on the presence/absence of a streak in
the image which is called streak certification. The certification is based purely on a single input image and a
public star catalog, using a minimalistic statistical model. Certification accuracy greater than 90% for streaks
of arbitrary orientation, longer than 500 pixels, and the signal-to-background log-ratio is better than −10dB is
achieved on the same dataset as in an earlier similar method, whose performance is thus exceeded, especially
for close-to-horizontal streaks. We also show that the certification decision indicates detection failure well.
1 INTRODUCTION
With the rise of spa tial traffic around Earth, Space Si-
tuational Awareness (SSA) gradually became an es-
tablished field (Bobrinsky and Del Monte, 2010). It
brought the need for object detection, most impor-
tantly space debris, which are unwanted man-made
passive objects of various sizes orbitin g Earth. Their
orbital parameters may be difficult to predict, due to
random influences, like solar win d, etc. Better de-
tection metho ds lead to safety increase in the Earth
orbit by improving collision prevention. Detection of
other near-Earth objects is also of interest (Yanagi-
sawa et al., 2005). Besides radar observations, optical
observations are widely considered a suitable moda-
lity for detection. Any automatic cataloging process
of a large number of such objects requires a statistical
assessment of d e te ction significance .
We co nsider optical observations of such objects.
In a typical setup, long-exposure images are taken in
a sequential manner. Objects of interest appear as st-
reaks in these images, an example is shown in Fig. 1.
A streak is a lin e segment parameterized b y position,
length, angular orientation, amplitude (or b rightness),
and cross-sectional profile (width). T he streak, orie n-
ted app roximately in a lower-left to upper-right di-
rection in Fig. 1 is not very difficult to detect although
it may not be visible to inexperienced reader at first
sight.
a
https://orcid.org/0000-0002-2032-5764
Figure 1: Input image, the green arrow points to the streak
(−38
◦
, SBR = −5.26 dB). Best viewed close-up, in PDF.
It is common that few images in an observation
sequence contain a streak. These images are hard
to select m anually. We therefore co nsider the fol-
lowing ta sk: Give n a single optical image like th e
one in Fig. 1, we wish to decide if the image c on-
tains a streak or not and deter mine the parameters of
the streak if it doe s. We discuss a f ormal framework
for the statistical decision part of the task that has
been c alled certification in (Sara and Cvrcek, 2017 ).
498
Cvr
ˇ
cek, V. and Šára, R.
Detection and Certification of Faint Streaks in Astronomical Images.
DOI: 10.5220/0007399804980509
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 498-509
ISBN: 978-989-758-354-4
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 2: Filter response (φ = −38
◦
) to the image from
Fig. 1, stars are not suppressed (Sara and Cvrcek, 2017).
Figure 3: Filter response (φ = −38
◦
) to the image from
Fig. 1 wi th star suppression.
In that view, the parameter inference (detection) is a
secondary task. The certification (or detection ) be-
comes progre ssively more difficult with decreasing
signal-to-background ratio (SBR) and decreasing st-
reak length. In addition, in case of a passive telescop e
(without sidereal tracking , as is the case in Fig. 1) the
certification and detection problems are not equally
difficult for all orientation angles because stars appear
as short streaks as well.
1.1 Related Work
The streak detection problem and its variations has
been studied for more than two decades (Leu, 1992).
Known methods can be divided to two broad cate-
gories: Single-frame meth ods that work with a sin-
gle image (Ciurte and Da nescu, 2014; Virtanen et al.,
2016; Tagawa et al., 2016) and mu ltif rame methods
that track the object (Yanagisawa et al., 2008; Sun
et a l., 2015; Uetsuhara and Ikoma, 20 14; Yanagisawa
and Kurosaki, 2012;
ˇ
S´ara et al., 2013) and/or use
streak-free images for background subtr action (Leu,
1992; Gural et al., 2005).
A long streak appears if the observed object moves
fast and appears in just a single frame. Some authors
also consid er slowly moving objects that are obser-
ved repeatedly over the course of several fram es (L eu,
1992; Uetsuhar a and Ikoma, 2014 ). The ‘streaks’ in a
single frame are then very shor t. To achieve reliable
detection, it must be coupled with tracking. We do
not consider such approaches in this paper and focus
on long streaks (at least 50 pixels, say).
Simple de te ction methods use matched filters (Gu-
ral et al., 2005). Each parameter vector defines a
convolutional filter that is applied to the image. Pa-
rameters inc lude streak shape and pose. Detection
is done by non-maximum suppression with threshol-
ding. The threshold can be learned (Schildknecht
et al., 2015). Th e matched-filter approaches perfor m
an exhaustive search, possibly with some speedup
heuristics (Schildknecht e t al., 2015). I n these me t-
hods there is a tradeoff betwe e n parameter space dis-
cretization step and detection accuracy.
A well-known method in the class of single-f rame
long-streak detection is based on image column me-
dians (Yanagisawa and Nakajima, 2005): Even a faint
vertical streak of sufficient length can be detected by
computing columnwise image medians and thresho l-
ding the result. This g ives the column position. The
streak is then localized within that column. Stre-
aks in other orientations are detected with the help
of image rotation. Th is method requir es a very fine
quantization o f angular space (around 360 discrete
angles in (Yanagisawa and Nakajima, 2005) for r e-
gion 700 × 700 pixels, big ger im ages require even fi-
ner qua ntization). On the other hand, the algorithm
is easily parallelizable which makes the method use-
ful. The method is robust: Bright stars and noise have
low impact on the median. A less robust but compu-
tationally e fficient methods ar e based on Radon trans-
form (Zimmer et al., 2013). These methods sh are the
limitation due to angular discretization.
Recent single-frame methods employ a bottom-up
proced ure of salient pixel detection, followed by per-
Detection and Certification of Faint Streaks in Astronomical Images
499

ceptual grouping (Virtanen et al., 2016). The method
does not d istinguish short/long streaks. It achieves
state of the art performance on a proprietary dataset.
Some recent approaches try avoiding early dec i-
sions, acknowledge the statistical nature of the pro-
blem and e mploy a formal classification/hypothesis
testing. An interesting method in this class is (Ko-
lessa, 2013). The method first considers local image
structure an d categorizes it to several classes (back-
ground/star/streak tracklet). Streaks a re then detected
by concatenating streak tracklets. Another statisti-
cally sound meth od is presented in (Dawson et al.,
2016). The methods maximizes image likelihood by
streak parameter space search.
A recent statistical method distinguishes two p ha-
ses of th e problem: Detection and certification (Sara
and Cvrcek, 2017). Detection infers streak parame-
ters in the Maximum a Posteriori (MAP) sense, assu-
ming there is a streak in the image. Certification is
a decision if the image contains a streak. These two
tasks are coupled in what the paper calls Multi-Level
Bayesian Inference (MLBI). The certification is d one
by Baye sian model selection. Two statistical models
are consider e d: (1) M
1
: image contains a streak, and
(2) M
0
: im age does not contain a streak. Model se-
lection is based on computing posterior marginals for
the two models and comparin g their value. The nice
property of the method is that the marginals can be
computed exactly with a low-order polynom ial algo-
rithm (Sara and Cvrcek, 2017). The method achie-
ved state-of-the art performance in a restricted streak
angle range: The p resence of axis-aligned CCD chip
artefacts (vertical, horizontal) an d star streaks (hori-
zontal) resulted in false-positive certification for these
angles, hence the algorithm worked with these angles
excluded.
The present paper aims to develop the method
from (Sara and Cvrcek, 2017) further. The under-
lying principles are the same. We removed the angu-
lar limitation of the previous m e thod by backg round
simulation an d subtraction in feature spac e, as de-
tailed in Sec. 2.1. This led to significant performance
improvement and push e d the performance bound ary
towa rds very faint streak certification, as shown in
Sec. 4. The main focus of this paper is on certifi-
cation. We nevertheless describe th e detectio n proce-
dure and verify c onsistency of the proposed certifica-
tion and ground-truth based detection rejection using
a threshold on location error of the detection.
Figure 4: Example of an oriented str eak template. The tem-
plate’s orientation is φ = −45
◦
.
2 METHOD
Each pixel x
i, j
(we might drop the indices i, j in sub-
sequent text) in the image X is r epresented by a fe-
ature vector f(i, j), of dimension d (d = 5). The fe-
ature vector f(i, j) rep resents a local region w.r.t. to
a certain family of templates (Marchant and Jackway,
2012a ). A streak segment template in Fig. 4 is repre-
sented by a vector t of size d that can be rotated in
O(d). Similarity be twe en region represen ted by f and
t rotated by φ is then computed in O(d) tim e. This
is faster than rotating the original streak te mplate in
Fig. 4 and convo lving with the input image for each
angle. Details how to construct f and t are provided
in (Marchant and Jackway, 2012a). Additional details
for compu ting similarity in an identical setting can be
found in (Sara and Cvrcek, 2017).
Some image objects resemble streaks (stars in a
passive telescope, CCD imager segment boundaries),
thus inducing high response (although th ey belong to
the backgro und). This often leads to false positives.
The paper (Sar a and Cvrcek, 2017) deals with this
problem by prohibiting problematic angles. Thus, the
angular degree interval [−90,−73.5] ∪ [−5.5, 5.5] ∪
[73.5, 90] was excluded in (Sara and Cvrcek, 2017).
But the n a streak with an orientation in that interval
leads to a false negative. In this paper, we wish to
extend the solu tion to every orientation of a streak.
To do this (1) we construct simulated background in
Sec. 2.1, and (2) we will show how to modify the fe-
ature vectors to compensate background artefacts in
Sec. 2.1.
2.1 Normalized Ima ge Representation
Our objects of interest are celestial o bjects th at pro-
duce streaks in long- exposure images. If the ob-
ject was not present, we would observe what we
call the background image. As discussed above,
the background image contains structures (stars and
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
500

image artefacts) tha t lead to false positive certificati-
ons/detections. In this paper, we will show how to
suppress these arte facts by modifying the feature re-
presentation of the imag e.
One can either obtain stars by detection, directly
in the input image (Schildknecht et al., 2015), or from
registering the image against a star catalog (Zimmer
et al., 2013). With the first approa ch, we risk de-
tecting a streak as a star, or ignoring a star altoget-
her. Rather than a truth we see the star catalog as
an independ ent but imperfect source of information.
We should note that automatically constructed cata-
logs are incomplete in objects of large apparent mag-
nitudes but up to the limiting magnitude of a typical
telescope it can be considered complete.
With a catalog or without, the usual approach is
to mask the stars out (Schildknecht et al., 2015), thus
loosing some data. We will avoid such early decisi-
ons b y using the star catalog and some characteristics
of the input image to simulate the background of the
input image in the space of afore mentioned features.
Assuming our back ground simulation was perfect,
then due to additivity, we could get the pure streak
image by simply subtracting the background im age
from the inpu t image. Unfortunately, simulating the
backgr ound in sufficient qua lity is very difficult since
the image is influenced by many ph ysical phenomena
(consider e.g. image saturation or blooming, or thin
clouds in the upper atmosphere partly dimming th e
stars and reflecting stray light from the Earth). We
found that if the su btraction is done in the space of
normalized image features, the idea works with even
a very coarse simulation. Mo reover, the simulation
tends to work very well for b right stars that tend to
attract the detector/skew certification. These kinds of
objects are causing most of typic al false positives in
previous methods (Zimmer et al., 2013).
Background simulation is done as follows. E a ch
star in the catalog has an apparent magnitud e M.
Magnitud e is not direc tly measura ble in the image.
We therefore recover the star magn itude-to-image
flux mapping. The images are first registered to the
catalog by the method u sed in (
ˇ
S´ara et al., 2013).
For each catalogued star and the given image expo-
sure time, an elongated star image region S is defi-
ned. Flux F
m
of the star in the image is computed by
integrating image values over S. This way we col-
lect (flux, magnitude) samples. Apparent m agnitu-
des M from the star catalog are matched to flux F
m
by robustly fitting a piece-wise line ar function to this
data. Catalogued stars are simulated by rendering a
line segment of length l proportional to exposure time
and amplitude proportional F
m
/l. T he resulting simu-
lated imag e is then convolved with a Gaussian point
spread function. Its σ pa rameter was learned from star
samples.
Finally, random Gaussian noise with zero mean
was added. The standard deviation of the noise was
learned as the sample standard deviation of the input
image, with image regions containing star s masked
out (solely) for this purpose.
Let f
im
(i, j) be steerable fea ture vector computed
at an inpu t image pixel (i, j) and f
sim
(i, j) be feature
vector computed at the corresponding pixel of the si-
mulated image. Th e features are spherical quadrature
filter respo nses (Marchant and Jackway, 2 012b) with
the zero-order filter excluded, see (Sara and Cvrcek,
2017) and references therein for deta ils. The exclu-
sion helps suppress additive artefacts. We then nor-
malize the vectors to suppress scaling artefacts and
then subtract them:
f
res
(i, j) =
f
im
(i, j)
kf
im
(i, j)k
−
f
sim
(i, j)
kf
sim
(i, j)k
, (1)
where k · k is the Euclidean norm.
The effect of this simulate d background sub-
traction in feature space can b e seen in Fig. 2 a nd 3.
We fo und that this feature modification dramatically
contributes to the overall succ e ss of the certifica-
tion/detection method a s the experimental results in
Sec. 3 show.
2.2 Model
We study two eve nts. In the fir st event, there is no sta-
tistically significant streak with an orientation φ in an
image X . We denote the Bayesian model f or the no-
streak event as p
0
(X,φ). The second event is a pre-
sence of a single statistically significant streak with
an or ie ntation φ and parameters θ (eg. starting an d en-
ding position) in the image X. We denote the Baye-
sian mo del fo r the single-streak event as p
1
(X,φ,θ).
We lift the image 2D grid to 3D grid by assuming
a discrete set of angles Φ. The lifted image element
value x
φ,i, j
is the n the similarity value be twe en the st-
reak segment templa te of the orientation φ and image
at th e pixel position (i, j). We denote similar ities for a
particular orientation X
φ
= {x
φ,i, j
| (i, j) ∈ X }, where
X is the image domain. The com plete 3D stack is
X
Φ
= {X
φ
| φ ∈ Φ}.
The quantiza tion Φ stems from the fact that stre-
aks are not infinitely thin. The orientation φ is then
a discrete ra ndom variable. The motivation for lifting
data to 3D is that we need to express the fact that a
possible streak can appear in just a single or ie ntation.
This is a substan tial m odification of the original m o-
del (Sara and Cvrcek, 2017). In summary, we assume
that p
0
(X,φ + ∆φ) ≈ ˆp
0
(X
φ
) and p
1
(X,φ + ∆φ,θ) ≈
Detection and Certification of Faint Streaks in Astronomical Images
501

ˆp
1
(X
φ
,φ,θ), when φ is fixed and |∆φ| is sufficiently
small.
First, we develop the two models ˆp
0
(X
φ
) and
ˆp
1
(X
φ
,φ,θ). Then, w e use the models to (1) find the
best streak in the image (detection), and (2) decide
about the statistical significance of the fou nded streak
(certification) .
2.2.1 No-streak Model Distributio n
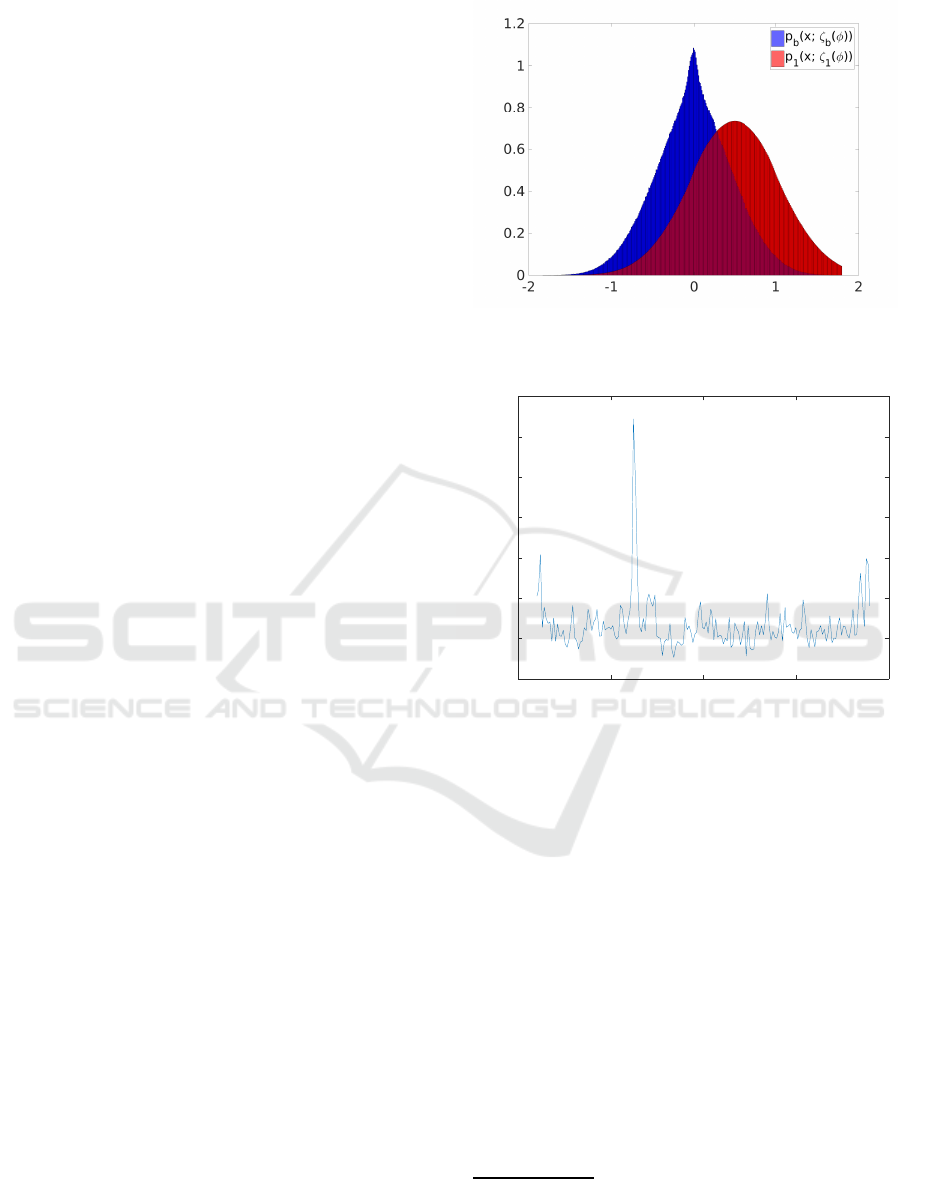
We first construct d istribution p
b
(x
φ,i, j
; ζ
b
(φ)) with
hyper-parameters ζ
b
(φ) that a single-pixel similarity
originates from a b ackground. Given a fixed orien-
tation φ ∈ Φ and the input image, we learn the dis-
tribution p
b
as a normalized histogram with hyper-
parameters ζ
b
(φ). The histogram is constructed from
all steered similarity responses x
φ,i, j
collected over the
image dom ain for a given angle φ. The effect of a pos-
sible strea k in the image is negligible in the histogram
due to its small support in the image. An example of
the background pixel-wise distribution p
b
is the blue
distribution in Fig. 5.
We assume pixel-wise independence and we con-
struct following joint image model distribution for
particular orientation φ
ˆp
0
(X
φ
) =
∏
i, j∈X
p
b
(x
φ,i, j
; ζ
b
(φ)). (2)
where X
φ
is the similarity map.
The distribution that the image is a background
p
0
(X) ≈ ˆp
0
(X
Φ
) is the joint distribution that every 3D
pixel is part of the backgrou nd
ˆp
0
(X
Φ
) = ˆp
0
(X
φ
1
,..,X
φ
k
) =
∏
φ∈Φ
ˆp
0
(X
φ
) =
∏
φ∈Φ
∏
i, j∈X
φ
p
b
(x
φ,i, j
; ζ
b
(φ)). (3)
The background model is hence param eterless.
2.2.2 Streak Model Distribution
We first construct distribution that a single-pixel simi-
larity originates from a streak p
1
(x
φ,i, j
;ζ
1
(φ)), which
is an analo gue to p
b
(x
φ,i, j
; ζ
b
(φ)) in (3). This is done
in a way similar to (Sara and Cvrcek, 2017). It is assu-
med that a streak adds an unknown additive quantity
to sim ilarity x
φ,i, j
. This is approximately true even
after normalization in (1) for small strea k am plitu-
des. Since the amplitude of the streak is unknown,
we assume a random variable of uniform distribution
p
u
(x;a,b), where x is a similarity shift and (a, b) is a
sufficiently wide shifts interval. The p
1
(x
φ,i, j
;ζ
1
(φ))
is the n given by
p
1
= p
b
∗ p
u
. (4)
Figure 5: Pixelwise distributions p
b
(x
φ,i, j
;ζ
b
(φ)) and
p
1
(x
φ,i, j
;ζ
1
(φ)) for φ = −38
◦
.
-100 -50 0 50 100
angle[ °]
50
100
150
200
250
300
350
400
log C (X )
angular profile
Figure 6: Angular profile of the i nput image in Fig. 1, with a
prominent peak corresponding to the streak orientation an-
gle.
Where ∗ represents convolution and ζ
1
(φ) are hyper-
parameters of a normalized histogram . A typical re-
sult is the red distribution in Fig. 5 .
Suppose we work at a given angle φ. We shea r
2
the domain X
Φ
to angle φ so that a streak is given by
its column position j and two end-points i
1,2
in that
column (Sara and Cvrcek, 2017).
3
Then the streak
parameters are θ
+
= (φ, j,i
1,2
) which defines its (she-
ared) domain Y (φ, j,i
1,2
). For the sake of brevity, we
assume that enumerating (φ, j,i) ∈ Y (θ
+
) is equiva-
lent to enumerating (φ, j, i
1,2
) ∈ Y (φ, j, i
1,2
).
We define the distribution that a particular stack in
2
The shear mapping is two times faster than a rotation.
3
After shearing the input image to angle φ a streak of
orientation φ becomes vertical, hence simpler to detect by
just searching image columns (Tagawa et al., 2016).
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
502

the X
Φ
contains a single streak with parameters θ
+
ˆp
1
(X
φ
| θ
+
) = ˆp
0
(X
φ
)
∏
(φ,i, j)∈Y (θ
+
)
p
1
(x
φ,i, j
; ζ
1
(φ))
p
b
(x
φ,i, j
; ζ
b
(φ)
,
(5)
that is analogous to (2). We define the distribution that
the image contains a single streak given pa rameters
θ
+
as
ˆp
1
(X
Φ
| θ
+
) = ˆp
0
(X
Φ\φ
) ˆp
1
(X
φ
| θ
+
) (6)
that is analogous to (3).
Then, we construct the joint distribution, given φ
ˆp
1
(X
φ
, j, i
1,2
| φ) =
ˆp
1
(X
φ
| φ, j, i
1,2
) ˆp
1
(i
1,2
| φ, j) ˆp
1
( j | φ) . (7)
We use uniformly distributed priors ˆp
1
(i
1,2
| φ, j) and
ˆp
1
( j | φ).
2.3 Certification
We compute the single streak evidence (given orienta-
tion) from the model by marginalizing the streak pa-
rameters
ˆp
1
(X
φ
| φ) =
n
φ
∑
j=1
m
φ
∑
i
1
=1
m
φ
∑
i
2
=i
1
ˆp
1
(X
φ
, j, i
1,2
| φ) . (8)
Where n
φ
is number of columns in the sheared image
and m
φ
is the number of rows.
The inner two sums in (8) are easily computed
with the help o f integral sums, using parametriza-
tion (φ, j, i
1,2
) in the sheared domain an d following
the Belmann principle of dy namic programming, as
in (Sara and Cvrc ek, 201 7).
We obtain the distribution for complete 3D stack
ˆp
1
(X
Φ
| φ) = ˆp
0
(X
Φ\φ
) ˆp
1
(X
φ
| φ) . (9)
Then the full Bayesian evidence required for cer-
tification is
ˆp
1
(X
Φ
) =
∑
φ∈Φ
ˆp
1
(X
Φ
| φ) ˆp
1
(φ). (10)
Where ˆp
1
(φ) is a uniform distribution.
We can effectively precompute the partial ele-
ments in (9) up to some constant background distri-
bution per individual level in 3D stack .
We have chosen the background distribution to
be parameterless and alread y have the required form
ˆp
0
(X
Φ
).
Certifying streak detection requires statistical de-
cision about the presence of a single streak in th e
image. We implement the decision as the Bayesian
model selection based on the evidences (10) and (3).
The Bayes model selection tells us that an image
contains a streak if and on ly if ˆp
1
(X
Φ
) > ˆp
0
(X
Φ
). In
practice, we study their ratio
C(X ) =
ˆp
1
(X
Φ
)
ˆp
0
(X
Φ
)
=
∑
φ∈Φ
ˆp
1
(X
φ
| φ) ˆp
1
(φ)
ˆp
0
(X
φ
| φ)
, (11)
which we call certification value and we say that
image contains a streak when
C(X ) > T , (12)
where the T is a given threshold. The (12) is then cer-
tification decision. This is equivalent to the de cision
rule used in (Sara and Cvrcek, 2 017). The need for
the threshold T arises from an imperfect power of the
statistical model to capture reality. The T then serves
as a way to bala nce the false po sitive/false negative
tradeoff.
The complete certification and detection algo-
rithm is summarized in Alg. 1.
2.4 Detection
Detection is a maximiza tion
(θ
+
)
∗
= argmax
(φ,i, j)∈Y (θ
+
)
ˆp
1
(X
Φ
| θ
+
), (13)
it can therefore be easily computed simultaneously
with certification. We simply replace summations
in (8) and (10) by m aximizations.
For clarity in subsequent text, we introduce the
following function
( j
∗
,i
∗
1,2
) = L(φ) = argmax
j,i
1,2
ˆp
1
(X
Φ
| φ, j, i
1,2
) , (14)
which selects the best streak segment, give n an angle
φ.
3 EXPERIMENTS
3.1 Certification
Certification is a decision task whose ROC curve is
generated by threshold T in (12). We therefore re -
port RO C curves and also AUC statistics. We used the
same experimenta l procedure as in (Sara and Cvrcek,
2017), which we call the MLBI method here. Note
that results in (Sara and Cvrcek, 2017) show ROC
curves and AUC with a su bset of streak orienta tion
angles ignored, as discussed in Sec. 2. Unlike MLBI,
here we are testing on the full angular range. This is
the reason the MLBI results re ported here are worse
than those reported in (Sara and Cvrcek, 2017 ).
The proposed method produces certification val-
ues C(X ), so does the MLBI method. False positive
Detection and Certification of Faint Streaks in Astronomical Images
503

Algorithm 1: Streak certification and detection.
Given: Input image X .
Output: Certificate value C(X), streak parameters
(φ
∗
, j
∗
,i
∗
1,2
).
1. G et a feature representation f
res
of the input image
using (1).
2. Initiate Φ to (−90,−85,..., 85, 90)[
◦
]:
3. For each angle φ ∈ Φ:
(a) Find response X
φ
to the template in Fig. 4 rotated by
φ.
(b) Shear response X
φ
by φ (streaks become vertical).
(c) Learn ζ
b
(φ).
(d) C ompute ζ
1
(φ) using (4) and ˆp
0
(X
φ
| φ) from (2).
(e) Compute ˆp
1
(X
φ
| φ) from (8).
(f) Fi nd the best segment L(φ) in angle φ using ( 14).
(g) Update Φ by using the branch and bound method.
4. Compute ˆp
0
(X
Φ
) from (3) and ˆp
1
(X
Φ
) from (10).
5. Find the maximum φ
∗
of L(φ) over φ ∈ Φ by fetching
results from Step 3f.
6. G iven φ
∗
use (14) to get ( j
∗
,i
∗
1,2
).
7. C(X) ← ˆp
1
(X
Φ
)/ ˆp
0
(X
Φ
).
occurs when C(X) exceeds the certification decision
threshold T . False negative occurs in a streak image
with the C (X ) lower than T .
To the best of our knowledge, there is no publicly
available benchmarkin g dataset. As a result, different
methods are evaluated on different datasets, which
are not p ublicly available. Even the largest publis-
hed study on the topic (Virtanen et al., 2016) do e s
not publish the dataset. Direct comparison with most
of o ther me thods is therefor e impossible. In order to
compare our results w ith the closest work, we used
a dataset very similar to that one that has been used
in (Sara and Cvrcek, 2017).
It is difficult to o btain streak images with verified
ground-truth . Manual ground-truth verification is n ot
feasible in very faint streaks, since there are many ob-
jects of high apparent magnitude that the human eye
cannot see. The difficulty may be acknowledged in
Fig. 1, which shows an example of a well detectable
streak but an untrained hum an eye can easily miss it.
Obtaining a ground-truth dataset would be a major ef-
fort in itself.
Therefore, a ground-truth dataset must be simu -
lated. In order to make the simulation realistic,
the (Sara and Cvrcek, 2017) used real images as a
backgr ound and simulated streaks of varying length ,
position, orientation, and amplitude in them. We use
the same method: One hundred real images a re se-
lected from the same large dataset, which either do not
contain a streak or contain streak(s) which can n ot be
manually confir med. The images were taken in Lulin
observatory in Taiwan (the same data as in (Yanagi-
sawa e t al., 2012; Sara and Cvrcek, 2017)). The 50 cm
telescope had FOV 1.3
◦
× 1.3
◦
, effective size of ima-
ges is 2049(V)×2047(H), 16 bit monochromatic and
5.9 s exposure time. Approximately 10 000 random
synthetic streaks were additively superimposed onto
the background images. Their amplitudes a are rela-
ted to signal-to-bac kground ratio (SBR) by
SBR = 20 log
10
a
σ
, [dB] (15)
where σ is the standard deviation of the backgroun d
values (upper half-percentile is clipped). This is equi-
valent to SBR defined in (Sara and Cvrcek, 2017).
The lower the SBR value the fainter the streak . The
streaks were generated so that the distribution of
their end points was uniform over the image dom-
ain and the ir SBRs have uniform distribution (SBR ∼
U(−30, 0)[dB]) in the dataset.
We pro totyped Algorithm 1 in MATLAB. The
processing time was measured on a m iddle-ran ge
laptop with Intel processor i5-6200U CPU @
2.30GHz ×4. The processing time of an input image
is determ ined by the SBR of a streak in th e input
image. The me thod takes up to several (3 -7) minutes
for stre ak-less images. If the image contains a stre ak
with higher SBR the processing times decreases to a
few (2-4) minutes.
3.2 Certification a nd Detection
Consistency
Detection is done over identical data as certification.
We ne ed to evaluate the accuracy o f detectio n, given
the ground truth data. The metric determinin g dis-
tance between a detected streak and g round truth is
problem dependent. From a practical point of view,
the most important param e te r of a detection is its
orientation angle φ. A somewhat less impo rtant pa-
rameter is the orthogonal distance of detec ted streak
from its corr ect position (corresponding a pprox ima-
tely to j). The least im portant parameters ar e the st-
reak endpoints (corresponding to i
1,2
).
For the purpose of this experiment, we chose
to measure the angu la r error between detected and
ground truth streak as
d(L
det
,L
gt
) = |φ
det
− φ
gt
|, (16)
where φ
det
and φ
gt
is the orientation of the detected
streak and the ground truth streak, respective ly.
We want to show that certification is consistent
with detection accuracy. For ea ch simulated image I,
we perform certification followed by streak detection.
We retain details abo ut th e simulation: The streak
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
504

length, orientation an d signal to background ratio. In
the results section, we study the relation between cer-
tification value C (X ) and detection. We would like to
see that the certification value C (X ) is related to streak
length an d to SBR and that the re exist a narrow in-
terval for the certification threshold T which predicts
streak detection failure, as measured by the accuracy
metric.
4 RESULTS AND DISCUSSION
4.1 Certification
Similarly as in (Sara and Cvrcek, 2017) we split the
dataset to several sub-groups based on the streak’s
SBR and length. As discussed above, short streaks
and/or streaks of low SBR are more difficult to certify
(and dete c t).
The results of ROC analysis (Fawcett, 2006) are
shown in Figs. 7, 8, 9 and 10 . Fig s. 8 an d 10 show
ROC curves of the proposed me thod. Figs. 7 and 9
show ROC analysis of the MLBI method presented
in (Sara and Cvrcek, 2017), this time with no orien-
tation restriction. Each point in Figs. 9 and 10 shows
AU C for the given subset. Since we do not restrict the
angular space as in (Sara and Cvrcek, 2017), the met-
hod in Figs. 7 and 9 show degraded results compared
to those reported in (Sara and Cvrcek, 2017).
As can be expected, long, sufficiently bright stre-
aks are easy to certify. In Fig . 10 we see that in the
interval of −10 dB to −5 dB, with the shortest stre-
aks, the AUC is 0.925. This means the err or rate (Fa-
wcett, 2006) is 7.5%. That is a 6-fold improvement
over the MLBI. For the long (∆ > 1200), ultra-faint
(SBR < −25 dB) streaks in Fig. 10 the error rate is
still less than 32 %. In this range the MLBI method
gives results not better than a c hance (AUC ≈ 0.5).
We conclude the proposed method significantly ex-
ceeds the MLBI method in performance when applied
to the f ull streak orienta tion domain.
4.2 Certification a nd Detection
Consistency
Certification works well when it is consistent with de-
tection: Only correctly detected streaks should be cer-
tified positively.
Box plots in Fig. 11 show dependency of angular
error on the SBR f or all de tections. We see in Fig. 12
that the error is significantly smaller in certified st-
reaks. Even very faint strea ks in the (−30, −20) dB
range achieve low median detection error.
0 0.2 0.4 0.6 0.8 1
False positive rate[-]
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
True positive rate[-]
ROC curve
(0.00,500.00]; SBR (-30.00,-20.00]; AUC = 0.528
(500.00,Inf]; SBR (-30.00,-20.00]; AUC = 0.491
(0.00,500.00]; SBR (-20.00,-15.00]; AUC = 0.518
(500.00,Inf]; SBR (-20.00,-15.00]; AUC = 0.542
(0.00,500.00]; SBR (-15.00,-5.00]; AUC = 0.510
(500.00,Inf]; SBR (-15.00,-5.00]; AUC = 0.717
(0.00,500.00]; SBR (-5.00,0.00]; AUC = 0.580
(500.00,Inf]; SBR (-5.00,0.00]; AUC = 0.868
Figure 7: ROC curves f or the MLBI method (Sara and Cvr-
cek, 2017) on the full angular domain. Colors represent
dataset subgroups (see the main text for a description) from
a Cartesian product l isted in the plot legends.
Table 1: Confusion matrix for real streaks, the certification
threshold is log (C(X)) > 200.
Ground truth
Streak Background
Certification
Streak
24 (TP) 4 (FP)
Backgr.
0 (FN) 18 (TN)
To probe further, the scatter plot in Fig. 13 shows
the dependency between the ang ular error and certi-
ficate value C(X ). We can see that almost all failed
detections occur under logC(X ) < 200. The red line
shows medians of data groups with a similar c e rtifi-
cation value. Th e sharp drop in that curve confirms a
stable decision thr eshold T ≈ 200 on logC(X).
4.3 Real Data Experiments
We manually selected 24 observations that contain a
streak and 22 observation that do not contain a streak.
An example of faint detected streak is in Fig. 14. We
run the detection and certification for these observati-
ons. The resulting confusion matrix is in Tab. 1.
False negative occurs when the streak is too
faint/short. Str e aks visible to human are a lmost al-
ways detec ta ble, hence the false negative count is
Detection and Certification of Faint Streaks in Astronomical Images
505

0 0.2 0.4 0.6 0.8 1
False positive rate[-]
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
True positive rate[-]
ROC curve
(0.00,500.00]; SBR (-30.00,-20.00]; AUC = 0.610
(500.00,Inf]; SBR (-30.00,-20.00]; AUC = 0.733
(0.00,500.00]; SBR (-20.00,-15.00]; AUC = 0.759
(500.00,Inf]; SBR (-20.00,-15.00]; AUC = 0.869
(0.00,500.00]; SBR (-15.00,-5.00]; AUC = 0.876
(500.00,Inf]; SBR (-15.00,-5.00]; AUC = 0.971
(0.00,500.00]; SBR (-5.00,0.00]; AUC = 0.964
(500.00,Inf]; SBR (-5.00,0.00]; AUC = 1.000
Figure 8: ROC curves for the proposed method, on the full
angular domain. Note the marked improvement over Fig. 7
on same-color curves.
-30 -25 -20 -15 -10 -5 0
SBR[dB]
0.4
0.5
0.6
0.7
0.8
0.9
1
AUC[-]
AUC plotted against length-SBR subsets
(10.00,580.00]
(580.00,900.00]
(900.00,1200.00]
(1200.00,1530.00]
(1530.00,2800.00]
Figure 9: AUC for the MLBI method (Sara and Cvrcek,
2017) on the full angular domain. Colors correspond to
streak length intervals, the SBR coordinate represents the
middle of a SBR interval.
zero. False positive occurs, wh e n the data are oversa-
turated (Fig. 15 ) or the catalog fails (Figs. 16 and 17).
Catalog fails, when the star in the catalog is either
significantly br ighter (Fig. 16) or significantly fainter
(Fig. 17). Both instances produc e a contrast tha t leads
to a false positive.
-30 -25 -20 -15 -10 -5 0
SBR[dB]
0.4
0.5
0.6
0.7
0.8
0.9
1
AUC[-]
AUC plotted against length-SBR subsets
(10.00,590.00]
(590.00,900.00]
(900.00,1200.00]
(1200.00,1540.00]
(1540.00,2730.00]
Figure 10: AUC for the proposed method, on the full angu-
lar domain. Note the improvement over Fig. 9.
[-30;-20] [-20;-15] [-15;-5] [-5;0]
SBR [-]
0
20
40
60
80
100
120
140
160
180
angular difference [ °]
angular distance of detection from ground truth
Figure 11: Angular error vs. SB R f or all detections. Blue
boxes show data from 25th to 75th percentile, red lines are
medians.
4.4 Comparison with other Methods
Comparison with other independent methods can only
be done indir ectly. The (Dawson et al., 2016) de -
monstrate their method on what they call ultra-faint
streaks. Their streak has amplitude lower than SBR
(a < RMS noise) and length ∆ ≈ 250 px. This means
authors are capable of de te cting a streak with SBR
lower than 0 dB. The lowest SBR we found in liter a-
ture is SBR ≈ −4.4 dB (amp litude ≈ 0 .6 σ (Zimmer
et al., 2013; Schildkn e cht et al., 2015 )). The method
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
506

[-30;-20] [-20;-15] [-15;-5] [-5;0]
SBR [-]
0
0.5
1
1.5
2
2.5
angular difference [ °]
angular distance of detection from ground truth
Figure 12: A ngular error vs. SBR for detections certified
with t he threshold of log(C(X)) > 200. Blue boxes show
data from 25th to 75th percentile, red lines are medians.
Note the scale change on the y axis.
150 200 250 300 350 400 450 500
certificate [-]
0
10
20
30
40
50
60
70
80
90
100
110
angular difference [ °]
angular difference of streaks
streaks
quantized streaks
Figure 13: Angular error d as a function of certification va-
lue logC(X ). One blue point corresponds to one image.
(Virtanen et al., 2016) is capable of detecting multi-
ple streaks in about 13 s in 2k-by-2k images. The true
positives are about 90% for SBR > 0dB for streaks
longer than 100 px. And w hen the SBR is lower than
−6 dB, the true positives are around 50%.
5 CONCLUSION
We have discussed a certification meth od, which sta-
tistically decides abo ut the presence of a streak in
the image. We have also shown th at ba ckground si-
Figure 14: Detection of a real faint streak, the certification
value is −325.
mulation (stars, some sensor artefacts) lea ds to su-
perior certification results, as demon stra te d on semi-
synthetic data. We have shown that th e certificatio n
value predicts detection failure in the sense of a de-
tection e rror metr ic .
We conducted experiments showing that on the
SBR in te rval of −5 dB to 0 dB, with streaks length
from 10 px to 500 px, we achieve AUC ≈ 0.97. This is
compara ble to results presented in (Sara and Cvrcek,
2017). However, unlike in (Sara a nd Cvrcek, 2017)
we can certify a streak regardless of its orientation.
The proposed method outperf orms (Sara and Cvrcek,
2017) in lower SBRs. Fig. 10 shows that even for the
SBR values from −30 dB to −25 dB the e rror rate of
the proposed method is still better than random gues-
sing (AUC > 0.5). Of the known methods this is the
best performance.
We also tested the method on a small set of real
data in Sec. 4.3. We have shown that the me thod is ca-
pable to detect faint streaks in r eal datasets. We have
also shown that the method often fails when the back-
ground compensation fails. This observation hints to-
ward further improvements.
The streak detec tion d omain pr ovides an example
of a problem, where the ob je c ts of interest are arbi-
trarily d ifficult to confirm. We have shown that it is
possible to construct a general mecha nism that c an
certify a detec tion while adapting to the input data in-
stance via constructing the p
b
distribution. The ge -
nerality of the approach follows from the generality
of Bay e sian inference. The nice prope rty of the st-
Detection and Certification of Faint Streaks in Astronomical Images
507

Figure 15: Detection fails because of the large saturated
star.
Figure 16: Detection fails because the star in the catalog
is too bright. The star is therefore overcompensated and
resulting contrast is detected as a streak. Best viewed close-
up, in PDF.
reak detection problem is that the marginals needed
for the inference can be comp uted exactly. It is there-
fore possible to study the utility of the Bayesian mo-
del selection principle in com puter vision problems.
Our results confirmed our (good) expectations.
Generalization to multip le streak certificatio n
is possible within the model selection framework.
Instead of consider ing just two models M
0
and M
1
,
Figure 17: Detection fails because the st ar in the catalog is
too faint. The undercompensated star residual response is
similar to a streak.
for no -streak and single-streak da ta interpretation, re-
spectively, one could consider a set M
i
for i = 0,... ,n.
As a result, one would get the a posteriori most pro-
bable nu mber of streaks in data. This is a topic for
further research.
ACKNOWLEDGMENTS
We ackn owledge the support of the CTU Internal
grant SGS18/18 4/OHK3/3T/13 and the OP VVV
MEYS funded proje ct CZ.02 .1.01/0.0/0.0/16
019/
0000765 “Resear ch Center for Informatics”.
Special thanks g o to Toshifumi Yanagisawa of
JAXA and the TAOS team who made th eir image data
available to us.
REFERENCES
Bobrinsky, N. and Del Monte, L. (2010). The space si-
tuational awareness program of the European Space
Agency. Cosmic Research, 48(5):392–398.
Ciurte, A. and Danescu, R. (2014). Automatic detection of
meo satellite streaks from single long exposure astro-
nomic images. In 2014 International Conference on
Computer Vision Theory and Applications (VISAPP),
volume 1, pages 538–544.
Dawson, W., Schneider, M., and Kamath, C. (2016). Blind
Detection of Ultra-faint Streaks with a Maximum Li-
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
508

kelihood Method. In Proceedings of the 2016 AMOS
Technical C onference, page 72.
Fawcett, T. (2006). An introduction to ROC analysis. Pat-
tern Recognition Letters, 27(8):861 – 874.
Gural, P. S., L arsen, J. A., and Gleason, A. E. (2005). Ma-
tched filter processing for asteroid detection. The As-
tronomical Journal, 130(4):1951.
Kolessa, A. E. (2013). Detection of Faint Space Debris Ele-
ments with Unknown Orbits. In 6th European Con-
ference on Space Debris, volume 723 of ESA Special
Publication, page 143.
Leu, J.-G. (1992). A computer vision process to detect and
track space debris using ground-based optical telep-
hoto images. In Proceedings 11th IAPR International
Conference on Pattern Recognition, pages 522–525.
Marchant, R. and Jackway, P. (2012a). Feature detection
from the maximal response to a spherical quadrature
filter set. In Proceedings International Conference on
Digital Image Computing Techniques and Applicati-
ons (DICTA), pages 1–8.
Marchant, R. and Jackway, P. T. (2012b). F eature detection
from the maximal response to a spherical quadrature
filter set. In DICTA, pages 1–8.
Sara, R. and Cvrcek, V. (2017). Faint st reak detection with
certificate by adaptive multi-l evel Bayesian i nference.
In 7th European Conference on Space Debris.
ˇ
S´ara, R., Matouˇsek, M., and Franc, V. (2013). RANSA-
Cing optical image sequences for GEO and near-GEO
objects. In Proceedings of the 2013 AMOS Technical
Conference, page 10.
Schildknecht, T., Schild, K., and Vannanti, A. (2015). St-
reak detection algorithm for space debris detection on
optical images. In Advanced Maui Optical and Space
Surveillance Technologies Conference, page 36.
Sun, R., Zhan, J., Zhao, C ., and Zhang, X. (2015). Algo-
rithms and applications for detecting faint space debris
in GEO. Acta Astronautica, 110:9 – 17.
Tagawa, M., Yanagisawa, T., Kurosaki, H., Oda, H., and
Hanada, T. (2016). Orbital objects detection algo-
rithm using faint streaks. Advances in Space Research,
57(4):929 – 937.
Uetsuhara, M. and Ikoma, N. (2014). Faint Debris De-
tection by Particle B ased Track-Before-Detect Met-
hod. In Advanced Maui Optical and Space Surveil-
lance Technologies Conference.
Virtanen, J., Poikonen, J., S¨antti, T., Komulainen, T.,
Torppa, J., Granvik, M., Muinonen, K., Pentik¨ainen,
H., Martikainen, J., N¨ar¨anen, J., Lehti, J., and Flohrer,
T. (2016). Streak detection and analysis pipeline for
space-debris optical images. Advances in Space Rese-
arch, 57(8):1607 – 1623.
Yanagisawa, T. and Kurosaki, H. (2012). Detection of
faint GE O objects using JAXA’s fast analysis met-
hods. Transactions of the Japan Society for Aeronauti-
cal and Space Sciences, Aerospace Technology Japan,
10(ists28):29 – 35.
Yanagisawa, T., Kurosaki, H., Banno, H., Kitazawa, Y.,
Uetsuhara, M., and Hanada, T. (2012). Comparison
between four detection algorithms for GEO objects.
In Proceedings of t he 2014 AMOS Technical Confe-
rence.
Yanagisawa, T., Kurosaki, H., and Nakajima, A. (2008).
The stacking method: The technique to detect small
size of GEO debris and asteroids. Technical report,
Japan Aerospace Exploration Agency (JAXA).
Yanagisawa, T. and Nakajima, A. (2005). Detection of
small LEO debris with line detection method. Tran-
sactions of the Japan Society for Aeronautical and
Space Sciences, 47(158):240–248.
Yanagisawa, T., Nakajima, A., Kadota, K ., Kurosaki, H.,
Nakamura, T., Yoshida, F., Dermawan, B., and Sato,
Y. (2005). Automatic detection algorithm for small
moving objects. Publications of the Astronomical So-
ciety of Japan, 57(2):399–408.
Zimmer, P. C., Ackermann, M. R., and McGraw, J. T.
(2013). G PU-accelerated faint streak detection for un-
cued surveillance of LEO. In Proceedings of the 2013
AMOS Technical Conference.
Detection and Certification of Faint Streaks in Astronomical Images
509