3D Cylinder Pose Estimation by Maximization of Binary Masks

Similarity: A simulation Study for Multispectral Endoscopy Image

Registration

O. Zenteno, S. Treuillet and Y. Lucas

PRISME, Univ. d’Orl

eans, F-45072 Orl

eans, France

Keywords:

Multispectral Endoscopy, Image Registration, Optical Biopsy.

Abstract:

In this paper we address the problem of simultaneous pose estimation for multi-modal registration of images

captured using a ﬁberscope (multispectral) inserted through the instrument channel of a commercial endoscope

(RGB). We developed a virtual frame using the homography-derived extrinsics parameters using a chessboard

pattern to estimate the initial pose of both cameras and simulate two types of ﬁberscope movements (i.e, inser-

tion and precession). The ﬁberscope pose is calculated by the maximization of similarity measures between

the 2D projection of the simulated ﬁberscope and the ﬁberscope tip segmentation from the endoscopic images.

We used the virtual frame to generate sets of synthetic ﬁberscope data at two different poses and compared

them after the maximization of similarity. The performance was assessed by measuring the reprojection error

of the control points for each pair of images and the pose absolute error in a sequential movement mimicking

scenario. The mean reprojection error was 0.38 ± 0.5 pixels and absolute error in the tracking scenario was

0.05 ± 0.07 mm.

1 INTRODUCTION

Gastrointestinal complications are usually produced

by a bacterial pathogen called Helicobacter pylori

(Hp). About 50% of the world’s population is infected

with Hp but most individuals remain asymptomatic

until developing clinical disease. The primary clinical

manifestations of the infection are chronic inﬂamma-

tion which produce cellular alterations of the gastric

mucosa (degeneration and inﬁltration) that can lead to

peptic ulcers and malignous complication.

Current early detection capabilities are primarily

based on gastro-endoscopic exploration under seda-

tion or anesthesia during which the clinician may per-

form a biopsy for further histopathological examina-

tion if needed. Some endoscopic systems propose

alternative spectral tools for helping gastric screen-

ing by the use of optical biopsies. Typical examples

are Fuji Intelligent Chromo Endoscopy (FICE), pro-

posed by Fuji and Narrow Band Imaging (NBI), pro-

posed by Olympus (Song et al., 2008). These techni-

ques have shown the beneﬁts of using multiple wave-

lengths to improve the visibility of blood vessels and

other important features. However, they are limited

in the number of wavelengths processed. We believe

that using a larger number of bands in the visible and

near infrared (400-1000 nm) could improve characte-

rization of reﬂectance properties of the gastric mucosa

varying between healthy tissue and inﬂammatory or

malignant lesions.

For this purpose we developed a multispectral-

augmented endoscopic prototype illustrated on Figure

1. It is based on a Olympus (Tokyo, Japan) EVIS

EXERA III endoscopic system and a ﬁberscope (IT-

Concepts microﬂex m2.5-2500) is inserted into the

operators canal and connected to a multispectral ca-

mera. This allows simultaneous acquisition of white

light (WL) and a multispectral video (i.e., 41 spectral

bands in the range of 470 to 975 nm). This prototype

offers a familiar protocol for the clinician: he ﬁrst

introduces the endoscope on the patient, then the ﬁ-

berscope into the operator’s canal and performs the

simultaneous multi-modal exploration as with a con-

ventional endoscope. The multispectral probe works

as a localized optical biopsy for medical exploration

with a much smaller ﬁeld of view.

There are several registration issues to overlay

both modalities (i.e., WL and multispectral): the two

images have different points of view, different reso-

lutions, different focal lengths and distortions. In ad-

dition, a conventional off-line static calibration using

a chessboard pattern can be used to estimate intrinsic

Zenteno, O., Treuillet, S. and Lucas, Y.

3D Cylinder Pose Estimation by Maximization of Binary Masks Similarity: A simulation Study for Multispectral Endoscopy Image Registration.

DOI: 10.5220/0007400808570864

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 857-864

ISBN: 978-989-758-354-4

857

Figure 1: Augmented multispectral prototype.

Figure 2: a) Fiberscopic Image b) Endoscopic Image c)

Multimodal-enhanced image.

parameters of each cameras (focal length and distor-

tions) but the relation of both cameras cannot be con-

sidered rigidly ﬁxed due to the ﬁberscope being re-

moved between patients for sterilization. Therefore, a

variation in the initial ﬁberscope insertion and a slight

bending of the ﬁberscope tip (precession) is always

present.

To perform the multimodal image registration du-

ring exploration we used the ﬁberscope’s tip, which

is always visible in the endoscopic image. A ﬁrst ap-

proach was proposed in (Zenteno et al., 2018) ba-

sed on an off-line training with a chessboard pattern

of an adaptive afﬁne transform. The transformation

compensates the zooming and decentering effect pro-

duced by the insertion/retraction movement of the ﬁ-

berscope during in-vivo exploration. Although this is

really useful for insertion and retraction, it does not

take into account more complex movements which

can be induced by ﬁberscope manipulation like pre-

cession or axis displacement.

This paper presents a new approach based on a 3D

cylinder model of the ﬁberscope to achieve a more ro-

bust tracking of the tip’s pose and improve the image

registration accuracy. The remainder of this docu-

ment is organized as follow: Section 2 makes a re-

view of related works, Section 3 describes the met-

hod, Section 4 the results obtained and Sections 5

concludes the manuscript.

2 RELATED WORKS

The present multimodal image registration problem is

similar to the pose estimation of a tubular instrument

which is a classic issue of visual servoing for lapa-

roscopy and has been presented before in the litera-

ture. The application of artiﬁcial landmarks is a com-

mon practice as in (Kim et al., 2003) or (Tonet et al.,

2007). However, in the case of surgical instruments

with direct contact to human tissue, particular medi-

cal requirements such as the biocompatibility and the

sterilisability of the artiﬁcial markers have to be met.

(Doignon et al., 2008) presents several 3-D pose esti-

mation algorithms and visual servoing-based tracking

of tubular instruments with monocular vision systems

such as endoscopes and CT scanners. Another ap-

proaches using the video information provided by the

endoscopic camera have been proposed in (Cabras

et al., 2017) and (Reilink et al., 2013). The ﬁrst relies

on colored markers attached onto the bending section.

The image of the instrument is segmented using a

graphbased method and the corners of the markers are

extracted by detecting the color transitions along Be-

zier curves ﬁtted on edge points. The latter uses the

positions of three markers in the endoscopic image or

three feature points to update the state of a kinematic

model of the endoscopic instrument. However, these

existing solutions does not use multimodal images or

have been applied to ad-hoc laboratory setup which

cannot be directly used for real surgical systems. In

this paper, we propose a landmark-free approach to

dynamically estimate the pose changes between the

two cameras using only a binary segmentation of the

ﬁberscope tip in the endoscopic images, for a robust

real time image registration.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

858

3 METHODOLOGY

3.1 Dual Camera Calibration

A set of chessboard pattern images is used to esti-

mate the intrinsic parameters and the distortion of

both cameras (endoscope and ﬁbroscope). Calibra-

tion from real images of a chess-board pattern gi-

ves a realistic initial pose for the two cameras using

the homography-derived extrinsics parameters which

provide the translation vector T and rotation matrix R

relative to the world coordinates. The reference fra-

mes attached to each camera take the optical center C

for origin with its optical axis Z and the image plane

XY designated as C

and C

respectively.

Figure 4 depicts the position of the three coordi-

nate reference frames used for the virtual modeliza-

tion:

- The world reference frame (W ) which origin is

at pattern’s left-top corner. W

correspond to the

pattern horizontal and vertical dimension and W

is oriented on the acquisition system opposite di-

rection.

- The Fiberscopic reference frame (FC) which its

origin is at the end of the ﬁbercope. FC

and FC

correspond to the camera plane and its camera op-

tical axis respectively.

- The Endoscopic reference frame (EC) which its

origin is at the end of the endoscope. EC

and

correspond to the camera plane and its ca-

mera optical axis respectively.

3.2 Fiberscope Model

The ﬁberscope is represented following its real geo-

metrical properties as a straight cylinder with a ﬁxed

diameter of 2.5mm. The cylinder’s pose is deﬁned by

two points: Z

and Z

, which are the two extremities

of its axis. The point Z

is ﬁxed behind the initial FC

to be used as a pivot point. The point Z

is at the end

of the tip and it moves with the center of the camera.

We modeled two different movements: insertion

and precession (Fig 3). To model insertion the lo-

cation of Z

is translated along FC

according to the

desired depth and to model precession the position of

moves in FC

by two values (p

and p

). All coor-

dinate points are then transformed into FC.

The ﬁnal extremity of the ﬁberscope’s tubular mo-

del (estimated camera location) is given by:

= R

· [p

, p

, depth]

+ L

(1)

= −T

· R

(2)

where L

is the initial pose given by the initial cali-

bration (i.e, extrinsics parameters of ﬁberscopic ca-

meras).

Therefore the ﬁberscopic camera pose will be de-

ﬁned by the vector [p

, p

, depth]

regarding FC.

Figure 3: Simulated ﬁberscope movements: insertion and

precession.

3.2.1 Image Projection

To simulate the observation of the ﬁberscope in the

endoscopic image the 3D cylindrical model is pro-

jected in 2D by using the projection matrix of the en-

doscopic camera deﬁned as follow

= P · MP = K





1 0 0 0

0 1 0 0

0 0 1 0





| T

] (3)

where

= Endoscopic 2D projection

P = Projection matrix

M = 3D point coordinates

= Endoscope calibration matrix

Figure 4 depicts the simulation interface where

the insertion depth, angles of precession of the ﬁ-

berscope and rotation of the camera can be modiﬁed

interactively. The lower part presents: c) the cylin-

der model and virtual pattern projection superposed

to the original endoscopic image, d) the original ﬁ-

berscopic image and e) the binary mask provided by

the projection of the world points in the 2D endosco-

pic plane.

3.3 Pose Estimation by Binary Mask

Similarity Maximization

The relative pose estimation between the two hetero-

geneous cameras (endoscopic/ﬁberscopic) is expres-

sed as a maximization problem by ﬁtting the pro-

jection of the 3D cylinder into the ﬁberscope’s seg-

mented tip in the endoscopic image. To do this we

maximize a similarity measure between two binary

masks A and B.

3D Cylinder Pose Estimation by Maximization of Binary Masks Similarity: A simulation Study for Multispectral Endoscopy Image

Registration

859

Figure 4: MATLAB simulator 3D view.

X = argmin[1 −S(A, B)] (4)

where X is the vector [p

,depth]

representing the

pose of the cylinder’s extreme point.

3.4 Similarity Index

To compare the two binary masks we tested three

commonly used indexes (Csurka et al., 2013). All

similarity index S comply the condition 0 ≤ S ≤ 1

3.4.1 Jaccard

The Jaccard index J, also known as intersection over

union is deﬁned as the size of the intersection divided

by the size of the union of the sample sets A and B. :

J(A, B) =

|A ∩ B|

|A ∪ B|

|A ∩ B|

|A| + |B| −|A ∩ B|

. (5)

3.4.2 Dice

Dice or Srensen’s measure it is deﬁned as twice the

number of elements common to both sets divided by

the sum of the number of elements in each set.

DSC(A, B) =

2|A ∩ B|

|A| + |B|

(6)

where |A| and |B| are the cardinalities of the two

sets (i.e. the number of elements in each set).

3.4.3 BF-score

The BF score measures how close the predicted boun-

dary of an object matches the ground truth boundary.

It is deﬁned as the harmonic mean of the precision

and recall values. Precision is the fraction of detecti-

ons that are true positives rather than false positives.

Recall is the fraction of true positives that are detected

rather than missed.

BF(A, B) = 2 ·

precision · recall

precision + recall

(7)

4 SIMULATION RESULTS AND

DISCUSSION

4.1 Objective Function

The behavior of the similarity indexes are observed

varying the three parameters of the ﬁberscope pose

(i.e., [p

,depth]

) as shown in Figure 5.

Althought the BF-score behaves as a strongly con-

vex function while evaluating the two precession pa-

rameters, it lacks of singular minimum values when

analyzing the insertion parameter. Jaccard and Dice

behave similarly in the three cases, describing a sin-

gular min value in the exact ﬁt case. However, Jac-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

860

Figure 5: Behavior of objective functions.

card’s function presents itself as a better option due to

the higher value of its local tangents which may lead

to a faster convergence.

4.2 Convergence Validation

Twelve scenarios including highly ill-posed initiali-

zation were simulated. An example of four represen-

tative cases is presented in Figure 6. The ﬁrst co-

lumn depicts the superposition of the initial and the

target segmentation. In the same manner, the second

column depicts the superposition of the ﬁnal and the

target segmentation. In both cases yellow and green

represent the intersecting and individual pixels to the

two segmentations. The third column describes the

evolution of the three parameters estimates trough ite-

rations, the dotted lines represent the expected values

and the crosses the estimated values on each iteration.

Finally, the fourth column compare the corners loca-

tion of the virtual grids for estimated pose vs ground

truth pose.

Detailed results including the error statistics for

the projected points and a comparison between the

initial and ﬁnal similarity measure for each case is

presented in Table 1. In addition a summary of sta-

tistics is presented in Table 1. The median error for

the sample set was 0.38 ± 0.5 pixels. We expected

the initial Jaccard similarity measure to be a determi-

nant for convergence. However, even when its value

is low (e.g., cases 5,6,7,9) the minimization can be

performed effectively. In contrast, we observed fai-

led convergences were more associated to inaccurate

ﬁnal estimates (i.e.,Table 1). This may be related to

the fact that large variations in the optimized parame-

ters lead to small variation in the projected images due

to non-linearity included in the perspetive projection

4.3 Tracking Scenario

Figure 7 depicts the evolution of the estimated para-

meters trough a simulation of combined movements

of the tip during an exploration. From initialization,

the pose of the ﬁberscope is estimated frame by frame

by using the ﬁnal estimate of the previous frame as

initial values for the current one. The trajectory was

determined by a combination of the parameters of in-

sertion and precession in an aleatory manner. The

overall mean absolute error in this measurements was

of 0.05 ± 0.07 mm. The number of iterations needed

for the initial ﬁt was 75 and the number of iterations

needed for the following cases was 35 ± 5. Indeed,

the initial ﬁt requires around the double of iterations

than the other points of the curve

We observe that in all cases the convergence was

achieved satisfactorily with high similarity measure

values and all differential errors being around zero.

This was expected due to the relative similarity bet-

ween successive frame. In addition, the convergence

3D Cylinder Pose Estimation by Maximization of Binary Masks Similarity: A simulation Study for Multispectral Endoscopy Image

Registration

861

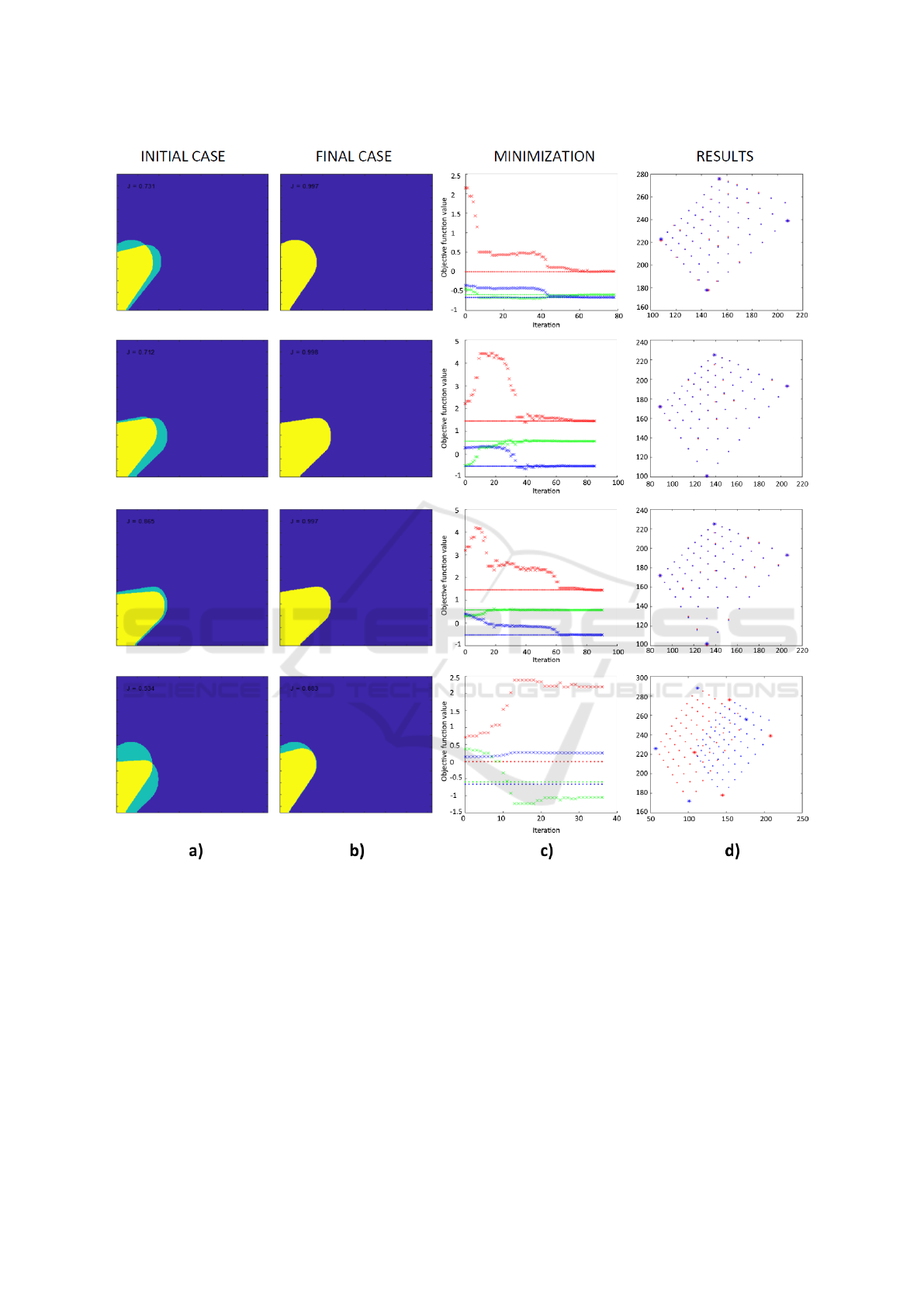
Figure 6: a) 2D projection of simulated sets before maximization, b) 2D projection of simulated sets after maximization, c)

Detail of the three objective function parameters over iteration time, d) reprojection results.

speed is also slower. So the minimization problem

could be critical for initialization in the ﬁrst frame

only. However the approach presented in (Zenteno

et al., 2018) can provide a precise ﬁrst initialization.

5 CONCLUSIONS

This paper has presented a method for simulating

and compensate two sources of movement encounte-

red during multi-spectral endoscopic acquisition for

multimodal registration (i.e, the insertion and preces-

sion motion of a ﬁberscope inserted in the instrument

channel of an endoscope). The technique relies on ap-

plying an homographic transformation between mo-

dalities by using a virtual reference pattern projected

in both frames as control points. The results showed

that the method can track the camera insertion and

precession motion. Although the pipeline is still cur-

rently executed off-line, this paper demonstrates the

potential of image-based tracking of a ﬁberscope.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

862

Table 1: Similarity measure comparison and projection error statistics.

Target pose (mm) Initial pose (mm) Estimated pose (mm) Jaccard E

Reprojection

No depth p

depth p

Initial Final Mean STD

1 3.17 0.00 0.00 1.62 0.00 0.00 3.177 -0.00 0.00 0.93 0.99 0.25 0.50

2 3.17 0.00 0.00 4.20 0.00 0.00 3.18 0.00 0.01 0.97 0.99 0.00 0.00

3 3.17 0.00 0.00 3.55 -0.21 -0.31 3.16 0.00 -0.00 0.87 0.99 0.00 0.00

4 3.17 0.00 0.00 3.55 0.64 0.29 4.29 -0.08 0.37 0.77 0.96 14.53 7.55

5 0.00 -0.59 -0.66 2.15 -0.44 -0.35 0.00 -0.59 -0.66 0.71 0.99 0.00 0.00

6 1.45 0.57 -0.52 2.21 -0.50 0.28 1.45 0.57 -0.52 0.86 0.99 0.25 0.50

7 1.45 0.57 -0.52 3.19 0.30 0.39 1.44 0.56 -0.52 0.53 0.88 43.87 6.10

8 0.00 -0.59 -0.66 0.71 0.37 0.13 2.19 -1.05 0.25 0.73 0.99 0.50 0.58

9 1.85 -0.59 0.66 2.21 0.36 -0.31 1.86 -0.58 0.66 0.68 0.99 0.25 0.50

10 1.85 -0.59 0.66 2.99 0.36 0.77 4.64 -0.99 1.74 0.66 0.92 39.52 17.68

11 2.34 0.00 0.00 2.41 -0.21 -0.16 2.22 0.03 -0.04 0.89 0.99 1.97 0.39

12 1.37 0.00 0.00 6.48 0.00 0.00 1.38 0.00 0.00 0.85 0.99 0.75 0.50

Figure 7: Comparison of estimated values versus ground truth along a 10 step sequential movement mimicking scenario.

3D Cylinder Pose Estimation by Maximization of Binary Masks Similarity: A simulation Study for Multispectral Endoscopy Image

Registration

863

ACKNOWLEDGEMENTS

This work was supported by the EMMIE (Endosco-

pie MultiModale pour les l

esions Inﬂammatoires de

l’Estomac) project funded by the ANR-15-CE17-

0015 grant.

REFERENCES

Cabras, P., Nageotte, F., Zanne, P., and Doignon, C. (2017).

An adaptive and fully automatic method for estima-

ting the 3d position of bendable instruments using

endoscopic images. The International Journal of

Medical Robotics and Computer Assisted Surgery,

13(4):e1812.

Csurka, G., Larlus, D., Perronnin, F., and Meylan, F. (2013).

What is a good evaluation measure for semantic seg-

mentation?. In BMVC, volume 27, page 2013. Cite-

seer.

Doignon, C., Nageotte, F., Maurin, B., and Krupa, A.

(2008). Pose estimation and feature tracking for robot

assisted surgery with medical imaging. In Unifying

perspectives in computational and robot vision, pages

79–101. Springer.

Kim, M., Lee, J., and Huh, J. (2003). Real time visual

servoing for laparoscopic surgery. In lnternational

Symposium on Artiﬁcial Life and Robotics, pages 0–

0. ISALR.

Reilink, R., Stramigioli, S., and Misra, S. (2013). 3d po-

sition estimation of ﬂexible instruments: marker-less

and marker-based methods. International journal of

computer assisted radiology and surgery, 8(3):407–

417.

Song, L. M. W. K., Adler, D. G., Conway, J. D., Diehl,

D. L., Farraye, F. A., Kantsevoy, S. V., Kwon, R., Ma-

mula, P., Rodriguez, B., Shah, R. J., et al. (2008). Nar-

row band imaging and multiband imaging. Gastroin-

testinal endoscopy, 67(4):581–589.

Tonet, O., Thoranaghatte, R. U., Megali, G., and Dario, P.

(2007). Tracking endoscopic instruments without a

localizer: a shape-analysis-based approach. Computer

Aided Surgery, 12(1):35–42.

Zenteno, O., Krebs, A., Treuillet, S., Lucas, Y., Benezeth,

Y., and Marzani, F. (2018). Dual-channel geometric

registration of a multispectral-augmented endoscopic

prototype. In VISIGRAPP (4: VISAPP), pages 75–82.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

864