
An Artificial Neural Network for Hand Movement Classification using
Surface Electromyography
Paulo L. Viana
1
, Victoria S. Fujii
1
, Larissa M. Lima
1
, Gabriel L. Ouriques
1
, Gustavo C. Oliveira
2
,
Renato Varoto
3
and Alberto Cliquet Jr.
1,2,3
1
Department of Electrical and Computer Engineering, Trabalhador S
˜
ao-Carlense Avenue, 400, S
˜
ao Carlos, Brazil
2
University of S
˜
ao Paulo Interunits Graduate Program in Bioengineering, University of S
˜
ao Paulo,
Trabalhador S
˜
ao-Carlense Avenue, 400, S
˜
ao Carlos, Brazil
3
Department of Orthopedics and Traumatology, University of Campinas, Cidade Universit
´
aria Zeferino Vaz,
Campinas, Brazil
Keywords:
Neural Networks, Hand Movement, Electromyography, Rehabilitation, Machine Learning.
Abstract:
In this paper we present the development of an artificial neural network that uses surface EMG data from two
forearm muscles to classify hand movements and gestures. We trained our network to classify three different
sets of movements, using EMG data from six healthy subjects. We were able to achieve hit rates of above 99%
in the training sets and hit rates of above 85% in all three test sets, with a maximum of 88.8% for the second
movement set. Advantages of the proposed method include small number of electrodes, reduced complexity,
computational cost and response time.
1 INTRODUCTION
For healthy individuals, the execution of daily tasks
(e.g feeding, bathing and dressing, for example) heav-
ily relies on the adequate motor control of the upper
limbs, which is performed by the central and periph-
eral nervous system. Unfortunately, there are many
pathological conditions that can impair one’s ability
to control his or her own arms and hands, such as
spinal cord lesions, stroke and cerebral palsy. Experi-
encing one of these conditions can lead to a reduced
sense of autonomy and negatively impact one’s qual-
ity of life (Guyton, 2010).
Many strategies have been employed over the
years to help individuals cope with reduced upper
limb motor control. One of these approaches is the
use of myoelectric controlled prosthesis, which began
to have a significant role in the rehabilitation of up-
per limb deficient patients in the 1970s. This type of
prosthesis makes use of the myoelectric signal, also
known as EMG, which is a group of electrical signals
that is generated by the body and precede mechanical
muscle activity. Its amplitude is small (1.5 mV RMS)
and random, and its frequency can range from 6 to
500 Hz, with most of its energy comprised between
20 to 150 Hz. These signals can be captured directly
from the skin, using surface electrodes, or from the
muscles, using needle electrodes (Englehart and Hud-
gins, 2003).
Myoelectric controlled prosthesis offer many ad-
vantages over other types. Firstly, the signal can be
acquired in a non-invasive manner, reducing risks for
the user. Secondly, small effort and muscle activity
is necessary to generate the control signals. Thir-
dle, its controller is relatively easy to adapt. Lastly,
there is no need for straps and harnesses that are re-
quired when using mechanical switch and body pow-
ered control (Englehart and Hudgins, 2003).
Although many myoelectric control systems are
currently available and have gained some success,
their application is relatively limited in the control
of multiple functions and devices. This is unfortu-
nate, since the capacity to offer multiple functions and
accurate movement selection is a critical feature that
could highly increase the functional benefits of pros-
thetic apparatuses (Englehart and Hudgins, 2003).
Exploring this context, many researchers have
developed strategies for a pattern-recognition-based
myoelectric control, which could be used to link de-
grees of freedom of the prosthetic apparatus to move-
ment classes. For small groups of movements, these
approaches have been successful. However, error
rates tend to increase with the number of movements
analyzed. For example, Glette et al. (2008) applied
a variety of machine learning techniques, such as k-
nearest neighbors, decision trees and support vector
machines, to identify 8 different movements using
surface EMG signals. Error rates of their classifiers
Viana, P., Fujii, V., Lima, L., Ouriques, G., Oliveira, G., Varoto, R. and Cliquet Jr., A.
An Artificial Neural Network for Hand Movement Classification using Surface Electromyography.
DOI: 10.5220/0007404201850192
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 185-192
ISBN: 978-989-758-353-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
185

ranged from 2.6% to 15.9%. Using support vector
machines, Boschmann et al. (2009) achieved a hit rate
of 98.6% in the classification of 6 movements. Tang et
al. (2012) used linear discriminant analysis to classify
11 different poses, with a hit rate of 94.8%. Atzori et
al. (2012) used support vector machines to classify 52
movements using EMG signals, with an error rate of
20.3%. Gijsberts et al. (2014) used kernel regularized
least squares to classify 40 poses, reaching hit rates
between 49.35% and 77.48%.
The aforementioned works have usually acquired
their EMG data using between 4 and 10 pairs of elec-
trodes. In general, as the number of electrodes in-
crease so will the number of data. This will then in-
crease the computing power required to process the
data and the preparation time before the system can
be used. In this paper, we present the development of
a relatively simple artificial neural network that uses
surface EMG data from less electrodes to classify a
number of different movements.
2 METHODOLOGY
2.1 Database Description
For the development of the neural network presented
in this paper we used the Ninapro Project database.
Ninapro stands for non-invasive adaptative prosthet-
ics and is an ongoing project that provides public
EMG datasets in order to help the development of ad-
vanced hand myoelectric prosthetics (Atzori, 2014).
The Ninapro database provides 7 different
datasets. Dataset 4, used in this work, includes fore-
arm EMG data from 10 healthy subjects, recorded us-
ing Cometa Wave Plus wireless sEMG system and its
miniWave sensors. Each sensor has a 10 Hz high-
pass filter and a 1 kHz low-pass filter, with a gain of
1000 and sample rate of 2kHz with 16 bits resolution.
Every sensor is connected to 2 Dormo SX-30 ECG
electrodes with 30mm diameter, covering the forearm
circumference without overlap and assuming the po-
sitions shown in the Figure 1 (Pizzolato et al., 2017;
Atzori, 2014).
The data is divided into 3 classes of movements:
basic wrist movements and isometric hand positions;
grasp and functional movements; and basic fingers
movements. Myoelectric signal is acquired using
12 wireless electrodes: 8 around the forearm in an
equally spaced disposition in correspondence to the
radio humeral joint, 2 electrodes are placed on the
main activity spots of the flexor digitorum and of the
extensor digitorum, 1 on the biceps and 1 on the tri-
ceps (Pizzolato et al., 2017; Atzori, 2014).
Figure 1: Electrode positions, adapted from (Pizzolato
et al., 2017).
Subjects performed 6 repetitions of 52 different
movements using their dominant hand. Each repeti-
tion consisted of 5 seconds of movement and 3 sec-
onds of resting (Pizzolato et al., 2017; Atzori, 2014).
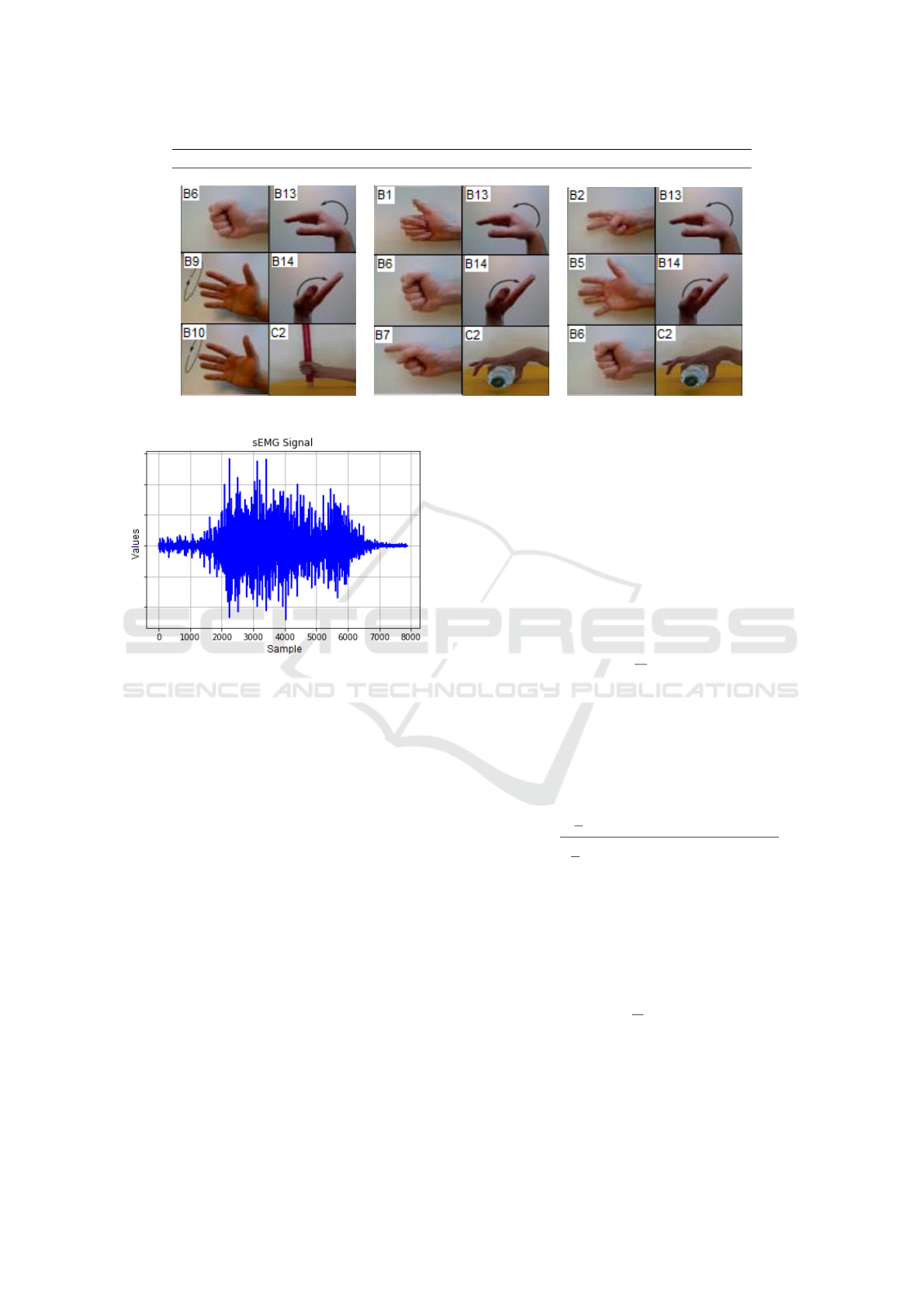
Of the 52 movements, 11 were selected and grouped
into 3 sets, which are described in Table 1 and illus-
trated in Figure 2.
Table 1: Description of the movements included in each set.
Set 1 Set 2
Closed hand (B6) Thumb up (B1)
Wrist supination (B9) Closed hand (B6)
Wrist pronation (B10) Pointing index (B7)
Wrist flexion (B13) Wrist flexion (B13)
Wrist extension (B14) Wrist extension (B14)
Grasp (small diameter) (C2) Ring grasp (C6)
Set 3
Extension of index and middle, flexion of others (B2)
Abduction of all fingers (B5)
Closed hand (B6)
Wrist flexion (B13)
Wrist extension (B14)
Ring grasp (C6)
For our classification network, we used as inputs
the EMG data from the main activity spots of the
flexor and extensor digitorum superficialis muscles
of 6 healthy subjects. EMG signals were segmented
based on the repetition variable, which indicates when
the subject is actually performing the gesture and also
give us the repetition number. Since data from the Ni-
napro Project database is provided in .mat files, we
converted each repetition signal from each movement
to a .csv file using Matlab, resulting in 3744 .csv files.
Figure 3 shows an example of one filtered surface
EMG signal that composes the dataset.
Using the data from the dataset 4 of the Ninapro
Database, we created 4 sets: 1 training set and 1 test
set for each of the 2 selected muscles. Since each sub-
ject from the NinaPro database performed 6 repeti-
tions of each hand gesture, we separated 4 repetitions
as the training set (66.7%), and 2 as the testing set
(33.3%). As we have 6 subjects, there are 24 signals
for training and 12 for testing, for each movement.
After performing the aforementioned preprocess-
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
186
Set 1 Set 2 Set 3
Figure 2: Hand movements performed by subjects.
Figure 3: Example of an surface EMG signal.
ing in Matlab, only Python scripts were used to train
and evaluate the neural network.
2.2 Parameter Extraction and Feature
Scaling
For the EMG signals that composed the dataset, 7 pa-
rameters were calculated to serve as inputs for our
neural network. In the time and frequency domain,
they are the arithmetic mean, the kurtosis, the root
mean square (RMS), the skewness, the standard de-
viation, the variance and the signal energy. In the
frequency domain, there is also the spectral centroid.
These parameters were chosen based on the literature
(B
´
urigo, 2014; Tang et al., 2012; Nilson, 2014). Af-
ter parameter extraction, the feature scaling method
was used. This is done to even the data to a mean
value of 0 and a standard deviation of 1. This mini-
mizes the potential danger of large numbers (like vari-
ance or the spectral centroid) dominating over small
numbers and to avoid computational difficulties dur-
ing calculations (B
´
urigo, 2014). In the remainder of
this subsection, we present the definition of each pa-
rameter and the equations used to calculate them. In
the equations shown, f
s
is the sampling rate, RMS(s)
is the root mean square value of a vector s, N is the
size of the respective array, emg
mean
is the mean value
of the respective array (emg array), and emg(n) is the
n
th
element of array emg.
2.2.1 Energy
The energy is calculated by multiplying the squared
RMS value by the time it exists, as shows Equation 1.
Energy =
N
f
s
× RMS(s)
2
(1)
2.2.2 Kurtosis
The kurtosis is a measure that determines the tailed-
ness of a probability distribution of a random variable.
It is defined as in Equation 2 (B
´
urigo, 2014).
Kurt[X] =
1
N
×
∑
N
n=1
(emg(n) −emg
mean
)
4
1
N
×
∑
N
n=1
(emg(n) −emg
mean
)
2
2
(2)
2.2.3 Mean Value
The mean value is the sum of all elements of an ar-
ray divided by the number of elements, defined as in
Equation 3 (B
´
urigo, 2014).
emg
mean
=
1
N
×
N
∑
n=1
emg(n) (3)
2.2.4 Root Mean Square
The Root Mean Square is also known as the quadratic
mean, simply being the square root of the mean
An Artificial Neural Network for Hand Movement Classification using Surface Electromyography
187

square of a set of data values, calculated as in Equa-
tion 4 (B
´
urigo, 2014).
RMS =
s
1
N
×
N
∑
n=1
emg(n)
2
(4)
2.2.5 Skewness
Skewness measures the asymmetry of the probability
function of a random variable, which in our case is
our sEMG signal. It is calculated as in Equation 5
(B
´
urigo, 2014).
Skewness =
1
N
×
∑
N
n=1
(emg(n) −emg
mean
)
3
q
1
N
×
∑
N
n=1
(emg(n) −emg
mean
)
2
3
(5)
2.2.6 Spectral Centroid
The spectral centroid is defined as the center of mass
of the spectrum. Given a array of magnitudes in the
frequency domain, the centroid is calculated as in
Equation 6 (B
´
urigo, 2014).
Centroid =
∑
N
n=1
n × emg(n)
∑
N
n=1
emg(n)
(6)
2.2.7 Standard Deviation
The standard deviation is the measure that quantifies
the variation or dispersion of a set of data values. It is
calculated as in Equation 7 (B
´
urigo, 2014).
σ =
s
1
N − 1
N
∑
n=1
(emg(n) −emg
mean
)
2
(7)
2.2.8 Variance
The variance, as the formula suggests, is also a mea-
sure of the dispersion of a dataset similar to the stan-
dard deviation. It is calculated as in Equation 8
(B
´
urigo, 2014).
σ
2
=
1
N − 1
N
∑
n=1
(emg(n) −emg
mean
)
2
(8)
2.3 Neural Network
The brain is a very complex and nonlinear infor-
mation processing system, capable of organizing its
small pieces of structure called neurons to perform
much better than any existing digital computer. This
is possible because the brain is able to connect the
neurons into a huge net called neural network us-
ing electrical signals that travel through a small gap
between the neurons, the synapse. Changing the
synapses will also change the influence of one neuron
on another and therefore change the brain’s response
to a stimulus (Sousa, 2011) (Haykin, 1999).
In an attempt to biomimic the brain and its struc-
ture the Artificial Neural Network (ANN) was cre-
ated. This network is an electronic circuit or a soft-
ware that uses massive connection of neurons to per-
form useful computations. The system receives an
input and through its connections and activations an
output is generated. ANNs have the ability to learn
through methods called learning algorithms. It can
also generalize the training, i.e. it can generate a rea-
sonable output with an input that has not been used in
its training (Haykin, 1999).
Figure 4 shows how a ANN is constructed. The
circles represent the neurons, the arrows represent the
synapses, the circle’s superscripts represent its layer
and its subscript represents the neuron number. The
layer 1 represents the input layer, and layer L rep-
resents the output layer. Neurons in the first row
(with subscript 0) are the bias neurons, which al-
ways produce the same value and don’t have incom-
ing synapses; the layers that are not input or output
layers are called the hidden layers. N(α) denotes the
number of neurons in the α
th
layer. The ANN im-
plemented in this work has 1 hidden layer with 12
neurons, with a bias neuron at the input layer and in
the hidden layer. This topology was chosen by tests
measuring the accuracy of 9 different topologies (with
1 and 2 hidden layers) over one of the datasets. It
receives 26 inputs (13 parameters from 2 electrodes)
and outputs 6 numbers, which represent the probabil-
ity of the input being from one of the six movements
in each movement set.
The values in the input layer are forwarded to the
next layer through the synapses. In the first layer
(layer 1), the input vector is [a
1
0
,a
1
1
,. . . ,a
1
N(1)
]. Each el-
ement of this vector is multiplied by a synaptic weight
ω
j
i
, and they are all added to generate the next layers’
neurons’ inputs. The activation function is applied to
this input, creating the neuron output. Each neuron
output value is calculated by Equation 10, with σ as
the sigmoid function (shown in Equation 9), which is
used as the activation function of the neurons. This is
called the feed-forward algorithm.
σ(x) =
1
1 + e
x
σ
0
(x) = σ(x)(1 − σ(x))
(9)
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
188

Figure 4: Artificial Neural Network diagram.
a
j
i
=σ
N( j)
∑
k=0
a
j−1
k
∗W
j−1
i
[k]
!
i ∈ [0,N( j)]
j ∈ [2, L]
(10)
The training algorithm used in this work is the
backpropagation algorithm. It is considered the algo-
rithm that brought light to neural networks, because
it is a computationally efficient method to train them
(Haykin, 1999). It calculates the partial derivatives
of the error signal with respect to the weights in the
synapses. This value is then summed to the weights
to minimize the error function E(w):
E(w) =
1
2
N
∑
n=1
k y(x
n
, w) −t
n
k
2
(11)
When we minimize this error, the ANN ap-
proaches its desired behavior. The backpropagation
algorithm work as follows. Given an input x
n
and
a target output t
n
, the real output y
n
of the ANN is
taken using the feed-forward algorithm, as shown in
Equation 10. The derivative of the error in the output
layer is calculated by
∂E
∂a
L
i
= t
i
−y
i
. From layer L−1 to
layer 1, the partial derivatives are calculated consider-
ing the values of the next layers’ errors and synaptic
weights that goes from the current layer to the next.
The mathematical steps and details are described by
Haykin, 1999.
The training set of the neural network has an in-
put vector x
n
associated to their corresponding target
vector t
n
, where n = 1, ...,N and N is the number of
samples in the input. The training stage has the objec-
tive of minimizing the error function in Equation 11
(Bishop, 2006). The hit rate percentage is calculated
by the number of right guesses divided by the total
number of signals to guess.
Having K > 2 separable binary classifications, it
is possible to apply a neural network with K outputs,
also considering that each output has sigmoid as acti-
vation function and has a binary class label t
k
∈ [0, 1],
where k = 1, ..., K, associated to it. Due to the input
vector, it can be considered the class labels as inde-
pendent and, therefore, the conditional distribution of
the targets is given by the Equation 12 (Bishop, 2006).
p(t|x, w) =
K
∏
k=1
y
k
(x, w)
t
k
[1 − y
k
(x, w)]
1−t
k
(12)
Then, the error function with more than one in-
put, originated by applying the negative logarithm in
the likelihood function, results in Equation 13, where
y
k
(x
n
, w) indicates the value in the k-unity in the n-
example, and t
nk
is the expected value in the k-unity
in the n-example (Bishop, 2006).
E(w) = −
N
∑
n=1
K
∑
k=1
t
nk
∗ ln(y
k
(x
n
, w))+
(1 −t
nk
) ∗ ln(1 −y
k
(x
n
, w))
(13)
In neural networks literature, there is the conven-
tion of considering the minimization of the error func-
tion instead of the maximization of the likelihood, but
both methods are equivalent (Bishop, 2006).
An Artificial Neural Network for Hand Movement Classification using Surface Electromyography
189
An Artificial Neural Network class was created in
Python programming language, using few and sim-
ple libraries. This is good for portability, in such a
way that a embedded system, for instance, would not
need to have installed a number of big libraries just for
using one feature of it, reducing hardware complex-
ity. The number of epochs during the training phase
was chosen empirically, in such a way that the ANN
reaches about 99% hit rate at the training set (after
this, the ANN will start overfitting). All codes related
to the artificial neural network creation, training and
evaluation were coded in Python language. The mod-
ules used are listed below:
• numpy
• numpy.fft
• csv
• scipy.signal
• scipy.stats
• cProfile
• matplotlib.pyplot
• random
• time
The codes were written in Python 2.7, and Spy-
der IDE version 3.2.6 was used to write, test and run
them. Spyder is ”a powerful scientific environment
written in Python, for Python, and designed by and for
scientists, engineers and data analysts” (as described
in Spyder Website). Spyder was used within Ana-
conda, a platform for Python and R data science and
machine learning, according to the Anaconda web-
site. All of this was processed on a Windows 10,
64bits machine, i5-4210U 2.4GHz CPU.
3 RESULTS
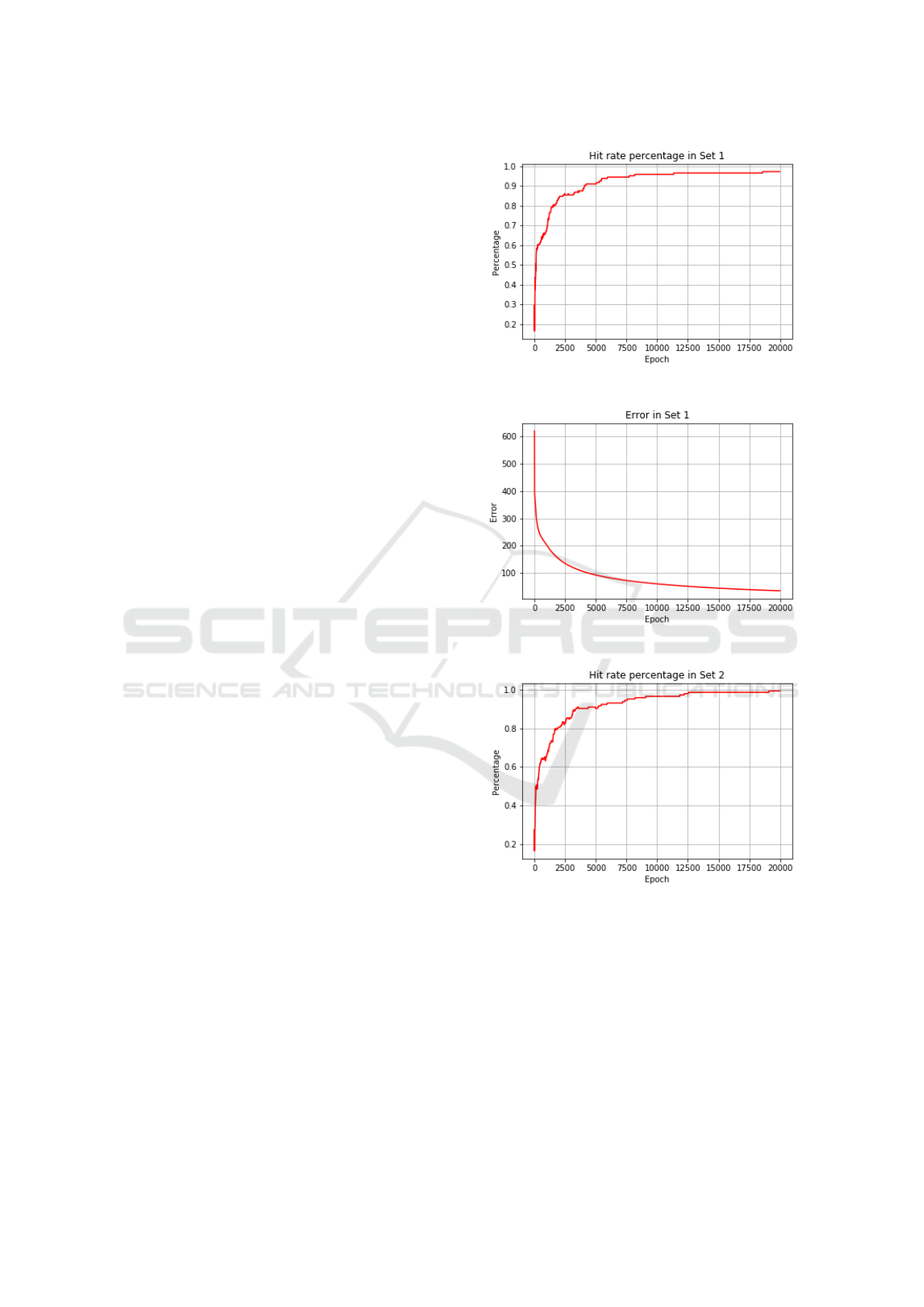
Figure 5 shows the hit rate by training epoch, while
Figure 6 shows the error by training epoch for move-
ment set 1. As we can see, the hit rate reaches 100%,
while the error decreases below 30. This number is
less important than the actual hit rate, but has interest-
ing implications, as we will see in Section 4. For this
dataset, the testing set hit rate achieved was 86.11%.
Figures 7 and 8 show the hit rate and error by
epoch for the training phase for movement set 2. The
hit rate in the testing set was 88.89%.
Figures 9 and 10 show the hit rate and error by
epoch for the training phase for movement set 3. The
hit rate achieved with this set was 87.5%.
The hit rate is a natural measure of the classifi-
cation method, but it does not account for mistakes
Figure 5: Hit rate achieved using set 1.
Figure 6: Error during training in set 1.
Figure 7: Hit rate achieved using set 2.
made by samples of a class over another class (Nil-
son, 2014). To verify which movements the ANN
classified correctly and which ones it did not, we con-
structed a confusion matrix for the movement set 1.
In this matrix, the columns show the actual move-
ment and the row shows which movement the ANN
guessed. As we can see in table 2, the ANN did
not have much problem classifying movements B6,
B13, B14 and C2, and had a lower hit rate classi-
fying movements B9 and B10. As we can see, the
ANN mistook movements B10 for B9 and B9 for B10
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
190

Figure 8: Error during training in set 2.
Figure 9: Hit rate achieved using set 3.
Figure 10: Error during training in set 3.
more often (wrist supination and pronation), which is
understandable because they are very similar move-
ments. Wrist supination had the lowest hit rate.
The classification time of the ANN was also mea-
sured. For this, the feed-forward algorithm was ap-
plied to the training set (144 repetitions) 10000 times.
The time measured was 173.596 seconds, what makes
an average of
16.55s
144∗10000
= 120.6µs spent on each repe-
tition. The time of reading the data from the .csv files,
pre-processing them, separating the movements of the
training and testing sets, and extracting the parame-
Table 2: Confusion Matrix for movement set 1.
Actual movement
B6 B9 B10 B13 B14 C2
Guessed mov.
B6 10 0 0 1 0 0
B9 0 7 2 0 0 0
B10 0 2 8 0 1 0
B13 0 1 1 10 0 0
B14 0 1 0 0 11 0
C2 2 1 1 1 0 12
ters was also measured as 200.19 seconds. The train-
ing time (during 20000 epochs) was 1064.97 seconds,
making an average of 53.2ms per epoch or 18.78
epochs per second. It’s important to note that our code
reads all the 52 movements from the dataset and only
saves in variables the movements that will be used to
train the ANN.
4 DISCUSSION
The hit rate for movement set 3 (the same as (Tang
et al., 2012)) was 87.5%. This means an 9.6% hit
rate increase compared to (B
´
urigo, 2014), and a de-
crease of 7.3% compared to (Tang et al., 2012), us-
ing a smaller number of electrodes. This reduction in
the number of electrodes brings many advantages to
a potential application in a myoelectric controlled de-
vice. It translates into less discomfort for the user, less
computational processing needed, less battery usage,
lower costs and weight.
We can notice that the error (from Equation 13)
achieved in sets 1, 2 and 3 was below 30. We can il-
lustrate the significance of this with an example. With
an error of 30, with 144 repetitions (6 subjects with 6
movements and 4 repetitions for each movement, in
the training set), the mean contribution of each move-
ment is
−30
144
= −0.208, and of each guess is
−0.208
6
=
−0.0347. Taking the exponential of this number (cal-
culating equation 13 backwards) and knowing that the
ANN output can be interpreted as the probability of
the guess being the right guess, we can see that the av-
erage “confidence” of the ANN is e
−0.0347
= 96.6%.
For instance, if this average was 60%, this error would
be −308.2.
We proposed using a feed-forward Neural Net-
work to solve the problem boarded in this work. How-
ever, there are many types of Neural Networks used
for Supervised Learning in the literature, such as
Convolutional Neural Networks and Recurrent Neu-
ral Networks. The former is used for the recognition
of 2D shapes (Haykin, 1999), which is not the case,
while the second could indeed be used for this kind of
task. However RNNs need many layers and more data
An Artificial Neural Network for Hand Movement Classification using Surface Electromyography
191

preprocessing, what would increase the training time.
Using time windows of 200 samples and assuming
just 1 second of gesture duration, with a sampling rate
of 2kHz, each gesture repetition would generate 1800
sets of 200 features per electrode (1800 sequences of
200 sampled signals), instead of our 1 set of 13 fea-
tures per electrode. This approach can be investigated
in a future work.
During coding and testing, the Python module
cProfile was used to identify which functions were
spending more time in the processor unit, enabling us
to fine tune some functions and methods to increase
overall performance. Additionally, using the sigmoid
as activation function had the benefit of reducing the
time spent on training the network, because its deriva-
tive can be written as a function of the function itself,
whose value was already calculated and stored.
Our neural network classifier proved to be very
fast, classifying sample signals in less than 1 ms.
It also does not need a lot of computational mem-
ory, because it only needs to store the weights in the
synapses after the training is complete. Reduced run-
time and complexity are valuable features, as they
help ensure the system has a reasonable response
time. Ideally, the delay introduced by a control sys-
tem should not be perceived, being kept below a
threshold of roughly 300 ms. However, there is a
trade-off between run-time, complexity and accuracy,
with the latter being critical for a correct operation.
This compromise should be considered in the design
of any system controlled by myoelectric signals (En-
glehart and Hudgins, 2003).
5 CONCLUSION
In this paper, we presented the development of a rela-
tively simple ANN that can classify hand movements
and gestures using surface EMG data from a reduced
number of electrodes. We achieved a hit rate of above
80% in all 3 test sets, with a maximum of 88.89% for
movement set 2, with small system complexity and
run time.
Future works may investigate how additions to
this ANN, such a regularization method, can be im-
plemented to improve its performance. The effi-
cacy of the proposed ANN’s performance on a big-
ger dataset with more subjects and a greater num-
ber of movements may also be examined in order
to test the ANN’s generalization power. Another in-
teresting possibility is to compare the performance
of the proposed ANN with different machine learn-
ing algorithms of similar complexity, number of in-
puts and computational time using the same dataset.
This could potentially generate a group of simple, fast
classifiers that combined, may achieve higher perfor-
mance levels.
REFERENCES
Atzori, M. (2014). Ninapro website. http://ninapro.hevs.ch/.
[Online]; accessed on October 21, 2018.
Bishop, C. (2006). Pattern Recognition and Machine
Learning, volume 29.
B
´
urigo, A. (2014). Classificac
˜
ao de Movimentos de M
˜
ao
Utilizando Eletromiografia de Superf
´
ıcie, Regress
˜
ao
Log
´
ıstica, Redes Neurais, M
´
aquina de Vetores de Su-
porte e Base de Dados NinaPro.
Englehart, K. and Hudgins, B. (2003). A Robust, Real-Time
Control Scheme for Multifunction Myoelectric Con-
trol. IEEE Transactions on Biomedical Engineering,
50(7):848–854.
Guyton, A; Hall, J. (2010). Textbook of Medical Physiology.
Haykin, S. (1999). Neural Networks: A Comprehensive
Foundation. Prentice Hall.
Nilson, C. D. E. P. (2014). Aquisic¸
˜
ao, Processamento de
Sinais Mioel
´
etricos e M
´
aquinas de Vetores de Su-
porte para Caracterizac¸
˜
ao de Movimentos do Seg-
mento M
˜
ao-Brac¸o.
Pizzolato, S., Tagliapietra, L., Cognolato, M., Reggiani, M.,
Mller, H., and Atzori, M. (2017). Comparison of six
electromyography acquisition setups on hand move-
ment classification tasks. PLOS ONE, 12(10):1–17.
Sousa, D. (2011). How the Brain Learns. SAGE Publica-
tions.
Tang, X., Liu, Y., Lv, C., and Sun, D. (2012). Hand mo-
tion classification using a multi-channel surface elec-
tromyography sensor. Sensors, 12(2):1130–1147.
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
192
