
Fine-grained 3D Face Reconstruction from a Single Image using
Illumination Priors
Weibin Qiu, Yao Yu, Yu Zhou and Sidan Du
∗
School of Electronic Science and Engineering, Nanjing University, Nanjing, China
Keywords:
3D Face Reconstruction, Morphable Model, Illumination Priors, Shape-from-Shading.
Abstract:
3D face reconstruction has a wide range of applications, but it is still a challenging problem, especially when
dealing with a single image. Inspired by recent works in face illumination estimation and face animation
from video, we propose a novel method for 3D face renconstruction with geometric details from a single
image by using three steps. First, a coarse 3D face is generated in morphable model space by landmarks
alignment. Afterwards, using the face illumination priors and surface normals generated from the coarse 3D
face, we estimate both illumination condition and facial texture, making it possible for the final step that refines
geometric details through shape-from-shading method. Experiments prove that our method outperforms state-
of-the-art method in terms of accuracy and geometric preservation.
1 INTRODUCTION
3D face reconstruction is useful for a variety of ap-
plications, such as facial animation (Cao et al., 2014)
and recognition (Zhu et al., 2015). Although the 3D
model can be reconstructed through multi-images or
special sensors, it still remains challenges to recon-
struct a 3D face from a single 2D image due to lack
of illumination and depth information.
In recent years, different methods have been pro-
posed for 3D face reconstruction from a single image.
Of these methods, the most common way is to use
a 3D Morphable Model (3DMM, (Blanz and Vetter,
1999)) to estimate its parameters via landmarks fitting
so that the model matches the input image. Besides,
Shape-from-shading (SFS) method (Kemelmacher-
Shlizerman and Basri, 2011) could also be introduced
to solve this reconstruction problem through recove-
ring depth field from the shading variation of the input
image. In addition, Convolutional Neural Network
(CNN) has been employed to recover 3D face directly
via volumetric regression (Jackson et al., 2017).
Although existing methods are capable of recove-
ring fine 3D face from a single image, they also have
some limitations. Since the 3DMM is a parametric
model of low-dimensional representation, it cannot
represent high-dimensional face information, that is,
facial features such as wrinkles cannot be recovered.
The problem of missing facial geometric details also
exists in the CNN volumetric regression method due
Figure 1: Our 3D face reconstruction from a single image.
Given an input image (left), we recover a 3D face with fine
geometric details (right, second column). The input image
is used as texture for the reconstructed face and making the
reslult intuitional (right, first column).
to its small number of model points. SFS method is
able to recover fine geometric details from images, but
it requires prior information about facial texture and
illumination to solve such ill-posed problem. Recon-
struction result would be far from the target face on
the overall shape if no prior knowledge is provided.
In this paper, we develop an intergrated method
based on 3DMM and SFS to recover a 3D face model
with geometric details (see Figure 1). Our method
consists of following three steps:
• First, we estimate a coarse 3D face that represents
876
Qiu, W., Yu, Y., Zhou, Y. and Du, S.
Fine-grained 3D Face Reconstruction from a Single Image using Illumination Priors.
DOI: 10.5220/0007406508760883
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 876-883
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 2: Pipeline of our method. We first estimate pose, shape and expression of the target face in 3DMM space. Afterwards,
lighting and texture parameters are estimated using both SH lighting prior and facial texture model. At last, we develop a SFS
method to refine facial geometric details.
the overall shape of the target face by fitting land-
marks between the 3DMM-based model and the
input image. We choose Basel Face Model (BFM,
(Paysan et al., 2009)), a dataset with large range in
identity and expression, as our morphable model.
• Afterwards, we analyze the Intrinsic Image (Land
and McCann, 1971) properties and face illumina-
tion prior knowledge. using the facial texture mo-
del and aforementioned solved overall shape, we
iteratively estimate the illumination condition and
face texture parameters of the target image, provi-
ding prior information for the SFS step.
• Finally, we utilize both the illumination and tex-
ture parameters to carry out shape refinement ba-
sed on the shading variation of the input image. A
height-field face model that captures the fine ge-
ometric details and preserves the overall shape of
the input image is eventually generated.
Our approach combines the advantages of the
3DMM-based method with the SFS method, while
avoiding their respective disadvantages. The 3DMM
method provides good overall face shape, and our in-
novative introduction of illumination priors makes the
SFS refinement more reliable. Experiments shows
that our method outperforms other method in terms
of accuracy and geometric preservation.
2 RELATED WORK
3DMM. Human faces have many common features,
which makes it possible to characterize 3D face model
using low-dimensional parameters. The most known
parametric face model is 3DMM (Blanz and Vetter,
1999), which is a PCA-based statistical model of fa-
cial shape and texture. 3DMM has been used in a
wide range of fields, such as 3D face reconstruction
(Roth et al., 2016), face recognition (Zhu et al., 2015)
and make-up suggestion (Scherbaum et al., 2011). In
the field of 3D reconstruction, one of the benefits of
using 3DMM is that it constrains the solution only to
the possible face space, which simplifies the problem
of 3D face reconstruction. Since 3DMM is derived
from a limited 3D face dataset and focus on the prin-
ciple components, its solutions cannot fully characte-
rize all faces and always lack fine geometric details.
Intrinsic Image and Lighting. Intrinsic Image De-
composition (IID, (Land and McCann, 1971)) is a
problem to decompose an image into its shading and
reflectance components. For decomposition of face
image , different prior information could be use to
facilitate the accuracy of decomposition (Li et al.,
2014). One of the latest face priors is the face ill-
lumination prior (Egger et al., 2018). The authors
propose a illumination estimation technique and ap-
ply it to face images under various illumination con-
ditions, resulting in a huge illumination dataset. The
prior is a probability distribution of natural illumina-
tion conditions and is modeled using first-three-bands
Spherical Harmonics (SH, (Ramamoorthi and Hanra-
han, 2001)). In this paper, we utilize such prior to
estimate intrinsic components of the face image.
Shape-from-shading. Shape-from-shading (SFS,
(Zhang et al., 1999; Durou et al., 2008)) is a tradi-
tional problem that recovers 3D shape from images
using shading variation. The SFS problem is extre-
mely ill-posed, which needs the knowledge of the re-
flectance and illumination information first to reco-
ver target geometry. Since such information is often
unable to achieved, corresponding priori assumptions
have been made for specific problems. For exam-
ple, assuming that the reflectance of the object is uni-
form and the light sources are all distant. As for 3D
face reconstruction, some people improve the robus-
tness of SFS by employing a separate reference face
(Kemelmacher-Shlizerman and Basri, 2011). In this
paper, we incorporate the prior knowledge about fa-
cial geometry, illumination condition and texture sol-
ved in previous steps to achieve reliable solution.
Fine-grained 3D Face Reconstruction from a Single Image using Illumination Priors
877

3 OVERVIEW
We provide an overview of our paper in this section.
The pipeline of our approach mainly consists of three
steps, as illustrated in Figure 2.
Our paper is organized as follows. Section 2 des-
cribes related work. Sections 4, 5 and 6 discuss the
three main steps of our reconstruction method, re-
spectively. Section 7 describes the experimental eva-
luations, and conclusions are drawn in Section 8.
To be more specific, in Section 4 we iteratively es-
timate the pose, identity and expression parameters of
the target face, resulting in a coarse 3D face model. In
section 5, we decompose the input image and extract
its texture and lighting parameters, by employing il-
lumination priors. In section 6, SFS process is carried
out to generate a fine geometric model.
4 SHAPE FITTING
3DMM is a linear combination of principle compo-
nents of face dataset. It could be represented as a
mesh with the same connectivity, and its vertex coor-
dinates V ∈ R
3n
v
are computed as
V(α, β) = µ + U
id
α + U
exp
β, (1)
where n
v
is the number of vertices, and µ ∈ R
3n
v
is the
mean face vector. U
id
is principle components matrix
of face identity whose size is 3n
v
× k, and α is the
identity parameter of 3DMM with length of k. Simi-
larly, U
exp
and β are principle components matrix and
parameter of facial expression respectively.
In this section, we align 3D landmarks on the
3DMM with corresponding 2D landmarks from the
input image. Since the 3DMM shares the same con-
nectivity under different parameters, its indices of 3D
landmarks would be fixed during reconstruction of
different images. Given an input image, we detect the
face and find out its corresponding landmarks using
the method in Dlib C++ library (King, 2009). Para-
meters of pose, identity and expression are estimated
iteratively in this section.
4.1 Pose Estimation
We suppose that the projective model is a weak per-
spective projection along the Z direction, so the pro-
jection just scale the X and Y coordinates of the face
object after it has been rotated and made translations.
Therefore, we can formulate the following energy
function to align the projection of 3D landmark verti-
ces with the detected 2D landmarks.
f (s, R, T, α, β) =
m
∑
i=1
k
sR ∗ V
c
i
(α, β) + T −W
i
k
2
2
(2)
Here W
i
is the i-th of the m landmarks on 2D image.
V
c
i
is the 3D landmark vertex that are corresponding
to W
i
, where c
i
is the the i-th fixed index of the 3D
landmarks in 3DMM. s is a scalar acting as the weak
perspective projection matrix. R is the first two rows
of the rotate matrix with a size of 2 ×3, which ommits
the effect of Z direction. T is a 2 × 1 vector represen-
ting image translations.
We first estimate the pose parameters by fixing the
parameters of face identity and expression. Thus the
problem is reduced to
s, R, T = arg min
s,R,T
f (s, R, T, α, β), (3)
which could be efficiently solved by SVD. Especially,
We set α = 0 and β = 0 at the first iteration.
4.2 Identity and Expression Estimation
Once the camera pose is solved, we turns to opti-
mize face identity parameters with pose and expres-
sion parameters fixed. We consider to add regulariza-
tion term in order to get rid of abnormal result. The-
refore the optimization turns to be
α = arg min
α
f (s, R, T, α, β) + γ
1
k
∑
i=1
α
i
σ
i
2
, (4)
where σ
i
is the corresponding singular values of the
identity components. This is a linear least-squares
problem and can be efficiently solved. Afterwards,
we fix the pose and identity parameters, and optimize
the expression parameters in the same way.
β = arg min
β
f (s, R, T, α, β) + λ
2
k
0
∑
i=1
β
i
σ
0
i
2
, (5)
where σ
0
i
is the corresponding singular values of the
expression components.
Since we just set α = 0 and β = 0 when estimate
pose at first, parameters {s, R, T } may not be accu-
rate enough. Besides, identity and expression soluti-
ons based on the previous pose parameters may also
deviate from the real result. Hence, we solve the
pose-identity-expression problem iteratively, until the
energy function converges. Finally, a parametric co-
arse model is generated.
5 IMAGE DECOMPOSITION
In this section, we firstly backproject the image to the
aligned coarse 3D model, and then decompose the
face image in model space. Both SH lighting priors
and 3DMM texture model are employed to estimate
corresponding parameters.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
878

Figure 3: Intrinsic Image Decomposition of an example
face image (left). It is decomposed into two components,
which are albedo (middle) and shading (right) respectively.
Shading could provide important cues for facial geometric
refinement.
We describe the fundamental equation for intrinsic
image decomposition as follow.
I(x, y) = A(x, y)S(x, y), (6)
where I(x, y) is the input RGB vector for pixel (x, y).
A(x, y) and S(x, y) are corresponding reflectance (or
says albedo) and shading vectors. For each channel,
this formulation takes element-wise multiplication. A
decomposition example is shown in Figure 3.
5.1 Spherical Harmonic Lighting
It is usually assumed that human face surfaces are
Lambertian and all light sources are distant. Hence,
3-order SH lighting would be sufficient for approxi-
mating shading effects (Ramamoorthi and Hanrahan,
2001). Based on these two assumptions, we employ
SH lighting to describe illumination condition.
S
c
(x, y) =
9
∑
k=1
L
c
k
Y
k
(n(x, y)), (7)
where S
c
(x, y) denotes shading effects of one single
channel c (c denotes either r, g, or b) at pixel (x, y).
L
c
k
is the corresponding SH lighting coefficient, with
1 ≤ k ≤ 9. The SH coefficient L
c
k
is estimated for
R,G,B color channels separately in order to acount
for color illumination. Y
k
(n(x, y)) denotes spherical
harmonics (SH) basis composed of surface normal
n(x, y) = (n
x
, n
y
, n
z
)
T
.
Y (n) = (1, n
y
, n
z
, n
x
, n
x
n
y
, n
y
n
z
,
3n
2
z
− 1, n
x
n
z
, n
2
x
− n
2
y
)
T
.
(8)
Therefore, we could rewrite the equation (7) in a
new form as follow.
S = Y(n) · L (9)
where S is a m × 3 matrix representing shading effect
in all m vertices, and Y(n) is a m × 9 matrix, and L is
a 9 × 3 matrix.
5.2 Lighting and Texture Estimation
We employ 3DMM texture model to represent the
face albedo. The formulation of texture model is si-
milar to that of shape model described in equation(1).
A(δ) = µ
tex
+ U
tex
δ, (10)
where µ
tex
is mean texture vector whose length is 3n,
U
tex
is principle components whose size is 3n × k, δ
is the texture parameter of 3DMM whose length is k.
In order to estimate lighting and texture parame-
ters, we form the data term of face image decomposi-
tion as follow.
f
sh
(L, δ) = kA(δ)Y(n)L − Ik
2
2
(11)
We innovatively employ a face illumination data-
set (Egger et al., 2018) to generate illlumination pri-
ors. This dataset consists of a wide range of illumi-
nation conditions (see Figure 4). Therefore, we add
a Gaussian-based regularization term to constrain SH
lighting parameters in a most probable range.
f
L
(L) = (L − µ
L
)
T
C
L
−1
(L − µ
L
), (12)
where µ
L
is the average of the illumination coeffi-
cients of the dataset, and C
L
is the corresponding co-
variance matrix.
Besides, similar to that of identity estimation, we
use the same regularization term for texture parameter
δ. Therefore, we could draw the full energy function
for lighting and texture estimation.
L, δ = arg min
L,δ
f
sh
(L, δ) + γ
3
f
L
(L) + γ
4
k
∑
i=1
δ
i
σ
i
2
(13)
We set δ = 0 at first, and estimate lighting and
texture parameters iteratively. This is a linear least-
squares problem and could be solved efficiently.
Figure 4: Samples from illumination dataset (Egger et al.,
2018) which represent a wide range of different real-world
illumination conditions. The samples are rendered with the
mean face of the Basel Face Model (top row) and a sphere
with the average face albedo (bottom row).
Fine-grained 3D Face Reconstruction from a Single Image using Illumination Priors
879

6 SHAPE-FROM-SHADING
In this section, we finally reconstruct a height field
surface model that has fine geometric details over the
face region of the input image. Using the known
parameters of lighting and texture solved in previ-
ous steps, we optimize a refined normal map that re-
presents geometric details of the target face. After-
wards, the refined normal map is integrated to recover
a height field surface as the final model.
6.1 Height Field Integration
Surface z(x, y) of the target face is pixelwise corre-
sponding to the input image I(x, y), and its surface
normal could be represented by two variables as
n(x, y) =
(p, q, −1)
T
p
p
2
+ q
2
+ 1
(14)
where
p(x, y) = z(x + 1, y) − z(x, y)
q(x, y) = z(x, y + 1) − z(x, y).
(15)
Obviously, the surface z(x, y) could be integrated by
z = arg min
z
∑
(
∂z
∂x
− p)
2
+ (
∂z
∂y
− q)
2
(16)
Once the surface normal map is refined, the height
field model could be easily solved by such a linear
least-squares optimization.
6.2 Surface Normal Refinement
Before integrating to surface height field, we should
optimize depth field gradient p and q by minimizing
following energy function.
f
sfs
(p, q) = f
data
+λ
1
f
grad
+λ
2
f
close
+λ
3
f
smo
+λ
4
f
int
(17)
For convenience, we denote the intensity differen-
ces between recovered result and input image as
D(p, q) = A(x, y)Y(n(x, y))L − I(x, y). (18)
First of all, using the lighting and texture parame-
ters obtained during previous step, we can gernerate a
2D image from the normal map according to Eq.(6).
It is naturally to force rendered image to be close to
the input image, which indicates the following energy
function.
f
data
(p, q) =
∑
(x,y)∈I
kD(p, q)k
2
2
(19)
However, if we only consider the intensity diffe-
rences, we may get unreliable results due to some ex-
treme lighting conditions such as highlights. There-
fore, we also minimize the difference in intensity gra-
dients between the input image and the reconstructed
one, resulting in following energy function.
f
grad
(p, q) =
∑
(x,y)∈I
∂D
∂x
2
2
+
∂D
∂y
2
2
(20)
Taking f
data
and f
grad
into consideration is not suf-
ficient for good results. Hence we employ three addi-
tional regularization terms for the surface normal and
height field. Firstly, since the coarse model genera-
ted in the 3DMM step captures overall shape of the
target face, we minimize the difference between nor-
mal map and the surface normals n
0
from the coarse
model.
f
close
(p, q) =
∑
(x,y)∈I
kn(x, y) − n
0
(x, y)k
2
2
(21)
Secondly, we create a Laplacian constraint to empha-
size smoothness of the surface normal map.
f
smo
(p, q) = k∆nk
2
2
(22)
At last, due to the property of integrity from gradient
p and q to surface height z, we force the gradient p, q
to satisfies the following formula.
p(x, y) + q(x + 1, y) − p(x, y + 1) −q(x, y) = 0 (23)
Hence we propose the last energy function about
height field integrability.
f
int
=
∑
(x,y)∈I
[p(x, y) + q(x + 1, y) − p(x, y + 1) − q(x , y)]
2
(24)
Now we combine all these five energy functions to
form a complete energy function as (17). p, q could
be optimized by
p, q = arg min
p,q
f
sfs
(p, q). (25)
After weights λ
1
, λ
2
, λ
3
and λ
4
are specified, we
solve this nonlinear least-squares problem using the
L-BFGS algorithm.
7 EXPERIMENT
In this section, we present several experimental re-
sults, and compare with other method to demonstrate
the reliability of our approach.
We develop our code in C++ and the recon-
struction algorithm is run on a PC with an Intel Core
i7-3770 3.40 GHz CPU and 16 GB RAM. The weig-
hts in optimization problems (4), (5), (13), (17) are
set as follows: γ
1
= γ
2
= 5.0 × 10
3
, γ
3
= 0.01, γ
4
=
1.0 × 10
4
;λ
1
= 8.0, λ
2
= 0.3, λ
3
= 0.3, λ
4
= 0.5; We
adopt the L-BFGS solver (Liu and Nocedal, 1989) to
solve the nonlinear optimization problem in the SFS
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
880
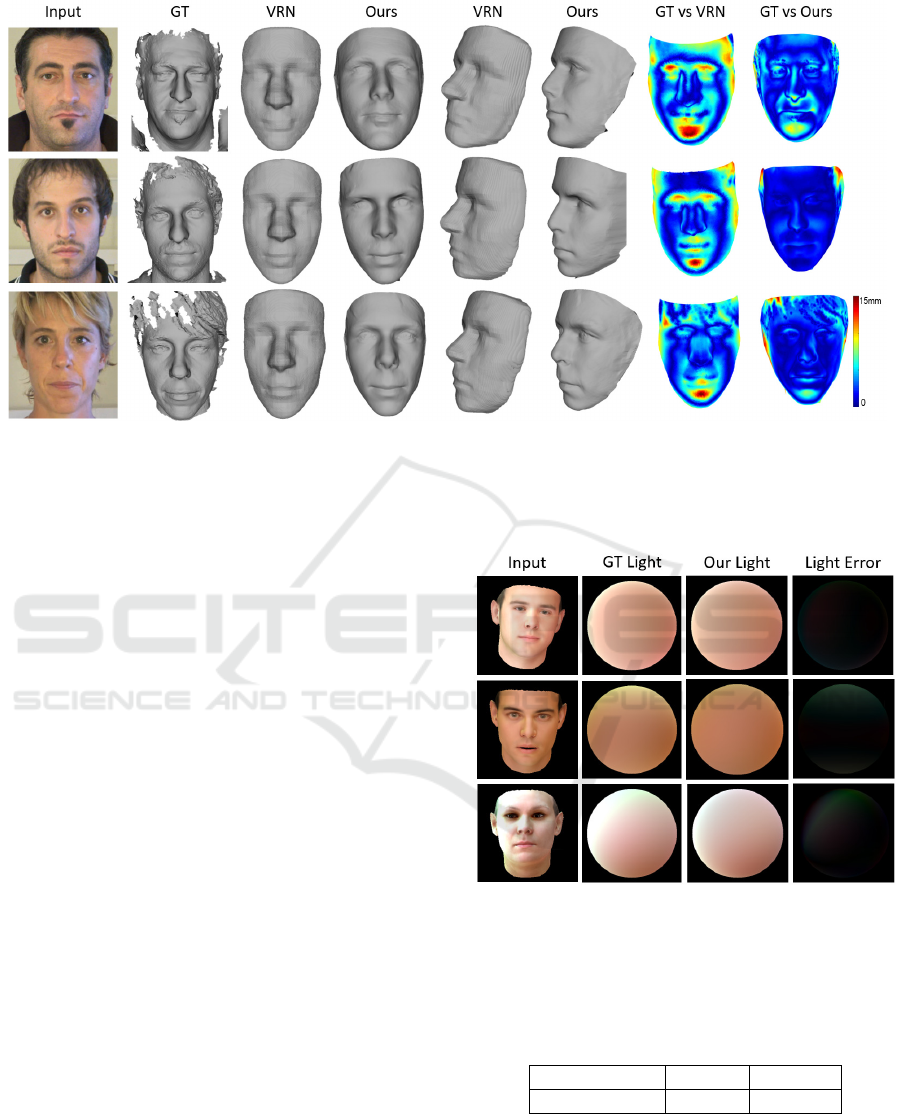
Figure 5: 3D Face reconstruction of three subjects from the MICC dataset. For each input image, we show the ground-truth
(GT) and the results using our method and VRN method in two viewpoints. We also show the error map (according to
3DRMSE) for these two methods.
process (25). In addition, we implement all derivative
functions by ourselves in order to speed up the opti-
mization. Our algorithm has no limit on the size of
the input image, but usually we take an image with a
size of around 480 × 480 as input, which would cost
about 30 milliseconds, 100 milliseconds, and 10 se-
conds respectively in corresponding steps.
7.1 Texture and Lighting Result
We first focus on the texture and lighting estimation.
Due to the lack of real-world face dataset about texure
and lighting condition, we synthesize 2D images from
3DDFA dataset (Zhu et al., 2016). Each image in the
dataset corresponds to relevant 3DMM parameters,
such as pose, texture, identity, and expression para-
meters, but except for SH lighting parameters. We
select SH lighting parameters from illumination prior
dataset (Egger et al., 2018), and apply them on the
3DDFA dataset to render corresponding 2D images.
For each rendered image, we estimate its facial
texure and illumination condition. For visualization,
we render the illlumination parameters onto a sphere
with the average face albedo. Then we calculate the
Mean Square Error (MSE) between rendered sphere
images and their corresponding ground-truths. Figure
6 shows several samples of our lighting results com-
pared with ground-truths. As for facial texture, the
MSE could be easily computed since the texture mo-
del shares semantic information and could be genera-
ted by multiplying principle component matrix with
texture parameter. The average MSE of texture and
lighting estimations are shown in Table 1.
Figure 6: Samples of lighting results by applying our al-
gorithm on synthesized images. Compared with those of
ground-truth, our results have low error, which proves the
accuracy of illumination estimation and guarantees the reli-
ability of SFS.
Table 1: Average MSE of texture and lighting by applying
our algorithm on synthesized dataset derived from 3DDFA.
Estimation Texture Lighting
Average MSE 0.0335 0.0238
Compared with traditional methods, we pay more
attention to analyzing the accuracy of image decom-
position components, which is an important prerequi-
site for geometric detail recovery. Both visualization
results and numerical errors prove that our algorithm
is reliable.
Fine-grained 3D Face Reconstruction from a Single Image using Illumination Priors
881

Figure 7: Face reconstrucion results from Internet images. We show results (with texture) using VRN method and our method,
respectively. In addition, we display our lighting estimations (without facial texture), in the last column.
7.2 3D Reconstruction Result
In order to demonstrate the effectiveness of our algo-
rithm, we evaluate 3D points reconstrucion error on
a ground-truth dataset. To measure such error, each
reconstructed model is aligned with its correspon-
ding ground-truth face using Iterative Closest Point
(ICP) method (Rusinkiewicz and Levoy, 2001). Af-
ter that, we compute the 3D Root Mean Square Error
(3DRMSE) between vertices of reconstructed model
and their corresponding vertices on ground-truth mo-
del by
3DRMSE =
r
∑
i
(Y − Y
gt
)
2
N
, (26)
where Y is the reconstructed model, Y
gt
is the ground-
truth, and N is the number of vertices of the recon-
structed model.
We compare our method with the VRN method
(Jackson et al., 2017) by applying on the MICC da-
taset (Bagdanov et al., 2011). The MICC dataset
contains 53 videos of different subjects and illlumi-
nation conditions. The ground-truths are generated
through a structured-light scanning approach. 42 sub-
jects with suitable image resolution and low noises in
point clouds are chosen for our experiment. We com-
pute the 3D reconstruction errors using the 3DRMSE
measurement described above. To be detailed, we ma-
nually choose the most frontal face image from the
videos for each subject, and reconstruct the 3D face
model by taking it as input using VRN method and
our method respectively. The mean and standard va-
riation of 3DRMSE are illustrated in Table 2.
Table 2: 3D reconstruction error comparison on the MICC
dataset. The mean and standard variation of 3DRMSE.
Method Mean of 3DRMSE Standard Variation
VRN 2.737 0.728
Ours 2.224 0.683
Table 2 shows that our reconstruction error is lo-
wer than that of VRN method (Jackson et al., 2017),
while Figure 5 and Figure 7 show in an intuitive way
that our method can recover more geometric details of
the face than the VRN method, whether using images
from MICC dataset or from Internet. Taking the third
row of Figure 7 as an example, wrinkles on the man’s
forehead are faithfully recovered in shape, rather than
in texture. Our lighting estimations from real-world
images are also show in the last column of Figure
7. We add facial geometric details to the target face
while keeping overall shape not changed. This is due
to our combination of 3DMM overall face fitting and
SFS detail recovery. It is clear that with the prior of
reliable illumination estimation and SFS refinement,
our approach have good estimations on single image
reconstruction.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
882

8 CONCLUSIONS
In this paper, we develop a novel approach to re-
construct a fine-grained 3D face model from a single
image using illumination priors. We generate a coarse
model in 3DMM space through landmarks alignment,
providing the overall shape for next optimizations.
By employing illumination priors and image intrin-
sic features, spherical harmonic lighting environment
and facial texture are accurately estimated. At last, a
shape-from-shading method is implemented to obtain
a fine-grained 3D face model. The experiments de-
monstrate that our method can effectively reconstruct
3D face model with fine geometric details from single
image.
REFERENCES
Bagdanov, A. D., Del Bimbo, A., and Masi, I. (2011). The
florence 2d/3d hybrid face dataset. In Proceedings of
the 2011 joint ACM workshop on Human gesture and
behavior understanding, pages 79–80. ACM.
Blanz, V. and Vetter, T. (1999). A morphable model
for the synthesis of 3d faces. In Proceedings of
the 26th annual conference on Computer graphics
and interactive techniques, pages 187–194. ACM
Press/Addison-Wesley Publishing Co.
Cao, C., Hou, Q., and Zhou, K. (2014). Displaced dynamic
expression regression for real-time facial tracking and
animation. ACM Transactions on graphics (TOG),
33(4):43.
Durou, J.-D., Falcone, M., and Sagona, M. (2008). Nume-
rical methods for shape-from-shading: A new survey
with benchmarks. Computer Vision and Image Under-
standing, 109(1):22–43.
Egger, B., Sch
¨
onborn, S., Schneider, A., Kortylewski, A.,
Morel-Forster, A., Blumer, C., and Vetter, T. (2018).
Occlusion-aware 3d morphable models and an illu-
mination prior for face image analysis. International
Journal of Computer Vision, pages 1–19.
Jackson, A. S., Bulat, A., Argyriou, V., and Tzimiropoulos,
G. (2017). Large pose 3d face reconstruction from
a single image via direct volumetric cnn regression.
In 2017 IEEE International Conference on Computer
Vision (ICCV), pages 1031–1039. IEEE.
Kemelmacher-Shlizerman, I. and Basri, R. (2011). 3d face
reconstruction from a single image using a single refe-
rence face shape. IEEE Transactions on Pattern Ana-
lysis and Machine Intelligence, 33(2):394–405.
King, D. E. (2009). Dlib-ml: A machine learning tool-
kit. Journal of Machine Learning Research, 10:1755–
1758.
Land, E. H. and McCann, J. J. (1971). Lightness and retinex
theory. Josa, 61(1):1–11.
Li, C., Zhou, K., and Lin, S. (2014). Intrinsic face image
decomposition with human face priors. In Euro-
pean Conference on Computer Vision, pages 218–233.
Springer.
Liu, D. C. and Nocedal, J. (1989). On the limited memory
bfgs method for large scale optimization. Mathemati-
cal programming, 45(1-3):503–528.
Paysan, P., Knothe, R., Amberg, B., Romdhani, S., and Vet-
ter, T. (2009). A 3d face model for pose and illumina-
tion invariant face recognition. In Advanced video and
signal based surveillance, 2009. AVSS’09. Sixth IEEE
International Conference on, pages 296–301. Ieee.
Ramamoorthi, R. and Hanrahan, P. (2001). An efficient re-
presentation for irradiance environment maps. In Pro-
ceedings of the 28th annual conference on Computer
graphics and interactive techniques, pages 497–500.
ACM.
Roth, J., Tong, Y., and Liu, X. (2016). Adaptive 3d face
reconstruction from unconstrained photo collections.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, pages 4197–4206.
Rusinkiewicz, S. and Levoy, M. (2001). Efficient variants
of the icp algorithm. In 3-D Digital Imaging and Mo-
deling, 2001. Proceedings. Third International Confe-
rence on, pages 145–152. IEEE.
Scherbaum, K., Ritschel, T., Hullin, M., Thorm
¨
ahlen, T.,
Blanz, V., and Seidel, H.-P. (2011). Computer-
suggested facial makeup. In Computer Graphics Fo-
rum, volume 30, pages 485–492. Wiley Online Li-
brary.
Zhang, R., Tsai, P.-S., Cryer, J. E., and Shah, M. (1999).
Shape-from-shading: a survey. IEEE transactions on
pattern analysis and machine intelligence, 21(8):690–
706.
Zhu, X., Lei, Z., Liu, X., Shi, H., and Li, S. Z. (2016). Face
alignment across large poses: A 3d solution. In Pro-
ceedings of the IEEE conference on computer vision
and pattern recognition, pages 146–155.
Zhu, X., Lei, Z., Yan, J., Yi, D., and Li, S. Z. (2015). High-
fidelity pose and expression normalization for face re-
cognition in the wild. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recog-
nition, pages 787–796.
Fine-grained 3D Face Reconstruction from a Single Image using Illumination Priors
883
