Virtual Flattening of a Clothing Surface by Integrating Geodesic
Distances from Different Three-dimensional Views
Yasuyo Kita and Nobuyuki Kita
Intelligent Systems Research Institute, National Institute of Advanced Industrial Science and Technology (AIST),
Tsukuba, Japan
Keywords:
Geodesic Distance, Virtual Flattening, Clothes Handling, Recognition of Deformable Objects, Robot Vision.
Abstract:
We propose a method of virtually flattening a largely deformed surface using three-dimensional images taken
from different directions. In a previous paper (Kita and Kita, 2016), we proposed a method of virtually fat-
tening a surface from a 3D depth image according to the calculation of geodesic lines, which are the shortest
paths between two points on an arbitrary curved surface. Although the work showed the promise of the pro-
posed approach, only gently curved surfaces can be flattened owing to the limit of the observation being made
from one direction. To apply the method to a wider range of surfaces, including sharply curved surfaces, we
extended the method to three-dimensional depth images taken from different directions integratively. This was
done by combining equations obtained from each observation through the surface points observed commonly
in different observations and by solving all the equations simultaneously. Experiments using actual clothing
items demonstrated the effect of the integration.
1 INTRODUCTION
Robots need to act more flexibly according to circum-
stance when their activities are extended from facto-
ries to the daily lives of people. To that end, com-
puter vision plays an important role in recognizing
various objects. Especially, the recognition of de-
formable daily objects presents difficulties that are
different from those presented by rigid objects that
have long been studied in factory automation. The
recognition of clothing items for the automatic han-
dling of clothing is a typical example.
The complex self-occlusion that accompanies the
large deformation of clothing items makes the task of
recognizing the items challenging. Figure 1 shows a
clothing item being handled by a robot. It is not easy
to determine the clothing type (e.g., trousers) or to
detect the best position to grasp next (e.g., the cor-
ner of the waist) from such deformed shapes. There-
fore, many studies on clothing recognition aimed at
automatic handling have tried to first spread the cloth-
ing item to reduce the level of self-occlusion (F. Os-
awa and Kamiya, 2007) (Hu and Kita, 2015) (D. Tri-
antafyllou and Aspragathos, 2016) (A. Doumanoglou,
2014). However, selecting proper positions to grasp
for good spreading is another difficult recognition
problem.
Figure 1: Our goal of obtaining the clothing shape flattened
on a two-dimensional plane from the observation of a three-
dimensionally deformed clothing item.
Meanwhile, a person can often imagine the flat-
tened shape from a three-dimensionally deformed
shape. Our aim is to realize this virtual flattening
function by transforming the three-dimensional (3D)
surface into a two-dimensional (2D) shape as shown
in Fig. 1. Hereafter, we refer to the shape after virtual
flattening as the flattened view. In a previous paper
(Kita and Kita, 2016), we proposed a method of vir-
tually flattening a clothing surface on a 2D plane from
a 3D depth image of the surface. The method formu-
lates the flattening of the observed 3D surface as a
problem of solving simultaneous equations given by
Kita, Y. and Kita, N.
Virtual Flattening of a Clothing Surface by Integrating Geodesic Distances from Different Three-dimensional Views.
DOI: 10.5220/0007410305410547
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 541-547
ISBN: 978-989-758-354-4
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
541

sets of the geodesic distance, which is the length of
the shortest path between two points on an arbitrary
curved surface. However, because only one depth im-
age is considered as the input in that paper, the target
is limited to the case that the whole surface can be
observed from one direction. In reality, most clothing
items can be seen only partially when they are held
in the air by one hand and do not satisfy this condi-
tion. The present paper extends the method to vir-
tually flatten a sharply curved surface by integrating
views taken from different directions.
Section 2 introduces the basic method of flatten-
ing proposed in the previous paper. Section 3 ex-
plains a method of integrating partial observations of
a deformed surface to flatten the whole surface. Ex-
perimental results using actual clothing items are pre-
sented in Section 4. Finally, the results and future
topics are discussed in Section 5.
2 BASIC FLATTENING METHOD
2.1 Calculation of the Geodesic Distance
Many methods of calculating the geodesic line use fi-
nite element meshes(P. Bose, 2011)(Zhong and Xu,
2006) or a voxel representation(R. Grossmann and
Kimme, 2002). However, both mesh-based and
voxel-based methods assume uniformly dense 3D
data of objects, which is not always the case for obser-
vation data in the real world. To calculate a geodesic
line directly from 3D point clouds obtained by a range
sensor or stereo cameras, we adopt an approach pro-
posed by Kawashima et al. (T. Kawashima, 1999) that
calculates geodesic lines in a mesh-free way.
To calculate the geodesic line between two points
on a surface, P
s
and P
e
, we set M nodes on the sur-
face to represent the line P
s
P
e
= p
1
p
2
....p
M
, where
p
1
= P
s
, p
M
= P
e
and p
i
= (x
i
,y
i
,z
i
) as shown in Fig.
2. The problem of obtaining the geodesic distance of
P
s
P
e
can be set as minimizing L
total
:
L
total
=
M− 1
∑
i=1
L
i
, (1)
L
i
=
q
(x
i+1
− x
i
)
2
+ (y
i+1
− y
i
)
2
+ (z
i+1
− z
i
)
2
.
We here represent the surface as z(x), x = (x,y).
To solve this minimization problem, z(x) at any place
on the surface should be continuously determined
from discontinuous observed 3D points of the sur-
face. For this purpose, the surface around the posi-
tion x = (x,y) is approximated by the local surface
function with continuous partial derivatives using the
Figure 2: Direct calculation of the geodesic line from a 3D
point cloud through surface interpolation.
element-free Galerkin method (T. Belytschko and Gu,
1994). Specifically, z(x) is approximated by a poly-
nomial function:
z(x) = P
T
(x)a(x), (2)
P
T
(x) = (1, x,y), a(x) = (a
1
(x),a
2
(x),a
3
(x))
T
.
The coefficient vector a(x) is locally determined
at each x by minimizing the difference of z(x) from
the observed points in the vicinity of x:
J =
N
r0
∑
l=1
w(r
l
)(z(x
l
) − z
l
)
2
, (3)
r
l
= |x − x
l
|,
where w(r) is a weight function defined by the
distance between the target point, x, and observed
points x
l
(l = 1,··· ,N
r0
) within a fixed distance, r
0
.
A fourth-order spline function is used as the weight
function in this paper.
The depth and normal at x are calculated using the
resultant a(x):
z(x) = a
1
(x) + a
2
(x)x+ a
3
(x)y, (4)
n(x) = (a
2
(x)/D,a
3
(x)/D,1/D), (5)
D =
q
a
2
(x)
2
+ a
3
(x)
2
+ 1.
Figure 2 shows an example of synthetic ob-
served points sampled from the surface of z =
p
25− (x− 5)
2
(red crosses). The green points in
Fig. 2 show an example of surface interpolation along
the line y = −x+ 10.
Because L
total
includes the term z(x) determined
using Eq. (2), it is a complicated function of x.
To stably minimize this function, we make the zero-
length spring analogy. Specifically, we assume that
each segment p
i
p
i+1
is a spring connecting two
nodes, p
i
and p
i+1
, with a basis length (i.e., the length
at neutral time) of zero and a spring constant k. The
total length of all springs, L
total
, is a minimum when
the spring system is at equilibrium.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
542

Because each node is constrained to move on the
surface, when a force F is exerted on a node, p
i
, only
the component of F along the surface,
˜
F , affects the
movement of p
i
:
˜
F = F − (F · n
i
)n
i
, (6)
where n
i
= (n
x
i
,n
y
i
,n
z
i
) is a unit vector in the nor-
mal direction at p
i
. The blue points in Fig. 2 show
the geodesic line obtained after the convergenceof the
successive approximation, using the green line as the
initial position.
2.2 Calculation of the Flattened View
We assume that a clothing surface can be flattened
onto a 2D plane, (u, v). If we then consider N points
on the clothing surface, P
i
(x
i
,y
i
,z
i
),i = 1, · · · , N, the
flattening can be formulated as the problem of calcu-
lating the 2D coordinates of P
i
when the surface is
flattened on the plane, (u
i
,v
i
).
The geodesic distance between P
i
and P
j
, G
i, j
, is
invariant regardless of the surface deformation and
equals the Euclidean distance between (u
i
,v
i
) and
(u
j
,v
j
) on the flattened 2D surface.
q
(u
i
− u
j
)
2
+ (v
i
− v
j
)
2
= G
i, j
, (7)
Although the number of equations of the form of
Eq. (7) is
N
C
2
if we consider all combinations of N
points, not all equations are required if the number
of equations related to one point is more than two,
which is the number of unknowns for the point. By
representing the use/disuse of G
i, j
as B(i, j) = {1,0},
the flattening becomes the minimization problem of
the equation
H(u,v) =
N−1
∑
i=1
N
∑
j=i+1
B(i, j)(
q
(u
i
− u
j
)
2
+ (v
i
− v
j
)
2
− G
i, j
)
2
.
(8)
The solution is then obtained by solving 2N simulta-
neous equations, where the two equations for each P
i
are
∂H(u,v)
∂u
i
= 0,
∂H(u,v)
∂v
i
= 0. (9)
3 INTEGRATION OF MULTIPLE
OBSERVATIONS
We assume the item is held in the air by a robot hand
and can be observed from different directions. Al-
though we plan to integrate several views in the fu-
ture, in this paper, we deal with the integration of two
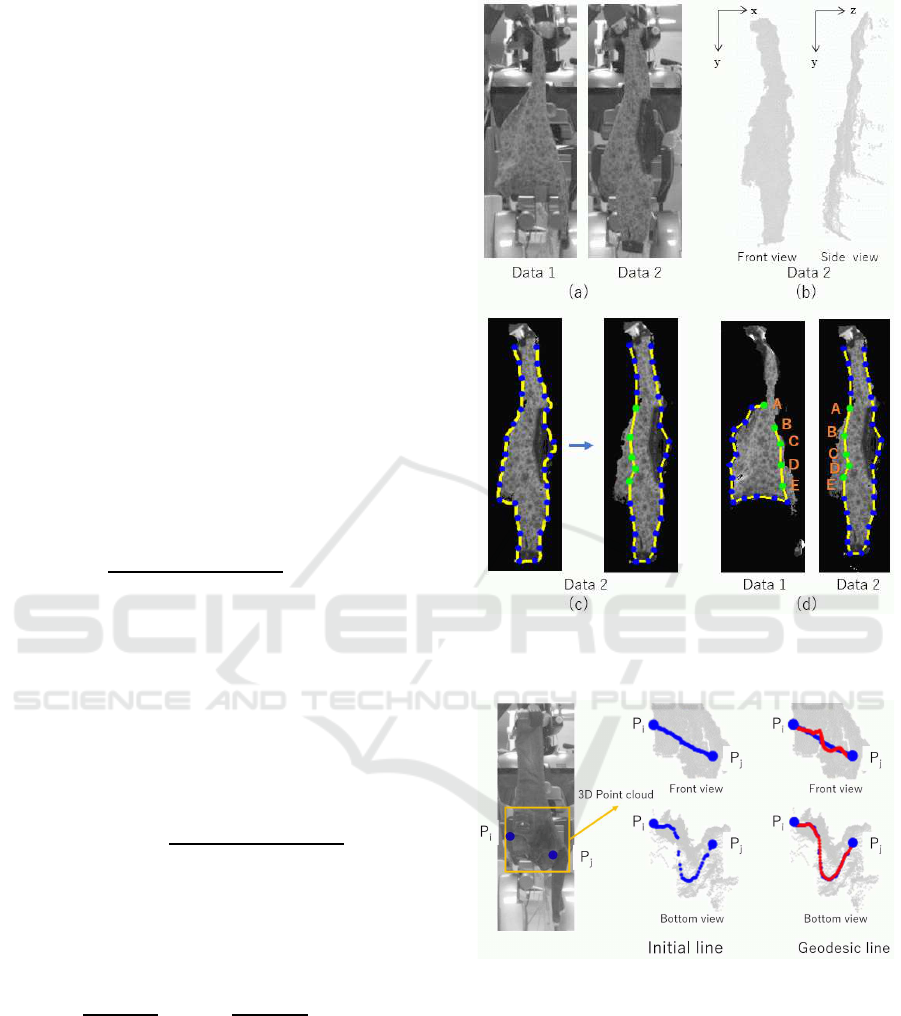
Figure 3: Selection of surface points from observation data:
(a) observation images; (b) 3D depth images; (c) selection
of surface points; (d) point correspondence.
Figure 4: Example of a geodesic line calculated from the
3D point cloud when observing a clothing surface.
views taken from largely different directions (sepa-
rated by about 90 to 120 degrees) as a first step. We
assume that the views are selected so that they cover
occluded parts of each other. Figure 3(a) shows an
example of a pair of such views.
The surface points commonly observed in the two
3D images are used to combine two sets of simulta-
neous equations of (u, v) that are obtained from each
observation. Although we plan to automatically de-
tect such point correspondences using 2D/3D char-
Virtual Flattening of a Clothing Surface by Integrating Geodesic Distances from Different Three-dimensional Views
543

acteristic points, we currently give the correspon-
dences manually. The steps described below are the
concrete procedure of combining two observations,
which cover one whole side of a clothing item by
complementing each other.
1. Point Setting
Figure 3(b) shows an example of 3D observation data,
where the observed3D points are illustrated with grey
dots. Basically, we choose points from the bound-
ary of the observed clothing region, P
i
(x
i
,y
i
,z
i
),i =
1,··· , N
b
, as shown by blue points in the left figure
of Fig. 3(c). Then, from the region observed in both
observation images, characteristics points that corre-
spond to the two images are selected and replaced as
shown by green points on the right of Fig. 3(c). Fig-
ure 3(d) shows an example of selected surface points
for the observation of Fig. 3(a) with the letters indi-
cating the correspondence between images.
2. Calculation of Geodesic Lines
Geodesic lines are calculated in each observation.
Pairs of two points for calculating geodesic distances
are selected such that the two points have similar
height. This is because folds on the surface occur
mainly in the vertical direction owing to the effect of
gravity. Figure 4 shows an example of the calcula-
tion of a geodesic line. An initial line, p
1
p
2
....p
M
, is
set between P
i
and P
j
through the uniform sampling
of (x,y) from the line between (x
i
,y
i
) and (x
j
,y
j
) and
calculating z(x,y) as described in Section 2.1. The
blue line in Fig. 4 shows an example of the initial line.
By minimizing Eq. (1), the geodesic line between P
i
and P
j
is calculated as shown by the red line.
The geodesic distance between P
m
i
and P
m
j
of ob-
servation m (in this paper, m = 1,2) is stored in
the array G
m
[i
m
][ j
m
], where G
m
[i
m
][ j
m
] = G
m
[ j
m
][i
m
].
Besides the geodesic distance, to maintain the lo-
cal shape, the Euclidean distance between the pair
of neighboring points, P
m
i
and P
m
i+1(2)
, is recorded in
G
m
[i
m
][i
m
+ 1(2)].
3. Integration of Geodesic Distances
After all G
m
are calculated, the arrays are integrated
to one array, G[i][ j], by merging the points observed
in common among the observations. During this pro-
cess, the x
m
and y
m
coordinates of each P
m
i
are re-
spectively recorded as initial values of u and v, u
0
and
v
0
. At this time, the x
m
and y
m
coordinates of m ≥ 2
observations are two-dimensionally translated and ro-
tated on the x − y plane so that the average coordi-
nates and direction of the corresponding points co-
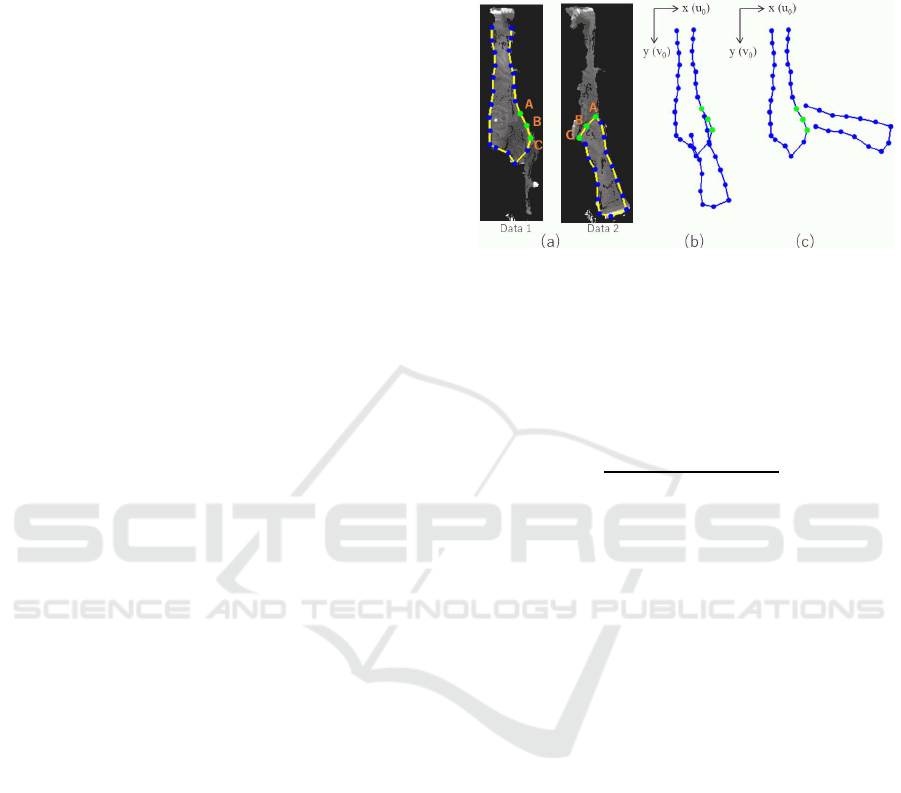
incide with those of another observation. Figure 5
shows an example, where three points (A, B and C)
on the fold are selected as the corresponding points of
the two observations. In Fig. 5(b), points from ob-
servation m = 2 are set using the original x
m
and y
m
.
Figure 5(c) shows their position after the 2D transfor-
mation.
Figure 5: Example of the initial location for merging: (a)
point correspondence; (b) (x
m
,y
m
); (c) (u
0
,v
0
).
4. Calculation of the Flattened View
The flattened view represented by (u,v) is calculated
via the minimization of
H
′
(u,v) =
N
∑
i=1
B(i, j)(
q
(u
i
− u
j
)
2
+ (v
i
− v
j
)
2
− G[i][ j])
2
,
(10)
where B(i, j) = {1,0} represents the use/disuse of the
pair of i and j. We solve this minimization using a
spring analogy by setting a spring between the pairs
of B(i, j) = 1 with a basis length of G[i][ j].
4 EXPERIMENTS
Experiments were conducted using two long-sleeve
shirts and two pairs of trousers. So that the situation
was similar to practical applications, the items were
hung by a robot hand, after the robot had picked them
up from a desk and had grasped their lowest part.
The target item was recorded by a trinocular stereo
vision system(Ueshiba, 2006) while the robot rotated
the item along the vertical axis through the holding
position. Two different views were manually selected
from the sequence of 3D data recorded during the ro-
tation. Three to five corresponding points between the
different views were manually given.
Figure 6 shows the result for the long-sleeve shirt
(LS1) in Fig. 3. The red lines in Fig. 6(a) show
geodesic lines calculated from 3D observation data.
Figure 6(b) and (c) shows the initial state set at
(u
0
,v
0
) obtained as described in Section 3 and the
resultant flattened view. Although there are small
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
544

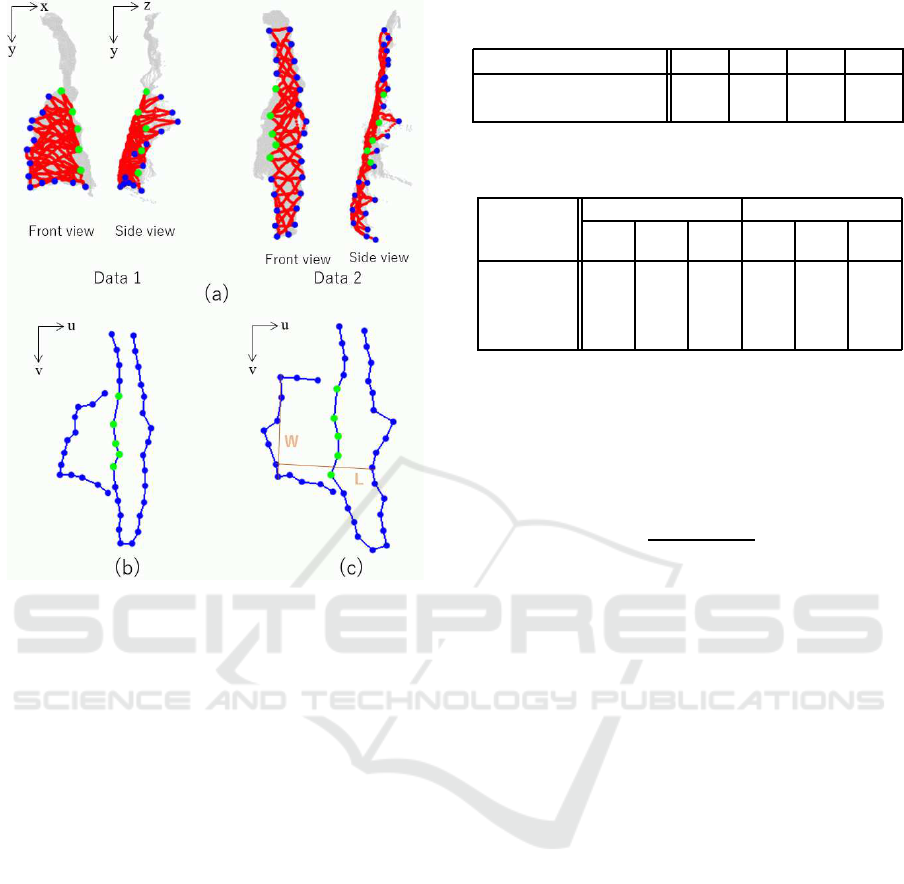
Figure 6: Experimental results of the virtual flattening of a
long-sleeve shirt (LS1): (a) geodesic lines; (b) initial state
of (u,v); (c) final state of (u,v).
zigzags owing to the inaccuracy of 3D observation
data along the region boundary, the shape of the long-
sleeve shirt when flattened on a table was globally
well estimated by the virtual flattening process.
Figure 7 shows the results for the other three sets,
LS2, TR1 and TR2. By combining two complemen-
tary views, the flattened views of the whole items
were roughly but well obtained. Especially in the case
of trousers, the acute fold of one leg can be unfolded
by this virtual flattening. In the case of TR2 (Fig.
7(c)), one leg was flattened in the wrong direction
with a shorter length. This resulted from large deep
creases marked by orange circles in Fig. 7(c), where
some hidden parts were not measured in both obser-
vations. The parts hidden by such deep creases would
be difficult to observe from any direction, until some
kind of action removes the creases.
The virtual flattened view can be directly matched
with the canonical shape of clothing items. This is a
great advantage for the analysis of largely deformable
objects. To examine this merit, we conducted a pre-
liminary experiment of category classification. Fig-
ure 8(a) shows clothing model images, I, calculated
from one of the typical shapes of each category, where
higher values represent a higher possibility of the con-
Table 1: Matching score with the canonical model images
of each category.
LS1 LS2 TR1 TR2
Long-sleeve shirts (LS) 0.65 0.78 0.43 0.47
Trousers (TR) 0.56 0.53 0.57 0.57
Table 2: Accuracy of the length measured for the flattened
shape.
W L
Data Result
(cm)
GT
(cm)
Error
(%)
Result
(cm)
GT
(cm)
Error
(%)
LS1 (Fig. 6) 35.6 36 1.1 34.2 35 2.3
LS2 (Fig. 7a) 35.6 39 8.7 38.1 40 4.8
TR1 (Fig. 7b) 25.7 25 2.8 64.2 62 3.5
TR2 (Fig. 7c) 26.0 27 3.7 55.8 67 16.7
tour of each category. When comparing the virtual
flattened view with the model images, the size of
the flattened view is normalized so that the longest
lengths of the view and the model typical shape be-
come the same. The matching criterion R is then cal-
culated as
R =
∑
N
c
n=1
I(i
n
, j
n
)
N
c
, (11)
where N
c
is the number of contour points of the flat-
tened view and (i
n
, j
n
)(n = 1,··· , N
c
)) denotes the co-
ordinates of the contour point on the image. While ro-
tating the contour after placing it on the model image
so that the centroid of the contour coincides with the
center of the image, the highest R is selected as the
matching score of the category. The resultant match-
ing score is summarized in Table 1, where the values
of the larger class are indicated in boldface. All views
are stably classified into the correct category. Figure
8(b) shows the matching results, where each view is
superposed on the model image with higher R.
To examine the accuracy of the virtual flattening,
we manually measured the width (W) and length (L)
of the resultant flattened views as marked by thin or-
ange lines in Fig. 6 and Fig. 7. The comparison
of those lengths with the actual length (GT: ground
truth) is summarized in Table 2. The errors are about
1–2 cm, or about 5%, except for the length error of
TR2 (Fig. 7(c)) owing to the flattening error as noted.
Combining the categorization result, the system can
describe the item such that “the observed item is a
long-sleeve shirt with width of about 35 cm and body
length of about 34 cm” for the case of Fig. 6.
Virtual Flattening of a Clothing Surface by Integrating Geodesic Distances from Different Three-dimensional Views
545

Figure 7: Experimental results of the virtual flattening of long-sleeve shirts and trousers: (a) LS2; (b) TR1; (c) TR2.
5 CONCLUSION
We proposed a method of virtually flattening a cloth-
ing surface onto a 2D plane from 3D depth images
of the surface taken from different directions. On the
basis that geodesic distances between surface points
equal 2D distances of the points on the flattened
plane, the method realizes flattening by solving simul-
taneous equations of the geodesic distances among
the surface points. Through points observed in com-
mon in different observations, the equations derived
from the observations are integrated and simultane-
ously solved to flatten the whole surface.
Experimental results for actual clothing items
show that the proposed method well estimates the
shape of a clothing surface when the clothing is flat-
tened on a table from two 3D observations of the de-
formed surface. The recognition of clothing items
having such shape is much easier than that for an ar-
bitrary shape. Accordingly, this allows a robot to rec-
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
546

Figure 8: Category classification using the flattened views:
(a) model images; (b) selected model.
ognize a clothing item during an ordinary handling
procedure, greatly benefiting the automatic handling
of clothing items. Category classification using the
resultant views demonstrated the good prospects of
using the virtual flattened view as a mediator between
canonical models and deformed items.
Although the corresponding points between dif-
ferent observations are manually given at present, au-
tomatic point correspondence should be possible us-
ing characteristic points of color (or intensity) fea-
tures and/or the particular 3D shape. As future work,
we plan to extend the method to integrate more obser-
vations, which will allow us to use more reliable 3D
data for all parts of the surface.
ACKNOWLEDGEMENTS
The authors thank Dr. Y. Kawai, Dr. Y. Domae, Mr.
T. Ueshiba and Mr. J. Hu for their support of this
research. This work was supported by a Grant-in-Aid
for Scientific Research, KAKENHI (16H02885).
REFERENCES
A. Doumanoglou, A. Kargakos, T.-K. K. S. M. (2014). Au-
tonomous active recognition and unfolding of clothes
using random decision forests and probabilistic plan-
ning. In International Conference in Robotics and Au-
tomation (ICRA) 2014, pages pp.987–993.
D. Triantafyllou, I. Mariolis, A. K. S. M. and Aspragathos,
N. (2016). A geometric approach to robotic unfolding
of garments. Robotics and Autonomous Systems, Vol
75:pp. 233–243.
F. Osawa, H. S. and Kamiya, Y. (2007). Unfolding of mas-
sive laundry and classification types by dual manip-
ulator. Journal of Advanced Computational Intelli-
gence and Intelligent Informatics, Vol. 11, No.5:457–
463.
Hu, J. and Kita, Y. (2015). Classification of the category
of clothing item after bringing it into limited shapes.
In Proc. of International Conference on Humanoid
Robots 2015, pages pp.588–594.
Kita, Y. and Kita, N. (2016). Virtual flattening of clothing
item held in the air. In Proc. of 23rd International
Conference on Pattern Recognition, pages pp.2771–
2777.
P. Bose, A. Maheshwari, C. S. a. S. W. (2011). A survey of
geodesic paths on 3d surfaces. Computational Geom-
etry, Vol 44:pp. 486–498.
R. Grossmann, N. K. and Kimme, R. (2002). Com-
putational surface flattening:a voxel-based approach.
IEEE Trans. on Pattern Anal. and Machine Intelli.,
vol. 24, no.4.
T. Belytschko, Y. Y. L. and Gu, L. (1994). Element-free
galerkin methods. International Journal for Numeri-
cal Methods in Engineering, Vol 37, No. 2:pp. 229–
256.
T. Kawashima, S. Yabashi, H. K. Y. (1999). Meshless
method for searching geodesic line by using moving
least squares interpolation. In Research Report on
Membrane Structures, pages pp. 1–6.
Ueshiba, T. (2006). An efficient implementation tech-
nique of bidirectional matching for real-time trinocu-
lar stereo vision. In Proc. of 18th Int. Conf. on Pattern
Recognition, pages pp.1076–1079.
Zhong, Y. and Xu, B. (2006). A physically based method
for triangulated surface flattening. Computer-Aided
Design, Vol. 38:pp. 1062–1073.
Virtual Flattening of a Clothing Surface by Integrating Geodesic Distances from Different Three-dimensional Views
547