
Performance Characterization of Absolute Scale Computation for 3D
Structure from Motion Reconstruction
Ivan Nikolov and Claus Madsen
Department of Architecture, Design and Media Technology, Aalborg University, Rendsburggade 14, Aalborg, Denmark
Keywords:
Scaling, 3D Reconstruction, Structure from Motion (SfM), GPS, Robustness.
Abstract:
Structure from Motion (SfM) 3D reconstruction of objects and environments has become a go-to process,
when detailed digitization and visualization is needed in the energy and production industry, medicine, culture
and media. A successful reconstruction must properly capture the 3D information and it must scale everything
to the correct scale. SfM has an inherent ambivalence to the scale of the scanned objects, so additional
data is needed. In this paper we propose a lightweight solution for computation of absolute scale of 3D
reconstructions by using only a real-time kinematic (RTK) GPS, in comparison to other custom solutions,
which require multiple sensor fusion. Additionally, our solution estimates the noise sensitivity of the calculated
scale, depending on the precision of the positioning sensor. We first test our solution with synthetic data to
find how the results depend on changes to the capturing setup. We then test our pipeline using real world data,
against the built-in solutions used in two state-of-the-art reconstruction software. We show that our solution
gives better results, than both state-of-the-art solutions.
1 INTRODUCTION
1.1 Object 3D Reconstruction
With the emergence of more and more powerful CPU
and GPUs, SfM software solutions have become wi-
despread and easier to use. This gives both more spe-
cialized industry, medicine and culture preservation
users the possibility to quickly capture objects and en-
vironments. Due to the nature of SfM, to create a de-
tailed reconstruction of both object and texture, users
need only a camera and the software. This gives SfM
solutions the edge, compared to other low-cost 3D re-
construction solutions, like the ones based on time-
of-flight (Corti et al., 2016), structured light (Sarbo-
landi et al., 2015) or stereo cameras (Sarker et al.,
2017). These solutions require appropriate hardware,
together with the specialized software, which gives
them a larger overhead, for users to get into. Exam-
ples of 3D reconstruction using these methods are ex-
tensively benchmarked by (Jamaluddin et al., 2017),
(Sch
¨
oning and Heidemann, 2016).
1.2 State of the Art
An important requirement for the state of the art SfM
software is for it to be both versatile and robust. This
is especially true for images taken in environments
with varying conditions and containing objects with
different shapes and sizes. Many of the state of the art
SfM solutions fall in the category of open-source soft-
ware like OpenSfM (VisualSFM, 2011), COLMAP
(Schonberger, 2016), etc. Other SfM solutions are de-
veloped as part of commercial products like Contex-
tCapture (Bentley, 2016), PhotoScan (Agisoft, 2010)
and RealityCapture (CapturingReality, 2016). All of
these solutions contain a whole processing pipeline
going from the input images to a dense point cloud
and mesh. One drawback that SfM has, is the am-
biguity of the scale of the reconstructed object. The
2D information extracted from images, does not al-
low determining of the absolute scale of the scanned
object. For obtaining this essential information, ad-
ditional information is needed from the user or from
external sensors.
This is why the programs also contain different
built-in solutions for scaling the final model. In most
cases these solutions are either using markers or ma-
nual distance measurement. This works only when
there is access to the reconstructed objects or surfa-
ces. This means that they are unfeasible for scanning
structures with drones or scanning hard to reach or
dangerous places. Another method is using the GPS
positions for finding the absolute scale of the object,
884
Nikolov, I. and Madsen, C.
Performance Characterization of Absolute Scale Computation for 3D Structure from Motion Reconstruction.
DOI: 10.5220/0007444208840891
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 884-891
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: The two sets of corresponding points. On the left an output screen from 3D reconstruction program with the camera
positions and a sparse point cloud, with unknown scale. On the right the same camera positions in a scaled real world metric
units from an external sensor. Establishing the absolute scale of the reconstruction involves estimation the transformation,
which will transfer the left set of points to the right.
but this way does not characterize the performance of
the scaling and do not take into consideration exter-
nal factors, which can influence the precision of the
scaling.
1.3 Using External Sensor Data for
Determining Scale and Noise
Sensitivity
We propose a solution for determining the absolute
scale for 3D SfM reconstructions using GPS posi-
tioning information, enhanced by RTK for a more
precise estimation of the camera for each image ta-
ken. Others have proposed method for using GPS
and RTK (Rabah et al., 2018), (Dugan, 2018) for ge-
oreferencing and enchanting the SfM reconstruction
workflow, but they do not focus on the scale of the
reconstructed objects. Our method is aimed at being
used as part of a unmanned aerial vehicle (UAV) so-
lution for scanning and 3D reconstruction of hard to
reach surfaces and objects. It also works only with
GPS data, in contrast with other methods using sen-
sor fusion (Sch
¨
ops et al., 2015). As the method is ai-
med for industrial and historical preservation use, not
only is the absolute scale needed, but also calculating
the uncertainty of said scale, as well as determining
how capturing conditions and external factors might
influence it. As an example, we show that when you
have 3 captured horizontally spaced camera positi-
ons from the reconstruction process, a scaled distance
of 100mm on a reconstructed object can be with un-
certainty of 0.1mm. While the same scaled distance,
when calculated from 18 captured horizontally spaced
camera positions has uncertainty of 0.007mm.
Our main contribution is this combination of esti-
mating the absolute scale and its sensitivity to noise,
which in the end gives both precise and robust results.
To test our approach, we first analyze the sensor
and determine its accuracy and precision. We then
do a series of simulated test scenarios to get a base-
line of the expected performance. Finally, we test the
method in a real world testing scenario and compare
results to the scaling results produced by the two 3D
reconstruction programs - ContextCapture and Pho-
toScan. We demonstrate that our method gives better
results than the state-of-the-art, while also providing
a reliable uncertainty metric.
2 METHODOLOGY
2.1 SfM Pipeline
To understand the proposed workflow, the SfM pi-
peline needs to be first explored. SfM relies on in-
formation captured from multiple images around the
scanned objects. Features are extracted from each
image and matched. Normally algorithms like SIFT
(Lowe, 2004), SURF (Bay et al., 2006) are used.
From these matched points a sparse 3D point cloud
can be triangulated using bundle adjustment (Triggs
et al., 1999) and the camera positions can be back-
projected. From these a dense point cloud and subse-
quent mesh can be created. The problem is that there
is no information in 2D images alone on how big the
scanned object is - is it a city or a model of a city?
This is also reflected in the calculated camera positi-
ons.
2.2 Least-squares Transformation
Estimation
When capturing the images, the positions of the ca-
meras can be saved in real world coordinates. The
GPS-RTK can be directly positioned on the camera
or on a drone caring the camera. To calculate the real
Performance Characterization of Absolute Scale Computation for 3D Structure from Motion Reconstruction
885
world scale of the reconstruction, the transformation
between the two sets of coordinates needs to be de-
termined - the ones calculated by the SfM software
and the ones given by the GPS-RTK. This is shown in
Figure1, where an output of SfM software is shown
on the left side and the GPS-RTK points are shown
on the right side.
Because there is clear a correspondence between
the SfM camera positions and the GPS-RTK posi-
tions and the unknown transformation consists only
of translation, rotation and uniform scaling, a sim-
ple least-squares estimation algorithm is conside-
red. An implementation of the classical algorithm by
(Umeyama, 1991) is chosen and customized for the
needs of the paper. For the algorithm to work the two
point sets need to have non-collinear points and no
outliers.
We need to also take into consideration the pro-
blem of the lever-arm offset between the GPS antenna
and the camera (Daakir et al., 2016). As an initial ca-
libration step the real-world distance between the two
is measured and used as an additional input for the
Least-Squares estimation algorithm.
a
i
= T (b
i
), a
i
∈ A, b
i
∈ B (1)
T =
sR
11
sR
12
sR
13
t
1
+ x
o f f
sR
21
sR
22
sR
23
t
2
+ y
o f f
sR
31
sR
32
sR
33
t
3
+ z
o f f
0 0 0 1
(2)
If the two point sets are A = [a
1
, a
2
, ..., a
m
], for the
known one and B = [b
1
, b
2
, ..., b
m
] for the unknown
one, where each set is comprised of m number of
points and each point has a x, y, z components. Then
the transformation matrix T between the two needs
to be calculated, such that it satisfies Equation 1. To
do that, the sum of squared errors e
2
shown in Equa-
tion 3 from (Umeyama, 1991), needs to be minimi-
zed, where s is the scale, R is the rotation and t is
the translation component of the transformation ma-
trix (Equation 2). The real world offset between the
two sensors is given as x
o f f
, y
o f f
, z
o f f
inputs.
e
2
(R, t, s) =
1
m
m
∑
i=1
||a
i
− (sRb
i
+t)||
2
(3)
To test out the algorithm’s results, a synthetic
point set of 18 points is created. The number of points
is chosen such that it coincides with the tests, perfor-
med later. A new set of points is then created, by gi-
ving the point set, a random translation, rotation and
scaling. The two sets are used in the least-square es-
timation algorithm. The result estimated transforma-
tion matrix is exactly the same as the one introduced
to the ground points to create the unknown ones. This
is seen in Figure 2, where the estimated transforma-
tion matrix is used on the Utah teapot, to transform it
to the coordinate’s initial position, together with the
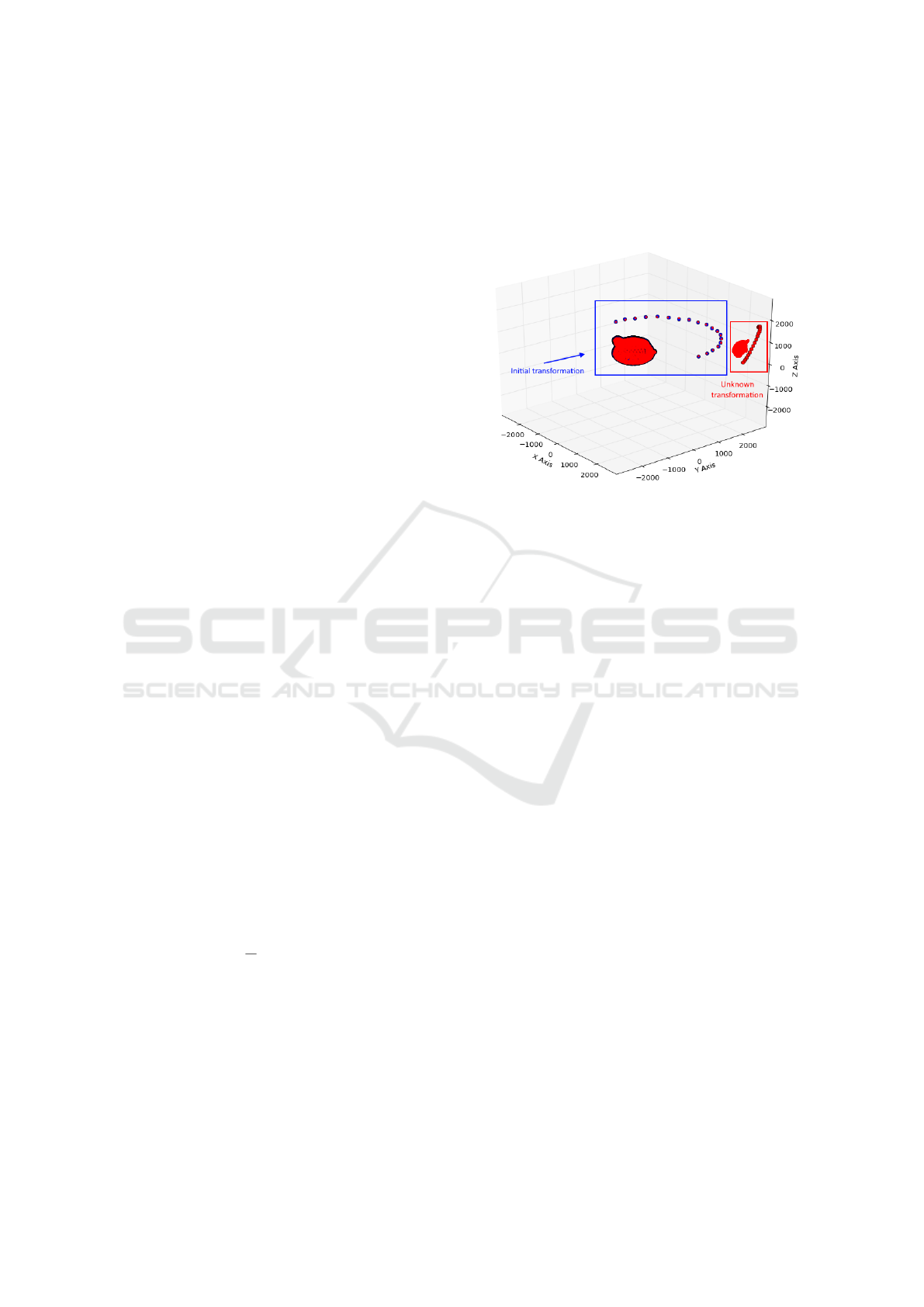
unknown positions.
Figure 2: Visualization of the output of the least-squares
transformation estimation algorithm. The initial position,
orientation and scale are first transformed to ”unknown”
ones. The estimation algorithm is then used to find the
transformation from the ”unknown” one to the initial one.
The Utah teapot is added for easier visualization.
In the real world this is not the case, as measuring
equipment is always a subject to additive noise. This
needs to be taken into consideration, when using the
least-squares estimation algorithm. This will trans-
form Equation 3, where C = A + N, with A being the
known locations and N = [n
1
, n
2
, ...n
m
] is the added
noise component, with each noise n
i
= [n
x
, n
y
, n
z
]
T
.
The next subsections will verify the sensor readings
and model the noise.
2.3 Verifying Sensor Readings
For the paper the sensor provided by DJI (DJI, 2017)
is used, as it has a very small margin of uncertainty in
the positioning information - less than 0.02m in ho-
rizontal direction and 0.03m vertically, in good we-
ather conditions. This precision needs to be verified,
before using it. Because the sensor works only when
attached to a drone controller, the whole platform is
used for the test. The sensor is started and its rea-
dings are saved each second for a period of 5 minu-
tes. The readings are taken when the whole platform
is on the ground, to eliminate inconsistencies from the
readings when the platform is in motion. The sen-
sor is then manually moved to another location and
the readings are again taken. The calculated position
standard deviation for the first point is 0.0175m in ho-
rizontal direction and 0.0244m in height and for the
second point the standard deviations are 0.0174m and
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
886
0.0251m respectively. The values are thus in the inter-
val given in the documentation by DJI. With the real
world positioning uncertainty verified, the next step
is to create a number of synthetic testing scenarios,
where the uncertainty is used as a noise component.
These scenarios are used to investigate aspects of how
the GPS-RTK noise influences scale noise.
2.4 Synthetic Testing Scenarios
For the synthetic tests to be as close to a real world
test, the point sets are setup as real SfM capturing
positions. The tests are designed to determine the
amount of camera positions needed and the amount
of vertical camera bands. To gather enough variation
in the calculated scale after the noise input in each of
the tests, the least-squares estimation step is done a
number of times, each time with a different sampling
of noise input.
2.4.1 Number and Sampling of Image Positions
The first synthetic test scenario looks at how the num-
ber of input camera positions affects the results of
the scale factor. The least-squares estimation method
requires at least two positions for estimation of the
transformation. In the paper by (Nikolov and Mad-
sen, 2016), a circular pattern of images is used, with
the position of each image, changing by 20 degrees.
This gave 18 images per circular pattern. For a sim-
pler and easier image capture for the real world test
scenarios described in the later sections, the circular
pattern is changed to a semi-circular one, leaving the
number of image positions to 18 again, giving a 10
degree separation between them. This gives the fi-
nal testing interval - 3 to 18 positions. The minimum
number of positions is set to 3, as at least 3 points are
needed to estimate the 3D transformation. To test this
we start with the full number of 18 positions going
from 0 to 180 degrees. Then every time we lower the
number of positions we do not just remove the last
one, but we resample the left ones so they always co-
ver the whole interval of 0 to 180 degrees, but have
larger distance between them.
The synthetic test is done once without resam-
pling, starting with 18 positions and removing posi-
tions, until only the first two are left. The second run
of the test is done with removing and resampling the
positions until only the 0 and 180 degree ones are left.
To model the positioning noise for each instance,
a random sampling of the uncertainty values captured
directly from the GPS-RTK. This of course introduces
the problem that not enough data has been captured
for a more diverse modeling of the uncertainty. We
will address this in the next subsection.
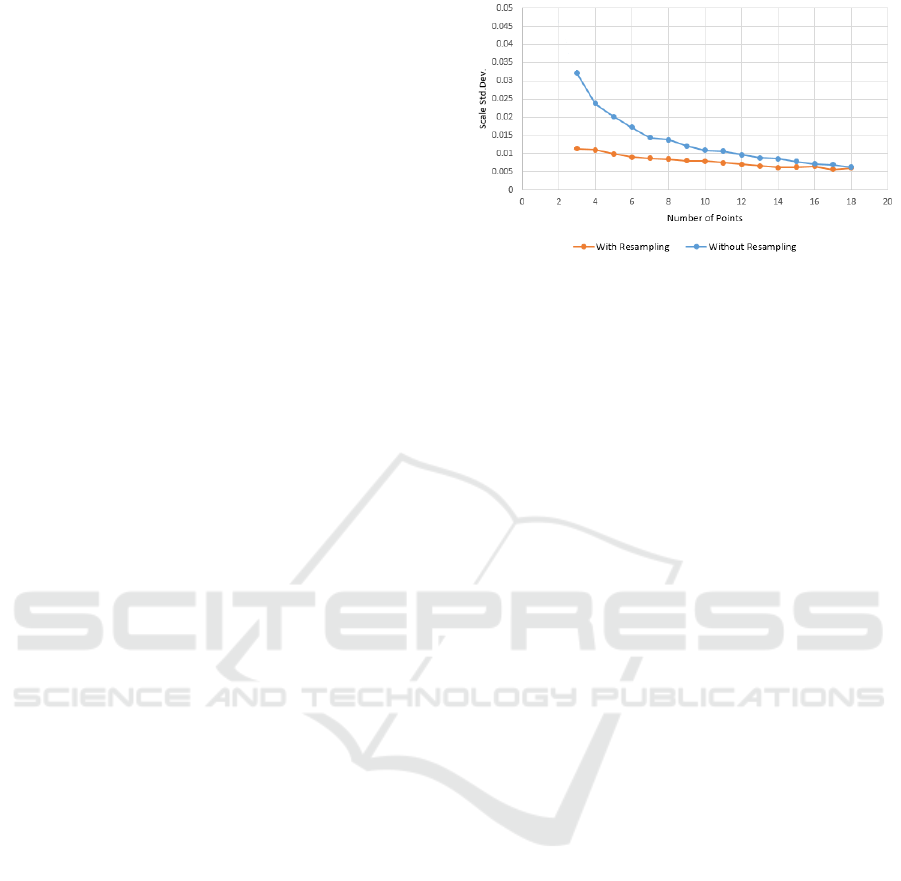
Figure 3: Results from the resampling versus no resampling
synthetic test. Resampling the captured positions so the first
and last one are always at 0 and 180 degrees, after removing
positioning information drastically lowers the standard de-
viation of the calculated scale.
The obtained results are shown in Figure 3. When
resampling the positions, as points are removed the
additional separation between points helps with lo-
wering the calculated scale’s error. This is especially
evident up until 10 image positions. After that the
two methods have comparable result standard devi-
ations, which converge at 16 image positions. This
shows that if not all image positions can be captured,
it is better that the captured ones have maximum se-
paration. In addition, the standard deviation settles at
around 12 or 13 image positions.
2.4.2 Number of Vertical Bands
The second test scenario is designed to check how
many vertical bands of images and image positions
are needed. The previous test showed that worse scale
uncertainty is achieved when no resampling of the
points is present. This test will explore if better scale
uncertainty can be achieved with more vertical sepa-
ration between the positions, if no resampling is used.
The work of (Nikolov and Madsen, 2016), shows that
three bands of photos give the best possible recon-
struction results. The paper however manually sca-
les the output meshes, so no conclusions are given on
how the scaling is affected by the bands. To test this
we choose to test with one, two and three position
bands respectively. This will determine if the additi-
onal spatial change between the positions in different
bands, given to the least-squares estimator, will make
a difference to the calculated scale factor.
The synthetic test is started with one band of ver-
tical separation and 18 camera positions. The number
of positions is reduced by one for each test until only
3 positions are left. The same is done for two and
three vertical band tests. The estimated scale factor
is calculated from each and standard deviation is cal-
culated from all the possible results. The results are
Performance Characterization of Absolute Scale Computation for 3D Structure from Motion Reconstruction
887

Table 1: Change in the scale standard deviation when going
from 1 to 2 bands and from 2 to 3 bands for the minimum
and maximum number of tested point positions. The change
from 2 to 3 bands is almost twice as small showing that the
gained accuracy, is not enough to offset the larger amount
of data, longer capturing time, etc.
Difference
Points 1 and 2 bands (%) 2 and 3 bands (%)
2 43.75 14.60
18 11.26 27.51
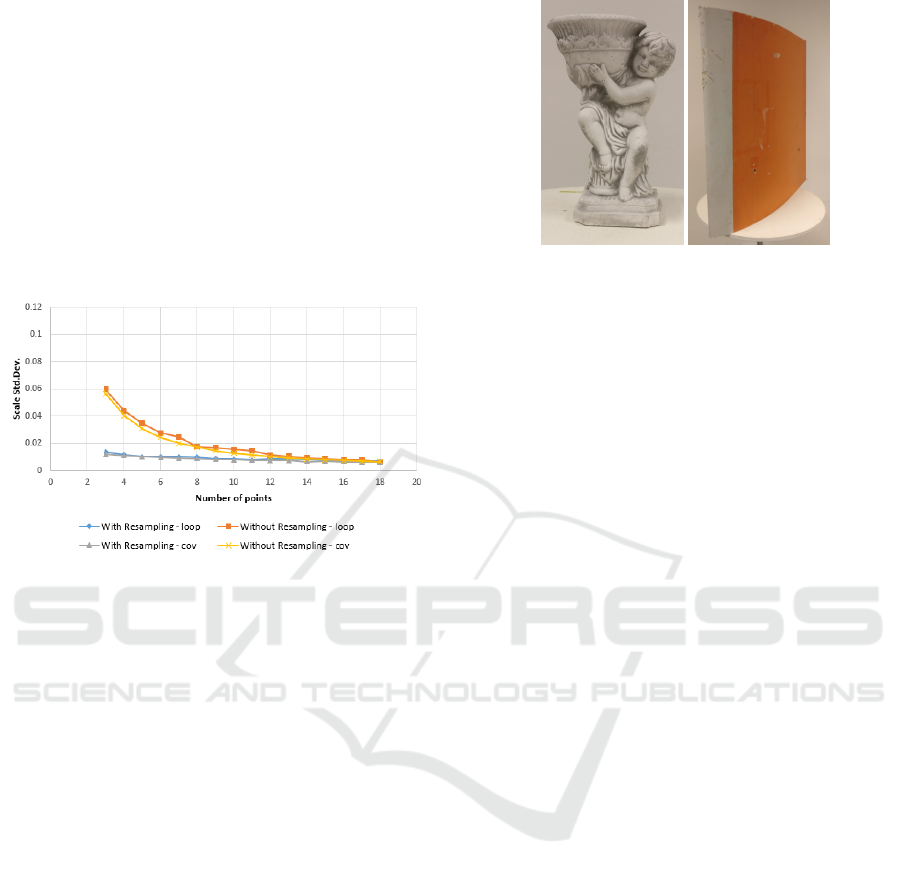
Figure 4: Results from capturing of positioning data from
different number of vertical bands. More vertical bands help
with the uncertainty of the scale. Both the larger number of
points and the additional spatial information help with that.
given in Figure 4.
As expected, the high standard deviation decre-
ases as we introduce additional vertical positions in
the form of more bands. This is both because of the
larger number of points and additional vertical sepa-
ration. If we look at the difference between the stan-
dard deviations of the calculated average scale we can
see a relation between the number of bands and num-
ber of points. The data is given in Table 1. When
more points are present in each band the gains won
by going from one to two bands are not big, but if
multiple bands need to be taken, then it will be much
better to capture three. When less points are present
in each band it is necessary to have as much bands
as possible, so the benefits from the additional num-
ber of points and separation can be felt. To strike a
balance between number of bands captured and scale
precision gains, we choose to use two bands for the
real world testing scenario for testing against the state
of the art.
2.5 Covariance Propagating of
Positioning Noise
The way the noise is introduced in these synthetic
tests and the performance characterization of the scale
calculation is found, can be cumbersome, as the test
needs to be done a large number of times. A better
solution to this is using covariance propagation (Ha-
ralick, 2000) of the noise. This will give the relation
between the uncertainty in each GPS-RTK position
and the uncertainty in the final calculated scale. The
idea has been shown to give good results (Madsen,
1997), as long as there are independent input parame-
ters, which are used in a function - no matter analyti-
cally or iteratively found, to calculate a set of output
parameters. As each captured GPS-RTK position is
used in the calculation of the scale factor through the
least-square estimation, this means that we can ex-
press the transformation calculation as represented as
s = f (C), where s is the estimated scale and C is the
GPS-RTK positioning set together with the introdu-
ced noise. We do not use the second positioning set B
obtained from the SfM reconstruction, as an input pa-
rameter, as it is treated as a constant. We use the met-
hod demonstrated in (Madsen, 1997), for determining
the covariance matrix of the input parameters. This of
course need to be done for each of the three dimensi-
ons for each of the points. The standard deviation of
the calculated scale will depend both on the standard
deviation of the uncertainty of the measured GPS-
RTK positions and the first derivative of the function.
To find the standard deviation of the scale, the first or-
der approximation needs to be done to the covariance
matrix, as seen in Equation 4 and then used together
with the dependence of the scale to the positions in
all 3 dimensions, as given in Equation 5. Where ∆ is
the covariance matrix of Q and is described as Equa-
tion 6, for each of its dimensions. Thus Q is a com-
bined vector containing all the dimensional data for
each position Q = [x
1
, y
1
, z
1
, ..., x
m
, y
m
, z
m
]
1x3m
∆ =
σ
2
x
1
0 0 . . . 0
0 σ
2
y
1
0 . . . 0
0 0 σ
2
z
1
. . . 0
. . . . . . . . . . . . . . . . . . . . . . . . .
0 . . . σ
2
x
m
0 0
0 . . . 0 σ
2
y
m
0
0 . . . 0 0 σ
2
z
m
3m×3m
(4)
σ
2
s
=
∂s
∂Q
∆
∂s
T
∂Q
(5)
∂s
∂Q
=
h
∂s
∂x
1
∂s
∂y
1
∂s
∂z
1
...
∂s
∂x
i
∂s
∂y
m
∂s
∂z
m
i
(6)
To test if the iterative approach and the covari-
ance propagation approach will yield the same re-
sults. Again the testing scenario of subsection 2.4.1
is used, both with and without resampled positioning
data. The results can be seen in Figure 5. The two
approaches achieve closely matched results for both
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
888
positioning data types. The average difference bet-
ween the calculated scale standard deviation from 3
to 18 points between the two approaches, without res-
ampling positioning data is 12.07%, while with res-
ampling the difference falls to 4.88%. In addition the
covariance propagation approach follows a smoother
overall curve of progression, meaning less chance for
random noise in the estimated scale standard devia-
tion. This also demonstrates that the covariance pro-
pagation method gives very accurate estimation of the
standard deviation of the scale, while bypassing the
assumptions about the nature of the uncertainty’s dis-
tribution.
Figure 5: Comparing the interations approach to the covari-
ance propagation approach for calculating scale uncertainty
from position uncertainty. The comparison is made for dif-
ferent number of input positions and a different way of res-
ampling the positions.
3 REAL WORLD TESTING
Two objects are chosen for the test. They can be seen
in Figure 6. The objects are chosen because they re-
present two different 3D reconstruction use cases - the
statue represents a digital heritage use case, while the
wind turbine blade represents an industrial use case.
Both cases require precise scale estimation.
For each of the two objects, two vertical bands of
18 images are taken in a semi-circle. The horizontal
separation between the images is 10 degrees, while
the vertical separation between bands is 20 degrees.
The images are taken with a Canon 5Ds at maxi-
mum resolution 8688x5792. This camera is chosen,
so enough information is captured from the objects
and the chance of the 3D reconstruction failing or ha-
ving errors is minimized.
The camera positions are manually determined
with a laser range finder. This is done so that any
possible random positioning accuracy fluctuations on
the GPS-RTK, caused by weather conditions, pres-
sure changes or environment effects are removed. A
second reason for this is that this way the experiment
(a) Angel Statue (b) Blade Segment
Figure 6: Two test objects used for 3D reconstruction.
Each represent different reconstruction challenges and re-
construction cases.
can be done in an indoor environment, removing the
possible illumination changes that can affect the final
reconstruction.
For the reconstruction both PhotoScan and Con-
textCapture software is used. The two solutions have
a number of built-in ways to scale a model - using
point markers that the user directly adds to the model
and have been measured beforehand, printing marker
trackers and putting them around the scanned object
and detecting them in the images, adding coordina-
tes to the camera positions from GPS. For testing our
proposed solution, we have chosen the method that
is most relevant - adding camera positions, together
with the images and using them to scale the object.
Because the built-in solutions do not have a mea-
surement of the uncertainty of the scaling, the compa-
rison will be done only on the basis of the calculated
scaling factors. For comparing the calculated scale
factors, the reconstructed objects will be scaled using
these factors and the distance will be measured ma-
nually on the real world object and the scaled recon-
struction.
As there are no ground truth scaled model to com-
pare the scales from the three methods, a manual me-
asuring of the objects is chosen. A number of parts of
the two real world objects are measured with a caliper,
which has a resolution of ±0.02mm, when measuring
objects below 100mm. The reconstructed and scaled
model are imported into CloudCompare (Girardeau-
Montaut, 2003) for measuring the same parts. By
measuring multiple parts of the models and averaging
the difference between the real world measurement
and the scaled model measurement, the effects of the
possible human errors, while manually measuring are
minimized.
The obtained scaled models are given in Figure 6.
Just by looking at the models, no observable diffe-
rence can be seen. Table 2 contains the average me-
Performance Characterization of Absolute Scale Computation for 3D Structure from Motion Reconstruction
889

(a) Angel Statue (b) Blade Segment
Figure 7: Reconstructed and scaled model. The ContextCapture and PhotoScan reconstructions are scaled using the built-in
solutions in the software. For our proposed solution(Paper), the unscaled ContextCapture reconstruction is used as basis. The
brightness difference in the models is due to the different ways the programs normalize the texture color. In addition the
model from PhotoScan reconstructed a larger portion of the blade and looks larger even though the scale is comparable.
asured distance errors from measuring ten different
parts in the real world and on the reconstructed ob-
jects, as well as the standard deviation from the mea-
surements. The results show that our proposed solu-
tion gives better results, because the mean error dis-
tance is the lowest compared to the other. Even if
we factor in the manual repeated measurement error,
shown as the standard deviation of the distance in the
table, the results obtained by our method are better or
the same as the build in solutions.
Table 2: Average distance error between measurements
from the real world object and the reconstructed model, for
the two tested objects - angel (A) and blade (B). The results
are in mm and the comparison is made between our pro-
posed solution (Paper) and the built-in scaling solutions in
ContextCapture (CC) and PhotoScan (PS).
Paper (mm) CC (mm) PS (mm)
A 0.35 ± 0.063 0.48 ± 0.069 1.04 ± 0.093
B 0.18 ± 0.012 0.23± 0.008 0.56 ± 0.009
σ
2
metric
= D
2
S f M
· σ
2
s
(7)
Furthermore the scale uncertainty in mm can be
also easily measured through our proposed solution.
We can take two random points from the unscaled
measured object and calculate the Euclidean distance
between them in unknown units - D
S f M
. As we have
calculated the scale uncertainty, denoted as σ
s
, we can
use Equation 7 as given in the book by (DeGroot and
Schervish, 2012), to calculate scaled distance uncer-
tainty σ
2
metric
in the chosen metric. To demonstrate
how this uncertainty can be useful, we recalculate the
real world reconstruction’s scale uncertainty, by using
different number of position data - from 2 to 18. Each
uncertainty is then used to find the metric uncertainty
of the distance between the same two randomly cho-
sen points. The results from the test can be seen in
Figure 8. The calculated metric uncertainty decreases
with the introduction of more and more point positi-
ons.
Figure 8: Correlation between the number of positions used
to calculate the scale uncertainty and the metric uncertainty
when measuring the real world distance between two points
on a object.
4 CONCLUSION AND FUTURE
WORK
In our paper we presented a pipeline for computing
the absolute scale of a 3D model reconstructed using
SfM. Our method relies on using external positioning
information from a GPS-RTK sensor, which has an
inherent uncertainty present in the provided data. We
provide an analysis of this uncertainty and how it pro-
pagates to the calculated absolute scale and results in
a scale uncertainty. Through a series of tests we de-
monstrated how changes to the number of positions
used and their spatial relationship can also influence
the scale uncertainty. We tested two ways to find the
scale uncertainty - an iterative method and a mathe-
matical covariance propagation of noise method.
Finally, we tested our proposed pipeline against
the scaling solutions available in state of the art SfM
software solutions - ContextCapture and PhotoScan.
We demonstrate that we achieve better results, on top
of providing more information about the scaling un-
certainty.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
890

As a extension to the current paper, we propose
testing the pipeline using data captured through drone
flights. This way the GPS-RTK positioning informa-
tion can be tested in different weather and environ-
ment conditions. Additionally the testing on objects
with different sizes will provide data on how the met-
hod scales with size and if the uncertainty depends on
the size of the scanned object. Finally, different po-
sitioning systems would also be tested and modeled -
both indoor and outdoor, to make the pipeline more
versatile.
ACKNOWLEDGEMENTS
This work is funded by the LER project no. EUDP
2015-I under the Danish national EUDP programme.
This funding is gratefully acknowledged.
REFERENCES
Agisoft (2010). Agisoft: Photoscan. http://www.agisoft.
com/. Accessed: 2018-09-06.
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:
Speeded up robust features. In European conference
on computer vision, pages 404–417. Springer.
Bentley (2016). Bentley: Contextcapture. https://www.
bentley.com/. Accessed: 2018-09-06.
CapturingReality (2016). Capturingreality: Reality capture.
https://www.capturingreality.com/. Accessed: 2018-
09-06.
Corti, A., Giancola, S., Mainetti, G., and Sala, R. (2016).
A metrological characterization of the kinect v2 time-
of-flight camera. Robotics and Autonomous Systems,
75:584–594.
Daakir, M., Pierrot-Deseilligny, M., Bosser, P., Pichard, F.,
Thom, C., and Rabot, Y. (2016). Study of lever-arm
effect using embedded photogrammetry and on-board
gps receiver on uav for metrological mapping purpose
and proposal of a free ground measurements calibra-
tion procedure. ISPRS Annals of Photogrammetry, Re-
mote Sensing & Spatial Information Sciences.
DeGroot, M. H. and Schervish, M. J. (2012). Probability
and statistics. Pearson Education.
DJI (2017). D-rtk gnss. https://www.dji.com/. Accessed:
2018-09-06.
Dugan, M. (2018). Rtk enhanced precision geospatial lo-
calization mechanism for outdoor sfm photometry ap-
plications. Robotics Research Journal.
Girardeau-Montaut, D. (2003). Cloudcompare. http://www.
cloudcompare.org/. Accessed: 2018-09-12.
Haralick, R. M. (2000). Propagating covariance in compu-
ter vision. In Performance Characterization in Com-
puter Vision, pages 95–114. Springer.
Jamaluddin, A., Mazhar, O., Jiang, C., Seulin, R., Morel,
O., and Fofi, D. (2017). An omni-rgb+ d camera rig
calibration and fusion using unified camera model for
3d reconstruction. In 13th International Conference
on Quality Control by Artificial Vision 2017, volume
10338.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International journal of computer
vision, 60(2):91–110.
Madsen, C. B. (1997). A comparative study of the robust-
ness of two pose estimation techniques. Machine Vi-
sion and Applications, 9(5-6):291–303.
Nikolov, I. and Madsen, C. (2016). Benchmarking close-
range structure from motion 3d reconstruction soft-
ware under varying capturing conditions. In Euro-
Mediterranean Conference, pages 15–26. Springer.
Rabah, M., Basiouny, M., Ghanem, E., and Elhadary, A.
(2018). Using rtk and vrs in direct geo-referencing of
the uav imagery. NRIAG Journal of Astronomy and
Geophysics.
Sarbolandi, H., Lefloch, D., and Kolb, A. (2015). Kinect
range sensing: Structured-light versus time-of-flight
kinect. Computer vision and image understanding,
139:1–20.
Sarker, M., Ali, T., Abdelfatah, A., Yehia, S., and Elaksher,
A. (2017). a cost-effective method for crack detection
and measurement on concrete surface. The Internatio-
nal Archives of Photogrammetry, Remote Sensing and
Spatial Information Sciences, 42:237.
Schonberger, J. L. (2016). Colmap. https://colmap.github.
io. Accessed: 2018-09-06.
Sch
¨
oning, J. and Heidemann, G. (2016). Taxonomy of 3d
sensors. Argos, 3:P100.
Sch
¨
ops, T., Sattler, T., H
¨
ane, C., and Pollefeys, M. (2015).
3d modeling on the go: Interactive 3d reconstruction
of large-scale scenes on mobile devices. In 3D Vision
(3DV), 2015 International Conference on, pages 291–
299. IEEE.
Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgibbon,
A. W. (1999). Bundle adjustmenta modern synthesis.
In International workshop on vision algorithms, pages
298–372. Springer.
Umeyama, S. (1991). Least-squares estimation of transfor-
mation parameters between two point patterns. IEEE
Transactions on Pattern Analysis & Machine Intelli-
gence, (4):376–380.
VisualSFM, C. W. (2011). A visual structure from motion
system.
Performance Characterization of Absolute Scale Computation for 3D Structure from Motion Reconstruction
891
