Mean and Variability in RNA Polymerase Numbers Are Correlated

to the Mean but Not the Variability in Size and Composition of

Escherichia Coli Cells

Bilena Almeida, Vatsala Chauhan, Vinodh Kandavalli and Andre Ribeiro

Laboratory of Biosystem Dynamics, BioMediTech Institute and Faculty of Biomedical Sciences and Engineering,

Tampere University of Technology, Tampere, Finland

Keywords: RNA Polymerase, Cell-to-cell Variability, Flow Cytometry, Single-cell Biology, Statistical Analysis.

Abstract: Cell morphology differs with cell physiology in general and with gene expression in particular. We

investigate the degree to which these relationships differ with medium richness. Using Escherichia coli cells

with ﬂuorescently tagged β’ subunits, flow cytometry, and statistical analysis, we study at the single-cell

level the correlation between parameters associated to cell morphology and composition (FSC, SSC, and

Width channels) and GFP tagged RNA polymerase (RNAp) levels (FITC channel). From measurements in

three media differing in richness (M63, LB, and TB) and, thus, cell growth rates, we find that the mean and

cell-to-cell variability in RNAp levels are correlated to the mean values of FSC, SSC, and/or Width.

Further, in all growth conditions considered, RNAp levels are positively correlated to FSC, SSC, and Width

at the single-cell level, with the correlation decreasing for increasing medium richness. Overall, the results

suggest that the mean and cell-to-cell variability in levels of RNAp, a master regulator of gene expression,

are correlated to the mean values of the parameters assessing the cellular morphology and composition, as

measured by flow cytometry, but they do not correlate to the degree of variability of these parameter values.

1 INTRODUCTION

In Escherichia coli, the concentration of RNA

polymerases (RNAp) is a key regulator of the rate of

transcription (McClure, 1980, 1985; Arkin, Ross and

McAdams, 1998; Kærn et al., 2005; Browning and

Busby, 2016). As this concentration differs even

between sisters cells (Cabrera and Jin, 2003;

Bratton, Mooney and Weisshaar, 2011; Yang et al.,

2014), it is an extrinsic factor for cell-to-cell

variability in gene expression (Elowitz et al., 2002;

Mäkelä, Kandavalli and Ribeiro, 2017).

One source of cell-to-cell variability in RNAp

numbers is the noise in the chemical processes

responsible for the production of RNAp (see e.g.

(Gillespie, 1977)). Other sources include variability

in cells’ health, morphology, and components

(Elowitz et al. 2002; Muthukrishnan et al., 2014;

Oliveira et al., 2016).

Here, we investigate the degree to which the

morphology and composition of the cells of a

population correlate with their mean and variability

in RNAp numbers. Since the environment is known

to affect the morphology and composition, we study

how this correlation differs with medium richness.

For this, we use E. coli strain RL1314 which has

GFP tagged β’ subunits (Bratton, Mooney and

Weisshaar, 2011). To assess both fluorescence levels

as well as parameters associated to cells’

morphology and composition, we use Flow

cytometry. Measurements are conducted in M63,

LB, and TB media, where growth rates differ. From

the measurements, we collect data on the cells’

green fluorescence intensity levels (a proxy for

RNAp numbers), and on the cells’ morphology

(size) and composition. Using the data, we searched

for statistically significant correlations between the

RNAp levels and morphology and composition, in

media differing in richness.

226

Almeida, B., Chauhan, V., Kandavalli, V. and Ribeiro, A.

Mean and Variability in RNA Polymerase Numbers Are Correlated to the Mean but Not the Variability in Size and Composition of Escherichia Coli Cells.

DOI: 10.5220/0007456102260233

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 226-233

ISBN: 978-989-758-353-7

2 METHODS

2.1 Bacterial Cells, Chemicals, Growth

Conditions, and Growth Rates

We used E. coli RL1314 with ﬂuorescently (GFP)

tagged β’ subunits (Bratton, Mooney and Weisshaar,

2011), generously provided by Robert Landick,

University of Wisconsin-Madison, U.S.A.. For cell

cultures, chemicals components for Luria-Bertani

(LB), terrific broth (TB) and M63 media were

purchased from LabM (UK) and Sigma-Aldrich.

Casamino acids and vitamins were purchased from

Gibco. LB medium components are 1 g tryptone, 0.5

g yeast extract and 1 g NaCl (pH – 7.0). Meanwhile,

the composition of TB medium per 100ml is 1.2 g

tryptone, 2.4 g yeast extract, 0.4% glycerol and TB

salts (KH2PO4 and K2HPO4). M63 medium was

prepared using M63 salts supplemented with 0.4%

glycerol, vitamins and 20% casamino acids.

Prior to flow cytometry, RL1314 cells were

grown overnight at 30 ºC with aeration and shaking

in the appropriate medium, diluted 1:1000 into the

fresh specific medium and allowed to grow at 37 ºC

at 250 rpm until an optical density at 600 nm

(OD

600

) of 0.4. Growth rates were measured by

growth curves obtained from cells at 37°C in the

appropriate medium (LB, TB and M63) with

antibiotics, using a spectrophotometer (Ultrospec 10;

GE Health Care). Cultures were grown overnight at

30°C with aeration and shaking at 250 rpm. Next,

overnight cultures were diluted into fresh medium to

an initial OD

600

of 0.01. The OD

600

values were

monitored every 20 min for 3.2 h.

2.2 Flow Cytometry

For flow cytometry (FC), cells from 5 ml of

bacterial culture were diluted 1:10000 into 1 ml PBS

vortexed for 10 seconds and a total of 50.000 cells

were tested in each run. Prior to every day

experiments, the analyzer was calibrated using

ACEA NovoCyte particle QC beads

(Cat.No.8000004). Data was collected using an

ACEA NovoCyte Flow Cytometer (ACEA

Biosciences Inc., San Diego USA) equipped with a

blue laser (488 nm) for excitation and the

fluorescein isothiocyanate channel (FITC) (530/30

nm filter) for detecting emitted light at a flow rate of

14 µl/minute and a core diameter of 7.7 µM. A PMT

voltage of 417 was used for FITC. To avoid

background signal from particles smaller than

bacteria, the detection threshold was set to 5000 in

FSCH analyses.

From the flow cytometry data, we study: i) FITC,

which measures the green fluorescence intensity

from a cell (a proxy for the number of RNA

polymerases in the cell); ii) Forward scatter (FSC),

which measures the light scattered at less than 10

degrees as a cell passes through the laser beam (a

proxy for cell size); iii) Side scatter (SSC), which

measures the light scattered at a 90 degree angle as a

cell passes through the laser beam (a proxy for cell

density); and, iv) Width (W), which measures the

duration of the signal, not impacted by the PMT

voltage, which also correlates with cell size. Except

for the Width, the FC informs on both the ‘Height’

(H) and ‘Area’ (A) of the signals. The H is the

maximum peak of the signal while the A is the

integration of the H measures over time.

Note that, in all conditions, we removed from the

data any cell with a negative or abnormally high or

low parameter value (which amounted to ~10-15%

of the cells in each medium condition). This is

necessary since, when ignoring one of the

parameters, the correlation between this and the

remaining ones cannot be obtained.

2.3 Correlations

Correlations between parameters extracted by FC

are obtained by linear regressions using the least-

squares fit method (95% confidence intervals),

applying the Matlab function fitlm that creates a

LinearModel object. We obtain the coefficient of

determination (R

) of the fitted regression line for

each case, along with the P-value of statistical

significance (derived from the F-test under the null

hypothesis that all regression coefficients equal

zero). If this P-value is smaller than 0.01, we reject

the null hypothesis that the line is a constant i.e., that

one variable does not differ with the other.

3 RESULTS

We investigate whether the cells’ morphology and

composition parameters measured by FC (FSC,

SSC, and Width channels) are correlated with RNAp

levels (FITC channel), and whether these

correlations differ with medium richness.

3.1 Growth Rates

We placed cells in LB (control), M63, and TB

media. For differences between conditions to be

significant,

cells should differ significantly in mean

Mean and Variability in RNA Polymerase Numbers Are Correlated to the Mean but Not the Variability in Size and Composition of

Escherichia Coli Cells

227

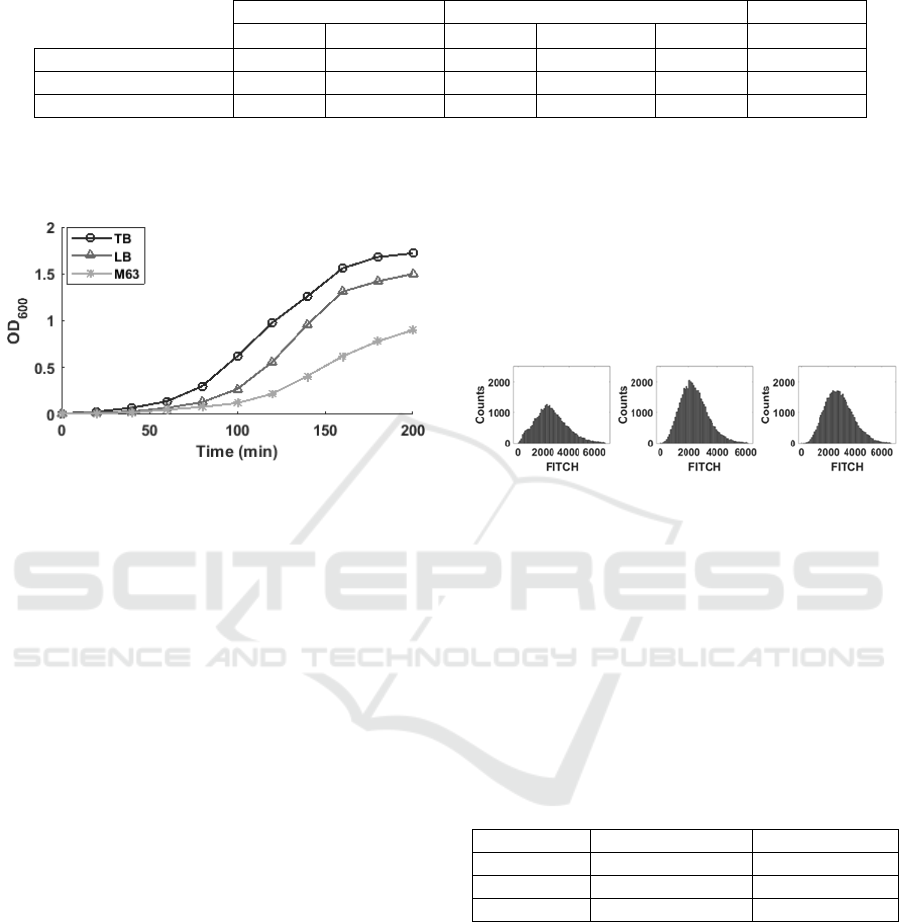
Table 1: Correlation (R

) between Height (H) and Area (A) for FITC, FSC and SSC in each medium.

M63 LB TB

P-value R

P-value

FITCA vs FITCH 0.86 <0.01 0.78 <0.01 0.73 <0.01

FSCA vs FSCH 0.94 <0.01 0.84 <0.01 0.83 <0.01

SSCA vs SSCH 0.98 <0.01 0.94 <0.01 0.96 <0.01

growth rates. This differences were verified in this

600

measurements.

Figure 1: Growth curves of cells of the RL1314 strain in

various media, as measured by OD

600

From Figure 1, M63, the poorest medium, has

the slowest growth rate, followed by LB and, finally,

TB, the richest medium with the fastest growth rate,

as expected from previous studies (see e.g.

(Goncalves et al, 2018)).

3.2 Correlation between Height (H)

and Area (A) of the Flow

Cytometer Parameters

Using FC, we extracted the values for FITC, FSC,

SSC and W for each cell. The flow cytometer also

informs on the ‘Height’ (H) and ‘Area’ (A) of the

signals, except for W. We evaluated the correlation

between the H and A signals of FITC, FSC, and SSC

by least-squares fits (Methods) to measure the R

fitted regression lines, along with the P-value of

statistical significance (Table 1).

In all cases we obtained ‘high’ positive R

values

indicating that the fit approximates well the data, in

a positive fashion. Further, all P-values are smaller

than 0.01, from which we conclude that the data is

well explained by a linear least-squares regression fit

between the pairs of variables. As such, from here

onwards, we only use the parameters FITCH, FSCH

and SSCH, along with W.

3.3 RNA Polymerase Numbers as a

Function of Medium Richness

For this, we measured the single-cell fluorescence

intensities of RNAp (FITCH channel) in each

medium. Figure 2 shows the distribution of the

number of cells with given FITCH values for each

medium.

Figure 2: Distribution of the number of cells with given

values of FITCH in each medium, as measured by flow

cytometry: Left: M63; Middle: LB; Right: TB.

To assess if the distributions differ statistically,

we performed Kolmogorov-Smirnov tests (KS-test)

of statistical significance between all pairs of

conditions (the null hypothesis is that the two data

sets belong to the same distribution). In all cases, the

P-value was smaller than 0.05, from which we

conclude that they differ in a statistical sense.

Table 2: Mean and coefficient of variation (CV) of the

distributions of FITCH (proxy for RNAp numbers) in each

medium condition.

Medium Mean(FITCH) CV(FITCH)

M63 2.6x10

0.47

LB 2.4x10

0.40

TB 2.8x10

0.37

To assess the behavioral trend of RNAp levels

with increasing medium richness, we first calculated

the mean and coefficient of variation (CV) of each

distribution. From Table 2, we find that the

CV(FITCH) decreases with medium richness, while

the mean(FITCH) is minimized in LB medium.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

228

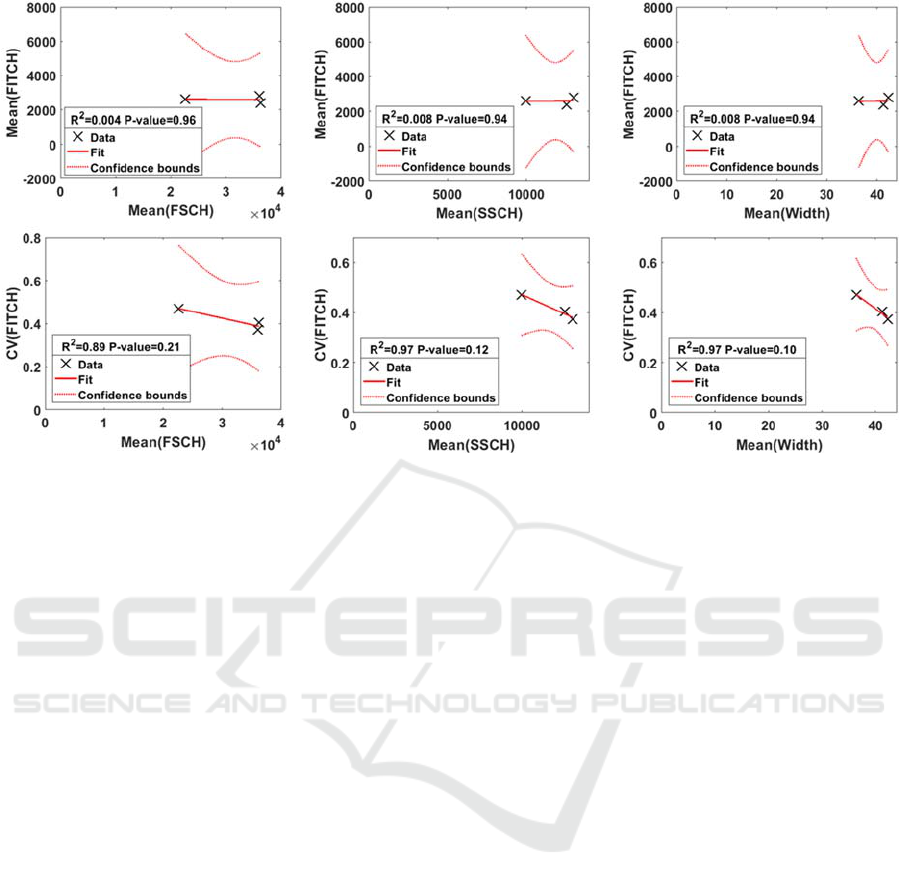
Figure 3: Top: Mean values of FITCH (proxy for RNAp numbers) plotted against the mean values of FSCH, SSCH and

Width (proxies for cell size and composition), respectively, in the three media considered (M63, LB, and TB), along with

the linear least-squares regression fits and confidence intervals. Bottom: coefficient of variation (CV) of FITCH values

plotted against the mean values of FSCH, SSCH and Width, respectively, in the three media considered (M63, LB, and TB),

along with the linear least-squares regression fits and confidence intervals.

3.4 Cell Morphology and Composition

as a Function of Medium Richness

Next, we investigated how the morphology and

composition as seen by parameters obtained by FC

differ, at the population level, with medium richness.

For this, we obtained the mean and CV of FSCH,

SSCH, and W at the single-cell level, in each

medium (Table 3). We find that, in general, the

mean values of FSCH, SSCH, and W increase with

increasing medium richness. Meanwhile, their CV

do not exhibit (linear) relationships with medium

richness.

3.5 Correlation between Cell

Morphology and Composition and

RNAp Levels against Medium

Richness

To validate the above conclusions, we tested for the

occurrence of linear correlations between the mean

values of FSCH, SSCH and W with the mean and

CV of RNAp levels as a function of medium

richness. Figure 3 (Top), shows that there are no

such statistically significant correlations.

Similarly, from Figure 3 (Bottom), there are no

statistically significant negative correlations between

the cell-to-cell variability in RNAp levels and the

mean values of FSCH, SSCH and W. However, if

more conditions were considered (e.g. medium of

intermediate richness between those tested), linear

correlations might become statistically significant.

Thus, we hypothesized that FSCH, SSCH and W,

which differ with medium richness, are negatively

correlated to the cell-to-cell variability in RNAp, but

not to the mean.

3.6 Correlation by Classes between

Cell Morphology and Composition

and RNAp Levels

From the data, it is visible the presence of much cell-

to-cell variability in FSCH, SSCH and W, even

within a given medium condition. This hampers the

ability to detect correlations between these

parameters and RNAp levels.

However, if such correlations exist, they should

become enhanced if, instead of analyzing the data

based on the growth condition, one instead classifies

the cells based on the values of FSCH, SSCH and W

(top panels in Figure 4).

Mean and Variability in RNA Polymerase Numbers Are Correlated to the Mean but Not the Variability in Size and Composition of

Escherichia Coli Cells

229

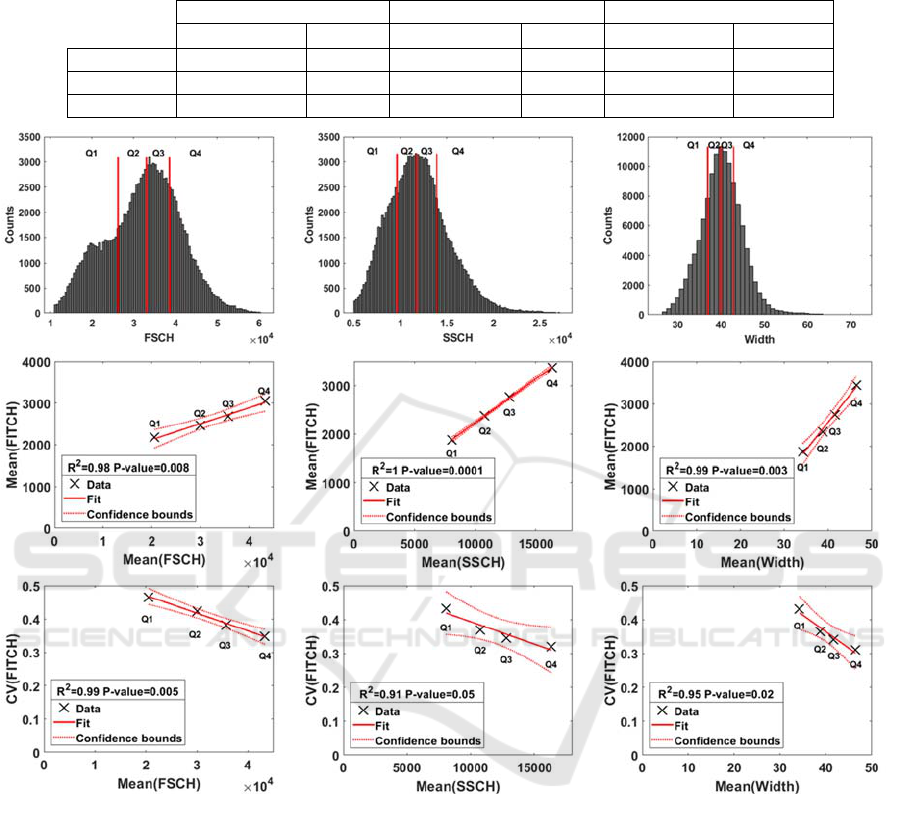
Table 3: Mean and coefficient of variation (CV) of FSCH, SSCH, and Width (proxies for cell size and composition) in each

medium condition.

M63 LB TB

Mean CV Mean CV Mean CV

FSCH 2.26x10

0.27 3.62x10

0.21 3.61x10

0.15

SSCH 9.98x10

0.27 1.26x10

0.28 1.30x10

0.21

W 36.41 0.12 41.30 0.01 42.29 0.09

Figure 4: Top: Distributions of FSCH, SSCH and Width (proxies for cell size and composition) values in individual cells

from all media; Center: Division of the data sets into quartiles and scatter plots Mean(FSCH) and Mean(FITCH, proxy for

RNAp numbers), Mean(SSCH) and Mean(FITCH) , and Mean(Width) and Mean(FITCH); Bottom: Division of the data sets

into quartiles and scatter plots Mean(FSCH) and CV(FITCH), Mean(SSCH) and CV(FITCH) , and Mean(Width) and

CV(FITCH).

We expect that, if the mean values of SSCH,

FSCH, and W can explain the CV(FITCH), then the

linear correlations should be equal or stronger than

when partitioning the data according to the medium.

Further, the P-values should be smaller than 0.01,

implying that the correlations are statistically

significant.

Figure 4 validates this hypothesis, i.e., when

partitioning cells according to the values of SSCH,

FSCH, and W, respectively, one finds strong,

statistically significant, negative linear correlations.

We conclude that the cell-to-cell variability in

RNAp levels decreases for increasing mean values

of FSCH, SSCH, and/or W, which are proxies for

cell size and/or density. Meanwhile, also from

Figure 4, mean RNAp levels increase with mean

values of FSCH, SSCH, and W.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

230

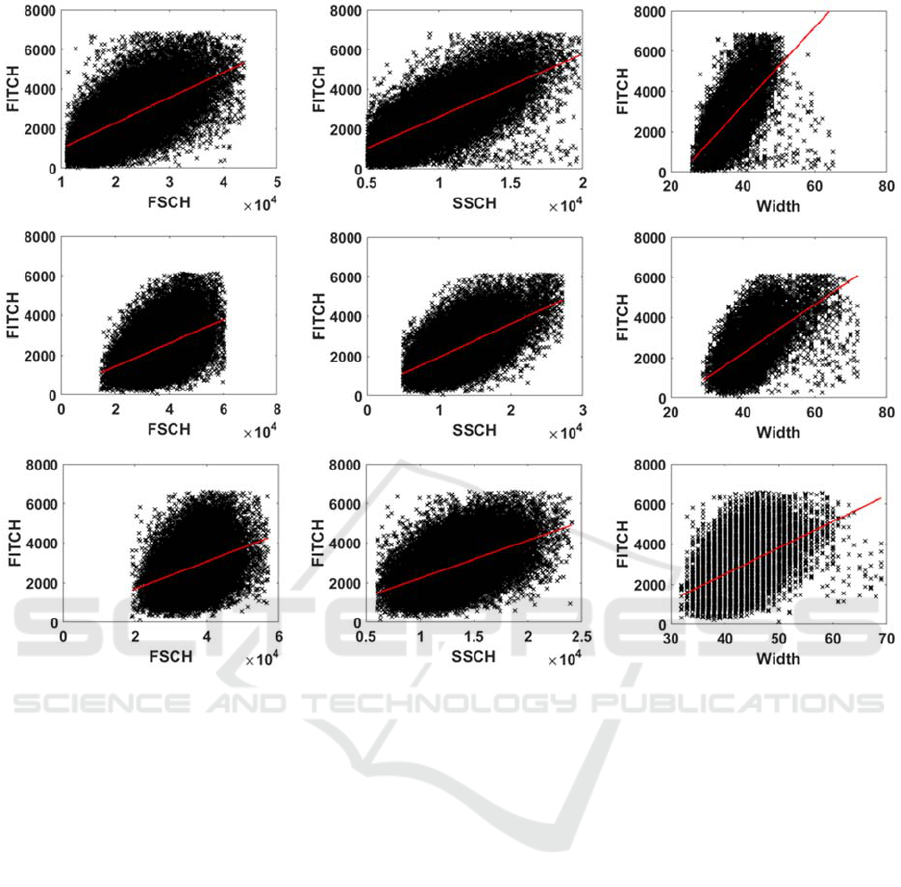
Figure 5: Scatter plots between single-cell values of FITCH (proxy for RNAp numbers) and FSCH, SSCH and Width

(proxies for cell size and composition), respectively, in each medium. Top: M63; Center: LB; Bottom: TB. The solid red

line is the linear least-squares regression fit.

3.7 Correlation by Classes between the

Cell-to-cell Variability in Cell

Morphology and Composition and

in RNAp Levels

We searched for correlations between the cell-to-cell

variability in cell morphology and composition and

the mean and the cell-to-cell variability in RNAp

levels. To obtain classes of cells with differing

variability in these parameters, we made use of

random sampling from the entire set of cells

gathered from all conditions. Namely, for

assembling the values for each class, we randomly

selected 10000 cells and obtained the CV of this set.

This was performed 1000 times. Next, from the

1000 sets, we selected the 10 sets with minimal and

the 10 sets with maximal cell-to-cell variability in

FSCH, SSCH, and W, respectively. We obtained the

CV of the parameter value for each set, and

calculated the average CV of the 10 sets of cells. For

each of these sets, we also obtained the mean and

CV of the RNAp levels of individual cells. As we

found no statistically significantly linear correlation

values below 0.15), we conclude that, unlike for

mean values, the cell-to-cell variability in SSCH,

FSCH, and W, cannot explain the mean and cell-to-

cell variability in RNAp numbers.

3.8 Relationship between Cell

Morphology and Composition and

the RNAp Levels at the Single-Cell

Level

Having found a correlation between the mean and

cell-to-cell variability in RNAp levels and the mean

values of FSCH, SSCH, and/or W of cell

populations, we studied whether such correlations

are significant at the single-cell level, i.e. in a

population of cells in the same medium.

Mean and Variability in RNA Polymerase Numbers Are Correlated to the Mean but Not the Variability in Size and Composition of

Escherichia Coli Cells

231

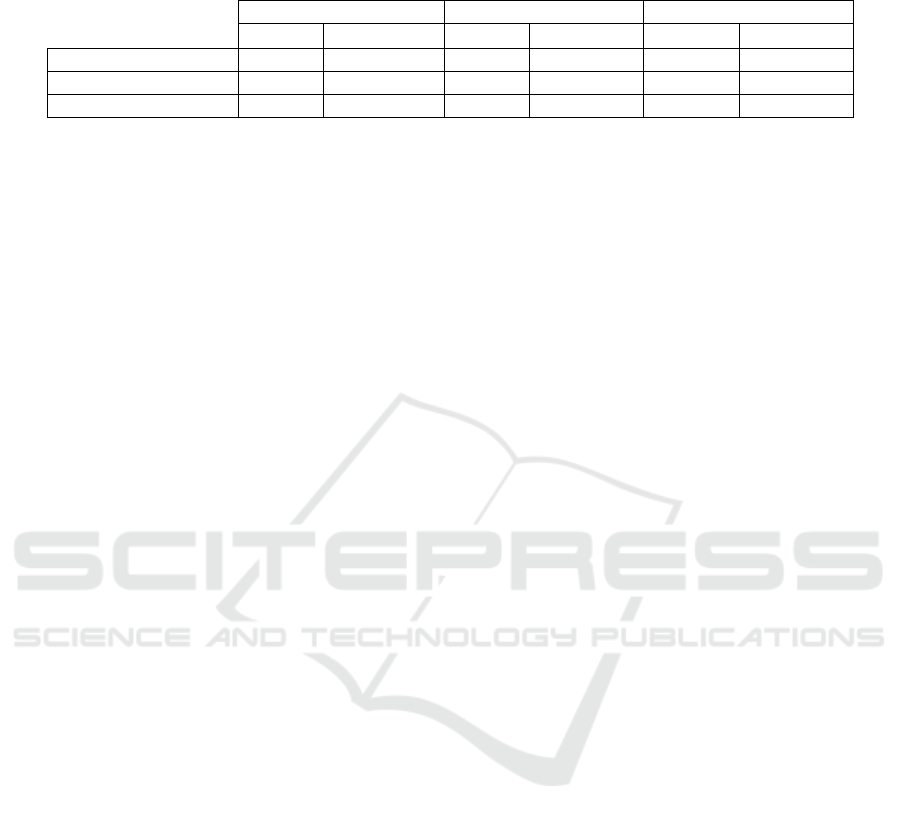
Table 4: Correlation (R

) between FITCH (proxy for RNAp numbers) and FSCH, SSCH, and Width (proxies for cell size

and composition) in each medium.

M63 LB TB

P-value R

P-value

FITCH vs FSCH 0.39 <0.01 0.21 <0.01 0.13 <0.01

FITCH vs SSCH 0.49 <0.01 0.36 <0.01 0.25 <0.01

FITCH vs W 0.47 <0.01 0.34 <0.01 0.24 <0.01

We searched for correlations between single-cell

values of FITCH and the respective values of FSCH,

SSCH and W (Figure 5), by performing fits by linear

regression (least-squares fit method). Also, we

obtained the P-values of statistical significance

(Table 4), by applying F-tests (Methods).

From Figure 5 and Table 4, in all media, the

linear fits are statistically significant, as the P-values

from the least-squares regression fits are smaller

than 0.01 (Table 4). Meanwhile, from the R

values,

we find that the goodness of fit decreases for

increasing medium richness.

4 CONCLUSIONS

Our results indicate that the mean and cell-to-cell

variability in RNAp numbers in E. coli cells differs

with parameter values associated to the cell size and

composition, as measured by flow cytometry. In

particular, the mean increases and the variability

decreases as each of these parameter values

increases. At the population level, these changes can

only be detected by classifying cells according to the

values of FSCH, SSCH and Width, respectively.

Analyzing the data at the single-cell level, one also

finds these correlations, being more pronounced in

poor growth medium.

We expect this knowledge to be relevant in

studies of gene expression dynamics in various

media, as the amount of RNAp is a key regulatory

mechanism of transcription dynamics. Namely, our

results suggest that the cell-to-cell variability in gene

expression may differ not only due to intrinsic noise

in gene expression and extrinsic factors, but also due

to the medium-dependence of the mean values of

FSCH, SSCH and Width.

At present, we cannot explain why the cell-to-

cell variability in SSCH, FSCH, and Width are not

correlated to the cell-to-cell variability in RNAp

numbers, while being correlated to the mean RNAp

numbers. An answer to this question may be of

relevance, as the RNAp is a master regulator of gene

expression in bacteria, and the answer may reveal

aspects of how their numbers are regulated. Thus,

the answers should contribute to a better

understanding of the modifications that these

organisms undergo following environmental

changes.

REFERENCES

Arkin, A., Ross, J. and McAdams, H. H. (1998)

‘Stochastic kinetic analysis of developmental pathway

bifurcation in phage λ-infected Escherichia coli cells’,

Genetics, 149(4), pp. 1633–1648. doi: 10.1016/0092-

8674(82)90456-1.

Bratton, B. P., Mooney, R. A. and Weisshaar, J. C. (2011)

‘Spatial distribution and diffusive motion of rna

polymerase in live Escherichia coli’, Journal of

Bacteriology, 193(19), pp. 5138–5146. doi:

10.1128/JB.00198-11.

Browning, D. F. and Busby, S. J. (2016) ‘Local and global

regulation of transcription initiation in bacteria’,

Nature Reviews Microbiology. Nature Publishing

Group, 14(10), pp. 638–650. doi:

10.1038/nrmicro.2016.103.

Cabrera, J. E. and Jin, D. J. (2003) ‘The distribution of

RNA polymerase in Escherichia coli is dynamic and

sensitive to environmental cues’, Molecular

Microbiology, 50(5), pp. 1493–1505. doi:

10.1046/j.1365-2958.2003.03805.x.

Elowitz, M. B. et al. (2002) ‘Stochastic gene expression in

a single cell: Supporting online material’, Science,

297, pp. 1183–1187.

Gillespie, D. T. (1977) ‘Exact stochastic simulation of

coupled chemical reactions’, Journal of Physical

Chemistry, 81(25), pp. 2340–2361. doi:

10.1021/j100540a008.

Kærn, M. et al. (2005) ‘Stochasticity in gene expression:

From theories to phenotypes’, Nature Reviews

Genetics, 6(6), pp. 451–464. doi: 10.1038/nrg1615.

Mäkelä, J., Kandavalli, V. and Ribeiro, A. S. (2017)

‘Rate-limiting steps in transcription dictate sensitivity

to variability in cellular components’, Scientific

Reports, 7(1), pp. 10588. doi: 10.1038/s41598-017-

11257-2.

McClure, W. R. (1980) ‘Rate-limiting steps in RNA chain

initiation.’, Proceedings of the National Academy of

Sciences, 77(10), pp. 5634–5638. doi:

10.1073/pnas.77.10.5634.

McClure, W. R. (1985) ‘Mechanism and Control of

Transcription Initiation in Prokaryotes’, Annual

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

232

Review of Biochemistry, 54(1), pp. 171–204. doi:

10.1146/annurev.bi.54.070185.001131.

Muthukrishnan, A. B. et al. (2014) ‘In vivo transcription

kinetics of a synthetic gene uninvolved in stress-

response pathways in stressed Escherichia coli cells’,

PLoS ONE, 9(9). doi: 10.1371/journal.pone.0109005.

NSM Goncalves et al (2018) Temperature-dependence of

the single-cell kinetics of transcription activation in

Escherichia coli. Physical Biology 15(2):026007.

DOI:10.1088/1478-3975/aa9ddf

Oliveira, S. M. D. et al. (2016) ‘Temperature-Dependent

Model of Multi-step Transcription Initiation in

Escherichia coli Based on Live Single-Cell

Measurements’, PLoS Computational Biology, 12(10).

doi: 10.1371/journal.pcbi.1005174.

Yang, S. et al. (2014) ‘Contribution of RNA polymerase

concentration variation to protein expression noise’,

Nature Communications, 5, pp. 1–9. doi:

10.1038/ncomms5761.

Mean and Variability in RNA Polymerase Numbers Are Correlated to the Mean but Not the Variability in Size and Composition of

Escherichia Coli Cells

233