Pattern Matching in Discrete Models for Ecosystem Ecology

Cinzia Di Giusto

, C

edric Gaucherel

, Hanna Klaudel

and Franck Pommereau

Universit

e C

ote d’Azur, CNRS, I3S, France

AMAP - INRA, CIRAD, CNRS, IRD, Universit

e Montpellier, France

IBISC, Univ Evry, Universit

e Paris-Saclay, Evry, France

Keywords:

Rewriting Systems, Similarity Rate, Pattern Matching, Ecosystems.

Abstract:

In this paper we consider discrete qualitative models of ecosystems viewed as collections of interacting living

(animals, plants. . . ) and nonliving entities (air, water, soil. . . ), whose conditions of appearance/disappearance

are controlled by a set of formal rules (i.e., processes). We present here a rule-based method allowing to

compare ecosystems. The method relies on a measure of similarity and on an optimization algorithm. In

addition, the proposed method allows to detect patterns (i.e., ecological processes or sets of processes) in

ecosystems. We have validated the method by applying it against a set of models and patterns provided by

ecologists.

1 INTRODUCTION

Ecosystems are deﬁned by complex processes of

highly different nature: e.g. bio-ecological, physico-

chemical and socio-economical. The dynamics of

such systems is difﬁcult to grasp as it is the result of

an intricate interplay between a large number of pro-

cesses: the functioning of living species (fauna and

ﬂora) and the dynamics of soil and climate. In ad-

dition, all these entities and processes are inﬂuenced

and often highly impacted by human activities.

Understanding the functioning of ecosystems is

thus crucial for a more sustainable management of

them. Indeed, we face today fast and dangerous

changes of most ecosystems (due to climate change,

to human activities. . . ) that we are compelled to un-

derstand so to appropriately react. Unfortunately, in

practice, the development and analysis of models of

ecosystems remain a challenge and constitutes a crit-

ical bottleneck as they are usually treated on a case-

by-case basis with few generalizations.

One relevant way of improving our understand-

ing of ecosystems functioning is to provide more for-

mal frameworks. They have proven to be valuable

for speeding up and better controlling the decision

procedures. Similarly to what happens in biology,

ordinary differential equations (ODE) are the dom-

inant modeling methodology for ecosystems (May,

1972, Lotka, 1925). The drawbacks of such models

are that: i) they usually need to quantify various pa-

rameters (mostly unknown). ii) They are not able to

faithfully represent the time scale required for obser-

vation of ecological processes which is usually large.

iii) On top of this, analytic solutions usually do not

exist and models often represent averaged and some-

times unrealistic behaviors of ecosystems. In contrast,

while discrete qualitative models are high level ab-

stractions of observed processes, they allow unrav-

eling the tangled causal relationships between sys-

tem’s entities (i.e. material constitutive components).

The success of discrete qualitative approaches is wit-

nessed, for instance, in systems biology with for-

malisms like Petri nets (Baldan et al., 2010), Boolean

networks (Thomas, 1973), process algebras (Cardelli,

2005) and rewriting systems (Giavitto et al., 2004), to

cite a few.

In ecology, discrete qualitative modelling is still

pioneering and under exploited. Approaches such

as (Gaucherel et al., 2012, Gaucherel et al., 2014),

where the authors study the driving rules needed to

change agricultural mosaics and model contrasted

landscapes, are promising. However, much more may

be obtained by developing original solutions based on

the suitable application of existing theory and associ-

ated (automated) tools. One of the goals of this paper

is to contribute in this regard.

As a starting point of our developments we take

a general discrete qualitative formalism proposed in

(Gaucherel and Pommereau, 2017). Ecosystems are

modeled as a set of (living and nonliving) entities

Di Giusto, C., Gaucherel, C., Klaudel, H. and Pommereau, F.

Pattern Matching in Discrete Models for Ecosystem Ecology.

DOI: 10.5220/0007485801010111

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 101-111

ISBN: 978-989-758-353-7

101

together with a set of rewriting rules expressing the

conditions of their appearance/disappearance (i.e., the

ecosystem component responses). These rules may

be interpreted as the functioning bricks of landscape

modelling. Each rule is, thus, part of a broader pro-

cess describing the behavior of the whole ecosystem.

Yet, there are processes that are common to sev-

eral ecosystems: e.g.–for species interactions– preda-

tion, competition, symbiosis. . . and it is crucial to be

able to identify them to better describe the ecosys-

tem under study. Hence, we can raise the following

questions: How can we detect whether a given pro-

cess is present in an ecosystem? Is the introduction

of a new entity causing the appearance of a known

process? Indeed, to detect wanted or unwanted inter-

action patterns would guide decisions for taking ac-

tions according to the management objectives, such

as preventing or reinforcing some ecosystemic pro-

cesses or states. Identify certain ecological processes

or interaction patterns –in a more computer science

oriented terminology– by employing classical graph-

theoretical methods on the state space is ineffective.

Indeed, in realistic ecosystem models, the modeled

dynamics usually leads to huge state spaces (often

hundreds of thousands of states). It is more efﬁcient

to search for patterns by referring only to the (limited)

syntactical system speciﬁcation as similar processes

look similar at the rule level.

From a more general point of view, a pattern

search corresponds to a variant of the problem of as-

sessing the similarity between models of ecosystems.

In order to compare two models of ecosystems, we

introduce a pair of mappings, the ﬁrst identifying en-

tities and the latter rules, and a similarity measure ex-

pressed as a scoring function. This scoring majors

the number of matched entities and rules, and penal-

izes those that do not perfectly match. Similarity is

then deﬁned as an optimization problem through the

scoring function. Indeed, the scoring function with

optimal value uniquely determines the mappings of

entities and rules. This way the deﬁnition of the scor-

ing function is used to search for interaction patterns

in the rule-based models of ecosystems. As the com-

plexity of this kind of search is exponential, it is not

always possible in realistic cases to ﬁnd optimal solu-

tions in a reasonable time. Nevertheless, optimization

tools generally allow obtaining a sub-optimal solution

quite efﬁciently, solutions that can then be reﬁned.

We implemented a prototype that allows encod-

ing the matching of two models into a pseudo-

Boolean optimization problem and invoking tool

Sat4j (Le Berre and Parrain, 2010) to solve it. We

applied this prototype to systematically match a col-

lection of predeﬁned interaction patterns against a set

of models of “real” ecosystems.

The paper is structured as follows: Section 3 in-

troduces the formal modeling of ecosystems we have

used and presents running examples. Section 4 de-

ﬁnes similarity measures used to compare ecosystems

and discusses possible extensions of them. Several

comparisons between ecosystems are used as illustra-

tions for the scoring function. In Section 5, we present

the results of our main case study: a search of inter-

action patterns in realistic ecosystems. Next section 2

is devoted to an overview of related work, while some

concluding remarks and perspectives are presented in

Section 6.

2 RELATED WORK

The model of ecosystems developed in this paper

is an instance of the more general family of rewrit-

ing systems (Terese, 2003). Such systems have been

shown convenient in formalizing models, in particu-

lar for systems biology and chemistry. In these do-

mains, we thus ﬁnd formalizations that are reminis-

cent of ours: the Biocham (Fages and Soliman, 2008),

the κ-calculus (Danos and Laneve, 2004), reaction

systems (Ehrenfeucht and Rozenberg, 2007), activity

networks (Delaplace et al., 2018), P-systems (Paun

et al., 2011), cellular automata (Gaucherel, 2006, Ag-

nihotri and Sharma, 2015) that describe the evolution

of cells and/or molecules applying rewriting rules.

Yet, the question of similarity appears rather novel

in rewriting systems. In a broader context, it is usu-

ally associated to the notion of equivalence. In con-

current systems like ours, equivalences are usually se-

mantics based, notable examples are partial ordering

equivalences, trace equivalence (van Glabbeek and

Goltz, 1989), bisimulation (Sangiorgi, 2011), prin-

cipal transition sequences (Wang et al., 2010), etc.

These notions are usually explored in theory and tai-

lored to highly abstracted languages, moreover com-

puted with a few existing tools. In practice, we can-

not expect to use such approaches on the huge state

spaces generated from detailed and realistic (qualita-

tive) models of ecosystems.

Works that are closer to ours can therefore be

found in domains in which models use structural as-

pects rather than their behaviors. For instance in

systems biology, several similarity measures can be

found (a good survey summarizing the used tech-

niques may be found in (Henkel et al., 2018)). Tech-

nically speaking, these methods include the anal-

ysis of similar pathways through a structural ap-

proach, namely the search of t-invariants in Petri net

models (Baldan et al., 2013a, Baldan et al., 2013b,

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

102

Grafahrend-Belau et al., 2008). They also deﬁne a

similarity score, but our goal and underlying mod-

elling are considerably different.

Another domain that focuses on similarity rates

is business process modeling. For instance in (Xiao

et al., 2009), the authors evaluate the similarity of

Petri nets by comparing the set of structural elements

such as places and transition arcs. Similarity is based

on rates of identical elements. Instead, our approach

is ﬁner-grained and more ﬂexible: the mappings al-

low different names of entities and rules, and we allow

partially matched rules. In (Bae et al., 2006), process-

based models are studied and similarity is deﬁned on

sets of nodes as the proportion of matched ones. Yet,

these authors do not deal with relations between them.

Likewise, in (Dijkman et al., 2011), other similarities

are explored. In this context the authors still compare

structural elements of workﬂows (e.g. sets of nodes),

but they allow different kinds of distance measures:

string-edit distance, labels synonyms and contextual

similarity. The latter measure is the closest to ours,

as we consider separately the input (or conditions, the

left hand side of a rule) and the output (realization, the

right hand side of a rule) of a node. Conversely, here,

we take into consideration penalties for elements that

are not matched. The work in (Dijkman et al., 2011)

shows how similarities in business process model are

linked to the semantic web domain, a survey of which

on corresponding metrics can be found in (Euzenat

and Shvaiko, 2007).

Finally, concerning explicitly the pattern search,

the work in (Milo et al., 2002) has analogous goals.

These authors search for patterns by counting the

number of occurrences of a given subgraph in spe-

ciﬁc networks (world wide web, electronic circuits,

. . . ) and comparing it to the number of occurrences in

random generated networks. This approach is com-

pletely different to ours, as their method applies to

graphs while ours applies to “hyper-graphs”. More-

over, they use techniques from statistics while we do

not.

3 MODELED ECOSYSTEMS

In this section, we recall the formal deﬁnition of a

model of an ecosystem as given in (Gaucherel and

Pommereau, 2017). An ecosystem consists of a set of

entities E that can be present (On) or absent (Oﬀ). We

assume that no entity may be simultaneously On and

Oﬀ. The status (the presence) of an entity a is called

polarity, we use a+ to denote that a is On, a− to de-

note that a is Oﬀ. The set of entities E with polarities

p ∈ {+, −} is E

= {a+,a− | a ∈ E}. The presence of

those entities is regulated by a sets of rewriting rules

R. More formally:

Deﬁnition 1 (Ecosystem). An ecosystem E is a tuple

(E,R) such that:

• E is a set of entities,

• R is a set of rewriting rules of the form r :

,α

−

 ω

,ω

−

, where r is the name of the rule,

and ω

are sets of entities that are On, and α

−

and ω

−

are sets of entities that are Oﬀ.

We denote by lhs(r) (respectively rhs(r)) the set

of entities in the left (respectively right) hand side of

the rule r.

An ecosystem state s is deﬁned by the information

about the presence or absence of all its entities. It is

described as the set of entities that are currently On:

thus s ⊆ E, and we assume that the remaining entities

E \ s are Oﬀ.

The dynamics of an ecosystem (E,R) is paramet-

ric over its initial state s

. It comprises all reachable

states obtained by asynchronously applying the rules

in R, in a non-deterministic way. A rule r is enabled

at a state s if the rule’s left hand side, i.e., (α

,α

−

matches the entities deﬁning s. It means that α

⊆ s

and α

−

∩s =

0. If it is the case, the rule may apply and

a new state s

is generated by updating s according to

the rule’s right hand side: s

= (s \ ω

−

) ∪ ω

Example 1 (Pond). We consider a toy-model of a

pond populated with two species of ﬁsh, piscivorous

and insectivorous ones. The pond behavior is de-

scribed by the following rules:

1. if the pond disappears, all ﬁsh species disappear

too,

2. in summer the pond dries and disappears,

3. if the pond is not dried, both species of ﬁsh may

live in it,

4. if the piscivorous ﬁsh are present, insectivorous

ﬁsh disappear,

5. if insectivorous ﬁsh disappear, piscivorous ﬁsh

disappear too.

It consists of four entities: the summer, the pond,

and two kinds of ﬁsh (piscivorous and insectivorous);

and seven rules (see Table 1): Rules 1–5 correspond

to items 1–5 above, and rules 6 and 7 are used to

simulate the change of the seasons.

As an example of the dynamics, let s

= {P} be

the initial state. Then rule 3 is enabled and its appli-

cation gives s

= {P,IF,PF}. The whole dynamics is

then a directed graph whose vertices are the reach-

able states and whose edges correspond to the appli-

cation of rules. 

Pattern Matching in Discrete Models for Ecosystem Ecology

103

Table 1: Entities and Rules for Example 1.

entities:

Su: Summer

P: Pond

PF: Piscivorous Fish

IF: Insectivorous Fish

rules:

1: P−  PF−, IF−

2: Su+  P−

3: P+  PF+, IF+

4: PF+  IF−

5: IF−  PF−

6: Su+  Su−

7: Su−  Su+

Example 2 (Pesticides). As a second small example,

consider a fragment of another ecosystem with four

entities: birds, insects, pesticides and rain.

Table 2: Entities and Rules for Example 2.

entities:

B: Birds

I: Insects

Pe: Pesticide

R: Rain

rules :

1’: B+  I−

2’: I−  B−

3’: Pe−, R+  I+

4’: Pe+  I−

5’: R+  Pe−

6’: B−, Pe−  I+

The ecosystem is governed by the following prin-

ciples: birds eat insects and if insects disappear, birds

will vanish as well. As a disturbing factor we add

pesticides that may kill insects. Pesticides are washed

away by the rain and when there are no pesticides

and it is still raining, insects proliferate. Similarly

insect proliferation happens when there are no pes-

ticides and no birds. We do not take into account

in this example, all the rules (and possibly entities)

that are necessary to regulate the presence/absence

of rain. Entities and rules are given in Table 2. 

4 SIMILARITY BETWEEN

ECOSYSTEMS

As mentioned in the introduction, our objective is to

identify interaction patterns. An interaction pattern

can be considered as a “tiny” ecosystem restricted to

few entities and rules. Thus it may be formalized in

the same syntax as the one for the whole ecosystem.

For example, the “habitat” interaction pattern is com-

posed of one entity featuring a speciﬁc environment

(aquatic, terrestrial, pond, . . . ) and several entities in-

habiting this environment:

1. if the environment disappears, all inhabitants dis-

appear as well.

Similarly, an interaction pattern for the “predation”

process is composed of two entities and two rules

only:

1. if predators are present, then prey disappear,

2. if prey disappear, then predators disappear too.

In the example of the pond ecosystem, instances

of both above patterns are present. The predation in-

stance is composed of piscivorous and insectivorous

species, and of rules 4 and 5; while the habitat in-

stance is composed of entities pond, piscivorous and

insectivorous species and of rule 1. Table 3 shows a

formal representation of the predation pattern.

Table 3: Interaction pattern for predation pattern.

entities:

Pred: Predator

Prey: Prey

rules:

: Pred+  Prey−

: Prey−  Pred−

We may observe that there is a syntactical “simi-

larity” between rules 4 and 5 in the pond ecosystems

and rules 1 and 2 in the predation pattern.

The concept of similarity will be the basis of

our investigation. Similarity is discussed in theory

(see for instance the philosophical work in (Tversky,

1977)) and also used in practice: in law (Mooiman,

2015), in natural sciences (Henkel et al., 2018) and

in various branches of computer science. Intuitively,

we express it in terms of how many groups of compo-

nents with the same roles are present in both ecosys-

tems. This means that, given two mappings, be-

tween entities and rules respectively, the similarity

rate is deﬁned as the number of mapped entities plus

how many mapped entities the rules have in common.

More formally, let E

= (E

) and E

= (E

)

be two ecosystems, and µ and ρ be two mappings be-

tween entities and rules respectively. The ﬁrst one is

µ : E

→ E

. The mapping µ is injective but not nec-

essarily total and polarities are consistent: i.e., if a+

is matched with b− then b+ is matched with a−. It is

encoded as a rectangular matrix X of size (|E

|×|E

of Boolean values deﬁned for each pair of entities

with polarities (m,n) ∈ E

× E

m,n

= 1 if µ(m) = n, 0 otherwise.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

104

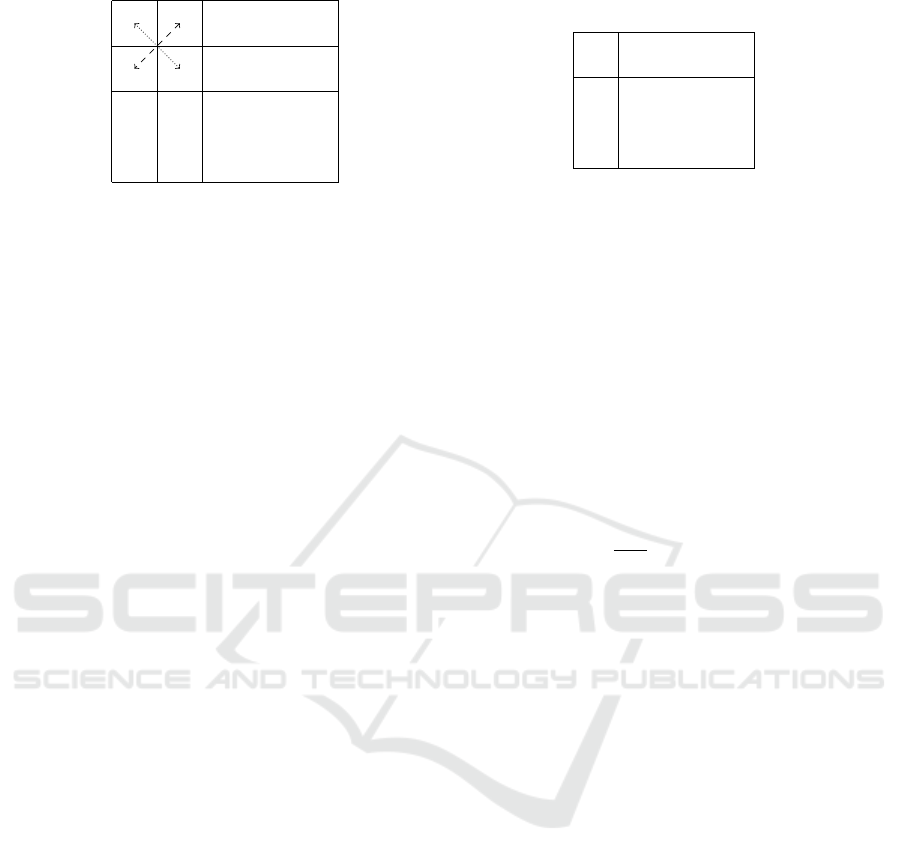
a−

...

b−

∑

≤1

∑

≤1

∑

≤1

∑

≤1

(a) The encoding into matrix X of the mapping µ

for entities and the illustration of corresponding

restrictions.

...

∑

≤1

∑

≤1

(b) The encoding of matrix Y of the mapping ρ for

the rules and the corresponding restrictions.

Figure 1: Encoding of mappings µ and ρ.

In order to implement injectivity and the corre-

spondence between polarities we introduce three re-

strictions (see Figure 1a):

1. There is at most one “1” in each line:

∀m ∈ E

∑

n∈E

m,n

≤ 1;

2. There is at most one “1” in each column:

∀n ∈ E

∑

m∈E

m,n

≤ 1;

3. Polarities are consistently matched:

∀a ∈ E

,b ∈ E

a+,b−

= X

a−,b+

∧ X

a+,b+

= X

a−,b−

Likewise, the mapping ρ : R

→ R

maps the rules.

Similarly as for entities, it is encoded as a rectangu-

lar matrix Y of size (|R

| × |R

|) of Boolean values

deﬁned for each pair of rules (u,v) ∈ R

× R

u,v

= 1 if ρ(u) = v, 0 otherwise.

It is subjected to the following restrictions that

implements injectivity (see Figure 1b):

1. There is at most one “1” in each line:

∀u ∈ R

∑

v∈R

u,v

≤ 1;

2. There is at most one “1” in each column:

∀v ∈ R

∑

u∈R

u,v

≤ 1.

For each pair of mappings (µ,ρ) between ecosys-

tems E

and E

we deﬁne a scoring function S. The

function assesses the quality of the matching rules

with respect to the number of matching entities. The

simplest way to express the score is to count, for each

pair of matching rules ρ(u) = v (i.e., Y

u,v

= 1), the

number of matching entities through function µ on

both the left and right hand side (i.e., for each pair

of entities n and m in rules u and v respectively, we

count the sum of all X

n,m

= 1). The scoring function

is a ratio between previous sum and a constant that

counts the number of rules times the maximal num-

ber of entities in a rule. More precisely:

(X,Y ) =

T · r

∑

u ∈ R

v ∈ R



u,v

∑

n∈u,m∈v

n,m



where r = min(|R

|,|R

|) is the cardinality of the set

of rules in the ecosystem having the smallest num-

ber of them, and T = max

u∈R

∪R

(|lhs(u)| + |rhs(u)|)

is the maximal number of entities in a rule in both

ecosystems, considering at the same time the left

(lhs(·)) and right (rhs(·)) hand side. However this

simple scoring does not take into account:

1. the different contribution of the left and right hand

side. This means, for instance, that a good match-

ing on the left hand side can compensate a bad

matching on the right hand one;

2. the proportion of entities that are not matched.

Scoring function S

does not differentiate between

two rule mappings that for a rule in one ecosystem

match the same number of entities but the size of

matched rules in the second system is different.

Example 3. For example, take the ecosystems R

with

one rule r

: A+, B+  C+ and R

with two rules

: A+, B+  C+ and r

: A+, B+,D−  C+ . The

score for ρ

mapping r

to r

should be greater than

mapping r

to r

as in the latter the mapping is less

perfect and there are entities that are not matched. 

We thus propose a better formulation for the scor-

ing function that takes into account these remarks.

The scoring function is now the sum of the scores of

Pattern Matching in Discrete Models for Ecosystem Ecology

105

the left hand side and the right hand side and can be

summarized as follows:

S(X,Y )

r · (L + R)

∑

u∈R

,v∈R

u,v

(left(u, v) + right(u,v))

where r = min(|R

|,|R

|) as above, L =

max

u∈R

∪R

(|lhs(u)|) and R = max

u∈R

∪R

(|rhs(u)|)

are the maximal numbers of entities occurring in the

left (respectively right) hand side of the rules from

both ecosystems, and left(u,v) and right(u,v) are the

scores for each pair of matching rules u ∈ R

and

v ∈ R

left(u, v) =

∑

n∈lhs(u),

m∈lhs(v)

n,m

−



min(|lhs(u)|,|lhs(v)|) −

∑

n∈lhs(u),

m∈lhs(v)

n,m



− abs(|lhs(u)| − |lhs(v)|)

= 2 ·

∑

n∈lhs(u),

m∈lhs(v)

n,m

− min(|lhs(u)|,|lhs(v)|)

− abs(|lhs(u)| − |lhs(v)|)

right(u, v) = 2 ·

∑

n∈rhs(u),

m∈rhs(v)

n,m

− min(|rhs(u)|,|rhs(v)|)

− abs(|rhs(u)| − |rhs(v)|)

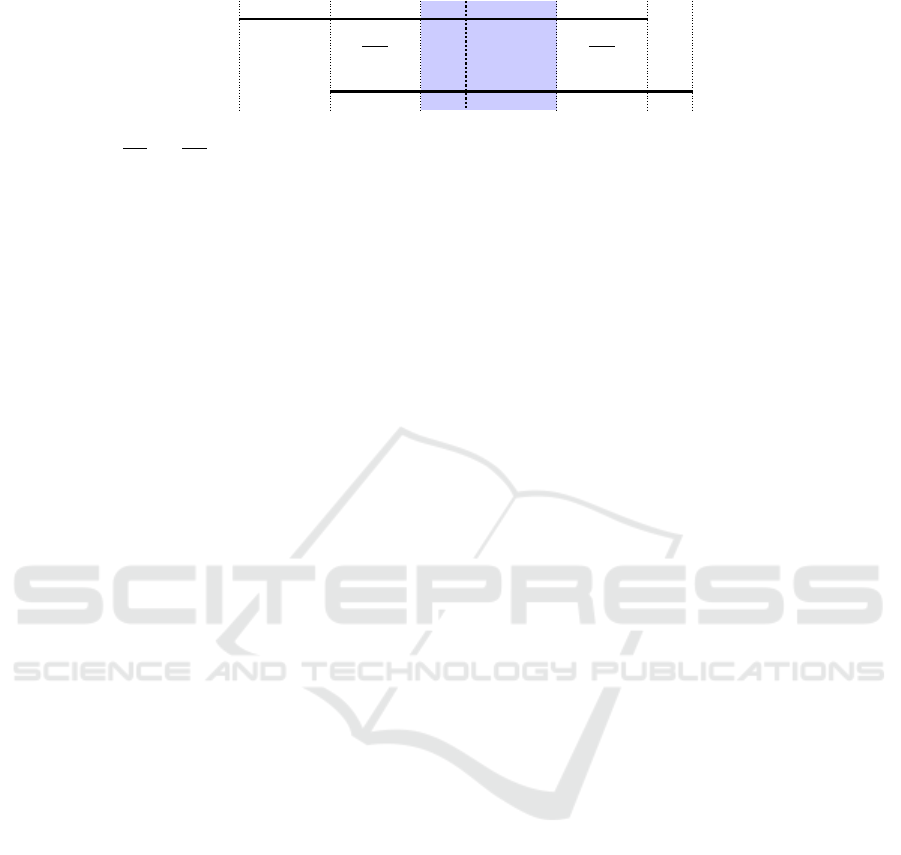
The construction of this scoring function is de-

picted in Figure 2 below. The part left(u, v) takes the

number of matching entities

∑

n∈lhs(u),m∈lhs(v)

n,m

and subtracts two penalties. The ﬁrst one:

min(|lhs(u)|,|lhs(v)|) − M

corresponds to the max-

imum number of entities, which could be matched

minus those that are actually matched. The second

one: abs(|lhs(u)| − |lhs(v)|) expresses the number of

entities which could never be matched because of the

difference in the length of the left hand sides of the

two rules. This score is maximal when left(u,v) =

min(|lhs(u)|,|lhs(v)|) and |lhs(u)| = |lhs(v)|, i.e., the

left hand sides of u and v have the same length, and all

their entities match. The part for the right hand sides

is deﬁned analogously. The overall score is normal-

ized with respect to the number of rules r times L plus

R. As an effect of penalties, the score can be negative

but it is always between -1 and 1.

Similarity is then deﬁned with respect to the scor-

ing function, as the maximal value it can have with

respect to all the possible mappings µ and ρ. It is pos-

sible to enumerate all solutions having a score greater

than a given threshold.

Also, depending on the speciﬁc objective, coefﬁ-

cients may be introduced in the scoring function to

weight preferences: the matching of entities and rules

can be guided adding additional restrictions or reg-

ulating the importance of penalties for not matching

parts of the rules.

Example 4 (Similarity). Let us consider the follow-

ing pairs of mappings between the ecosystems from

Examples 1 and 2:











PF+ → Pe+

IF+ → R+

Su+ → B+

P+ → I+











1 → 1

2 → 2

3 → 3

4 → 4

5 → 5

6 → 6

S(µ

,ρ

) = −12/24











PF+ → Pe+

IF+ → I+

Su+ → R+

P+ → B+











1 → 3

2 → 5

3 → 1

4 → 4

5 → 2

S(µ

,ρ

) = −3/24











PF+ → B+

IF+ → I+

Su+ → R+

P+ → Pe−











1 → 4

2 → 5

3 → 3

4 → 1

5 → 2

S(µ

,ρ

) = 5/24

The ﬁrst pair of mappings is the trivial one, where

we match entities and rules in the same order as they

appear. In this case and as expected, the similarity

score is rather low as there are only hazardous corre-

spondences. The second and the third one have better

scores and they are closer to the optimal solution that

is discussed in the next section. The third matching

suggests that birds and insects have the same role as

piscivorous and insectivorous ﬁsh respectively, while

the presence of the pond can be assimilated to the ab-

sence of pesticides. 

Ecosystems may be compared through the scoring

function. In particular, if one of the ecosystems repre-

sents an interaction pattern we can search for it using

the same method, as shown in Example 5.

Example 5. Take the interaction pattern of predation

in Table 3.

The scores that we obtain for some mappings be-

tween the pattern above and the ecosystems from Ex-

amples 1 and 2 are given below.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

106

left hand side

right hand side



∆

Figure 2: Schema of the scoring function for rules u and v represented as two horizontal lines; M

and M

are the matching

parts of u and v; M

and M

are the parts which do not match while the length of the rules would allow to do so, and ∆

and

∆

are the parts which cannot match because of the different length of the rules.



Pred+ → Pe+

Prey+ → R+



→ 1

→ 2

S(µ

,ρ

) = −4/6



Pred+ → Pe+

Prey+ → I+



→ 4

→ 2

S(µ

,ρ

) = 2/6



Pred+ → B+

Prey+ → I+



→ 1

→ 2

S(µ

,ρ

) = 4/6

One may observe that the third pair of mappings,

having also the best score among the three matches,

matches perfectly the entities and the rules, i.e., we

may easily identify that B plays the role of the preda-

tor and I the role of the prey. It turns out that this is in-

deed an optimal solution, i.e., a pair of mappings that

maximizes the scoring function. The second match

also gives a good but less perfect score as rule 2

and 2 do not match on their outputs. Nevertheless,

this second mapping suggests that pesticides, even if

they are not living entities, may also be interpreted as

predators. The ﬁrst match is more arbitrary and as

expected its score is also the lowest among the three

matches. 

5 EXPERIMENT: SEARCHING

PATTERNS INTO MODELS OF

ECOSYSTEMS

In order to evaluate how practical our matching

method is, we have implemented a prototype tool

and used it to search patterns into various models

of ecosystems. Both patterns and models are origi-

nated from previous works involving realistic ecosys-

tem modeling. This tool performs the following steps

that use the deﬁnition of scoring function given above:

1. Read models E

of the pattern and E

of the

ecosystem in which the pattern is searched for.

2. Build the variables in matrices X and Y , and the

scoring function S(X,Y ) as explained in the pre-

vious section.

3. Encode S(X,Y ) into a pseudo-Boolean opti-

mization (PBO) problem following the require-

ments of the competitions of pseudo-Boolean

solvers (Roussel and Manquinho, 2012, PB16,

2016).

4. Call a PBO solver and extract its solution. The

solution can be interpreted back as the mappings

of entities and rules that gives the best score.

As PBO solver, we have used Sat4j that appears to

be quite fast and can be interrupted during its com-

putation, in which case it proposes the best solution

found so far. This is a very nice feature consider-

ing that searching for an optimal solution may be

very long while non-optimal solutions may already

correspond to interesting matches for the modeler.

The prototype itself was implemented in Python us-

ing SymPy (SymPy development team, 2016) to build

the scoring function as deﬁned above and simpliﬁed

to match the constraints of the PBO format.

This is illustrated in Figure 3 where we see how

our prototype executes on the ecosystems from Ex-

amples 1 and 2: it prints the values of the scoring

function as soon as Sat4j ﬁnds them. At any time, it is

possible to kill Sat4j which interrupts its computation

and force it to print the best solution it has discov-

ered so far. It is interesting to note that this solution

corresponds to none of those proposed in Example 4

which are all matches that have been crafted manually

and corresponded to our intuition about the two mod-

els. So, this shows that our method is able to propose

something new, i.e., something that a modeler would

not necessarily imagine even on small examples.

5.1 Benchmark

Using this prototype, we have systematically searched

for 12 patterns into 21 models of ecosystems. These

patterns and models are all originated from various

Pattern Matching in Discrete Models for Ecosystem Ecology

107

### reading ’pond.rr’

### 4 variables / 7 rules / 0 constraints

### reading ’pest.rr’

### 4 variables / 6 rules / 0 constraints

### building model

### running sat4j

... satisfiable [0:00:00.637612]

... objective function=2/24 [0:00:00.639101]

... objective function=4/24 [0:00:01.144709]

... objective function=6/24 [0:00:01.649645]

... optimum found

=== done running sat4j in 0:00:03.193784

*** OPTIMAL SAT => 6/24

### states

P+ ==> Pe+

IF+ ==> I+

Su+ ==> R+

PF+ ==> B+

### rules

R5: IF- >> PF- ==> R2: I- >> B-

R4: PF+ >> IF- ==> R1: B+ >> I-

R2: Su+ >> P- ==> R5: R+ >> Pe-

### normal exit

Figure 3: A sample run of our prototype searching matches

between the Pond and Pesticides models presented in Ex-

amples 1 and 2.

works performed by ecologists, in particular master

students who have modeled contrasted ecosystems.

The models are representation of ecosystems from the

south of France (Camargue), the Alpes (Chamrousse)

and ecosystems in Africa (Uganda, Karamoja). The

patterns searched are mainly species interactions such

as predation, competition, symbiosis, etc. It is out

of the scope of this paper to describe these interac-

tions, but we would like to pinpoint that they are all

patterns and models that ecologists are actually inter-

ested in and not arbitrary examples. In particular, we

did not include the “pond” and “pesticides” models

in this benchmark, because they have been designed

to illustrate this paper and have no ecological interest.

For each search, we have deﬁned a timeout of 3 min-

utes (180 seconds)

after which Sat4j was interrupted.

Among the 252 searches resulting from this bench-

mark, 194 (77%) returned an optimal solution before

the timeout, and 58 (23%) have been interrupted re-

sulting in a non-optimal solution, as summarized in

Figure 4. Even if the search time is short, we can ob-

serve that an optimal solution is found in most cases.

For the other ones a solution, even if not optimal, is

found anyway.

A more detailed view of this benchmark is pro-

vided in the “heat-map” depicted in Figure 5 that

shows for each pattern and each model a color cor-

responding to the search time. In this heat-map, mod-

els are named with an upper-case letter, and patterns

The choice of 3 minutes is arbitrary.

with a lower-case letter; names are followed by pairs

of numbers e/r where e is the number of entities and

r the number of rules in the model or pattern. For

instance, the “prey-predator” and “live-in” patterns

we have presented in the introduction are e and d re-

spectively. Columns and rows have been sorted with

respect to the sum of the values in the column and

row, which allows to group larger search times in the

lower-right corner. From this plot we can draw the

following observations:

• neither patterns nor models size seem to be the

key factor that lead to the signiﬁcant search time

increase. For instance, models S and J have very

similar sizes but do not yield similar search times.

The same remark applies to patterns e and g to j;

• however, the shape of the heat-map shows that a

key factor lies in patterns as pattern choice may

yield a signiﬁcant increase of search time, while

increasing is more progressive with respect to

model choice;

• for toy models (A to F at the top), the solution is

always quickly found;

• for large, more detailed, models (O to U at the bot-

tom), the pattern structure is the key factor to de-

termine if a timeout occurs;

• this is conﬁrmed on intermediary models (G to N

in the middle) where we can observe that more

searches timeout as we go down the plot and, pat-

terns all have the same size while models are not

necessarily ordered by size.

So far, we have not identiﬁed what is the key factor

that forbids a quick search. For sure pattern size is

a factor as we can see for patterns k and l (or mod-

els O to U), but what we observe from patterns g—j

and models F—L shows that this is not the only as-

pect. Considering our scoring function, search time is

probably linked to the size of rules in the pattern and

in the model, but this question will deserve further

work to examine more in depths the characteristics of

patterns that lead to the observed increasing of search

times.

As a conclusion of this benchmark, we observe

that searching a pattern in a model is always possible,

usually in a very short time. Moreover, in every case,

a solution has been found quickly, which allows the

user to interrupt the search very soon and yet get a

match that is not optimal with respect to the scoring

function but may be interesting already.

A future extension of the implementation would

be to enable re-injecting found matches in the PBO

problem as negative constraints, in order to forbid the

search to ﬁnd them again. In addition, this would give

a way to enumerate matches. It is indeed particularly

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

108

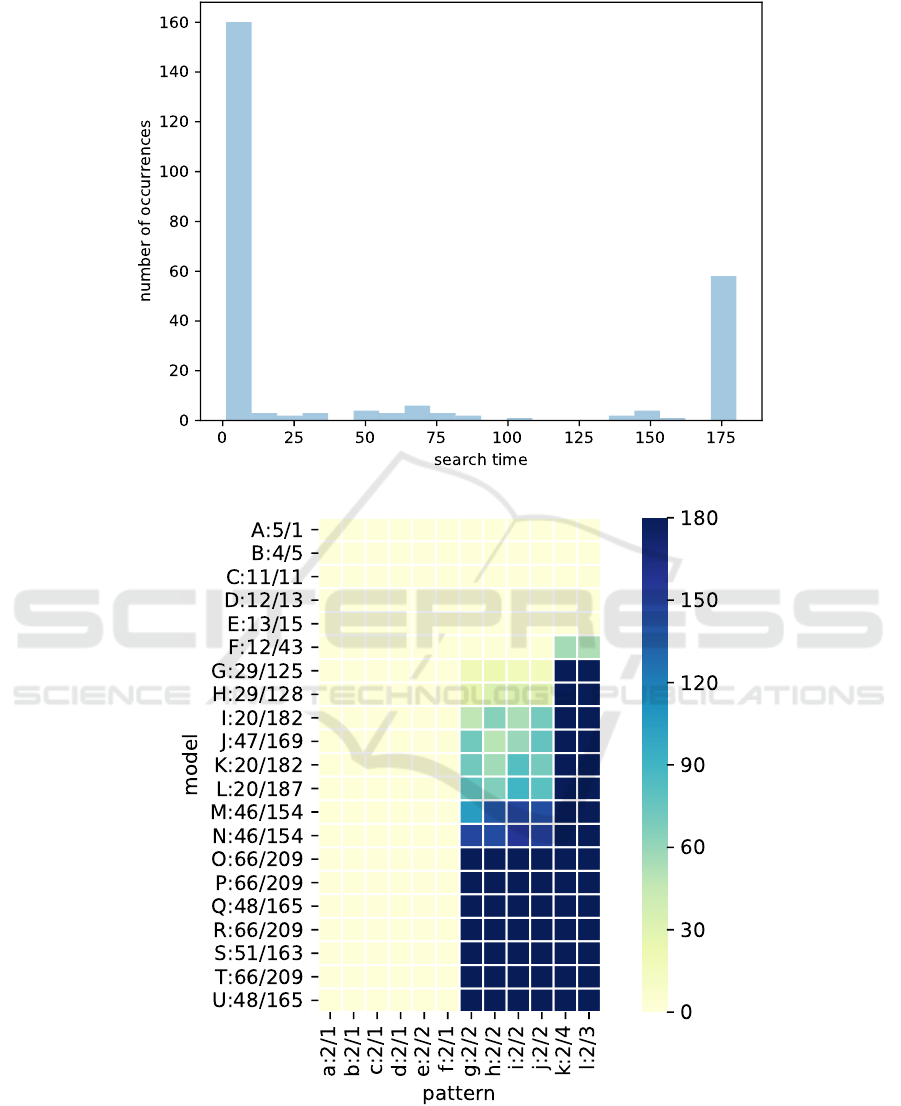
Figure 4: Histogram of search times (in seconds) in the benchmark.

Figure 5: Search times (in seconds) with respect to models and patterns. Models are indicated with an upper-case letter,

patterns with a lower-case letter. Model and pattern names are followed by pairs of numbers e/r: e is the number of entities

and r the number of rules.

relevant for ecologists to (automatically) identify sev-

eral instances of the same interaction pattern (ecologi-

cal processes) in the ecosystem dynamics under study.

Pattern Matching in Discrete Models for Ecosystem Ecology

109

6 CONCLUSION AND

PERSPECTIVES

In this paper, we have presented a method for auto-

matically comparing and assessing similarity between

ecosystems deﬁned as speciﬁc kinds of rewriting sys-

tems. We have deﬁned a scoring function that takes

into account not only the number of matching enti-

ties and rules, but also the quality of partial mappings

between the left and right hand sides of rules. The ap-

proach has been successfully applied to the search of

known interaction patterns (i.e., ecological processes)

in models of ecosystems.

The results we have obtained in our benchmark

are promising: we quickly obtain optimal solutions

for the vast majority of the cases studied. For the re-

maining ones, we obtain a solution that is not optimal

in a short time, but we have no assessment of how far

from optimal it is. A possible option to solve this is-

sue could be to add ecological information to assess

the quality of a match (with a relevance score) closer

to the modeler’s expectations. In other words, a big-

ger match is not necessarily a better match. So far,

our method searches for bigger matches. When the

search is interrupted and yields to a sub-optimal so-

lution, a relevance score may help deciding whether

it is already a “good” match or not. In practice, the

matching of entities (here, ecosystemic entities) and

rules (ecological processes) can be guided by adding

additional constraints, such as to:

• enforce the matching/identity between subsets of

entities or rules. For example, if the model al-

lows different categories of rules (each category

possibly having a different semantics), the scor-

ing function could be adapted to take into account

this extension;

• enforce the matching between entities/rules of

the same category (for example match carnivores

among them);

• diminish the importance of some entities/rules

(i.e., set a different weight for each matching up

to forget some, if necessary).

Finally, as a long term perspective, we may use

our method to discover invariant patterns that are not

known in advance, thus increasing the understand-

ing about ecosystem functioning. This could account

for using our concept of similarity to identify match-

ing parts of ecosystems and extract from those the

new patterns. Experiments we have conducted so far

in this direction showed bad performances as search

time becomes prohibitive (as if we would have used

patterns whose sizes are close to the studied models’

sizes). However, sub-optimal patterns may provide

interesting matches (which remains to be studied), or

we may ﬁnd a way to guide the search with respect to

additional constraints (related to the previous idea of

a relevance score).

ACKNOWLEDGMENT

We would like to thank David Monniaux for his ad-

vise on MAXSAT and PBO solvers, and Daniel Le

Berre who has recommended Sat4j and has been very

helpful concerning its installation and use.

REFERENCES

Agnihotri, K. and Sharma, N. (2015). Developments in eco-

logical modeling based on cellular automata. 6.

Bae, J., Liu, L., Caverlee, J., and Rouse, W. B. (2006). Pro-

cess mining, discovery, and integration using distance

measures. In 2006 IEEE International Conference on

Web Services (ICWS’06), pages 479–488.

Baldan, P., Bocci, M., Cocco, N., and Simeoni, M.

(2013a). Comparing metabolic pathways through

potential ﬂuxes: a selective opening approach. In

BioPPN@Petri Nets.

Baldan, P., Cocco, N., Giummol

e, F., and Simeoni, M.

(2013b). Comparing metabolic pathways through re-

actions and potential ﬂuxes. Trans. Petri Nets and

Other Models of Concurrency, 8:1–23.

Baldan, P., Cocco, N., Marin, A., and Simeoni, M. (2010).

Petri nets for modelling metabolic pathways: a survey.

Natural Computing, 9(4):955–989.

Cardelli, L. (2005). Abstract machines of systems biol-

ogy. Transactions on Computational Systems Biology,

3737:145–168.

Danos, V. and Laneve, C. (2004). Formal molecular biol-

ogy. TCS, 325(1):69–110.

Delaplace, F., Di Giusto, C., Giavitto, J., and Klaudel, H.

(2018). Activity networks with delays an application

to toxicity analysis. Fundamenta Informaticae, to ap-

pear.

Dijkman, R., Dumas, M., van Dongen, B., K

arik, R., and

Mendling, J. (2011). Similarity of business process

models: Metrics and evaluation. Information Systems,

36(2):498 – 516. Special Issue: Semantic Integration

of Data, Multimedia, and Services.

Ehrenfeucht, A. and Rozenberg, G. (2007). Reaction sys-

tems. Fund. Inform., 75(1-4):263–280.

Euzenat, J. and Shvaiko, P. (2007). Ontology Matching.

Springer-Verlag New York, Inc., Secaucus, NJ, USA.

Fages, F. and Soliman, S. (2008). Formal cell biology

in biocham. In Proceedings of the Formal Meth-

ods for the Design of Computer, Communication, and

Software Systems 8th International Conference on

Formal Methods for Computational Systems Biology,

SFM’08, pages 54–80, Berlin, Heidelberg. Springer-

Verlag.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

110

Gaucherel, C. (2006). Inﬂuence of spatial patterns on eco-

logical applications of extremal principles. Ecological

Modelling, 193:531–542.

Gaucherel, C., Boudon, F., Houet, T., Castets, M., and

Godin, C. (2012). Understanding patchy landscape

dynamics: Towards a landscape language. PLoS ONE,

7(9):16.

Gaucherel, C., Houllier, F., AUCLAIR, D., and Houet, T.

(2014). Dynamic Landscape Modelling : The Quest

for a Unifying Theory. Living reviews in landscape

Research, 8(2):5–31.

Gaucherel, C. and Pommereau, F. (2017). Using Petri nets

to identify basins of attraction and tipping points of an

ecosystem. submitted.

Giavitto, J.-L., Malcolm, G., and Michel, O. (2004).

Rewriting systems and the modelling of biological

systems. Comparative and Functional Genomics,

5:95–99.

Grafahrend-Belau, E., Schreiber, F., Heiner, M., Sackmann,

A., Junker, B. H., Grunwald, S., Speer, A., Winder,

K., and Koch, I. (2008). Modularization of biochem-

ical networks based on classiﬁcation of Petri net t-

invariants. BMC Bioinformatics, 9(1):90.

Henkel, R., Hoehndorf, R., Kacprowski, T., Kn

upfer, C.,

Liebermeister, W., and Waltemath, D. (2018). Notions

of similarity for systems biology models. Brieﬁngs in

Bioinformatics, 19(1):77–88.

Le Berre, D. and Parrain, A. (2010). The Sat4j library, re-

lease 2.2. Journal on Satisﬁability, Boolean Modeling

and Computation, 7.

Lotka, A. J. (1925). Elements of physical biology. Williams

& Wilkins Company, Baltimore.

May, R. M. (1972). Will a large complex system be stable?

Nature, 238:413 EP –.

Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N.,

Chklovskii, D., and Alon, U. (2002). Network motifs:

Simple building blocks of complex networks. Science,

298(5594):824–827.

Mooiman, L. (2015). Comparing stories with the use of

Petri nets. Technical report, University of Amsterdam.

Paun, A., Paun, M., Rodr

ıguez-Pat

on, A., and Sidoroff, M.

(2011). P systems with proteins on membranes: a sur-

vey. Int. Journal of Foundations of Computer Science,

22(1):39–53.

PB16 (2016). Pseudo-Boolean competition 2016. http:

//www.cril.univ-artois.fr/PB16. Satellite event

of SAT’16.

Roussel, O. and Manquinho, V. (2012). Input/output

format and solver requirements for the competi-

tions of pseudo-Boolean solvers. http://www.cril.

univ-artois.fr/PB12/format.pdf.

Sangiorgi, D. (2011). Introduction to Bisimulation and

Coinduction. Cambridge University Press, New York,

NY, USA.

SymPy development team (2016). SymPy. http://www.

sympy.org.

Terese (2003). Term Rewriting Systems, volume 55 of Cam-

bridge Tracts in Theoretical Computer Science. Cam-

bridge University Press.

Thomas, R. (1973). Boolean formalisation of genetic con-

trol circuits. Journal of theoretical biology, 42:565–

583.

Tversky, A. (1977). Features of similarity. Psychological

Review, 84(4):327–352.

van Glabbeek, R. and Goltz, U. (1989). Equivalence notions

for concurrent systems and reﬁnement of actions. In

Kreczmar, A. and Mirkowska, G., editors, Mathemat-

ical Foundations of Computer Science 1989, pages

237–248, Berlin, Heidelberg. Springer Berlin Heidel-

berg.

Wang, J., He, T., Wen, L., Wu, N., ter Hofstede, A. H. M.,

and Su, J. (2010). A behavioral similarity measure

between labeled Petri nets based on principal transi-

tion sequences. In On the Move to Meaningful Inter-

net Systems: OTM 2010 - Confederated International

Conferences: CoopIS, IS, DOA and ODBASE, Her-

sonissos, Crete, Greece, October 25-29, 2010, Pro-

ceedings, Part I, pages 394–401.

Xiao, L., Zheng, L., Xiao, J., and Huang, Y. (2009). A

graphical query language for querying Petri nets. In

Yang, J., Ginige, A., Mayr, H. C., and Kutsche, R.-

D., editors, Information Systems: Modeling, Develop-

ment, and Integration, pages 514–525, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Pattern Matching in Discrete Models for Ecosystem Ecology

111