
Towards an Efficient Verification Method for Monotonicity Properties of
Chemical Reaction Networks
Roberta Gori, Paolo Milazzo and Lucia Nasti
Dipartimento di Informatica, Universit
`
a di Pisa, Largo Bruno Pontecorvo, Pisa, Italia
Keywords:
Chemical Reaction Network, ODEs, Monotonicity.
Abstract:
One of the main goals of systems biology is to understand the behaviour of (bio)chemical reaction networks,
which can be very complex and difficult to analyze. Often, dynamical properties of reaction networks are
studied by performing simulations based on the Ordinary Differential Equations (ODEs) models of the re-
actions’ kinetics. For some kinds of dynamical properties (e.g. robustness) simulations have to be repeated
many times by varying the initial concentration of some components of interest. In this work, we propose
sufficient conditions that guarantee the existence of monotonicity relationships between the variation of the
initial concentration of an “input” biochemical species and the concentration (at all times) of an “output”
species involved in the same reaction network. Our sufficient conditions allow monotonicity properties to be
verified efficiently by exploring a dependency graph constructed on the set of species of the reaction network.
Once established, monotonicity allows us to drastically restrict the number of simulations required to prove
dynamical properties of the chemical reaction network.
1 INTRODUCTION
The dynamics of biological systems can be very dif-
ficult to analyze, because they often consist of a huge
number of components that interact with each other
as a system. This is true in particular for systems con-
sidered at the molecular level, in which components
interact essentially through chemical reactions.
From the computational viewpoint, the dynamics
of (bio)chemical reaction networks is often studied by
performing simulations. The two most common ap-
proaches to the simulation of reaction networks are
the deterministic and the stochastic ones (Barnes and
Chu, 2010). The deterministic approach is usually
based on a description of the behaviour of the system
in terms of Ordinary Differential Equations (ODEs).
The stochastic approach usually requires the appli-
cation of Gillespie’s simulation algorithm (Gillespie,
1977), or of one of its more recent (and efficient) vari-
ants (Cao et al., 2006; Salis and Kaznessis, 2005).
In the deterministic approach the time evolution of
the model is studied as a continuous process. Concen-
trations are continuous values and reactions change
their values in a continuous way. In the stochas-
tic approach, concentrations are discretized (these ap-
proaches actually deal with number of species, rather
than concentrations) and reactions occur one by one
in discrete time steps. In both the deterministic and
the stochastic cases, simulations can become com-
putationally very expensive. For this reason, other
less accurate analysis approaches are often consid-
ered, which are based for instance on a qualitative
description of the system behaviour, or on abstrac-
tions. Examples of analysis approaches of this kind
are those based on Boolean networks (Shmulevich
et al., 2002; Schlitt and Brazma, 2007; Barbuti et al.,
2018), on interaction graphs (Jeong et al., 2001; Stelzl
et al., 2005; Brohee and Van Helden, 2006), on ab-
stract interpretation (Fages and Soliman, 2008; Gori
and Levi, 2010; Bodei et al., 2015; Fages et al., 2017;
Carvalho et al., 2018) and, in general, on logic and
symbolic approaches (Eker et al., 2001; Antoniotti
et al., 2003; Barbuti et al., 2016a; Barbuti et al., 2015;
Barbuti et al., 2016b).
In this paper, we focus on how to make more effi-
cient the analysis of the dynamics of a biological sys-
tems in a deterministic setting. One of the problems in
this case is that often the behaviour has to be studied
by varying the initial concentrations of some species.
This happens, for example, when the initial concen-
trations of some species is not precisely known, or
when a complex or general biological property (e.g.
robustness (Kitano, 2004; Fages and Soliman, 2018))
is investigated. In principle, this requires performing
250
Gori, R., Milazzo, P. and Nasti, L.
Towards an Efficient Verification Method for Monotonicity Properties of Chemical Reaction Networks.
DOI: 10.5220/0007522002500257
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 250-257
ISBN: 978-989-758-353-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

many simulations, or to analytically solve the non-
linear differential equations by considering many ini-
tial conditions.
In this context it would be very useful to assess
monotonicity properties between species that could
allow us to significantly reduce the set of initial
conditions that have to be considered. This is the
aim of this work: to define sufficient conditions for
chemical reactions networks that guarantee the exis-
tence of monotonic relationships between the chem-
ical species involved in the network. More in de-
tail, given two species, that we call input and out-
put species of the network, we say that they are in
a monotonicity relation if the concentration of output
species at any time either increases or decreases due
to an increase in the initial concentration of the input.
This result would allow us to reduce substantially the
number of simulations required to explore the system.
Indeed, if two species are in a monotonicity relation-
ship and we are interested in studying the dynamics
of the output when varying the input, we can avoid
to simulate the chemical reaction network for all pos-
sible values of the initial concentrations of the input
species.
It is worth noting that the idea of finding sufficient
conditions that guarantee some biological properties
useful to analyze the behaviour of chemical reaction
networks is not completely new. In (Angeli et al.,
2006), the authors show a graphical method to study
a global notion of monotonicity for certain classes of
chemical reaction networks. The sufficient conditions
they propose says that a chemical reaction network is
globally monotone if a particular form of graph asso-
ciated to the chemical reaction network under study
contains only certain kinds of loop (see (Angeli et al.,
2006) for details). However, global monotonicity is
a very strong property, since it is based on a unique
ordering on the whole set of species of the reaction
network. Unfortunately, such a strong property does
not hold on most realistic chemical reaction network.
For this reason we introduce new definitions of mono-
tonicity concerning the relation between a given input
and output species. We then propose sufficient condi-
tions for verifying our monotonicity relations.
Another example of sufficient conditions pro-
posed to infer dynamical properties of chemical re-
action networks are related with the study of absolute
concentration robustness (Shinar and Feinberg, 2010;
Shinar and Feinberg, 2011). This property holds for a
species of a reaction systems if its concentration at the
steady state is independent from perturbations in the
initial concentration of some other species. In (Shinar
and Feinberg, 2010; Shinar and Feinberg, 2011) the
authors propose a sufficient condition on the structure
of the reaction network that allows absolute concen-
tration robustness to be assessed without performing
simulations. In this case, both the considered prop-
erty (absolute concentration robustness) and the suffi-
cient condition are very strong, and can be applied to
a limited class of networks. For this reason, more gen-
eral notions of robustness have been proposed (Rizk
et al., 2009), but for which verification requires con-
siderable efforts. In (Nasti et al., 2018) we proposed a
notion of concentration robustness based on concen-
tration intervals, which is more general than absolute
concentration robustness and for which an efficient
verification method could be designed by exploiting
the monotonic properties we are considering in this
paper.
We proceed by introducing some basic definition
in Section 2, which are assumed in the rest of the pa-
per. In Sections 3 and 4 we give our new definitions
of monotonicity and propose sufficient conditions to
assess them. In Section 5, we apply our methodol-
ogy on some simple systems and to study the case of
the ERK signaling pathway. Finally, in Section 6 we
draw our conclusions and discuss future work.
2 BACKGROUND
A chemical reaction is a transformation that involves
one or more chemical species, in a specific situation
of volume and temperature.
The chemical species that are transformed are
called reactants; while those that are the result of the
transformation are called products. We can represent
a chemical reaction as an equation, showing all the
species involved in the process.
A simple example of chemical reaction is the fol-
lowing elementary reaction:
aA + bB
k
1
k
−1
cC + dD (1)
In this case, A, B, C, D are the species involved in the
process: A and B are the reactants, C and D are the
products. The parameters a, b, c, d are called stoichio-
metric coefficients and represent the number of reac-
tants and products participating in the reaction. They
are always integer, because elementary reactions in-
volve the whole participants. The arrow is used to in-
dicate the direction in which a chemical reaction takes
place. When we have only one arrow, it means that the
reaction is irreversible, that is it is not possible to have
the opposite process. To describe the dynamical be-
haviour of the chemical reaction network, we can use
the law of mass action, which states that: the rate of a
reaction is proportional to the product of the reactants.
Towards an Efficient Verification Method for Monotonicity Properties of Chemical Reaction Networks
251

Applying the law of mass action to the system, we ob-
tain, for each chemical species, a differential equation
describing the production and the consumption of the
considered species. Considering the generic chemical
equation 1, we obtain:
d[A]
dt
=
direct reaction
term
z }| {
−ak
1
[A]
a
[B]
b
inverse reaction
term
z }| {
+ak
−1
[C]
c
[D]
d
d[B]
dt
= −bk
1
[A]
a
[B]
b
+ bk
−1
[C]
c
[D]
d
d[C]
dt
= +ck
1
[A]
a
[B]
b
− ck
−1
[C]
c
[D]
d
d[D]
dt
= +dk
1
[A]
a
[B]
b
− dk
−1
[C]
c
[D]
d
.
where, in each equation, we isolated the term describ-
ing the direct reaction from the one describing the in-
verse reaction. With these two terms, we implicitly
considered, for each element, the processes of con-
sumption and production.
3 DEFINITION OF
MONOTONICITY
We start with a formal definition of chemical reaction.
Definition 1 (Reaction). Given a set of species S,
a reaction is a tuple (u,v,k) denoted u
k
−−→ v, where
u,v ∈ S
∗
(multisets over S) and k ∈ R
+
.
Consider a set of reactions R, over a set of
species S = S
1
,...S
n
. Let us indicate with S
I
the in-
put and with S
O
the output species. Moreover, let
dS
1
dt
= f
S
1
(S),...,
dS
n
dt
= f
S
n
(S) be the ODEs obtained
from R according to the mass action kinetics. With
F
S
i
(t,S
0
1
,...,S
0
n
) we indicate the solution of the ODEs
for the species S
i
considering S
0
1
,...,S
0
n
as the initial
values of the species S
1
,...,S
n
in R.
The following two definitions describe the con-
cept of monotonicity that we are interested in. Our
properties of monotonicity describe whether the out-
put species react in a monotone way to the increase of
the input concentration.
Definition 2 (Positive Monotonicity). Given a set of
reactions R, species S
O
is positively monotonic with
respect to S
I
in R if and only if, for every time t ∈ R
≥0
:
S
0
I
< S
0
I
=⇒ F
S
O
(t,S
0
1
,..., S
0
I
,...S
0
n
) ≤ F
S
O
(t,S
0
1
,..., S
0
I
,...S
0
n
)
Definition 3 (Negative Monotonicity). Given a set of
reactions R, species S
O
is negatively monotonic with
respect to S
I
in R if and only if, for every time t ∈ R
≥0
:
S
0
I
< S
0
I
=⇒ F
S
O
(t,S
0
1
,..., S
0
I
,...S
0
n
) ≥ F
S
O
(t,S
0
1
,..., S
0
I
,...S
0
n
)
Example 1. Consider a network R consisting of the
following chemical reactions:
A + B
k
1
C (R
1
)
D + B
k
2
E (R
2
)
The differential equations describing the be-
haviour of R are the following
d[A]
dt
= −k
1
[A][B]
d[B]
dt
= −k
1
[A][B] −k
2
[B][D]
d[C]
dt
= +k
1
[A][B]
d[D]
dt
= −k
2
[B][D]
d[E]
dt
= +k
2
[B][D]
Consider A as the input species and C as the output
species. Assume now that the initial concentrations
of species B, D, C and E are fixed, but that the initial
concentration of species A can vary from 10 to 1000.
In principle, in order to study the dynamics of the con-
centration of C we would need to perform many sim-
ulations, one for each possible (continuous) value of
the initial concentration of A. However, if species C
is positively monotonic w.r.t. A, then just two simu-
lations are necessary: one with A = 10 and one with
A = 1000. The dynamics of C in all the other (inter-
mediate) cases is included in the results we obtained
from these two simulations. A similar simplification
could be done by assessing the negatively monotonic-
ity of E w.r.t. A. In addition, if the species to vary
were two, say A and B with the latter varying from 20
to 200, and if species C was also positively monotonic
w.r.t. B, then just two simulations would be neces-
sary to study the behaviour of C: one with A = 10
and B = 20 and another with A = 1000 and B = 200.
Finally, if we could prove that species E is positively
monotonic w.r.t. B then, to study its behaviour we
would need at most four different simulations, A = 10
and B = 20, A = 10 and B = 200, A = 100 and B = 20,
and A = 100 and B = 200.
It is worth noting that interesting weaker notions
of monotonicity could be defined. For example, for
some reaction networks it could be interesting to
study steady state monotonicity, defined (in its pos-
itive formulation) as follows.
Definition 4. S
O
in R is steady state positively mono-
tonic with respect to S
I
if and only if S
0
I
< S
0
I
implies
lim
t→∞
F
S
O
(t,S
0
1
,..., S
0
I
,...S
0
n
) ≤ lim
t→∞
F
S
O
(t,S
0
1
,..., S
0
I
,...S
0
n
)
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
252

Figure 1: Dependency graph of the reaction network in Ex-
ample 1. The red edges have sign − and express competi-
tion among reactions, the remaining ones have sign +.
4 EFFICIENT ASSESSMENT OF
MONOTONICITY
We now define a dependency graph on species that we
will use to define our sufficient conditions. Intuitively,
the graph highlights the positive or negative influence
that each species has on each reaction.
In the following, we denote the cardinality of a
set S with ]S, and the number of instances of s in a
multiset u with ]
s
u = ]{a | a = s and a ∈ u}.
Definition 5 (Dependency graph). Given a finite set
of reactions R over a set of species S, the depen-
dency graph G of R is the tuple hS, R, E
+
,E
−
i, where
E
+
⊆ (S × R) ∪ (R × S) and E
−
⊆ (S × R), are such
that given s ∈ S, u
k
−−→ v ∈ R:
• (s,u
k
−−→ v) ∈ E
+
⇐⇒ s ∈ u
• (u
k
−−→ v,s) ∈ E
+
⇐⇒ s ∈ v ∧ ]
s
v > ]
s
u
• (s,u
k
−−→ v) ∈ E
−
⇐⇒ s /∈ u ∧ ∃ u
0
k’
−−→ v
0
∈ R (u ∩
u
0
6=
/
0 ∧ s ∈ u
0
)
Consider again the reaction network R of Example
1. The corresponding dependency graph is shown
in Figure 1. The nodes representing species are de-
picted as circles, while nodes representing reaction as
squares. To build the dependency graph, we draw an
edge labelled with the sign + between each reactant
and its reaction, and between each reaction and each
of its product. Moreover, if a species is a reactant
of two or more reactions (like B, in the example) we
build an edge with the sign − between all the species
that are not in common and each competing reaction.
Considering the example, we build an edge with sign
− between A and reaction R
2
since reaction R
2
com-
petes with reaction R
1
for species B. Analogously, we
draw an edge with sign − between D and the compet-
ing reaction R
1
.
We are interested in characterizing the paths over
the previously defined dependency graph.
Definition 6 (Path). Given a dependency graph
hS,R,E
+
,E
−
i, a path is a finite sequence
S
o
R
1
S
1
R
2
...R
n
S
n
where S
o
,...,S
n
∈ S, R
1
,...,R
n
∈ R
and ∀i ∈ [1, n] (S
i−n
,R
i
) ∈ E
+
∪ E
−
and (R
i
,S
i
) ∈ E
+
.
A path is positive iff ]{(S
i−1
,R
i
) ∈ E
−
|i ∈ (1,n)} is
even. A path is negative otherwise.
Going back to the dependency graph depicted in
Figure in 1, we can observe that there is a positive
path from species A to C, while there is a negative path
from species A to E. Analogously, there is a negative
path from D to C and a positive path from D to E.
Finally, there are positive paths from B to D and E.
We are now ready to present our conjectures.
Conjecture 1 (Positive Paths). Given a set of reac-
tions R over a set of species S. Let G = hS,R,E
+
,E
−
i
be the dependency graph of R. Let S
I
,S
O
∈ S. If paths
from S
I
to S
O
in G are all positive, then S
O
is posi-
tively monotonic with respect to S
I
.
Conjecture 2 (Negative Paths). Given a set of reac-
tions R over a set of species S. Let G = hS,R,E
+
,E
−
i
be the dependency graph of R. Let S
I
,S
O
∈ S. If paths
from S
I
to S
O
in G are all negative, then S
O
is nega-
tively monotonic with respect to S
I
.
As a consequence of our conjectures, in the reac-
tion network of Example 1, we can affirm that C is
positively monotonic with respect to A and B, while
it is negatively monotonic with respect to D. Anal-
ogously, we can conclude that E is positively mono-
tonic with respect to D and B, while it is negatively
monotonic with respect to A.
5 APPLICATION EXAMPLES
We show the application of our methodology to two
small examples of reaction networks and to the case
study of the ERK signaling pathway.
5.1 Example of Monotonic Behaviours
Consider again the reaction network of Example 1 and
let A be the input species. By applying our conjectures
we can derive (by observing paths in the dependency
graph in Figure 1) that C is positively monotonic w.r.t.
A, and E is negatively monotonic w.r.t. A. This be-
haviour is confirmed by the simulation results shown
in Figures 2 and 3: by increasing the initial concen-
tration of A, the concentration of C is (at all times)
increased, while that of E is (at all times) decreased.
In the simulations, initial concentrations of B, C, D
and E are B
0
= 20, C
0
= 0, D
0
= 10, and E
0
= 0.
Towards an Efficient Verification Method for Monotonicity Properties of Chemical Reaction Networks
253

0 1 2 3 4 5 6 7 8 9 10
Time
0
2
4
6
8
10
12
14
16
18
20
Concentrations
C(1) with A
0
=20
C(2) with A
0
=25
C(3) with A
0
=100
Figure 2: Simulation results of Example 1. Changes in the
dynamics of species C by varying the initial concentration
of species A.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Time
0
1
2
3
4
5
6
7
Concentrations
E(1) with A
0
=20
E(2) with A
0
=25
E(3) with A
0
=1000
Figure 3: Simulation results of Example 1. Changes in the
dynamics of species E by varying the initial concentration
of species A.
For this particular example, monotonicities be-
tween species that can be deduced from our conjec-
tures are stated in the following proposition.
Proposition 1. In the reaction network of Example 1,
species C and D are positively monotonic w.r.t. A, and
species B and E are negatively monotonic w.r.t. A.
An empirical assessment of the validity of the pre-
vious proposition can be obtained by using the small
tool we developed and we made available at http://
www.di.unipi.it/msvbio/software/MonotoneExample.
html. The tool executes 1000 simulations of the re-
action network of Example 1 by using the Euler
method. Each simulation actually computes two sets
of variables: A, B,C, D, E and A
0
,B
0
,C
0
,D
0
,E
0
. The
dynamics of both sets of variables is governed by
the same ODEs, but the initial value of variable A
0
is
greater than the initial value of variable A (the initial
value of each other primed variable is the same as
that of the corresponding unprimed variable). In this
way the tool can compare step by step the dynamics
of the reaction network with the dynamics of the
same network with a (positive) perturbation in the
initial concentration of the input species A.
In each of the 1000 simulations, the initial values
of the variables, the perturbation of the input species
and the values of the kinetic constants are randomly
chosen. To assess the validity of Proposition 1, at each
step of each simulation the tool checks whether the
following inequalities hold: A
0
i
≥ A
i
, B
0
i
≤ B
i
, C
0
i
≥ C
i
,
D
0
i
≥ D
i
and E
0
i
≤ E
i
. If one of such inequalities does
not hold, an error message is displayed.
We ran the tool 10 times, corresponding to 10000
simulations overall. The error message never ap-
peared.
5.2 Example of Non-monotonic
Behaviour
Example 2. Consider the following example of chem-
ical reaction network
A + B
k
1
C
A + E
k
2
N
E
k
3
C
for which, applying the law of mass action, we
obtain the following system of ODEs:
d[A]
dt
= −k
1
[A][B] −k
2
[A][E]
d[B]
dt
= −k
1
[A][B]
d[C]
dt
= +k
1
[A][B] +k
3
[E]
d[E]
dt
= −k
2
[A][E] − k
3
[E]
d[N]
dt
= +k
2
[A][E]
The dependency graph is shown in Figure 4. Consid-
ering A as the input species and the C as the output of
the chemical reaction network, we observe two dif-
ferent paths, one positive and one negative, relating
species A and C. Hence, the sufficient conditions of
our conjectures do not apply and we cannot conclude
anything on the monotonicity of the selected species.
However, observing the differential equations, we
can notice that the behaviour of the chemical species
A is ambivalent with respect to the chemical species
C. Indeed, A produces C in R
1
, but - at the same
time - consumes the chemical species E (another re-
actant producing C) in the reaction R
2
. This intuition
is confirmed by the result of simulations where we
augmented the concentration of A and plot the con-
centration of C (see Figure 5). The simulations shows
that in this case C is not monotonic with respect to the
variation of the initial concentration of A. Initial con-
centrations considered in the simulations are B
0
= 10,
C
0
= 0, E
0
= 20 and N
0
= 10.
5.3 Application to the ERK Signaling
Pathway
We now apply our method to a more complex ex-
ample. We consider the mathematical modeling of
the influence of RKIP on the ERK signaling path-
way presented in (Kwang-Hyun et al., 2003), a se-
ries of chemical transformations which contributes to
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
254

Figure 4: Dependency graph of the reaction network in Ex-
ample 2.
0 10 20 30 40 50 60 70 80 90 100
Time
0
2
4
6
8
10
12
14
16
18
20
Concentrations
C(1) with A
0
=1
C(2) with A
0
=20
C(3) with A
0
=50
Figure 5: Simulation results of Example 2. Changes in the
dynamics of species C by varying the initial concentration
of species A.
the control of a large number of cellular processes.
The activated kinase Ra f 1 phosphorylates the ki-
nase MAPK/ERK (MEK), which phosphorylates and
activates the Extracellular Signal Regulated kinase
(ERK).
Example 3. This chemical reaction network consists
of 11 chemical species and 11 reactions:
Raf
1
+ Rkip
k
1
k
2
Raf
1
/Rkip
Raf
1
/Rkip + Erkpp
k
3
k
4
Raf
1
/Rkip/Erkpp
Raf
1
/Rkip/Erkpp
k
5
Raf
1
+ Erk + Rkipp
Mekpp + Erk
k
6
k
7
Mekpp/Erk
Mekpp/Erk
k
8
Mekpp + Erkpp
Rkipp + Rp
k
9
k
10
Rkipp/Rp
Rkipp/Rp
k
11
Rkip + Rp
To assess monotonicity relationships between the
chemical species, we build the dependency graph of
the chemical reaction network, shown in Figure 6. In
this case, we notice that only reactions R
2
and R
4
have
common reactants, that is the species Ra f 1/Rkip.
Hence, in the dependency graph, we build only a neg-
ative edge between the species Erkpp and the reac-
tion R
2
.
Once the dependency graph is constructed, we in-
spect all possible paths among the species in order
to verify the conditions of our conjectures. Our con-
jectures allow us to draw conclusions on the mono-
tonicity of many pairs of species, that we validated by
performing simulations.
As an example, consider the species Mekpp and
Erk, respectively as input and output of the chemi-
cal reaction network. The paths from Mek pp to Erk
in the dependency graph are all positive. Hence, ac-
cording to our conjecture Erk is positively monotonic
with respect to Mekpp. This is confirmed by the
result of simulations, shown in Figure 7, where we
increase the initial concentration of Mekpp to study
the concentration variation of Erk. Consider now the
species Ra f 1/Rkip/Erkpp and Ra f 1/Rkip as input
and output, respectively, of the chemical reaction net-
work. In this case we find two paths (one positive
and one negative) which link the two species. Hence,
Ra f 1/Rkip could be not monotonic with respect to
Ra f 1/Rkip/Erkpp. Indeed, the fact that Ra f 1/Rkip
does not react in a monotonic way to the increase of
the initial concentration of Ra f 1/Rkip/Erk pp is ver-
ified by the result of simulations (see Figure 8). Pa-
rameters and initial concentrations are as in (Kwang-
Hyun et al., 2003).
Figure 6: Dependency graph of the ERK signaling pathway.
Towards an Efficient Verification Method for Monotonicity Properties of Chemical Reaction Networks
255
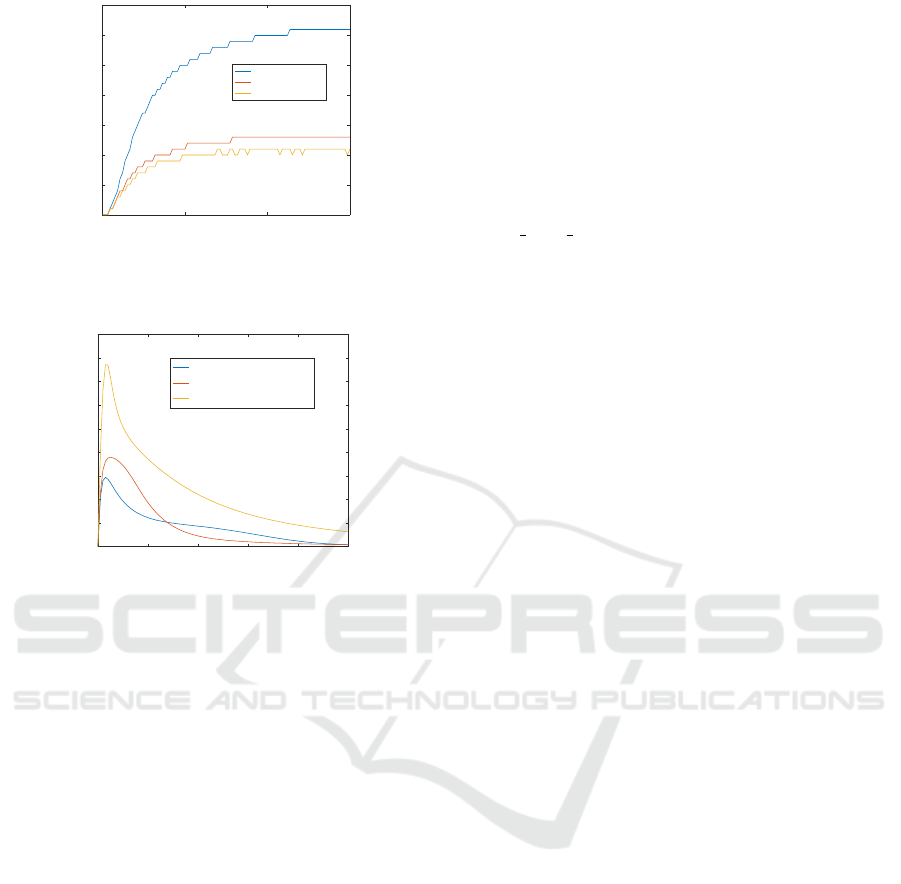
0 5 10 15
Time
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
Concentrations
ERK(1) with Mekpp
0
=2.5
ERK(2)with Mekpp
0
=5.5
ERK(3) with Mekpp
0
=6.5
Figure 7: Simulation results of Example 3. In this case, we
increase the initial concentration of Mekpp and compare the
concentrations of the output Erk. The results show that Erk
is monotonic with respect to the variation of the input.
0 5 10 15 20 25
Time
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Concentrations
Raf1/Rkip(1) with Raf1/Rkip/Erkpp
0
=1
Raf1/Rkip(2) with Raf1/Rkip/Erkpp
0
=25.5
Raf1/Rkip(3) with Raf1/Rkip/Erkpp
0
=300
Figure 8: Simulation results of Example 3. In this case, we
increase the initial concentration of Ra f 1/Rkip/Erk pp and
compare the concentrations of the output Ra f 1/Rkip. The
results show that Ra f 1/Rkip is not monotonic with respect
to the variation of the input.
6 CONCLUSION AND FUTURE
WORK
In this paper we have studied dynamical properties
of chemical reaction networks. We have given a new
notion of monotonicity, for which two species, con-
sidered as input and output of the network, are mono-
tonic if the variation of the initial concentration of the
input implies a monotonic variation in the concentra-
tion of the output. We have proposed new sufficient
conditions based on a dependency graph that guaran-
tee the monotonicity property to hold. Monotonicity
assessment can drastically reduce the number of sim-
ulations necessary to study the dynamical behaviour
of a chemical reaction network. We have shown the
application of our sufficient conditions to two small
models and to the quite complex model of the ERK
signaling pathway (Kwang-Hyun et al., 2003).
As regards ongoing and future work, we are work-
ing on the proof of our conjectures and we plan to
validate the approach by applying it extensively to a
benchmark collection of models of chemical reaction
networks as we did, for example, in (Pardini et al.,
2014) to validate an algorithm for the modularization
of biochemical pathways.
ACKNOWLEDGEMENTS
This work has been supported by the project
“Metodologie informatiche avanzate per l’analisi di
dati biomedici” funded by the University of Pisa
(PRA 2017 44). We thank Federico Poloni and Gi-
acomo Tommei for their useful suggestions.
REFERENCES
Angeli, D., De Leenheer, P., and Sontag, E. D. (2006). On
the structural monotonicity of chemical reaction net-
works. In Decision and Control, 2006 45th IEEE Con-
ference on, pages 7–12. IEEE.
Antoniotti, M., Mishra, B., Piazza, C., Policriti, A., and
Simeoni, M. (2003). Modeling cellular behavior
with hybrid automata: Bisimulation and collapsing.
In International Conference on Computational Meth-
ods in Systems Biology (CMSB 2003), pages 57–74.
Springer.
Barbuti, R., Bove, P., Gori, R., Levi, F., and Milazzo, P.
(2018). Simulating gene regulatory networks using re-
action systems. In Concurrency Specification & Pro-
gramming (CS&P 2018), CEUR-WS, volume 2240,
pages 119–132.
Barbuti, R., Gori, R., Levi, F., and Milazzo, P. (2015). Spe-
cialized predictor for reaction systems with context
properties. In Int. Workshop on Concurrency, Specifi-
cation and Programming, CS&P 2015, pages 31–43.
Barbuti, R., Gori, R., Levi, F., and Milazzo, P. (2016a).
Investigating dynamic causalities in reaction systems.
Theoretical Computer Science, 623:114–145.
Barbuti, R., Gori, R., Levi, F., and Milazzo, P. (2016b). Spe-
cialized predictor for reaction systems with context
properties. Fundamenta Informaticae, 147(2-3):173–
191.
Barnes, D. J. and Chu, D. (2010). Introduction to Model-
ing for Biosciences. Springer Publishing Company,
Incorporated, 1st edition.
Bodei, C., Gori, R., and Levi, F. (2015). Causal static anal-
ysis for brane calculi. Theoretical Computer Science,
587:73–103.
Brohee, S. and Van Helden, J. (2006). Evaluation of clus-
tering algorithms for protein-protein interaction net-
works. BMC bioinformatics, 7(1):488.
Cao, Y., Gillespie, D. T., and Petzold, L. R. (2006). Ef-
ficient step size selection for the tau-leaping sim-
ulation method. The Journal of chemical physics,
124(4):044109.
Carvalho, R. V., Verbeek, F. J., and Coelho, C. J. (2018).
Bio-modeling using petri nets: A computational ap-
proach. In Theoretical and Applied Aspects of Systems
Biology, pages 3–26. Springer.
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
256

Eker, S., Knapp, M., Laderoute, K., Lincoln, P., Meseguer,
J., and Sonmez, K. (2001). Pathway logic: Sym-
bolic analysis of biological signaling. In Biocomput-
ing 2002, pages 400–412. World Scientific.
Fages, F., Le Guludec, G., Bournez, O., and Pouly, A.
(2017). Strong turing completeness of continuous
chemical reaction networks and compilation of mixed
analog-digital programs. In International Conference
on Computational Methods in Systems Biology, pages
108–127. Springer.
Fages, F. and Soliman, S. (2008). Abstract interpretation
and types for systems biology. Theoretical Computer
Science, 403(1):52–70.
Fages, F. and Soliman, S. (2018). On robustness computa-
tion and optimization in biocham-4. In 16th Int. Conf.
on Computational Methods in Systems Biology.
Gillespie, D. T. (1977). Exact stochastic simulation of
coupled chemical reactions. The journal of physical
chemistry, 81(25):2340–2361.
Gori, R. and Levi, F. (2010). Abstract interpretation based
verification of temporal properties for bioambients.
Information and Computation, 208(8):869–921.
Jeong, H., Mason, S. P., Barab
´
asi, A.-L., and Oltvai, Z. N.
(2001). Lethality and centrality in protein networks.
Nature, 411(6833):41.
Kitano, H. (2004). Biological robustness. Nature Reviews
Genetics, 5(11):826–837.
Kwang-Hyun, C., Sung-Young, S., Hyun-Woo, K., Wolken-
hauer, O., McFerran, B., and Kolch, W. (2003). Math-
ematical modeling of the influence of rkip on the erk
signaling pathway. In International Conference on
Computational Methods in Systems Biology, pages
127–141. Springer.
Nasti, L., Gori, R., and Milazzo, P. (2018). Formalizing
a notion of concentration robustness for biochemical
networks. In International Conference on Software
Engineering and Formal Methods, collocated work-
shop DataMod 2018. Springer, in press. Draft avail-
able at http://pages.di.unipi.it/datamod/edition-2018/.
Pardini, G., Milazzo, P., and Maggiolo-Schettini, A. (2014).
Identification of components in biochemical path-
ways: extensive application to sbml models. Natural
Computing, 13(3):351–365.
Rizk, A., Batt, G., Fages, F., and Soliman, S. (2009). A
general computational method for robustness analysis
with applications to synthetic gene networks. Bioin-
formatics, 25(12):i169–i178.
Salis, H. and Kaznessis, Y. (2005). Accurate hybrid stochas-
tic simulation of a system of coupled chemical or bio-
chemical reactions. The Journal of chemical physics,
122(5):054103.
Schlitt, T. and Brazma, A. (2007). Current approaches to
gene regulatory network modelling. BMC bioinfor-
matics, 8(6):S9.
Shinar, G. and Feinberg, M. (2010). Structural sources of
robustness in biochemical reaction networks. Science,
327(5971):1389–1391.
Shinar, G. and Feinberg, M. (2011). Design principles for
robust biochemical reaction networks: what works,
what cannot work, and what might almost work.
Mathematical biosciences, 231(1):39–48.
Shmulevich, I., Dougherty, E. R., Kim, S., and Zhang,
W. (2002). Probabilistic boolean networks: a rule-
based uncertainty model for gene regulatory networks.
Bioinformatics, 18(2):261–274.
Stelzl, U., Worm, U., Lalowski, M., Haenig, C., Brem-
beck, F. H., Goehler, H., Stroedicke, M., Zenkner, M.,
Schoenherr, A., Koeppen, S., et al. (2005). A human
protein-protein interaction network: a resource for an-
notating the proteome. Cell, 122(6):957–968.
Towards an Efficient Verification Method for Monotonicity Properties of Chemical Reaction Networks
257
