FDMO: Feature Assisted Direct Monocular Odometry

Georges Younes

1,2

, Daniel Asmar

and John Zelek

Mechanical Engineering Department, American Univsersity of Beirut, Beirut, Lebanon

Department of Systems Design, University of Waterloo, Waterloo, Canada

Keywords:

Feature-based, Direct, Odometry, Localization, Monocular.

Abstract:

Visual Odometry (VO) can be categorized as being either direct (e.g. DSO) or feature-based (e.g. ORB-

SLAM). When the system is calibrated photometrically, and images are captured at high rates, direct methods

have been shown to outperform feature-based ones in terms of accuracy and processing time; they are also

more robust to failure in feature-deprived environments. On the downside, direct methods rely on heuristic

motion models to seed an estimate of camera motion between frames; in the event that these models are

violated (e.g., erratic motion), direct methods easily fail. This paper proposes FDMO (Feature assisted Direct

Monocular Odometry), a system designed to complement the advantages of both direct and featured based

techniques to achieve sub-pixel accuracy, robustness in feature deprived environments, resilience to erratic

and large inter-frame motions, all while maintaining a low computational cost at frame-rate. Efﬁciencies are

also introduced to decrease the computational complexity of the feature-based mapping part. FDMO shows

an average of 10% reduction in alignment drift, and 12% reduction in rotation drift when compared to the

best of both ORB-SLAM and DSO, while achieving signiﬁcant drift (alignment, rotation & scale) reductions

(51%, 61%, 7% respectively) going over the same sequences for a second loop. FDMO is further evaluated on

the EuroC dataset and was found to inherit the resilience of feature-based methods to erratic motions, while

maintaining the accuracy of direct methods.

1 INTRODUCTION

Visual Odometry (VO) is the process of localizing one

or several cameras in an unknown environment. Two

decades of extensive research have led to a multitude

of VO systems that can be categorized based on the

type of information they extract from an image, as di-

rect, feature-based, or a hybrid of both (Younes et al.,

2017). While the direct framework manipulates pho-

tometric measurements (pixel intensities), the feature-

based framework extracts and uses visual features as

an intermediate image representation. The choice of

feature-based or direct has important ramiﬁcations on

the performance of the entire VO system, with each

type exhibiting its own challenges, advantages, and

disadvantages.

One disadvantage of particular interest is the sen-

sitivity of direct methods to their motion model. This

limitation is depicted in Fig. 1 (A) and (B), where a

direct VO system is subjected to a motion that violates

its presumed motion model, and causes it to errone-

ously expand the map as shown in Fig. 1 (C) and (D).

Inspired by the invariance of feature-based methods

across relatively large motions (as shown in Fig. 1 (E)

and (F)), this paper proposes to address the shortco-

mings of direct methods, by detecting failure in their

frame to frame odometry component, and accordingly

invoking an efﬁcient feature-based strategy to cope

with large inter-frame motions, hereafter referred to

as large baselines. We call our approach Feature assis-

ted Direct Monocular Odometry, or FDMO for short.

We show that by effectively exploiting information

available from both direct and feature-based frame-

works, FDMO considerably improves the robustness

of monocular VO by succesfully achieving simultane-

ously the following properties:

1. Sub-pixel accuracy for the odometry system.

2. Robustness in feature-deprived environments.

3. Low computational cost at frame-rate, and a re-

duced computational cost for feature-based map

optimization.

4. Resilience to erratic and large inter-frame moti-

ons.

Younes, G., Asmar, D. and Zelek, J.

FDMO: Feature Assisted Direct Monocular Odometry.

DOI: 10.5220/0007524807370747

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 737-747

ISBN: 978-989-758-354-4

737

C D

A B

Figure 1: Direct methods failure under large baseline mo-

tion. (A) and (B) show the trajectory estimated from a direct

odometry system, before and after going through a relati-

vely large baseline between two consecutive frames (shown

in (C) and (D). Notice how the camera’s pose in (B) de-

railed from the actual path to a wrong pose. (C) and (D)

show the projected direct point cloud on both frames re-

spectively after erroneously estimating their poses. Notice

how the projected point cloud is no longer aligned with the

scene. On the other hand, (E) and (F) show how features

can be matched across the relatively large baseline, allo-

wing feature-based methods to cope with such motions.

2 BACKGROUND

Visual odometry can be broadly categorized as being

either direct or feature-based.

2.1 Direct VO

Direct methods process raw pixel intensities with the

brightness constancy assumption (Baker and Mat-

thews, 2004):

(x) = I

t−1

(x + g(x)), (1)

where x is the 2-dimensional pixel coordinates (u, v)

and g(x) denotes the displacement function of x be-

tween the two images I

and I

t−1

. Frame-to-frame

tracking is then a byproduct of an image alignment

optimization (Baker and Matthews, 2004) that mini-

mizes the photometric residual (intensity difference

between the two images) over the geometric transfor-

mation that relates them.

2.1.1 Traits of Direct Methods

Since direct methods rely on the entire image for

localization, they are less susceptible to failure in

feature-deprived environments, and do not require a

time-consuming feature extraction and matching step.

More importantly, since the alignment takes place at

the pixel intensity level, the photometric residuals can

be interpolated over the image domain ΩI, resulting

in an image alignment with sub-pixel accuracy, and

relatively less drift than feature-based odometry met-

hods (Irani and Anandan, 2000). However, the ob-

jective function to minimize is highly non-convex;

its convergence basin is very small, and will lock to

an erroneous conﬁguration if the optimization is not

accurately initialized. Most direct methods cope with

this limitation by adopting a pyramidal implementa-

tion, by assuming small inter-frame motions, and by

relying on relatively high frame rate cameras; howe-

ver, even with a pyramidal implementation that slig-

htly increases the convergence basin, all parameters

involved in the optimization should be initialized such

that x and g(x) are within 1-2 pixel radii from each ot-

her.

2.1.2 State of the Art in Direct Methods

Direct Sparse Odometry (DSO) (Engel et al., 2017)

is currently considered the state of the art in direct

methods. It is a keyframe-based VO that exploits

the small inter-frame motions nature of a video feed

to perform a pyramidal implementation of the for-

ward additive image alignment (Baker and Matthews,

2004). DSO’s image alignment optimizes a variant of

the brightness constancy assumption over the incre-

mental geometric transformation between the current

frame and a reference keyframe. The aligned patches

are then used to update the depth estimates for each

point of interest as described in (Engel et al., 2013).

2.2 Feature-based VO

Feature-based methods process 2D images to ex-

tract locations that are salient in an image. Let x =

(u, v)

represent a feature’s pixel coordinates in the 2-

dimensional image domain ΩI. Associated with each

feature is an n-dimensional vector Q

(x), known as

a descriptor. The set ΦI{x, Q(x)} is an intermediate

image representation after which the image itself be-

comes obsolete and is discarded.

2.2.1 Traits of Feature-based Methods

On the positive side, features with their associated

descriptors are somewhat invariant to viewpoint and

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

738

illumination changes, such that a feature x ∈ ΦI

one image can be identiﬁed as x

∈ ΦI

in another,

across relatively large illumination and motion base-

lines. However, the robustness of the data association

relies on the distinctiveness of each feature from the

other, a condition that becomes more difﬁcult to sa-

tisfy the higher the number of features extracted in

each scene; thereby favouring sparse, versus dense,

feature representations. On the downside, and as a

result of their discretized image representation space,

feature-based solutions offer inferior accuracy when

compared to direct methods, as the image domain

cannot be interpolated for sub-pixel accuracy.

2.2.2 State of the Art in Feature-based Methods

ORB-SLAM (Mur-Artal et al., 2015), currently con-

sidered the state of the art in feature-based methods,

associates FAST corners (Rosten and Drummond,

2006) with ORB descriptors (Rublee et al., 2011) as

an intermediate image representation. Regular fra-

mes are localized by minimizing the traditional ge-

ometric re-projection error; the 3D points are trian-

gulated using Epipolar geometry (Hartley and Zisser-

man, 2003), from multiple observations of the fea-

ture {x

, Q(x

)} in two or more keyframes. The con-

sistency of the map is maintained through a local

bundle adjustment minimization. Both, localization

and mapping optimizations are resilient to relatively

large inter-frame baseline motions and have a rela-

tively large convergence radius. To further increase

its performance and cut down processing time, ORB-

SLAM resorts to various methods for data association

such as the covisibility graph (Strasdat et al., 2011)

and bag of visual words. (Galvez-L

opez and Tardos,

2012).

3 RELATED WORK

When the corresponding pros and cons of both

feature-based and direct frameworks are placed side

by side, a pattern of complementary traits emerges

(Table 1). An ideal framework would exploit both di-

rect and feature-based advantages to beneﬁt from the

direct formulation accuracy and robustness to feature-

deprived scenes, while making use of feature-based

methods for large baseline motions.

In an attempt to achieve the aformentioned proper-

ties, hybrid direct-feature-based systems were previ-

ously proposed in (Forster et al., 2014), (Krombach

et al., 2016) and (Ait-Jellal and Zell, 2017); however,

(Forster et al., 2014) did not extract feature descrip-

tors, it relied on the direct image alignment to perform

Table 1: Comparison between the feature-based and direct

methods. The more of the symbol +, the higher the attribute.

Trait Feature-based Direct

Large baseline +++ +

Robust to Feature

Deprivation

+ +++

Recovered scene

point density

+ +++

Accuracy + +++

Optimization Non-

Convexity

+ ++

data association between the features. While this led

to signiﬁcant speed-ups in the processing required for

data association, it could not handle large baseline

motions; as a result, their work was limited to high

frame rate cameras, which ensured frame-to-frame

motion is small. On the other hand, both (Krombach

et al., 2016) and (Ait-Jellal and Zell, 2017) adopted a

feature-based approach as a front-end to their system,

and subsequently optimized the measurements with a

direct image alignment; as such, both systems suffer

from the limitations of the feature-based framework,

i.e. they are subject to failure in feature-deprived en-

vironments and therefore not able to simultaneously

meet all of the desired traits of Table 1. To address

this issue, both systems resorted to stereo cameras.

In contrast to these systems, FDMO can ope-

rate using a monocular camera, and simultaneously

achieve all of the desired traits. FDMO can also

be adapted for stereo and RGBD cameras as well.

FDMO’s source code will be made publicly available

on this URL upon the acceptance of this work.

4 PROPOSED SYSTEM

To capitalize on the advantages of both feature-based

and direct frameworks, our proposed approach con-

sists of a local direct visual odometry, assisted with a

feature-based map, such that it may resort to feature-

based odometry only when necessary. Therefore,

FDMO does not need to perform a computationally

expensive feature extraction and matching step at

every frame. During its feature-based map expan-

sion, FDMO exploits the localized keyframes with

sub-pixel accuracy from the direct framework, to ef-

ﬁciently establish feature matches in feature-deprived

environments using restricted epipolar search lines.

Similar to DSO, FDMO’s local temporary map is

deﬁned by a set of seven direct-based keyframes and

2000 active direct points. Increasing these parame-

ters was found by (Engel et al., 2017) to signiﬁcantly

increase the computational cost without much impro-

FDMO: Feature Assisted Direct Monocular Odometry

739

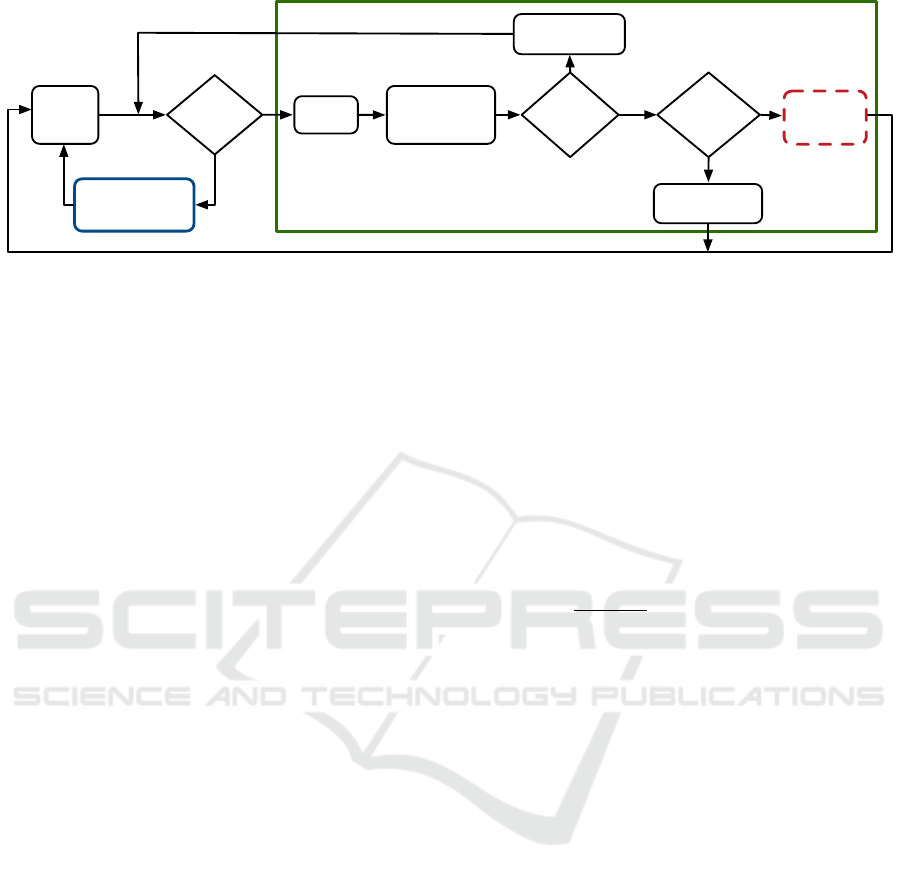
Direct Odometry

New

Frame

CVMM

Pyramidal

FAIA (Eq.2)

in M

If FAIA

diverged

If Track

Disable M

Feature-based

tracking

recovery

Update direct

depth map

Is KF

add new

Figure 2: Front-end ﬂowchart of FDMO. It runs on a frame by frame basis and uses a constant velocity motion model

(CVMM) to seed a Forward Additive Image Alignment (FAIA) to estimate the new frame’s pose and update the direct map

depth values. It also decides whether to invoke the feature-based tracking or add a new keyframe into the system. The blue

(solid line) and red (dashed line) boxes are further expanded in ﬁgures 3 and 4 respectively.

vement in accuracy. Direct keyframe insertion and

marginalization occurs frequently according to con-

ditions described in (Engel et al., 2017). In con-

trast, the feature-based map is made of an undetermi-

ned number of keyframes, each with an associated set

of features and their corresponding ORB descriptors

Φ(x, Q(x)).

4.1 Notation

To address any ambiguities, the superscript d will be

assigned to all direct-based measurements and f for

all feature-based measurements; not to be confused

with underscript f assigned to the word frame. There-

fore, M

refers to the temporary direct map, and M

to the feature-based map, which is made of an un-

restricted number of keyframes κ

and a set of 3D

points X

. I

refers to the image of frame i and T

,KF

is the se(3) transformation relating frame i to the la-

test active keyframe KF in the direct map. We also

make the distinction between z referring to depth me-

asurements associated with a 2D point x and Z refe-

ring to the Z coordinate of a 3D point.

4.2 Odometry

4.2.1 Direct Image Alignment

Frame by frame operations are handled by the ﬂow-

chart described in Fig. 2. Similar to (Engel et al.,

2017), newly acquired frames are tracked by minimi-

zing

argmin

,KF

∑

x∈N(x

)

Ob j(I

(ω(x, z,T

,KF

)−I

(x, z))),

(2)

where f

is the current frame, KF

is the latest added

keyframe in M

, x

∈ ΩI

is the set of image locati-

ons with sufﬁcient intensity gradient and an associa-

ted depth value d. N(x

) is the set of pixels neighbou-

ring x

and w(·) is the projection function that maps a

2D point from f

to KF

The minimization is seeded from a constant velo-

city motion model (CVMM). However, erratic mo-

tion or large motion baselines can easily violate the

CVMM, erroneously initializing the highly-non con-

vex optimization, and yielding unrecoverable tracking

failure. We detect tracking failure by monitoring the

RMSE of Eq. (2) before and after the optimization;

if the ratio

RMSE

a f ter

RMSE

be f ore

> 1 + ε we consider that the

optimization has diverged and we invoke the feature-

based tracking recovery, summarized in the ﬂowchart

of Fig. 3. The ε is used to restrict feature-based inter-

vention when the original motion model used is accu-

rate, a value of ε = 0.1 was found as a good trade-

off between continuously invoking the feature-based

tracking and not detecting failure in the optimization.

To avoid extra computational cost, feature extraction

and matching is not performed on a frame by frame

basis, it is only invoked during feature-based tracking

recovery and feature-based KF insertion.

4.2.2 Feature-based Tracking Recovery

Our proposed feature-based tracking operates in M

When direct tracking diverges, we consider the

CVMM estimate to be invalid and seek to estimate a

new motion model using the feature-based map. Our

proposed feature-based tracking recovery is a vari-

ant of the global re-localization method proposed in

(Mur-Artal et al., 2015); we ﬁrst start by detecting

Φ f

= Φ(x

, Q(x

)) in the current image, which are

then parsed into a vocabulary tree. Since we consider

the CVMM to be invalid, we fall back on the last piece

of information the system was sure of before failure:

the pose of the last successfully added keyframe. We

deﬁne a set κ

of feature-based keyframes KF

con-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

740

nected to the last added keyframe KF

through a co-

visibility graph (Strasdat et al., 2011), and their asso-

ciated 3D map points X

Blind feature matching is then performed between

Φ f

and all keyframes in κ

, by restricting feature ma-

tching to take place between features that exist in the

same node in a vocabulary tree (Galvez-L

opez and

Tardos, 2012); this is done to reduce the computatio-

nal cost of blindly matching all features.

Once data association is established between f

and the map points, we set up an EPnP (Efﬁcient

Perspective-n-Point Camera Pose Estimation) (Lepe-

tit et al., 2009) to solve for an initial pose T

using

3D-2D correspondences in an non-iterative manner.

The new pose is then used to deﬁne a 5 × 5 search

window in f

surrounding the projected locations of

all 3D map points X

∈ κ

. Finally the pose T

reﬁned through the traditional feature-based optimi-

zation. To achieve sub-pixel accuracy, the recovered

pose T

is then converted into a local increment over

the pose of the last active direct keyframe, and then

further reﬁned in a direct image alignment optimiza-

tion Eq. (2).

Note that the EPnP step could have been skip-

ped in favour of using the last correctly tracked keyf-

rame’s position as a starting point; however, data as-

sociation would then require a relatively larger se-

arch window, which in turn increases its computati-

onal burden in the subsequent step. Data association

using a search window was also found to fail when

the baseline motion was relatively large.

4.3 Mapping

FDMO’s mapping process is composed of two com-

ponents: direct, and feature-based as described in Fig.

4. The direct map propagation used here is the same

as suggested in (Engel et al., 2017); however we ex-

pand its capabilities to propagate the feature-based

map. When a new keyframe is added to M

, we cre-

ate a new feature-based keyframe KF

that inherits

its pose from KF

. ΦKF

, Q(x

)) is then extrac-

ted and data association takes place between the new

keyframe and a set of local keyframes κ

surrounding

it via epipolar search lines. The data association is

used to keep track of all map points X

visible in the

new keyframe and to triangulate new map points.

To ensure an accurate and reliable feature-based

map, typical feature-based methods employ local

bundle adjustment (LBA)(Mouragnon et al., 2006) to

optimize for both the keyframes poses and their asso-

ciated map points; however, employing an LBA may

generate inconsistencies between both map represen-

tations, and is computationally expensive; instead, we

make use of the fact that the new keyframe’s pose

is already locally optimal, to replace the typical lo-

cal bundle adjustment with a computationally less de-

manding structure only optimization deﬁned for each

3D point X

argmin

∑

i∈κ

Ob j(x

i, j

− π(T

)), (3)

where X

spans all 3D map points observed in all

keyframes ∈ κ

. We use ten iterations of Gauss-

Newton to minimize the normal equations associated

with Eq. (3) which yield the following update rule per

3D point X

per iteration:

t+1

= X

− (J

W J)

−1

We (4)

Where e is the stacked reprojection residuals e

asso-

ciated with a point X

and its found match x

in keyf-

rame i. J is the stacked Jacobians of the reprojection

error which is found by stacking:

0 −

−

(5)

and R

is the 3 × 3 orientation matrix of the keyf-

rame observing the 3D point X

. Similar to ORB-

SLAM, W is a block diagonal weight matrix that

down-weighs the effect of residuals computed from

feature matches found at high pyramidal levels

and

is computed as



S f

0 S f



(6)

where S f is the scale factor used to generate the py-

ramidal representation of the keyframe (we use S f =

1.2) and n is the pyramid level from which the feature

was extracted (0 < n < 8). The Huber norm is also

used to detect and remove outliers. We have limited

the number of iterations in the optimization of Eq. (3)

to ten, since no signiﬁcant reduction in the feature-

based re-projection error was recorded beyond that.

4.4 Feature-based Map Maintenance

To ensure a reliable feature-based map, the following

practices are employed. For proper operation, di-

rect methods require frequent addition of keyframes,

resulting in small baselines between the keyframes,

which in turn can cause degeneracies if used to trian-

gulate feature-based points. To avoid numerical insta-

bilities, following the suggestion of (Klein and Mur-

ray, 2007), we prevent feature triangulation between

Features matched at higher pyramidal levels are less

reliable.

FDMO: Feature Assisted Direct Monocular Odometry

741

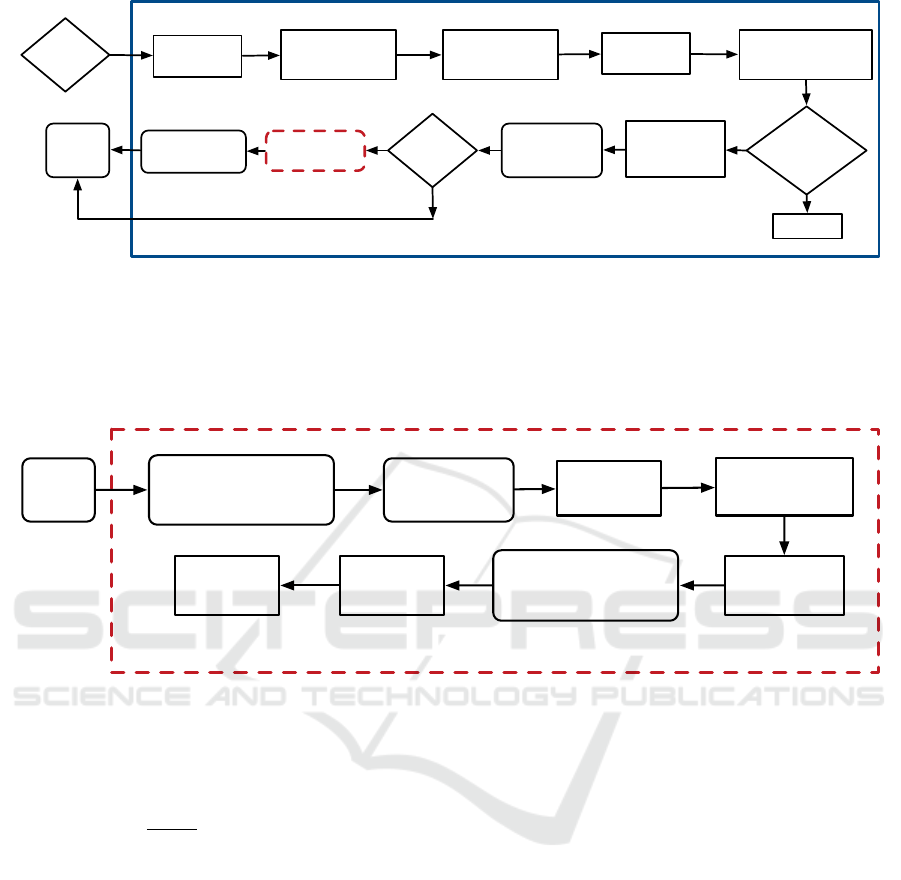
Extract

ɸ(x,Q(x))

Feature based tracking recovery

New

Frame

Blind feature

matching in

vocabulary tree

EPnP

Get κ

from

covisibility graph

Guided data

association with a

search window

Motion only

optimization

in M

Is KF

Add new KF

If not enough

matches

Update direct

depth map

Fail

Pyramidal

FAIA (Eq.2)

in M

If Track

Figure 3: FDMO Tracking Recovery ﬂowchart. Only invoked when direct image alignment fails, it takes over the front end

operations of the system until the direct map is re-initialized. FDMO’s tracking recovery is a variant of ORB-SLAM’s global

failure recovery that exploits the information available from the direct framework to constrain the recovery procedure locally.

We start by extracting features from the new frame and matching them to 3D features observed in a set of keyframes κ

connected to the last correctly added keyframe from KF

. Efﬁcient Perspective-n-Point (EPnP) camera pose estimation is

used to estimate an initial guess which is then reﬁned by a guided data association between the local map and the frame. The

reﬁned pose is then used to seed a Forward additive image alignment step to achieve sub-pixel accuracy.

Add new KF

New

Photometric

optimization in M

add T

Extract

ɸ(x,Q(x))

Get κ

from

covisibility graph

Feature

triangulation

Structure only

optimization (Eq.3) in

map

maintenance

map

maintenance

Figure 4: Our proposed mapping ﬂowchart, is a variant of DSO’s mapping backend; we augment its capabilities to expand

the feature-based map with new KF

. It operates after or parallel to the direct photometric optimization of DSO, by ﬁrst

establishing feature matches using restricted epipolar search lines; the 3D feature-based map is then optimized using a com-

putationally efﬁcient structure-only bundle adjustment, before map maintenance ensures the map remain outliers free.

keyframes with a

baseline

depth

ratio less than 0.02 which is

a trade-off between numerically unstable triangulated

features and feature deprivation problems. We exploit

the frequent addition of keyframes as a feature quality

check. In other words, a feature has to be correctly

found in at least 4 of the 7 keyframes subsequent to

the keyframe it was ﬁrst observed in, otherwise it is

considered spurious and is subsequently removed. To

ensure no feature deprivation occurs, a feature can-

not be removed until at least 7 keyframes have been

added since it was ﬁrst observed. Finally, similar to

(Mur-Artal et al., 2015) a keyframe with ninety per-

cent of its points shared with other keyframes is re-

moved from M

only once marginalized from M

The aforementioned practices ensure that sufﬁ-

cient reliable map points and features are available

in the immediate surrounding of the current frame,

and that only necessary map points and keyframes are

kept once the camera moves on.

5 EXPERIMENTS AND RESULTS

To evaluate FDMO’s tracking robustness, experi-

ments were performed on several well-known data-

sets (Burri et al., 2016) and (Engel et al., 2016), and

both qualitative and quantitative appraisal was con-

ducted. To further validate FDMO’s effectiveness,

the experiments were also repeated on state of the

art open-source systems in both direct (DSO) and

feature-based (ORB-SLAM2). For fairness of com-

parison, we evaluate ORB-SLAM2 as an odometry

system (not as a SLAM system); therefore, similar to

(Engel et al., 2017) we disable its loop closure thread

but we keep its global failure recovery, local, and glo-

bal bundle adjustments intact. Note that we’ve also

attempted to include results from SVO (Forster et al.,

2014) but it continuously failed on most datasets, so

we excluded it.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

742

5.1 Datasets

5.1.1 TUM MONO Dataset

(Engel et al., 2016) Contains 50 sequences of a ca-

mera moving along a path that begins and ends at

the same location. The dataset is photometrically ca-

librated: camera response function, exposure times

and vignetting are all available; however, ground truth

pose information is only available for two small seg-

ments at the beginning and end of each sequence;

fortunately, such information is enough to compute

translation, rotation, and scale drifts accumulated

over the path, as described in (Engel et al., 2016).

5.1.2 EuRoC MAV Dataset

(Burri et al., 2016) Contains 11 sequences of stereo

images recorded by a drone mounted camera. Ground

truth pose for each frame is available from a Vicon

motion capture system.

5.2 Computational Cost

The experiments were conducted on an Intel Core

i7-4710HQ 2.5GHZ CPU, 16 GB memory; no GPU

acceleration was used. The time required by each of

the processes was recorded and summarized in Table

2. Both DSO and ORB-SLAM2 consist of two pa-

rallel components, a tracking process (at frame-rate

)

and a mapping process (keyframe-rate

). On the ot-

her hand, FDMO has three main processes: a direct

tracking process (frame-rate), a direct mapping pro-

cess (keyframe-rate), and a feature-based mapping

process (keyframe-rate). Both of FDMO’s mapping

processes can run either sequentially for a total com-

putational cost of 200 ms on a single thread, or in pa-

rallel on two threads. As Table 2 shows, the mean

tracking time for FDMO remains almost the same

that of DSO: we don’t extract features at frame-rate;

feature-based tracking in FDMO is only performed

when the direct tracking diverges; the extra time is

reﬂected in the slightly increased standard deviation

of the computational time with respect to DSO. Ne-

vertheless, it is considerably less than ORB-SLAM2’s

23 ms. The highest computational cost during FDMO

tracking occurs when the recovery method is invoked,

with a highest recorded processing time during our

experiments of 35 ms. As for FDMO’s mapping pro-

cesses, its direct part remains the same as DSO, whe-

reas the feature-based part takes 153 ms which is also

occur at every frame.

occur at new keyframes only.

Table 2: Computational time (ms) for processes in DSO,

FDMO and ORB-SLAM2. (Empty means the process does

not exist).

Process DSO FDMO

ORB-

SLAM2

Tracking

(frame-rate)

12.35±

9.62

13.54±

14.19

23.04±

4.11

Direct

mapping

(Keyframe-

rate)

46.94±

51.62

46.89±

65.21

—

Feature-based

mapping

(Keyframe-

rate)

—

153.8±

58.08

236.47±

101.8

signiﬁcantly less than ORB-SLAM2’s feature-based

mapping process that requires 236 ms.

5.3 Quantitative Results

We assess FDMO, ORB-SLAM2 and DSO using the

following experiments.

5.3.1 Two Loop Experiment

In this experiment, we investigate the quality of

the estimated trajectory by comparing ORB-SLAM2,

DSO, and FDMO. We allow all three systems to

run on various sequences of the Tum Mono dataset

(Engel et al., 2016) across various conditions, both

indoors and outdoors. Each system is allowed to

run through every sequence for two continuous loops

where each sequence begins and ends at the same lo-

cation. We record the positional, rotational, and scale

drifts at the end of each loop, as described in (Engel

et al., 2016). The drifts recorded at the end of the ﬁrst

loop are indicative of the system’s performance across

the unmodiﬁed generic datasets, whereas the drifts re-

corded at the end of the second loop consist of three

components: (1) the drift accumulated from the ﬁrst

loop, (2) an added drift accumulated over the second

run, and (3) an error caused by a large baseline mo-

tion induced at the transition between the loops. The

reported results are shown in Table 3 and some of the

recovered trajectories are shown in Fig. 5.

5.3.2 Frame Drop Experiment

While the ﬁrst experiment reports on the system’s per-

formance across large scale scenes in various con-

ditions, this experiment investigates the effects erra-

tic and large baseline motions have on the camera’s

tracking accuracy. Erratic motion can be deﬁned

as a sudden acceleration in the opposite direction of

FDMO: Feature Assisted Direct Monocular Odometry

743

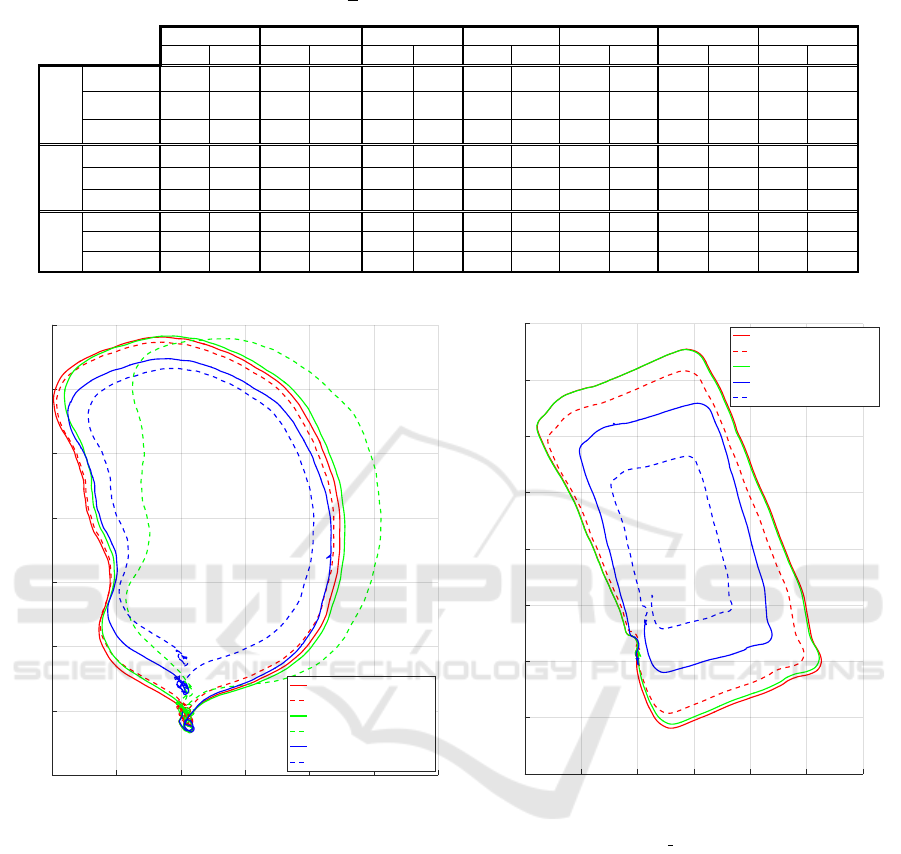
Table 3: Measured drifts after ﬁnishing one and two loops over various sequences from the TumMono dataset. The alignment

drift (meters), rotation drift (degrees) and scale(

) drifts are computed similar to (Engel et al., 2016).

Loop 1

Loop 2 Loop 1 Loop 2 Loop 1 Loop 2

Loop 1

Loop 2

Loop 1

Loop 2

Loop 1 Loop 2

Loop 1

Loop 2

FDMO

0.752 1.434 0.863 1.762 0.489 1.045 0.932 2.854 2.216 4.018 1.344 2.973 1.504 2.936

DSO

0.847

－

0.89 3.269 0.728 5.344 0.945

－

2.266 4.251 1.402 8.702 1.813

－

ORB SLAM

4.096 8.025 3.722 8.042 2.688 4.86 1.431 2.846

－－

8.026 12.69 6.72 13.56

FDMO

1.4 1.192 1.154 2.074 0.306 0.317 1.425 6.246 3.877 6.524 0.522 5.595 0.448 1.062

DSO

1.607

－

1.278 7.699 0.283 18.9 2.22

－

4.953 19.89 0.462 23.17 0.594

－

ORB SLAM

26.92 53.28 2.373 4.647 2.982 4.549 3.676 6.498

－－

3.707 7.375 3.243 6.668

FDMO 1.079 1.161 1.113 1.238 1.033 1.071 1.072 1.211 1.109 1.219 1.082 1.106 1.107 1.224

DSO 1.089

－

1.116 1.424 1.045 1.109 1.067

－

1.118 1.226 1.084 1.023 1.133

－

ORB SLAM 1.009 1.019 1.564 2.403 1.199 1.373 1.094 1.206 －－ 1.867 2.574 1.7 2.675

Sequence 45

Sequence 50

Alignment

Rotation

Scale

Sequence 20

Sequence 25

Sequence 30

Sequence 35

Sequence 40

-10 -5 0 5 10 15 20

X (m)

-5

Y (m)

Sequence 30

FDMO Loop 1

FDMO Loop 2

DSO Loop 1

DSO Loop 2

ORB SLAM Loop 1

ORB SLAM Loop 2

-10 -5 0 5 10 15 20

X (m)

-10

-5

Y (m)

Sequence 50

FDMO Loop 1

FDMO Loop 2

DSO Loop 1

ORB SLAM Loop 1

ORB SLAM Loop 2

Figure 5: Sample paths estimated by the various systems on Sequences 30 and 50 of the Tum Mono dataset. The paths are all

aligned using ground truths available at the beginning and end of each loop. Each solid line corresponds to the ﬁrst loop of

a system while the dashed line correspond to the second loop. Ideally, all systems would start and end at the same location,

while reporting the same trajectories across the two loops. Note that in Sequence 50, there is no second loop for DSO as it

was not capable of dealing with the large baseline between the loops and failed.

motion, and is quite common in hand-held devices

or quad-copters. Another example of erratic motion

occurs when the camera’s video feed is being trans-

mitted over a network to a ground station where com-

putation is taking place; communication issues may

cause frame drops which are seen by the odometry

system as large baseline motions; therefore it is impe-

rative for an odometry system to cope with such mo-

tions. To quantize the inﬂuence of erratic motions on

an odometry system, we set up an experiment to emu-

late their effects, by dropping frames and measuring

the recovered poses before and after dropping them.

The experiment is repeated at the same location and

the number of frames dropped is increased by ﬁve fra-

mes each time until each system fails. Various factors

can affect the obtained results, such as the distance to

the observed scene, skipping frames towards a previ-

ously observed or unobserved scene, and/or the type

of camera motion (i.e., sideways, forward moving, or

rotational motion), to name a few. Therefore we re-

peat the above experiment for each system in various

locations covering the above scenarios. We chose to

perform the experiments on the EuroC dataset (Burri

et al., 2016) whose frame to frame ground truth is

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

744

known; thus allowing us to compute the relative Eu-

clidean distance Translation = ||F

− F

||, and the

orientation difference between the recovered poses at

and F

as the geodesic metric of the normalized

quaternions on the unit sphere deﬁned by Rotation =

cos

−1

(2|F

· F

− 1). We report on the percent error

%Error = 100 ×

|Measured−GroundTruth|

GroundTruth

for the recove-

red Euclidean distance and relative orientation before

and after the skipped frames. The obtained results for

FDMO, DSO and ORB-SLAM2 are shown in Fig. 6.

0 0.5 1 1.5 2 2.5 3

Ground Truth Translation (meters)

100

% Error

Camera motion parallel to its optical axis

0 10 20 30 40

Ground Truth rotation (degrees)

100

% Error

Pure rotation motion

FDMO (forward) FDMO (Backward)

DSO (forward) DSO (Backward)

ORB SLAM (forward) ORB SLAM (Backward)

0 1 2 3 4 5

Ground Truth Translation (meters)

% Error

Camera motion perpendicular to its optical axis

100

Figure 6: %Error v.s. ground truth motion measured by

dropping frames and estimating the relative rotation and

translation before and after the frames were dropped. Af-

ter every measurement, the system is restarted and the num-

ber of dropped frames is increased/decreased by 5 frames

for forward and backward jumps respectively, until failure

occurs. The experiments were conducted on various se-

quences of the EuroC dataset (Burri et al., 2016): Expe-

riment (A) in the sequence MH01 with forward starting at

frame 200 and backward starting at 250; Experiment (B) in

the sequence MH02 with forward starting at frame 510 and

backward at 560. Experiment (C) in the sequence MH03

with forward starting at frame 950 and backward starting at

frame 1135.

5.4 Qualitative Assessment

Fig. 7 compares the resilience of FDMO and ORB-

SLAM2 to feature-deprived environments. FDMO

exploits the sub-pixel accurate localized direct keyfra-

mes to propagate its feature-based map, therefore its

capable of generating accurate and robust 3D land-

marks that have a higher matching rate even in low

textured environments. In contrast, ORB-SLAM2

fails to propagate its map causing tracking failure.

FDMO ORB SLAM

Figure 7: Features matched of FDMO (left) and ORB-

SLAM2 (right) in a feature deprived environment (sequence

40 of the Tum mono dataset).

5.5 Discussion

The results reported in the ﬁrst experiment (Table. 3)

demonstrate FDMO’s performance in large-scale ind-

oor and outdoor environments. The importance of

the problem FDMO attempts to address is highligh-

ted by analyzing the drifts incurred at the end of the

ﬁrst loop; while no artiﬁcial erratic motions nor large

baselines were introduced over the ﬁrst loop, i.e. un-

modiﬁed dataset, FDMO was able to outperform the

best of either DSO and ORB-SLAM2 in terms of po-

sitional and rotational drifts, by an average of 10%

and 12% respectively on most sequences. The impro-

ved performance is due to FDMO’s ability to detect

and account for inaccuracies in the direct framework

using its feature-based map, while beneﬁting from the

sub-pixel accuracy of the direct framework. Further-

more, FDMO was capable of expanding both its direct

and feature-based maps in feature-deprived environ-

ments (e.g. Sequence 40) whereas ORB-SLAM2 fai-

led to do so. FDMO’s robustness is further proven by

analyzing the results obtained over the second loop.

The drifts accumulated toward the end of the second

loop are made of three components; mainly, the drift

that occurred over the ﬁrst loop, the drift that occurred

over the second, and an error caused by a large base-

line separating the frames at the transition between

the loops. If the error caused by the large baseline

is negligible, we would expect the drift at the second

loop to be double that of the ﬁrst. While the measured

drifts for both ORB-SLAM2 and FDMO does indeed

exhibit such behaviour, the drifts reported by ORB-

FDMO: Feature Assisted Direct Monocular Odometry

745

SLAM2 are signiﬁcantly larger than the ones repor-

ted by FDMO as Fig. 5 also highlights. On the other

hand, DSO tracking failed entirely on various occa-

sions, and when it did not fail, it reported a signiﬁ-

cantly large increase in drifts over the second loop. As

DSO went through the transition frames between the

loops, its motion model estimate was violated, errone-

ously initializing its highly non-convex tracking op-

timization. The optimization got subsequently stuck

in a local minimum, which led to a wrong pose esti-

mate. The wrong pose estimate was in turn used to

propagate the map, thereby causing large drifts. On

the other hand, FDMO was successfully capable of

handling such a scenario, reporting an average impro-

vement of 51%, 61% and 7 % in positional, rotatio-

nal, and scale drifts respectively, when compared to

the best of both DSO and ORB-SLAM2, on most se-

quences.

The results reported in the second experiment

(Fig. 6) quantify the robustness limits of each sy-

stem to erratic motions. Various factors may affect the

obtained results, therefore, we attempted the experi-

ments under various types of motion and by skipping

frames towards a previously observed (herein referred

to as backward) and previously unobserved part of the

scene (referred to as forward). The observed depth of

the scene is also an important factor: far-away sce-

nes remain for a longer time in the ﬁeld of view, thus

improving the systems’ performance. However, we

cannot model all different possibilities of depth vari-

ations; therefore, for the sake of comparison, all sy-

stems were subjected to the same frame drops at the

same locations in each experiment where the obser-

ved scene’s depth varied from three to eight meters.

The reported results highlight DSO’s brittleness to

any violation of its motion model; where translations

as little as thirty centimeters and rotations as small

as three degrees introduced errors of over 50% in its

pose estimates. On the other hand, FDMO was ca-

pable of accurately handling baselines as large as 1.5

meters and 20 degrees towards previously unobser-

ved scene, after which failure occurred due to feature-

deprivation, and two meters toward previously obser-

ved parts of the scene. ORB-SLAM2’s performance

was very similar to FDMO in forward jumps, howe-

ver it signiﬁcantly outperformed it by twice as much

in the backward jumps; ORB-SLAM2 uses a global

map for failure recovery whereas FDMO, being an

odometry system, can only make use of its immediate

surroundings. Nevertheless FDMO’s current limitati-

ons in this regard are purely due to our current imple-

mentation as there are no theoretical limitations of de-

veloping FDMO into a full SLAM system. However,

using a global relocalization method has its downside;

the jitter in ORB-SLAM2’s behaviour (shown in Fig.

6 (C)) is due to its relocalization process erroneously

localizing the frame at spurious locations. Another

key aspect of FDMO, visible in this experiment, is

its ability to detect failure and not incorporate it into

its map. In contrast, toward their failure limits, both

DSO and ORB-SLAM2 incorporate spurious measu-

rements for few frames before failing completely.

6 CONCLUSION

This paper successfully demonstrated the advantages

of integrating direct and feature-based methods in

VO. By relying on a feature-based map when direct

tracking fails, the issue of large baselines that is cha-

racteristic of direct methods is mitigated, while main-

taining the high accuracy and robustness to feature-

deprived environments of direct methods in both

feature-based and direct maps, at a relatively low

computational cost. Both qualitative and quantitative

experimental results proved the effectiveness of the

collaboration between direct and feature-based met-

hods in the localization part.

While these results are exciting, they do not make

use of a global feature-based map; as such we are

currently developing a more elaborate integration be-

tween both frameworks, to further improve the map-

ping accuracy and efﬁciency. Furthermore, we antici-

pate that the beneﬁts to the mapping thread will also

lead to added robustness and accuracy to the motion

estimation within a full SLAM framework.

ACKNOWLEDGEMENTS

This work was funded by the University Research

Board (UBR) at the American University of Beirut,

and the Canadian National Science Research Council

(NSERC).

REFERENCES

Ait-Jellal, R. and Zell, A. (2017). Outdoor obstacle avoi-

dance based on hybrid stereo visual slam for an auto-

nomous quadrotor mav. In IEEE 8th European Con-

ference on Mobile Robots (ECMR).

Baker, S. and Matthews, I. (2004). Lucas-Kanade 20 Years

On: A Unifying Framework. International Journal of

Computer Vision, 56(3):221–255.

Burri, M., Nikolic, J., Gohl, P., Schneider, T., Rehder, J.,

Omari, S., Achtelik, M. W., and Siegwart, R. (2016).

The euroc micro aerial vehicle datasets. The Interna-

tional Journal of Robotics Research.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

746

Engel, J., Koltun, V., and Cremers, D. (2017). Direct sparse

odometry. IEEE Transactions on Pattern Analysis and

Machine Intelligence, PP(99):1–1.

Engel, J., Sturm, J., and Cremers, D. (2013). Semi-dense

Visual Odometry for a Monocular Camera. In Com-

puter Vision (ICCV), IEEE International Conference

on, pages 1449–1456. IEEE.

Engel, J., Usenko, V., and Cremers, D. (2016). A photo-

metrically calibrated benchmark for monocular visual

odometry. In arXiv:1607.02555.

Forster, C., Pizzoli, M., and Scaramuzza, D. (2014). Svo :

Fast semi-direct monocular visual odometry. In Robo-

tics and Automation (ICRA), IEEE International Con-

ference on.

Galvez-L

opez, D. and Tardos, J. D. (2012). Bags of Binary

Words for Fast Place Recognition in Image Sequen-

ces. Robotics, IEEE Transactions on, 28(5):1188–

1197.

Hartley, R. and Zisserman, A. (2003). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press.

Irani, M. and Anandan, P. (2000). About direct methods. In

Proceedings of the International Workshop on Vision

Algorithms: Theory and Practice, ICCV ’99, pages

267–277, London, UK, UK. Springer-Verlag.

Klein, G. and Murray, D. (2007). Parallel Tracking and

Mapping for Small AR Workspaces. 6th IEEE and

ACM International Symposium on Mixed and Aug-

mented Reality, pages 1–10.

Krombach, N., Droeschel, D., and Behnke, S. (2016). Com-

bining feature-based and direct methods for semi-

dense real-time stereo visual odometry. In Internati-

onal Conference on Intelligent Autonomous Systems,

pages 855–868. Springer.

Lepetit, V., Moreno-Noguer, F., and Fua, P. (2009). EPnP:

An Accurate O(n) Solution to the PnP Problem. Inter-

national Journal of Computer Vision, 81(2):155–166.

Mouragnon, E., Lhuillier, M., Dhome, M., Dekeyser, F.,

and Sayd, P. (2006). Real time localization and 3d

reconstruction. In 2006 IEEE Computer Society Con-

ference on Computer Vision and Pattern Recognition

(CVPR’06), volume 1, pages 363–370.

Mur-Artal, R., Montiel, J. M. M., and Tardos, J. D. (2015).

ORB-SLAM: A Versatile and Accurate Monocular

SLAM System. IEEE Transactions on Robotics,

PP(99):1–17.

Rosten, E. and Drummond, T. (2006). Machine Learning

for High-speed Corner Detection. In 9th European

Conference on Computer Vision - Volume Part I, Pro-

ceedings of the, ECCV’06, pages 430–443, Berlin,

Heidelberg. Springer-Verlag.

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.

(2011). ORB: An efﬁcient alternative to SIFT or

SURF. In International Conference on Computer Vi-

sion (ICCV), pages 2564–2571.

Strasdat, H., Davison, A. J., Montiel, J. M. M., and Ko-

nolige, K. (2011). Double Window Optimisation for

Constant Time Visual SLAM. In International Confe-

rence on Computer Vision, Proceedings of the, ICCV

’11, pages 2352–2359, Washington, DC, USA. IEEE

Computer Society.

Younes, G., Asmar, D., Shammas, E., and Zelek, J. (2017).

Keyframe-based monocular slam: design, survey, and

future directions. Robotics and Autonomous Systems,

98:67 – 88.

FDMO: Feature Assisted Direct Monocular Odometry

747