Limitations of Metric Loss for the Estimation of Joint Translation and

Rotation

Philippe P

erez de San Roman

1,2,3

, Pascal Desbarats

1,2

, Jean-Philippe Domenger

1,2

and Axel Buendia

3,4,5

Universit

e de Bordeaux, Bordeaux, France

LaBRI, Talence, France

ITECA, Angoulłme/Paris France

SpirOps, Paris, France

CNAM-CEDRIC, Paris, France

jean-philippe.domenger@u-bordeaux.fr, axel.buendia@cnam.fr

https://www.u-bordeaux.com/, http://www.labri.fr/, http://iteca.eu/, http://www.spirops.com/, https://cedric.cnam.fr/

Keywords:

Object Localization, Deep Learning, Metric Loss.

Abstract:

Localizing objects is a key challenge for robotics, augmented reality and mixed reality applications. Images

taken in the real world feature many objects with challenging factors such as occlusions, motion blur and

changing lights. In manufacturing industry scenes, a large majority of objects are poorly textured or highly

reﬂective. Moreover, they often present symmetries which makes the localization task even more complicated.

PoseNet is a deep neural network based on GoogleNet that predicts camera poses in indoor room and outdoor

streets. We propose to evaluate this method for the problem of industrial object pose estimation by training

the network on the T-LESS dataset. We demonstrate with our experiments that PoseNet is able to predict

translation and rotation separately with high accuracy. However, our experiments also prove that it is not

able to learn translation and rotation jointly. Indeed, one of the two modalities is either not learned by the

network, or forgotten during training when the other is being learned. This justiﬁes the fact that future works

will require other formulation of the loss as well as other architectures in order to solve the pose estimation

general problem.

1 INTRODUCTION

Over the past decades, the growing interest for Deep

Convolutional Neural Networks for image and object

recognition (Le Cun et al., 1990; Krizhevsky et al.,

2012; Szegedy et al., 2015; Simonyan and Zisserman,

2014) has seen more ambitious works emerged for

image segmentation (Ronneberger et al., 2015) and

object localization (Kendall et al., 2015; Rad and Le-

petit, 2017; Do et al., 2018; Li et al., 2018; Xiang

et al., 2017). Object localization is a key component

for augmented reality applications where information,

visual effects or data are added to real world objects.

This allows the user to be better informed about his

environment, most often by wearing an augmented

reality headset (Microsoft Hololens

, 2017). Aug-

mented reality is applied in video-game industry and

shopping Industry (IKEA, 2017). It is also useful in

the medical domain (Collins et al., 2014) and in ma-

nufacturing industry (Didier et al., 2005).

Typical augmented reality headsets have a trans-

parent screen inserting visuals on the foreground of

the user’s ﬁeld of view. As for now, headsets such

as the (Microsoft Hololens

, 2017) provide limi-

ted data about user environment (RGB video, surface

mesh of nearby objects). They have also limited me-

mory and computational power. It is thus difﬁcult to

align the created visuals on the real world objects, es-

pecially if high precision is required as it is the case

in many industrial or medical applications. To ena-

ble the deployment of such technologies in applica-

tive ﬁelds with high robustness constraints, the preci-

sion of object localization as to be drastically increa-

sed. Moreover, challenging objects (namely: objects

without texture, objects with metallic materials and

symmetric objects) have to be correctly handled.

In this paper we are interested in localizing indus-

trial objects with high precision for augmented reality

590

Roman, P., Desbarats, P., Domenger, J. and Buendia, A.

Limitations of Metric Loss for the Estimation of Joint Translation and Rotation.

DOI: 10.5220/0007525005900597

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 590-597

ISBN: 978-989-758-354-4

applications in the manufacturing industry. We aim

to deploy such solutions on augmented reality head-

sets. To that extent, we selected PoseNet (Kendall

et al., 2015) as the backbone architecture and trai-

ned it on the T-LESS dataset(Hoda

n et al., 2017) as

it features 30 industrial objects and it consists in very

detailed training data which perfectly suits our needs

in order to train a CNN to localize objects. In this

particular setup, we will focus on the inﬂuence of the

two parameters of PoseNet in order to ﬁnd the best

weighting to ensure optimal pose estimation. These

two parameters weigh the importance of the transla-

tion estimation and rotation estimation respectively.

Therefore, we provide a thorough evaluation of their

impact on the training using PoseNet when applied to

the T-LESS dataset. Our experiments will show that

the network is not able to correctly learn both moda-

lities together as one modality always overtakes the

other.

Overview of the Paper. In the next part we present

the state of the art in object localization and available

datasets. Then we detail the experimental protocol

used measure if translation and rotation can be lear-

ned jointly, starting with the dataset: T-LESS (Hoda

et al., 2017), the network proposed by A. Kendall and

al: PoseNet (Kendall et al., 2015), the loss function

optimized during training, and the accuracy measu-

rement performed. Following section describes the

results we obtained that prove that translation and ro-

tation can be learned separately but not together. Fi-

nally we interpret these results with regards to the task

of augmented reality for manufacturing industry, and

we propose possible solutions that we intent to ex-

plore in the near future.

2 STATE OF THE ART

The task of object / camera pose estimation has been

widely covered in previous works. Structure-From-

Motion algorithms (H

aming and Peters, 2010) can re-

trieve the position and orientation of a camera given a

set of images using descriptors such as SIFT (Lowe,

1999) or SURF (Bay et al., 2006) and RANSAC re-

gression. More recently, deep-learning methods have

overpassed manual descriptors as they are now able

to learn more speciﬁc features for each application,

providing better results on most challenges. Modern

CNNs such as PoseNet (Kendall et al., 2015) can be

used to directly predict the pose of an object. These

methods were extended to predict the pose of multi-

ple parts (Crivellaro et al., 2015a) in order to increase

the robustness of the network towards occlusions. Ot-

her approaches aim at regressing the position of the

8 corners of the bounding-box of the object in the

image plane to recover 3D coordinates using PnP al-

gorithms (Rad and Lepetit, 2017). Methods with mul-

tiple regression branches have also been proposed in

(Do et al., 2018; Xiang et al., 2017). Finally, methods

with iterative reﬁnement on the estimated pose have

recently appear (Li et al., 2018) in order to increase

overall precision. Pose detection applied to augmen-

ted reality requires real-time performances as well as

low memory consumption. Thus, multi-part / multi-

branches approaches are oversized for our application

scenario. Moreover, object of attention is usually lo-

cated in the center of the image, on the foreground.

Therefore, the robustness towards occlusion is not re-

levant here. Therfore, we chose the PoseNet architec-

ture as the backbone of the presented work.

The Extented ACCV (Crivellaro et al., 2015b) da-

taset is designed for training methods on 3D models.

However, it has shown limitations in its usage as each

image has to be rendered to generate training data-

set. Datasets for autonomous driving such as (Gei-

ger et al., 2012) have been widely used because of

their high quality. However, such datasets focus on

outdoor scenarios at metric precision. On the other

hand, the T-LESS (Hoda

n et al., 2017) dataset focu-

ses on industrial objects with centimetric precision in

the groundtruth. Moreover, it depicts objects without

textures that are typically found in industrial environ-

ment (electrical parts). Thus, the T-LESS dataset per-

fectly ﬁts our requirements in terms of precision and

object diversity.

3 EXPERIMENTAL SETUP

We aim to ﬁnd the 3D position of industrial objects in

RGB video for augmented reality applications using

deep learning techniques. The goal of the experiments

reported in this paper are to show that the Euclidean

loss does not allow training the (Kendall et al., 2015)

network to predict accurate pose estimation of trans-

lation and rotation on the selected dataset. In this

section we ﬁrst present in depth the dataset we use:

T-LESS(Hoda

n et al., 2017), then we describe the ar-

chitecture of the network proposed in (Kendall et al.,

2015), followed by the loss function used to train the

network, and ﬁnally the accuracy metrics that are ap-

plied in our experiments.

T-LESS Dataset. The T-LESS dataset (Hoda

et al., 2017) features objects with no discriminating

colors, metallic parts, intern similarities and symme-

tries. Therefore, it is a very challenging dataset to

Limitations of Metric Loss for the Estimation of Joint Translation and Rotation

591

work on. The training set only depicts a single ob-

ject on a black background in each image. On the

opposite, the testing set consists in many objects on

various backgrounds for each image. As we are fo-

cused on selecting the optimal α and β parameters of

the loss function Equation (1), the network is trained

on a split of the training set and accuracy is computed

on the rest of the training set.

PoseNet Architecture. PoseNet (Kendall et al.,

2015) is among the ﬁrst networks that successfully

tackled the problem of camera re-localization. It is a

20 modules deep convolutional neural network. The

fact that it based on GoogleNet (Szegedy et al., 2015)

gives it interesting properties: low memory usage

(only 4 million parameters), fast evaluation and the

ability to work with features at different scales. We

apply the same weight to the auxiliary classiﬁer as in

(Szegedy et al., 2015) (0.3, 0.3, 1) For details about

the complete architecture of the network we invite the

interested reader to read the work of (Szegedy et al.,

2015) and (Kendall et al., 2015) but we also provi-

ded a graphical representation of the architecture in

the Figures 1,2 in appendices.

Joint Euclidean Loss. The network is trained to op-

timize the following joint euclidean loss function:

)=α×

−t

+β×



−



(1)

Where i ∈ [0, b] is the index of the example in a batch

of size b,

is the predicted translation (3D vector),

the predicted rotation, t

is the translation label (3D

vector) and q

is the rotation label.

The weighting factors α and β are used to respecti-

vely weight the translation error, and the rotation er-

ror. The quaternion error if both

q and q are unit

length, is bounded in [0, 2] although in the ﬁrst step

where the network weight are randomly initialized,

this loss value could actually be higher. The same is

true for the translation error but it is mostly inﬂuenced

by the scale and the unit in which data are presented

to the network. T-LESS data are provided in milli-

meters, the maximum distance is 700mm. This me-

ans that the error could be of at least of 3880mm × b

and more for the 3 classiﬁcation branches used during

training (where b is the batch size).

Such high values for a loss are challenging be-

cause they can lead to numerical error when compu-

ting the gradient. Thus the α and β parameters have

tremendous impact on the training stability and as we

will see on accuracy of the network at prediction time.

loss =

(2 × (700mm + 700mm))

= 2800mm, and

lossglobal = loss + 0.6 × loss = 3880mm

Input

shape: 224x224x3

Convolution 2D

kernel: 7x7, ﬁlters:64,

strides: 2x2, padding: SAME

Max-Pooling 2D

pooling: 3x3, strides:2x2,

padding: SAME

Convolution 2D

kernel: 3x3, ﬁlters: 192,

strides: 1x1, padding: SAME

Max-Pooling 2D

pooling: 3x3, strides: 2x2 ,

padding: SAME

Inception Module B

ﬁlters: 64, 96, 128, 16, 32, 32

Inception Module B

ﬁlters: 128, 128, 192, 32, 96,

Max-Pooling 2D

pooling: 3x3, strides: 2x2 ,

padding: SAME

Inception Module B

ﬁlters: 192, 96, 208, 16, 48, 64

Inception Module B

ﬁlters: 160, 112, 224, 24, 64,

Inception Module B

ﬁlters: 128, 128, 256, 24, 64,

Inception Module B

ﬁlters: 112, 144, 288, 32, 64,

Inception Module B

ﬁlters: 256, 160, 320, 32, 128,

128

Inception Module B

ﬁlters: 256, 160, 320, 32, 128,

128

Max-Pooling 2D

pooling: 3x3, strides: 2x2,

padding: SAME

Inception Module B

ﬁlters: 384, 192, 384, 48, 128,

128

Average-Pooling 2D

pooling: 3x3, strides: 2x2,

padding: SAME

Dropout

rate: 0.4

Dense

units: 2048

Dropout

rate: 0.4

Linear

units: 7

Translation

shape: 3

Rotation

shape: 4

Auxiliary

Classiﬁer 2

Auxiliary

Classiﬁer 1

Figure 1: Backbone architecture of PoseNet(Kendall et al.,

2015) with parameters of each layers. The two auxiliary

classiﬁers detailed in ﬁgure 2 and the dropout layers are

only used during training.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

592

Average-Pooling 2D

pooling: 5x5, strides: 3x3 ,

padding: SAME

Convolution 2D

kernel: 1x1, ﬁlters:128,

strides: 1x1, padding: SAME

Dense

units: 1024

Dropout

rate: 0.7

Translation

shape: 3

Rotation

shape: 4

Linear

units: 7

Feature Maps

Figure 2: Architecture of the two auxiliary classiﬁers of Po-

seNet(Kendall et al., 2015) with parameters of each layers

used only during training.

The intuition here is that scaling α down will prevent

the translation from dominating the loss, allowing ro-

tation to train as well and ensuring computational in-

tegrity. β can also be scaled up to better focus the

training on rotation.

Euclidean Accuracy. We advocate that the accu-

racy is directly inﬂuenced by the ability of the net-

work to learn jointly translation and rotation which is

controlled by the α and β parameters in Equation (1).

The translation accuracy can be measured by the

euclidean distance to τ:

Acc

(

t,t,τ)=

∑

i=0









t −t



≤ τ

0 otherwise

(2)

A predicted translation

t (in cm) is considered correct

if the euclidean distance between the prediction

(in cm) and the label t (in cm) is less than a given

threshold τ (in cm).

One way to compute the rotational accuracy is

using the angle at τ:

Acc

(

q,q,τ) =

∑

i=0

(

if angle(

q, q) ≤

τ×π

180

0 otherwise

(3)

angle(

q, q) = arccos(2 × h

− 1) (4)

A predicted rotation

q (quaternion) is considered cor-

rect if the angle (in degree) between the prediction

(quaternion) and the label q (quaternion) is less than

a given threshold τ (in degree). Note that angle(

q, q)

gives an angle in radians thus we convert the threshold

τ to radians in the above equation.

Complete Setup. We train the PoseNet net-

work(Kendall et al., 2015) to regress translation (3D

vector) and rotation (4D quaternion) by optimizing

an euclidean loss as deﬁned in Equation (1) like in

(Kendall et al., 2015) on data from the T-LESS data-

set (Hoda

n et al., 2017). The images of a subset of

the training set of the dataset are re-sized to a ﬁxed

size of 224x224 (RGB). We do not take crops nor ap-

ply any data augmentation. The learning rate is set

to γ = 0.0001 for all training runs. We do this trai-

ning several time with various values of α and β to

show the effect of these two parameters on the trai-

ning in terms of convergence speed, stability, and on

the accuracy for both translation and rotation (measu-

red on the remaining examples of training set).

4 RESULTS

Choosing the right value for α and β is a very com-

plicated task. In this section we detail all the training

run and provide interpretation of the results. We ﬁrst

produced baseline results for translation and rotation

where one of the two weight is set to 0 only allowing

one of the two to train. Then following our intuition

we ﬁxed β to 1 and attempted to scaled down α. And

ﬁnally we ﬁxed α and scaled β up in an attempt to

better learn rotation.

Baseline Results. We ﬁrst set the parameters to α =

0.01, β = 0 (only optimizing translation). Results are

presented in Figure 3 (a). In order to visualize the re-

sults we rendered the objects at ground truth position

and ground truth rotation in green, and overlay a ren-

der of the object at predicted position and at ground

truth rotation in transparent red. As expected the net-

worked learned to predict accurate translation but not

rotation. The accuracy for the translation is equal to

20% for τ = 5cm and is equal to 100% for τ ≥ 20cm.

Then we set the parameters to α = 0, β = 1 (only

optimizing rotation). Figure 3 (b) features objects

rendered at the ground truth position and ground truth

rotation in green and objects rendered at the ground

truth position but predicted rotation in red. This time

the network is very accurate on rotation and inaccu-

rate on translation. With Accu

(

q, q, 5

) = 26% and

for τ ≥ 20

then Accu

(

q, q, τ) ≈ 100%. Translation

accuracy is close to 0 for any values of τ ≤ 65cm.

We recall that object are at most 70cm away from the

Limitations of Metric Loss for the Estimation of Joint Translation and Rotation

593

(a) α = 0, β = 1 (b) α = 0.01, β = 0

Figure 3: (a) Results for a network trained to only optimize rotation (α = 0, β = 1). Green: objects at the ground truth

t and q, red: objects at the ground truth t but predicted

q. (b) Results for a network trained to only optimize translation

(α = 0.01, β = 0). Green: object at the ground truth t and q, red: objects at the ground truth q but predicted

camera in T-LESS so for any value of τ > 65cm the

accuracy will always be close to 100%.

Together these two classiﬁers provide a good so-

lution to the problem of object localization in terms

of accuracy. But we would like to combine these two

results in one network following the work of (Kendall

et al., 2015) to save memory and computational time

as well as providing a uniﬁed solution to the problem.

Down-scaling Translation. In order to prevent the

translation loss from taking to large values with re-

spect to the rotation loss, and also to ensure compu-

tational integrity of the gradient we ﬁxed the β para-

meter to 1 and started tuning the α parameter. Results

on the loss (translation and rotation) can be found in

Figure 4 (a) and results on the accuracy can be found

in Figure 4 (b).

Setting α ≥ 0.0075 does not allow rotation to be

trained at all. This is equivalent to the baseline result

where β is set to 0. Then if we set α to 0.005 or 0.006

we can see on Figure 4 (b) (second row) that rotation

is learned but then as training progresses, it is forgot-

ten to allow translation to be learned. This is also

visible in Figure 4 (a): as soon as translation loss de-

creases, rotation loss increases drastically. Even if the

rotation loss then slowly decreases, it never returns to

its previous minimum, and accuracy never increases

again. Finally α ≤ 0.001 does not allow translation

to be trained. Loss and accuracy are equivalent to the

ones for α = 0 (baseline result).

As we can see, setting only α is not enough. If

we do no not decrease it, rotation will not be learned

for sure. But decreasing it (without changing β) will

only delay the translation from taking over. And if we

decrease it too much we quickly fall back to the case

where it is equal to 0.

Up-scaling Rotation. In the previous experiment

we saw that α = 0.005 is a key value where the loss

”hesitates” between the translation and rotation. We

also concluded that only tuning α is not enough to

balance translation and rotation. In this set of experi-

ments we wanted rotation to train just like it did be-

fore in the early stages of training, thus we set α to

0.005. But we also wanted it to not be forgotten by

the network. To ensure this we increased β in values

ranging from 1 to 3.Results are presented in Figure 5

(a) and (b). We ﬁrst set β to 0.5 and we saw as ex-

pected that this leads to rotation not being learned at

all just like in our baseline result where β was set to

0. Then we increased β to 1.2 and 1.5. Results pre-

sented in Figure 5 (b) (second row) show that rotation

is indeed learned longer, thus better. But we see the

same phenomena as before: when translation is lear-

ned, rotation is forgotten. Thus we decided to furt-

her increase β and set it to 2 and 3. For these values

translation accuracy did not increased, and the corre-

sponding loss remains constantly high. This result is

equivalent to the baseline result where α = 0.

Once again this set of experiment shows that trans-

lation is favored to rotation during training. Trans-

lation and rotation can never be learned jointly with

high accuracy for both. Rotation is either not lear-

ned at all, or forgotten. This is due to the fact that it

is more proﬁtable for the network to learn translation

with respect to the implemented loss.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

594

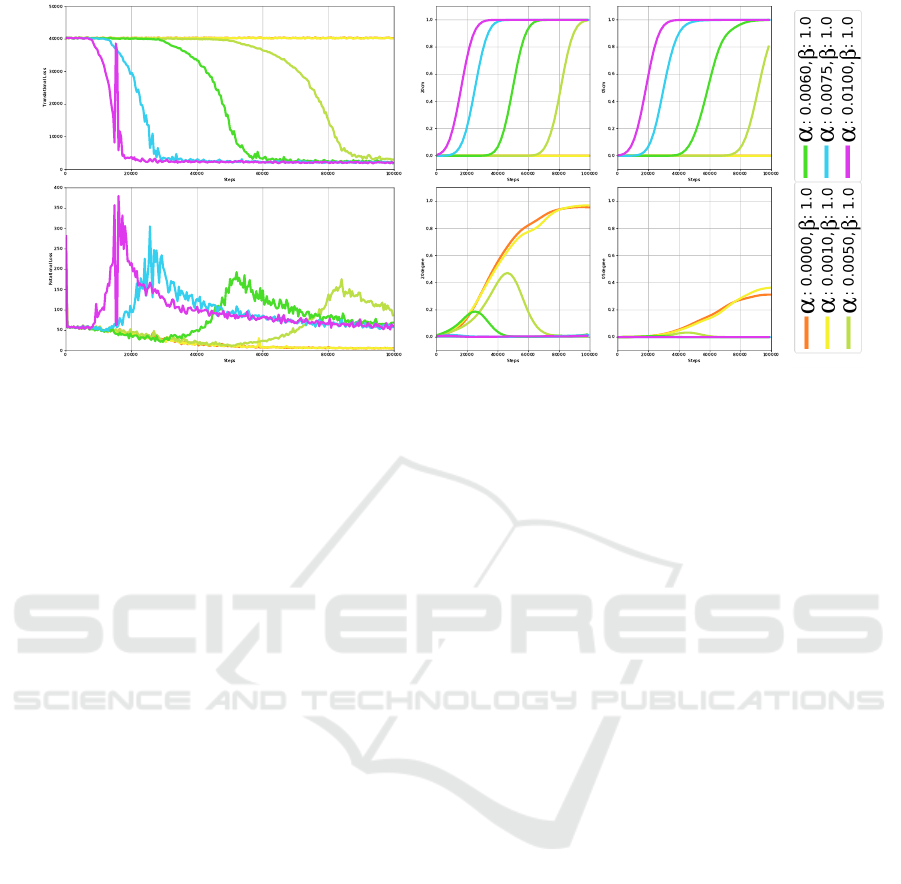
(a) Translation and rotation losses (b) Translation and rotation accuracies (c) Legend

Figure 4: First row: translation, second row: rotation. (a) Euclidean loss over training steps for different α values and β = 1.0

(b) Accuracy at τ = 20 and τ = 5 over training steps for different α values and β = 1.0.

5 CONCLUSIONS

Regressing both translation and rotation using a sin-

gle regression branch is a very hard task for a network

as it has to model different concepts (with different

units) at the same level of abstraction. They are no va-

lues of the weighting parameters α and β that enable

the network to learn jointly rotation and translation.

If α > 0, conﬂicts between translation and rotation

occur, and translation overtakes rotation. The only ef-

fect of increasing β was to delay the overtaking of the

translation.

The fact that we can see so clearly the PoseNet

(Kendall et al., 2015) forgetting one of the two mo-

dality in favor of the other in the results proves that

when used on the T-LESS dataset it is failing to le-

arn translation and rotation jointly. This is mainly be-

cause the scale, and the range of viewpoints of the

data is not the same as the original use case. Pose-

Net is meant for large scene where object are bigger

and observed from further away and from less point

of views. In our case the positional data in millime-

ter leads to large translation error that is not bounded.

The rotational loss on the other hand is bounded by

deﬁnition. Thus the translation always takes over in

the training at some point.

Perspectives. To solve the problem of the euclidean

loss not being able to learn jointly the translation and

rotation, one could investigate the use of other los-

ses that already exist, such as 3D geometrical loss for

application that require absolute precision, or 2D ge-

ometrical loss computed in the image plane that are

suitable for augmented reality applications (Br

egier

et al., 2016). These losses are very interesting be-

cause they can be modiﬁed to include symmetries.

Other networks architectures that have separate re-

gression branches for translation and rotation can also

help training the two jointly (Do et al., 2018; Xiang

et al., 2017). New types of network such as Capsu-

les Network (Hinton et al., 2011; Sabour et al., 2017)

that have vectorial activation values could better mo-

del translation and rotation that are vectorial data.

ACKNOWLEDGEMENTS

We would like to thank Pierre Biasutti for the long

talk we had on the results presented in the paper and

Arnaud Favareille, who both helped with the paper.

REFERENCES

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). SURF:

Speeded up robust features. In In ECCV, pages 404–

417.

egier, R., Devernay, F., Yeyrit, L., and Crowley, J. L.

(2016). Deﬁning the pose of any rigid object and an

associated distance. CoRR, abs/1612.04631.

Collins, T., Pizarro, D., Bartoli, A., Canis, M., and Bour-

del, N. (2014). Computer-assisted laparoscopic myo-

mectomy by augmenting the uterus with pre-operative

mri data. In 2014 IEEE International Symposium on

Mixed and Augmented Reality (ISMAR), pages 243–

248.

Limitations of Metric Loss for the Estimation of Joint Translation and Rotation

595

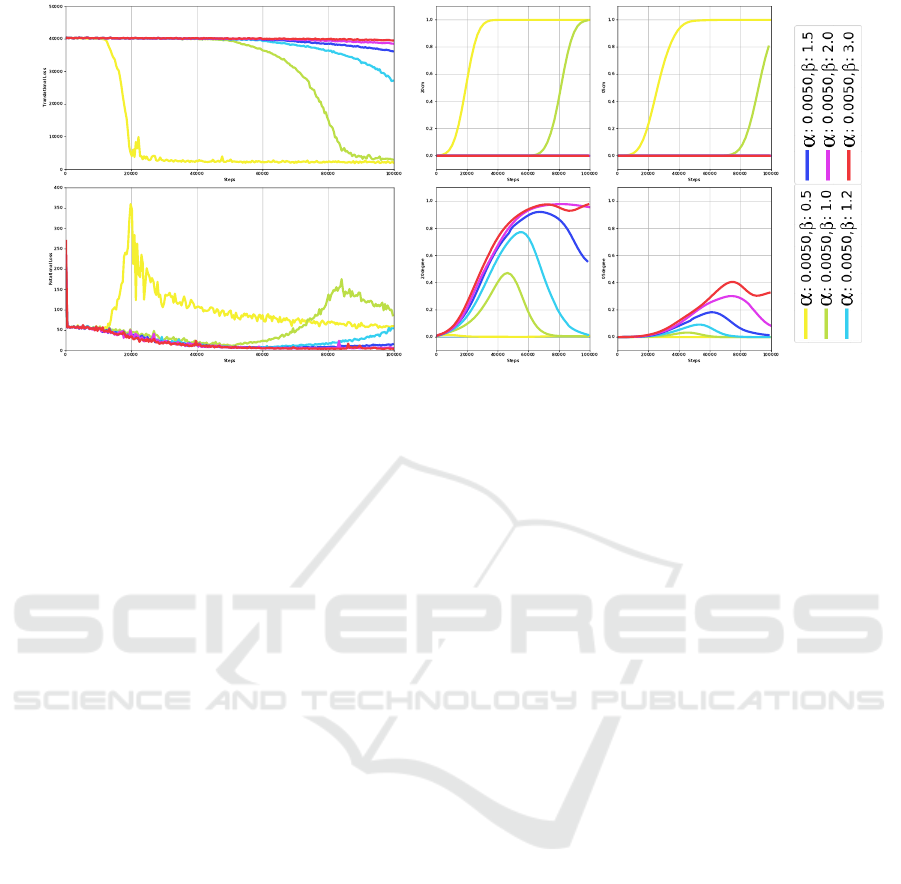
(a) Translation and rotation losses (b) Translation and rotation accuracies (c) Legend

Figure 5: First row: translation, second row: rotation. (a) Euclidean loss over training steps for α = 0.005 and various values

of β. (b) Accuracy at τ = 20 and τ = 5 over training steps for α = 0.005 and various values of β.

Crivellaro, A., Rad, M., Verdie, Y., Yi, K., Fua, P., and Le-

petit, V. (2015a). A novel representation of parts for

accurate 3d object detection and tracking in monocu-

lar images. In 2015 IEEE International Conference on

Computer Vision (ICCV), pages 4391–4399.

Crivellaro, A., Rad, M., Verdie, Y., Yi, K. M., Fua, P., and

Lepetit, V. (2015b). A novel representation of parts

for accurate 3d object detection and tracking in mo-

nocular images. In Proceedings of the 2015 IEEE In-

ternational Conference on Computer Vision (ICCV),

ICCV ’15, pages 4391–4399, Washington, DC, USA.

IEEE Computer Society.

Didier, J.-Y., Roussel, D., Mallem, M., Otmane, S., Naudet,

S., Pham, Q.-C., Bourgeois, S., M

egard, C., Leroux,

C., and Hocquard, A. (2005). AMRA: Augmented re-

ality assistance for train maintenance tasks. In Works-

hop Industrial Augmented Reality, 4th ACM/IEEE In-

ternational Symposium on Mixed and Augmented Re-

ality (ISMAR 2005), page (Elect. Proc.), Vienna, Au-

stria.

Do, T., Cai, M., Pham, T., and Reid, I. D. (2018). Deep-

6DPose: Recovering 6D object pose from a single

RGB image. CoRR, abs/1802.10367.

Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we ready

for autonomous driving? the KITTI vision benchmark

suite. In 2012 IEEE Conference on Computer Vision

and Pattern Recognition, pages 3354–3361.

aming, K. and Peters, G. (2010). The structure-from-

motion reconstruction pipeline a survey with focus

on short image sequences. Kybernetika, 5.

Hinton, G., Krizhevsky, A., and Wang, S. (2011). Transfor-

ming auto-encoders. In Honkela, T., Duch, W., Giro-

lami, M., and Kaski, S., editors, Artiﬁcial Neural Net-

works and Machine Learning – ICANN 2011, pages

44–51. Springer Berlin Heidelberg.

Hoda

n, T., Haluza, P., Obdr

alek,

S., Matas, J., Lourakis,

M., and Zabulis, X. (2017). T-LESS: An RGB-D da-

taset for 6D pose estimation of texture-less objects.

IEEE Winter Conference on Applications of Compu-

ter Vision (WACV).

IKEA (2017). Place app.

Kendall, A., Grimes, M., and Cipolla, R. (2015). PoseNet:

A convolutional network for real-time 6-DOF camera

relocalization. CoRR, abs/1505.07427.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).

Imagenet classiﬁcation with deep convolutional neu-

ral networks. In Proceedings of the 25th Internatio-

nal Conference on Neural Information Processing Sy-

stems - Volume 1, NIPS’12, pages 1097–1105, USA.

Curran Associates Inc.

Le Cun, Y., Jackel, L. D., Boser, B., Denker, J. S., Graf,

H. P., Guyon, I., Henderson, D., Howard, R. E.,

and Hubbard, W. (1990). Handwritten digit recog-

nition: Applications of neural net chips and automa-

tic learning. In Souli

e, F. F. and H

erault, J., editors,

Neurocomputing, pages 303–318, Berlin, Heidelberg.

”Springer Berlin Heidelberg.

Li, Y., Wang, G., Ji, X., Xiang, Y., and Fox, D. (2018). Dee-

pIM: Deep iterative matching for 6D pose estimation.

CoRR, abs/1804.00175.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. In Proceedings of the Seventh

IEEE International Conference on Computer Vision,

volume 2, pages 1150–1157 vol.2.

Microsoft Hololens

 (2015-2017). Webpage.

Rad, M. and Lepetit, V. (2017). BB8: A scalable, accurate,

robust to partial occlusion method for predicting the

3d poses of challenging objects without using depth.

2017 IEEE International Conference on Computer Vi-

sion (ICCV), pages 3848–3856.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-

Net: Convolutional networks for biomedical image

segmentation. CoRR, abs/1505.04597.

Sabour, S., Frosst, N., and Hinton, G. (2017). Dynamic

routing between capsules. CoRR, abs/1710.09829.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

596

Simonyan, K. and Zisserman, A. (2014). Very deep con-

volutional networks for large-scale image recognition.

CoRR, abs/1409.1556.

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., An-

guelov, D., Erhan, D., Vanhoucke, V., and Rabinovich,

A. (2015). Going deeper with convolutions. In 2015

IEEE Conference on Computer Vision and Pattern Re-

cognition (CVPR), pages 1–9.

Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2017).

PoseCNN: A convolutional neural network for 6d

object pose estimation in cluttered scenes. CoRR,

abs/1711.00199.

APPENDICES

A T-LESS Viewpoints

Figure 6: Position where each object is photograp-

hed to produce the training data-set. Objects 19

and 20 have a full vertical symmetry, this is why

they are only sampled from one side of the sam-

pling sphere. All point-of-view are bounded in the

rectangle (−652.975mm, −652.252mm, −635.481mm) to

(651.928mm, 653.682mm, 635.049mm).

The Figure 6 presents the positions where the ca-

mera shot the picture used to create the training set of

the T-LESS dataset.

B Network Architecture

The architecture of the network as well as conﬁgura-

tion parameters of every layers are provided in Figure

1. The auxiliary classiﬁers used during training are

both designed following the Figure 2.

C Combined Loss

During training the euclidean loss is applied to all 3

classiﬁcation branches. It is integrated using the fol-

lowing formula:

Global

(

t, t,

q, q) = λ

× L

Aux0

(

Aux0

,t, [q

Aux0

, q)

+ λ

× L

Aux1

(

Aux1

,t, [q

Aux1

, q)

+ λ

× L

Top

(

Top

,t,

Top

, q) (5)

Where L

Top

, L

Aux1

and L

Aux2

are computed using

Equation (1) with the same labels but with predictions

coming from the different regression branches.

The authors of GoogleNet (Szegedy et al., 2015)

suggested to use λ

= 0.3, λ

= 0.3 and λ

= 1.0, this

is what is used in PoseNet (Kendall et al., 2015), thus

we stick with these values for all our experiments.

D Remarks

Baseline Architecture. Setting α = 0.01, β = 0 is

not equivalent to having a network predicting only

translation (7 logits instead of 3), and setting α =

0, β = 1 is not equivalent to having a network pre-

dicting only rotation (7 logits instead of 4): the extra

”unused” weights (4 or 3) in the network contribute

to the gradient computations and to the regularization

terms. Indeed

is often used to prevent the weig-

hts values from taking too large values, where W is the

matrix containing all the weights of the network.

Unit Quaternion. The predicted quaternion

q is not

normalized but the network is optimized with respect

to a normalized ”label” quaternion

, thus it is trai-

ned to predict unit length quaternion, but they are no

hard constraints for it. This is actually a better idea

than to normalize the predicted quaternion

q in the

loss, as it would not penalize the training if a non-unit

quaternion was predicted by the network. Although at

test time the predicted quaternion can be normalized

for example to later convert it to Euler angles.

Limitations of Metric Loss for the Estimation of Joint Translation and Rotation

597