Subgroup Anomaly Detection using High-confidence Rules:

Application to Healthcare Data

Juan L. Domínguez-Olmedo

, Jacinto Mata

, Victoria Pachón

and Manuel Maña

Escuela Técnica Superior de Ingeniería, University of Huelva, Huelva, Spain

Keywords: Anomaly Detection, Rules Discovery, Breast Cancer.

Abstract: In real datasets it often occurs that some cases behave differently from the majority. Such outliers may be

caused by errors, or may have differential characteristics. It is very important to detect anomalous cases, which

may negatively affect the analysis from the data, or bring valuable information. This paper describes an

algorithm to address the task of automatically detect subgroups and the possible anomalies with respect to

those subgroups. By the use of high-confidence rules, the algorithm determines those cases that satisfy a rule,

and the cases discordant with that rule. We have applied this method to a dataset regarding information about

breast cancer patients. The resulting subgroups and the corresponding outliers have been presented in detail.

1 INTRODUCTION

Anomaly detection refers to the task of discovering

patterns in data which do not conform to the

“expected” behavior. These nonconforming patterns

are often referred to as anomalies, outliers, discordant

observations, exceptions, peculiarities, or

contaminants in different application domains. The

detection of anomalies can be used in a wide variety

of domains, such as fraud detection, insurance or

medical care, detection of intruders for cyber-

security, fault detection, military surveillance, or

event detection in sensor networks. Its importance is

due to the fact that anomalies present in the data often

result in significant information that can be analysed

(Chandola et al., 2009).

Anomaly detection in health domains usually

employs patient records. The data may have

anomalies due to several reasons, such as abnormal

patient condition, or recording errors. The detection

of anomalies is a very critical problem in this domain,

requiring a high degree of precision (Wong et al.,

2003); (Sipes et al., 2014). Outliers can sometimes

be treated as noise, or incorrect data, resulting from

some error.

https://orcid.org/0000-0001-5083-2313

https://orcid.org/0000-0001-5329-9622

https://orcid.org/0000-0003-0697-4044

https://orcid.org/0000-0002-7551-2401

Outlier detection may be carried out as a data

preprocessing step, in an initial preparation and

cleaning phase. But outliers can be thought as element

with different characteristics from the rest of the data.

In this sense, they would be considered as anomalies

in the data being analysed. In studies dealing with

medical data, outlier detection is applied both as the

preprocessing stage aiming to identify noise and

errors or as the process of anomaly detection (Duraj,

2017).

In this work we describe an algorithm to address

the task of automatically detect subgroups and the

possible anomalies with respect to those subgroups.

In summary, the algorithm determines those cases

that satisfy a rule and the cases discordant with that

rule, using for that purpose a list of high-confidence

rules.

The rest of the paper is organized as follows.

Section 2 gives a description of the methods

employed in this work. The experimental setup and

results are presented in Section 3. Section 4 treats

some discussion. And the last section presents the

conclusions.

Domínguez-Olmedo, J., Mata, J., Pachón, V. and Maña, M.

Subgroup Anomaly Detection using High-conﬁdence Rules: Application to Healthcare Data.

DOI: 10.5220/0007555104310435

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 431-435

ISBN: 978-989-758-353-7

431

2 METHODS EMPLOYED

2.1 Robust Statistics

Computing descriptive statistics about a set of data

can yield important information to be used in the

detection of anomalies. Although a basic measure as

the mean maybe useful, the median is more robust

against an outlier. Similarly, a robust measure of scale

is the median of all absolute deviations from the

median (MAD) (Rousseeuw et al., 2018):

MAD = median ( | X

– median(X) | ) (1)

One rule that can be used to detect outliers is

based on the z-scores (normal scores) of the

observations, given by:

z-score =



µ- x

(2)

where µ is the mean and σ the standard deviation of

the data.

Using robust estimators of location and scale,

such as the median and the MAD, yields the robust z-

score measure (rz-score):

rz-score =

MAD(X)

median(X) - x

(3)

which is a much more reliable outlier detection tool

(Rousseeuw et al., 2018).

2.2 Extraction of Rules

In machine learning, one of the methods often used to

extract knowledge from data is association rules. An

association rule takes the form

A → C, where A (the

antecedent) and

C (the consequent) express a

condition (or a conjunction of conditions) on

variables of the dataset (Agrawal et al., 1993);

(Domínguez-Olmedo et al., 2012).

The measures

support and confidence are used to

express the quality of the association rules. The

support measure evaluates the number of cases in

which both the antecedent and the consequent of the

rule hold. The confidence measure is the ratio

between the support of the rule and the number of

cases in which the antecedent holds:

confidence(A → C) =

support(A)

C) support(A 

(4)

Also, the values minsup (minimum support) and

minconf (minimum confidence) are the thresholds

that a rule has to satisfy to be considered interesting

by the user.

Subgroup discovery is a type of descriptive

induction whose main objective is to discover

properties of a population by obtaining significant

rules, using only one variable in the consequent: the

class or target variable (Wrobel, 1997); (Gamberger

et al., 2003).

2.3 Algorithm Description

In this work we have approach the task of identifying

possible anomalies in subgroups. In this sense,

“subgroup outliers” can be defined as patterns in a

subgroup of data that do not conform to the general

characterization of that subgroup.

To acomplish this objective, we employ a list of

high-confidence rules, in order to identify the cases

that although satisfying the antecedent of a rule, do

not belong to the class indicated by the consequent.

The rules with a confidence value of 1 (100% of

confidence) would not be useful for this purpose; this

is because in such a rule all the cases satisfying the

antecedent also satisfy the consequent (the rule

describes a "subgroup without anomalies").

The algorithm SAD (Subgroup Anomaly

Detection) is shown in Algorithm 1. Using the list of

rules provided, each of the rules is examined

iteratively, considering only those that have a

confidence less than 1 and not inferior to the value of

the minimum confidence parameter (lines 1-2).

Algorithm 1: SAD.

Input: Dataset D, list of rules R, minconf

Output: Description of possible subgroups and outliers

1: for each rule r in R do

2: if confidence(r)[minconf, 1) then

3: S = cases in D that satisfy r

4: show statistics of S

5: for each case o in antecedent(r) do

6: if o ∉ S then

7: show values and statistics of o

8: end if

9: end for

10: end if

11:

nd for

Descriptive statistics (minimum, maximum,

mean, standard deviation, median and MAD) are

calculated for the subgroup, that is, the set of cases

that satisfy the rule (lines 3-4). Next, outlier cases are

shown: those cases that satisfy the antecedent of the

rule but not its consequent. For each of such outlier

case, the values in each variable are shown, as well as

the corresponding z-score and rz-score values (lines

5-9).

HEALTHINF 2019 - 12th International Conference on Health Informatics

432

3 EXPERIMENTAL SETUP

3.1 Dataset Description

In an application example, we have tested the

proposed algorithm in a dataset regarding clinical

features observed or measured for 64 patients with

breast cancer and 52 healthy controls (Patricio et al.,

2018).

This dataset (Breast Cancer Coimbra) was

obtained from the UCI Machine Learning Repository

(Dua et al., 2017). It contains data which can be

collected in routine blood analyses. The names and

units of the variables can be seen in Table 1.

Table 1: Variables and units of the dataset.

Variable Units/Values

Age years

BMI kg/m2

Glucose mg/dL

Insulin µU/mL

HOMA real

Leptin ng/mL

Adiponectin µg/mL

Resistin ng/mL

MCP-1 pg/dL

Classification Healthy, Patient

3.2 Experimental Results

First, in order to obtain a list of high-confidence rules,

we have employed the algorithm DEQAR-SD

(Domínguez-Olmedo et al., 2015); (Domínguez-

Olmedo et al., 2017). This algorithm does not carry

out a discretization of numeric attributes before the

rule induction process; it obtains the conditions for

these attributes during a depth-first search with

backtracking.

After applying DEQAR-SD to the Breast Cancer

Coimbra dataset, with the limit of 2 variables in the

antecedent of the rules, the resulting rules were

processed with the algorithm SAD, using a value of

0.95 for minconf. The corresponding output is

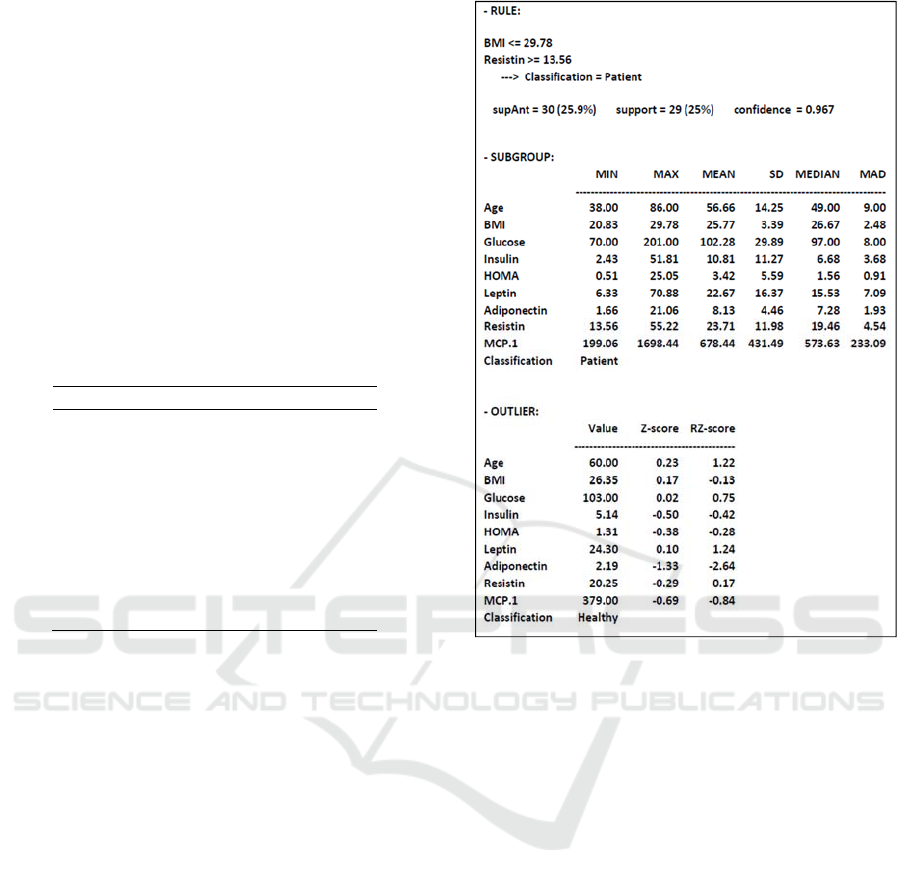
displayed in Figure 1.

As can be seen, the rule associates two conditions

(for the variables BMI and Resistin) with the class

"Patient", having a confidence of 96.7%. The support

of the antecedent (supAnt), that is, the number of

cases that satisfy those conditions, is 30. And of those

30 cases, 29 satisfy the consequent. That is, the rule

describes a subgroup of 29 cases of type "Patient".

Only one case of those ones satisfying the antecedent

does not satisfy the consequent (it is of "Healthy"

type).

Figure 1: Subgroup and outlier resulting from a rule.

The values of this outlier are shown, as well as the

z-score and rz-score values for each variable. It can

be seen that the variable Adiponectin presents a

somewhat low value, in comparison with the

corresponding values of the subgroup.

Figure 2 shows the graph for the two variables

used in the antecedent of that rule. In the upper left

quadrant, the cases in the subgroup ("Patient") can be

seen together with the outlier ("Healthy").

We have also executed DEQAR-SD to find rules

with a maximum of 4 variables in the antecedent. The

resulting rules were processed using the SAD

algorithm (minconf = 0.95), yielding 2 final rules.

These rules and their corresponding subgroups and

outliers are shown in Figures 3 and 4.

The first of these rules describes a subgroup of 25

"Healthy" cases. With a confidence of 96.2%, it uses

the variables Glucose, Insulin, HOMA and Resistin.

One outlier "Patient" case was described. Looking at

its z-score and rz-score values, it presents somewhat

low values for the variables Insulin, Leptin and

Adiponectin, and a somewhat high value for Resistin,

in comparison with the corresponding values in the

subgroup.

Subgroup Anomaly Detection using High-conﬁdence Rules: Application to Healthcare Data

433

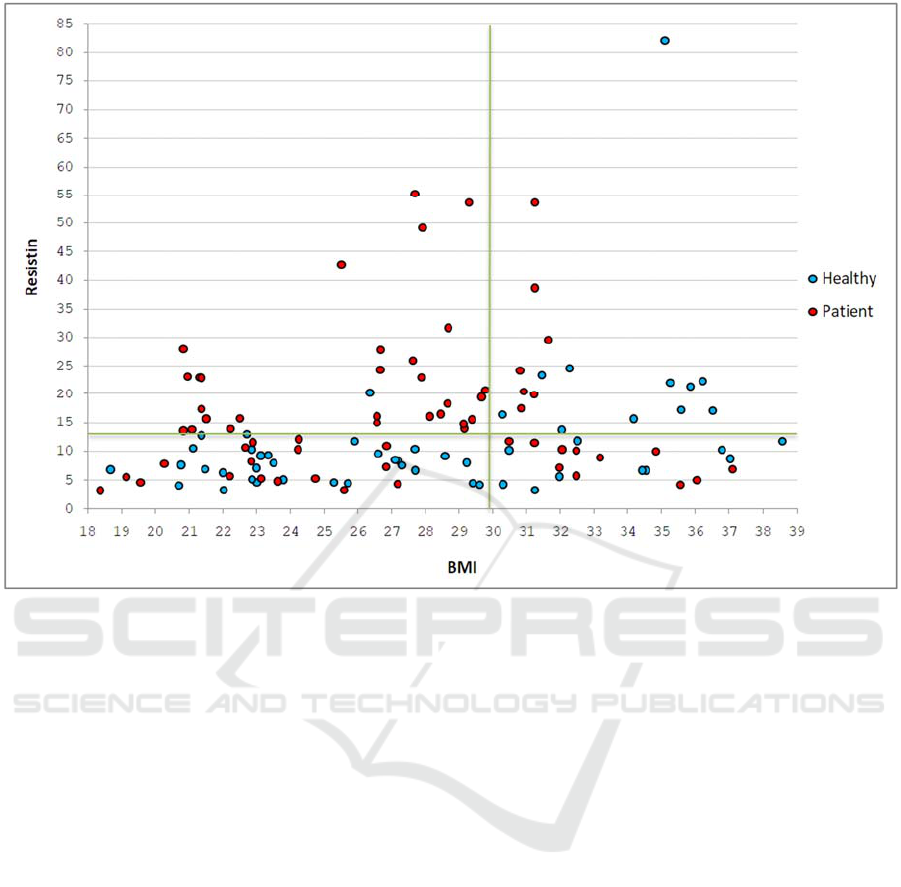
Figure 2: Graphical representation of the data and the quadrants resulting from two conditions.

The second rule describes a subgroup of 36

"Patient" cases, with a confidence of 97.3%. It

employs the variables BMI, Glucose, Leptin and

Resistin. One outlier "Healthy" case was described. It

can be seen that it presents a somewhat low value for

the variable Adiponectin, in comparison with the

corresponding values in the subgroup.

4 DISCUSSION

The proposed algorithm, applied to a healthcare

dataset, has achieved to describe subgroups of cases

(both for the "Patient" and "Healthy" classes)

employing some high-confidence rules. The size

(support) of such subgroups was around 25% of the

cases in the dataset.

For each subgroup, possible outlier cases have

been identified, and their values together with some

statistical information were showed. Although their

values fit into the corresponding ranges of each

variable in the subgroup, the additional statistical

information allows us to suggest those variables that

most differ from the corresponding ones in the

subgroup.

A medical expert could analyse this information

carefully and possibly obtain interesting knowledge.

5 CONCLUSIONS

In this work we have described a method to

automatically detect subgroups and possible

anomalies that could be present in a dataset. By using

high-confidence rules, the algorithm determines those

cases that satisfy a rule (forming a subgroup) and

those ones that don't fully satisfy the rule (outliers).

In some way, the final determination of anomalies

or outliers is a subjective task; but in any case, the

suggested anomalies bring the opportunity to carry

out a deeper analysis on the data, and eventually

obtain useful information.

As future work, additional information for each

detected anomaly could be presented, e. g. the cases

in the subgroup which are closest to the outliers.

REFERENCES

Chandola, V., Banerjee, A. and Kumar, K., 2009. Anomaly

Detection: A Survey. ACM Computing Surveys, (41)3.

HEALTHINF 2019 - 12th International Conference on Health Informatics

434

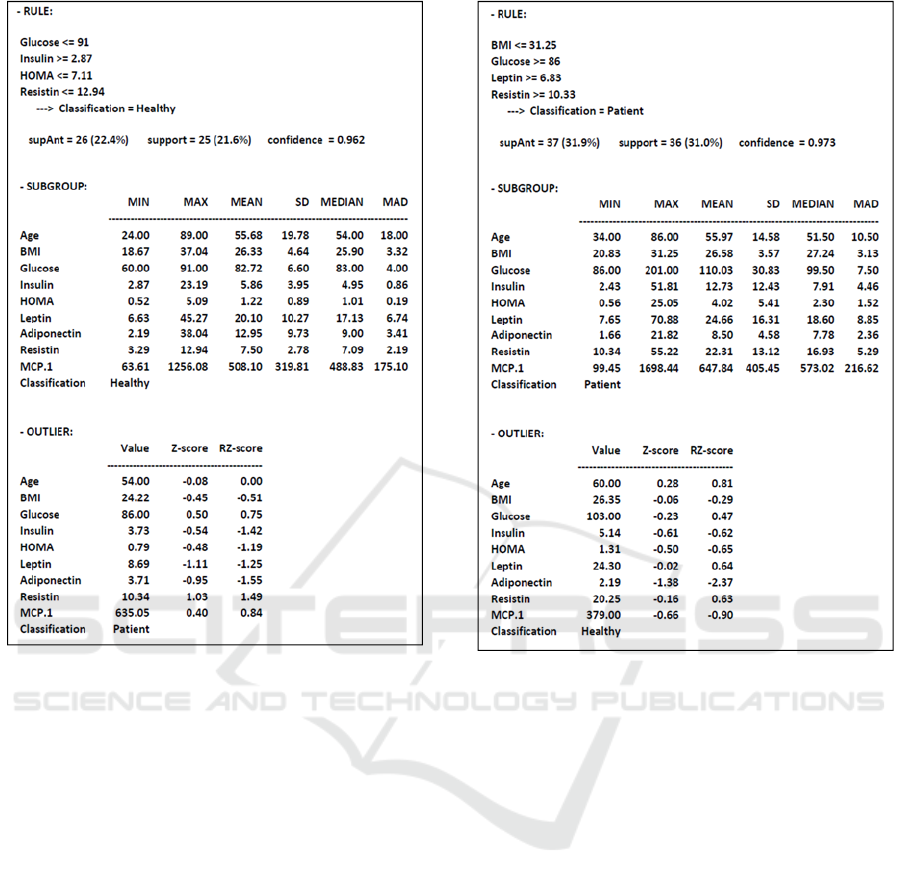
Figure 3: Subgroup and outlier resulting from a rule.

Wong, W.-K., Moore, A., Cooper, G., and Wagner, M.,

2003. Bayesian network anomaly pattern detection for

disease outbreaks. In Proceedings of the 20th

International Conference on Machine Learning, AAAI

Press, 808–815.

Sipes, T., Jiang, S., Moore, K., Li, N., Karimabadi, H. and

Barr, J.R., 2014. Anomaly Detection in Healthcare:

Detecting Erroneous Treatment Plans in Time Series

Radiotherapy Data. International Journal of Semantic

Computing, (8)3, 257-278.

Duraj, A., 2017. Outlier detection in medical data using

linguistic summaries. In Proceedings of the IEEE

International Conference on INnovations in Intelligent

SysTems and Applications (INISTA).

Rousseeuw, P.J. and Hubert, M., 2018. Anomaly detection

by robust statistics. WIREs Data Mining Knowledge

Discovery, 8:e1236.

Agrawal, R., Imielinski, T. and Swami, A., 1993. Mining

Association Rules between Sets of Items in Large

Databases. In Proceedings of ACM SIGMOD ICMD,

207-216.

Domínguez-Olmedo, J.L., Mata, J., Pachón, V. and Maña,

M., 2012. Rule extraction from medical data without

discretization of numerical attributes. In Proceedings of

the International Conference on Health Informatics

(HEALTHINF), 397-400.

Figure 4: Subgroup and outlier resulting from a rule.

Wrobel, S., 1997. An algorithm for multi-relational

discovery of subgroups. Principles of data mining and

knowledge discovery, 78-87.

Gamberger, D., Lavrac, N. and Krstacic, G., 2003. Active

Subgroup Mining: A Case Study in Coronary Heart

Disease Risk Group Detection. Artificial Intelligence in

Medicine 28, 27–57.

Domínguez-Olmedo, J.L., Mata, J. and Pachón, V., 2015.

Deterministic Extraction of Compact Sets of Rules for

Subgroup Discovery. In Proceedings of Intelligent

Data Engineering and Automated Learning – IDEAL,

138-145.

Domínguez-Olmedo, J.L. and Mata, J., 2017. Obtaining

Significant and Interpretable Rules for Subgroup

Discovery Tasks. IEEE Latin America Transactions

15(10), 2012-2016.

Patrício, M., Pereira, J., Crisóstomo, J., Matafome, P.,

Gomes, M., Seiça, R. and Caramelo, F., 2018. Using

Resistin, glucose, age and BMI to predict the presence

of breast cancer. BMC Cancer, 18(1).

Dua, D. and Karra Taniskidou, E. (2017). UCI Machine

Learning Repository [http://archive.ics.uci.edu/ml].

University of California, School of Information and

Computer Science.

Subgroup Anomaly Detection using High-conﬁdence Rules: Application to Healthcare Data

435