
Cataglyphis Ant Navigation Strategies Solve the Global Localization
Problem in Robots with Binary Sensors
Nils Rottmann, Ralf Bruder, Achim Schweikard and Elmar Rueckert
Institute for Robotics and Cognitive Systems, University of Luebeck, Ratzeburger Allee 160, 23562 Luebeck, Germany
Keywords:
Global Localization, Binary Measurements, Land Navigation, Path Integration, Cataglyphis.
Abstract:
Low cost robots, such as vacuum cleaners or lawn mowers, employ simplistic and often random navigation
policies. Although a large number of sophisticated localization and planning approaches exist, they require
additional sensors like LIDAR sensors, cameras or time of flight sensors. In this work, we propose a global
localization method biologically inspired by simple insects, such as the ant Cataglyphis that is able to return
from distant locations to its nest in the desert without any or with limited perceptual cues. Like in Cataglyphis,
the underlying idea of our localization approach is to first compute a pose estimate from pro-prioceptual
sensors only, using land navigation, and thereafter refine the estimate through a systematic search in a particle
filter that integrates the rare visual feedback.
In simulation experiments in multiple environments, we demonstrated that this bioinspired principle can be
used to compute accurate pose estimates from binary visual cues only. Such intelligent localization strategies
can improve the performance of any robot with limited sensing capabilities such as household robots or toys.
1 INTRODUCTION
Precise navigation and localization abilities are cru-
cial for animal and robots. These elementary skills
are far developed in complex animals like mammals
(O’keefe and Nadel, 1978), (Redish et al., 1999).
Experimental studies have shown that transient neu-
ral firing patterns in place cells in the hippocam-
pus can predict the animals location or even com-
plete future routes (Pfeiffer and Foster, 2013), (Fos-
ter and Wilson, 2006), (Johnson and Redish, 2007),
(Carr et al., 2011). These neural findings have in-
spired many computational models based on attractor
networks (Hopfield, 1982), (Samsonovich and Mc-
Naughton, 1997), (McNaughton et al., 2006), (Er-
dem and Hasselmo, 2012) and have been successfully
applied to humanoid robot motion planning tasks
(Rueckert et al., 2016), (Tanneberg et al., 2019).
In this work we took inspiration from simpler in-
sects which are able to precisely navigate by using
sparse perceptual and pro-prioceptual sensory infor-
mation. For example, the desert ant Cataglyphis (Fig-
ure 1a) employs basic path integration, visual piloting
and systematic search strategies to navigate back to
its nest from distant locations several hundred meters
away (Wehner, 1987). While computational models
of such navigation skills lead to better understanding
(a) ”Cataglyphis nodus”
by (Bobzin, 2013).
(b) Create 2
Figure 1: The Cataglyphis ant and the robot Create 2 from
the company iRobot.
of the neural implementation in the insect (Lambri-
nos et al., 2000), they also have a strong impact on a
large number of practical robotic applications. Espe-
cially, non-industrial autonomous systems like house-
hold robots (Figure 1b) or robotic toys require precise
navigation features utilizing low-cost sensory hard-
ware (Lee and Jung, 2012), (Miller and Slack, 1995),
(Nebot and Durrant-Whyte, 1999).
Despite this obvious need for precise localiza-
tion in low cost systems, most related work in mo-
bile robot navigation can be categorized into two ex-
treme cases. Either computational and monetary ex-
pensive sensors like cameras or laser range finders
are installed (Su et al., 2017), (Feng et al., 2017),
(Ito et al., 2014) or simplistic navigation strategies
such as a random walks are used like in the current
214
Rottmann, N., Bruder, R., Schweikard, A. and Rueckert, E.
Cataglyphis Ant Navigation Strategies Solve the Global Localization Problem in Robots with Binary Sensors.
DOI: 10.5220/0007556102140223
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 214-223
ISBN: 978-989-758-353-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
purchasable household robots (Tribelhorn and Dodds,
2007). When using limited sensing, only few navi-
gation strategies have been proposed. O’Kane et al.
investigated how complex a sensor system of a robot
really has to be in order to localize itself. Therefore,
they used a minimalist approach with contact sen-
sors, a compass, angular and linear odometers in three
different sensor configurations (O’Kane and LaValle,
2007). Erickson et al. addressed the localization
problem for a blind robot with only a clock and a
contact sensor. They used probabilistic techniques,
where they discretized the boundary of the environ-
ment into small cells. A probability P
k,i
of the robot
being in the cell i at the time step k is allocated to each
one and updated in every iteration. For active local-
ization, they proposed an entropy based approach in
order to determine uncertainty-reducing motions (Er-
ickson et al., 2008). Stavrou and Panayiotou on the
other hand proposed a localization method based on
Monte Carlo Localization (Dellaert et al., 1999) us-
ing only a single short-range sensor in a fixed position
(Stavrou and Panayiotou, 2012). The open challenge
however that remains is how to efficiently localize a
robot equipped only with a single binary sensor and
odometer. Such tasks arise, for example, especially
with autonomous lawn mowing robots. They usu-
ally use a wire signal to detect whether they are on
the area assigned to them or not. There are also sen-
sors that detect the moisture on the surface and can
thus detect grass (Bernini, 2009). All these sensors
usually return a binary signal indicating whether the
sensor is in the field or outside. The aforementioned
approaches can either not be applied to such local-
ization tasks because they require low-range sensors
(Stavrou and Panayiotou, 2012) or they are trying to
solve the problem with even less sensor information
(Erickson et al., 2008). A direct comparison between
these approaches and our method is not possible since
different sensors types are used. However, to be able
to compare the estimation accuracy of our methods
with the aforementioned algorithms, we created our
test environments similar to the test envrionment used
in (Stavrou and Panayiotou, 2012).
We propose an efficient and simple method for
global localization based only on odometry data and
binary measurements which can be used in real time
on a low-cost robot with only limited computational
resources. This work demonstrates for the first time
how basic navigation principles of the Cataglyphis ant
can be implemented in an autonomous outdoor robot.
Our approach has the potential to replace the currently
installed naive random walk behavior in most low cost
robots to an intelligent localization and planning strat-
egy inspired by insects. The methods we used are
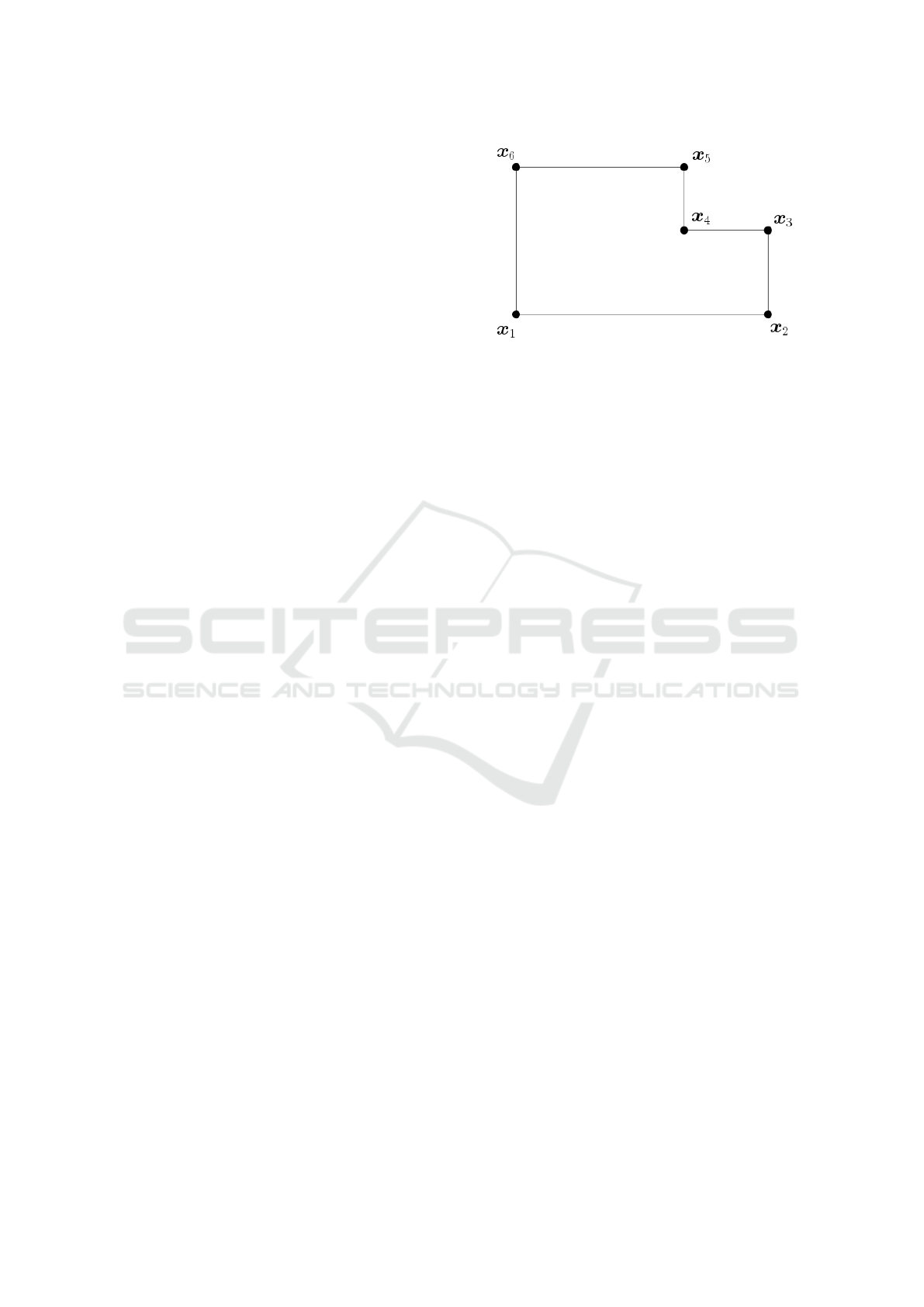
Figure 2: Boundary Map: An example map of an envi-
ronment which defines the boundary by connecting vertices
X = [x
x
x
1
, x
x
x
2
, ..., x
x
x
6
] to a polygon shape.
discussed in Section II. We first present a wall fol-
lowing scheme which is required to steer the robot
along the boundary line of the map based on the bi-
nary measurement data. Inspired by path integration
we determine dominant points (DPs) to represent the
path estimated by the odometry. We then generate a
first estimate of the pose of the robot using land nav-
igation. Therefore, we compare the shape of the esti-
mated path with the given boundary line. The gener-
ated pose estimate allows to systematically search for
the true pose in the given area using a particle filter.
This leads to a more accurate localization of the robot.
Here a particle filter is required since other localiza-
tion techniques, such as Kalman Filter, are not able to
handle binary measurement data. In Section III, we
evaluate our approach in two simulated environments
and show that it leads to accurate pose estimates of
the robot. We conclude in Section IV.
2 METHODS
For our proposed localization method, we assume
that a map of the environment is given as a bound-
ary map M defined as a polygon with vertices
X = [x
x
x
1
, x
x
x
2
, ..., x
x
x
n
] with x
x
x
i
∈ R
2
, ∀i ∈ [1, n]. In Fig-
ure 2 such a boundary map is shown. As sensor sig-
nals we only receive the binary information s ∈ {0, 1},
where 0 means that the sensor is outside of the map
and 1 means the sensor is within the boundary de-
fined by the polygon. We are using a simple differ-
ential drive robot controlled by the desired linear and
angular velocities v and ω. Furthermore, odometry
information is assumed to be given. We assume the
transform between the sensor position and the odom-
etry frame, which is also the main frame of the robot
and has the position [x
r
, y
r
]
>
in world coordinates, is
known as
x
s
y
s
=
x
r
y
r
+ R
R
R(ϕ
r
)
∆x
∆y
. (1)
Cataglyphis Ant Navigation Strategies Solve the Global Localization Problem in Robots with Binary Sensors
215
Here, R
R
R(ϕ
r
) is the two dimensional rotation matrix
with the orientation angle ϕ
r
of the robot and ∆x, ∆y
the distances between odometry frame and sensor po-
sition in robot coordinates. In Figure 3 the setup for
the differential drive robot is depicted. For our pro-
posed localization method, it is required that there is
a lever arm between the robots frame and the sensor,
such that if only the orientation of the robot changes
the position of the sensor changes too.
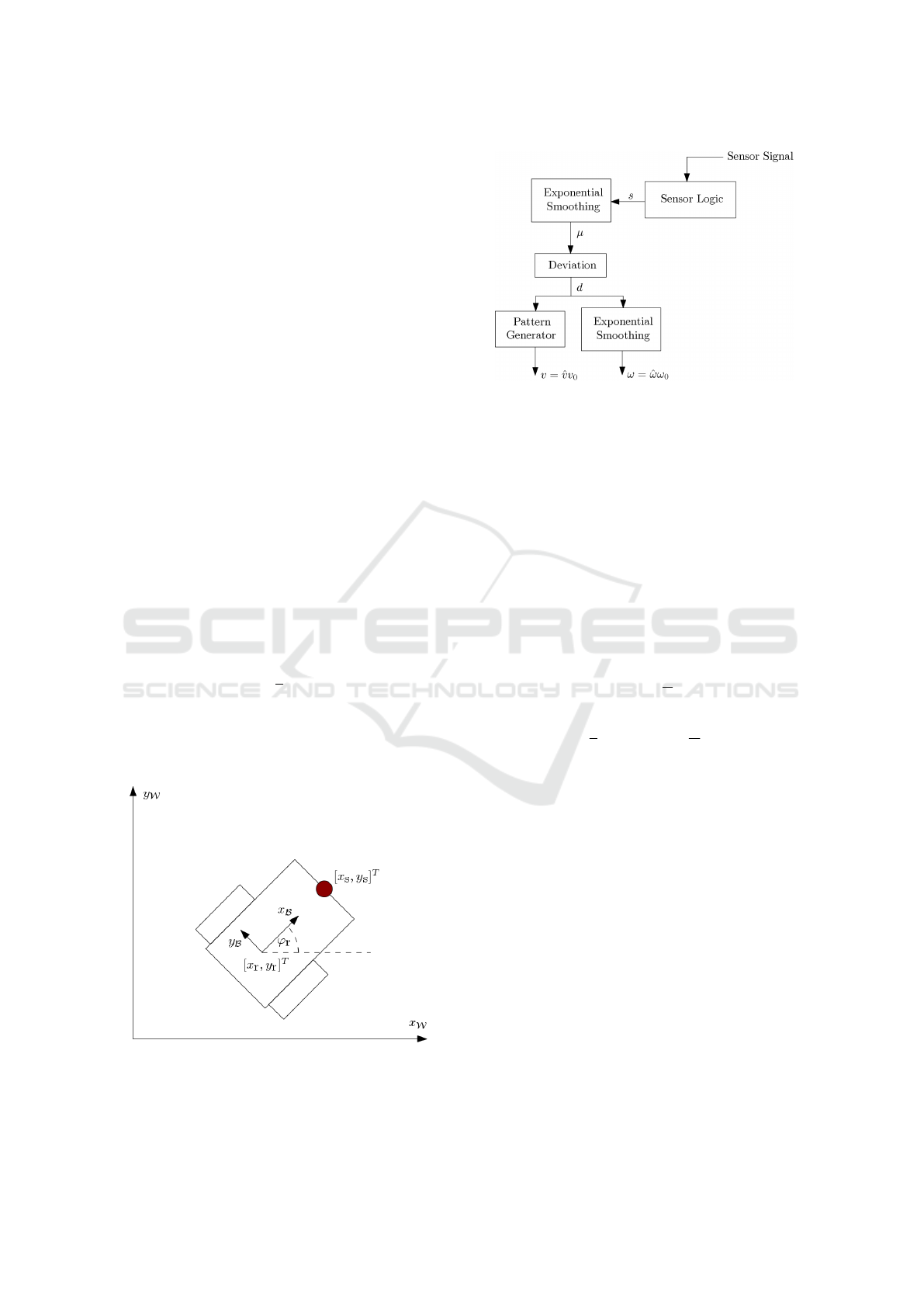
2.1 Wall Follower
Since only at the boundary we are able to generate
sensor data useful for localization, a wall follower
is required. The proposed control algorithm allows
to navigate the robot along the boundary line even
if the binary measurements are corrupted by noise.
Thereby, to increase the scanning area, the robot
moves in wiggly lines along the boundary such that
the mean of the sensor detection is µ
d
= 0.5. For the
update step of the sensor mean we use exponential
smoothing
µ
d
← a
µ
µ
d
+ (1 −a
µ
)s, (2)
starting with an initial mean of µ
d
= 1.0 (assumption:
start within the field). Here a
µ
defines the update rate
of the mean µ
d
. We then calculate the difference be-
tween the desired mean and the actual mean
d = 2
1
2
− µ
d
. (3)
The difference is scaled onto the range [−1, 1]. We
now use relative linear and angular velocities ˆv and
ˆ
ω
for the control algorithm. They have to be multiplied
Figure 3: A differential drive robot within the
2-dimensional world frame given by W . The robots
main frame B is determined by the frame for the odometry.
The robots position is given by x
r
, y
r
and the sensor position
by x
s
, y
s
.
Figure 4: Wall Follower: Control method blocks represent-
ing the wall following algorithm.
with the maximum allowed velocities for the given
robotic system v
0
and ω
0
in order to get the desired
velocities v and ω. Using the difference d from Equa-
tion (3), we update the relative forward velocity for
the differential drive robot ˆv using again exponential
smoothing
ˆv ← a
v
ˆv + (1 − a
v
)(1 −|d|). (4)
Here, a
v
defines an update rate and |d| the absolute
value of d. The relative velocity increases the longer
and better the desired mean of µ
d
= 0.5 is reached.
Thereby, the relative velocity is always in the range of
ˆv ∈ [0, 1]. The relative angular velocity of the robot is
determined using the deviation d to the desired mean
and a stabilizing term cos
2π
c
M
to ensure robustness
against noise corrupted measurements
ˆ
ω =
1
2
d + cos
2π
k
K
. (5)
Here, k is a counter variable and K the counter di-
vider. Thus, K should be chosen accordingly to the
frequency of the operating system. A diagram of the
controller as well as pseudo code can be found in Fig-
ure 4 and Algorithm (1) respectively.
2.2 Path Integration / Land Navigation
In order to get a first pose estimate for the robot we
use land navigation between the given map M and the
driven path P along the boundary line.
First, we start by generating a piecewise linear
function of the orientation of the boundary line in re-
gard to the length θ
b
= θ
b
(x). This function repre-
sents the shape of the boundary and is defined as
θ
b
(x) = φ
i
for l
i
≤ x < l
i+1
, i = 1, 2, . . . , 2n. (6)
with
φ
i+1
= φ
i
+ ∆θ
i
l
i+1
= l
i
+ ||v
v
v
i
||.
(7)
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
216

Algorithm 1: Wall Follower.
• Parameters
K, a
µ
, a
v
, v
0
, ω
0
• Inputs
s
• Outputs
v, ω
1: k = 0
2: µ
d
= 1.0 start within the field
3: while true do
4: if Mode == 0 then search for boundary
5: µ
d
← a
µ
µ
d
+ (1 − a
µ
)s
6: if µ
d
> 0.5 then
7: v = v
0
8: ω = 0
9: else
10: Mode = 1
11: end if
12: else if Mode == 1 then wall following
13: µ
d
← a
µ
µ
d
+ (1 − a
µ
)s
14: d = 2 · (0.5 − µ
d
)
15: ˆv ← a
v
ˆv + (1 − a
v
)(1 − ||d||)
16: v = ˆvv
0
17: ω =
d + cos
2π
k
K
· 0.5 · ω
0
18: end if
19: k ← k + 1
20: return v, ω
21: end while
Here, ||v
v
v
i
|| defines the Euclidean norm
for the vector v
v
v
i
. We start with φ
1
= 0
and l
1
= 0. Thereby, v
v
v
i
=
ˆ
X
i+1
−
ˆ
X
i
with
ˆ
X = [x
x
x
1
, x
x
x
2
, ..., x
x
x
n
, x
x
x
1
, x
x
x
2
, ..., x
x
x
n
, x
x
x
1
] consisting of
the vertices X of the map and ∆θ
i
as the difference in
orientation between v
v
v
i
and v
v
v
i−1
.
Second, in order to represent the path driven by
the robot as vertices connected by straight lines (sim-
ilar to the map representation), we generate dominant
points (DPs). Therefore, we are simply using the esti-
mated position from the odometry of our robot start-
ing with DP = [x
x
x
0
] at the first contact with the bound-
ary line. We also initialize a temporary set S = [x
x
x
0
]
which holds all the actual points which can be com-
bined to a straight line. We start by adding in every it-
eration step the new position estimate from the odom-
etry data x
x
x to our temporary set S ← [S, x
x
x] and then
check if
L
min
> ||DP
end
− S
end
|| (8)
and
e
max
>
1
N − 2
N−1
∑
i=2
e
i
(9)
are both true. If this is the case we add the point
Algorithm 2: DP Generation.
• Parameters
L
min
, e
max
• Inputs
x
x
x
• Outputs
DP
1: DP = [x
x
x
0
]
2: S = [x
x
x
0
]
3: if new x
x
x available then
4: d = ||DP
end
− x
x
x||
5: if d < L
min
then
6: S ← [S, x
x
x]
7: else
8: S
tmp
= [S, x
x
x]
9: e = errorLineFit(S
tmp
)
10: if e < e
max
then
11: S ← S
tmp
12: else
13: DP ← [DP, S
end
]
14: S ← [S
end
, x
x
x]
15: end if
16: end if
17: end if
S
end−1
to the set of DPs and set the temporary set back
to S = [S
end
, x
x
x]. Here, e
i
defines the shortest distance
between the point S
i
and the vector given by S
end
−S
1
.
Pseudo code for the algorithm can be found in Algo-
rithm (2). The parameters L
min
and e
max
are problem
specific and have to be tuned accordingly.
Third, every time a new DP is accumulated we
generate a piecewise orientation function θ
r
as pre-
sented above using the actual set of DPs, as long as
the accumulated length between the DPs is larger then
U
min
× Map Circumference. This ensures that the al-
gorithm does not start too early with the compari-
son. The parameter U
min
∈ [0, 1] represents the mini-
mal required portion of the boundary line to identify
unique positions and has to be chosen or trained ac-
cording to the given map. We then compare θ
r
with
θ
b
for all vertices x
x
x
i
, i = 1, 2, . . . , n of the boundary
line in order to find a suitable vertex at which the
robot could be. Therefore, we adjust θ
b
such that
θ
b,i
(x) = θ
b
(x + l
i
) − φ
i
, i = 2n, 2n − 1, . . . , n + 1. We
now evaluate these functions at N linearly distributed
points from −L to 0 which results into vectors θ
θ
θ
b,i
.
Here, L is the path length driven by the robot along
the boundary line. We then calculate the correlation
error
c
c
c
i
=
1
N
N
∑
k=1
|θ
θ
θ
b,i,k
− θ
θ
θ
r
|, (10)
Cataglyphis Ant Navigation Strategies Solve the Global Localization Problem in Robots with Binary Sensors
217
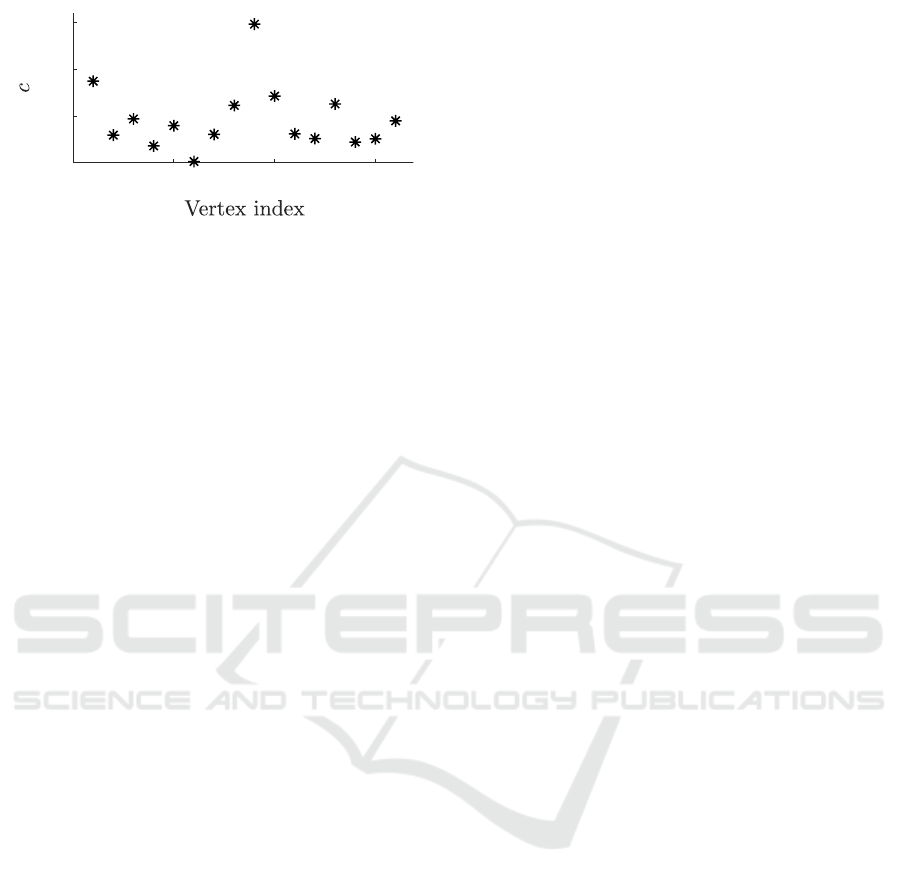
0 5 10 15
0
5
10
15
Figure 5: Correlation errors between the actual DP and the
vertices of the map are shown. Here the vertex with the
index 6 fulfills the required conditions and is chosen for the
first position estimate.
where θ
θ
θ
r
is the evaluation of the function
ˆ
θ
r
(x) = θ
r
(x + L) − θ
r
(L) in the range from −L
to 0 at N linearly distributed points. We now have
correlation errors between the actual driven path by
the robot along the boundary line and every vertex of
the polygon map. In Figure 5 correlation errors are
graphically displayed.
Fourth, we search for the vertex with the mini-
mal correlation error and check if the error is below
a certain threshold c
min
. The parameter c
min
has to
be trained accordingly to the given map and the given
robotic system. If we do not find a convenient vertex,
we simply drive further along the wall until finding
a vertex which follows the condition above. Thereby,
we limit the stored path from the robot to the length of
the circumference of the map. If a convenient vertex
is found, we call this vertex from now on matching
vertex, the first guess of the robots position can be
determined as x
x
x
est
, where x
x
x
est
is the matching vertex.
Moreover, we can also define a orientation estimate
as
ϕ
est
= atan2(v
v
v
est,y
, v
v
v
est,x
), (11)
where v
v
v
est
= x
x
x
est
− x
x
x
est−1
.
2.3 Systematic Search
Using the land navigation from above we now have a
first estimate on where the robot is located. Based on
this estimate we are able to start a systematic search in
this region to determine a more accurate and certain
pose estimate. Therefore, we use a particle filter since
other localization techniques, such as Kalman Filter,
can not handle binary measurement data. The gen-
eral idea of the particle filter (Thrun et al., 2005) is to
represent the probability distribution of the posterior
by a set of samples, called particles, instead of using
a parametric form as the Kalman Filter does. Here,
each particle
X
t
= x
x
x
[1]
t
, x
x
x
[2]
t
, . . . , x
x
x
[N]
t
(12)
represents a concrete instantiation of the state at time
t, where N denotes the number of particles used. The
belief bel(x
x
x
t
) is then approximated by the set of par-
ticles X
t
. The Bayes filter posterior is used to include
the likelihood of a state hypothesis x
x
x
t
x
x
x
[i]
t
∼ p(x
x
x
t
|z
z
z
1:t
, u
u
u
1:t
). (13)
Here z
z
z
1:t
and u
u
u
1:t
represent the measurement history
and the input signal history respectively.
The idea of our method is to reduce the particles re-
quired for global localization with a particle filter ex-
tensively by just sampling particles in an area around
the position estimate retrieved by land navigation as
shown above. This is nothing else than the transfor-
mation from a global localization problem to a lo-
cal one. Therefore, we simply use a Gaussian dis-
tribution N (µ
µ
µ, Σ
Σ
Σ) with the mean µ
µ
µ = [x
x
x
T
est
, ϕ
est
]
T
and
parametrized covariance matrix Σ
Σ
Σ = diag[σ
x
, σ
y
, σ
ϕ
].
The parameters σ
x
, σ
y
, σ
ϕ
can be chosen accordingly
to the mean and uncertainty of the error of the initial
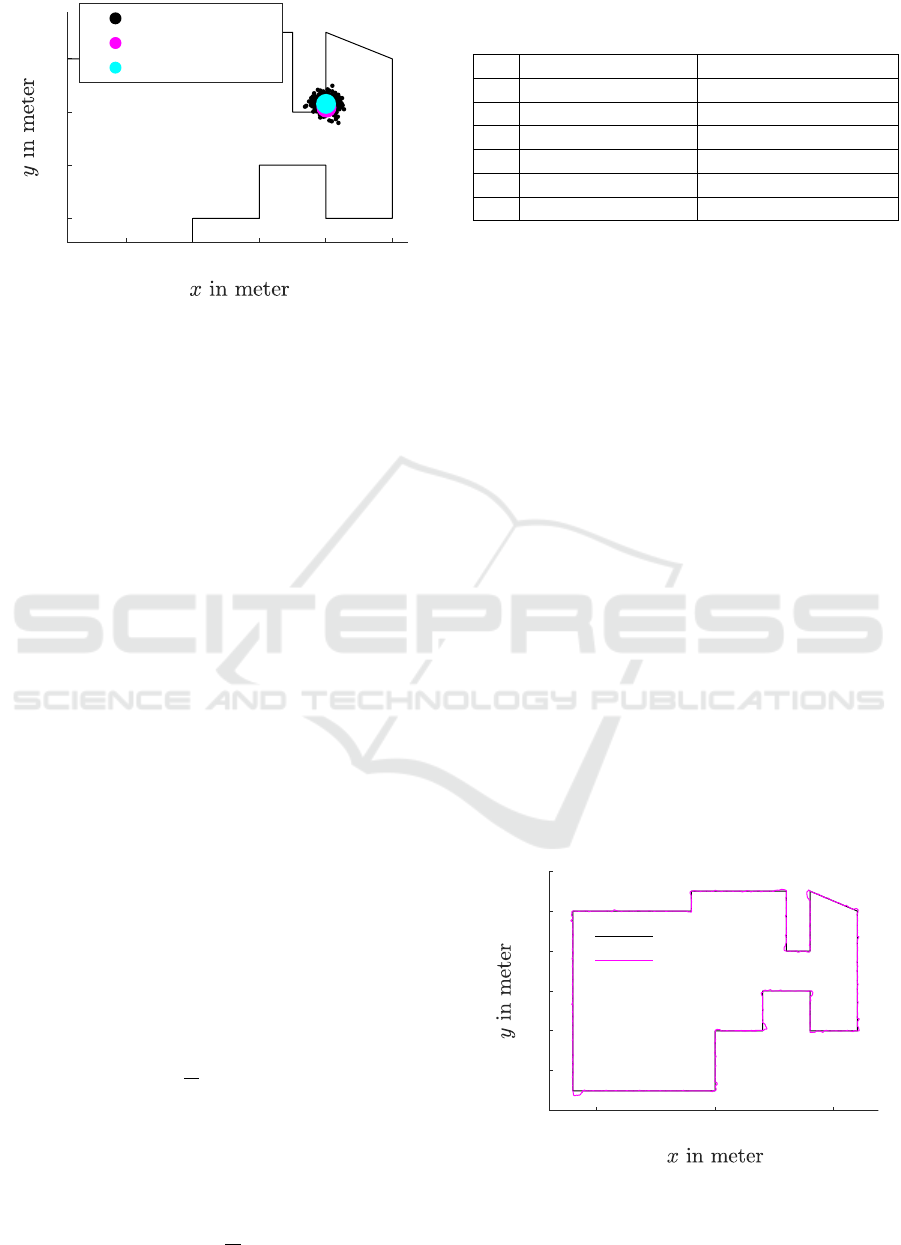
pose estimate as we will see in Section 3. In Figure 6
an example distribution of the particles around the
estimated pose is shown. After sampling the particles
we now are able to further improve the localization
executing a systematic search along the border line
using the particle filter. Thereby, the weighting of the
particles happens as follows: If a particle would see
the same as the sensor has measured, then we give this
particle the weight w
i
= ˆw, where w
i
is the weight
of the i-th particle. If the particle would not see the
same, then w
i
= (1 − ˆw). Here the parameter ˆw has to
be larger then 0.5.
3 RESULTS
In this section, we evaluate the proposed algorithms
in regard to stability and performance. Stability is de-
fined as the fraction of localization experiments were
the robot could localize itself from an initially lost
pose in the presence of sensor noise. For that the Eu-
clidian distance between the true and the estimated
pose had to be below a threshold of 0.3 m. Perfor-
mance is defined as the mean accuracy of the pose
estimation and the time required to generate the pose
estimate. Therefore, we created a simulation environ-
ment using Matlab with a velocity and an odometry
motion model for a differential drive robot as pre-
sented in (Thrun et al., 2005). For realistic condi-
tions, we calibrated the noise parameters in experi-
ments to match the true motion model of a real Viking
MI 422P, a purchasable autonomous lawn mower. For
this calibration, we tracked the lawn mower move-
ments using a visual tracking system (OptiTrack) and
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
218
-2 0 2 4 6
0
2
4
6
Particles
Real Pose
Estimated Pose
Figure 6: Sampled Particles: Particles have been sampled
around the first pose estimate generated using land naviga-
tion.
computed the transition model parameters through
maximum likelihood estimation. The parameters can
be found in Table 1. We used a sampling frequency of
f = 20 Hz for the simulated system and the maximum
linear velocity v
0
= 0.3 m s
−1
and angular velocity
ω = 0.6s
−1
. These values correspond approximately
to the standard for purchasable low-cost robots. We
set the number of K = 100 which leads to a period
time of the wiggly lines T = 5 s. This is a trade-
off between the enlargement of the scanning surface
and the movement that can be performed on a real
robot. The relative position of the binary sensor in
regard to the robot frame, Equation (1), is given by
[∆x, ∆y]
T
= [0.3 m, 0.0 m]
T
.
3.1 Wall Follower
As mentioned before, only at the boundary we are
able to generate data useful for localization since only
there we can detect differences in the signal generated
by the given binary sensor. Hence, we first evaluate
the performance of the presented wall following al-
gorithm. Therefore, we use the mean squared error
(MSE) to measure the deviation of the path of the sen-
sor to the given boundary line of the map. An example
of such a path along the map is given in Figure 7. Let
x
x
x
i
be the i-th position of the sensor and s
s
s
i
the closest
point at the boundary line to x
x
x
i
, then
MSE =
1
N
N
∑
i=1
||s
s
s
i
− x
x
x
i
||
2
, (14)
where N represents the number of time steps required
to complete one round along the boundary line. We
also evaluate the mean velocity of the robot driving
along the boundary
v
µ
=
U
T
, (15)
Table 1: Measured parameters for the velocity and odome-
try motion model from (Thrun et al., 2005).
Vel. Motion Model Odom. Motion Model
α
1
0.0346 0.0849
α
2
0.0316 0.0412
α
3
0.0755 0.0316
α
4
0.0566 0.0173
α
5
0.0592 -
α
6
0.0678 -
where U is the circumference of the map and T the
time required by the robot to complete one round. In
Figure 8, Figure 9 and Figure 10, the average sim-
ulation results over 10 simulations for different noise
factors in Equation (2) and Equation (4) are presented.
The used map is shown in Figure 7. The noise factor
hereby determines the randomness of the binary sig-
nals, thus a factor of 0 leads to always accurate mea-
surements whereas a factor of 1 implies total random
measurement results. Hence, a noise factor of 40 %
signals that 40 % of the output signals of the binary
sensor are random.
The presented wall follower leads to a stable
and accurate wall following behavior as exemplarily
shown in Figure 7. With increasing noise factor, the
MSE becomes larger. However, the algorithm is sta-
ble enough to steer the robot along the boundary line
even by noise factors around 40 %. The algorithm
seems to work best, thus leading to small MSE, for
small a
µ
. However, a small value for a
µ
leads to large
changes in the linear and angular velocities which
may not be feasible on a real robot or may cause large
odometry erros. We discuss this problem more inten-
sively in Section 4. The parameter a
v
seems to have
no strong influence neither on the MSE nor on the
mean velocity.
-5 0 5
-4
-2
0
2
4
6
8
Map
Sensor Path
Figure 7: Example of a path along the boundary line gen-
erated using the presented wall following algorithm with
a
µ
= 0.7, a
v
= 0.7, M = 100 and a sensor noise of 10 %.
Cataglyphis Ant Navigation Strategies Solve the Global Localization Problem in Robots with Binary Sensors
219

0
1
0.01
1
0.8
0.02
0.8
0.6
0.6
0.05
1
0.1
1
0.8
0.15
0.8
0.6
0.6
Figure 8: MSE and mean velocity for a noise factor of 0 %
and varying parameters a
µ
and a
v
. The results shown are
the average values over 10 iterations.
0
1
0.05
1
0.8
0.1
0.8
0.6
0.6
0
1
0.2
1
0.8
0.4
0.8
0.6
0.6
Figure 9: MSE and mean velocity for a noise factor of 20%
and varying parameters a
µ
and a
v
. The results shown are
the average values over 10 iterations.
0
1
0.2
1
0.8
0.4
0.8
0.6
0.6
0
1
0.2
1
0.8
0.4
0.8
0.6
0.6
Figure 10: MSE and mean velocity for a noise factor of
40% and varying parameters a
µ
and a
v
. The results shown
are the average values over 10 iterations.
3.2 Land Navigation
In order to evaluate the performance and stability of
the proposed shape comparison method we simulated
the differential drive robot 100 times in two different
maps (Figure 11) with randomly chosen starting po-
sitions. We trained the parameters specifically for the
given maps under usage of the proposed wall follow-
ing algorithm with a
µ
= 0.7, a
v
= 0.7, M = 100 and a
simulated sensor noise of 10 %. The resulting param-
eters are presented in Table 2.
Table 2: Trained parameters for the presented maps from
Figure 11.
L
min
e
max
c
min
U
min
Map 1 0.5 0.01 0.2 0.5
Map 2 0.5 0.01 0.3 0.4
We then calculated the difference of the estimated
position and the true position ∆x = ||x
x
x
true
− x
x
x
est
|| as
well as for the estimated orientation and true orien-
0 2 4 6 8 10
0
5
10
-5 0 5
-4
-2
0
2
4
6
8
Figure 11: Maps used for the simulation. Map 1 is at the top
and map 2 at the bottom. The circumferences for the maps
are U
1
= 40m and U
2
= 53.23m.
tation ∆ϕ = ||ϕ
true
− ϕ
est
||. Histograms of these er-
rors are depicted in Figure 12 and Figure 13. The
mean time for finding this first pose estimate is around
T
1
= 336s for map 1 and T
2
= 382s for map 2. The re-
sults show that the proposed algorithm is able to com-
pute accurate estimates of the robots poses. Those es-
timates can then be further used to sample particles
for a particle filter to systematically search in the re-
gion of interest for the correct pose.
3.3 Systematic Search
We now demonstrate how the position estimate from
above can be further used to systematically search for
a better estimate and for executing planning tasks. As
proposed, we first sample particles around the posi-
tion estimate using Gaussian distributions
x
y
ϕ
∼
N (x
est
, µ
∆x
+ 3σ
∆x
)
N (y
est
, µ
∆x
+ 3σ
∆x
)
N (ϕ
est
, µ
∆ϕ
+ 3σ
∆ϕ
)
. (16)
The standard deviation µ+3σ, depending on the mea-
surement results from Section 3.2, ensures that the
particles are sampled in an area large enough around
the initial pose estimate. In Figure 15 and Figure 16,
the particles and the pose estimate are shown as well
as the true position of the robot. In the following step
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
220

Figure 12: Evaluation results for map 1: Histogram
of the difference between position and orientation es-
timate and true position and orientation after matching
through shape comparison with µ
∆x
= 0.13, µ
∆ϕ
= 0.55,
σ
∆x
= 0.06, σ
∆ϕ
= 0.09.
Figure 13: Evaluation results for map 2: Histogram
of the difference between position and orientation es-
timate and true position and orientation after matching
through shape comparison with µ
∆x
= 0.23, µ
∆ϕ
= 0.25,
σ
∆x
= 0.20, σ
∆ϕ
= 0.15.
we systematically search for the true pose of the robot
by following the boundary line. The particle filter al-
gorithm weights the particles and does a resampling if
required. We stop the wall following if we are certain
enough about the pose of the robot, hence the variance
of the particles is less then a certain treshold. In Fig-
ure 17 the robot after the systematic search for a better
pose estimate is shown. Now we are able to execute
certain tasks with the robot, for example mowing the
lawn. Thereby, the robot has to move away from the
boundary and the pose estimate becomes more un-
certain as shown in Figure 18. After reaching again
the boundary line the particle filter is able to enhance
the pose estimate based on the new information as de-
picted in Figure 19.
We also evaluated the performance of the pro-
Figure 14: Histogram of the difference between position
and orientation estimate and true position and orientation
after the systematic search using the particle filter with
µ
∆x
= 0.13, µ
∆ϕ
= 0.04, σ
∆x
= 0.086, σ
∆ϕ
= 0.04.
posed systematic search. Therefore, we simulated the
differential drive robot 100 times sampling the parti-
cles as proposed in Equation (16). We then followed
the boundary line until the standard deviation of the
orientation has been below 0.2. Again, we evaluated
the difference between position and orientation esti-
mate and true position and orientation. Here, 3 times
the particle filter has not found a sufficient accurate
pose estimate. If this happens, we simply can restart
the procedure by finding a pose estimate using land
navigation. In Figure 14 a histogram depicting the re-
sults are shown. The systematic search for the pose
of the robot using a particle filter improves the orien-
tation estimate compared to the initial estimate pre-
sented in section 3.2.
4 CONCLUSION
We have presented a method for global localization
based only on odometry data and one binary sensor.
This method, inspired by insect localization strate-
gies, is essential for efficient path planning methods
as presented in (Hess et al., 2014) or (Galceran and
Carreras, 2013) which require an accurate estimate of
the robots pose. Our approach combines ideas of path
integration, land navigation and systematic search to
find a pose estimate for the robot.
Our method relies on a stable and accurate wall fol-
lowing algorithm. We showed that the proposed al-
gorithm is robust even under 40 % sensor noise and,
if convenient parameters are chosen, leads to an accu-
rate wall following behavior.
The proposed approach for finding a first pose esti-
mate is robust and accurate. Given this pose estimate
we are able to sample particles around this position
Cataglyphis Ant Navigation Strategies Solve the Global Localization Problem in Robots with Binary Sensors
221

-5 0 5
-4
-2
0
2
4
6
8
Particles
Real Pose
Estimated Pose
Figure 15: Randomly sampled particles around the position
estimate x
x
x
est
.
5 5.5 6
-0.5
0
0.5
Figure 16: Randomly sampled particles around the position
estimate x
x
x
est
in close up view.
5.2 5.4 5.6 5.8 6 6.2 6.4
1.2
1.4
1.6
1.8
Figure 17: Pose estimate of the robot after the systematic
search.
3.5 4 4.5 5
1
1.5
Figure 18: Moving within the map increases the uncertainty
of the pose estimate.
3.5 4 4.5
0.5
1
Figure 19: New information collected at the boundary leads
to an improvement in pose estimation.
for starting a systematic search with a particle filter
algorithm. Therefore, we maintain the wall follow-
ing behavior until the uncertainty of the pose esti-
mate of the particle filter is below a certain threshold.
The proposed search method improves the orientation
estimate intensively while maintaining the accuracy
of the position estimate. As mentioned in the Intro-
duction, it is not possible to compare our approach
directly with other approaches since different types
of sensors are used. However, comparing our local-
ization results with the results presented in (Stavrou
and Panayiotou, 2012) for a particle filter with a sin-
gle low-range sensor, we reach a similar accuracy for
the position estimate by only using a binary sensor.
Thereby, the accuracy is in the range of around 0.1 m.
Using the generated pose estimate we are now able to
execute given tasks by constantly relocating the robot
at the boundary lines. For example, using bioinspired
neural networks for complete coverage path planning
(Zhang et al., 2017). Open research questions in re-
gard to the proposed approach are which methods can
be used to learn the algorithm parameters L
min
, e
max
,
c
min
, U
min
on the fly. Also, the algorithm has to be
evaluated on a real robotic system in a realistic gar-
den setup.
REFERENCES
Bernini, F. (2009). Lawn-mower with sensor. US Patent
7,613,552.
Bobzin, C. (2013). Cataglyphis nodus. CC BY-SA 3.0,
https://de.wikipedia.org/wiki/Cataglyphis.
Carr, M. F., Jadhav, S. P., and Frank, L. M. (2011). Hip-
pocampal replay in the awake state: a potential sub-
strate for memory consolidation and retrieval. Nature
neuroscience, 14(2):147.
Dellaert, F., Fox, D., Burgard, W., and Thrun, S. (1999).
Monte carlo localization for mobile robots. In
Robotics and Automation, 1999. Proceedings. 1999
IEEE International Conference on, volume 2, pages
1322–1328. IEEE.
Erdem, U. M. and Hasselmo, M. (2012). A goal-directed
spatial navigation model using forward trajectory
planning based on grid cells. European Journal of
Neuroscience, 35(6):916–931.
Erickson, L. H., Knuth, J., O’Kane, J. M., and LaValle,
S. M. (2008). Probabilistic localization with a blind
robot. In Robotics and Automation, 2008. ICRA 2008.
IEEE International Conference on, pages 1821–1827.
IEEE.
Feng, L., Bi, S., Dong, M., Hong, F., Liang, Y., Lin, Q.,
and Liu, Y. (2017). A global localization system for
mobile robot using lidar sensor. In 2017 IEEE 7th An-
nual International Conference on CYBER Technology
in Automation, Control, and Intelligent Systems (CY-
BER), pages 478–483. IEEE.
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
222

Foster, D. J. and Wilson, M. A. (2006). Reverse replay of
behavioural sequences in hippocampal place cells dur-
ing the awake state. Nature, 440(7084):680.
Galceran, E. and Carreras, M. (2013). A survey on coverage
path planning for robotics. Robotics and Autonomous
systems, 61(12):1258–1276.
Hess, J., Beinhofer, M., and Burgard, W. (2014). A prob-
abilistic approach to high-confidence cleaning guar-
antees for low-cost cleaning robots. In Robotics and
Automation (ICRA), 2014 IEEE International Confer-
ence on, pages 5600–5605. IEEE.
Hopfield, J. J. (1982). Neural networks and physical sys-
tems with emergent collective computational abili-
ties. Proceedings of the national academy of sciences,
79(8):2554–2558.
Ito, S., Endres, F., Kuderer, M., Tipaldi, G. D., Stachniss,
C., and Burgard, W. (2014). W-rgb-d: floor-plan-
based indoor global localization using a depth camera
and wifi. In Robotics and Automation (ICRA), 2014
IEEE International Conference on, pages 417–422.
IEEE.
Johnson, A. and Redish, A. D. (2007). Neural ensembles
in ca3 transiently encode paths forward of the ani-
mal at a decision point. Journal of Neuroscience,
27(45):12176–12189.
Lambrinos, D., M
¨
oller, R., Labhart, T., Pfeifer, R., and
Wehner, R. (2000). A mobile robot employing insect
strategies for navigation. Robotics and Autonomous
systems, 30(1-2):39–64.
Lee, H. and Jung, S. (2012). Balancing and navigation con-
trol of a mobile inverted pendulum robot using sensor
fusion of low cost sensors. Mechatronics, 22(1):95–
105.
McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I.,
and Moser, M.-B. (2006). Path integration and the
neural basis of the’cognitive map’. Nature Reviews
Neuroscience, 7(8):663.
Miller, D. P. and Slack, M. G. (1995). Design and testing of
a low-cost robotic wheelchair prototype. Autonomous
robots, 2(1):77–88.
Nebot, E. and Durrant-Whyte, H. (1999). Initial calibration
and alignment of low-cost inertial navigation units for
land vehicle applications. Journal of Robotic Systems,
16(2):81–92.
O’Kane, J. M. and LaValle, S. M. (2007). Localization
with limited sensing. IEEE Transactions on Robotics,
23(4):704–716.
O’keefe, J. and Nadel, L. (1978). The hippocampus as a
cognitive map. Oxford: Clarendon Press.
Pfeiffer, B. E. and Foster, D. J. (2013). Hippocampal
place-cell sequences depict future paths to remem-
bered goals. Nature, 497(7447):74.
Redish, A. D. et al. (1999). Beyond the cognitive map: from
place cells to episodic memory. MIT press.
Rueckert, E., Kappel, D., Tanneberg, D., Pecevski, D., and
Peters, J. (2016). Recurrent spiking networks solve
planning tasks. Nature Publishing Group: Scientific
Reports, 6(21142).
Samsonovich, A. and McNaughton, B. L. (1997). Path inte-
gration and cognitive mapping in a continuous attrac-
tor neural network model. Journal of Neuroscience,
17(15):5900–5920.
Stavrou, D. and Panayiotou, C. (2012). Localization of a
simple robot with low computational-power using a
single short range sensor. In Robotics and Biomimet-
ics (ROBIO), 2012 IEEE International Conference on,
pages 729–734. IEEE.
Su, Z., Zhou, X., Cheng, T., Zhang, H., Xu, B., and Chen,
W. (2017). Global localization of a mobile robot using
lidar and visual features. In Robotics and Biomimet-
ics (ROBIO), 2017 IEEE International Conference on,
pages 2377–2383. IEEE.
Tanneberg, D., Peters, J., and Rueckert, E. (2019). Intrin-
sic motivation and mental replay enable efficient on-
line adaptation in stochastic recurrent networks. Neu-
ral Networks - Elsevier, 109:67–80. Impact Factor of
7.197 (2017).
Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic
robotics. MIT press.
Tribelhorn, B. and Dodds, Z. (2007). Evaluating the
roomba: A low-cost, ubiquitous platform for robotics
research and education. In ICRA, pages 1393–1399.
Wehner, R. (1987). Spatial organization of foraging behav-
ior in individually searching desert ants, cataglyphis
(sahara desert) and ocymyrmex (namib desert). In
From individual to collective behavior in social in-
sects: les Treilles Workshop/edited by Jacques M.
Pasteels, Jean-Louis Deneubourg. Basel: Birkhauser,
1987.
Zhang, J., Lv, H., He, D., Huang, L., Dai, Y., and Zhang, Z.
(2017). Discrete bioinspired neural network for com-
plete coverage path planning. International Journal of
Robotics and Automation, 32(2).
Cataglyphis Ant Navigation Strategies Solve the Global Localization Problem in Robots with Binary Sensors
223
