
Bayesian Optimization of 3D Feature Parameters for 6D Pose Estimation
Frederik Hagelskjær, Norbert Kr
¨
uger and Anders Glent Buch
Maersk Mc-Kinney Moller Institute, University of Southern Denmark, Odense, Denmark
Keywords:
Pose Estimation, Object Detection, Feature Matching, Optimization, Bayesian Optimization, Machine
Learning.
Abstract:
6D pose estimation using local features has shown state-of-the-art performance for object recognition and pose
estimation from 3D data in a number of benchmarks. However, this method requires extensive knowledge
and elaborate parameter tuning to obtain optimal performances. In this paper, we propose an optimization
method able to determine feature parameters automatically, providing improved point matches to a robust
pose estimation algorithm. Using labeled data, our method measures the performance of the current parameter
setting using a scoring function based on both true and false positive detections. Combined with a Bayesian
optimization strategy, we achieve automatic tuning using few labeled examples. Experiments were performed
on two recent RGB-D benchmark datasets. The results show significant improvements by tuning an existing
algorithm, with state-of-art performance.
1 INTRODUCTION
Pose estimation is the task of determining the position
and orientation of one or multiple objects in a scene,
e.g. as seen in Fig. 1. The scene data could be either
2D or 3D data coming from one or multiple sensors.
A wide range of new sensors, with the Kinect (Zhang,
2012) at the forefront, has enabled easy access to 3D
data. This has resulted in 3D feature matching as a vi-
able tool for pose estimation. The pose is represented
by a transformation matrix consisting of a translation
and rotation, which can be passed on for further use,
e.g. during robotic grasping.
A widely used method for addressing the task of
pose estimation in 3D data is feature matching using
local shape descriptors. This method goes back 20
years with the well-known Spin Images (Johnson and
Hebert, 1999) and has become the de facto standard
for 3D pose estimation (Guo et al., 2014). Matches
between object and scene points are found in feature
space and are used to find the transform between the
to point clouds. This approach is especially suitable
for scenarios where parts of the object are occluded,
as the matching is performed locally. Many different
features have been developed, e.g. SHOT (Salti et al.,
2014), FPFH (Rusu et al., 2009), and USC (Tombari
et al., 2010). A fundamental limitation when applying
such descriptors is that the performance depends he-
avily on careful parameter tuning, the size of the lo-
Figure 1: Multi-instance pose estimation example for a
scene from the dataset of (Tejani et al., 2014). To the top is
shown an example with non-optimized feature parameters,
resulting in two correct (green) and one incorrect detection
(red). The CAD model of the object is shown in the middle.
Our parameter optimization improves the pose estimation
algorithm, giving correct detection of all the three instances
of the object shown at the bottom.
cal support radius is shown to be extremely important
(Guo et al., 2016), which must be set to a compromise
between descriptive power and occlusion tolerance.
If set incorrectly, the matching will perform badly
Hagelskjær, F., Krüger, N. and Buch, A.
Bayesian Optimization of 3D Feature Parameters for 6D Pose Estimation.
DOI: 10.5220/0007568801350142
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 135-142
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
135

Figure 2: Full pipeline of our parameter optimization approach. ’p’ training scenes are selected and for each scene ’m’
objects are present. Resulting in m*p object detections. A: First a parameter set is used for object recognition. B: The scoring
function then determines the performance. C: The Gaussian Process fits a distribution to the results. D: The decision selects
the next parameters sets to test. A number of preselected parameter sets are used to build the Gaussian Process, after which the
Bayesian Optimization runs for n-iterations. E: the full set of parameters and scores is fit to an additional Gaussian Process
and the expected best parameter set is found F.
and so will the pose estimation algorithm, which uses
these matches for the sampling process.
In a comparison of different features, this varia-
bility is shown as an error greatly influencing perfor-
mance (Guo et al., 2016). And in papers presenting
the performance of new features the tuning is done by
the author who searches for the best performance, and
leaves out all other results. We believe the parameter
values to be fundamental in the feature matching task
and propose a systematic approach to choosing the
best parameters.
Although the data-driven approach for object re-
cognition for 3D data is old (Oshima and Shirai,
1983), the knowledge-driven fine tuning is the one of-
ten seen in benchmarking. In this paper we focus on
the data-driven approach. Scenes are split into a trai-
ning and test set, but compared to modern approaches
towards 3D tasks, e.g. (Qi et al., 2017), we also show
good results with much smaller training samples. Ad-
ditionally, we employ Bayesian Optimization (Snoek
et al., 2012) to search the parameter space. But as we
are only searching a small dataset, instead of using
a single maximum value we fit a Gaussian process
(Rasmussen, 2004) to the results to avoid local maxi-
mums. An overview of the full method can be seen in
Fig. 2.
In a study of the usage of pose estimation, the me-
dian time to setup a system was found to be between
1–2 weeks (Hagelskjær et al., 2017), with most of
the work being done on the software side. To enable
an easier use of object recognition in real applicati-
ons, automatic optimization approaches can be help-
ful. This paper presents a principled method for doing
so, with a focus on some of the most important para-
meters for local shape descriptor computation. Our
method, however, can be applied in a wide range of
applications.
The remaining article is structured as follows:
Section 2 outlines the methods used for pose estima-
tion along with other optimization approaches. Our
method is presented in Section 3. Section 4 contains
experimental results of our method compared with
current methods. Finally, we outline the conclusion
of our work and the further perspectives of this ap-
proach.
2 PROPOSED METHOD
Parameter tuning using Bayesian Optimization has
begun to be widely used in machine learning. Despite
this, to the best of our knowledge, automatic parame-
ter tuning has not yet been seen for 3D feature des-
criptors. Although e.g. (Jørgensen et al., 2018) cover
optimal camera placements in a robotic setup, it does
not go into the parameters of feature matching. We
start by outlining the feature matching for pose esti-
mation task, then we outline the Bayesian Optimiza-
tion method and finally we describe how it is used to
tune parameters.
2.1 Pose Estimation with Feature
Matching
Pose estimation based object recognition is the task
of determining the position of one or multiple ob-
jects in a scene. A typical strategy towards a solu-
tion to this problem is to represent the scene by a
2D image, wherein template matching of object views
are performed (Hinterstoisser et al., 2012). This ap-
proach, however, is not well suited to handle occlusi-
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
136

Figure 3: The important descriptor parameters for a single point in a point cloud. To the left is shown a representation of
parameters: For each point, the Normal Radius is used to select nearby points for calculating the normal vector. All points
within the Keypoint Radius is then used to compute the descriptor. In the middle the size of feature radius is shown, the 30
mm represent 10 % of the object size. To the right is shown a 10 mm normal radius, zoomed.
ons of the object. Feature based methods such as e.g.
SIFT (Lowe, 1999) were developed, which describe
local patches. At roughly the same time, new descrip-
tors were also developed for 3D data, e.g. the Spin
Image descriptor(Johnson and Hebert, 1999). The
Spin image is a local descriptor based on the idea of
an object-centered viewpoint. In the 2D case the lo-
cal descriptor is calculated with orientation towards
the camera, as the geometry is unknown. In the 3D
case the normal vector at the point can be calculated
and instead of using the coordinate system of the ca-
mera, a local coordinate system is found. This makes
the descriptor much more robust to both translation
and rotation in depth (Hagelskjaer et al., 2017). The
object-centered viewpoint is used for many of the fol-
lowing descriptors which have later been developed.
The Spin Image encodes the number of points that fall
into nearby spatial bins, relative to the surface point
being described. This use of relational information
has been used in many following descriptors, for in-
stance SHOT (Salti et al., 2014), FPFH (Rusu et al.,
2009), and USC (Tombari et al., 2010), to name a few.
In this work we use local shape descriptor which col-
lects four simple relations for each point in the spher-
ical neighborhood around the point to be described.
These relations are taken from the point pair feature
(PPF) (Drost et al., 2010) and rely on the computation
of surface normals, similar to the majority of other
shape descriptors available. The relations are binned
into a number of histograms, which together describe
the local shape variation. This descriptor has been
successfully used earlier for pose estimation and ob-
ject recognition tasks (Buch et al., 2017). An illus-
tration of the computation of the PPF based feature
in a scene with corresponding parameters is shown in
Fig. 3. Using training-data for pose estimation have
also been performed using deep learning (Kehl et al.,
2017; Rad and Lepetit, 2017; Do et al., 2018). These
approaches show impressive performance, but have a
number of limitations. The trained network is a com-
plex model with many parameters requiring a large
amount of well representing data. This restricts the
setup of new systems as training data needs to either
collected or generated. These methods expects the ob-
ject standing on a table and have not been tested on the
bin-picking dataset. Compared to this our approach is
based on methods only requiring a CAD model.
2.2 Optimization Strategy
In the previous section the importance of choosing
correct values for shape descriptor parameters where
highlighted. It is, therefore, necessary to explore the
parameter space and obtain an optimum configuration
according to some criterion. An exhaustive search of
the full parameter space is intractable, thus it is desi-
rable to derive a proper search strategy.
2.2.1 Optimization Algorithms
Optimization algorithms in general is a widely stu-
died subject, and a number of different methods exist.
One of the more straightforward approaches is gra-
dient descent wherein the gradient of the loss function
is used to update the parameter setting. Thus, given
a starting point, the parameters are gradually updated
until a maximum is found. This also has the advan-
tage that it can be easily specified when to terminate
the optimization. For the pose estimation problem
two difficulties for gradient descent arise. First, the
loss function cannot be expected to be either smooth
or convex. Fundamentally, the score is the number of
correct detections, which is a subset of the list of natu-
ral numbers N. The gradient of this function cannot be
expected to be non zero. As a limited number of sce-
nes are used for our purposes, the score function will
be expected to fluctuate. It is, therefore, necessary
to perform non-smooth non-convex optimization, for
which many different methods have been developed
(Rios and Sahinidis, 2013).
Bayesian Optimization of 3D Feature Parameters for 6D Pose Estimation
137

(a) Score for different para-
meters set run on the training
data.
(b) The resulting mean of the
fitted Gaussian Process.
(c) The resulting variance of
the fitted Gaussian Process.
(d) The Upper Confidence
Bound plot by combining
mean and variance.
Figure 4: Loop of a single bayesian optimization. Notice the variance is zero at each data point. The next iteration will be at
the highest point in the Upper Confidence Bound plot.
2.2.2 Bayesian Optimization
We decided to use Bayesian optimization, a method
for bounded global optimization (Snoek et al., 2012).
Bayesian optimization has been employed success-
fully for tuning machine learning parameters as well
as many other applications (Bergstra et al., 2013), and
an implementation is readily available (Snoek et al.,
2012). Bayesian optimization is also a good approach
when evaluations are expensive as is the case of pose
estimation. Benchmarking of optimization algorithms
have shown Bayesian Optimization with state-of-art
performance(Jones, 2001). Compared with other non-
gradient methods, i.e. evolutionary algorithms and
particle filters Bayesian Optimization use qualified
guesses and not random mutations and sampling and
thus requires fewer iterations.
In Bayesian optimization all previous samples are
used to fit a surrogate model and using this surro-
gate model the next sample to evaluate is selected.
A number of initial samples are made using random
uniform sampling within the bounds for the parame-
ters. The used surrogate model is a Gaussian process
(Rasmussen, 2004), a non-parametric method which
utilizes all previous samples to create the model. Ad-
ditionally, the Gaussian process also provides a pro-
bability of the prediction. The well-known Upper
Confidence Bound (UCB) is used as the acquisition
function (Snoek et al., 2012). As the name implies the
confidence bound over the current maximum is used
to select the next parameter setting to investigate. An
illustration of the a single step in the Bayesian opti-
mization can be seen in Fig. 4.
2.3 Our Approach
The pose estimation system we optimize is based on
the voting approach presented in (Buch et al., 2017).
This algorithm is freely available online
1
and direct
comparison can be performed with existing results.
1
https:://www.gitlab.com/caro-sdu/covis
We decide to optimize the size of the feature radius
and the normal radius, as these parameters are fun-
damental to all feature matching algorithms and are
easily understood. The goal of our approach is to find
the parameter set which gives the best performance
for pose estimation. For the datasets used in this work,
recall and maximum F1-score were used (Hinterstois-
ser et al., 2012; Tejani et al., 2014) to evaluate perfor-
mance of a recognition system. Recall is defined as
the number of correct detections found from the full
dataset. A detection is defined as correct if the transla-
tion distance is less than 50 mm and the angular error
for the Z-axis is less than 15
◦
. F1-score is defined as a
combination of both recall and precision, where preci-
sion is the number of correct detections to the number
of returned detections.
2.3.1 Scoring the Detections
To optimize for stable detections, we utilize the score
given from the detection algorithm to create a new
score for the optimization system. We split the sco-
res given by the system into correct (true positives,
TPs) and wrong detections (false positives, FPs), thus
getting respectively KDE
T P
and KDE
FP
. The KDE
is the output kernel density score for a pose pro-
vided by the underlying pose voting method (Buch
et al., 2017) used for the estimation, but any scoring
function could in principle be used here. We then use
the TP/FP ratio as the score, as seen in (1), penalizing
has high scores for wrong detections and rewarding
high scores for correct detections. The score function
is log-transformed for numerical reasons, as this leads
to more stable performance when invoking the opti-
mization algorithm.
score(KDE)
=
(
log(
∑
KDE
T P
∑
KDE
FP
), if
∑
KDE
T P
≥
∑
KDE
FP
0, otherwise
(1)
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
138

Figure 5: Result of fitting a Gaussian process to the samples from the Bayesian optimization. The best parameter set is then
found by the maximum position of the resulting fit.
2.3.2 Gaussian Process Regression for Mode
Finding
As only a small training set is used, there is a risk
of overfitting the parameters to only the particular set
of training scenes seen during training. To decrease
the risk of wrong parameters we additionally employ
a Gaussian Process to regress over the finished set of
evaluations, which is then used to predict the best pa-
rameter set in a more smooth and robust manner.
Other approaches have also been made to
avoid overfitting Bayesian optimization techniques to
sparse training sets. In (Dai Nguyen et al., 2017) a
term is added to the acquisition function which pe-
nalizes sharp peaks. In our approach we focus on ex-
ploration, but use the classical Bayesian optimization,
and then fit all explored points with a Gaussian Pro-
cess to determine a stable maximum. The number of
explored points, n, can be described as the matrix con-
sisting of the parameters X and the resulting score y.
X, y = {(x
i
, f (x
i
) ) | i = 1, ..., n} (2)
To predict the expected score at new parameter va-
lues with a Gaussian Process, a distribution is requi-
red. Here ˆx is denoting a new untested parameter set.
y
ˆx
∼
K K
T
ˆx
K
ˆx
K
ˆx ˆx
(3)
Where K is a covariance matrix given by a se-
lected kernel, k(x
1
, x
2
), wherein each index is calcu-
lated by the relationship of two parameter sets. This
gives that K
nxn
, K
nx1
and K
ˆx ˆx
. We are now able to
find the expected value of the new parameter set by
the mean and the uncertainty as the variance (Ebden,
2008).
E( ˆx) = K
ˆx
K
−1
y (4)
var( ˆx) = K
ˆx ˆx
− K
ˆx
K
−1
K
T
ˆx
(5)
To make the Gaussian process more stable to
noise, a second term is added to the covariance
function, compared with the Bayesian Optimization
(Snoek et al., 2012), giving a Matern-kernel and a
White Noise kernel, as shown in (6). Here the ker-
nel function K takes distance d as input, combining
the Matern covariance C
ν
and a diagonal noise term
N.
K(d) = C
ν
(d) + N(d) (6)
Γ and J denote the gamma function and the Bessel
function, respectively. The white noise (8) adds the
uncertainties in the evaluation as the full dataset is not
used. An illustration of a 2D regression can be seen
in Fig. 5, representing the scores for parameters sets
trained the training images shown in Fig. 6.
C
ν
(d) = σ
2
+
2
1−ν
Γ(ν)
√
2ν
d
ρ
ν
J
ν
√
2ν
d
ρ
(7)
N(d) =
(
σ, if d = 0
0, otherwise
(8)
This kernel is used create the covariance matrices,
but before the prediction can be calculated, parame-
ters for (7) and (8) needs to be determined. A minimi-
zation using (Byrd et al., 1995) is performed that fits
the parameter values to the known score y while fix-
ing the ν value, i.e. how much distant points interact
with predicted result. This is to ensure a more smooth
prediction of parameters. With these values the kernel
can be calculated and a more robust function for the
expected parameter space can be created.
Using the training data and the scoring system the
parameter space is explored using Bayesian optimi-
zation and a number of samples are collected. These
samples are then used to fit a Gaussian process as seen
in (6) from which a maximum parameter set is found.
Bayesian Optimization of 3D Feature Parameters for 6D Pose Estimation
139
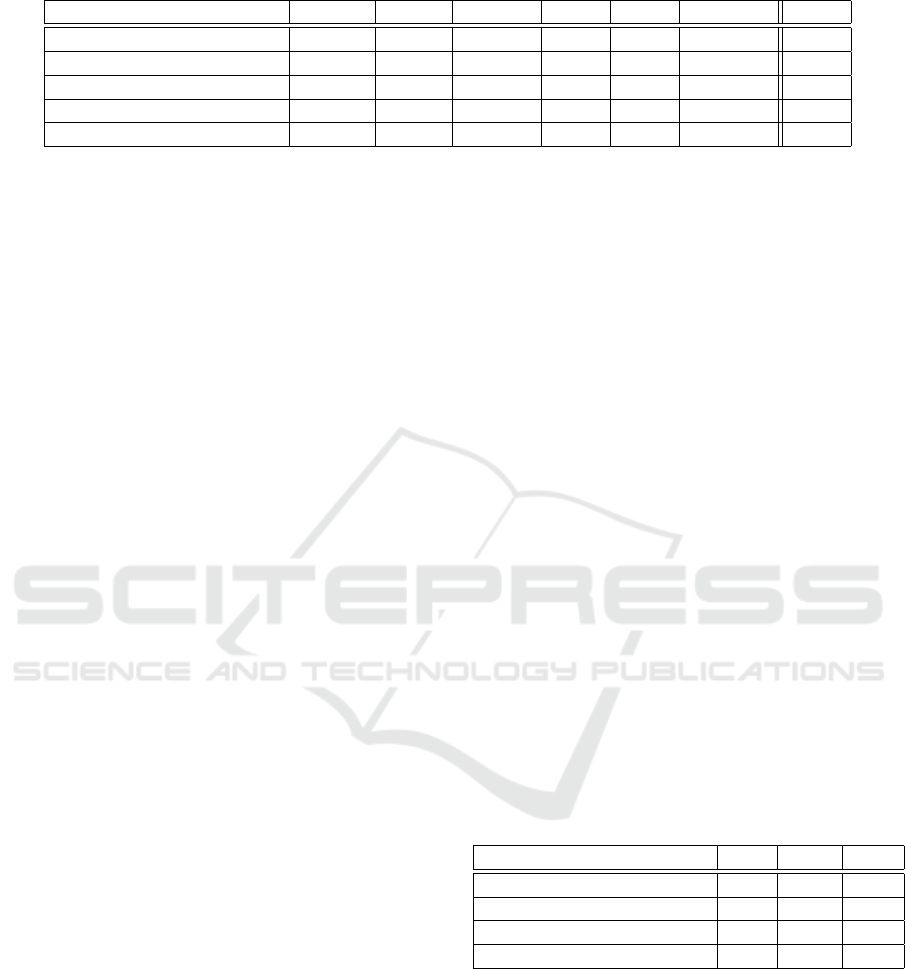
Table 1: Results for the tabletop dataset (Tejani et al., 2014). All results are given as F1 scores.
Method Camera Coffee Joystick Juice Milk Shampoo Avg
(Doumanoglou et al., 2016) 0.903 0.932 0.924 0.819 0.510 0.735 0.803
(Kehl et al., 2017) 0.603 0.991 0.937 0.977 0.954 0.859 0.856
(Li and Hashimoto, 2018) 0.741 0.983 0.997 0.919 0.780 0.999 0.910
Org (Buch et al., 2017) 0.711 0.993 0.973 0.975 0.776 0.709 0.856
Ours 0.853 0.999 0.994 0.973 0.859 0.796 0.912
3 EXPERIMENTS
We ran extensive evaluations on two commonly used
RGB-D based object recognition datasets. The first
dataset of Tejani et al. (Tejani et al., 2014) contains
six tabletop sequences for multi-instance pose estima-
tion (see Fig. 1 for an example). The scenes contain
large amounts of cluttering and background structu-
res. The second dataset of Doumanoglou et al. (Dou-
manoglou et al., 2016) contains two objects (a coffee
cup and a juice box) and three test sequences, all sho-
wing multiple instances of the objects in a bin. There
is a dedicated sequence per object and a mixed se-
quence, where both objects appear in the bin.
3.1 Selection of Training Images
The tested datasets unfortunately do not have training
scenes, which required us to take some out for trai-
ning. In (Brachmann et al., 2016) a scheme for se-
lecting training data in already existing datasets have
been proposed. This scheme has been reused in a
number of papers (Rad and Lepetit, 2017; Tekin et al.,
2018). This approach samples the full range of poses
in the dataset by adding all images that deviate more
than 15 degrees from images already in the training
set. An example of the difference between each trai-
ning image is shown in Fig. 6. As this would cover
33 percent of the dataset for the bin picking dataset a
different approach is chosen in this article.
From each dataset, we collected eight random sce-
nes for training, considerable less than the more than
100 used in (Brachmann et al., 2016; Rad and Lepetit,
2017; Tekin et al., 2018).
For our optimization, ten initial parameter sam-
ples drawn uniformly in space and 25 subsequent ite-
rations were made using Bayesian optimization with
our KDE scoring. Lastly the Gaussian process regres-
sion model was fitted and a maximum was calculated.
A specific example can be seen in Fig. 1, where our
method enable successful recognition of all three in-
stances of a model in a scene from the tabletop data-
set.
3.2 Results
Comparison was done with the original pose voting
method (Buch et al., 2017) and for the tabletop data-
set we included the current state of the art (Doumano-
glou et al., 2016; Li and Hashimoto, 2018) from the
literature. Compared with the original pose voting al-
gorithm, we obtain a 7% increase in performance on
the tabletop scenes on average (second column from
the right). Interestingly, our optimization also allows
the pose voting method to surpass state of the art on
this dataset. For completeness, we have additionally
included a rightmost column where we do not include
the eight training scenes in the testing to show that
this causes a marginal difference in results.
For the bin picking dataset (Doumanoglou et al.,
2016) no current method seems to outperform (Buch
et al., 2017), we decided to include two other known
methods to show not only compare with the original
approach. The results can be seen in Tab. 2. Here we
substantially outperform the baseline on average, but
perform slightly worse on the coffee cup. We believe
this is because the performance on this object close to
saturated already, with the chosen parameters.
Table 2: Results for bin picking dataset (Doumanoglou
et al., 2016). All results are given as recall rates, as per
the protocol for this dataset.
Method Coff Juice Avg.
(Tejani et al., 2014) 31.4 24.8 28.1
(Doumanoglou et al., 2016) 36.1 29.0 32.6
Org (Buch et al., 2017) 63.8 44.9 54.4
Ours 63.4 51.7 57.6
3.3 Sensitivity to the Number of
Training Images
We also wanted to test the ability of our method to
generalize to the test set using a varying number of
training scenes. This experiment was performed on
the bin picking dataset. It is clear from Fig. 7 that the
number of scenes is important for the resulting per-
formance. As the number of scenes increases, so does
the performance in general, although eight scenes in
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
140
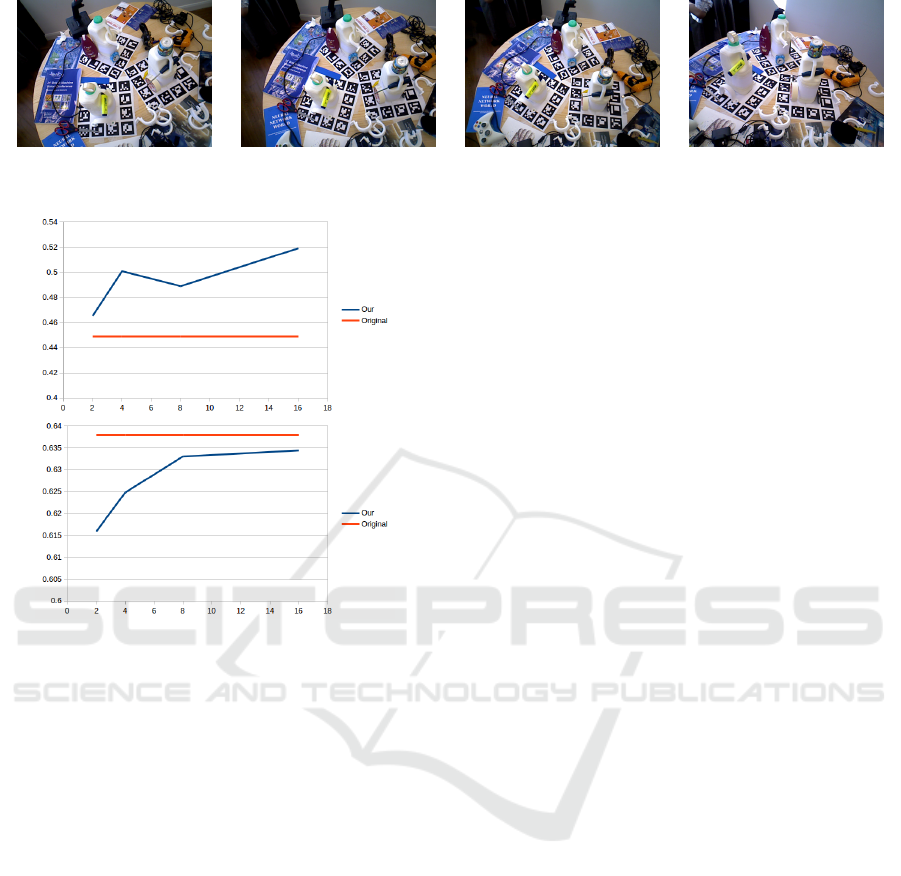
Figure 6: Sequence of the first four images used for the training of object ”05” of the Tejani dataset. There is atleast a 15
degree angle between each object.
Figure 7: Results of fitting a Gaussian process to increasing
training set sizes from the bin picking dataset. To the left
is shown the result of varying the number of training scenes
for the juice, and to the right the same for the coffee cup.
the juice dataset gives a drop. This is likely from an
unfortunate random sample of a subset of scenes that
do not properly represent the full data. For the coffee
cup dataset the performance is slightly increasing as
more samples are added, although it is still not able
to outperform the original. A 1 dimensional grid se-
arch was performed on the full dataset which shows
that the original performance is actually at the best
possible and all our found parameter sets are circling
around this performance.
4 CONCLUSIONS
In this work we have demonstrated the feasibility
of using Bayesian optimization in combination with
Gaussian Process regression for automatically deter-
mining optimal parameters for an existing 3D shape
descriptor based object recognition and pose estima-
tion system. Our method is useful for bounded global
optimization within a chosen parameter space that is
crucial to the performance of the method that is to
be tuned. We have demonstrated our approach on a
recent pose estimation algorithm, optimizing two of
the most important hyper-parameters for the descrip-
tor calculation process.
Our method is able to significantly improve the
performance on the chosen pose estimation algorithm,
providing improved results compared to state the art
algorithms on two RGB-D datasets. We see our met-
hod as more generally applicable for optimization of
many other parameters than the two descriptor pa-
rameters used in this work. We will pursue this di-
rection for future work.
ACKNOWLEDGEMENTS
This work has been supported by the H2020 project
ReconCell (H2020-FoF-680431).
REFERENCES
Bergstra, J., Yamins, D., and Cox, D. D. (2013). Making
a science of model search: Hyperparameter optimiza-
tion in hundreds of dimensions for vision architectu-
res. Journal of Machine Learning Research.
Brachmann, E., Michel, F., Krull, A., Ying Yang, M., Gum-
hold, S., et al. (2016). Uncertainty-driven 6d pose esti-
mation of objects and scenes from a single rgb image.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, pages 3364–3372.
Buch, A. G., Kiforenko, L., and Kraft, D. (2017). Rota-
tional subgroup voting and pose clustering for robust
3d object recognition. In International Conference on
Computer Vision (ICCV).
Byrd, R. H., Lu, P., Nocedal, J., and Zhu, C. (1995). A
limited memory algorithm for bound constrained op-
timization. SIAM Journal on Scientific Computing,
16(5):1190–1208.
Dai Nguyen, T., Gupta, S., Rana, S., and Venkatesh, S.
(2017). Stable bayesian optimization. In Pacific-Asia
Conference on Knowledge Discovery and Data Mi-
ning, pages 578–591.
Do, T.-T., Cai, M., Pham, T., and Reid, I. (2018). Deep-
6dpose: Recovering 6d object pose from a single rgb
image. arXiv preprint arXiv:1802.10367.
Bayesian Optimization of 3D Feature Parameters for 6D Pose Estimation
141

Doumanoglou, A., Kouskouridas, R., Malassiotis, S., and
Kim, T.-K. (2016). Recovering 6d object pose and
predicting next-best-view in the crowd. In Internati-
onal Conference on Computer Vision and Pattern Re-
cognition (CVPR), pages 3583–3592.
Drost, B., Ulrich, M., Navab, N., and Ilic, S. (2010). Model
globally, match locally: Efficient and robust 3d object
recognition. In International Conference on Computer
Vision and Pattern Recognition (CVPR), pages 998–
1005.
Ebden, M. (2008). Gaussian processes for regression: A
quick introduction. the website of robotics research
group in department on engineering science. Univer-
sity of Oxford: Oxford.
Guo, Y., Bennamoun, M., Sohel, F., Lu, M., and Wan,
J. (2014). 3d object recognition in cluttered scenes
with local surface features: a survey. IEEE Transacti-
ons on Pattern Analysis and Machine Intelligence,
36(11):2270–2287.
Guo, Y., Bennamoun, M., Sohel, F., Lu, M., Wan, J., and
Kwok, N. M. (2016). A comprehensive performance
evaluation of 3d local feature descriptors. Internatio-
nal Journal of Computer Vision, 116(1):66–89.
Hagelskjaer, F., Buch, A. G., et al. (2017). A novel 2.5 d
feature descriptor compensating for depth rotation. In
International conference on Computer Vision Theory
and Applications (VISAPP).
Hagelskjær, F., Kr
¨
uger, N., and Buch, A. G. (2017). Does
vision work well enough for industry? International
conference on Computer Vision Theory and Applica-
tions (VISAPP).
Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski,
G., Konolige, K., and Navab, N. (2012). Model based
training, detection and pose estimation of texture-less
3d objects in heavily cluttered scenes. In Asian confe-
rence on computer vision (ACCV), pages 548–562.
Johnson, A. E. and Hebert, M. (1999). Using spin images
for efficient object recognition in cluttered 3d scenes.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 21(5):433–449.
Jones, D. R. (2001). A taxonomy of global optimization
methods based on response surfaces. Journal of global
optimization, 21(4):345–383.
Jørgensen, T. B., Iversen, T. M., Lindvig, A. P., and Kr
¨
uger,
N. (2018). Simulation-based optimization of camera
placement in the context of industrial pose estimation.
In International conference on Computer Vision The-
ory and Applications (VISAPP).
Kehl, W., Manhardt, F., Tombari, F., Ilic, S., and Navab, N.
(2017). Ssd-6d: Making rgb-based 3d detection and
6d pose estimation great again. In Proceedings of the
International Conference on Computer Vision (ICCV
2017), Venice, Italy, pages 22–29.
Li, M. and Hashimoto, K. (2018). Accurate object pose
estimation using depth only. Sensors, 18(4):1045.
Lowe, D. G. (1999). Object recognition from local scale-
invariant features. In International conference on
Computer Vision (ICCV), volume 2, pages 1150–
1157.
Oshima, M. and Shirai, Y. (1983). Object recognition using
three-dimensional information. IEEE Transactions on
Pattern Analysis and Machine Intelligence, (4):353–
361.
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017). Pointnet:
Deep learning on point sets for 3d classification and
segmentation. International Conference on Computer
Vision and Pattern Recognition (CVPR), 1(2):4.
Rad, M. and Lepetit, V. (2017). Bb8: A scalable, accu-
rate, robust to partial occlusion method for predicting
the 3d poses of challenging objects without using
depth. In International Conference on Computer Vi-
sion (ICCV).
Rasmussen, C. E. (2004). Gaussian processes in machine
learning. In Advanced lectures on machine learning,
pages 63–71. Springer.
Rios, L. M. and Sahinidis, N. V. (2013). Derivative-free op-
timization: a review of algorithms and comparison of
software implementations. Journal of Global Optimi-
zation, 56(3):1247–1293.
Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast point
feature histograms (fpfh) for 3d registration. In In-
ternational Conference on Robotics and Automation
(ICRA), pages 3212–3217.
Salti, S., Tombari, F., and Di Stefano, L. (2014). Shot: Uni-
que signatures of histograms for surface and texture
description. Computer Vision and Image Understan-
ding, 125:251–264.
Snoek, J., Larochelle, H., and Adams, R. P. (2012). Practi-
cal bayesian optimization of machine learning algo-
rithms. In Advances in Neural Information Processing
Systems (NIPS), pages 2951–2959.
Tejani, A., Tang, D., Kouskouridas, R., and Kim, T.-K.
(2014). Latent-class hough forests for 3d object de-
tection and pose estimation. In European Conference
on Computer Vision (ECCV), pages 462–477.
Tekin, B., Sinha, S. N., and Fua, P. (2018). Real time se-
amless single shot 6d object pose prediction. In Inter-
national Conference on Computer Vision and Pattern
Recognition (CVPR).
Tombari, F., Salti, S., and Di Stefano, L. (2010). Unique
shape context for 3d data description. In Proceedings
of the ACM workshop on 3D object retrieval, pages
57–62.
Zhang, Z. (2012). Microsoft kinect sensor and its effect.
IEEE multimedia, 19(2):4–10.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
142
