
Robust Fitting of Geometric Primitives on LiDAR Data
Tekla T
´
oth and Levente Hajder
Department of Algorithm and Applications, E
¨
otv
¨
os Lor
´
and University,
Pazmany Peter stny. 1/C, Budapest 1117, Hungary
Keywords:
Surface Fitting, Geometric Primitives, Light Detection and Ranging, Robust Fitting.
Abstract:
This paper deals with robust surface fitting on spatial points measured by a LiDAR device. The point clouds
contain hundreds of thousands data points. Therefore, the time demand of the algorithms is crucial for fast
operation. We present two novel algorithms based on the RANSAC method: one for plane detection and
one for other object detection. The execution time of the novel algorithms is significantly lower as only one
random sampling is required because a deterministic teqnique selects the other data points. The accuracy of
the novel methods are validated on synthesized data as well as real indoor and outdoor measurements.
1 INTRODUCTION
3D vision (Hartley and Zisserman, 2003) is one of
the most challenging research topic of computer sci-
ence. There are many different sensors for machine
perception systems that can produce accurate spatial
data from our 3D world. Vision applications are usu-
ally based on digital cameras. However, other sensors
become popular recently.
The aim of this paper is to show that LiDAR
(Light Detection And Ranging) technology can be ef-
fectively used for 3D object detection. It is a survey-
ing method that measures distance to a target by illu-
minating the target with pulsed laser light and measur-
ing the reflected pulses with a sensor. Differences in
laser return times and wavelengths can then be used to
create digital 3-D representations of the target. (Defi-
nition of LiDAR is from Wikipedia (TM)).
It is demonstrated in this paper that the accuracy
of a LiDAR scans is enough to detect geometric prim-
itives such as planes, spheres and cylinders. The for-
mer and the latter ones are especially important ob-
jects as they usually appear in real-world scenes: the
ground and the walls of the buildings are planes, and
advertising columns and lamp posts form cylinders.
The challenge of 3D object fitting algorithms is
that LiDAR devices can scan only one side of the
object, because more than half of the objects are oc-
cluded.
1.1 Related Work
Fitting geometric primitives on LiDAR point clouds is
a relatively new research topic. The main idea here is
to adapt efficient fitting methods to point clouds taken
by LiDAR devices.
This paper deals with the fitting of planes, spheres
and cylinders. The latter two tasks are more challeng-
ing as only part of the object can be measured due to
self-occlusion. Plane fitting seems to be significantly
simpler, but this task can be speeded up if specialties
of urban scenes are considered.
Plane Fitting. LiDAR technology has become
popular for the last decade although the price of the
devices are quite high. To the best of our knowledge,
the first solved task using LiDAR was the plane
fitting (Tsai et al., 2010) which is a long-time
researched problem in 3D geometry with efficient
solutions (Pratt, 1987; Eberly, c; Eberly, b). Detected
planes can be used for several purposes, e.g. motion
registration (Grant et al., 2013) or reconstruction of
buildings via roof detection (Awrangjeb and Fraser,
2014).
Sphere Fitting. Although spheres are relatively sim-
ple geometric objects that can be reconstructed effi-
ciently (Eberly, c), the detection of spheres on Li-
DAR data is not frequently addressed, maybe because
spheres do not usually appear in urban environment.
However, (Pereira et al., 2016) showed that spheres
are very useful for registering different point clouds,
taken by LiDAR devices, into a common system.
622
Tóth, T. and Hajder, L.
Robust Fitting of Geometric Primitives on LiDAR Data.
DOI: 10.5220/0007572606220629
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 622-629
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Cylinder Fitting. Cylinder fitting (Eberly, a) is more
challenging than reconstruction of spheres, neverthe-
less, advertising columns often appear in large cities,
therefore cylinder fitting is a realistic problem for
machine perception. To the best of our knowledge,
cylinder fitting is addressed only on laser scanned
data (Nurunnabi and andoderik Lindenbergh, 2017).
In this paper, we show how planes, spheres, and
cylinders can be reconstructed from LiDAR point
clouds. The main challenge of these problems is that
only part of the observed object is visible due to self-
occlusion. The contributions of our paper are as fol-
lows: (i) a novel modification of RANSAC algorithm
is introduced for robust plane fitting; another similar
modification is applied for sphere and cylinder fitting.
(ii) The appendix contains basic and precise geomet-
ric methods for plane, sphere and cylinder fitting that
can yield accurate object parameters even if the meth-
ods are supported by LiDAR data; (iii) The efficiency
of the methods are validated both on synthesized and
real data-world data.
2 PROPOSED METHODS
In this section, we introduce novel robust fitting meth-
ods. Development issues are also discussed here.
2.1 Robust Model Estimation
Our shape detection is based on RANSAC (Fischler
and Bolles, 1981) (RAndom SAmpling Consensus)
algorithm. RANSAC is a method which fits a model
from randomly sampled subset of an observed dataset.
It works with arbitrary model. For line fitting, the
basic steps of the RANSAC algorithm is visualized in
Figure 1. These are as follows:
1. Randomly select a subset from the original
dataset. Usually, the size of the subset is the min-
imal one. For example, two/three points are se-
lected for line/plane fitting.
2. Model is fitted to the selected subset.
3. Classification of all the points of the dataset to
inliers/outliers based on an error function. For
line/fitting, a point is an inlier if it is closer to the
line/plane than a given threshold. It is a disadvan-
tage of the method that this threshold is usually
given empirically. The set of inliers is called con-
sensus set..
4. The estimated model is accepted if the consensus
set is large enough.
5. Modification of the accepted model by refitting it
from the inliers.
(a) Step 1 (b) Step 2 (c) Step 3 (d) Step 4-
5
(e) Step 6
Figure 1: Illustration of RANSAC algorithm for line fitting.
The titles of the subfigures denote the steps of the algorithm.
6. Repeat steps 1-5 several times. Repetition number
can be calculated if outlier ratio is approximately
known. If we reach one or more successfully fitted
results, the model with the largest consensus set is
chosen.
RANSAC is a reliable method. However, for
multi-model fitting it is not a viable solution as the
number of iterations is extremely high if only a small
portion of the data points belong to an object. Table 1
shows the required number of iterations. Remark that
at least three data points are necessary for plane and
cylinder fitting, while spheres require more than that.
If only five percent of the dataset corresponds to
a plane, more than 36.000 iterations are required to
obtain good result with 99% probability. It is very
time-consuming even if GPU is applied for the com-
putation.
2.1.1 Plane Detection
The original algorithm can be parallelized to make it
faster, but there are several properties in case of Li-
DAR point clouds which can improve the algorithm.
Our modified RANSAC algorithm of plane detection
is based on two observations.
Observation 1. The planes in urban environment are
principally the ground or the walls of the buildings,
hence they contain a huge amount of points, up to half
of the whole cloud. Therefore, one can reduce the
search time with sampling, and we can construct a
more focused detection algorithm.
Table 1: Number of iterations required for original
RANSAC (Fischler and Bolles, 1981) algorithm if confi-
dence is set to 99%. N denotes the number of sample points.
Both plane and cylinder fitting requires at least 3 points. For
sphere fitting, the minimum number is 4. Columns are vary-
ing w.r.t. outlier ratio from 50% to 95%. It is well seen that
N = 1 case is drastically faster than the others.
N 50% 65% 80% 90% 95%
1 7 11 20 44 90
3 35 106 573 4602 ∼ 10
4
4 72 305 2875 ∼ 10
4
∼ 10
5
Observation 2. The normal vectors of the planes are
usually either vertical or horizontal. With minimal
Robust Fitting of Geometric Primitives on LiDAR Data
623

Figure 2: Synthetic point generation and the planes along
the synthetic directions, yielding sets Ω
x
(green), Ω
y
(blue),
Ω
z
(red).
rotation can be reached that the planes are parallel to
two of the three coordinate axes.
Instead of taking a subset of sampling points, we
choose only one point P = (p
x
, p
y
, p
z
) of the origi-
nal set. Four synthetic points are calculated along the
three planes perpendicular to the axes of the coordi-
nate system with a given t distance in the following
way, yielding point sets Ω
x
, Ω
x
, and Ω
z
as
Ω
x
= {(p
x
, p
y
, p
z
), (p
x
, p
y
+t, p
z
+t), (p
x
, p
y
+t, p
z
−t),
(p
x
, p
y
−t, p
z
+t), (p
x
, p
y
−t, p
z
−t)}
Ω
y
= {(p
x
, p
y
, p
z
), (p
x
+t, p
y
, p
z
+t), (p
x
+t, p
y
, p
z
−t),
(p
x
−t, p
y
, p
z
+t), (p
x
−t, p
y
, p
z
−t)}
Ω
z
= {(p
x
, p
y
, p
z
), (p
x
+t, p
y
+t, p
z
), (p
x
+t, p
y
−t, p
z
),
(p
x
−t, p
y
−t, p
z
), (p
x
−t, p
y
−t, p
z
)}.
(1)
This calculation is illustrated in Figure 2. Assume
that the red, green and blue colors denote axes X, Y
and Z. In the figure, the coordinates of point P is
(0, 0, 2), and the distance threshold parameter is set
to t = 2. The synthetic points of Ω
x
, Ω
y
and Ω
z
are
the middle point of the edges: there are four green,
four blue and four red points.
The input points of the plane fitting algorithm are
the closest real points in the pointcloud to the syn-
thetic points. Point P is unchanged, but the other four
points are replaced for the closest one in the whole
pointcloud. We evaluate the minimal needed distance
from P during the tests. Furthermore, if the plane
searching parameter is t, the algorithm can detect the
planes, rectangles with area least t
2
.
After searching the closest real points, one can fit
the planes to Ω
x
, Ω
y
and Ω
z
sets. Thus the three prin-
cipal planes, drawn by red, blue, and green in the fig-
ure, are separately processed, they obtain three differ-
ent candidate planes. Then the consensus set of all the
planes is collected similarly to the original RANSAC
algorithm.
2.1.2 Sphere and Cylinder Detection
In case of a sphere or a cylinder, we can use a sim-
ilarly modified RANSAC algorithm. However, the
result depends on more parameters. After plane de-
tection, the remaining surfaces are built from partly
Figure 3: Estimation of the sphere center. Each candidate
point pair of the sphere determines a plane. The sphere cen-
ter is the intersections of these planes.
covered but continuous pointsets and they are easily
separable in space. Hence the search to find the can-
didate spherical and cylindrical objects can run in par-
allel. The algorithm randomly chooses a single point
and takes the closest points within a predefined dis-
tance. The inliers are the points with neighboring
point which Euclidean distance is smaller than a given
threshold parameter t. When the pointset contains less
then k points, it is discarded. k are set in an empirical
way, see the test section for our setting. Then the sur-
face fitting is carried out on the selected points, yield-
ing a candidate model. The further steps are similar
to the original RANSAC. The final model contains the
most inliers.
2.2 Surface Fitting Methods
The main goal is to detect planes, spheres and cylin-
ders from noise point clouds, therefore very effective
and robust fitting algorithms are needed. We suggest
efficient fitting methods, the suggested algorithms are
written in the Appendix in detail. However, in case of
the LiDAR data, we have to modify the algorithms,
because of the special properties of the LiDAR point
clouds. The following two subsection introduce our
new methods for sphere and cylinder fitting.
Estimation of the Center of a Sphere. A good es-
timation for the center of the sphere is the average of
the sample points, as it is discussed in the appendix if
the surface of the sphere is uniformly sampled. How-
ever, this is a bad approximation in case of LiDAR
data where only one segment of the sphere is known,
because this solution needs too many iterations.
We implemented our method based on a geomet-
rical approach, which is visualized in Figure 3. The
center of the sphere can be estimated from the equa-
tions of its four points. Bisecting plane of two points
contains the center itself, and the intersection of three
bisecting planes is a good estimation for the center.
To our experience, 10 points are enough to select
because synthetic tests showed that it is an accurate
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
624

Figure 4: Hemisphere of the possible directions of the cylin-
der. The initial step evaluates the errors at the purple points.
Pink points denote the directions after bisecting the initial
intervals.
estimation, and more points yield increased computa-
tion time. Hence when there is a larger input pointset,
one can get a good estimation using 10 randomly cho-
sen points. After this, the fixpoint-iteration gives the
local optimal solution.
Estimation of the Direction of the Cylinder. To
estimate the direction of the cylinder axis, we repre-
sent vector W with a two dimensional parameter. Vec-
tor W with spherical coordinates is given by Equation
4. The original method, written in the appendix, finds
this vector by exhaustive search. It splits the interval
of the two parameters into 1024 and 512 equal parts.
This gives a very accurate result because of the fine
sampling.
However, most of the calculations are unneces-
sary. To reach the same result, an incremental approx-
imation is applied, yielding significantly less time de-
mand. Figure 4 shows the initial step of the method,
where the hemisphere represents the set of the possi-
ble unit length directional vectors. At first, we cal-
culate the fitting error in the nine directions denoted
by the purple points, which are obtained by the equal
partitioning of the intervals of θ
0
and θ
1
into 4 and 3
parts, respectively. If the direction of minimal error
value is the labeled by point P, the optimal direction
is located within the pink part of the sphere. There-
after we iteratively bisect the intervals of θ
0
and θ
1
until the desired accuracy is reached.
3 TESTS AND RESULTS
The proposed algorithms are implemented in MAT-
LAB. The methods are tested both on synthetic and
real LiDAR datasets. The synthetic tests and indoor
data, measured by Velodyne HDL-64 and Velodyne
VLP-16-LiDAR, are made for sphere and cylinder fit-
ting, and the outdoor data is designed to fit planes and
cylinders.
Figure 5: Synthetic datapoints for cylinder (up) and sphere
fitting (down). Left: Noise added to points. Middle: Oc-
cluded points removed. Right: pointset made sparser. In the
figures, blue dots represent original pointset, green when
the noise/point removing is moderate, yellow when high
amount of noise/point removing is applied. Best viewed in
color.
3.1 Test Data
The synthetic tests contain randomly generated points
of a plane, sphere or cylinder with given parameters.
The results were observed in the presence of growing
noise, occlusion and the number of the sample points.
The real tests are indoor and outdoor LiDAR mea-
surements. The difficulty is, that the HDL-64 data is
very noisy, and the outdoor data is only available with
this device, which was equipped on a car. The in-
door tests were made in a room with exact test objects,
however, the scene were fully continuous against the
street tests.
3.2 Synthetic Tests
In order to quantitatively test the robust fitting meth-
ods, synthetic test sequences are generated. The main
goal for the test generation is to simulate the real mea-
surement. For this reason, three parameters can be
changed in our environment:
1. Noise. LiDAR technology has been improved
for the last decade, yielding more accurate mea-
surements. The precision of Velodyne HDL-64
is approximately 100 mm, that of VLP-16 is a
bit smaller. Remark that Velodyne VLP-16 is the
newer technology.
2. Occlusion. Normally, 3D scanning by a LiDAR
device can measure only one side of an object due
to self-occlusion. This effect can also be simu-
lated in our testing environment.
Robust Fitting of Geometric Primitives on LiDAR Data
625
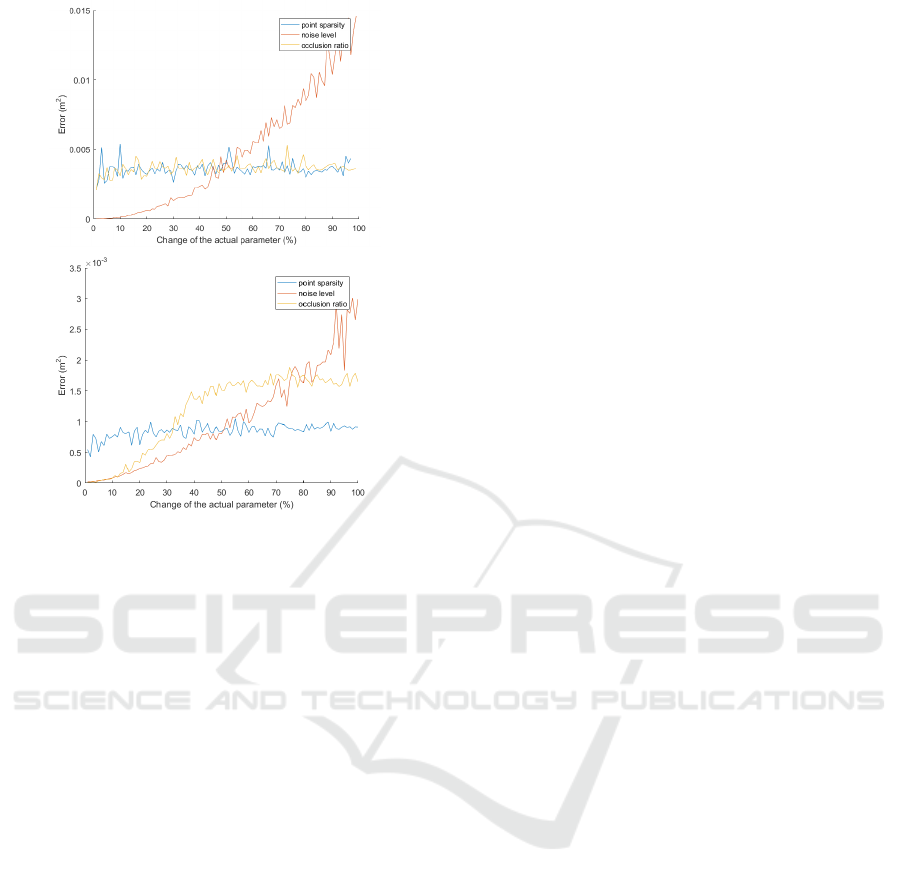
Figure 6: Error of sphere (top) and cylinder (bottom) fit-
ting. Data are synthetically generated. Red, yellow, and
blue curves are noise level, occlusion ratio, and point spar-
sity, respectively. Vertical axis shows the fitting error. Best
viewed in color.
3. Density of the Point Cloud. For real measure-
ment, density is determined by the applied LiDAR
device. It mainly depends on the number of the
beams. E.g. Velodyne HDL-64 and VLP-16 have
64, and 16 beams, the point cloud measured by
the former one is significantly denser.
For the synthesized tests, a sphere with 0.375 m
radius, and a cylinder with 1.3 m height and 0.35 m
radius are generated. The fitting of the two objects are
separately tested. The objects are translated in order
to make them viewable from the location of the syn-
thesized LiDAR. The object is rotated as well, how-
ever, it does not influence the sphere fitting as spheres
are rotational symmetric.
Then noise is added to all the points in order to
simulate the measurement noise of the LiDAR tech-
nique. Finally, points are removed to simulate self-
occlusion and measurement by sparse devices. The
synthesized spheres and cylinders are visualized in
Figure 5.
Test results are plotted in Figure 6. The three
different test types are visualized in the same chart.
They are distinguished by different colors.
The tests show that the fitting quality is principally
based on noise in both cases as the error increases
monotonically. The influence of the self-occlusion is
not significant, but the sparsity of the point cloud af-
fects the results of the cylinder. These tests are run
100 times because of the random parameters, and the
same results are obtained.
As it is expected, the error is increasing in all test
cases: it is evident that noise, self-occlusion and point
removal make a fitting less accurate.
3.3 Real Indoor Tests
The fitting methods are tested on point clouds taken
in both indoor and outdoor environment. The indoor
tests are discussed first. Some examples for sphere
and cylinder fitting are shown in Figure 7 and 8.
An important task of the experiments is to tune
the free parameters of the algorithms on real datasets.
In case of plane detection, it is observed that if the
distance between the real point and the one generated
by the proposed method is less or equal than 5 cm,
the result becomes inaccurate. Furthermore, the op-
timal value of t is between 0.3 and 0.5 m, hence the
algorithm detects planes with dimensions greater than
[0.6×0.6]−[1.0 ×1.0]m. The plane detector requires
some trade-offs near the line where two planes cut
each oder. The first time detected plane contains all
points inside the threshold t from both planes. So if t
is higher, the fitting is very inaccurate, but if t is lower,
many good points are lost. For practical reasons, we
implemented a re-selection of the points near these
cutting lines.
The improved RANSAC needs less iterations, be-
cause it has to select only a single point from a plane,
the other four points are generated synthetically. If
we run the algorithms with the same iteration num-
ber, the modified algorithm selects the greatest plane
more times, so we get more accurate result.
The parameter t is set to 0.4 m in case of sphere
and cylinder fitting, because real tests contains cylin-
ders with 1 − 2 m height. The minimal number of
points (k) is 15, because it approaches the expected
fitting. Moreover, the improved sphere fitting algo-
rithm needs one fifth of the iterations to reach the
same sphere parameters as the original method.
3.4 Real Outdoor Tests
Outdoor tests are taken to test the plane and cylin-
der fitting algorithm. There are many planes in urban
environment: the ground, building walls, side of vehi-
cles, etc. Cylinders also appear near the roads: adver-
tising columns can be modeled as regular cylinders.
Unfortunately, sphere testing is missing in the case
of outdoor testing as regular spheres do not appear in
cities to the best of our knowledge.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
626

Figure 7: Fitted spheres. Point clouds in the left two
columns were taken by Velodyne HDL-64, right columns
by VLP-16. Red and blue dots visualize the measured and
fitted data, respectively. The self-occlusion is the highest in
the middle column.
Figure 8: Fitted cylinders. Point clouds in the right two
columns were taken by Velodyne HDL-64, left columns by
16. Red and blue dots visualize the measured and fitted
data, respectively. The self-occlusion is the highest in the
middle.
Figure 9 shows an example for plane fitting. The
point cloud is taken in a crossroads where five verti-
cal walls around the measuring device. All of them
are successfully segmented. They are plotted by dif-
ferent colors in the figure. Table 2 consists of the time
demand, in seconds, of the original RANSAC and our
modified algorithm on this test scenario.
There are challenges even for plane fitting: disad-
vantage of noisy points is demonstrated in Figure 10,
where the points of the same plane form different
quasi-parallel planes because of the mirroring of the
widows. It seems to impossible to filter out these
planes, because they really create false planes in the
pointcloud. The obtained plane parameters of this ex-
ample are shown in Table 3.
Geometrically, advertising columns or lamp posts
are cylinders. However, the number of the points cor-
responding to this objects are not too high. Real ex-
amples for cylinder fitting is visualized in Figure 11,
the obtained parameters are listed in Table 4.
Table 2: Time demand of the plane detectors. T
original
and
T
proposed
denote the original RANSAC and the proposed
algorithm. Test results are visualized in Figure 9. Tests
were run 1000-times and average values are listed.
color N T
original
T
proposed
1. green 52857 16.434 17.945
2. yellow 4904 10.323 9.675
3. red 2239 8.932 7.830
4. light blue 2101 7.525 7.333
5. dark blue 1866 7.292 6.752
6. magenta 1518 7.043 6.425
7. orange 1344 6.992 6.182
(a) Outdoor measurement
(b) Real environment
Figure 9: The figure shows the similarity between the fitted
planes to an outdoor measurement, and the map of the real
environment. Best viewed in color.
4 CONCLUSION
The paper proposes novel fitting algorithms which
can reconstruct sphere, cylinder and plane. The goal
was to detect and reconstruct the given objects in a
sparse pointcloud.
The fitting algorithms are efficient and fast. The
RANSAC algorithm is modified to get fewer itera-
tion, decreasing the time demand. This modification
is based on some special properties of the sparse point
cloud taken of urban environments.
The methods are tested on synthetic point clouds,
varying the amount of noise, the number of the points
and the self-occlusion. Real indoor and outdoor test
results are also presented, the advantages and limits
of the algorithms are discussed.
Robust Fitting of Geometric Primitives on LiDAR Data
627

Table 3: Parameters of the detected planes in Figure 10. N denotes the number of points for which the plane fitting is carried
out. Vectors P
0
and n denote a point of the plane, and the plane normal. Five out of the six plane are quasi parallel, the blue
one is perpendicular to the others.
color N P
0
n
1. green 31 743 (1.881, 0.999, -0.191) (-0.098, -0.995, 0,013)
2. magenta 10 328 (-2.486, 0.998, -1.071) (-0.059, -0.959, 0.055)
3. purple 9007 (-1.394, 0.996, 0.7974) (-0.235, -0.961, -0.148)
4. rose 4076 (-2.203, 0.989, -1.2377) (0.021, -0.940, 0.340)
5. blue 5698 (0.459, -0.041, 5.0901) (0.893, -0.449, 0.013)
6. orange 2428 (-2.086, 0.976, -0.572) (-0.143, 0.867, 0.478)
Table 4: Parameters of the detected cylinders in Figure 11. N denotes the number of the points of a cylinder. Vectors C and
W denote a point of the axis and the direction of the axis. r and h are the radius and the height value of the cylinder, finally,
E denotes the fitting error given in Euclidean distance.
N C W r h E
1. 660 (5.560, 0.029, -0.432) (0.000,0.000, 1.000) 0.127 2.257 0.001
2. 782 (6.203, 7.609, -0.174) (-0.024,0.074, 0.996) 0.559 2.464 0.002
3. 263 (6.687, 16.955, 0.340) (0.000,0.078, 0.996) 0.487 2.352 0.006
Figure 10: Fitted planes of an outdoor test in case of high
noise because of mirroring.
Figure 11: Fitted cylinders of some outdoor measurements.
ACKNOWLEDGEMENTS
EFOP-3.6.3-VEKOP-16-2017-00001: Talent Man-
agement in Autonomous Vehicle Control Technolo-
gies – The Project is supported by the Hungarian
Government and co-financed by the European Social
Fund.
REFERENCES
Awrangjeb, M. and Fraser, C. S. (2014). Automatic seg-
mentation of raw LIDAR data for extraction of build-
ing roofs. Remote Sensing, 6(5):3716–3751.
Bj
¨
orck,
˚
A. (1996). Numerical Methods for Least Squares
Problems. Siam.
Eberly, D. Fitting 3D Data with a Cylinder. http://
www.geometrictools.com/Documentation/Cylinder
Fitting.pdf. Online; accessed at 5th November 2018.
Eberly, D. Least Squares Fitting of Segments by Line or
Plane. https://www.geometrictools.com/Documentati
on/FitSegmentsByLineOrPlane.pdf. Online; accessed
at 5th November 2018.
Eberly, D. Least Squares Fitting on Data. http://www.geo
metrictools.com/Documentation/LeastSquaresFitt
ing.pdf. Online; accessed at 5th November 2018.
Fischler, M. and Bolles, R. (1981). RANdom SAmpling
Consensus: a paradigm for model fitting with appli-
cation to image analysis and automated cartography.
Commun. Assoc. Comp. Mach., 24:358–367.
Grant, W. S., Voorhies, R., and Itti, L. (2013). Finding
planes in lidar point clouds for real-time registration.
In International Conference on Intelligent Robots and
Systems, pages 4347–4354.
Hartley, R. and Zisserman, A. (2003). Multiple view geom-
etry in computer vision. Cambridge University Press.
Nurunnabi, A. and andoderik Lindenbergh, Y. S. (2017).
Robust cylinder fitting in three-dimensional point
cloud dara. In The International Archives of the Pho-
togrammetry, Remote Sensing and Spatial Informa-
tion Sciences, pages 63–70.
Pereira, M., Silva, D., Santos, V. M. F., and Dias, P. (2016).
Self calibration of multiple lidars and cameras on au-
tonomous vehicles. Robotics and Autonomous Sys-
tems, 83:326–337.
Pratt, V. (1987). Direct Least-squares Fitting of Algebraic
Surfaces. In Proceedings of the 14th Annual Con-
ference on Computer Graphics and Interactive Tech-
niques, SIGGRAPH ’87, pages 145–152.
Tsai, A., Hsu, C., Hong, I.-C., and Liu, W.-K. (2010). Plane
and boundary extraction from lidar data using cluster-
ing and convex hull projection. In IAPRS, pages 175–
179.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
628

APPENDIX
Plane Fitting. The implicit form of a 3D plane is
usually given as
a b c d
x y z 1
T
= 0.
It can be written as P
T
X = X
T
P = 0 in short,
where P =
a b c d
T
and X =
x y z 1
T
con-
tain the plane parameters and the point coordinates
in homogeneous form. If the plane is represented
by a point P
0
and normal n, then the implicit form
is written as n
T
ˆ
X − P
0
= 0, where
ˆ
X =
x y z
T
.
The two plane representations are equivalent if
P =
n
T
−
n
T
P
0
T
and X =
ˆ
X 1
.
Plane fitting algorithms usually find the plane that
is the closest one to the points. It can be carried out
by minimizing the algebraic error: if a point set {P
i
},
i = {1, 2, . . . , N} is given, the cost function to be min-
imized becomes
∑
N
i=1
X
T
i
P
2
.
This is equivalent to minimize the square of the
norm of the matrix-vector product AP:
k
AP
k
2
2
, where
A =
X
T
1
X
T
2
. . . X
T
N
T
. It is well-known (Bj
¨
orck,
1996) that the optimal solution for this problem is
that P is the eigenvector of matrix A
T
A corresponding
to the smallest eigenvalue if the length of the vector,
consisting of the plane parameters, is one: P
T
P = 1.
Sphere Fitting. We have tried several sphere fitting
algorithms on LiDAR point clouds, it was found that
the method of (Eberly, c) is the most efficient one for
this purpose, based on our experiences.
The equation of a general sphere is written
as (x − a)
2
+ (y − b)
2
+ (z − c)
2
= r
2
, where
C = [a b c]
T
is the center, and r the radius of the
sphere.
The sphere fitting algorithm is based on min-
imizing squared error, where the error is defined
as the difference between the estimated and real
distance from a surface point to the center of
the sphere: E(a, b, c, r) =
∑
N
i=1
(l
i
− r)
2
,where l
i
=
p
(x
i
− a)
2
+ (y
i
− b)
2
+ (z
i
− c)
2
is the length of the
radius to the i-th point (x
i
, y
i
, z
i
).
The partial derivates of E with respect to r, a, b
and c must be equal to zero at the minima. This leads
to the following equations:
a =
1
N
N
∑
i=1
x
i
+
1
N
N
∑
i=1
r
a − x
i
l
i
, b =
1
N
N
∑
i=1
y
i
+
1
N
N
∑
i=1
r
b − y
i
l
i
,
c =
1
N
N
∑
i=1
z
i
+
1
N
N
∑
i=1
r
c − z
i
l
i
, r =
1
N
N
∑
i=1
l
i
.
(2)
If one substitutes r into the last three equations,
the center coordinates of the sphere can be estimated
by fixpoint-iteration. The offset value is the average
of the points. The four optimization steps are run one
after the other until convergence.
Cylinder Fitting. We suggest to apply the method
of (Eberly, a) for cylinder fitting.
A cylinder can be represented by a point C of the
middle axis, and a direction, represented by unit vec-
tor W, of the axis, and radius r. Furthermore, it can be
defined two more unit vectors U and V, which form in
conjunction with W a right-handed orthonormal co-
ordinate system. A surface point X of the cylinder
can be written as X = C + kU + uV + vW = C + RY,
where R =
U V W
T
is a rotation matrix and
Y =
k u v
T
contains the coordinates of the point in
the cylindric coordinate system.
When the distance between the axis and the sur-
face point X
i
is denoted by r
i
, similar to the sphere,
the error function becomes: E(r
2
, C, W) =
∑
N
i=1
(r
2
i
−
r
2
)
2
,where r
2
i
= u
2
i
+ v
2
i
is the distance of the point to
the cylinder axis. The approximation of the radius is
the average of the estimated radius lengths from the
input surface points: r =
1
N
∑
N
i=1
r
i
.
The axis point can be calculated by an iteration,
where there is an offset value of the point, e.g. the
mean of the input points, and every iteration replace
the old value C for C + αU + βV. The α and β coef-
ficients are obtained by the solution of the following
expression:
N
∑
i=1
u
2
i
u
i
v
i
u
i
v
i
v
2
i
α
β
=
1
2
N
∑
i=1
(u
2
i
+ v
2
i
)u
i
(u
2
i
+ v
2
i
)v
i
, (3)
which is an inhomogeneous system of linear equa-
tions. Althought the solution seems to depend on U
and V, it can be justified that the axis point can be
expressed with the X
i
input points and only the W
direction vector, because of U, V and W form an or-
thonormal system by definition. Hence, the direction
vector has to be approximated before the axis point.
The direction vector itself can be written by two
parameters θ
0
and θ
1
:
W = (cos θ
0
sinθ
1
, sin θ
0
sinθ
1
, cos θ
1
)
θ
0
∈ [0,2π) θ
1
∈ [0,
π
2
] w
z
(θ
0
, θ
1
) ≥ 0.
(4)
An exhaustive search finds the optimal parameters
in our approach minimizing the cost function defined
in Equation 4.
Robust Fitting of Geometric Primitives on LiDAR Data
629
