Acceleration Data Structures for Ray Tracing on Mobile Devices

Nuno Sousa

, David Sena

, Nikolaos Papadopoulos

and Jo

ao Pereira

Instituto Superior T

ecnico/Inesc-ID, Universidade de Lisboa, Lisboa, Portugal

Samsung R&D UK, Staines, U.K.

Keywords:

Ray Tracing, Acceleration Structures, Mobile Environment, Android, OpenGL ES.

Abstract:

Mobile devices are continuously becoming more efﬁcient at performing computationally expensive tasks,

such as ray tracing. A lot of research effort has been put into using acceleration data structures to minimize

the computational cost of ray tracing and optimize the use of GPU resources. However, with the vast majority

of research focusing on desktop GPUs, there is a lack of data regarding how such optimizations scale on

mobile architectures where there are a different set of challenges and limitations. Our work bridges the gap

by providing a performance analysis of not only ray tracing as a whole, but also of different data structures

and techniques. We implemented and proﬁled the performance of multiple acceleration data structures across

different instrumentation tools using a set of representative test scenes. Our investigation concludes that a

hybrid rendering approach is more suitable for current mobile environments, with greater performance beneﬁts

observed when using data structures that focus on reducing memory bandwidth and ALU usage.

1 INTRODUCTION

The hardware of mobile devices has improved signif-

icantly over the past few years. There are, however,

limitations, and developers are always searching for

optimizations that allow them to make the best use of

available hardware. Nevertheless, today a mobile de-

vice is capable of rendering graphically intensive ap-

plications with reasonable quality and performance.

Ray tracing is a rendering technique capable of

producing highly realistic results at higher computa-

tional cost than rasterization based approaches. With

the release of technologies like DirectX Raytracing

(DXR), native support for hardware accelerated ray

tracing is starting to become more accessible to an

end user.

The high computational cost of ray tracing can be

reduced with the use of acceleration data structures,

a topic that has been primarily researched for desktop

computers. Our main objective is to present a compar-

ative study of the performance of these data structures

on mobile platforms and document their characteris-

tics.

2 PREVIOUS WORK

The idea of using ray shooting for the generation of

images was ﬁrst introduced by (Appel, 1968). Sev-

eral other techniques have since been developed that

provide much higher visual ﬁdelity by simulating vi-

sual effects like reﬂections (Whitted, 1979), soft shad-

ows (Cook et al., 1984), depth-of-ﬁeld (Cook et al.,

1984) and even global illumination (Kajiya, 1986).

This, however, is outside the scope of our work. The

focus of this research is the performance of accelera-

tion data structures and not the visual ﬁdelity achieved

with different ray tracing techniques.

2.1 Acceleration Data Structures

Acceleration data structures can be used to reduce the

number of ray-primitive intersection tests. An accel-

eration data structure algorithm transforms scene data

to a format that minimizes the number of intersection

tests at runtime and optimizes the use of hardware.

For our research we focused on the traversal per-

formance of KD-Trees and Bounding Volume Hier-

archy (BVH). Both structures make use of Surface

Area Heuristic (SAH) (Goldsmith and Salmon, 1987)

to determine the best splitting point for each node that

is being subdivided.

332

Sousa, N., Sena, D., Papadopoulos, N. and Pereira, J.

Acceleration Data Structures for Ray Tracing on Mobile Devices.

DOI: 10.5220/0007575403320339

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 332-339

ISBN: 978-989-758-354-4

2.1.1 Bounding Volume Hierarchies

Bounding Volume Hierarchies are based on bound-

ing volumes (Kay and Kajiya, 1986). A BVH is a

tree in which the root consists of a bounding volume

that encloses the whole scene. Each internal node is

a bounding volume of a subset of objects of its par-

ent node. The leaves contain actual geometry to test

against.

The BVH can be subdivided, for example, by us-

ing the median of the centroids of the enclosed objects

or by using SAH.

In this work we chose to focus on the following

traversal algorithms:

• Stack-less Parent-Link Traversal - a link-based al-

gorithm that tries to provide the same traversal

order of the stack based algorithm while being

stack-less (Hapala et al., 2011).

• Restart Trail Traversal - This algorithm tries to

adapt the KD-restart algorithm used to traverse

KD-trees, to be used with Bounding Volume Hi-

erarchies (BVHs) (Laine, 2010).

2.1.2 KD-Trees

First introduced as a method for searching of points

in a k-dimensional space (Bentley, 1975), KD-trees

are a speciﬁc case of binary space partitioning Binary

Space Partitioning (BSP).

Just like BVHs spatial subdivision can be based

on SAH. An optimised O(NlogN) construction algo-

rithm introduced by (Wald and Havran, 2006) which

used an ordered event list with special list splitting

rules.

Our work focused on Graphics Processing Unit

(GPU) based algorithms (Hapala and Havran, 2011),

more speciﬁcally:

• Kd-Push-Down Traversal - this algorithm expands

Kd-Restart (Horn et al., 2007), which works by

moving a point along the ray and ﬁnding the leaf

where the point is located. By keeping the low-

est depth-wise node that contains the interval of

intersection in its entirety, this node can then be

used instead of the root node when restarting the

search.

• Kd-Backtrack Traversal - this algorithm adds to

each node the corresponding bounding box and a

pointer to the parent node (Foley and Sugerman,

2005) to avoid restarting the search from the root

node.

2.2 Mobile Environment

The system on chip architectures of mobile devices

have restrictions on the amount of power they can

draw and, due to the small form factor, the amount

of heat they are able to dissipate. As a result, com-

putational resources are more limited than on desktop

computers.

3 IMPLEMENTATION

This research focuses on mobile environments, run-

ning Android, and was conducted in partnership with

Samsung UK. The following sections will describe

how the application was implemented, which ray trac-

ing algorithms were used as well as which data struc-

tures were implemented. We also describe the differ-

ent rendering approaches used.

3.1 Ray Tracing Implementation

We implemented Whitted ray tracing (Whitted, 1979)

with a ray spawned for each pixel of the framebuffer

and a subsequent ray spawned for each light visibility

query when an intersection is found. We implemented

the ray-triangle intersection algorithm by (M

oller and

Trumbore, 2005) and for Axis Aligned Bounding Box

(AABB) ray intersections we used the ray-box inter-

section algorithm by (Williams et al., 2005).

We implemented different data packing arrange-

ments of primitives using Shader Storage Buffer Ob-

ject (SSBO). Our initial approach was to store

each triangle vertex and each normal as a vec3 with

padding. In our second approach we used the padding

of the three vertices to store the ﬁrst normal and min-

imize the size per primitive. Our last approach was

based on the fact that, while doing intersection test-

ing, normals are not used. We split the vertices and

normals into separate SSBOs to reduce redundant

memory accesses.

3.2 Implementation of Acceleration

Data Structures

For the GPU rendering methods we chose to imple-

ment only KD-Trees and BVHs instead of Regular

Grids because they are consistently outperformed by

BVHs and KD-Trees apart from very speciﬁc situa-

tions (Thrane and Simonsen, 2005).

Acceleration Data Structures for Ray Tracing on Mobile Devices

333

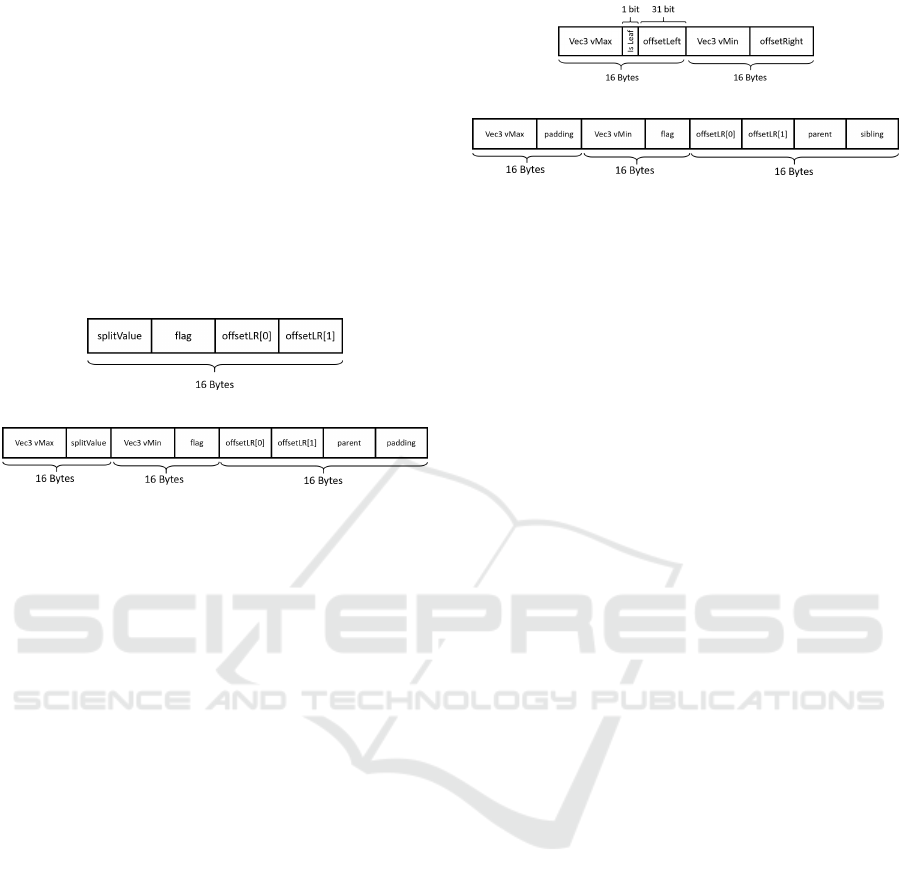
3.2.1 KD-Tree Implementation

The construction of KD-Trees in our implementation

is done using the SAH algorithm (Wald and Havran,

2006). Our implementation allows for the creation

of empty leaf nodes but does not perform triangle

clipping. By experimenting with different values for

traversal

and C

intersection

, we concluded that mobile ar-

chitectures tend to favour wider and shallower trees.

We found a value of 3.0 for C

traversal

and 1.5 for

intersection

to yield good results.

The memory layout for KD-Tree nodes varies ac-

cording to which traversal algorithm is being used.

(a) KD-Pushdown node layout

(b) KD-Backtrack node layout

Figure 1: Layouts of KD-Tree nodes. vMin and vMax rep-

resent the node bounding box.

Another difference between trees for the two

traversal methods is that while building the tree for the

KD-Backtrack traversal method, we do not allow for

perfectly ﬂat nodes, i.e. nodes that have zero length

on one of the axis. This is done to avoid precision

related issues while traversing the tree. We imple-

mented the KD-Pushdown and KD-Backtrack algo-

rithms using the node layouts shown in Figure 1.

3.2.2 BVH Implementation

In our implementation, the construction of BVHs is

done using an altered version of the construction algo-

rithm (Wald and Havran, 2006) that was also used in

the KD-Trees construction. Like with KD-Trees, af-

ter experimenting with several values, we came to the

conclusion that, again, wider, shallower trees tend to

perform best. As such, the values chosen for C

traversal

and C

intersection

were, again, 3.0 and 1.5 respectively.

The memory layout for BVH nodes also varies ac-

cording to which traversal method is being used. The

possible layouts are shown in Figure 2.

For GPU traversal we implemented Trail traversal

along with the Parent-Link traversal algorithm.

3.3 GPU Rendering Methods

Our implementation used multiple rendering ap-

proaches. Regardless of the rendering method cho-

(a) BVH Trail traversal node layout

(b) BVH Parent traversal node layout

Figure 2: Layout of BVH nodes. vMin and vMax represent

the node bounding box.

sen, our implementation starts by constructing the se-

lected acceleration structure along with the auxiliary

structures for primitive storage. These structures are

then copied to GPU memory as Shader Storage Buffer

Objects (SSBOs). The application also creates and

uploads a Vertex Array Object (VAO) containing a

full-screen quad that is then used for every render-

ing method. The drawing process, however, changes

according to which rendering approach is selected:

• Fragment Shaders - the application renders a full-

screen quad using a very simple vertex shader.

The fragment shader is then responsible for ray

tracing the corresponding pixel. In this case, all

the code for ray tracing and structure traversal is

contained in the fragment shader.

• Compute Shaders - the application performs a two

step process. In the ﬁrst step, the application

dispatches the necessary compute workgroups so

that each thread processes a pixel of the ﬁnal im-

age. The result of this ﬁrst step is stored in an

Image Buffer which is then utilized in the second

step as an input texture. The second pass simply

draws a full-screen quad, using the texture gener-

ated in the ﬁrst step.

• Hybrid Shading - the application, not only cre-

ates a VAO containing the full-screen quad, but

also a second VAO containing the entire geom-

etry for the scene being rendered. This second

VAO is used in the ﬁrst phase of the rendering pro-

cess, where the application issues a drawcall that

rasterizes all primitives. This ﬁrst phase stores

the calculated normals into a color attachment.

From this ﬁrst step a depth buffer is also gener-

ated. These two buffers are then used on the sec-

ond phase of the drawing process where the full-

screen quad is rendered. The values in the buffers

are used to create and cast the shadow ray which

then triggers a structure traversal. For this ren-

dering method, all the ray tracing logic is in the

fragment shader of the second pass.

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

334

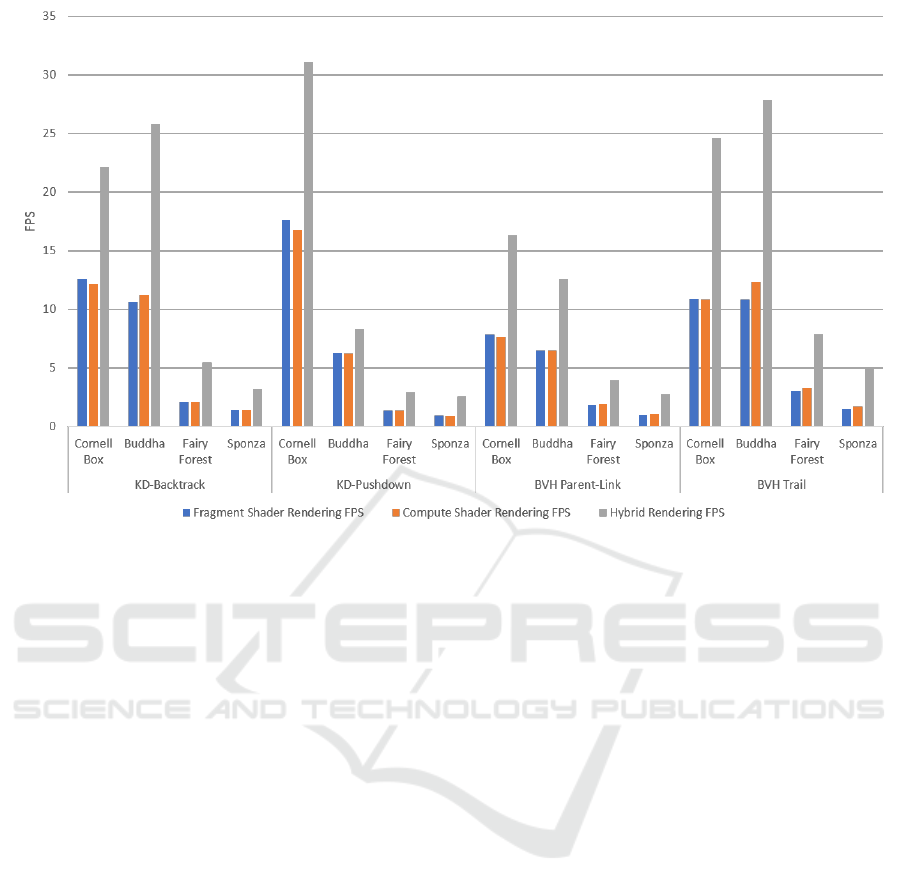
Figure 3: Graph comparing the performance of different rendering methods.

4 EVALUATION

To evaluate the performance of the different algo-

rithms, we proﬁled our implementation by collect-

ing metrics in app and using external instrumentation

tools.

The application was developed using OpenGL ES

and tested on a Samsung Galaxy S8 (Model SM-

G950U) with a 64 bit Qualcomm Snapdragon 835

system-on-chip with a Qualcomm Adreno 540 GPU

provided by Samsung Research, UK.

4.1 Application Metrics

At the rendering stage, several measurements are col-

lected in order to evaluate overall performance:

• Framerate - How many times the image is updated

per second. Frametime expressed in milliseconds,

while more accurate, is harder to measure on mo-

bile due to hardware and architectural restrictions.

• Rays per Second - expressed in millions of rays

per second. Rays-per-Second (RPS) more accu-

rately describes the raw ray tracing power of the

underlying hardware.

• Structure Size - expressed in KBytes. Repre-

sents the overall size of the generated acceleration

structure.

The application allows to visualize a heatmap rep-

resenting the number of node traversals for each pixel.

As an effort to keep results consistent, we consider

that a node is traversed when it is fetched from the

acceleration structure SSBO.

4.2 External Tools

The Qualcomm Snapdragon Proﬁler allows develop-

ers to proﬁle devices with Snapdragon processors.

The application provides several metrics of interest to

our work:

• SP Memory Read - Number of bytes read from

memory by the Shader Processors per second.

• % Shader ALU Capacity Utilized - % of maxi-

mum shader ALU capacity that is being utilized.

• % Time ALUs Working - % of time the ALUs are

working while the shaders are busy.

• ALU/Fragment - Average number of ALU in-

structions performed per fragment.

4.3 Test Scenes and Test Methodology

For our tests we used a number of different scenes

such as the Cornell Box, the Cornell Buddha, the

Fairy Forest and the Crytek Sponza.

Acceleration Data Structures for Ray Tracing on Mobile Devices

335

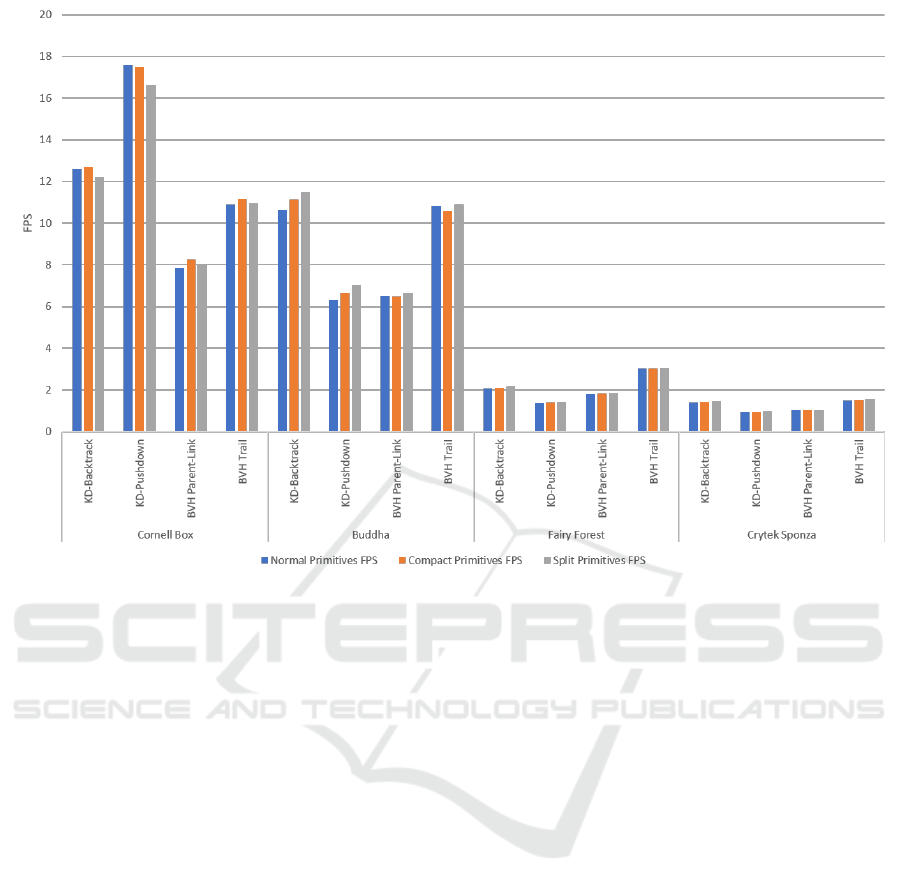
Figure 4: Graph showing performance for different primitive layouts.

The application always renders the resulting im-

age at 1024x1024 resolution. We also restart the ap-

plication between every test.

5 RENDERING TECHNIQUES

COMPARISON

We implemented three different rendering ap-

proaches, and for each approach we proﬁled the per-

formance of different traversal methods across differ-

ent scenes. While Fragment and Compute rendering

had similar performance, as shown in Figure 3, the

hybrid rendering approach distinguished itself by hav-

ing better performance. This is due to the higher com-

putational cost of ray tracing when compared with

rasterization.

Overall, our results show that using hybrid ren-

dering is the best approach when implementing ray

tracing on mobile. However, different ray tracing al-

gorithms may beneﬁt from using Fragment and Com-

pute Shader based rendering.

6 PRIMITIVE LAYOUT

COMPARISON

As shown in Figure 4, we ran a series of tests to anal-

yse the performance of the different primitive layouts.

Results show that a compact layout does not always

equate to better performance as it needs a few extra

instructions to retrieve the stored normal. The split

layout on the other hand, consistently yields either

similar or better results.

To better understand the impact of these changes

when accessing memory, we performed a bandwidth

analysis using the Cornell Box and Buddha scenes.

The results are shown in Figures 5 and 6.

The results show that there is a reduction in mem-

ory bandwidth from using the compact and split lay-

outs, with split layout producing the best results. Hav-

ing vertices and normals separated means that no

bandwidth is wasted on normals that are not being

used. This maximizes the number of vertices fetched

each time which means the number of overall fetches

is reduced.

Scenes with higher complexity require more ac-

cesses to the data structures containing the geometry

and thus, optimization of primitive layout becomes

more important because of the impact in memory

bandwidth utilization.

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

336

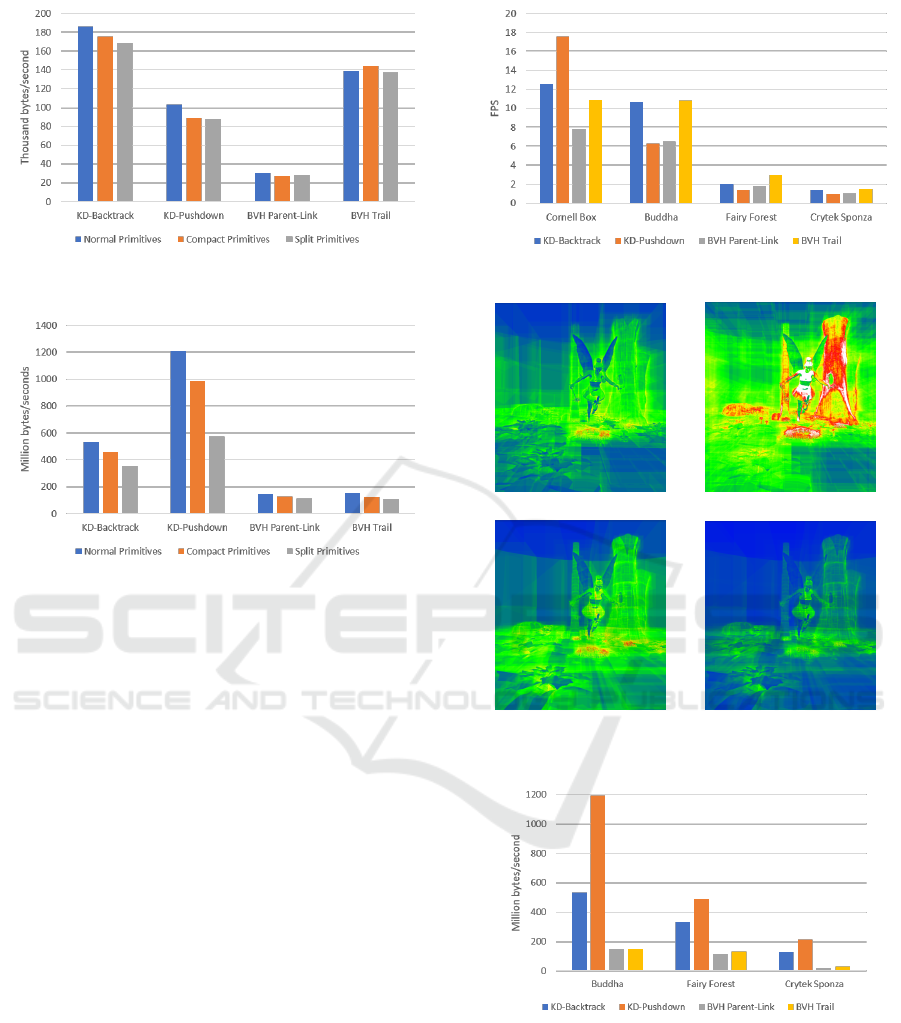
Figure 5: Memory bandwidth usage when varying primitive

layout for the Cornell Box Scene.

Figure 6: Memory bandwidth usage when varying primitive

layout for the Buddha Scene.

7 ACCELERATION DATA

STRUCTURE COMPARISON

Acceleration data structures are essential for the efﬁ-

ciency of ray tracing algorithms and as such have an

impact on performance. In the following sections we

will present and discuss the results we obtained with

regards to computation cost and memory utilization.

7.1 Performance

To evaluate the performance of the different data

structures, we conducted a series of tests for the

traversal methods we chose across different scenes.

For these particular tests we only used the Fragment

Shader renderer along with a normal primitive layout.

Figure 7 shows the results obtained from all

the test runs. Whilst the performance of the KD-

Pushdown traversal excels in scenes with a lower

number of primitives, it quickly deteriorates in scenes

with higher geometric complexity. In contrast, BVH

Trail traversal performs better in more complex

scenes.

To understand the performance difference be-

tween traversal methods, we created heatmaps for

Figure 7: Performance values for acceleration structures.

(a) KD-Backtrack (b) KD-Pushdown

Figure 8: Heatmap of the fairy scene for all structures.

Figure 9: SP Memory Read values for each structure. Val-

ues for the Cornell Box were not visible at this scale.

each traversal method and each scene. Figure 8 shows

a subset of the generated heatmaps.

We obtained the best results using BVH Trail.

KD-Backtrack and BVH-Parent-Link followed up,

yielding similar results to each other. This veriﬁes

our previous observations and shows that the number

of traversed nodes correlates to the performance of

Acceleration Data Structures for Ray Tracing on Mobile Devices

337

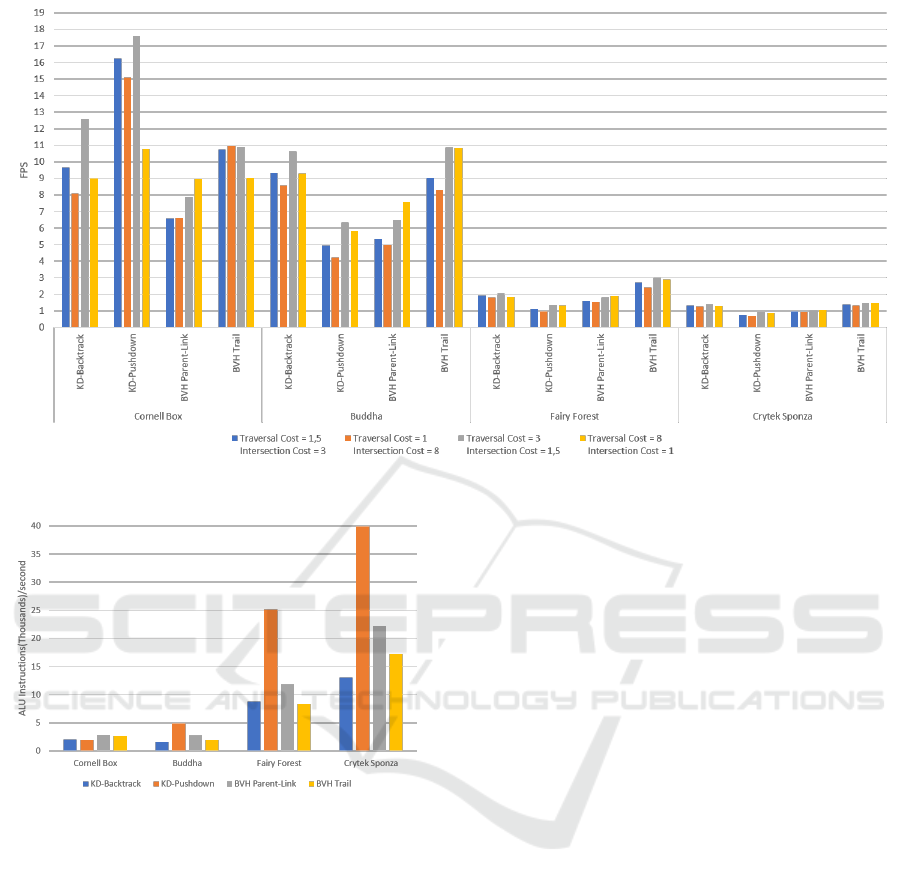
Figure 10: Performance comparison for different SAH cost values.

Figure 11: ALU instructions per fragment.

the algorithm. Due to the high cost of bandwidth, we

measure its impact. The results are shown in Figure 9.

Algorithms based on KD-Trees consume higher

memory bandwidth than those based on BVHs. One

explanation is that the increased number of nodes gen-

erated by KD-Trees boosts the probability of execut-

ing a memory fetch for each new traversed node. This

is because each local memory fetch request is less

probable to contain the next node that needs to be tra-

versed. In Figure 11 we also analyse the ALU in-

structions per fragment.

Results show that, the KD-Backtrack algorithm

requires the least overall amount of ALU instructions.

This is due to the fact that it performs no near-far clas-

siﬁcation, and, consequently, uses fewer instructions

per node traversed than other traversal methods.

On the opposite end, the traversal method with

most ALU instructions per fragment is the KD-

Pushdown due to the increased number of nodes and

extra traversal steps it takes. This, combined with

higher memory bandwidth utilization, results in the

worst performance across all the traversal methods.

Results show that traversal methods with fewer

ALU instructions per fragment have better perfor-

mance. There is however the exception of the KD-

Backtrack traversal, that despite using less ALU in-

structions has its traversal slowed down due to the

high memory bandwidth requirements.

According to these results the performance of the

traversal algorithms is limited by a combination of

ALU, memory accesses and bandwidth. However,

the strongest limitation appears to be the number of

traversed nodes, i.e. the number of accesses to the

SSBOs that contain the acceleration structure.

7.2 SAH Costs Comparison

One of the ways to optimize KD-Trees and BVHs

built using the SAH is to tweak the values for traversal

and intersection cost given to the construction func-

tion. Usually, having the intersection cost higher than

the traversal yields better results. To test this we used

four different cost values and a combination of all the

scenes and traversal methods.

As shown in Figure 10, having an intersection cost

lower than the traversal cost provides the best perfor-

mance. The results also show that it is best to keep the

traversal cost only slightly higher than the intersec-

tion cost. Reducing the cost of traversal equates to a

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

338

higher number of node traversals necessary per pixel.

The performance numbers shown in Figure 10 corrob-

orate the previous results showing that the number of

traversals correlate to the performance of the traversal

algorithm.

8 CONCLUSIONS

Our work focused on providing a performance anal-

ysis of different acceleration data structures for ray

tracing on mobile devices. Our main goal was to es-

tablish a basis for future research into the potential of

mobile environments. As for future work, we want to

explore the performance of construction methods for

dynamics scenes to provide further insight on current

mobile hardware capabilities.

ACKNOWLEDGEMENTS

This work was supported by national funds through

Fundac¸

ao para a Ci

encia e T

ecnologia (FCT) with ref-

erence UID/CEC/50021/2019.

REFERENCES

Appel, A. (1968). Some techniques for shading machine

renderings of solids. In Proceedings of the AFIPS

Conference, pages 37–45.

Bentley, J. (1975). Multidimensional binary search trees

used for associative searching. Commun. ACM,

18(9):509–517.

Cook, R., Porter, T., and Carpenter, L. (1984). Distributed

ray tracing. In Proceedings of the 11th Annual Con-

ference on Computer Graphics and Interactive Tech-

niques, pages 137–145.

Foley, T. and Sugerman, J. (2005). Kd-tree acceleration

structures for a gpu raytracer. In Proceedings of

the ACM SIGGRAPH/EUROGRAPHICS conference

on Graphics hardware, pages 15–22.

Goldsmith, J. and Salmon, J. (1987). Automatic creation

of object hierarchies for ray tracing. IEEE Comput.

Graph. Appl., 7(5):14–20.

Hapala, M., Davidovi

c, T., Wald, I., Havran, V., and

Slusallek, P. (2011). Efﬁcient Stack-less BVH Traver-

sal for Ray Tracing. In Proceedings of the 27th Spring

Conference on Computer Graphics, pages 7–12.

Hapala, M. and Havran, V. (2011). Review: Kd-tree Traver-

sal Algorithms for Ray Tracing. Computer Graphics

Forum, 30(1):199–213.

Horn, D. R., Sugerman, J., Houston, M., and Hanrahan, P.

(2007). Interactive kd tree gpu raytracing. In Proceed-

ings of the 2007 symposium on Interactive 3D graph-

ics and games, pages 167–174.

Kajiya, J. (1986). The rendering equation. In Proceedings

of the 13th Annual Conference on Computer Graphics

and Interactive Techniques, pages 143–150.

Kay, T. L. and Kajiya, J. T. (1986). Ray tracing complex

scenes. In ACM SIGGRAPH computer graphics, vol-

ume 20, pages 269–278.

Laine, S. (2010). Restart Trail For Stackless BVH Traver-

sal. In Proceedings of the Conference on High Perfor-

mance Graphics, pages 107–111.

oller, T. and Trumbore, B. (2005). Fast, minimum storage

ray/triangle intersection. In ACM SIGGRAPH 2005

Courses.

Thrane, N. and Simonsen, L. O. (2005). A comparison

of acceleration structures for gpu assisted ray tracing.

Master’s thesis.

Wald, I. and Havran, V. (2006). On building fast kd-Trees

for Ray Tracing, and on doing that in O(N log N).

In Proceedings of the IEEE Symposium on Interactive

Ray Tracing, pages 61–69.

Whitted, T. (1979). An improved illumination model for

shared display. In Proceedings of the 6th Annual Con-

ference on Computer Graphics and Interactive Tech-

niques.

Williams, A., Barrus, S., Morley, R. K., and Shirley, P.

(2005). An efﬁcient and robust ray-box intersection

algorithm. In ACM SIGGRAPH 2005 Courses.

Acceleration Data Structures for Ray Tracing on Mobile Devices

339