
Loop Grammars to Identify RNA Structural Patterns
Michela Quadrini, Emanuela Merelli and Riccardo Piergallini
School of Science and Technology, University of Camerino, Via Madonna della Carceri 9, 62032, Camerino, Italy
Keywords:
RNA Secondary Structures, Relations, Hairpins, String Pattern Matching.
Abstract:
The biological functions of an RNA molecule are largely determined by molecular configuration. Understand-
ing the link between the structure and the biological functions has been considered one of the challenges in
biology. In this study, we face the problem of identifying a given structural pattern into an RNA pseudoknot-
free secondary structure. We introduce a context-free grammar, Loop Grammar, that formalizes the primary
and secondary structure of an RNA molecule as a composition of loops. Such composition is expressed as
to concatenation or nesting of the simplest structural elements, hairpins, generated during the folding process
when a bond between two nonconsecutive nucleotides is established. Then, we formalize the concatenation
and nesting on Fatgraphs, oriented surfaces with boundary, and we define a Surface Loop Grammar, whose
algebraic expressions uniquely identify such surfaces associated with given RNA structures. The terms of
the Loop Grammar allow us to face the problems of identifying substructures considering both the primary
and secondary structures, while the strings generated by Surface Loop Grammar permit to identify a given
structural pattern in a secondary structure in terms of relations among hairpins. Both use the string pattern
matching.
1 INTRODUCTION
RNA is a single strand polymer, named primary struc-
ture, that consists of four different nucleotides, Ade-
nine (A), Guanine (G), Cytosine (C) and Uracil (U),
linked together by phosphodiester bonds, referred to
as strong bonds. RNA folds back on itself deter-
mining complex three-dimensional shapes known as
secondary and tertiary structures (Dill, 1990; Ferr
´
e-
D’Amar
´
e and Doudna, 1999). During the folding
process, each nucleotide can interact with another
one by establishing a hydrogen bond, referred to as
weak bound, mainly Watson-Crick (G-C and A-U)
and wobble (G-U) base pairs. RNA molecules play
numerous roles in cellular, and they are classified ac-
cording to the functions that perform in the cell. Main
classes of RNA are messenger RNA (mRNA), trans-
fer RNA (tRNA) and ribosomal RNA (rRNA), each
of which performs different but cooperative functions
in protein synthesis. Functional RNA families such
as tRNA and rRNA exhibit a highly conserved shape
of the secondary structure, but little sequence simi-
larity (H
¨
ochsmann et al., 2004). Therefore, it is of
great interest the possibility of comparing and iden-
tifying RNA secondary structures directly, i.e., with-
out relying on sequence similarity (Jiang et al., 2002),
while the identification of common primary and sec-
ondary structures is useful to study the consequences
of the RNA secondary structures changes in the RNA-
RNA interactions. Moreover, searching for sequence
motifs has been a powerful tool for analysis of DNA
and proteins; but this approach does not work as ef-
fectively with RNA because conserved RNA struc-
tures may have no detectable sequence similarity (Li
et al., 2008). In the literature, several approaches have
been studied over the years for finding common pat-
terns. Wang et al. proposed an algorithm for finding
the largest approximately common substructures be-
tween two trees (Wang et al., 1998). H
¨
ochsmann et
al. gives a method for finding local patterns in a tree-
representation of RNAs (H
¨
ochsmann et al., 2003).
Algorithms based on tree data structures were also
proposed in (Mauri and Pavesi, 2005). Backofen and
Sielbert introduced an approach for computing com-
mon sequential and structural patterns based on dy-
namic programming (Backofen and Siebert, 2007).
According to Waterman (Waterman and Smith,
1978), an RNA secondary structure is composed of
five basic structural elements namely hairpins, inter-
nal loops, bulges, helixes (or stacks) and multi-loops,
illustrated in Figure 3 of Section 2. Each of them,
characterized by strong and weak bonds, is a loop.
They are generated when at least one base pair is
formed. Disregarding the spatial configuration of the
302
Quadrini, M., Merelli, E. and Piergallini, R.
Loop Grammars to Identify RNA Structural Patterns.
DOI: 10.5220/0007576603020309
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 302-309
ISBN: 978-989-758-353-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
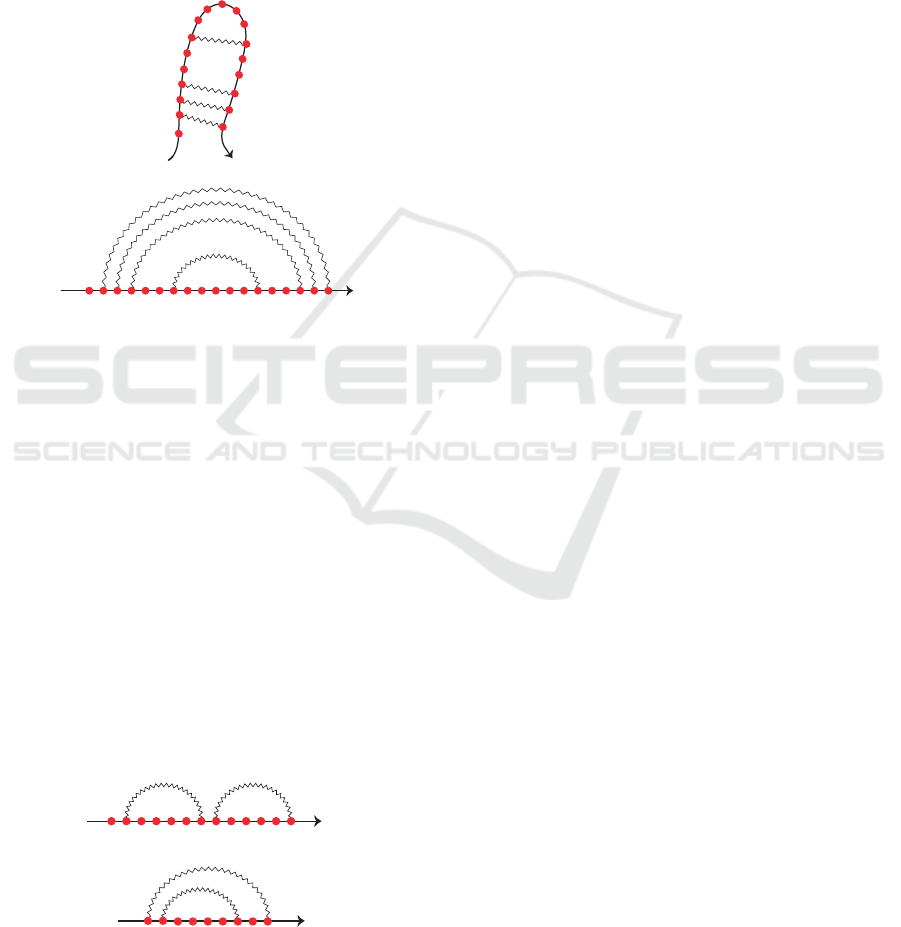
molecule and reducing nucleotides to dots, an RNA
secondary structure can be schematically represented
by a squiggle-plot representation like the one in Fig-
ure 1-A, where solid and zigzag lines represent strong
and weak bonds, respectively. Another way is the
arc diagram, where the nucleotides are represented
by vertices on a straight line (backbone) and the base
pairs are depicted by arcs in the upper half-plane, as
illustrated in Figure 1-B.
5’
3’
U G C U U C C U U ACU G A G G G
U
U
U
U
C
A
G
C
G
G
U
3’
C
U
U
C
G
U
5’
A
G
( A )
( B )
Figure 1: The secondary structure of homo sapiens miR-
516a-3p predicted by Mfold (Zuker, 2003). (A) A squiggle-
plot representation and (B) the arc diagram of the molecule
is illustrated.
Taking advantage of the arc diagram representa-
tion, it is possible to observe that given two loops
there are only two possible cases: a loop follows
the other, referred to as loop concatenation, or it is
nested into the other, referred to as loop nesting, as
shown in Figure 2, respectively. In this work, we
do not consider crossing between loops since we face
the problem of identifying structural patterns in RNA
pseudoknot-free secondary structures.
In this paper, we define a context-free grammar,
called Loop Grammar. Each term of the grammar
represents both primary and secondary structure of
an RNA molecule as a composition of loops. The
5’
5’
3’
U U C C U U ACU G A G G
3’
C U A U ACG U G
( B )
( A )
Figure 2: Concatenation and Nesting of two hairpins on top
and in the bottom, respectively.
proposed composition is expressed as concatenation
and nesting of hairpins, considered as base loops.
Both concatenation and nesting are also formalized
on surfaces. Such formalization permits to intro-
duce another grammar, called Surface Loop Gram-
mar, whose algebraic expressions uniquely identify
fatgraphs, oriented surfaces with boundary, associ-
ated with given RNA structures (Penner et al., 2010).
In other words, a string obtained by Loop Grammar
models an RNA structure, while the corresponding
term of Loop Surface Grammar identifies the surface
associated with the given structure. The terms of the
grammars allows us to identify RNA structural pattern
in terms of the strings matching, which consists of
finding all the matching strings occurrences of a pat-
tern string in other string, and string pattern matching,
that tries to find a place where one or several strings
are found within a larger string or text.
The paper is organized as follows. In Section 2,
we introduce some preliminary concepts. Firstly, the
concept of the loop and the corresponding RNA de-
composition are presented. Secondly, some mathe-
matical definitions related to RNA secondary struc-
tures and the corresponding topological concepts are
recalled. In Section 3, we introduce a context-free
grammar, Loop Grammar. In Section 4, we define
two topological operators over fatgraphs and formu-
late the Surface Loop Grammar taking advantage of
the topological operators. In Section 5, we discuss
the obtained results. The paper ends with some con-
clusions and future perspective, Section 6.
2 BASIC CONCEPTS
In this section, we introduce preliminary notions.
The concept of the loop and the corresponding
RNA decomposition are presented in Section 2.1,
whereas some mathematical representations of RNA
secondary structures and some topological concepts
are recalled in Section 2.2.
2.1 RNA Secondary Structure: Loops
as Structural Elements
Each RNA secondary structure is characterised by
strong and weak bonds. Strong bonds link two con-
secutive nucleotides, whereas weak bonds connect
two non-consecutive nucleotides. According to Wa-
terman (Waterman and Smith, 1978), each RNA sec-
ondary structure can be uniquely decomposed into
five basic structural elements, namely hairpin, inter-
nal loop, bulge, helix, and multi loop, illustrated in
Loop Grammars to Identify RNA Structural Patterns
303

( A ) ( B ) ( C )
( D ) ( E )
Figure 3: Basic structural elements of RNA secondary
structures: hairpin (A), internal loop (B), bulge (C), helix
(D), and multi-loop (E). A strong bond is depicted with a
line, a weak bond is drawn with a zigzag line and several
consecutive strong bond are represented by a dashed line.
Figure 3. Each of them is a loop made of a set of
nucleotides linked by strong and weak bonds.
A hairpin, depicted in Figure 3-A, is a loop char-
acterised by one weak bond enclosing a sequence of
nucleotides linked by strong bonds. An internal loop,
represented in Figure 3-B, is defined by two weak
bonds alternating with two non-empty sequences of
nucleotides linked by strong bonds. A bulge, shown
in Figure 3-C, is a special case of internal loop in
which one of the two sequences of nucleotides is
empty. A helix, illustrated in Figure 3-D, is also a
special case of internal loop in which both sequences
are empty. Finally, a multi-loop, depicted in Figure 3-
E, consists of more than two weak bonds separated by
non-empty sequences of nucleotides linked by strong
bonds.
2.2 Representations and Topology of
RNA Secondary Structures
An RNA secondary structure can be schematically
represented by a squiggle-plot representation like the
one in Figure 1-A, where solid and zigzag lines rep-
resent strong and weak bonds, respectively. A special
case of this representation is the arc diagram, which
is obtained from the mentioned above depicting each
vertex on a straight line and connecting two non-
consecutive vertices by an arc, which corresponds to
weak bound, in the upper half-plane.
Definition 1 (Arc Diagram). An Arc Diagram is a
labeled graph over the vertex set [`] = {1,..., `}, in
which each vertex has degree ≤ 3, and the edges are
all the segments [i, i + 1] for i = 1,... ,` −1 and some
semi-circular arcs (i, j) in the upper half-plane, with
1 ≤ i < j ≤ `.
For each arc diagram, it is possible to associate
the linear chord diagram deleting the unpaired nu-
Fattening
(A) (B)
Figure 4: (A) The linear chord diagram and (B) The fat-
graph of miR-516a-3p secondary structure molecules, illus-
tarted Figure 1-B.
cleotides, i.e. nucleotides that do no any crossing.
Definition 2 (Linear Chord Diagram). A linear chord
diagram consists of a line segment, called its back-
bones, to which are attached a number n
0
of chords
with distinct endpoints.
As an example, the linear chord diagram associ-
ated with the miR-516a-3p secondary structure illus-
trated in Figure 1-B is shown in Figure 4-A.
Each linear chord diagram admits a fattening. A
fatgraph F is a graph equipped with a cyclic order on
the edges incident on each vertex, as shown in Fig-
ure 4-B. It uniquely determines an oriented surface
with boundary. For more details regarding the con-
cept of fatgraph, interested readers can refer to (Pen-
ner et al., 2010).
3 LOOP GRAMMAR
Several context-free grammars have been proposed
in the literature. Knudsen and Hein proposed a
very simple grammar (Knudsen and Hein, 1999),
which has been implemented into the secondary struc-
ture prediction software Pfold (Knudsen and Hein,
2003). Other proposed grammars are (Dowell and
Eddy, 2004; Sakakibara et al., 1994). Each term of
these grammars is the primary structure of an RNA
molecule, while the parse tree has a natural corre-
spondence with its secondary structure. Other gram-
mars, such as RNAFeatures, are designed to explicitly
designate the different structural features (Giegerich,
2014), while others describe RNA structures in dot-
parenthesis notation such as (Anderson et al., 2012).
We introduce a context-free grammar that models the
RNA secondary structure in terms of loops. Differ-
ently from RNAFeatures, the Loop Grammar does not
explicitly identify structural components since it rep-
resents each RNA secondary structure as a composi-
tion of hairpins. As a consequence, the Loop gram-
mar is characterized by a set of 5 productions, while
Grammar RNAFeatures is defined using more of 20
rules. The Loop grammar is unambiguous and im-
poses a particular order to add a new weak bond.
Definition 3. Let Σ
RNA
= {A,U,G,C} be the
alphabet of RNA nucleotides, and let Σ
RNA
=
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
304

{(A,U),(U,A),(G,C),(C,G),(G,U), (U,G)} be the
alphabet of weak bonds, whose elements represent
pairs of nucleotides. The Loop Grammar is L
RNA
=
(V
N
,V
T
,P,S) where V
N
= {S,S
0
,H}, V
T
= Σ
RNA
∪
Σ
RNA
∪{[,]} , and the set of productions P is
S ::= ε empty structure
| S
0
non-empty structure
S
0
::= sS primary structure
| HS secondary structure
H ::= x[S
0
] base loop
where x ∈ Σ
RNA
and s ∈ Σ
RNA
.
The start symbol S formalizes empty or non-empty
RNA structure, whereas non-terminal symbol S
0
rep-
resents any RNA primary and secondary structure. A
primary structure, a sequence of unpaired nucleotides,
can be uniquely represented applying production S →
S
0
followed by S
0
→ sS. The secondary structure,
HS, is composed by a loop H followed by a struc-
ture S. Each loop H is formalized by production
H → x[S
0
], where S
0
could be both primary and sec-
ondary structure. If S
0
is a sequence of unpaired nu-
cleotides the grammar generates a hairpin, otherwise
one of the other four loops (internal loop, helix, multi-
loop, bulge) is formalized as a composition of base
loops. Note that this representation permits to nat-
urally associate the Loop Energy Model, where the
total energy E of a structure S is the sum over the en-
ergy contributions of each constituent loop H (Zuker
and Stiegler, 1981). As a consequence, associating a
probability distribution over the production rules we
can also use this formalization to predict the RNA sec-
ondary structures based on this energy model.
As an example, we use Loop Grammar to repre-
sent the molecule illustrated in Figure 1. The first
step is to formalize that the structure is not empty by
rule S →S
0
and to represent the head composed of the
unpaired nucleotide U by S
0
→ sS. This unpaired se-
quence is followed by loops formalized by rule S
0
→
HS. Such loop, generated by the weak bond between
the second and the last nucleotide, is formalized by
production H → x[S
0
]. In this case, the substructure is
determined by the weak bond that involves the third
and the second to the last nucleotide and it is formal-
ized by the only possible sequence of rules S
0
→ HS,
S → ε and H → x[S
0
]. The same sequence must be
used to model the weak bond between the fourth and
the third to the last nucleotide. Instead, to represent
the sub-motif that involves the nucleotides from the
fifth to the fifteenth one, it is necessary to include at
the beginning and at the ending of the previous se-
quence the production S
0
→ sS for representing the
two unpaired sequences of nucleotides, UC and AG.
Lastly, the unpaired sequence nested to the innermost
weak bond is formalized using the production S
0
→
sS. The string associated to the considered molecule
is U(G,U)[(C,G)[(U,G)[UC(C,G)[UUUCA]AG]]].
Such scheme works in general to give a unique al-
gebraic expression of each motif of RNA secondary
structure. This observation yields the following:
Theorem 1. The Loop Grammar, L
RNA
generates
uniquely all RNA structures.
It is equivalent to prove that the grammar L
RNA
is
not ambiguous. A technique for proving it is by in-
duction over nucleotides and loops or proving that the
grammar is LR(1), but it is omitted since it is essen-
tially the same as the proof of Theorem 2.
Corollary 1. Each derivation path of the Loop Gram-
mar, L
RNA
, corresponds uniquely to an RNA sec-
ondary structure.
Each term obtained by grammar L
RNA
uniquely rep-
resents a particular molecule. It is a word over
Σ = Σ
RNA
∪ Σ
RNA
∪ { [,] }, where Σ
RNA
and Σ
RNA
are the alphabets of unpaired nucleotides and weak
bonds, respectively. In this work, we assumed that
only Watson-Crick and wobble base pairs character-
ize the RNA molecule; if we want to add also the non-
canonical weak bonds, it is enough to add the corre-
sponding pairs in Σ
RNA
. Instead, the extra symbols,
00
[ , ]
00
, are introduced to model the fact that a weak
bond is contained into another one. In other words, a
loop is nested into another one. By abuse of notation,
we do not introduce another type of extra symbols to
model that a weak bond is followed by is another one.
The abuse consists in the fact that the usual concate-
nation has been used to concatenate both nucleotides
and loops.
4 TOPOLOGICAL
FORMALIZATION
In this section, we will focus on the relations, nest-
ing or concatenation, among hairpins. We define two
topological operators, nesting and concatenation, in
Section 4.1. They permit to define the Surface Loop
Grammar in Section 4.2.
4.1 Topological Operators
Each RNA secondary structure can be uniquely de-
composed into loops. Each of them can be expressed
as a composition of hairpins, as defined by Loop
Grammar in Section 3. The proposed composition
is based on nesting and concatenation. Briefly, nest-
ing corresponds to the insertion of a structure into
Loop Grammars to Identify RNA Structural Patterns
305

another one, as shown in Figure 2-A for the simple
case in which a hairpin is nested into another one;
while concatenation is used to represent a motif in
which a structure is followed by another one, as il-
lustrated in Figure 2-B for two simple hairpins. The
two operators are described over fatgraph, which is a
two-dimensional topological object that uniquely de-
termines an oriented surface with boundary as intro-
duced in Section 2. In topology, cutting and gluing are
two methods for analysing surfaces. Taking advan-
tage of these two methods, we define the following
two operations: cutting backbone and gluing back-
bone. The former cuts the backbone of a fatgraph in
two parts, as shown on top of Figure 5; the latter glues
two parts of backbone, as illustrated in the bottom of
Figure 5.
Cutting
Backbone
Gluing
Backbone
Figure 5: The cutting and the gluing backbone operations
are illustrated on top and in the bottom, respectively.
The two topological operators, nesting and con-
catenation, are defined as follows
Definition 4 (Concatenation). Given two fatgraphs,
F
1
and F
2
, the concatenation, F
1
F
2
, is a fatgraph
defined as F
1
followed by F
2
, whose backbones are
glued.
As an example, we consider the two fatgraphs, F
1
and F
2
, illustrated in Figures 6-A and 6-B, respec-
tively, whose concatenation, F
1
F
2
, is shown in Fig-
ure 6-C.
(A)
(B)
(C)
(D)
Figure 6: (A) The fatgraph F
1
; (B) the fatgraph F
2
; (C) the
concatenation of F
1
and F
2
; (D) a nesting of F
1
and F
2
.
Definition 5 (Nesting). Given two fatgraphs, F
1
and
F
2
, the nesting, F
1
e F
2
, is a fatgraph defined by cut-
ting the backbone under an arch of F
1
once and by
gluing F
2
, where the backbone of F
1
has been cut.
Differently from the concatenation, the resulting
of a nesting, F
1
e F
2
, is not unique fatgraph, since it
depends on where the backbone of F
1
is cut. As an
example, we again consider the two surfaces of Fig-
ures 6-A and 6-B, and a possible nesting is shown in
Figure 6-D. Moreover, another resulting structure can
also be obtained cutting the backbone in the last com-
ponents and gluing the backbone of fatgraph F
2
that
corresponds to the concatenation. In fact, from the
topological point of view, both operators correspond
to the connected sum (Gilbert and Porter, 1994).
4.2 Loop Surface Grammar
The two topological operators defined above allows
us to formalize the surface associated with an RNA
secondary structure using a term of a language of ex-
pressions whose grammar would look like the follow-
ing one:
F ::= ε empty structure
| L base loop
| F F concatenation of fatgraphs
| F e F nesting of two fatgraphs
where F is a generic fatgraph and L is the loop base.
Each fatgraph F can be defined in terms of nesting
and concatenation of other fatgraphs. Such grammar
can generate different derivation trees representing
the same fatgraph, but this problem has been solved
by the ordered given by the backbone.
Definition 6. The Surface Loop Grammar is S
RNA
=
(V
N
,V
T
,P,S), where V
N
= {S, S
0
,L}, V
T
= {(x, ¯x)},
and the set of productions P is
S ::= ε empty structure
| S
0
non-empty structure
S
0
::= L S concatenation
L ::= L e S
0
nesting
| (x, ¯x) base loop
The start symbol S represents any surfaces asso-
ciated with RNA secondary structures, empty or non-
empty. If a secondary structure is not empty, the as-
sociated fatgraph is composed of the surface associ-
ated a base loop, L := (x, ¯x), concatenated to another
structure, eventually empty, or the considered surface
contains another structure not empty.
Theorem 2. The Surface Loop Grammar S
RNA
is
context-free and it generates uniquely the surface as-
sociated to the RNA structures.
The proof is reported in Appendix A.
Corollary 2. Each derivation path of the Surface
Loop Grammar, S
RNA
, corresponds uniquely to the
surface associated to an RNA secondary structure.
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
306

5 RESULTS AND DISCUSSION
In this study, we have defined two context-free gram-
mars, Loop Grammar and Surface Loop Grammar.
The former models both RNAs primary and sec-
ondary structure in terms of a string as a composi-
tion of loops. The proposed composition is based on
concatenation or nesting of hairpins, considered as
base loops. These two operators have been also de-
scribed over fatgraphs, two-dimensional topological
objects that uniquely determine oriented surfaces with
boundary. The operators have permitted to define a
Surface Loop grammar, whose algebraic expressions
uniquely identify fatgraphs. Each term of the gram-
mar represents an RNA secondary structure without
relying on sequence similarity in terms of hairpins
and relations among them. To prove that the grammar
is unambiguous, we have associated with it the gener-
ating function, which determines the Catalan numbers
able to enumerate all possible linear chord diagrams
without any crossings. The terms obtained by the two
grammars allow us to face the problem of identify-
ing substructures considering both the primary and
secondary structures in terms of both strings match-
ing and string pattern matching. In the literature, the
problem has been widely addressed using trees as data
structures (Cserkuti et al., 2006). Considering only
pseudoknot-free structures represents a limitation of
our approach due to the use of context-free grammar.
This formalism is inadequate to model RNA pseudo-
knotted structures (Harrison, 1978).
To test the approach, we have considered the Ver-
tebrate Telomerase RNAs. Telomerase is a ribonu-
cleoprotein enzyme that maintains telomere length by
adding telomeric sequence repeats onto chromosome
ends. The most remarkable feature of this molecule
is the evolutionary conservation of four structural do-
mains: the pseudoknot domain, the CR4-CR5 do-
main, the Box H/ACA domain, and the CR7 do-
main (Chen et al., 2000). In this test, we have consid-
ered the CR4-CR5 domain from human, quoll, Xeno-
pus, and Typhlonectes telomerase RNAs. We have
represented them as strings using Loop Grammar and
Surface Loop Grammar. The terms obtained with
the former are reported in Tables 1, while terms ob-
tained with Surface Loop Grammar are the same for
each species. It is S = L e L e L e L e L e L e
L e L e L. The term of the human CR4-CR5 do-
main obtained by Surface Loop Grammar matches
with the strings that identify the ones of other con-
sidered species. Such string matching has been done
using Notepad++ 7.6 as a text editor. Moreover, us-
ing the strings obtained with the Loop Grammar, we
have identified the pattern (C, G)[(C,G)[·]·], where
the symbol · identifies everything, in each consid-
ered molecules, while we have identified the pattern
(C,G)[(C,G)[(C, G)[(C,G)[·]·]·]·] only in human and
in Quoll CR4-CR5 domain. To identify these string
patterns, we have developed a prototype Java tool
based on regular expressions and Java Regular Ex-
pression Tester (Expression Tester, 2018). The regu-
lar expressions allow us to recognize the correspond-
ing closed bracket of the weak interaction.
Table 1: The terms of CR4-CR5 domain of Human, Quoll,
Xenopus and Typhlonectes obtained with Loop Grammar.
S
o
h
,S
o
q
,S
o
x
,S
o
t
are the substructure omitted due to lack of
space.
Human S
h
= (C, G)[(C,G)[(C,G)[(G,C)[S
o
h
]]]]
Quoll S
q
= (C, G)[(C,G)[(C,G)[(G,C)[S
o
q
]]]]
Xenopus S
x
= (C, G)[(C,G)[(C,G)[(C, G)[S
o
x
]]]]
Typhlonectes S
t
= (C, G)[(C,G)[(A,U)[(C, G)[S
o
t
]]]]
6 FUTURE PERSPECTIVES
The biological functions of RNAs are largely deter-
mined by molecular configuration. In this work, we
have faced the problem of the identification of a given
structural pattern into an RNA pseudoknot-free sec-
ondary structure in terms of string introducing two
context-free grammars able to represent both primary
and secondary structure of an RNA molecule. We
are working on the development of a toolchain that
implements the presented methodology and takes as
input dot-bracket notation, an output of RNAStrand
database (Andronescu et al., 2008). We have planned
to compare our tool with the existing ones using
an appropriate benchmark to study technical features
such as scalability. Moreover, the tool will be tested
on real RNAs. It will be carried out in collaboration
with experts of the biological domain in order to test
the impact of our approach on the creation of new bi-
ological knowledge.
As a future work, we want to generalize the string
pattern matching of RNA secondary structures with
arbitrary pseudoknots. A promising approach is based
on our preliminary results (Quadrini et al., 2017;
Quadrini et al., 2018; Quadrini and Merelli, 2018)
since it is able to model each kind of pseudoknots
differently classical approaches, such as (Rivas and
Eddy, 2000). Another direction of future work is to
face the problem of RNAs classification using the Sur-
face Loop Grammar. A suitable database of func-
tional molecules is RNA Strand Database (Harrison,
1978). Moreover, the problem of folding of RNA
without pseudoknots can be also addressed with the
Loop Grammar defining an opportune probability dis-
tribution.
Loop Grammars to Identify RNA Structural Patterns
307

REFERENCES
Anderson, J. W., Tataru, P., Staines, J., Hein, J., and Lyngsø,
R. (2012). Evolving stochastic context-free grammars
for RNA secondary structure prediction. BMC bioin-
formatics, 13(1):78.
Andronescu, M., Bereg, V., Hoos, H. H., and Condon, A.
(2008). RNA STRAND: the RNA secondary structure
and statistical analysis database. BMC bioinformatics,
9(1):340.
Backofen, R. and Siebert, S. (2007). Fast detection of com-
mon sequence structure patterns in RNAs. Journal of
Discrete Algorithms, 5(2):212–228.
Chen, J.-L., Blasco, M. A., and Greider, C. W. (2000). Sec-
ondary Structure of Vertebrate Telomerase RNA. Cell,
100(5):503–514.
Chomsky, N. and Sch
¨
utzenberger, M. P. (1963). The al-
gebraic theory of context-free languages. In Studies
in Logic and the Foundations of Mathematics, vol-
ume 35, pages 118–161. Elsevier.
Cserkuti, P., Levendovszky, T., and Charaf, H. (2006).
Survey on Subtree Matching. In 2006 International
Conference on Intelligent Engineering Systems, pages
216–221. IEEE.
Dill, K. A. (1990). Dominant forces in protein folding. Bio-
chemistry, 29(31):7133–7155.
Dowell, R. D. and Eddy, S. R. (2004). Evaluation of sev-
eral lightweight stochastic context-free grammars for
RNA secondary structure prediction. BMC bioinfor-
matics, 5(1):71.
Expression Tester (2018). Java Regular Expression Tester.
Accessed 20 November 2018.
Ferr
´
e-D’Amar
´
e, A. R. and Doudna, J. A. (1999). Rna folds:
insights from recent crystal structures. Annual review
of biophysics and biomolecular structure, 28(1):57–
73.
Giegerich, R. (2014). Introduction to stochastic context
free grammars. In RNA Sequence, Structure, and
Function: Computational and Bioinformatic Meth-
ods, pages 85–106. Springer.
Gilbert, N. and Porter, T. (1994). Knots and Surfaces. Ox-
ford University Press, UK.
Harrison, M. A. (1978). Introduction to Formal Language
Theory. Addison-Wesley Longman Publishing Co.,
Inc.
H
¨
ochsmann, M., Toller, T., Giegerich, R., and Kurtz, S.
(2003). Local similarity in RNA secondary structures.
In Bioinformatics Conference, 2003. CSB 2003. Pro-
ceedings of the 2003 IEEE, pages 159–168. IEEE.
H
¨
ochsmann, M., Voss, B., and Giegerich, R. (2004). Pure
Multiple RNA Secondary Structure Alignments: A
Progressive Profile Approach. IEEE/ACM Transac-
tions on Computational Biology and Bioinformatics,
1(1):53–62.
Jiang, T., Lin, G., Ma, B., and Zhang, K. (2002). A General
Edit Distance between RNA Structures. Journal of
Computational Biology, 9(2):371–388.
Knudsen, B. and Hein, J. (1999). RNA secondary structure
prediction using stochastic context-free grammars and
evolutionary history. Bioinformatics, 15(6):446–454.
Knudsen, B. and Hein, J. (2003). Pfold: RNA sec-
ondary structure prediction using stochastic context-
free grammars. Nucleic Acids Research, 31(13):3423–
3428.
Li, K., Rahman, R., Gupta, A., Siddavatam, P., and Grib-
skov, M. (2008). Pattern matching in RNA struc-
tures. In International Symposium on Bioinformatics
Research and Applications, pages 317–330. Springer.
Mauri, G. and Pavesi, G. (2005). Algorithms for pattern
matching and discovery in RNA secondary structure.
Theoretical Computer Science, 335(1):29–51.
Penner, R. C., Knudsen, M., Wiuf, C., and Andersen, J. E.
(2010). Fatgraph models of proteins. Communica-
tions on Pure and Applied Mathematics, 63(10):1249–
1297.
Quadrini, M., Culmone, R., and Merelli, E. (2017). Topo-
logical Classification of RNA Structures via Intersec-
tion Graph. In Theory and Practice of Natural Com-
puting. TPNC 2017, volume 10687 of Lecture Notes
in Computer Science, pages 203–215. Springer.
Quadrini, M. and Merelli, E. (2018). Loop-loop Interaction
Metrics on RNA Secondary Structures with Pseudo-
knots. In Proceedings of the 11th International Joint
Conference on Biomedical Engineering Systems and
Technologies - Volume 4: BIOINFORMATICS, pages
29–37, Set
´
ubal, Portugal.
Quadrini, M., Tesei, L., and Merelli, E. (2018). An Al-
gebraic Language for RNA Pseudoknots Comparison.
Accepted by BMC Bioinformatics.
Rivas, E. and Eddy, S. R. (2000). The language of RNA: a
formal grammar that includes pseudoknots. Bioinfor-
matics, 16(4):334–340.
Sakakibara, Y., Brown, M., Hughey, R., Mian, I. S.,
Sj
¨
olander, K., Underwood, R. C., and Haussler, D.
(1994). Stochastic context-free grammers for tRNA
modeling. Nucleic Acids Research, 22(23):5112–
5120.
Wang, J. T., Shapiro, B. A., Shasha, D., Zhang, K., and
Currey, K. M. (1998). An algorithm for finding the
largest approximately common substructures of two
trees. IEEE Transactions on Pattern Analysis & Ma-
chine Intelligence, (8):889–895.
Waterman, M. S. and Smith, T. F. (1978). RNA secondary
structure: A complete mathematical analysis. Mathe-
matical Biosciences, 42(3-4):257–266.
Zuker, M. (2003). Mfold web server for nucleic acid folding
and hybridization prediction. Nucleic Acids Research,
31(13):3406–3415.
Zuker, M. and Stiegler, P. (1981). Optimal computer fold-
ing of large RNA sequences using thermodynamics
and auxiliary information. Nucleic Acids Research,
9(1):133–148.
APPENDIX A
Taking advantage of the Chomsky-Schutzenberger
enumeration theorem, that allows one to construct an
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
308

algebraic equation whose power series expansion pro-
vides the enumeration (Chomsky and Sch
¨
utzenberger,
1963), we can associate to the considered grammar
the following generating function observing that op-
erator concatenation and nesting over surface corre-
spond to the connected sum from a topology point of
view
S(z) = 1 + zS(z)
2
(1)
Equation 1 is just a quadratic equation in S(z) which
we can solve using the quadratic formula. In a more
familiar form, we can rewrite it as: zS(z)
2
−S(z)+1 =
0 whose soluzion is
S(z) =
1 ±
√
1 −4z
2z
Since it is known that S(0) = 1 and for z →0
+
, S(z) →
+∞, choosing the positive sign in the quadratic for-
mula. Thus, the only possible solution is
S(z) =
1 −
√
1 −4z
2z
whereas for z → 0
+
,
lim
z→0
+
C(z) = lim
z→0
+
2(1 −4z)
−
1
2
2
= 1
since lim
z→0
+
C(z) is an indetermined form of 0/0
type. To expand S(z) we will just use the binomial
formula on
p
(1 −4z) = (1 −4z)
−
1
2
whence
S(z) =
1 −
√
1 −4z
2z
=
2
1 +
√
1 −4z
Using of the binomial formula with fractional ex-
ponents follows
C(z) =
1
2z
1−
√
1 −4z
=
1
2z
1−
∑
n≤0
1/2
n
(−4z)
n
(2)
Since
α
n
=
α(α −1) .. .(α −n + 1)
n!
it follows that
(−4)
n
α
n
=
1
2
(
1
2
−1). .. (
1
2
−n + 1)
n!
·(−4)
n
=
1
2
(−
1
2
)···(
−2n+3
2
)
n!
˙
( −1)
n
·(2 ·2)
n
=
3 ·5.. .(−3 + 2n)
n!n!
2
n
·n ·(n −1).. .1
= −
3 ·5.. .(3 −2n)
n! n!
·2n ·(2n −2).. .2
= −
(2n)!
n! n!(2n −1)
= −
2n
n
1
2n −1
(3)
Substituting 3 into equation 2, we obtain
S(z) =
1
2z
1 +
∑
n≤0
2n
n
·
1
2n −1
z
n
=
1
2z
1 −1 +
∑
n≥1
2n
n
·
1
2n −1
z
n
=
1
2
∑
n≥0
2(n + 1)
n + 1
·
1
2(n + 1) −1
z
n
(4)
Applying the definition of the binomial formula fol-
lows that
C(z) =
∑
n≥0
1
n + 1
2n
n
z
n
where
s
n
=
2n!
(n + 1)!n!
with n is the number of base loops, and s
n
is the
Catalan numbers, i.e., the number of all possible lin-
ear chord diagrams without crossing. This proves the
corresponding surface context-free language is unam-
biguous.
Loop Grammars to Identify RNA Structural Patterns
309
