Predicting Respiratory Depression in Neonates using Intra-arterial

Pressure Measurements

Aleksandar Jeremic

and Dejan Nikolic

Department of Electrical and Computer Engineering McMaster University, Hamilton, ON, Canada

Physical Medicine and Rehabilitation, University Children’s Hospital, Faculty of Medicine, University of Belgrade,

Belgrade, Serbia

Keywords:

Inter-arterial Pressure Measurements, Signal Models.

Abstract:

Respiratory problems are one of the most common reasons for neonatal intensive care unit (NICU) admis-

sion of newborns. It has been estimated that as much as 29% of late preterm infants develop high respiratory

morbidity. To this purpose invasive ventilation is often necessary for their treatment in NICU. These patients

usually have underdeveloped respiratory system with deﬁciencies such as small airway caliber, few collateral

airways, compliant chest wall, poor airway stability, and low functional residual capacity. Consequently ven-

tilation control has been subject of considerable research interest. In this paper we propose an algorithm for

detection of respiratory depression by predicting the onset of pO

depressions using intra-arterial pressure

measurements and second order statistical properties of these signals. We calculate the average covariance

matrix of intra-arterial pressure measurements in the absence of respiratory depression. We then use this

matrix as a reference measure and monitor the changes in the actual covariance matrix measurements. We

predict the onset of respiratory depression once the distance is larger than empirically determined threshold.

We demonstrate the applicability of our results using a real data set.

1 INTRODUCTION

Newborn intensive care is one of the great medical

success of the last 20 years. Current emphasis is

upon allowing infants to survive with the expectation

of normal life without handicap. Clinical data from

follow up studies of infants who received neonatal

intensive care show high rates of long-term respira-

tory and neurodevelopmental morbidity. As a conse-

quence, current research efforts are being focused on

reﬁnement of ventilated respiratory support given to

infants during intensive care (Revow et al., 1989).

The main task of the ventilated support is to

maintain the concentration level of oxygen (O

) and

carbon-dioxide (CO

) in the blood within the phys-

iological range until the maturation of lungs occur.

Failure to meet this objective can lead to various

pathophysiological conditions. Therefore one of the

most critical components in the neonatal intensive

care units (NICU) is an adequate ventilation control.

In addition, due to a fragile state of neonatal lungs

the ventilation control has to be designed very care-

fully as neither hyperventilation nor hypoventilation

are acceptable.

In our previous work (Jeremic and Tan, 2007)

we developed a deterministic inverse mathematical

model of the CO

partial pressure variations in the ar-

terial blood of a ventilated neonate. We evaluated the

applicability of the proposed modelusing clinical data

sets obtained from neonatal multi-parameter intra-

arterial sensor which enables intra-arterial measure-

ments of partial pressures. Using this model we de-

veloped statistical signal processing model (Jeremic

and Tan, 2009) that predicts both inter-arterial pres-

sure measurements and corresponding conﬁdence in-

tervals.

In this paper we present a new statistical signal

processing model for predicting the onset of respi-

ratory depression. We focus on advance detection

of falling edge events of oxygen partial pressure and

consequently rising edge events of carbon-dioxide

partial pressure measurements. To this purpose we

propose to detect the change by calculating distance

between the sample covariance matrix and reference

matrix obtained in the training stage. In Section 2

we describe the training procedure in which the ref-

erence estimate of the covariance matrix is calculated

and operating mode in which the actual sample co-

Jeremic, A. and Nikolic, D.

Predicting Respiratory Depression in Neonates using Intra-arterial Pressure Measurements.

DOI: 10.5220/0007576802370240

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 237-240

ISBN: 978-989-758-353-7

237

variance matrix is calculated using the sliding win-

dow approach. The sample covariance matrices are

calculated by using Frechet mean by utilizing our pre-

viously developed algorithms (Jahromi et al., 2015).

In Section 3 we present experimental results obtained

by applying our algorithms to real data set. Finally in

Section 4 we present conclusions and discuss possi-

bilities for future research.

2 SIGNAL PROCESSING

MODELS

To examine the applicability of the proposed algo-

rithms we apply them to the data set obtained in the

Neonatal Unit at St. James’s University Hospital. The

data set consists of intra-arterial partial pressure mea-

surements obtained from twenty ventilated neonates.

The sampling time was set to 10s and the expiratory

rate was set to 1 breathe per second. In Figure 1 we

illustrate a sample of intra-arterial pressure measure-

ments.

0 500 1000 1500 2000 2500

Time[ms]

2 [kPa]

Figure 1: Sample of intra-arterial pressure measurements.

In order to predict the onset of respiratory depres-

sion (hypo-ventilating) condition we propose to cal-

culate the sample covariance matrix and compare it to

a reference value obtained from the training period.

In order to achieve this goal we ﬁrst select a training

data set by selecting time intervals without respira-

tory depression event. Note that these intervals have

to be selected for every patient by a trained neonatolo-

gist. Then we calculate the sample covariance matrix

by using the sliding window over the measured intra-

arterial pressure measurements. To determine the size

of the window we ﬁrst calculate the autocorrelation

function, see Figure 3.

Note that there are various techniques for detect-

ing signal jumps / edges in arbitrary signals. However

since our goal is to predict the onset of these events,

i.e. detect conditions that lead to hypoventilation we

propose to use second-order statistical properties in-

1 2 3 4 5 6 7 8 9 10

Lag

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Autocorrelation

Figure 2: Autocorrelation function.

stead of simple trend changes. Namely, our prelimi-

nary results indicate that trend changes are frequent in

intra-arterial pressure measurements due to the nature

gas exchange and hence lead to signiﬁcant number of

false positives.

In order to calculate the sample covariance ma-

trix we propose to use Frechet mean (Jahromi, 2014)

which is given as the point which minimizes the sum

of the squared distances (Barbaresco, 2008):

S = argmin

S ∈M

∑

i=1

,S ) (1)

where {S

}

i=1

represents the symmetric positive deﬁ-

nite matrices and d(., .) denotes the metric being used

respectively. Therefore the above expression can be

interpreted as a way of calculating an averaged sam-

ple covariance matrix using a sliding window where

represents an i−th window sample covariance es-

timate.

In this paper we propose to use log-Riemannian

distance measure given by (Moakher, 2005):

(A,B) =



log(A

−

)



∑

i=1

log

)

(2)

where the L

’s are the eigenvalues of the matrix A

−1

(Absil et al., 2009) where A and B are arbitrary M× M

matrices. In our particular application matrix A refers

to sample covariance matrix of the measured signal

and B is the reference covariance matrix obtained in

the training phase i.e. on an interval where no depres-

sion events were recorded.

In order to determine the threshold for distance

comparison between the reference and testing co-

variance matrices we propose to use multiple signal

segments and calculate multiple reference covariance

matrices. Using these matrices we then calculate the

histogram of mutual distances and pick the thresh-

old based on the desired percentage of false positives.

Note that as a preliminary approach we choose to use

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

238

the same distance measure both for training and eval-

uating performance although other distance measures

(e.g. square root, Frobenius norm) could be used as

well.

Let y

be the i-th sample of inter-arterial pressure

measurements. Then the outline of the algorithm is as

follows

• within the training data set create windows

data

= [y

(k−1)∗l1+1

,· ·· , y

k∗l1−1

] where l1 is the

length of the window

• within the above window select subwindows of

length l2 and label them

data

where j = 1, l1 −

l2+ 1

• remove the sample mean from the window vectors

• calculate rank 1 sample covariances

data

j,T

data

and average them using Frechet mean instead of

commonly used addition

3 RESULTS

We evaluate the performance of the proposed algo-

rithms using the data set obtained at the Neonatal

Intensive Care Unit, at McMaster University Hospi-

tal. At each cot in the Neonatal Intensive Care Unit

at the McMaster Children’s Hospital there is a cot-

side monitor displaying the physiological parameters

measured. Moreover, these monitors are linked in a

network with a central station into which data can be

rapidly exported via Draeger Inﬁnity Gateway soft-

ware. Data is stored in the central station for 24 hours.

The ﬁnal dataset contained 16 patients with the num-

ber of recorded days for each patient varying between

1 and 90 with a mean of 32 days.

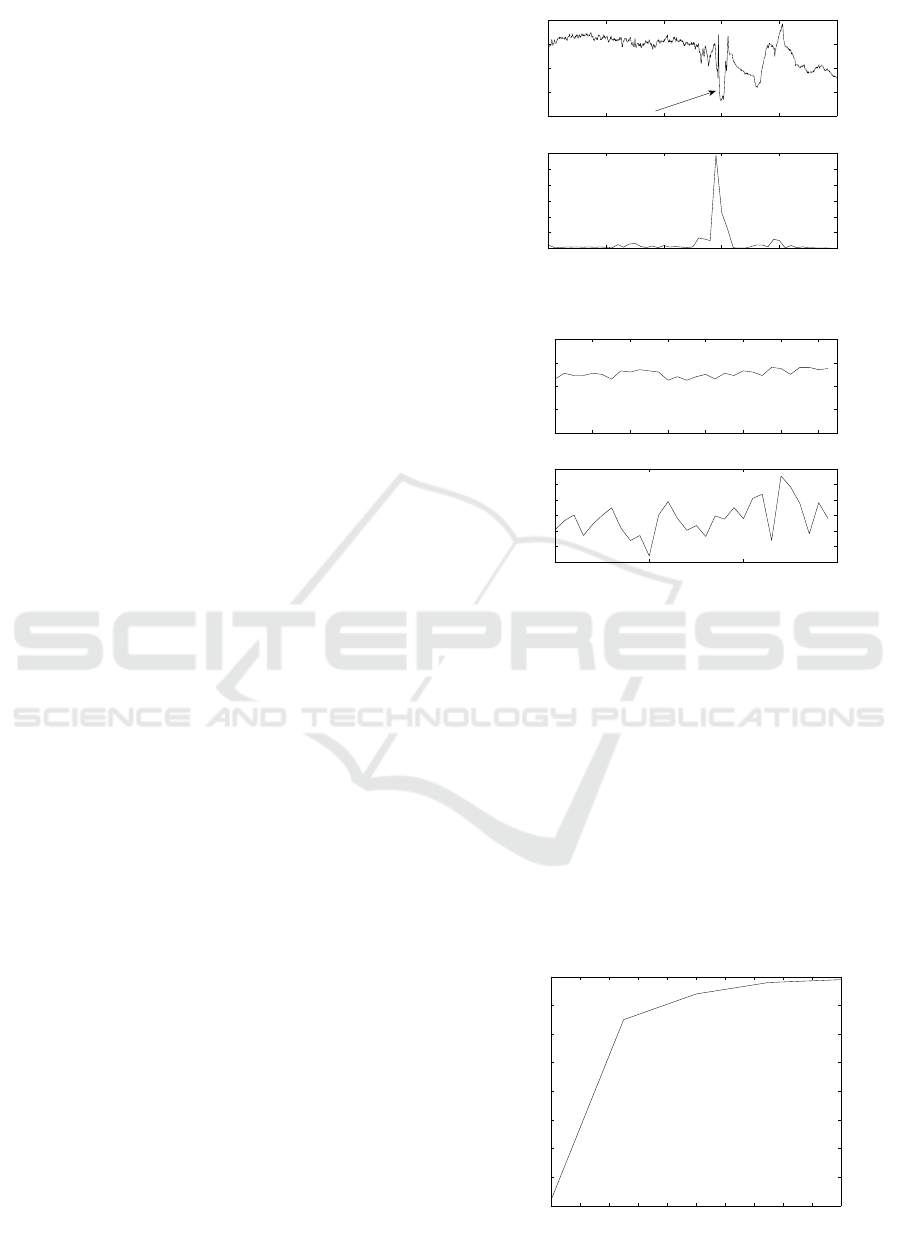
In Figure 4 (a) we illustrate the event correspond-

ing to the respiratory depression and in Figure 4 (b)

we illustrate the corresponding change in the covari-

ance distance calculated using the aforementioned

logarithmic Riemannian distance. In Figure 5 we il-

lustrate the same results but in the absence of respira-

tory depression. Note that the dynamic range of the

distance is much smaller compared to Figure 4.

As we stated before the performance of the algo-

rithm will be dependent on adequate threshold selec-

tion. As a preliminary approach we arbitrarily set the

false positives rate to 10% and calculated the corre-

sponding threshold empirically using the part of data

set (for each patient) without hypoventilation events.

Using sliding window we calculate multiple sample

covariance matrix estimates. Then we use the testing

part of the data set and detect onsets of hypoventila-

tion events by comparing distance between training

0 500 1000 1500 2000 2500

a) Time [ms]

2 [kPa]

0 500 1000 1500 2000 2500

b) Time[ms]

0.1

0.2

0.3

0.4

0.5

0.6

Distance

Figure 3: a) Sample of inter-arterial partial pressure b) Co-

variance distance calculated using logarithmic measure.

200 400 600 800 1000 1200 1400

a) Time[ms]

2 [kPa]

0 500 1000 1500

b) Time[ms]

0.002

0.004

0.006

0.008

0.01

0.012

Distance

Figure 4: a) Sample of inter-arterial partial pressure b) Co-

variance distance calculated using logarithmic measure.

set covariance estimates to reference covariance ma-

trices. In both cases we calculate sample covariances

using sliding window of 100 samples and within that

window we use 5 samples to construct 5-dimensional

vector of lagged measurements which are then aver-

aged using Frechet mean in order to calculate sample

covariances.

In order to evaluate the performance of the pro-

posed algorithm we count the number of detected on-

sets and compare it to the actual count performed by

trained physicians. In Figure 6 we illustrate the per-

formance of our algorithm as a function of the false

alarm positives.

0 2 4 6 8 10 12 14 16 18 20

False positives [%]

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Detection probability

Figure 5: Detection probability as a function of false posi-

tives.

Predicting Respiratory Depression in Neonates using Intra-arterial Pressure Measurements

239

In Figure 6 we illustrate the performance mea-

sures for all the patients. Note that due to the

large patient-to-patient variability the performance

may vary signiﬁcantly. This may partially be due

to the fact that the respiratory patterns are very de-

pendent on the gestation length and hence an effort

should be made in selecting adequate training sets.

0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13 0.14 0.15

0.74

0.76

0.78

0.8

0.82

0.84

0.86

0.88

0.9

0.92

Figure 6: Scatter plot of performance parameters for all the

patients.

4 CONCLUSIONS

One of the most important tasks that affect both long-

and short-term outcomes of neonatal intensive care is

maintaining proper ventilation support. To this pur-

pose in this paper we develop signal processing algo-

rithms for predicting the onset of hypoventilation in

order to increase efﬁcient control of ventilation sys-

tem in timely manner. This is especially important for

neonates due to a fragile state of their lungs and hence

predicting the decrease oxygen levels can potentially

enable us to control the ventilator with smaller dy-

namic range.

In this paper we propose to predict the onset us-

ing second order statistical properties by calculating

sample covariance matrices using Frechet mean. Our

experimental results indicate that the structure of co-

variance matrix is slowly changing once the hypoven-

tilation begins. Due to the fact that the trend changes

of intra-arterial pressure occur continuously they may

not serve as a good indicator due to a large number of

false positives. To this purpose we focus our attention

on the second order properties i.e. covariance matrix

and utilize Frechet mean as it is know to be able to

capture different information about matrix structure

depending on the distance measure used. We evalu-

ate the performance of our algorithm using a real data

set previously labeled by trained physicians. In fu-

ture work we propose to develop multichannel infor-

mation fusion system that will use different distance

measures as onset detectors. In addition, we will com-

pare performance of our algorithm versus threshold-

ing. Note however that currently used thresholding

algorithms detect depression once it starts to occur

while our algorithm attempts to predict the onset of

the depression.

REFERENCES

Absil, P.-A., Mahony, R., and Sepulchre, R. (2009). Opti-

mization algorithms on matrix manifolds. Princeton

University Press.

Barbaresco, F. (2008). Innovative tools for radar signal pro-

cessing based on cartan’s geometry of spd matrices &

information geometry. In Radar Conference, 2008.

RADAR’08. IEEE, pages 1–6. IEEE.

Jahromi, M. (2014). Frechet means with respect to rieman-

nian distances: Evaluations and applications. Ma.Sc.

Thesis.

Jahromi, M., Jeremic, A., and Wong, K. (2015). Estimating

positive deﬁnite matrices using frechet mean. Biosig-

nals, 3:295–299.

Jeremic, A. and Tan, K. (2007). Estimating respiratory pa-

rameters using intra-arterial partial pressure measure-

ments. Asilomar, 2:851–854.

Jeremic, A. and Tan, K. (2009). Estimating respiratory

parameters using intra-arterial partial pressure mea-

surements and stochastic differential equations. 2009

Canadian Conference on Electrical and Computer

Engineering, 2:559–564.

Moakher, M. (2005). A differential geometric approach

to the geometric mean of symmetric positive-deﬁnite

matrices. SIAM Journal on Matrix Analysis and Ap-

plications, 26(3):735–747.

Revow, M., England, S., Beirne, H., and Bryan, A. (1989).

A model of the maturation of respiratory control in

the newborn infant. IEEE Trans. on Biomedical Engi-

neering, 36(4):415–423.

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

240