
Compact Color Texture Representation by Feature Selection in Multiple
Color Spaces
M. Alimoussa
1
, N. Vandenbroucke
2
, A. Porebski
2
, R. Oulad Haj Thami
1
, S. El Fkihi
1
and D. Hamad
2
1
Advanced Digital Entreprise Modeling and Information Retrieval Laboratory, ENSIAS, Rabat, Morocco
2
Laboratoire d’Informatique Signal et Image de la C
ˆ
ote d’Opale, 62228 Calais, France
rachid.ouladhajthami@gmail.com, elfkihi.s@gmail.com, denis.hamad@univ-littoral.fr
Keywords:
Color Texture Classification, Feature Selection, Color LBP Histogram, Chromatic Cooccurrence Matrix.
Abstract:
This paper presents a compact color texture representation based on the selection of features extracted from
different configurations of descriptors computed in multiple color spaces. The proposed representation aims
to take simultaneously into account several spatial and color properties of different textures. For this purpose,
texture images are coded in five different color spaces. Then, texture descriptors with different neighborhood
and quantization parameter settings, are calculated from this images in order to extract a high dimensionality
feature vector describing the textures. Compact representation is finally obtained by means of a feature se-
lection scheme. Our approach is applied with two well-known color texture descriptors for the classification
of three benchmark image databases.
1 INTRODUCTION
Texture classification is one of the most complex pro-
cess in computer vision and image processing. It has
been an active topic of research for many years and
an important step in many applications such as con-
tent based image retrieval, medical image analysis,
face recognition, machine vision and many more (Liu
et al., 2018). Texture classification is typically cate-
gorized into two sub-problems of representation and
decision. Texture representation is a fundamental step
of texture analysis that consists in extracting features
that describe texture information. Texture informa-
tion refers to the spatial organization of a set of ba-
sic elements that requires the analysis of a neighbor-
hood and depends on observation conditions (illumi-
nation, field of view, spatial resolution, orientation,
viewpoint, deformation, etc). In order to deal with
texture appearance variations caused by the change of
these conditions, numerous texture descriptors have
been proposed in the last decades, firstly for gray le-
vel images. Liu et al. proposed an updated survey
of advances in texture representation based on Bag of
Words (BoW) and on Convolutional Neural Network
(CNN) (Liu et al., 2018). Although CNN-based met-
hods have provided impressive performances last ye-
ars, they suffer from the difficulty to understand the
representation that they generate. The choice of the
adequate descriptor for classifying textures is there-
fore a crucial but difficult problem, being agree that
classification results depend on the choice of the tex-
ture features as well as the tuning of their parameters.
In addition, many studies have proved that the use
of color impacts the discrimination of textures and im-
proves classification accuracy (Alvarez and Vanrell,
2012; Khan et al., 2015). That is why many tex-
ture descriptors, like Gray Level Cooccurrence Ma-
trix (GLCM), Local Binary Pattern (LBP) and others,
were extended to color. These descriptors combine
spatial and color information to generate color tex-
ture features following two main approaches depen-
ding on whether they are considered jointly or inde-
pendently (M
¨
aenp
¨
a
¨
a and Pietik
¨
ainen, 2004; Bianconi
et al., 2011). There is a wide variety of color spaces
that belong to different families depending on their
properties. It is known that the choice of the color
space impacts texture classification results too but the
prior determination of a suitable color space is a com-
plex problem (Bello-Cerezo et al., 2016; Cernadas
et al., 2017).
Many authors propose to combine various texture
descriptors in several color spaces in order to take into
account their different properties (Khan et al., 2015;
Cusano et al., 2016). Because these approaches ge-
nerate high-dimensional features spaces, they suffer
from the curse of dimensionality and require to ex-
436
Alimoussa, M., Vandenbroucke, N., Porebski, A., Thami, R., El Fkihi, S. and Hamad, D.
Compact Color Texture Representation by Feature Selection in Multiple Color Spaces.
DOI: 10.5220/0007578704360443
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 436-443
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
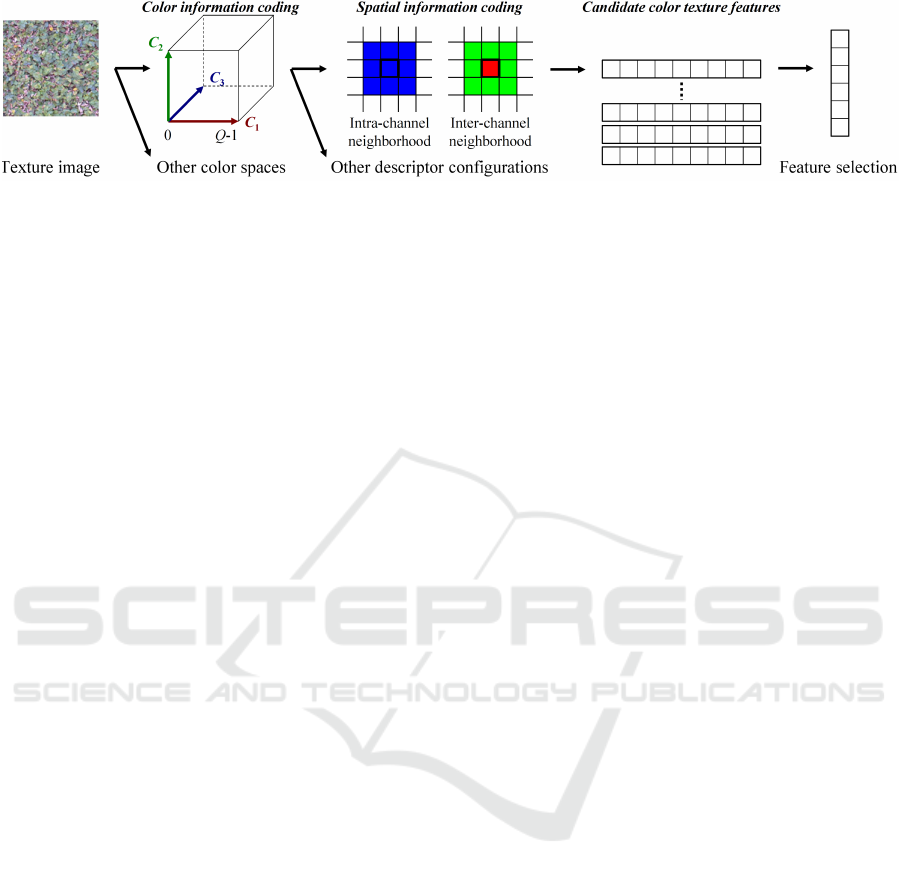
Figure 1: Compact color texture representation.
tract a limited number of relevant features in order to
provide compact texture representations that improve
classification performance in terms of accuracy and
processing time (Porebski et al., 2013b). In most of
these works, the parameter settings of the used des-
criptors, including the chosen color space, are a priori
predefined. However, the properties of the textures of
different classes may be so different that they require
to be represented with different descriptor configura-
tions. At the same time, texture representation has to
take into account possible intraclass property varia-
tions due to changes in illumination, rotation, scale,
shape, etc.
In this paper, we propose a compact color tex-
ture representation where texture features are com-
puted and selected from different configurations of
a same descriptor in multiple color spaces (see fi-
gure 1). The proposed approach is applied with two
well-known color descriptors that process spatial and
color information jointly: Reduced Size Chromatic
Cooccurrence Matrix (RSCCM) (Palm, 2004) and
Extended Opponent Color Local Binary Pattern (EO-
CLBP) (Pietik
¨
ainen et al., 2011). Intra-channel and
inter-channel neighborhoods are both used to extract
color texture features from these descriptors. For the
first descriptor, Haralick features are extracted from
different configurations of RSCCM. For the second
one, we propose to extract statistical features from
histograms of many color LBP configurations. The
extraction of features proposed for this latter descrip-
tor is original because it differs from the classical ap-
proaches that use the bins of LBP histograms as tex-
ture features and so, it limits the number of candidate
features. Another original contribution is to repre-
sent a color texture by combining features from se-
veral configurations of a same descriptor in order to
take advantage of their different spatial and color pro-
perties simultaneously. The proposed approach thus
overcomes the difficulty of choosing a relevant des-
criptor configuration and aims to provide a compre-
hensible and interpretable representation of textures.
The second section of this paper presents the im-
portance of color spaces used in texture classifica-
tion problems. The two descriptors used in this pa-
per for illustrating our approach are presented in the
third section. Section four presents how a compact
representation is determined from texture features ex-
tracted from a descriptor. Experimental results on
three benchmark databases are presented in the fifth
section. The last section offers different perspectives
for future work in order to improve our approach.
2 COLOR SPACES
The color of pixels can be represented in different co-
lor spaces which respect different physical, physiolo-
gic, and psycho-visual properties. They can be ca-
tegorized into four families: the primary spaces, the
luminance-chrominance spaces, the perceptual spaces
and the independent color component spaces (Poreb-
ski et al., 2013b).
Since the choice of a color space impacts directly
the classification results, many authors tried to com-
pare results obtained by using different color spa-
ces in order to find the most suited one for a given
application (M
¨
aenp
¨
a
¨
a and Pietik
¨
ainen, 2004; Bello-
Cerezo et al., 2016; Cernadas et al., 2017). The
synthesis of these works shows that there is no color
space well suited to represent all types of textures. To
solve this problem, few studies propose multi-color
space approaches (Porebski et al., 2018). They ex-
ploit the properties of multiple color spaces simulta-
neously by combining them and overcomes the diffi-
culty of choosing a single relevant color space. Alt-
hough these approaches have shown their relevance
with variable numbers of considered color spaces, it
appears that a limited number of color spaces repre-
sentative of each family is sufficient to improve classi-
fication performances. Moreover, many of these spa-
ces require to know the properties of the illumina-
tion and the acquisition device. That is why we pro-
pose to describe textures with only five color spaces
that do not need this knowledge: the RGB acquisition
image color space with one color space of each fa-
mily: YCbCr luminance-chrominance space, I1I2I3
independent color component space, HSV perceptual
space and RGB
n
normalized primary space.
Compact Color Texture Representation by Feature Selection in Multiple Color Spaces
437

3 TEXTURE DESCRIPTORS
In this paper, we propose to apply our approach with
two popular and efficient texture descriptors: the
cooccurrence matrix and the LBP operator known for
their computational simplicity.
3.1 Haralick Features Extracted from
Chromatic Cooccurrence Matrices
3.1.1 Chromatic Cooccurrences Matrices
This descriptor is the extension to color of the GLCM
operator that is considered as a two-dimensional his-
togram of pairs of neighbor pixels. An important pro-
perty of this operator is its invariance to orientation
changes. Chromatic Cooccurrence Matrix (CCM)
considers both the spatial interactions within and be-
tween the color components of neighbor pixels in
the image plane and the color distribution in a color
space (Palm, 2004).
Let Q, be the number of levels used to quantify
the color components C
1
, C
2
and C
3
of a given color
space. A Reduced Size Chromatic Cooccurrence Ma-
trix (RSCCM) is a Q × Q CCM, where the parameter
Q is reduced in order to decrease the memory storage
cost and so, the time required to extract texture featu-
res from these matrices (Porebski et al., 2013b).
The normalized RSCCM m
C
k
,C
k
0
N
[I] measures the
spatial interactions in the neighborhood N between
the two color components C
k
and C
k
0
of an image I
(k, k
0
∈ {1, 2, 3}). The neighborhood N is a second
parameter defined by the user.
For an image coded in a color space C
1
C
2
C
3
with a quantization level Q and a given neighbor-
hood N , six normalized RSCCM are computed:
three within-component matrices (k = k
0
) and three
between-component matrices (k 6= k
0
) where m
C
k
,C
k
0
N
[I]
and m
C
k
0
,C
k
N
[I] are symmetric.
3.1.2 RSCCM Configurations
Before calculating a chromatic cooccurrence matrix,
a number of parameters have to be set and adjusted.
This configuration is complex when the color and spa-
tial properties of the analyzed textures are heterogene-
ous. It principally depends on:
• Q, the image quantization level that defines the
size of the RSCCM,
• N , the pixel neighborhood in which cooccurren-
ces are counted. N is controlled by two other pa-
rameters:
– the neighborhood direction: four 2-directional
neighborhoods are usually used to compute
direction-dependent cooccurrence matrices: 0
◦
,
45
◦
, 90
◦
and 135
◦
. In order to take simulta-
neously into account all the possible directions
of an observed texture, an isotropic 3 × 3 neig-
hborhood is generally used with a number of 8
neighbors located in the 4 directions.
– the neighborhood distance: this distance, deno-
ted D, is the spatial infinity-norm distance se-
parating each pixel from its neighbors.
We propose to adjust RSCCM configurations de-
pending on two parameters: the quantization level Q
and the neighborhood distance D since we believe
these two parameters control the representation of
texture acquired with different observation conditi-
ons. Haralick features are so extracted from each of
the following RSCCM configurations (D, Q):
(1, 16) (1, 32) (1, 64) (1, 128) (1, 256)
(2, 16) (2, 32) (2, 64) (2, 128) (2, 256)
(3, 16) (3, 32) (3, 64) (3, 128) (3, 256)
(5, 16) (5, 32) (5, 64) (5, 128) (5, 256)
(10, 16) (10, 32) (10, 64) (10, 128) (10, 256)
3.1.3 Haralick Features Extracted from
RSCCM
The cooccurrence matrices are able to represent the
texture but they are not directly used for color texture
classification purposes because of the large amount of
information they contain. To reduce it while preser-
ving the relevance of these descriptors, Haralick pro-
posed statistical features that can be extracted from
each matrix (Palm, 2004). We propose to use the
first 13 Haralick features: homogeneity, contrast, cor-
relation, variance, inverse difference moment, sum
average, sum entropy, entropy, difference variance,
difference entropy and measures of correlation I and
II.
A color texture is then represented by Haralick fe-
atures extracted from RSCCM with different configu-
rations and computed from images coded in multiple
color spaces.
3.2 Texture Features Extracted from
Color LBP Histograms
3.2.1 Color LBP Histogram
Color LBP are extensions to color of the Local Bi-
nary Pattern operator that captures the local texture
properties of a gray level image (Pietik
¨
ainen et al.,
2011). An important property of this operator is its
invariance to monotonic gray-scale changes caused,
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
438

for example, by illumination variations. In order to
characterize the whole color texture image, the LBP
operator is applied on each pixel and for each pair of
components in the color space C
1
C
2
C
3
. Considering
a pair of component (C
k
, C
k
0
), (k, k
0
∈ {1, 2, 3}), the
color LBP labels a pixel with the component C
k
by
thresholding its neighborhood N in the component
C
k
0
and by encoding the result as a binary number.
The consideration of the Extended Opponent Co-
lor LBP (EOCLBP) operator gives rise to nine LBP
images: three within-component LBP images (k = k
0
)
and six between-component (k 6= k
0
). These images
are usually not exploited directly and most of authors
prefer to use LBP histograms and consider histogram
bins as texture features (Pietik
¨
ainen et al., 2011).
Instead of using the bins of EOCLBP histograms,
we propose to extract two different types of statistical
features from these histograms. In order to characte-
rize textures acquired with different observation con-
ditions, these features are extracted from many EO-
CLBP configurations.
3.2.2 EOCLBP Configurations
Due to its popularity, many variants of the basic LBP
operator, like the rotation invariant LBP or the uni-
form LBP for feature dimensionality reduction, as
well as their few extensions to color, have been pro-
posed the last two decades (Pietik
¨
ainen et al., 2011).
The definition of the original LBP operator with
its 3 × 3 neighborhood has then been generalized by
using a circular neighborhood N defined by:
• P, the number of neighbor pixels that determines
the dimensionality of the LBP histograms. For ex-
ample, a 3 ×3 neighborhood with P = 8 neighbors
gives rise to a 2
8
= 256-dimensional LBP histo-
gram. For each pair of color components, a color
texture is thus described by a 2
P
-dimensional his-
togram.
• R, the distance between each pixel and its neig-
hbors. This distance is equal to the radius of the
circle around the central pixel. Generally, when
a neighbor pixel is not confused with the circle, a
bi-linear interpolation is used to estimate its loca-
tion. Here, the neighborhood is thus pre-sampled.
With these two parameters, many LBP configura-
tions are available in order to characterize textures in
different scales. In this paper, we propose to consider
the following EOCLBP configurations (P, R):
(8, 1) (8, 2) (8, 3) (8, 5) (8, 10)
(16, 2) (16, 3) (16, 5) (16, 10)
(24, 3) (24, 5) (24, 10)
3.2.3 Statistical Features Extracted from
EOCLBP Histograms
With the EOCLBP operator, a color texture is re-
presented by 9 LBP histograms that are concatena-
ted to constitute a vector containing 9 × 2
P
features
for a given color space C
1
C
2
C
3
. Several approaches
have been proposed to reduce the dimensionality of
such a feature space, like the uniform LBP opera-
tor. Some authors select the most discriminant bins
that constitute the LBP histograms (Pietik
¨
ainen et al.,
2011). Others authors reduce the number of histo-
grams with only the three within-component LBP his-
tograms or by adding only three out of six between-
component LBP histograms, assuming that the oppo-
nent pairs such as (C
1
, C
2
) and (C
2
, C
1
) are highly re-
dundant (M
¨
aenp
¨
a
¨
a and Pietik
¨
ainen, 2004). Another
approach consists in selecting, out of the nine LBP
histograms, the most discriminant ones for the consi-
dered application (Porebski et al., 2018).
In this paper we propose to extract statistical fea-
tures from each LBP histogram and concatenate them
to form a reduced dimensionality statistical feature
vector. For this purpose, two types of statistical fe-
atures are proposed:
• 7 first order statistical features: mean, median,
mode, standard deviation, symmetry around the
average and two inter quartile ranges.
• 11 second order statistical features extended
from the first 11 Haralick features presented in
section 3.1.3 and adapted to deal with histograms.
We propose to extract these 18 features from his-
tograms of different EOCLBP configurations for re-
presenting color textures.
4 COMPACT COLOR TEXTURE
REPRESENTATION
Supervised texture classification aims to assign a gi-
ven texture to one of a set of known texture catego-
ries for which training samples have been given. This
process is divided into two successive stages: a lear-
ning stage in which a classifier is trained and a de-
cision stage in which this classifier operates. During
the learning stage, texture images are represented by
descriptors from which texture features are extracted.
The extraction of discriminant texture features plays
an essential role in the success of the classification.
So the learning stage has to provide a powerful tex-
ture representation for the decision stage.
The previously proposed descriptors are able to
take into account the heterogeneity of color textu-
Compact Color Texture Representation by Feature Selection in Multiple Color Spaces
439

res to be analyzed. However, they tend to produce
high dimensionality feature vectors, especially when
the number of configurations increases or when it is
applied to color images. It is well-known that the
performance of a classifier is generally dependent on
the dimension of the feature space due to the curse
of dimensionality. Thus, dimensionality reduction
methods are needed to reach satisfying classification
accuracies while decreasing the memory storage and
the computation time.
To reduce the dimensionality of the feature space,
two main strategies are proposed: feature extraction
and feature selection. Because feature extraction met-
hods require the computation of all candidate fe-
atures during the decision stage to build the new
low-dimensional feature subspace, they are time-
consuming. So, feature selection methods that just
require the computation of a reduced number of se-
lected features are preferred here.
So, the proposed compact color texture represen-
tation consists in selecting the most discriminant color
texture features among a set of candidate ones during
a learning stage.
4.1 Candidate Color Texture Features
4.1.1 Features Extracted from Multiple RSCCM
Configurations
In order to take advantage of the specific properties
of several color spaces simultaneously, each image is
first coded in 5 color spaces described in section 2.
Then, for each of the 25 RSCCM configurations des-
cribed in subsection 3.1, 6 RSCCM are computed
and the 13 Haralick features are extracted from each
RSCCM.
Using Haralick features extracted from different
RSCCM configurations, a color texture is firstly re-
presented by 5 × 25 × 6 × 13 = 9750 candidate featu-
res.
4.1.2 Features Extracted from Histograms of
Multiple EOCLBP Configurations
To extract statistical features from histograms of mul-
tiple EOCLBP configurations, each image is first co-
ded in 5 color spaces descried in section 2. Then, for
each of the 12 EOCLBP configurations described in
subsection 3.2, 9 LBP images are computed and 18
statistical features are extracted from each EOCLBP
histogram.
Using statistical features extracted from EOCLBP
histograms, a color texture is firstly represented by
5 × 12 × 9 × 18 = 9720 candidate features.
4.2 Feature Selection
Many authors have chosen to use sequential feature
selection methods in order to build a reduced dimen-
sion feature subspace during the learning stage of the
classification process. Porebski et al. were among the
first to use sequential forward selection (SFS) scheme
to select the most discriminant Haralick features ex-
tracted from cooccurrence matrices of images coded
in 28 different color spaces (Porebski et al., 2013b).
Because these scheme have shown their efficiency,
a SFS scheme is applied in this paper for a compact
representation of color textures. SFS scheme is a
bottom-up approach that starts with an empty set and
adds features at each step of the procedure in order
to constitute candidate feature subspaces to be evalu-
ated. An evaluation function then measures the ca-
pacity of the feature subspaces built during the gene-
ration step to correctly classifying the given textures
and selects the most discriminant subspace. The pro-
cedure continues until a stopping criterion is satisfied.
In order to highlight the interest of our appro-
ach, a wrapper model evaluates each candidate fea-
ture subspace by using the classification accuracy as
the evaluation function in a supervised context. In
this context, wrapper models require to split up the
initial image database to a training, a validation, and
a testing image subset, according to a holdout par-
tition. At each step s of this procedure, the classi-
fication accuracy C
s
is measured with the validation
image subset in order to evaluate the discriminant po-
wer of each candidate subspace. The candidate sub-
space with the highest accuracy is selected as the most
discriminant s-dimensional subspace. In this paper,
the classification accuracy is estimated as the percen-
tage of the validation images that have been correctly
classified by the nearest neighbor classifier because of
its parameter-independence and its simplicity of im-
plementation. Although the wrapper model is time-
consuming and classifier-dependent, it gives good re-
sults and easily determines the dimensionality of the
feature subspace by searching the best classification
accuracy. The procedure runs until the dimensionality
of the selected feature space reaches a maximum va-
lue s
max
equal to 100 in our experiments. The dimen-
sionality ˆs of the finally selected subspace is equal to
the iteration step for which the classification accuracy
is maximum.
In order to select uncorrelated color texture featu-
res, correlation levels between all candidate features
are measured before performing the SFS scheme. In
our approach, candidate features are considered as re-
dundant if their correlation measure is greater than a
threshold equal to 0.95 and are thus removed.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
440

5 EXPERIMENTS
In order to evaluate the efficiency of our approach,
we perform an evaluation on the three well known
and largely used benchmark color texture databases
Outex-TC-00013
1
, NewBarkTex
2
and USPtex
3
.
Each database has been chosen to measure the re-
levance of our approach by comparing the classifica-
tion accuracies with those of previous works under
the same experimental protocol (number of classes,
size of images, number of images for each class, total
number of images, and accuracy evaluation method).
They are representative of different color texture clas-
sification problems with different numbers of classes
as shown in table 1
Table 1: Experimented texture databases.
Dataset Image size #classes #images
Outex-TC-00013 128 × 128 68 1360
NewBarkTex 64 × 64 6 1632
USPtex 128 × 128 191 2292
Let us note that the considered databases are given
with only two image subsets according to a holdout
evaluation method: half of the images defines a trai-
ning subset and the other half a testing subset. Howe-
ver, our approach needs three subsets because it uses
a wrapper model associated to the nearest neighbor
classifier for the feature selection scheme. For com-
parison with other works, this classifier has to use the
same training subset. We thus propose to use the tes-
ting subset as a validation subset and to consider that
the classification accuracies are measured during the
feature selection scheme of the learning stage. The-
refore, the classification results can be interpreted as
optimistic but they can be compared with other works
using the same split into training and testing subsets.
5.1 Experimental Results
5.1.1 Haralick Features Extracted from
Different RSCCM Configurations
Table 2 presents results obtained with the proposed
approach using a combination of Haralick features ex-
tracted from the multiple RSCCM configurations pro-
posed in section 3.1.
1
available at: http://www.outex.oulu.fi/index.php?
page=classification#Outex TC 00013
2
available at: https://www-lisic.univ-littoral.fr/
∼
porebski/BarkTex image test suite.html
3
available at: https://www-lisic.univ-littoral.fr/
∼
porebski/USPtex image set.html
In addition, this table shows the results obtained in
multiple color spaces with only one predefined con-
figuration. As mentioned by Porebski et al., when
Q = 16 and D = 1, RSCCM analysis reaches sa-
tisfying classification results while significantly redu-
cing the processing time (Porebski et al., 2013b).
Table 2: Classification accuracies for different RSCCM
configurations in multiple color spaces.
Dataset (D, Q) C
ˆs
ˆs
Outex-TC-00013
multiple 98.53 29
(1, 16) 97.20 33
NewBarktex
multiple 86.39 75
(1, 16) 84.50 93
USPtex
multiple 98.87 38
(1, 16) 95.98 54
This table highlights the interest of our approach
that produces higher classification accuracies with lo-
wer dimensionality feature spaces compared to a pre-
defined descriptor configuration.
5.1.2 Statistical Features Extracted from
Different EOCLBP Configurations
Table 3 presents results obtained with the proposed
approach using a combination of statistical features
extracted from histograms of the multiple EOCLBP
configurations proposed in section 3.2.
In addition, this table shows the results obtained in
multiple color spaces with only one predefined confi-
guration. We choose to use the original LBP configu-
ration with P = 8 and R = 1 in two cases: without and
with a bin selection (BS) scheme (Pietik
¨
ainen et al.,
2011).
Table 3: Classification accuracies for different EOCLBP
configurations in multiple color spaces.
Dataset (P, R) C
ˆs
ˆs
Outex-TC-00013
multiple 96.91 18
(8, 1) 96.61 47
(8, 1) with BS 97.50 75
NewBarktex
multiple 89.82 20
(8, 1) 89.46 66
(8, 1) with BS 86.76 66
USPtex
multiple 97.64 18
(8, 1) 96.71 49
(8, 1) with BS 93.45 41
This table shows that our approach provides repre-
sentations with a lower dimensionality than the other
approaches and with a bit higher classification accu-
racies. Moreover, statistical features extracted from
EOLBP histograms give comparable results than clas-
sical bin selection approach with a lower dimensiona-
lity feature space too. This result underlines the rele-
vance of this original LBP representation.
Compact Color Texture Representation by Feature Selection in Multiple Color Spaces
441
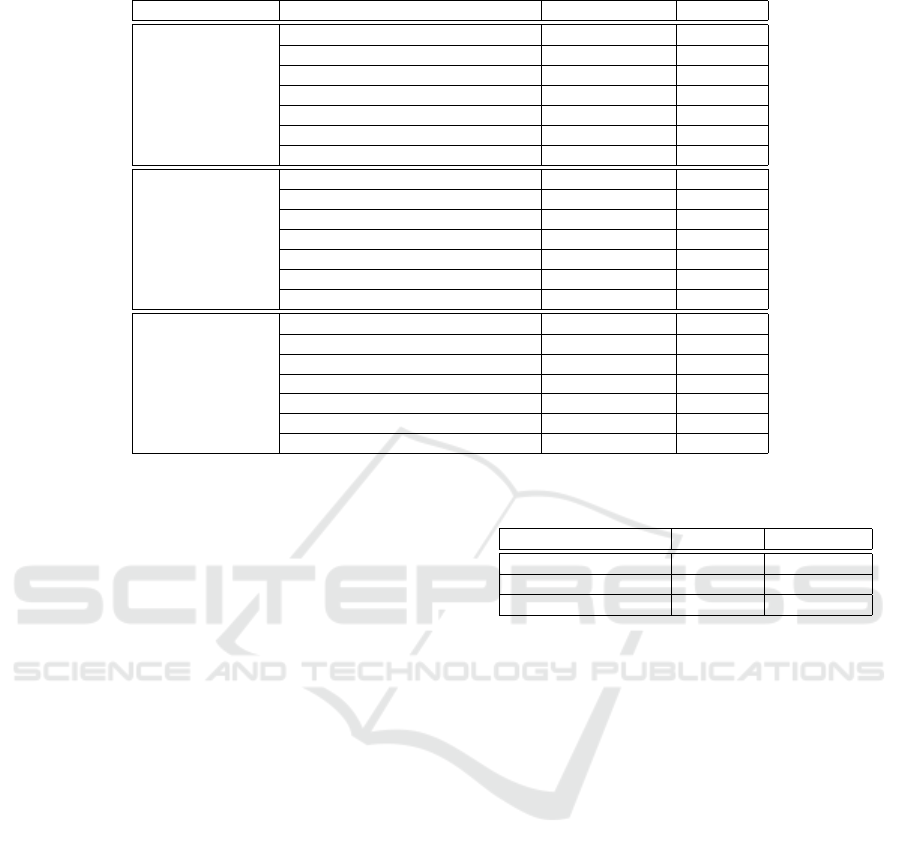
Table 4: Comparison between the classification accuracies reached with the 1-NN classifier.
Dataset Descriptor Color space Accuracy
Outex-TC-00013
Our approach with RSCCM 5 color spaces 98.5
Our approach with EOCLBP 5 color spaces 96.9
(Porebski et al., 2013b) 28 color spaces 96.6
(Porebski et al., 2018) 9 color spaces 95.6
(M
¨
aenp
¨
a
¨
a and Pietik
¨
ainen, 2004) HSV 95.4
(Qazi et al., 2011) IHLS 94.5
(Alvarez and Vanrell, 2012) RGB 94.1
NewBarkTex
Our approach with EOCLBP 5 color spaces 89.8
Our approach with RSCCM 5 color spaces 86.4
(Porebski et al., 2018) 9 color spaces 88.0
(Kalakech et al., 2018) RGB 81.4
(Porebski et al., 2013a) RGB 81.4
(Ledoux et al., 2016) RGB 77.7
(Porebski et al., 2014) RGB 75.9
USPtex
Our approach with RSCCM 5 color spaces 98.9
Our approach with EOCLBP 5 color spaces 97.6
(Porebski et al., 2018) 9 color spaces 97.6
(Liu et al., 2017) RGB 95.9
(Guo et al., 2016) RGB 93.9
(Kalakech et al., 2018) YUV 93.2
(Ledoux et al., 2016) RGB 84.2
5.2 Comparisons and Discussion
Table 4 reports the classification results reached by ot-
her method applied on the three experimented bench-
mark datasets with the same experimental protocol. In
order to achieve classifier-independent comparisons,
only the five better texture classification results rea-
ched with the nearest neighbor classifier (1-NN) and
the same training subset are presented.
As we can notice, the results obtained by our ap-
proach is competitive with other approaches and are
very promising. Obviously, other results with other
classifiers and other protocols are available in the li-
terature (Cernadas et al., 2017; Bello-Cerezo et al.,
2016). This table also confirms that multi-color space
approaches outperform approaches using a single co-
lor space. For the Outex-TC-00013 and USPtex da-
tasets, the best result is reached by our approach with
RSCCM whereas for the NewBarkTex dataset, it is
reached by EOCLBP. So, none of these descriptors is
more relevant than the other.
5.3 Processing Time
5.3.1 Learning Stage
Table 5 compares the processing time required by the
learning stage of 1360 images of the Outex-TC-00013
image test suite, for both training and testing images.
These times are obtained using Matlab software on a
PC cadenced at 2.00 GHz and with 4 MB RAM.
Table 5: Processing time of the learning stage for the 1360
training and testing images of the Outex-TC-00013 dataset.
Descriptor RSCCM EOCLBP
Feature computation 287 800 s 1 369 240 s
Feature selection 10 911 s 9 266 s
Total 289 711 s 1 378 506 s
The learning stage seems time-consuming be-
cause a wrapper model is used here to select color
texture features. With this model, the classification
of all validation images is needed in order to esti-
mate the classification accuracy for each candidate
subspace and to determine the dimension of the fea-
ture subspace under construction. The solution to this
problem is to prefer filter or embedded models for the
feature selection evaluation in future work.
The learning time required with the EOCLBP des-
criptor is high because of the computation of features
extracted from the configuration using P = 24 neig-
hbors which consumes the most part of this time. In-
deed, with this parameter value, 2
24
= 16 777 216-
dimensional histograms are analyzed.
5.3.2 Decision Stage
Table 6 shows the processing time required in order
to classify a 128 × 128 Outex sub-image. This time
depends on the selected color texture features and the
dimensionality of the feature space.
This table shows that the classification time is very
low for RSCCM compared to EOCLBP because of
the analysis of high dimensional histograms when the
number of neighbors is high.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
442

Table 6: Processing time of the decision stage for one 128×
128 testing image of the Outex-TC-00013 dataset.
Descriptor RSCCM EOCLBP
Feature computation 933 ms 3 000 ms
Classification 3 ms 3 ms
Total 936 ms 3 003 ms
6 CONCLUSION
In this paper, we have proposed a compact color tex-
ture representation based on the combination of tex-
ture features extracted from various configurations of
descriptors in multiple color spaces. This representa-
tion takes into account different color and spatial pro-
perties of the textures to be analyzed and overcomes
the difficulty of a prior parameter settings. In addi-
tion, a novel family of features computed from histo-
grams of LBP has been proposed in this paper.
Compared to others approaches, experiments car-
ried out on three benchmark texture databases give
competitive results that are very promising for future
work. The proposed approach should be improved by
using a filter model for feature selection rather than
the wrapper model chosen in this paper. Since filter
model is classifier-independent, it should greatly re-
duce the execution time of the learning stage. For the
decision stage, it would be interesting to apply more
performing classifiers like SVM.
Finally, in order to increase the classification accu-
racies, we plan to extend our approach to the com-
bination of texture features extracted from manifold
descriptors (RSCCM, EOCLBP and others) with dif-
ferent configurations and several color spaces.
REFERENCES
Alvarez, S. and Vanrell, M. (2012). Texton theory revisited:
A bag-of-words approach to combine textons. Pattern
Recognit., 45(12):4312–4325.
Bello-Cerezo, R., Bianconi, F., Fern
´
andez, A., Gonz
´
alez,
E., and Mar
´
ıa, F. D. (2016). Experimental comparison
of color spaces for material classification. J. Electron.
Imag., 25(6):061406.
Bianconi, F., Harvey, R., Southam, P., and Fernandez, A.
(2011). Theoretical and experimental comparison of
different approaches for color texture classification. J.
Electron. Imag., 20(4):043006.
Cernadas, E., Fern
´
andez-Delgado, M., Gonz
´
alez-Rufino,
E., and Carri
´
on, P. (2017). Influence of normalization
and color space to color texture classification. Pattern
Recognit., 61:120–138.
Cusano, C., Napoletano, P., and Schettini, R. (2016). Com-
bining multiple features for color texture classifica-
tion. J. Electron. Imag., 25(6):061410.
Guo, J.-M., Prasetyo, H., Lee, H., and Yao, C.-C. (2016).
Image retrieval using indexed histogram of void-and-
cluster block truncation coding. Signal Processing,
123:143–156.
Kalakech, M., Porebski, A., Vandenbroucke, N., and Ha-
mad, D. (2018). Unsupervised local binary pattern
histogram selection scores for color texture classifica-
tion. J. Imaging, 4(10):1–17.
Khan, F. S., Anwer, R. M., van de Weijer, J., Felsberg, M.,
and Laaksonen, J. (2015). Compact color-texture des-
cription for texture classification. Pattern Recognit.
Lett., 51:16–22.
Ledoux, A., Losson, O., and Macaire, L. (2016). Color
local binary patterns: compact descriptors for texture
classification. J. Electron. Imag., 25(6):061404.
Liu, L., Fieguth, J. C. P., Zhao, G., Chellappa, R., and Pie-
tik
¨
ainen, M. (2018). From BoW to CNN: Two decades
of texture representation for texture classification. Int.
J. Comput. Vis., pages 1–36.
Liu, P., Guo, J., Chamnongthai, K., and Prasetyo, H. (2017).
Fusion of color histogram and LBP-based features for
texture image retrieval and classification. Inf. Sci.,
390:95–111.
M
¨
aenp
¨
a
¨
a, T. and Pietik
¨
ainen, M. (2004). Classification with
color and texture: jointly or separately? Pattern Re-
cognit., 37(8):1629–1640.
Palm, C. (2004). Color texture classification by inte-
grative co-occurrence matrices. Pattern Recognit.,
37(5):965–976.
Pietik
¨
ainen, M., Zhao, G., Hadid, A., and Ahonen, T.
(2011). Computer Vision Using Local Binary Pat-
terns. Number 40 in Computational Imaging and Vi-
sion. Springer.
Porebski, A., Hoang, V. T., Vandenbroucke, N., and Hamad,
D. (2018). Multi-color space local binary pattern-
based feature selection for texture classification. J.
Electron. Imag., 27(1):011010.
Porebski, A., Vandenbroucke, N., and Hamad, D. (2013a).
LBP histogram selection for supervised color texture
classification. In IEEE Int. Conf. on Image Proces-
sing, pages 3239–3243, Melbourne, Australia.
Porebski, A., Vandenbroucke, N., and Macaire, L. (2013b).
Supervised texture classification: color space or tex-
ture feature selection? Pattern Anal. Applic., 16(1):1–
18.
Porebski, A., Vandenbroucke, N., Macaire, L., and Hamad,
D. (2014). A new benchmark image test suite for
evaluating color texture classification schemes. Mul-
timed. Tools Appl., 70(1):543–556.
Qazi, I., Alata, O., Burie, J., Moussa, A., and Fernandez-
Maloigne, C. (2011). Choice of a pertinent color
space for color texture characterization using parame-
tric spectral analysis. Pattern Recognit., 44(1):16–31.
Compact Color Texture Representation by Feature Selection in Multiple Color Spaces
443
