Separation of Foreign Patterns from Native Ones: Active Contour based
Mechanism
Piotr S. Szczepaniak
Institute of Information Technology, Lodz University of Technology, Lodz, Poland
Keywords:
Pattern Recognition, Native and Foreign Patterns, Classification, Active Contour, Quality of Data.
Abstract:
This position paper presents an approach to the problem of foreign pattern rejection from a data set containing
both native and foreign patterns. On the one hand, the approach may be regarded as classic in the sense that
it is based on well-known concepts: class-contra-all-other classes or class-contra-class, but on the other hand,
the novelty lies in the (embedding) application of potential active hypercontour, which is a powerful method
for solving classification problems and may be applied as a binary or multiclass classifier.
1 INTRODUCTION
The definitions of the term pattern may be divided
into application- or context-oriented ones. A pattern
may be considered as a representative sample (vector)
which is an example or type for others of the same
classification. The definition of classification is gi-
ven in Section 2 of the paper. Classification is usually
performed on the basis of a set of features observed or
determined for the objects under consideration, which
are called patterns. Here, we speak of classification of
vectors of features which are elements of a certain fe-
ature space. The space is chosen or defined for the
task to be performed and for methods to be used. For
the sake of clarity, in the following discussion the vec-
tors of features are composed of numerical values re-
presenting only real numbers.
In the area of machine learning, and thus also in
the present discussion, pattern recognition is under-
stood as the assignment of a label to a given input
vector representing an object. The goal of pattern re-
cognition applied to a set of patterns is to divide it
into subsets of patterns marked by the same label, i.e.,
classified as belonging to the same group of similar
objects.
In general, patterns can be divided into two types
(Homenda et al., 2017; Homenda and Pedrycz, 2018):
• native - known at the stage of recognizer con-
struction;
• foreign - positioned outside of native sets.
The frequent requirement is to reject the foreign
objects from a given set of patterns, as they deteriorate
the quality of classification. The reason is that they do
not belong to any of the classes defined at the moment
of recognizer construction. In the machine learning
approach, the native database is collected and deter-
mined by objects labelled and present in the learning
set. Note that f oreign and outlier are two different
concepts.
Data sets are frequently non-homogeneous, i.e.,
they may contain data that are atypical, subject to me-
asurement errors, or those that take unusual or erro-
neous values. A classifier constructed using the stan-
dard methods, which do not assume the presence of
any atypical elements at the construction stage, is sup-
posed to assign each input pattern to one of the pre-
viously defined classes. This leads to a foreign pat-
tern being identified as belonging to one of the set of
classes. It will be misclassified, since the presence
of unknown, foreign instances was not taken into ac-
count in the training set. This leads to an increase of
the processing error – here measured in terms of clas-
sification accuracy.
Example: if an IT tool is designed for letter recog-
nition and the training set contains only letters (native
patterns), then the presence of digits and other sym-
bols (here: foreign patterns) among the data analy-
zed will pose a problem. They will be assigned to
one of the previously designed classes, thus affecting
classification correctness, unless the machine is able
to identify and reject the foreign patterns. Other ex-
amples could be given: bicycles among motorbikes,
butterflies among birds etc. In the literature, there
have been relatively few attempts to investigate the
problem of existence and separation of native and fo-
150
Szczepaniak, P.
Separation of Foreign Patterns from Native Ones: Active Contour based Mechanism.
DOI: 10.5220/0007579101500154
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 150-154
ISBN: 978-989-758-353-7
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

reign patterns. The most prominent research achie-
vements in this field are reported in the already menti-
oned works of Homenda et al. (Homenda et al., 2017;
Homenda and Pedrycz, 2018).
The paper is organized as follows. Section 2 pre-
sents the concept of the adaptive potential active hy-
percontour (APAH) and its application to the classifi-
cation problem. Section 3 introduces two foreign pat-
tern rejection mechanisms which incorporate APAH.
Finally, the rule-based approach is briefly described.
2 ACTIVE CONTOUR BASED
CLASSIFICATION
Classification, which is the last stage of the recogni-
tion process, consists in assigning a given vector re-
presenting an object to one of a set of previously de-
fined categories. Thus, it may be regarded as a type
of decision-making problem, in which, of course, the
number of wrong decisions should be reduced to the
minimum.
The classifier is a function
κ : X → Λ(L) (1)
where:
X – vector of features;
L – number of labels (a natural number);
Λ(L) - set of labels;
A standard classification task may be expressed as
follows:
The following number of unknown objects is given
{x},x ∈ X
p
(2)
where:
p – the dimension of a vector x,
X
p
– observation space.
Assign a proper label from Λ(L) to every object.
There are many classification methods, i.e., many
correctly constructed classifiers, which take into ac-
count the following factors:
• vector of features x (as a basic information about
the object),
• surrounding elements (the presence of other cor-
rectly labelled objects, or unlabelled objects),
• expert knowledge, and other.
The question may be posed: which classifier is best
suited to a given problem, i.e., which is the optimal
one?
Generalization of the concept of contour (with the
number of features n = 2 and number of labels L = 2)
has led to the formulation of the term hypercontour,
which operates in R
n
.
The concept of active hypercontours (AH) was de-
veloped as a generalization of the traditional active
contour techniques, as reported in (Tomczyk, 2005).
The hypercontour can be used to separate any set of
objects described by features in metric space X into
an arbitrarily chosen number of classes (regions) L.
Let us recall the formal definition of the term, which
was introduced in (Tomczyk and Szczepaniak, 2006);
see also (Tomczyk et al., 2007):
Definition 2.1. Let ρ denote any metric in X, L =
{1,..., L} denote the set of labels and let K(x
0
,ε) =
{x ∈ X : ρ(x
0
,x) < ε} denote the sphere with centre
x
0
∈ X and radius ε > 0. The set h ⊆ X with infor-
mation about labels of regions it surrounds, is called
a hypercontour if and only if there exists a function
f : X → R and p
0
= −∞, p
1
∈ R,. .., p
L−1
∈ R, p
L
= ∞
(p
1
< p
2
< ·· · < p
L−1
) such that:
h = {x ∈ X : ∃
l
1
,l
2
∈L,l
1
6=l
2
∀
ε>0
∃
x
1
,x
2
∈K(x,ε)
ω(x
1
,l
1
) ∧ ω(x
2
,l
2
)}
(3)
where condition ω(x,l) is true only when p
l−1
≤
f (x) < p
l
and the region {x ∈ X : ω(x, l)} represents
class l ∈ L.
The concept of active hypercontour may be con-
veniently applied in the theoretical context. However,
for practical application, it requires a specific imple-
mentation approach. A possible solution is the poten-
tial active hypercontour (PAH) proposed in (Tomczyk
and Szczepaniak, 2006). It may be generalized for
any metric space, as presented in Def. 2.2.
Definition 2.2. Let feature space X be a metric space
with metric ρ : X × X → R. The potential hypercon-
tour is defined by means of a set of labelled con-
trol points: D
c
= {(x
c
1
,l
c
1
),..., (x
c
N
c
,l
c
N
c
)} where
x
c
i
∈ X and l
c
i
∈ L for i = {1, ...,N
c
}. Each point is
a source of potential, the value of which decreases as
the distance from the source point increases. Classi-
fier k and, consequently, the corresponding hypercon-
tour h that it generates, is defined by:
∀
x∈X
k(x) = argmax
l∈L
N
c
∑
i=1
P
Ψ
i
µ
i
(x
c
i
,x)δ(l
c
i
,l) (4)
where δ : L × L → {0,1}, l
1
6= l
2
⇒ δ(l
1
,l
2
) = 0, l
1
=
l
2
⇒ δ(l
1
,l
2
) = 1 and P : X × X → R is a potential
function, e.g., the exponential potential function:
P
1Ψ
µ
(x
0
,x)
= Ψe
−µρ
2
(x
0
,x)
(5)
or the inverse potential function:
P
2Ψ
µ
(x
0
,x)
=
Ψ
1 + µρ
2
(x
0
,x)
(6)
Separation of Foreign Patterns from Native Ones: Active Contour based Mechanism
151

In both cases, Ψ ∈ R and µ ∈ R represent the para-
meters characterizing the potential field. Those pa-
rameters and the distribution of control points fully
describe the classifier.
As stated before, the principal advantage of the
active hypercontour method is its ability to define
energy (the objective function) in an almost arbitrary
way.
A classifier assigns a class label to each vector
from the feature space and divides it into L regions
of diferent topology. The boundaries of those regi-
ons are interpreted as a visual representation of the
hypercontour. As it is clear from the definition and
description of the hypercontour, it is not restricted to
images, but it can perform classification in any me-
tric space. Let us consider a special case determined
by n = 2 and L = 2, where an image is divided into
two regions, and the boundary of the part interpreted
as the object is in fact a visual representation of the
contour.
Figure 1: Sample hypercontour, L = 2 classes (the values of
parameters Ψ and µ are 1.0 and 5.0, respectively).
Fig. 1 displays a sample result of the poten-
tial active hypercontour applied to the IRIS database
(Dheeru and Taniskidou, 2017) using the first and the
fourth feature. The subspace with a positive potential
(bottom right) is referred to as the ob ject while the
remaining space is defined as the background. The
dataset consisted of L = 3 classes representing three
types of iris plants (iris setosa, iris versicolour and
iris virginica). Each class was represented by 50 ob-
jects and each object was described using n = 4 fea-
tures (sepal length, sepal width, petal length and petal
width).
Compared with Def. 2.1, the above illustration
provides another proof for the close connection bet-
ween contours and classifiers. In formal terms, the
classification task in the adaptive potential active con-
tour (APAH) method may be expressed as:
k(x) = sign[
∑
P
Ψ
i
,µ
i
(ρ(x, p
i
))] (7)
where:
p
i
∈ X denotes a source of potential (potential point)
in feature space X,
P : R → R is the potential function of distance from
point x
i
with additional parameters Ψ
i
, µ,
ρ : X × X → R is a distance function in feature space
X.
As demonstrated in (Tomczyk, 2005), a hyper-
contour can be regarded as similar to a classifier
if X = R
n
and n ∈ N. This is true for any other
metric space X (there are hardly any differences
in the proofs). It follows from the above that each
classifier generates a hypercontour in each metric
space X which has a suficient discriminative power
to distinguish classified objects, and conversely,
each hypercontour unambiguously generates the
corresponding classification function. The term
hypercontour is used to emphasize the relationship
of the proposed technique with the active contour
methods. The connection between active contour
methods and the classifier construction techniques
was first investigated in (Tomczyk and Szczepaniak,
2005).
Summarizing comments:
1. The energy function applied to contour evalua-
tion can be chosen to suit either the supervised or
unsupervised mode of learning optimization.
2. In feature space X, it sets an arbitrary number of
potential source points that define a potential field
comparable to an electric field found in physics.
Each of the points is a source of potential assigned
to one of labels L.
3. In the case of a binary classifier, it divides the fea-
ture space into two subspaces, one with a positive
and the other with a negative potential.
4. The adaptive potential active contour may serve
as a binary or multiclass classifier. The above re-
marks are crucial for the formulation of foreign
pattern rejection mechanisms, which are discus-
sed in more detail in the next section.
3 SEPARATION OF PATTERNS
As mentioned in the Introduction, the frequent
requirement is to reject the foreign objects from
the given set of patterns because they decrease the
quality of classification.
The three following approaches:
(A) separation of foreign from native patterns, follo-
wed by classification of native patterns;
BIOIMAGING 2019 - 6th International Conference on Bioimaging
152

(B) classification of native patterns followed by re-
jection of foreign patterns;
(C) simultaneous classification and rejection;
and the two rejecting mechanisms
(a) class-contra-all-other-classes;
(b) class-contra-class.
are recommended in (Homenda and Pedrycz, 2018).
Both a) and b) can be used in all three approaches.
Let us consider approach A with application of
method a) implemented as adaptive potential active
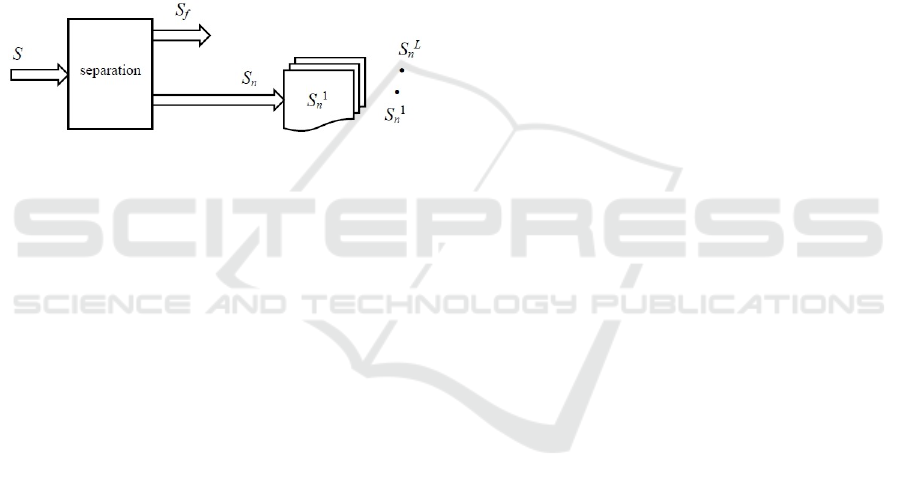
hypercontour (APAH). The set of patterns S to be ana-
lyzed is a mixture of native patterns which form the
set S
n
(of L classes), and foreign patterns – S
f
: S =
S
n
∪ S
f
.
Figure 2: Approach A. Separation of foreign from native
patterns, and classification of native patterns.
To apply method a), the set of L binary classifiers
k
1
(x), k
1
(x), .. . , k
L
(x) of the form class-contra-all-
other-classes must be first constructed. Here, they are
in the form of (3) and one has to train the APAH on
the set of known patterns divided L-times as follows:
class | all-other-classes.
Given a set of unknown patterns {x},x ∈ X
p
, as
defined in (2).
Rejection Mechanism 1 (Using Binary
Classifiers)
Stage 1.
Each unknown pattern x is classified by each binary
APAH-classifier k
l
(x), l = 1,2, ...,L. The result are
sets: patterns of the known classes – native patterns,
and patterns classified as others – foreign ones.
Stage 2.
Use the results of Stage 1 or perform again the
classification of patterns recognized as native in the
Stage 1.
Rejection Mechanism 2 (Using a
Multiclass Classifier)
Each unknown pattern x is classified by the APAH-
multiclass-classifier. The result: L sets of the cor-
rectly classified native patterns, and other patterns –
separated as foreign ones.
Rejection Quality
The rejection performance can be evaluated in a stan-
dard way. In (Homenda and Pedrycz, 2018), six me-
asures are given: accuracy, native sensitivity, native
precision, foreign sensitivity (fs), foreign precision
(fpr), and F-measure. For example:
f s = T N/(T N + FP) and f pr = T N/(T N + FN)
(8)
where the values of FP, FN, TN and TP are as follows:
FP – the number of foreign patterns incorrectly clas-
sified as native ones - false positives;
FN – the number of native patterns incorrectly classi-
fied as foreign ones - false negatives;
TN – the number of foreign patterns correctly classi-
fied as foreign ones - true negatives;
TP – the number of native patterns classified as fo-
reign ones - true positives (both correct and incorrect
class).
More detailed description of both rejection methods,
and more separability measures can be found in (Ho-
menda and Pedrycz, 2018).
Separation Rules
The representation of rules as a hypercube with axis-
parallel planes in the variable space is a human-
friendly approach, which provides the ability to ex-
plain various phenomena and to gain an understan-
ding of the cause-outcome relationship.
The term rule can be used to refer to any logical
condition that assigns a label to an object evaluated
under that condition. For the sake of user-friendly
rule determination and presentation, it is recommen-
ded to associate a rule as an hyperrectangle in space X
where the hypercontour is defined (Szczepaniak and
Pierscieniewski, 2018).
Definition 3.1. The Cartesian product of intervals is
called a hyperrectangle in the space X ⊆ R
n
of n fea-
tures
H
i
n
= [a
i
1
,b
i
1
] × [a
i
2
,b
i
2
] × ·· · × [a
i
n
,b
i
n
] (9)
where [a
i
j
,b
i
j
] are closed intervals, and j =
1,2,... ,n.
It follows from the above that H
i
n
enclosing a set
of patterns determined by feature vectors in R
n
can
be constructed by giving endpoints of the intervals
shown in (9), i.e., the minimum or maximum value of
the respective feature. If each class of patterns (here,
Separation of Foreign Patterns from Native Ones: Active Contour based Mechanism
153

native or foreign ones) is enclosed in one of the hy-
perrectangles H
j
n
( j = 1, 2,. .., n) then obviously H
n
includes all the examined patterns
H
n
= H
n
1
∪ H
n
2
∪ ·· · ∪ H
n
n
(10)
It is possible to optimally match the hyperrec-
tangles to the regions where the native or foreign
patterns are detected by the active hypercontour
applied. Let us call them native-hyperrectangles
and foreign-hyperrectangles, respectively. The rules
associated with those rectangles are of the form:
if for each n x
n
∈ H
i
n
then label of x is l
i
(11)
where l
i
denotes the label associated with native or
foreign patterns, and i determines the respective label.
Of course, the quality of separation by rules is
worse than that obtained by hypercontours. The fol-
lowing five criteria for evaluation of rule quality can
be considered:
• Accuracy – the ability of the ruleset to perform
correct classification of previously unseen exam-
ples.
• Covering – the number of samples covered by the
set of rules.
• Fidelity – the ability of the ruleset to mimic the
behaviour of the hypercontour from which it was
extracted by capturing the information represen-
ted in that hypercontour.
• Consistency – the capability of the ruleset to be
consistent under variable sessions of rules gene-
ration; the finally obtained ruleset produces the
same classifications of unseen examples from the
test set.
• Comprehensibility – this criterion refers to the
size of the ruleset (measured in terms of the num-
ber of rules and the number of antecedents per
rule).
The above criteria bear a close resemblance to those
considered in the problem of rule extraction from ar-
tificial neural networks (Diedrich, 2008).
4 CONCLUSIONS
This paper has presented an approach to the problem
of separating foreign patterns from native ones. It has
proposed two foreign pattern rejection mechanisms
incorporating adaptive potential active hypercontours
(APAH). The potential of this approach lies in the
classification power of APAH, which – as the very
name suggests – is an adaptive, i.e., flexible method.
If a human-friendly interpretation is requested, then
the logical classification rules can be associated with
the results generated by APAH.
ACKNOWLEDGEMENTS
The author appreciates the assistance of L. Pierscie-
niewski who has performed the experiments on IRIS
database shown in Fig. 1, and the assistance of J. La-
zarek in the editorial work. Both persons are with
Lodz University of Technology, Poland.
REFERENCES
Dheeru, D. and Taniskidou, K. (2017). Iris dataset. UCI
machine learning repository.
Diedrich, J. (2008). Rule extraction from support vector
machines. Studies in Computationa Intelligence, 80.
Homenda, W., Jastrzebska, A., and Pedrycz, W. (2017).
Unsupervised mode of rejection of foreign patterns.
Applied Soft Computing, 57:615–626.
Homenda, W. and Pedrycz, W. (2018). Pattern Recognition
A Quality of Data Perspective. Wiley.
Szczepaniak, P. and Pierscieniewski, L. (2018). Rule ex-
traction from active contour classifiers. Journal of Ap-
plied Computer Science JACS, 26(1):76–83.
Tomczyk, A. (2005). Active hypercontours and contextual
classification. In 5th Int. Conference on Intelligent
Systems Design and Applications (ISDA), pages 256–
261. IEEE Computer Society Press.
Tomczyk, A. and Szczepaniak, P. S. (2005). On the relati-
onship between active contours and contextual clas-
sification. In Proceedings of the 4th International
Conference on Computer Recognition Systems (CO-
RES05), pages 303–311. Springer-Verlag.
Tomczyk, A. and Szczepaniak, P. S. (2006). Adaptive po-
tential active hypercontours. In 8th Int. Conference on
Artificial Intelligence and Soft Computing (ICAISC),
pages 692–701. Springer-Verlag.
Tomczyk, A., Szczepaniak, P. S., and Pryczek, M. (2007).
Supervised web document classification using dis-
crete transforms, active hypercontours and expert kno-
wledge. In WImBI 2006, LNAI 4845, pages 305–323.
Springer-Verlag.
BIOIMAGING 2019 - 6th International Conference on Bioimaging
154