
Grid-based Exploration of OCT Thickness Data of Intraretinal Layers
Martin R
¨
ohlig
1
, J
¨
org St
¨
uwe
1
, Christoph Schmidt
1
, Ruby Kala Prakasam
2
, Oliver Stachs
2
and Heidrun Schumann
1
1
Institute of Computer Science, University of Rostock, Albert-Einstein-Str. 22, Rostock, Germany
2
Department of Ophthalmology, University of Rostock, Doberaner Str. 140, Rostock, Germany
Keywords:
Visual Analysis of OCT Data, Optical Coherence Tomography, Modified ETDRS Grids, Intraretinal Layers.
Abstract:
Optical coherence tomography (OCT) enables high-resolution 3D imaging of the human retina to understand
a variety of retinal and systemic disorders. Commonly, the thickness of segmented intraretinal layers is used to
assess the condition of the retina. However, the thickness data are complex and thus, need to be considerably
reduced prior to further processing and analysis. This leads to a loss of information and may hinder the
discovery of subtle and localized retinal changes, which are important for an early detection of certain diseases.
On this account, we propose an enhanced grid-based reduction of OCT thickness data. We adapt established
grid types for retinal thickness data and suggest alternative grids that capture more information. We integrate
our data reduction approach into a visual analysis tool that supports an automated computation and interactive
exploration of different grids. We demonstrate the application of our tool and show how it can be used to
support experts in choosing and comparing appropriate grid representations for given OCT thickness data.
1 INTRODUCTION
Optical coherence tomography (OCT) is a widely-
used noninvasive technique to capture high-resolution
3D images of retinal substructures. Ophthalmolo-
gists analyze the resulting data to understand a va-
riety of retinal and systemic disorders, e.g., diabe-
tic retinopathy, age-related macular degeneration, and
glaucoma. Particularly, the thickness of segmented
intraretinal layers is used to assess the condition of
the retina. However, derived thickness data are com-
plex, as one thickness value is typically computed for
every single point of each intraretinal layer. On the
one hand, this enables a spatially precise judgment of
the layers. On the other hand, the large amounts of
thickness values are difficult to deal with, and a ge-
neral summary of thickness changes in larger retinal
areas is missing. Hence, ophthalmologists typically
rely on considerable data reduction prior to further
processing and analysis of the data.
Established data reduction approaches for OCT
thickness data are commonly based on retinal grids.
These grids are used to spatially divide the retina into
few large regions and to derive aggregated thickness
measures for each region. This helps to get a quick
overview of the layers’ thickness in anatomically pre-
defined areas. Moreover, it drastically reduces the
amount of information to be analyzed, particularly if
the layer thickness in larger studies with dozens or
hundreds of OCT datasets has to be evaluated. Yet,
due to the spatial aggregation, information loss may
occur. This is because small and localized variations
in thickness are not always reasonably represented via
aggregated values of large regions. Capturing such in-
formation is, however, mandatory for detecting early
signs of certain diseases or investigating progressions.
We aim at supporting ophthalmologists in their
grid-based visual analysis of intraretinal layer
thickness. We propose an enhanced data reduction
scheme together with a visual analysis tool for the ex-
ploration of alternative grids. Our approach helps to
strike a balance between obtaining a compact grid re-
presentation of thickness data and being able to cap-
ture more relevant information of intraretinal layers.
Our contributions are:
New Grid Design: We propose an enhanced grid-
based reduction scheme for OCT thickness data.
New grid layouts are derived based on radial and
sector-wise subdivision of well-established grids.
Data-driven Adaptation: We introduce a procedure
to compute the suitability of different grid layouts
for given thickness data. The grids are rated and
best options are suggested to the user.
Röhlig, M., Stüwe, J., Schmidt, C., Prakasam, R., Stachs, O. and Schumann, H.
Grid-based Exploration of OCT Thickness Data of Intraretinal Layers.
DOI: 10.5220/0007580001290140
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 129-140
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
129

Grid-based Exploration: We develop a new vi-
sual analysis tool for grid-based exploration of
thickness data. Grids are interactively adjusted,
compared to other grids of different datasets, and
grid-related details are investigated on demand.
2 BACKGROUND
Our work is motivated and driven by advances in the
detection of retinal diseases. Particularly, the dyna-
mic development of OCT technology with respect to
image quality, e.g., the improvement of the axial and
lateral resolution, offers a unique possibility of dif-
ferentiating and precisely measuring substructures of
the retina. Modern OCT devices are able to capture
even subtle retinal changes and allow to accurately
monitor the progression of a disease. Based on the
data, ophthalmologists aim at performing both:
• Patient-specific assessments of the retinal condi-
tion of individuals
• Group-specific evaluations of experimental and
prospective studies in ophthalmic research
In this context, they often need to compare multi-
ple intraindividual datasets, e.g., follow-up examina-
tions of a single patient, and interindividual datasets,
e.g., examinations of patients in relation to normative
data of controls. Yet, the data analysis can be complex
and the available analysis methods differ between ex-
isting software tools. In this regard, our work is rela-
ted to the visual analysis of retinal OCT data in gene-
ral, and to the representation of retinal layer thickness
via grids in particular.
2.1 Visual Analysis of OCT Data
Current analysis procedures are based on a combina-
tion of commercial OCT software, non-commercial
OCT software, and general-purpose analysis soft-
ware. Segmentation of intraretinal layers and measu-
rement of layer thickness are supported by both com-
mercial software and non-commercial software (Gar-
vin et al., 2009; Mayer et al., 2010; Mazzaferri et al.,
2017). Commercial OCT software is commonly dis-
tributed by OCT device manufactures. Currently, se-
veral major platforms are available, including soft-
ware from Nidek, Optovue, Zeiss, Topcon, Heidel-
berg Engineering and others. The provided software
platforms are predominantly used in clinical practice
as well as for ophthalmic research. Besides commer-
cial software, few approaches for visually analyzing
retinal OCT data exist. Examples are the research-
oriented Iowa Reference Algorithms (Garvin et al.,
2009), the open-source software ImageJ (Schindelin
et al., 2015) and its application to OCT data (Garrido
et al., 2014), a 3D visualization of OCT data based on
ray-tracing (Glittenberg et al., 2009), and a recent vi-
sual analysis framework based on multiple coordina-
ted views (R
¨
ohlig et al., 2018). These software tools
are typically applied in ophthalmic research. In gene-
ral, all available analysis software packages support at
least one of three fundamental presentation methods
for OCT data: cross-sectional views, 3D views, and
top-down views.
Cross-sectional views show individual 2D image
slices of volumetric OCT data together with overlaid
profiles of segmented intraretinal layers. This allows
to view details but flipping through the images is time-
consuming, as OCT datasets can consist of hundreds
of slice images. 3D views show an entire OCT dataset
as a 3D volume rendered tomogram. This provides
an overview of the data but combined 3D visualizati-
ons of the tomogram and the layers are only provided
by few tools, e.g., (R
¨
ohlig et al., 2018). Top-down
views show a fundus image of the interior surface of
the eye around the OCT acquisition area together with
superimposed retinal layers. This facilitates a layer-
centric analysis of the data and helps to link the lay-
ers to retinal areas in the fundus image. In general,
cross-sectional views and 3D views are mainly used
for the visual analysis of individual datasets, whereas
top-down views are also applied to anatomically lo-
calize and compare areas under investigation in mul-
tiple OCT datasets. In this regard, top-down views are
most relevant to our work.
Instead of showing the raw OCT data, top-down
views typically represent intraretinal layers via their
derived layer thickness. The layer thickness is dis-
played either via thickness maps or via spatially
aggregated thickness grids. This helps to reveal
even subtle retinal changes, which may be difficult
to identify by visualizing the raw OCT data alone.
While there recently have been advances in the ap-
plication of thickness maps for the analysis of OCT
data (R
¨
ohlig et al., 2018), thickness grids are still pre-
dominantly used in most opthalmic applications. On
the other hand, the design of thickness grids has been
hardly investigated in previous work, despite the con-
tinuous development of OCT technology and asso-
ciated analysis methods. On this account, we parti-
cularly focus on the grid-based exploration of retinal
thickness data.
IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications
130

Figure 1: Grid representation of retinal layer thickness. An OCT scan captures the area around the macula and the optic
disk (a). The resulting volumetric data consists of multiple 2D image slices (B-scans) (b). Several intraretinal layers are ex-
tracted from each B-scan (c) and thickness values are computed for every pixel along the horizontal image axes by measuring
the vertical distance between the upper and lower layer boundaries (d). The thickness values are combined across all B-scans
per retinal layer (e) and spatially aggregated into corresponding grid representations (f).
Figure 2: The layout of the ETDRS grid. The grid divides
the retina into nine regions defined by three rings, i.e., cen-
tral, pericentral, and peripheral, and four sectors, i.e., nasal,
temporal, superior, and inferior.
2.2 Representation of Retinal Layer
Thickness via Grids
The most common grid type to represent retinal
thickness data was established by the Early Treatment
Diabetic Retinopathy Study (ETDRS) (Chew et al.,
1996). The cells of ETDRS grids divide the retina into
nine large regions, i.e., a central foveal ring with 1mm
diameter, an inner macula ring (pericentral) with 3mm
diameter, and an outer macula ring (peripheral) with
6mm diameter. The inner and outer rings are further
divided into four quadrants, namely nasal, temporal,
superior, and inferior. For each grid cell and intrare-
tinal layer, typically one aggregated thickness measu-
rement is stored. Figure 1 illustrates how such grid re-
presentations are obtained and Figure 2 shows the la-
yout of the ETDRS grid. The grid design enables the
localization and assessment of anatomically impor-
tant areas of the macula near the center of the retina.
Thus, ETDRS grids have been widely applied for va-
rious purposes in ophthalmic research, including in-
vestigations of early structural changes of the retina
for a variety of diseases, e.g., diabetes mellitus (G
¨
otze
et al., 2018) and glaucoma (Chen et al., 2017). Alt-
hough other grid types exist, they have been mos-
tly designed for special applications, e.g., rectangular
grids for asymmetry analysis of retinal thickness for
glaucoma diagnosis (Asrani et al., 2011).
A major advantage of ETDRS grids is their com-
pact representation of the complex thickness data with
only few aggregated values for each intraretinal layer,
i.e., typically one arithmetic mean thickness value per
grid cell. This allows a quick overview and judgment
of thickness changes in predefined retinal areas. Mo-
reover, the applied data reduction eases the evalua-
tion and comparison of multiple datasets. Particularly
in case of larger studies, it is easier to handle fewer
data values for statistical analysis and interpretation
of the data. That is because ophthalmologists conven-
tionally export ETDRS thickness values from OCT
software to external spreadsheet software or statistics
software to compile study groups and to perform ba-
tched or non-batched statistical analyses. On top of
that, the fixed grid cells enable the comparison of re-
sults from different studies that used ETDRS grids.
On the downside, the main problem with ETDRS
grids is that they do not necessarily faithfully repre-
sent underlying thickness data (Fig. 3). Due to the
considerable spatial data reduction, localized variati-
ons in thickness of an intraretinal layer are not accu-
rately captured via a single aggregated thickness va-
lue per grid cell. This is the case for both small vari-
ations in thickness within a grid cell and variations
divided by the boundary of two or more grid cells
(Fig. 3c). Moreover, when evaluating deviations bet-
ween thickness data of multiple OCT datasets, aggre-
gation artifacts may bear an additional risk of infor-
mation loss. The reason for this is that localized po-
sitive and negative deviations within a grid cell may
be nullified during data reduction (Fig. 3g). This can
Grid-based Exploration of OCT Thickness Data of Intraretinal Layers
131

Figure 3: Data representation with ETDRS grids. The thickness of an intraretinal layer is shown via a thickness map (a) and
an ETDRS grid (b). Small and localized regions of high thickness (dark red) in the map are not accurately represented in all
cells of the grid, e.g., cell (c) with regions of high thickness has almost the same aggregated value as cell (d) without such
regions. In addition, localized regions of positive and negative deviations in thickness (dark red and dark blue) in the map (e)
are nullified in certain cells of the grid (f), e.g., averaging artifacts of grids cells (g).
lead to false normal findings. Detecting such infor-
mation is, however, vital for the identification of early
retinal changes of certain diseases.
3 GRID DESIGN
Given both the discussed benefits and drawbacks of
ETDRS grids, we aim at designing alternative grids
that combine the advantages of ETDRS grids with the
possibility to capture more relevant information. To
this end, we identified design requirements, devised a
new subdivision scheme that allows to compare diffe-
rent grid layouts, and developed a method to rate the
representation quality of grids for given data.
3.1 Requirements
The grid-related design requirements reflect the ex-
perts’ needs with regard to processing and analyzing
OCT thickness data. We derived the following list by
talking with the experts about current limitations and
about the way they utilize existing grids to analyze
thickness data of intraretinal layers.
Layout based on ETDRS Grid (GR
1
): The basic
layout of alternative grids should correspond to
the ETDRS grid. This is to maintain the ability
to localize anatomically important areas of the
macula near the center of the retina.
Compact Data Representation (GR
2
): In general,
the number of grid cells should be small and the
content of a grid cell should be mainly represen-
ted by only a single descriptive value. Nevert-
heless, an appropriate representation of thickness
data should be facilitated.
Compariability of Grid Layouts (GR
3
):
Alternative grid layouts should be compara-
ble to both the basic ETDRS grid and other
alternative grids. This is to ensure that analysis
results from multiple datasets with different grids
are relatable.
3.2 Subdivision of Grids
Based on the experts’ demands, we design alterna-
tive grids that meet requirements GR
1
and GR
2
. Our
approach is based on subdivisions of existing grid la-
youts. Taking the ETDRS grid as a basis, we employ
a radial or a sector-wise partition strategy of ETDRS
grid cells. This allows us to obtain alternative grids
that represent the underlying thickness data at diffe-
rent levels of granularity. Figure 4a exemplifies both
partition strategies.
Radial partitions add rings to a grid. The resulting
grid cells enable a more fine-grained analysis of areas
with respect to the distance from the foveal center.
For example, intraretinal layer thickness of macula
rings can be investigated in-depth via secondary peri-
central or peripheral cells. Sector-wise partitions add
separating lines at certain angles to a grid. The ge-
nerated grid cells facilitate a more direction-centric
analysis of areas with respect to the foveal center.
For example, by adding further directional cells, the
thickness of areas facing nasally may be evaluated in
greater detail in relation to areas facing temporally.
Radial and sector-wise partitions can also be combi-
ned to obtain fine grids that support analyses with fo-
cus on both properties.
To restrict the number of all possible combinati-
ons of subdivisions, we suggest to start by equally di-
viding grid cells and to increase the number of radii
or sectors in power of two steps. By dividing grid
cells in half for each radial or sector-wise subdivision
IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications
132
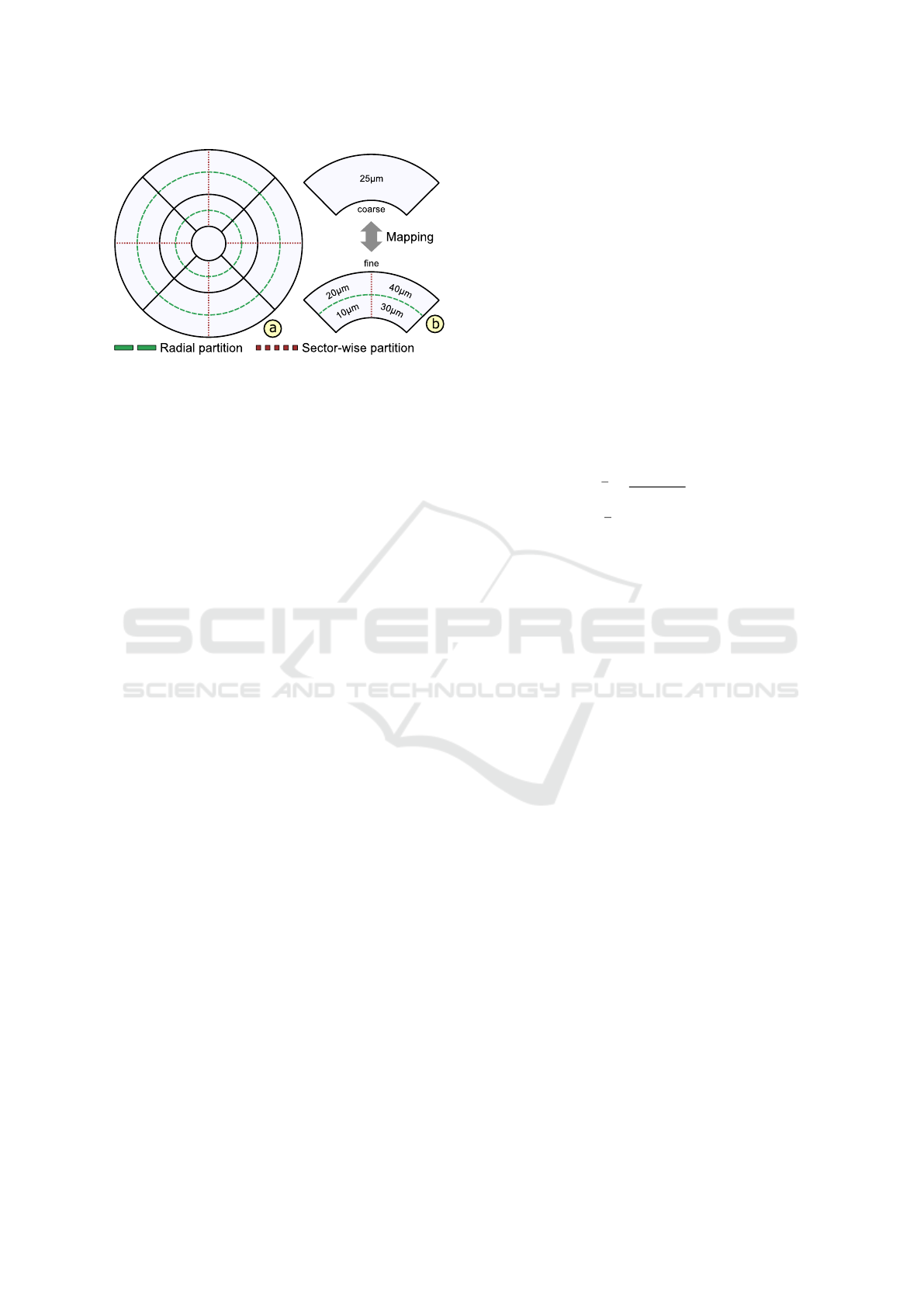
Figure 4: Subdivision and mapping of grids. The ETDRS
grid layout is subdivided via radial (dashed line) or sector-
wise (dotted line) partitions to derive alternative grids (a).
To ensure the comparability of grids, a coarse grid is map-
ped to a fine grid or vice versa by subdividing or merging
corresponding grid cells (b).
pass, the amount of information stored in a subdivi-
ded grid is increased in constant steps. The resulting
set of grids can then be refined interactively. Just like
conventional ETDRS grids, we represent the content
of each grid cell via one aggregated thickness mea-
surement. Optionally, additional summary statistics,
e.g., mean, percentiles, and standard deviation, may
be stored per cell to provide further information on
the distribution of the underlying thickness data.
Utilizing the well-known ETDRS grid as a basis
for radial or sector-wise subdivisions helps experts
to familiarize themselves with the layout of derived
grids. The simple and fixed subdivision scheme eases
the localization of areas under investigation and the
interpretation of the data. This in turn increases the
acceptance of alternative grids. Next, we discuss how
to further support experts in choosing an appropriate
grid from a set of alternatives for their given data.
3.3 Rating of Grids
In general, no single grid layout exists that fits all pos-
sible spatial distributions of thickness data. Instead of
trying to create such an all-solving solution, we pro-
vide a set of alternative grids to choose from. Yet,
given all available grid layouts, experts now face the
problem that they have to decide which grid actually
matches their given data. To support experts in this
decision, we developed a rating procedure based on
a quantitative measure of the representation quality
for each grid under consideration. With our rating of
grids we are able to address the second aspect of de-
sign requirement GR
2
.
We determine the overall representation quality of
a grid by measuring the homogeneity of thickness va-
lues of all data points within each grid cell. This is
based on the assumption that a cell with high homo-
geneity covers thickness values that are more or less
equal, whereas a cell with low homogeneity encloses
strongly varying thickness values. Thus, an aggrega-
ted thickness value of a grid cell with high homoge-
neity matches the thickness values within that cell. In
contrast, a cell with low homogeneity indicates infor-
mation loss, e.g., due to averaging of localized vari-
ations. Consequently, a grid composed of cells with
high homogeneity corresponds to a good representa-
tion of the underlying thickness data and vice versa.
One possible measure to quantify the amount of
variation or homogeneity of a set of thickness values
inside a grid cell is the standard deviation. Based on
this simple measure, we obtain the overall rating of a
grid via the weighted arithmetic mean of the compu-
ted standard deviations of all grid cells.
x =
∑
n
i=1
w
i
x
i
∑
n
i=1
w
i
In this equation, x represents the final rating of the
grid, n denotes the number of grid cells, x
i
is the stan-
dard deviation of a cell, and w
i
is the weight for that
cell given by the normalized amount of enclosed data
points (equal to the size of the cell). Based on the final
ratings, we compute a ranking for a set of alternative
grids and suggest a best fit for thickness data of one
retinal layer while considering secondary expert con-
straints. Such constraints are a specified maximum
number of allowed grid cells or a preference for either
radial or sector-wise subdivisions. This promotes a
more patient-specific analysis in contrast to generali-
zing all given thickness data to just the ETDRS grid
representation. Likewise, the rating and ranking can
be adapted to support a group-specific assessment of
grids. The procedures allow to find one best fitting
grid for multiple layers of one dataset or even for one
or several layers of multiple datasets, e.g, to obtain
one grid to represent the data of all patients in a study.
The resulting rankings are then used to steer the grid-
based visual exploration of thickness data.
3.4 Comparability of Grids
Ophthalmologists are often interested in relating
grid-based analysis results from multiple datasets
(cf. GR
3
). In a patient-specific analysis scenario, each
of these individual datasets may be best represented
by another grid with a different layout. To ensure the
comparability of the grids, we support mapping a fine
grid to a coarse grid and vice versa. This is possible
as in our design a fine grid is basically a subdivided
version of a coarse grid. Figure 4b illustrates both
mapping strategies. In addition, in a group-specific
Grid-based Exploration of OCT Thickness Data of Intraretinal Layers
133

analysis scenario, grids of a patient group may have
to be compared to grids of another patient group or of
a control group. On this account, we allow to compile
a set of multiple source grids of a group into a single
aggregated grid. The aggregated grid cells can then be
mapped and assigned values can be directly related.
Mapping a fine grid to a coarse grid entails that
subdivided grid cells have to be merged together to
the granularity level of the cells of the coarse grid.
The values of the merged cells are determined by ag-
gregating the values of the corresponding subdivided
cells, e.g., by computing and storing their arithmetic
mean. The most prominent example for this mapping
strategy is to trace alternative grids back to the ini-
tial ETDRS grid. As a practical example, this allows
to compare new analysis results obtained via our grid
design to results of previous ophthalmic studies based
on the ETDRS grid. Another example is to select the
coarsest subdivision grid from a set of alternatives as
reference and to map the other grids to that reference.
This is necessary if the underlying thickness data are
no longer available and thus, merging finer cells and
aggregating associated values are the only options.
Mapping a coarse grid to a fine grid involves that
coarse grid cells are subdivided to the granularity le-
vel of the cells of the fine grid. The values of the sub-
divided cells are then assigned either by recomputing
them based on the underlying thickness data or sim-
ply by copying the values of corresponding coarser
cells. A precondition for the second case is however
that the coarse grid is a good representation of that
data and consequently, a subdivided version of that
grid represents the data equally well, i.e, it just con-
sists of more grid cells. An advantage of this mapping
strategy is that no details stored via finer grid cells are
lost during the comparison. Practically this is impor-
tant if, for example, a fine grid representing a patient
with abnormal localized variations in thickness has to
be compared to a coarser grid representing normative
data of healthy controls, which commonly show less
variations in thickness and only in larger areas.
Compiling an aggregated grid implies that mul-
tiple source grids are transformed into a single grid
representation. First, a layout for the aggregated grid
is determined and then the source grids are mapped to
that common layout. The aggregated grid represents
the source grids via one descriptive value per cell,
e.g., the arithmetic mean of corresponding source cell
values. In addition, summary statistics of source va-
lues may be stored per aggregated grid cell. To ana-
lyze two or more aggregated grids, they are mapped
using one of the above strategies and related based on
corresponding cell values. This way, a grid of a single
patient or an aggregated grid of a patient group can be
compared to an aggregated grid of a control group.
In summary, our grid design allows to obtain com-
pact representations of retinal thickness data compa-
rable to well-established ETDRS grids, while also
being able to capture more relevant information.
Thus, our solution is a first step towards supporting
ophthalmologists in choosing thickness grids that fit
the OCT data under investigation. In addition, we de-
signed an interactive visualization tool that supports
the exploration of different grids and adjusting their
visual representation.
4 GRID-BASED VISUAL
EXPLORATION
We aim at supporting users in their grid-based analy-
sis of OCT thickness data of intraretinal layers. For
this purpose, we design a visualization tool based on
multiple coordinated views. Figure 5 shows an over-
view of the user interface. Our tool supports: (i) vi-
sualizing grids, (ii) showing grid details on demand,
(iii) interactively adapting grids to facilitate explora-
tion, and (iv) comparing different grids.
4.1 Presentation of Grids
In order to enable a comprehensive analysis of
thickness grids, we visualize different grids together
with related information. To this end, we design a
top-down view for coloring and labeling of grids and
a measurement view for showing details of grid cells.
The top-down view provides an overview of diffe-
rent thickness grids with regard to the interior surface
of the eye (Fig. 5a). A fundus image depicts the OCT
acquisition area. Colored grids of selected intraretinal
layers are visualized on top of the fundus image. The
opacity of the grid overlay can be adjusted using a sli-
der to help to relate attribute values in the maps to no-
ticeable structures in the subjacent fundus image. All
other intraretinal layers are shown as grid thumbnails
on the side, ordered according to their anatomical lo-
cation within the retina (Fig. 5c). This view design
presents grids for all layers in one image without ha-
ving to flip through them manually. Thus, layers with
abnormal characteristics can be easily discovered.
The coloring of grids is based on suitable and ad-
justable palettes (Harrower and Brewer, 2003). Se-
quential palettes encode the actual thickness of indi-
vidual grids or the averaged thickness of aggregated
multiple grids. The cells are colored by evaluating
the stored thickness values with respect to clinically
established thresholds. Two boundary values are gi-
ven for all cells of each retinal layer. Low thickness
IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications
134

Figure 5: Overview of our prototypical visual analysis tool. In the left top-down view (a), an intraretinal layer (b) is selected
in the layer overview (c) and the associated thickness grid is enlarged and superimposed over a fundus image. Aggregated
thickness values per cell are color-coded, labels indicate cell values close to specified thresholds, and borders of cells with low
ratings are highlighted (purple). Details about the underlying thickness data of a selected grid cell (d) are shown in a linked
measurement view (e). In the right top-down view (f), the selected grid is mapped and compared to reference data of a control
group and deviations are color-coded. Details of a selected cell (g) are shown in a second measurement view (h) in relation to
the distribution of the reference data.
values are assigned to light colors, high thickness va-
lues to dark colors, and thickness values outside the
specified thickness ranges to distinctively lighter or
darker colors. Figure 5a shows an example. This al-
lows to judge the thickness data globally in relation
to the given boundaries. The coloring on the basis of
common thresholds also allows to relate grid presen-
tations across different datasets.
The labeling of grids enriches the colored grid
presentation with additional text labels and highligh-
ted cell borders. Text labels are added to show values
of grid cells in detail. Optionally, only text labels of
selected cells or of cells with values outside of speci-
fied thresholds are displayed. This is to prevent visual
clutter in the image, particularly in fine grids with a
lot of small cells. Instead of showing numeric cell va-
lues, the textual labeling can be switched to encode
location-oriented cell names. To this end, existing na-
ming conventions of the ETDRS grid (cf. Fig. 2) can
be adapted to derived grids, e.g., by adding suffixes
like pericentral inner or outer for radially partitioned
cells. Alternatively, naming schemes based on notati-
ons of time and partial distances can be applied. For
instance, the location of a cell is denoted by 11:0.25,
which stands for a cell in the direction of the 11th hour
on a 12-hour clock at one-quarter of the distance bet-
ween the foveal center and the outer macular border.
Next to text labels of cells, cell borders are outlined
to illustrate the structure of grids and to highlight spe-
cific cells. By default, all cell borders are outlined.
This presentation can be adjusted to match selecti-
vely shown text labels of abnormal cells or to mark
the ETDRS grid layout in subdivided grids (Fig. 6a).
This further facilitates the localization of cells. Fi-
nally, cell borders may be emphasized to reflect the
computed rating of grid cells, e.g., to indicate infor-
mation loss in cells with low homogeneity (Fig. 6b).
The measurement view helps to go beyond the ba-
sic grid presentation and to show further details about
the underlying thickness data (Fig. 5e). Thickness va-
lues of selected cells in the top-down view are visu-
alized as lines and numerical text labels on top of a
color legend in the measurement view. The legend re-
flects the applied coloring and specified thresholds of
the grid presentation. Next to the legend, summary
statistics associated with selected cells are optionally
shown as statistical plots. For individual grids, the
distribution of the contained thickness data is visuali-
zed via box-and-whisker plots and histograms toget-
her with numerical labels of descriptive values. This
helps to judge the grid representation and to under-
stand the rating of cells, e.g., by showing the distribu-
tion of highlighted cells with low homogeneity. For
aggregated grids, the statistical plots encode the dis-
tribution of thickness values assigned to correspon-
ding cells of all source grids. This allows to assess the
variability of thickness values of a group of patients.
4.2 Interactive Exploration of Grids
To promote an in-depth analysis of retinal thickness
data, the data have to be explored at appropriate level
of granularity. We support users in specifying initial
grids to start the exploration, browsing through grids
at different levels of granularity, adapting grids on de-
mand, and comparing different grids.
Specifying initial grids is possible via interactive
grid design and based on automated grid suggestions.
To interactively design a grid, the respective layout
parameters, i.e., the number of radii and sectors, have
Grid-based Exploration of OCT Thickness Data of Intraretinal Layers
135

Figure 6: Interactive exploration of grids. The ETDRS grid
layout is marked on a subdivided grid to support the locali-
zation of cells (a). Grid cells with low ratings (purple bor-
ders) are interactively subdivided to investigate details (b).
to be set. This first option offers the most freedom
to the expert and allows to obtain a set of grids that
reflects specific needs. The second option is to auto-
matically suggest fitting grids for given thickness data
based on the computed rating and ranking of a prede-
fined set of alternative grid layouts. Such a predefined
set of alternatives may consist of increasingly finer
subdivisions of the ETDRS grid using combinations
of both radial and sector-wise partition strategies. An
expert may further steer the automated selection by
setting additional constraints, e.g, the maximum num-
ber of allowed grid cells. This helps to obtain grids at
an appropriate level of granularity, i.e., grids that cap-
ture even small and localized variations in thickness.
Browsing through grids is supported by interactive
selections from a set of specified grid layouts. Se-
lected grids are immediately presented in the top-
down view with cells colored and labeled. By flip-
ping through these grids, the data can be explored at
different levels of granularity. For instance, selecting
increasingly finer subdivision of the ETDRS grid al-
lows to analyze the data from overview, i.e., coarsest
grid, to detail, i.e., finest grid. This helps to under-
stand the data and to localize areas of interest.
Interactively adapting grids allows to refine a se-
lected grid layout. On demand, one or multiple grid
cells may be selected and then merged together or
subdivided by means of the provided partitioning stra-
tegies (cf. Sect. 3.2). This helps to fine-tune grids
for given data based on the expertise of experts. For
instance, while browsing through alternative grids,
a specific grid is selected, cells are visualized, and
information about the underlying thickness data is
shown. Individual grid cells with low ratings are then
further subdivided to investigate respective areas in
greater detail and the remaining cells are merged to-
gether to provide context information of less relevant
areas. Figure 6b exemplifies the adaption of grids.
Comparison of different grids is enabled by juxta-
position of views, explicit encoding of deviations, and
application of statistical tests. The juxtaposition of
Figure 7: Comparison of different grids. The top-down
view (a) and the linked measurement view (b) show a group-
specific comparison of an aggregated grid of a patient group
to an aggregated grid of a control group. The juxtaposed
small multiple views (c) show an overview of grids of all
individual members of the patient group compared to the
aggregated grid of the control group. Thickness deviations
are explicitly encoded using a diverging color palette.
views supports the comparison of several individual
grids (Fig. 5a, f). In the user interface, multiple in-
stances of the top-down view and measurement view
can be dynamically added and freely arranged. For
a patient-specific analysis, different grids of the same
patient, e.g., follow-up examinations, or of related pa-
tients, e.g., similar medical cases, can be assigned to
these view instances. Linking the view instances en-
sures that matching parts of the data are shown. For a
group-specific analysis, individual grids of all mem-
bers of a group are shown as small multiple views
(Fig. 7c). This provides a quick overview and allows
to detect differences between group members.
The explicit encoding of deviations facilitates a di-
rect comparison of a grid to a reference grid. For this
purpose, the coloring of the grid presentation is swit-
ched. The cells are colored using diverging palettes
and by evaluating the stored thickness values with re-
spect to threshold intervals of an aggregated reference
grid. The boundary values vary cell by cell for each
layer, e.g., confidence intervals or percentile bounda-
ries per reference cell. Small deviations from a re-
ference are represented via a light neutral color and
larger negative or positive deviations via respective
darker colors. Displaying deviations helps to evalu-
ate a thickness grid locally in relation to a reference
IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications
136

grid. Figure 5f and Figure 7a exemplify comparisons
of a grid of a single patient and of an aggregated grid
of an entire patient group to intervals ranging between
the 2.5
th
and 97.5
th
percentile boundaries stored in an
aggregated grid of a control group, respectively.
The application of statistical tests allows to quan-
tify the differences between multiple aggregated
grids. For example, for the comparison of aggrega-
ted grids of two different groups, e.g., patients and
controls, an independent two-sample Student’s t-test
is applied and for aggregated grids of more groups an
one-way analysis of variance is performed. The re-
sulting measurements of statistical significance, i.e.,
p-values, and effect size are shown as numerical la-
bels. In addition, statistical plots for the cells of each
grid under consideration are shown in the measure-
ment view (Fig. 7b). This illustrates the difference
between the thickness distributions and provides ad-
ditional details about the color-coded deviations in the
comparative grid presentation. Altogether, the functi-
onality eases the evaluation of studies with a lot of
datasets, as this conventionally requires to first export
the data of all source grids and then to statistically
analyze them using external software (cf. Sect. 2.2).
5 APPLICATION
We applied and evaluated our research prototype in
cooperation with domain experts. We particularly ai-
med at assessing the utility of our solutions in the con-
text of experimental studies. Here, we briefly describe
one use case, present exemplary results, and reflect on
benefits and limitations of our approach.
5.1 Use Case
In this use case, we applied our solutions to study if
early retinal changes in adult patients suffering from
age-related macular degeneration (AMD) can be cap-
tured via different grid representations. In addition,
we were interested in relating the obtained results to
grid representations of healthy control subjects.
A common early sign of AMD is the presence of
drusen in the macula. Drusen are small accumula-
tions of extracellular material that build up between
Bruch’s membrane and the retinal pigment epithelium
(RPE) of the eye (Yoshimura and Hangai, 2014). The
high sensitivity of OCT and the analysis of OCT data
support detecting such small and localized changes,
and hence may contribute to an early diagnosis and
immediate intervention. Yet, in the thickness data of
the RPE, these retinal changes are reflected by small
Figure 8: Examples of alternative grids evaluated in our use
case. Three partitioning strategies were applied to derive in-
creasingly finer grids: radial (a), sector-wise (b), and radial
and sector-wise partitions (c).
and localized increases in thickness. We hypothe-
size that conventional ETDRS grids may not always
accurately represent the thickness data in this situa-
tion (cf. Sect. 2.2). In fact, the principal goal of this
study was to assess alternative grids for early retinal
changes in all datasets of participating AMD patients.
The study data were acquired via OCT examinati-
ons of two groups of subjects. The first group consists
of 8 adults with AMD and the second group of 20 he-
althy controls. For each subject, the thickness data
of the RPE from one OCT dataset of the macula was
selected for further investigation (28 datasets in total).
Starting from the ETDRS grid, three partitioning stra-
tegies were applied: radial, sector-wise, or radial and
sector-wise partitions. The numbers of radii and sec-
tors were increased in constant steps per strategy up
to a maximum of 129 radii, 256 sectors, and 17 radii
plus 32 sectors respectively. The finest grid had 513
cells for each strategy. In total, a set of 21 grids, i.e.,
7 grids per strategy, was defined (Fig. 8). In a pre-
process, grid representation were computed and rated
for the thickness data of each dataset in both groups.
The ratings were then summarized per grid to judge
the overall representation quality for each group.
Figure 9 shows an overview of the obtained re-
sults. Note that these results are only meant as a proof
of concept example to demonstrate the feasibility of
our approach. We are aware of the possible bias indu-
ced by the small sample size, which prevents drawing
any medical conclusions. Nonetheless, from a data-
centric perspective, we are able to reason about the
utility of our approach and to summarize our insig-
hts gained from interpreting the results. In this con-
nection, we assume that a superior data representation
is reflected by a better rating of grids using the measu-
res introduced in Sect. 3.3, i.e., a good representation
is equal to a low mean standard deviation.
Grid-based Exploration of OCT Thickness Data of Intraretinal Layers
137
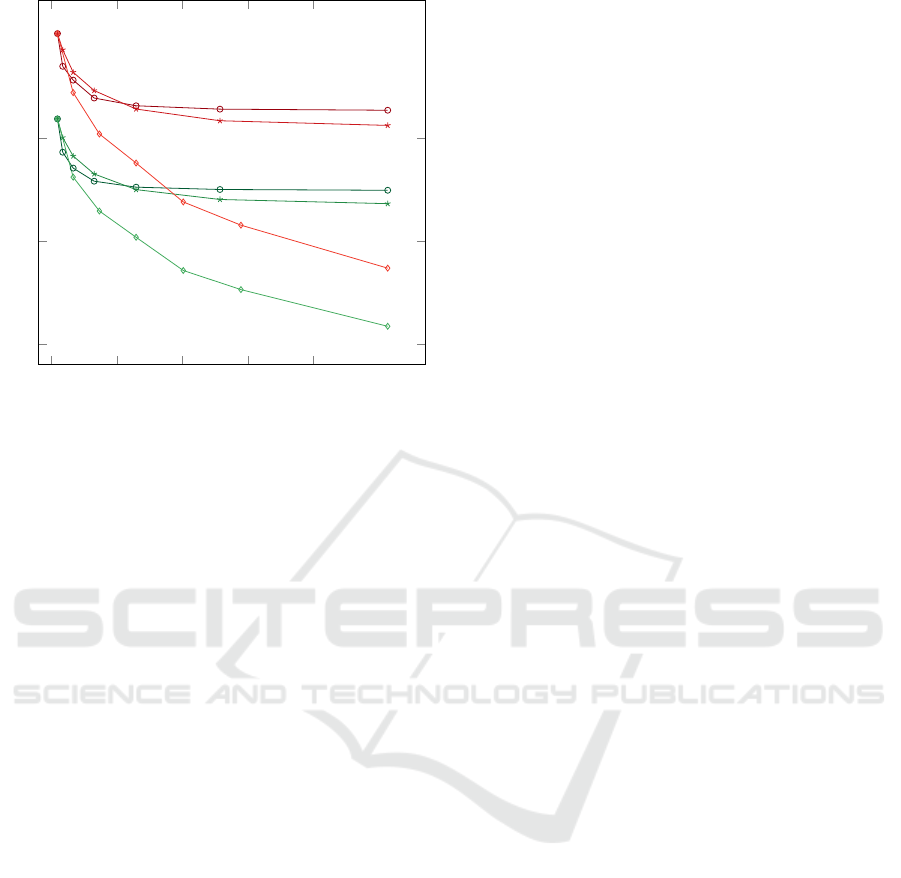
0 100 200 300 400
0.3
0.4
0.5
d
e
f
a
b
c
Cells
Rating
Figure 9: Overview of the study results. The line plot
shows ratings of grids, i.e., summarized standard deviati-
ons, with respect to cell counts. The ratings are depicted for
the thickness data of patients (red) and controls (green) in
relation to three partitioning strategies: radial (a, d), sector-
wise (b, e), and radial and sector-wise (c, f).
In general, all subdivided grids showed better ra-
tings than the ETDRS grid. For the thickness data of
patients, grids based on sector-wise partitions perfor-
med slightly better than grids based on radial partiti-
ons (Fig. 9a, b). Interestingly, for both partition stra-
tegies, an increase in cell count only resulted in better
ratings up to a certain point. In contrast, for combi-
ned radial and sector-wise partitions, an increase in
cell count showed steadily improved ratings (Fig. 9c).
A possible explanation is that early drusen often come
in the form of small, roughly circular-shaped regions
of high thickness. Hence, grid cells that match such
shapes, e.g., cells of grids subdivided via combined
radial and sector-wise partitions, will result in better
overall ratings of respective grids.
For the thickness data of controls, we observed
patterns in the grid ratings that are similar to the re-
sults of patients (Fig. 9d, e, f). This similarity can
probably be explained due to the consideration of pa-
tients with early signs of AMD in the study, i.e., while
the patients’ thickness data showed some noticeable
changes, they were still not too far from the data of
healthy controls. One remarkable difference was, ho-
wever, that the control data generally required fewer
cells to obtain equally good ratings of grids. This is
probably due to the fact that thickness data of healthy
eyes contains less localized variations in thickness.
Thus, an appropriate grid representation of the data
can be achieved with fewer and coarser cells.
5.2 User Feedback and Lessons
Learned
Our solutions are the result of a participatory design
process starting from prior work (R
¨
ohlig et al., 2018).
We cooperated with two groups of domain experts,
including ophthalmic research scientists and a team
of technical and medical professionals from a major
commercial OCT device manufacturer. Throughout
the development, we had close contact with primarily
two ophthalmic experts. Together, we applied and tes-
ted our prototype in collaborative data analysis sessi-
ons using a pair analytics approach (Arias-Hernandez
et al., 2011). We also held repeated demonstration
and feedback sessions with around ten participants of
both expert groups. We jointly identified challenges
and specified respective requirements (cf. Sect. 3.1).
Their informal feedback helped us to devise suitable
grid designs and visualization techniques.
During the discussions, the experts stated that they
liked the visual analysis tool because it allowed them
to explore their thickness data at different levels of
granularity. They also appreciated the consideration
of the established ETDRS grid in our grid design.
At the same time, they reassured us that the provi-
ded methods for subdivision, rating, and comparabi-
lity of grids are meaningful enhancements to obtain
appropriate data representations. In fact, the experts
reported that there is a need to find grids that match
certain ophthalmic applications, as existing grids are
not always the best choice for their analysis tasks.
In this regard, the results of our experimental
study suggest that our approach can be a useful aid
for identifying appropriate grids for given thickness
data. However, arbitrarily fine subdivided grids are
practically unfeasible for some applications. For ex-
ample, choosing a grid with a large number of cells
may impede further utilization of the data. On this
account, the experts approved to have the rating and
ranking of grids at their disposal. It helped them to de-
cide how much variance they are willing to accept in
a grid with a certain amount of cells. They considered
such decisions to be particularly easy to make in case
of grids that showed only minimally improved ratings
in further subdivision with a certain partitioning stra-
tegy (cf. Fig. 9). Thus, with the provided functiona-
lity, they were able to balance the granularity of grids
and the amount of encoded information.
As another major advantage, the ophthalmic ex-
perts identified the ability to compare multiple and
possibly differing grids with each other and to the
conventional ETDRS grid. The interlinked top-
down and measurement views helped them to quickly
switch between grids of different layers or datasets
IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications
138

and to show grid-related details when necessary. For
the analysis of larger studies, they considered the vi-
sualization of deviations between aggregated grids of
groups and the integrated quantification of differen-
ces based on statistical tests to be particular useful.
They concluded that reducing the manual analysis ef-
fort and being able to obtain results with higher spatial
accuracy compared to the current analysis procedures
are great benefits.
6 CONCLUSION
We presented an enhanced grid-based data reduction
approach for retinal thickness data. A new grid design
helps to strike a balance between obtaining a compact
data representation and being able to capture more re-
levant information. A coordinated visual analysis tool
supports a grid-based exploration of thickness data at
different levels of granularity. Different grids from
multiple datasets are compared. Alternative grids are
rated and ranked to facilitate the selection of best fit-
ting grids for given thickness data. Our approach con-
stitutes a systematic enhancement of existing work
and hence, provides a first step towards supporting
ophthalmologists in their grid-based analysis of intra-
retinal layer thickness.
Our data reduction is based on subdivisions of the
widely-used ETDRS grid layout. This allows to ad-
dress various ophthalmic applications while promo-
ting a more patient-specific analysis. Beyond taking
the ETDRS grids as a basis, the main ideas of subdivi-
sion, rating, and comparability together with coordi-
nated visualization are applicable to other grid types
as well. This may help to support fine-grained ana-
lyses in more specific ophthalmic applications, e.g.,
asymmetry analysis of retinal thickness for glaucoma
diagnosis using rectangular grids (Asrani et al., 2011).
During demonstration and feedback sessions, our
experts reported that it is not always known which
grid helps to solve a given analysis task. Hence, re-
search effort exists to find new grids that adequately
represent retinal changes of specific diseases. In this
regard, our rating and ranking of grids may help in
evaluating newly designed grids and sorting out ex-
isting grid types. So far, we used a data-driven ap-
proach to judge the representation quality of grids.
An interesting extension is to also support diagnosis-
driven grid ratings. This requires defining custom me-
asures that match different ophthalmic analysis tasks,
e.g. asymmetry analysis of thickness data. Moreo-
ver, assistance in choosing suitable rating cutoffs for
the selection of grids has to be provided. That way,
automated grid suggestions for specific tasks or ap-
plication are possible. However, to fully support such
efforts, more work is needed to be able to compare
and rank different grid types.
We ascertained the general utility of our solutions
in first tests with domain experts. To improve our de-
sign, we plan further evaluations of our tool in the
context of experimental studies. In this connection, an
interesting open question is how our grid-based analy-
sis approach can be combined with recent map-based
analysis approaches for thickness data of intraretinal
layers, e.g., (R
¨
ohlig et al., 2018). To utilize the be-
nefits of both approaches, identifying and evaluating
best practices for each solution is required with re-
spect to an ophthalmic analysis workflow.
ACKNOWLEDGEMENTS
This work has been supported by the German Rese-
arch Foundation (project VIES).
REFERENCES
Arias-Hernandez, R., Kaastra, L. T., Green, T. M., and Fis-
her, B. D. (2011). Pair analytics: Capturing reasoning
processes in collaborative visual analytics. In Pro-
ceedings of the Hawaii International Conference on
System Sciences, pages 1–10, Washington, DC, USA.
IEEE Computer Society.
Asrani, S., Rosdahl, J., and Allingham, R. (2011). Novel
software strategy for glaucoma diagnosis: Asymme-
try analysis of retinal thickness. Archives of Ophthal-
mology, 129(9):1205–1211.
Chen, Q., Huang, S., Ma, Q., Lin, H., Pan, M., Liu, X.,
Lu, F., and Shen, M. (2017). Ultra-high resolution
profiles of macular intra-retinal layer thicknesses and
associations with visual field defects in primary open
angle glaucoma. Scientific Reports, 7:41100.
Chew, E., Klein, M., Ferris, F., Remaley, N., Murphy, R.,
Chantry, K., Hoogwerf, B., and Miller, D. (1996). As-
sociation of elevated serum lipid levels with retinal
hard exudate in diabetic retinopathy: Early treatment
diabetic retinopathy study (ETDRS) report 22. Archi-
ves of Ophthalmology, 114(9):1079–1084.
Garrido, M. G., Beck, S. C., M
¨
uhlfriedel, R., Julien, S.,
Schraermeyer, U., and Seeliger, M. W. (2014). To-
wards a quantitative OCT image analysis. PLOS ONE,
9(6):1–10.
Garvin, M. K., Abramoff, M. D., Wu, X., Russell, S. R.,
Burns, T. L., and Sonka, M. (2009). Automated 3-
D intraretinal layer segmentation of macular spectral-
domain optical coherence tomography images. IEEE
Transactions on Medical Imaging, 28(9):1436–1447.
Glittenberg, C., Krebs, I., Falkner-Radler, C., Zeiler, F.,
Haas, P., Hagen, S., and Binder, S. (2009). Advan-
tages of using a ray-traced, three-dimensional rende-
ring system for spectral domain cirrus HD-OCT to vi-
Grid-based Exploration of OCT Thickness Data of Intraretinal Layers
139

sualize subtle structures of the vitreoretinal interface.
Ophthalmic Surgery Lasers and Imaging, 40(2):127–
134.
G
¨
otze, A., von Keyserlingk, S., Peschel, S., Jacoby, U.,
Schreiver, C., K
¨
ohler, B., Allgeier, S., Winter, K.,
R
¨
ohlig, M., J
¨
unemann, A., Guthoff, R., Stachs, O.,
and Fischer, D.-C. (2018). The corneal subbasal nerve
plexus and thickness of the retinal layers in pediatric
type 1 diabetes and matched controls. Scientific Re-
ports, 8(1).
Harrower, M. and Brewer, C. A. (2003). Colorbrewer.org:
An online tool for selecting colour schemes for maps.
The Cartographic Journal, 40(1):27–37.
Mayer, M. A., Hornegger, J., Mardin, C. Y., and Tornow,
R. P. (2010). Retinal nerve fiber layer segmentation
on FD-OCT scans of normal subjects and glaucoma
patients. Biomedical Optics Express, 1(5):13581383.
Mazzaferri, J., Beaton, L., Hounye, G., N. Sayah, D., and
Costantino, S. (2017). Open-source algorithm for au-
tomatic choroid segmentation of OCT volume recon-
structions. Scientific Reports, 7.
R
¨
ohlig, M., Schmidt, C., Prakasam, R. K., Schumann, H.,
and Stachs, O. (2018). Visual analysis of retinal chan-
ges with optical coherence tomography. The Visual
Computer, 34(9):1209–1224.
Schindelin, J., Rueden, C. T., Hiner, M. C., and Eliceiri,
K. W. (2015). The ImageJ ecosystem: An open plat-
form for biomedical image analysis. Molecular Re-
production and Development, 82(7-8):518–529.
Yoshimura, N. and Hangai, M. (2014). OCT Atlas. Sprin-
ger, Berlin, Germany.
IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications
140
