Detecting Neonatal Seizures using Sample Covariance Estimation
Aleksandar Jeremic
1
and Dejan Nikolic
2
1
Department of Electrical and Computer Engineering McMaster University, Hamilton, ON, Canada
2
Physical Medicine and Rehabilitation, University Childrens Hospital, Faculty of Medicine, University of Belgrade,
Belgrade, Serbia
Keywords:
Seizure Detection, Information Fusion.
Abstract:
One of the most frequent of neurological dysfunctions in prematurely born infants is the presence of frequent
seizures. As they may be related to serious neurological problems they require immediate detection which is
most commonly done using electroencephalography (EEG) systems that enable trained physicians to detect
them in the real time. Due to the length of neonatal period (first 28 days) it would be extremely beneficial
to have an automated system that is able to detect seizures as it would enable more efficient use of expert
time. In this paper we propose a new multichannel technique for detecting seizure in neonates that calculates
distance measure using second order statistical properties and Frechet mean. We have demonstrated previously
that Frechet mean in certain cases can outperform clustering/detection algorithms that are based on first order
distances.
1 INTRODUCTION
A seizure is defined clinically as a paroxysmal alter-
ation in neurologic function, i.e., behavioural, mo-
tor, or autonomic function. It is a result of excessive
electrical discharges of neurones, which usually de-
velop synchronously and happen suddenly in the cen-
tral nervous system (CNS). It is critical to recognize
seizures in newborns, since they are usually related to
other significant illnesses. Seizures are also an initial
sign of neurological disease and a potential cause of
brain injury (Volpe, 2001).
In a clinical settings physicians are able to detect
seizures based on EEG data however the process may
be time consuming considering the number of cot-
beds in regular size NICU department. To this pur-
pose developmentof computer-aided diagnosis would
be extremely beneficial as such system would be im-
portant from both academic and clinical standpoint
of view. From the academic stand point automatic
recording of seizures and consequently analysis of
these data would provide insight into frequency of
occurrence and correlate it with the dynamic of neu-
rological development. From clinical standpoint it
could be useful tool for adjusting level of medical care
based on the neurological state of the brain with re-
spect to seizures.
In our previous work, we proposed several dis-
tributed detection algorithms for neonatal seizure de-
tection using some of the commonly used seizure de-
tection algorithms. In this paper we propose new local
detectors based on the Frechet mean of the EEG sig-
nal covariance calculated using sliding window. First,
we present an estimator of the Frechet mean of the
covariance matrices on the manifold M using the dif-
ferent measures of Riemannian distances. Then we
introduce the Fr´echet mean based on several Rieman-
nian distances and discuss computational algorithms
for calculating the proposed distance means. In Sec-
tion 3 we illustrate applicability of our results using
data set of NICU patients. Finally, in Section 4 we
discuss future directions.
2 SIGNAL MODEL
2.1 Frechet Mean Local EEG Detectors
We use the notion of Fr´echet mean to unify the
method of finding the mean of positive definite ma-
trices. The Fr´echet mean is given as the point which
minimizes the sum of the squared distances (Bar-
baresco, 2008):
ˆ
S = argmin
S ∈M
n
∑
i=1
d
2
(S
i
,S ) (1)
where {S
i
}
n
i=1
represents the symmetric positive defi-
246
Jeremic, A. and Nikolic, D.
Detecting Neonatal Seizures using Sample Covariance Estimation.
DOI: 10.5220/0007580302460250
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 246-250
ISBN: 978-989-758-353-7
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

nite matrices and d(.,.) denotes the metric being used
respectively. Therefore the above expression can be
interpreted as a way of calculating an averaged sam-
ple covariance matrix using a sliding window where
S
i
represents an i−th window sample covariance es-
timate. Then the overall estimate of the covariance
matrix is calculated using a particular metric. We will
use this technique to calculate sample covariance ma-
trix of EEG signal in the absence of seizures assuming
that these intervals of no-seizures were properly iden-
tified by an expert.
To measure the distance between two M ×M co-
variance matrices A and B on manifold of positive
definite matrices M , we consider the metrics which
have been developed to measure distance between
two points on the manifold itself.
The first metric is obtained by measuring distance
between projections on the subspace spanned by uni-
tary matrices (Li and Wong, 2013)
d
R
1
(A,B) =
q
Trace(A) + TraceB) −2Trace(A
1
2
BA
1
2
)
1
2
In general for any positive definite matrix A its square
root is defined as A
1
2
= S
√
LD
H
; where A = SLD
H
is
the eigenvalue value decomposition of matrix A with
diagonal matrix L consisting of eigenvalues of A.
The second metric is obtained by measuring the
distance between their projections on the subspace
spanned by identity matrices. It has been shown (Li
and Wong, 2013) that this distance is equivalent to:
d
R
2
(A,B) =
q
Trace(A) + Trace(B) −2Trace(A
1
2
B
1
2
)
(2)
Finally, as a last local detector we propose to use
the log- Riemannian metric is given as (Moakher,
2005):
d
R
3
(A,B) =



log(A
−
1
2
BA
−
1
2
)



2
=
s
M
∑
i=1
log
2
(L
i
)
(3)
where the L
i
’s are the eigenvalues of the matrix A
−1
B
(Absil et al., 2009).
In order to solve the corresponding minimization
problems we presented detailed computational algo-
rithms for calculating these distances in (Jahromi et
al., 2015). In all the cases certain iterative proce-
dures are necessary however we demonstrated exis-
tence of unique solutions (means) for all the proposed
distances.
In order to define local detectors we first identify
no-seizure segments and define overlapping windows
which are used to calculate covariance matrices in the
absence of seizures. using the following algorithm:
Let y
i
be the i-th sample of inter-arterial pressure mea-
surements. Then the outline of the algorithm is as fol-
lows
• within the training data set create windows
~
d
k
=
[y
(k−1)∗l1+1
,··· ,y
k∗l1−1
] where l1 is the length of
the window
• within the above window select subwindows of
length l2 and label them
~
d
j
k
where j = 1,l1−l2+
1
• remove the sample mean from the windowvectors
• calculate rank 1 sample covariances
~
d
j,T
k
~
d
j
k
and
average them using Frechet mean instead of com-
monly used addition
These sample covariances are then used as a clus-
ter of reference covariance matrices in which the cen-
tre of the cluster is defined using the above met-
rics. The threshold is then calculated as a function
of predefined probability of false alarm i.e. incorrect
seizure detection. Therefore by setting a false alarm
ratio to α we can empirically calculate threshold for
a particular patient by using event-free segments of
EEG recordings.
2.2 Distributed Detection System
Each of the metric detectors v presented in the previ-
ous section can be considered as a single channel i.e.
local detector. In order to improve the overall perfor-
mance of a single detectors we propose to combine
the existing single detectors and utilize their strengths
by extending previous results on blind multichannel
information fusion (Liu et al., 2007).
Local
Detector LD
Local
Detector LD
Local
Detector LD
Phenomenon
Fusion
Center
u
u
u
1
2
n
y
1
y
2
y
n
u
0
1
2
n
Figure 1: Parallel Distributed Detection System.
Figure 1 shows the structure of a typical parallel
distributed detection system with N detectors. The
local detectors transmit local decisions u
n
based on
a particular metric that they are using. Obviously in
our case there are three local detectors as we are us-
ing three different metrics. All the local decisions are
then sent to the fusion centre, where the global de-
cision u
0
is made based on a fusion rule in order to
minimize the overall probability of error. Additional
Detecting Neonatal Seizures using Sample Covariance Estimation
247

detectors can be added into the system whenever more
information is required to make final decision.
The local decisions u
n
, n = 1,2,3 can be expressed
as
u
n
=
(
0, thenth detector favoursH
0
1, thenth detector favoursH
1
(4)
where ”favours” should be interpreted as the distance
between actual sample covariance estimate and refer-
ence covariance estimate is smaller than the empiri-
cal threshold for a particular false alarm rate. We use
P(H
0
) to denote prior probability that the seizures are
not present in a particular signal segment. A com-
mon assumption used here is the local observations
y
n
are conditionally independent, given the unknown
hypothesis H
i
.
After receiving the local decisions, the fusion cen-
tre makes the global decision by applying an optimal
fusion rule in order to minimize the final error prob-
ability. For a binary hypothesis testing problem, the
error probability P
e
is given by
P
e
= P(H
0
)P(u
0
= 1|H
0
) + P(H
1
)P(u
0
= 0|H
1
) (5)
The authors provided the optimality criterion for N
local detectors in the sense of minimum error prob-
ability in (Varshney, 1986). We recall it here for the
case of N = 3.
u
0
=
(
1, if w
0
+
∑
3
n=1
w
n
> 0
0, otherwise
(6)
where, w
0
= log

P
1
P
0

(7)
and w
n
=
(
log((1−P
m
n
)/P
f
n
), if u
n
= 1
log(P
m
n
/(1−P
f
n
)), if u
n
= 0
(8)
The probabilities of false alarm and missed detec-
tion of the nth local detector are denoted as P
f
n
and
P
m
n
, respectively. The optimal fusion rule tells us that
the global decision u
0
is determined by the a priori
probability and the detector performances, i.e., P
1
, P
f
n
and P
m
n
. However, they are all unknown in our seizure
detection problem, which is usually the case in many
other real applications (Mirjalily, 2003),(Liu et al.,
2007). In order to make the final decision, we need
to utilize the information available to us: the local bi-
nary decisions u
n
.
Suppose the decision combination {u
1
= i, u
2
=
j and u
3
= k} is represented by ℓ = (ijk)
2
, where
i, j,k = 0 or 1 (Mirjalily, 2003). In our system, the
number of all the possible local decision combina-
tions is 2
3
and will be denoted as L in the remainder of
this paper. The joint probability of decision {u
1
= i,
u
2
= j and u
3
= k} is also the occurrence probability
of the ℓth decision combination, given by
P
ℓ
= Pr(u
1
= i, u
2
= j, u
3
= k)
= P(u
1
= i|H
1
)P(u
2
= j|H
1
)P(u
3
= k|H
1
)P
1
+P(u
1
= i|H
0
)P(u
2
= j|H
0
)P(u
3
= k|H
0
)(1−P
1
)
(9)
P(u
n
= i|H
1
) =
(
1−P
m
n
, if i = 1
P
m
n
, if i = 0
(10)
P(u
n
= i|H
0
) =
(
P
f
n
, if i = 1
1−P
f
n
, if i = 0
(11)
In this nonlinear system, only seven out of eight
equations are independentsince
∑
P
ℓ
= 1 and there are
seven unknowns P
1
, P
f
n
and P
m
n
, for n = 1,2,3. Thus,
it can be solved when P
ℓ
are known. Although P
ℓ
is
usually unavailable in practice, it could be replaced
by empirical probability defined as
P
ℓ
= Pr(u
1
= i,u
2
= j,u
3
= k)
≃
number ofu
1
= i,u
2
= j,u
3
= k
number of local decisionsN
t
(12)
where N
t
is the number of decisions made by one
of the local detectors. The analytical solution to
the above nonlinear equations is given in (Mirjalily,
2003).
Note that in a particular setting if the data size is
limited and/or the number of events needed for accu-
rate calculation of anomalies is not sufficient we de-
veloped a maximum likelihood based algorithm that
exploits the multinomial probability mass function
describing the decision vector and utilized in order to
estimate the anomalies as well as prior probabilities
(seizure and no-seizure). We presented the details of
these algorithms in (Liu et al., 2014).
3 RESULTS
We evaluate the performance of the proposed algo-
rithms on the data set consisting of preterm infants
(GA less than 32 weeks) admitted to the Neonatal In-
tensive Care Unit at McMaster Hospital. Due to phys-
ical limitations we were able to obtain prior expect
knowledge on a very limited time length and hence
all of the non-seizure epoch were shorter than 400
samples using single C3 channel with minimal mo-
tion artefacts.
For illustrational purposes in Figures 2-4 , we il-
lustrate the detection performance as a scatter dia-
gram of windows selected from testing data. Note that
in the presence of motion artifacts the actual perfor-
mance will actually vary significantly. Furthermore
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
248

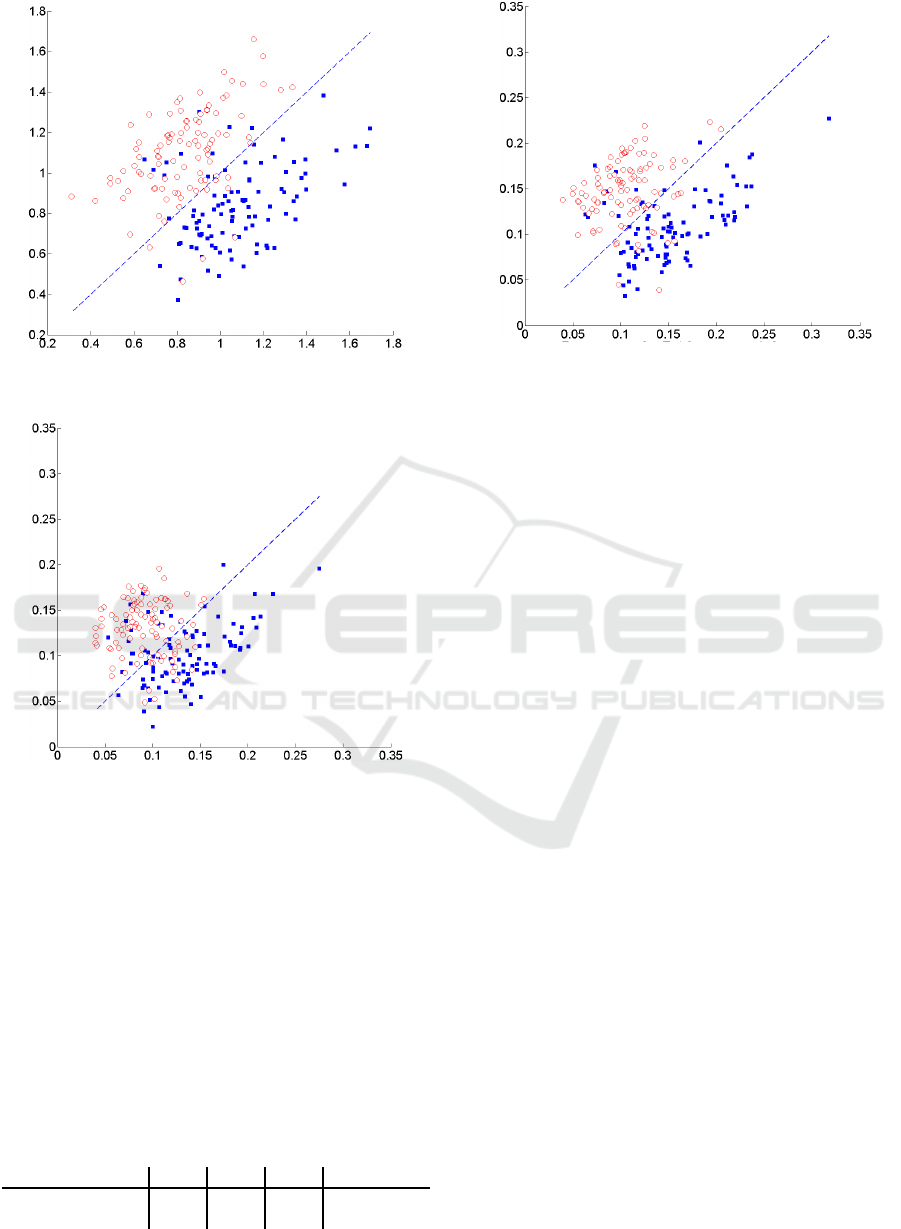
Figure 2: Scatter plot of detection performance using metric
d
R1
.
Figure 3: Scatter plot of detection performance using metric
d
R2
.
because the original system design was based on no-
seizures the system was calibrated so that the prob-
ability of false alarm is controlled. Due to motion
artifacts and reaction to pain stimuli during medical
procedures in NICU it is quite likely that local detec-
tors will identify these manifestation in EEG as false
seizure. The x and y axes represent distances to co-
variance matrices corresponding to signal segments
with and without seizures. Note that in order to test
applicability of the proposed techniques we selected
signal segments in which the prior probabilities are
approximately the same.
Table 1: Average seizure detection performance.
d
R1
d
R2
d
R3
ML-Fused
false seizures 0.07 0.09 0.12 0.05
missed seizures
0.09 0.08 0.11 0.07
Figure 4: Scatter plot of detection performance using metric
d
R3
.
4 CONCLUSIONS
Automatic systems for seizure detection have been
subject of considerable research interest in the past.
One of main advantages lies in the fact that expert
time is potentially required only during the training
session. Furthermore, for newborn patients admit-
ted to NICU such systems enable continuous moni-
toring of seizure events and hence can provide bet-
ter insight into neurological development. In recent
years significant effort has been placed on develop-
ing systems that predict seizures in order to poten-
tially counter them with appropriately generated elec-
trical stimuli. To this purpose in this paper we ex-
amine possibility of detecting seizures by measuring
different distances between sample covariance matrix
estimates. Since different second order distances fo-
cus on various structural information we propose to
combine their decisions by minimizing overall prob-
ability of error. To achieve this goal we define lo-
cal detectors using empirically determined threshold
and fuse their local decisions using our previously de-
veloped information fusion algorithm for seizure de-
tection. We demonstrate the applicability of the pro-
posed algorithms using a real data set consisting of
multiple NICU patients.
In future work we plan to improve performance
by including mean based local detectors as well as
instantaneous frequency based detectors as they may
account for features that are not accounted for in the
proposed covariance based detectors. Furthermore
the performance of these detectors should be inves-
tigated in scenarios in which priors may have differ-
ent values as the training of the proposed system de-
pends on seizure occurrence frequency. Finally an ef-
fort should be made to evaluate performance when
Detecting Neonatal Seizures using Sample Covariance Estimation
249

the training set includes epoch intervals that include
seizures. In this case we expect that the problem
can be easily formulated as a classification problem
in which case the Frechet-mean based algorithms of-
ten improve performance when combined with mean
based algorithms (such as k-means).
REFERENCES
Absil, P.-A., Mahony, R., and Sepulchre, R. (2009). Opti-
mization algorithms on matrix manifolds. Princeton
University Press.
Barbaresco, F. (2008). Innovative tools for radar signal pro-
cessing based on Cartan’s geometry of SPD matrices
& information geometry. Radar Conference, 2008.
RADAR’08. IEEE, pages 1–6.
Jahromi et al., M. (2015). Estimating Positive Definite Ma-
trices Using Frechet Mean. In Biosignals 2015.
Li, Y. and Wong, K. M. (2013). Riemannian distances for
EEG signal classification by power spectral density.
IEEE journal of selected selected topics in signal pro-
cessing.
Liu, B., Jeremic, A., and Wong, K. (2007). Blind adaptive
algorithm for M-ary distributed detection. In IEEE In-
ternational Conference on Acoustics, Speech and Sig-
nal Processing, 2007. ICASSP 2007, volume 2.
Liu, B., Jeremic, A., and Wong, K. (2014). Optimal dis-
tributed detection of multiple hypotheses using blind
algorithm. IEEE Trand. on Aerospace and Electronic
Systems, 50:1190–1203.
Mirjalily, G. e. (2003). Blind adaptive decision fusion
for distributed detection. IEEE Transactions on
Aerospace and Electronic Systems, 39(1):34–52.
Moakher, M. (2005). A differential geometric approach
to the geometric mean of symmetric positive-definite
matrices. SIAM Journal on Matrix Analysis and Ap-
plications, 26(3):735–747.
Varshney, P. (1986). Optimal data fusion in multiple sen-
sor detection systems. IEEE Trans. on Aerospace and
Electronic Systems, pages 98–101.
Volpe, J. (2001). Neurology of the newborn. WB Saunders
Co.
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
250