Towards the Modelling of Osseous Tissue

F. D. P

erez and J. J. Jim

enez

Graphics and Geomatics Group, University of Ja

en, Ja

en, Spain

Keywords:

Modelling, Image reconstruction, Virtual, Bone, Tissue.

Abstract:

The virtual representation of bone tissue is one of the pending challenges of infographics in the ﬁeld of trau-

matology. This advance could mean a reduction in the time and effort that is currently used in the analysis of a

bank of medical images, as it is done manually. Our proposal aims to lay the foundations of the elements that

must be taken into account not only geometrically, but also from a medical point of view. In this article we

focus on the segmentation of a bone model, establish the limits for its representation and introduce the main

characteristics of the microstructures that form in the bone tissue.

1 INTRODUCTION

Computer graphics applied to medicine is a ﬁeld of

research with many open lines and continues to boom

due to the advancement of technologies. In the ﬁeld of

traumatology, the creation of computer-assisted tech-

niques has made it possible to reduce the intervention

time, minimise the risk of error and advances in re-

search to microscopic levels in order to predict and

reduce the possibility of suffering a fracture. Stud-

ies at microscopic levels are generally based on the

use of computed tomographic images (CT). These im-

ages contain more detailed information than X-rays

and are 2D grayscale images, which can be converted

into a 3D volume, where the intensity of the pixel cor-

responds to the coefﬁcient of absorption of the mate-

rial. In addition to the difﬁculty of obtaining a quality

image bank to work, the radiation used to obtain the

images can cause serious tissue damage and mean a

signiﬁcant health risk to patients. Therefore, there is

a need to ﬁnd a way to replace them. Our main objec-

tive is the generation of virtual bone tissue that will

allow us to advance through the substitution of these

images by providing a much richer and more varied

database than the one traditionally obtained with CT

images without endangering the health of patients. In

addition, it will make it possible to analyse and ob-

tain certain data that normally have to be examined

manually which take a long time. To compare the re-

sults obtained with those of specialists in the study of

bone tissue, the generation of tissue must be in 2D al-

though the importance of certain structural aspects of

the bone and the effects on the different structures that

form the bone at microscopic levels make it necessary

for it to be previous representated in three dimensions.

The structure of the article is as follows: section

2 reviews current knowledge of bone tissue represen-

tation. The representation of the model, the selection

of boundaries and the main characteristics of the mi-

croosseous structures are described below. Finally,

the conclusions obtained as well as the future work

is highlighted.

2 RELATED WORK

2.1 Hierarchy of Osseous Structures

The hierarchical structure of bones is a fundamental

point to take into account for this study. They have a

very complex structure that, in addition to providing

mechanical support, allows the reserve of minerals.

The complexity of this structure causes the bones to

have a great resistance. The following is a description

of the hierarchical structure of bone, from the macro-

scale to the nanoscale (Fig. 1):

• Macroscale: this is the level of the entire bone

that includes both types of bone: cortical and tra-

becular. In cortical bone, the lamellae come to-

gether in concentric circles to form osteons, while

in trabecular bone they come together irregularly

to form trabeculae.

• Mesoscale: this layer represents both the cortical

bone, which is composed of osteons embedded in

the interseptal bone, and the trabecular bone com-

posed of a porous network of trabeculae with ir-

regular shapes (Sabet et al., 2015).

340

Pérez F. and Jiménez J.

Towards the Modelling of Osseous Tissue.

DOI: 10.5220/0007580803400345

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 14th International Conference on

Computer Graphics Theory and Applications), pages 340-345

ISBN: 978-989-758-354-4

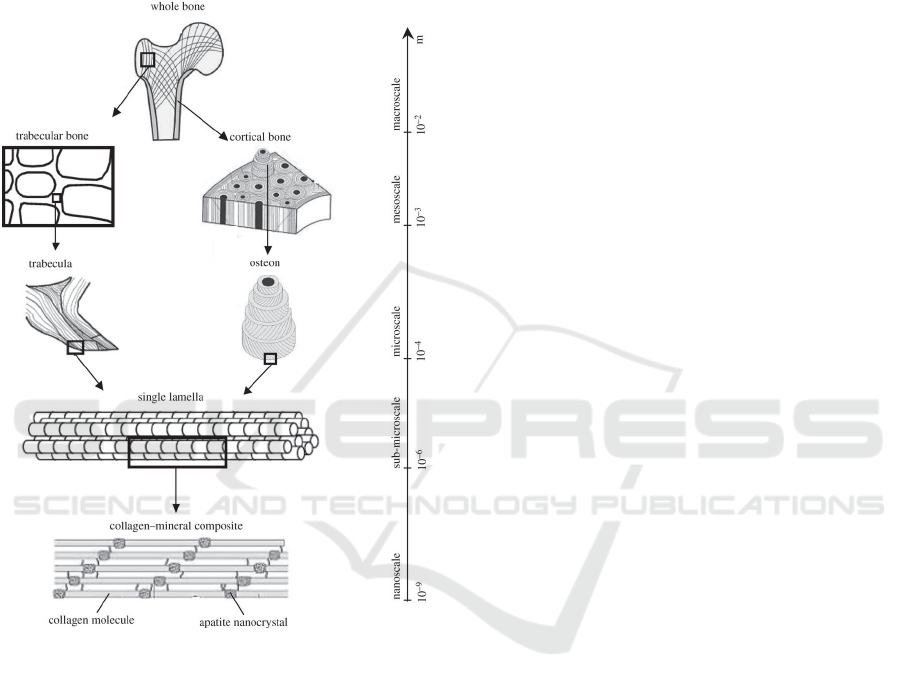
• Microscale: lamellae are assembled to form two

different types of bone tissue: cortical and trabec-

ular.

• Sub-microscale: at this level, collagen ﬁbers are

assembled into sheet-like structures.

• Nanoscale: this level is composed of mineralized

collagen ﬁbers.

Figure 1: Hierarchical structure of the bone, from

macroscale to nanoscale in (Sabet et al., 2015).

Most studies usually focus on predicting the risk

of fracture in a bone or on the inﬂuence of mi-

crostructural features on the behaviour of the prop-

agation of a crack through a bone (Ural, 2011).There

seems to be a consensus among the main author on

the fundamental microstructural parameters that inﬂu-

ence fractures such as the percentage of osteonal area

(On.Ar), the density of osteons (On.Dn) and the per-

centage of porosity(Po) (Demirtas et al., 2016; Tong

et al., 2015). Currently, there are no tools to repre-

sent bone tissue and the microscopic structures (mi-

crostructures) that compose it. Therefore, these stud-

ies use approximation of the microstructure, as the

one carried out by Demirtas (Demirtas et al., 2016)

where it uses an approximate representation in which

only the relevant characteristics for its study are in-

cluded, when the importance of their shape is proved

by Raeisi Najaﬁ et al. (Najaﬁ et al., 2007). Some

of the most important microstructures which compose

the cortical bone are osteons, trabeculae, lamellae or

pores, haversian canals, etc. In addition, it must be

borne in mind that the bone structure is not homo-

geneous, so the properties must be determined indi-

vidually according to the structural level taking into

account their involvement at the global level.

2.2 3D Representation of Bone

The irregularity of the cortical bone as well as

some parameters depending on the longitudinal axis

(Gao et al., 2013) of the bone make representation

at macroscale level a fundamental preliminary step

when generating bone tissue. There are many ap-

proaches to obtaining the representation of a bone

structure in three dimensions. All forms of represen-

tation are based on 3d scanning or 2D image analy-

sis. The process to scan a model consists of differ-

ent stages: calibration, scanning, noise removal, scan

alignment and merging of the aligned parts to close

the gaps. Sometimes it is also necessary to close cer-

tain parts manually because of the noise. As for image

analysis, there are different techniques based on the

sheetness measure (Descoteaux et al., 2006), region

growing (Justice et al., 1997) or graph cuts (Boykov

and Funka-Lea, 2006) that allow us to segment and

classify 2D images to obtain a geometric model in

three dimensions. Paulano (Paulano et al., 2014) de-

scribed a method which needs a user to place a seed

within a region that forms a bone. To segment sev-

eral fragments of bone would have to repeat the pro-

cess. After placing the seeds, an algorithm based on

the growth of a 2D region is used for each seed and all

seeds are propagated through the image pile discard-

ing those regions containing a certain noise, in other

words, very small regions. A curvature ﬂow ﬁlter is

also applied to each cut before each 2D segmentation

process to smooth the images. This algorithm also re-

solves certain special cases where overgrowth occurs

in the regions.

2.3 Microstructure of Bone Tissue

Our study focuses on the virtual representation of the

cortical part of the bone at microscopic levels. The

two main structural features of the cortical bone are:

the osteons and the Havers canal. There are sev-

eral studies aimed at increasing knowledge of biome-

chanics or the peculiarities of these structures such

as those performed by Britz (Britz et al., 2009) or

Doblar

e (Doblar

e et al., 2004) which parameters such

Towards the Modelling of Osseous Tissue

341

as the size, shape or distribution of osteons are ana-

lyzed. It is generally accepted that osteons are circu-

lar in cross-section and that deviations of this shape

are attributed to deviations of longitudinal orientation.

The study conducted by Hennig (Hennig et al., 2015)

shows that osteons are not circular in the cross sec-

tion, but tend to be elliptical in shape, and that there is

no clear way to explain the deviation from the circular

shape(Fig. 2). In the same study, it is also suggested

that parameters such as age most affect the shape of

the osteons regardless of their orientation. Therefore,

the typical and classical idea of representing these

structures as perfect circles is far from their natural

shape. In terms of their distribution, articles such as

written by Gao (Gao et al., 2013) show that osteons

have a random distribution and are embedded in an

interstitial matrix surrounded by a thin layer known

as the cement line.

Figure 2: Computed tomography image (CT).

In most of the studies where CT images have been

used as a reference, the microstructure has been an-

alyzed manually, carrying a slow and tedious pro-

cess for a large volume of data. The work done by

ornquist (T

ornquist, 2017), is as similar as we can

ﬁnd in terms of the virtual representation of bone tis-

sue. T

ornquist performs segmentation, analysis and

modeling of bone tissue through CT images main-

taining the main geometric characteristics and with-

out using approximations as occurs in the studies of

Gao (Gao et al., 2013) and Nobakhti (Nobakhti et al.,

2014) where bone tissue is represented without much

accuracy.

3 MODELLING VIRTUAL BONE

TISSUE

Due to the limitations that currently exist to achieve

advances in the ﬁeld of health, the generation of vir-

tual bone tissue is a fundamental issue to achieve ad-

vances that are not currently reached due to lack of

data and time. Most of the research at microscopic

levels within the health ﬁeld focuses on the analysis

of CT 2D and 3D images manually.

3.1 Model Representation

For the generation of virtual bone tissue, it is es-

sential to have good input data. The irregularity of

the bone and the dependence on microstructural fea-

tures such as the distribution of the osteons /cite-

Het1994 or their inclination within the cortical bone

/citeGao2013 make their representation at the macro

level a necessary preliminary step for the generation

of bone tissue. To obtain this representation, we have

studied two different approaches: 3D scanning of a

bone model and segmentation of a bone from CT im-

ages. The biggest problems of the ﬁrst approach are

the time it takes to perform the scan and the segmen-

tation of the model, the difﬁculty to have real bones

and that in the model obtained we only have infor-

mation from the external but not the internal corti-

cal part. The second approach solves most of the

problems of the ﬁrst approach, and although obtain-

ing medical images can be a problem, it is a much

faster, more precise process and allows us to obtain in-

formation about the internal part of the cortical bone.

Paulano (Paulano et al., 2014) conducted a study fo-

cusing on segmentation of fractured bones from CT

images. This study concludes that traditional meth-

ods of segmentation work well for segmentation of

healthy bones, but are unable to identify fractured

bones. Since our input data contain healthy and frac-

tured bones, we have used a method based on 2D re-

gion growing [(Justice et al., 1997),(Fan et al., 2005)],

proposed by Paulano (Paulano et al., 2014), because

the results obtained are better as demonstrated in their

article(Fig. 3).

The segmentation of bone models, besides help-

ing us to generate virtual bone tissue, could also help

us to create a bank of bone fractures using different

methods such as those studied in (P

erez et al., 2018)

where the suitability of a library of geometric fractur-

ing is analyzed for the different fracture approaches

of geometric models examined by Paulano (Paulano-

Godino et al., 2017).

GRAPP 14th International Conference on Computer Graphics Theory and Applications - 14th International Conference on Computer

Graphics Theory and Applications

342

Figure 3: Results obtained by the different methods in

(Paulano et al., 2014). The ﬁrst row corresponds to a

healthy bone while the second row corresponds to a frac-

tured bone.

3.2 Setting Boundaries

As the automatic generation of all bone tissue from a

bone can be a slow process and most scientiﬁc articles

focus on the manual analysis of 2D images, we con-

sider that the generation of virtual bone tissue should

be in 2D. This will allow us to compare the results ob-

tained directly with the values obtained by specialists

when studying bone tissue.Therefore, for the gener-

ation of the tissue we have used a plane to manually

select the area of the bone over which we want to gen-

erate the bone tissue (Fig. 4).

Figure 4: Representation of the bone and the plane to de-

limit the area to be generated.

In order to be able to work in 2D, the points of

contact of the bone and the plane are aligned with

the Z axis by applying a series of simple transforma-

tions. The points of contact between the bone geomet-

ric model and the plane form the inner and outer limits

of the area of the fabric to be generated (Fig. 5). So

we have to use an algorithm to establish which points

form each of the limits like the alpha shape algorithm

[(Edelsbrunner et al., 1983), (Akkiraju et al., 1995)],

based on the extraction of polygons from a cloud of

points. The criterion used to obtain the smallest value

with which the algorithm is capable of detecting both

parts has been to start from the mean distance between

the different points forming the collision zone and re-

duce the value iteratively by a percentage established

by default at 1. The problem with this approach is

that it greatly decreases the precision of the areas de-

limiting the cortical part of the bone and is not valid

for obtaining limits in areas where the bone is frac-

tured (Fig. 5c). Therefore, the criterion that we have

followed has been the union of the adjacent points

by distances. In some cases it may be necessary to

manually clean some points, which would cause a cer-

tain loss of precision, but the morphology of a natural

bone and the process to virtualize it followed through-

out this article make this type of cases very isolated.

To determine the points that form part of the different

limits that can form part of the virtual bone tissue, we

have used the smallest value that the alpha shape algo-

rithm needs to generate two polygons. From the outer

limit of the bone structure calculated with the alpha

shape algorithm and this value, we can delimit which

points are within and out of range, thus generating the

inner and outer limits. As can be seen in (Fig. 5), the

algorithm used improves precision and has no prob-

lems when it comes to delimiting the limits for gener-

ating bone tissue in fractured areas. This will allow us

to obtain measurements of greater weight compared

to other studies based on approximate representations.

Figure 5: Comparison between the results obtained with the

alpha shape algorithm(A,C) and with our method(B,d). Im-

ages A and B correspond to a healthy bone while images C

and D correspond to a fractured area. The white dots are ob-

tained by projecting the areas of contact between the bone

and the plane while the red lines delimit the contour of the

area where the bone tissue will be generated.

Once the limits have been established, we can take

the next step in our research and focus on the cre-

ation of the different microstructures that make up the

Towards the Modelling of Osseous Tissue

343

Figure 6: CT image used to obtain the model with which

tests have been carried out.

bones, taking into account all their characteristic fea-

tures, without using perfect or accepted forms that

may cause changes in the morphology of the bone

structure, and thus achieve the creation of a quality

virtual bone tissue that facilitates future research. Our

study could be validated since we limit ourselves to

the use of real medical images of human bones, so

the geometric models we use are replicas as similar

as possible to the real ones. Figure 7 (Fig. 6) cor-

responds to an image of the computed axial tomog-

raphy scan (CAT) used to recreate one of the models

used throughout this study. As can be seen, the limits

of the bone are almost identical those obtained by the

study in ﬁgure (Fig. 5d).

3.3 Microstructure Modelling

Most studies study the modelling of microstructures

at sub-microscale and smaller scales which collagen

ﬁbers are assembled into sheet-like structures. In this

section we will focus on the different characteristics

and inputs that must be taken into account for the rep-

resentation of the cortical bone tissue at microscopic

levels. Osteons are the most important structure of

the compact bone. The shape of the osteons is a key

point in studies of the spread of fractures through the

cortical bone (Najaﬁ et al., 2007). They consist of a

series of concentric layers called lamellae, which sur-

rounding a central canal, which is a cavity through

which blood vessels and nerves pass, known as the

Havers canal. Osteons are limited by a line known

as the cement line that separates them from the rest

of the bone tissue. The part of the osseous tissue be-

tween two osteons is formed by some layers known

as interstitial laminae. These parameters can be stud-

ied through image analysis such as the study about

bone porosity by Cardoso (Cardoso et al., 2013) or

the study conducted by Lin (Lin and Xu, 2010) that

focused on the analysis of the lacunar-canalicular net-

work (Fig. 7). Although they do not focus on the

microstructures that make up the bone tissue directly,

their different characteristics are studied due to their

importance and involvement in them.

Figure 7: Microscopic images of the osseous structures ob-

tained from Cardoso’s study (Cardoso et al., 2013) Labels in

panel a indicate the Haversian canal (H), lacuna (L), and ce-

ment line (CL). In panel b, canaliculi rich (CR) and canali-

culi free (CF) areas are distinguished.

For the representation of the virtual osseous tissue

it is necessary to know the characteristics of different

elements that compose the tissue. In addition to geo-

metrical parameters such as dimensions, shape or dis-

tribution of them, it is necessary to know other param-

eters such as porosity (Po), osteons density(On.Dn),

osteonal area (On.Ar), tissue volume (TV), canal vol-

ume (Ca.V) or bone volume(BV) as demonstrated in

the studies of Demirtas or Tong (Demirtas et al., 2016;

Tong et al., 2015) . These parameters are key to ob-

taining a realistic tissue as well as for its study in

ﬁelds such as fracturing. So, to represent the vir-

tual osseous tissue realistically, it is necessary to go

beyond the geometric representation of the structures

allowing it to be useful and to replace the basis for

future research.

4 CONCLUSIONS

The generation of virtual bone tissue is an unexplored

ﬁeld. There are many studies that focus on micro-

scopic analysis of bones. In these studies, manual

analysis of CT images is performed. The develop-

ment of a virtual bone generation tool can help signif-

icantly reduce the time spent analyzing microscopic

images of bones and provide more information for

further analysis. In addition, most of the geometric

representations that exist on the bone tissue, use ap-

proximations and do not follow the standards that are

GRAPP 14th International Conference on Computer Graphics Theory and Applications - 14th International Conference on Computer

Graphics Theory and Applications

344

used within traumatology, so their validity when rep-

resenting these microstructures remain in no man’s

land and can not be exploited by specialists. This

study aims to lay the foundations for the virtual gener-

ation of bone tissue not only from a geometric point of

view, but also from a medical point of view. The study

of the segmentation of the bone model, how it should

be generated in order to evaluate and compare it later,

and the establishment of a series of limits serve as a

starting point for achieving this ambitious objective.

For the future it would be interesting to generate the

different microstructures that make up the bone tis-

sue taking into account all those elements that are

scientiﬁcally relevant such as the different measures

used. What other types of structural parameters could

be included to make the tissue generated more useful

within the different ﬁelds of study?

ACKNOWLEDGEMENTS

This work has been subsidized by the Ministry of

Economy and Competitiveness and the European

Union (via ERDF funds) through the research project.

DPI2015-65123-R.

REFERENCES

Akkiraju, N., Edelsbrunner, H., Facello, M., Fu, P., Mucke,

E., and Varela, C. (1995). Alpha shapes: deﬁnition

and software. IEEE Transactions on Information The-

ory, 63(1):66–70.

Boykov, Y. and Funka-Lea, G. (2006). Graph cuts and efﬁ-

cient n-d image segmentation.

Britz, H. M., Thomas, C. D. L., Clement, J. G., and Cooper,

D. M. (2009). The relation of femoral osteon geome-

try to age, sex, height and weight. Bone, 45(1):77–83.

Cardoso, L., Fritton, S. P., Gailani, G., Benalla, M., and

Cowin, S. C. (2013). Advances in assessment of bone

porosity, permeability and interstitial ﬂuid ﬂow. Jour-

nal of Biomechanics, 46(2):253–265.

Demirtas, A., Curran, E., and Ural, A. (2016). Assessment

of the effect of reduced compositional heterogeneity

on fracture resistance of human cortical bone using

ﬁnite element modeling. Bone, 91:92–101.

Descoteaux, M., Audette, M., Chinzei, K., and Siddiqi, K.

(2006). Bone enhancement ﬁltering: Application to

sinus bone segmentation and simulation of pituitary

surgery. Computer Aided Surgery, 11(5):247–255.

Doblar

e, M., Garc

ıa, J., and G

omez, M. (2004). Modelling

bone tissue fracture and healing: a review. Engineer-

ing Fracture Mechanics, 71(13-14):1809–1840.

Edelsbrunner, H., Kirkpatrick, D., and Seidel, R. (1983).

On the shape of a set of points in the plane. IEEE

Transactions on Information Theory, 29(4):551–559.

Fan, J., Zeng, G., Body, M., and Hacid, M.-S. (2005).

Seeded region growing: an extensive and comparative

study. Pattern Recognition Letters, 26(8):1139–1156.

Gao, X., Li, S., Adel-Wahab, A., and Silberschmidt, V.

(2013). Effect of random microstructure on crack

propagation in cortical bone tissue under dynamic

loading. Journal of Physics: Conference Series,

451:012033.

Hennig, C., Thomas, C. D. L., Clement, J. G., and Cooper,

D. M. L. (2015). Does 3d orientation account for vari-

ation in osteon morphology assessed by 2d histology?

Journal of Anatomy, 227(4):497–505.

Justice, R., Stokely, E., Strobel, J., Ideker, R., and Smith, W.

(1997). Medical image segmentation using 3d seeded

region grow-ing. Medical Imaging 1997: Image Pro-

cessing, 3034:900–910.

Lin, Y. and Xu, S. (2010). AFM analysis of the lacunar-

canalicular network in demineralized compact bone.

Journal of Microscopy, 241(3):291–302.

Najaﬁ, A. R., Arshi, A., Eslami, M., Fariborz, S., and

Moeinzadeh, M. (2007). Micromechanics fracture in

osteonal cortical bone: A study of the interactions

between microcrack propagation, microstructure and

the material properties. Journal of Biomechanics,

40(12):2788–2795.

Nobakhti, S., Limbert, G., and Thurner, P. J. (2014). Ce-

ment lines and interlamellar areas in compact bone

as strain ampliﬁers – contributors to elasticity, frac-

ture toughness and mechanotransduction. Journal of

the Mechanical Behavior of Biomedical Materials,

29:235–251.

Paulano, F., Jim

enez, J. J., and Pulido, R. (2014). 3d seg-

mentation and labeling of fractured bone from CT im-

ages. The Visual Computer, 30(6-8):939–948.

Paulano-Godino, F., Jim

enez-P

erez, J. R., and Jim

enez-

Delgado, J. J. (2017). Issues on the simulation of geo-

metric fractures of bone models. In VipIMAGE 2017,

pages 467–475. Springer International Publishing.

erez, F. D., Jim

enez, J. J., and Jim

enez, J. R. (2018).

Blast Features and Requirements for Fracturing Os-

seous Models. In Garc

ıa-Fern

andez, I. and Ure

na,

C., editors, Spanish Computer Graphics Conference

(CEIG). The Eurographics Association.

Sabet, F. A., Najaﬁ, A. R., Hamed, E., and Jasiuk, I.

(2015). Modelling of bone fracture and strength at

different length scales: a review. Interface Focus,

6(1):20150055.

Tong, X., Burton, I. S., Isaksson, H., Jurvelin, J. S., and

oger, H. (2015). Cortical bone histomorphome-

try in male femoral neck: The investigation of age-

association and regional differences. Calciﬁed Tissue

International, 96(4):295–306.

ornquist, E. (2017). Segmentation, analysis, and mod-

elling of microstructure in cortical bone, based on x-

ray microtomography. Student Paper.

Ural, A. (2011). Cohesive modeling of bone fracture at mul-

tiple scales. Procedia Engineering, 10:2827–2832.

Towards the Modelling of Osseous Tissue

345