Natural Stereo Camera Array using Waterdrops

for Single Shot 3D Reconstruction

Akira Furukawa, Fumihiko Sakaue and Jun Sato

Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Japan

Keywords:

Natural Stereo Camera System, Water Drop Stereo, Camera Parameters By Optical Aberration.

Abstract:

In this paper, we propose a stereo 3D reconstruction from a single image including multiple water drops.

Water drops on a surface, e.g. camera lens, refract light rays and the refracted rays are roughly converged to

a point. This indicates that water drops can be regarded as approximately small lens. Therefore, sub-images

refracted by water drops can be regarded as images taken from different viewpoints. That is, virtual stereo

camera systems can be constructed from a single image by using these raindrop characteristics. In this paper,

we propose an efﬁcient description of this virtual stereo camera system using water drops. Furthermore, we

propose methods for the estimation of the camera parameters and for the reconstruction of the scene. We

ﬁnally display several experimental results and discuss the validation of our proposed camera model from the

results.

1 INTRODUCTION

In ﬁeld of computer vision, 3D reconstruction is

one the most traditional and important aspects, and

hence, various methods have been studied extensi-

vely(Newcombe et al., 2011; Klein and Murray, 2009;

Cheung et al., 2000; Posdamer and Altschuler, 1982;

Kolmogorov and Zabih, 2002). In general, 3D recon-

struction methods require two or more than two came-

ras since depth information is lost in a single image.

Therefore, multiple camera systems, known as stereo

camera systems, are used for 3D scene reconstructi-

ons in general.

However, the stereo camera system does not al-

ways require explicit multiple cameras because the

system just requires images that are taken from dif-

ferent viewpoints. Therefore, 3D reconstruction can

be achieved by using single camera if the camera can

take such images. The most representative 3D recon-

struction method that uses a single camera is Structure

from Motion (SfM)(Klein and Murray, 2009; New-

combe et al., 2011). In this method, a single camera

moves around the target object and takes several ima-

ges from different viewpoints. From these images,

the 3D shape of the target object can be reconstructed

by using ordinary stereo reconstruction techniques.

Although these methods are considerably convenient

since the method can be utilized by using only a sin-

gle camera, the method cannot be applied when the

target object is not rigid. This is because stereo cor-

respondences that are used for stereo reconstruction

may be changed when the target object is not rigid,

and thus, the stereo constraints for 3D reconstruction

are not satisﬁed in this case.

In order to avoid this problem, another approach

that uses a special lens, as shown in Fig.1(a) and

2(a), are proposed. In this approach, multiple images

that are taken from different viewpoints are virtually

obtained from a single image. These methods can be

classiﬁed into two techniques based on lens size and

lens position.

In the ﬁrst technique, micro-lens array as shown

in Fig 1(a) is used(Levoy and Hanrahan, 1996; Chen

et al., 2014). The micro-lens array is equipped on the

image plane such as a CCD and it achieves special

image photography as shown in Fig. 1(b). This spe-

cial image includes multiple images taken from diffe-

rent viewpoints, and then, the image can be separated

into multiple images. Therefore, 3D scenes can be

reconstructed from the images by using an ordinary

technique. In general, cameras that are equipped with

micro-lens arrays are known as light-ﬁeld cameras.

The second approach uses large-lens array as

shown in Fig 2(b). The array is placed in front of

the camera, and then, images that include multiple

sub-images from different viewpoints can be taken di-

rectly as shown in Fig.2(b). By using the sub-images

in the input image, 3D reconstruction can be achieved.

Furukawa, A., Sakaue, F. and Sato, J.

Natural Stereo Camera Array using Waterdrops for Single Shot 3D Reconstruction.

DOI: 10.5220/0007582609010907

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theor y and Applications (VISIGRAPP 2019), pages 901-907

ISBN: 978-989-758-354-4

901

(a) micro-lens array (b) obtained image

Figure 1: Multiple image photography using micro-lens ar-

ray equipped on the image plane.

(a) lens array (b) obtained image

Figure 2: Multiple image photographing using lens array

placed in front of the main camera.

The approaches using special lens arrays achieve

stereo 3D reconstruction from single images. Howe-

ver, the special lens cannot be utilized always. There-

fore, the convenience of these methods may become

lesser than an ordinary stereo method using multi-

ple cameras. In order to overcome this problem,

several methods that use natural optical phenomena

have been proposed(Arvind V. Iyer, 2018; You et al.,

2016). In these methods, natural optical lenses such

as water drops as shown in Fig.3(a) are utilized as lens

arrays. When the water drops are placed in front of

the camera, the input image includes multiple sub-

images as shown in Fig.3(b). Therefore, 3D recon-

struction can be achieved from a single image using

natural objects alone.

Although these methods are signiﬁcantly conve-

nient, they require large computational cost for 3D

reconstruction as the method has to compute com-

plicated optical refractions by water drops that have

complicated shapes. In this paper, we propose an ef-

ﬁcient camera model for describing these complica-

ted optical phenomena. In this model, we focus not

on the shape of water drop, but rather on the optical

refraction by the water drop; moreover, we do not re-

construct the shape of the water drop explicitly. In our

model, the optical refraction is described using only a

few parameters. Therefore, the computational cost for

3D reconstruction can be drastically reduced. In ad-

dition, the robustness of the reconstruction becomes

higher as the constraint of the model is powerful. In

this paper, we explain this camera model and indicate

the calibration and 3D reconstruction method using

the model as well.

(a) water drops (b) obtained image

Figure 3: When a water drop is put on the lens, the water

drop can be regarded as natural lens array.

Figure 4: Overview of our proposed camera model.

2 WATER DROP CAMERA

MODEL

We ﬁrst deﬁne a camera model that describes the

image projection from a 3D scene to the image plane

using water drops. Figure 4 shows the overview of our

camera model. As shown in this ﬁgure, we assume

that the main lens of the camera can be approximated

by a pinhole and water drops are placed on a trans-

parent plane set in front of the main camera. In this

case, input light rays are refracted by the water drops

at ﬁrst. Thereafter, the rays pass through the pinhole

and are received by pixels on an image plane.

In general, a surface normal direction is required

to compute the refraction of light rays. Speciﬁcally,

explicit shape description and reconstruction is ne-

cessary for describing the behavior of the light rays

to the image plane. In addition, light ray refractions

by not only the water drops, but transparent planes

as well should be considered for describing accurate

light rays. When this description is used, the com-

putational cost becomes burdensome if a lot of water

drops are placed on the plane. Therefore, we propose

an efﬁcient description model that focuses on optical

aberration by water drops.

When the water drop is an ideal optical lens, in-

put light rays are converged to a pinhole as shown

in Fig.5(a). However, the light rays are not conver-

ged into the point owing to inaccuracies such as com-

plicated shapes of the lens in general, as shown in

Fig.5(b). This phenomenon can be described by the

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

902

(a) ideal lens

(b) ordinary shape

Figure 5: Optical aberration caused by water drops. Fi-

gure(a) shows an ideal case where the light rays are conver-

ged to a point . Figure(b) shows an ordinary case where the

light rays are not converged to a point.

optical aberration model(Tyson, 2010; Geary, 1995;

Roddier, 2004) efﬁciently. In our case, water drops

can be regarded as incorrect optical lenses; thereafter

the behavior of the light rays can be described by the

optical aberration model efﬁciently.

For this objective, Zernike polynomial is generally

used as the model can describe the aberration efﬁ-

ciently. In this model, optical aberration is represen-

ted using a few parameters. Therefore, we employ the

Zernike aberration model in our proposed method.

Here, we describe the details of the Zernike aber-

ration model. In this model, optical aberration is re-

presented by the linear combination of the Zernike ba-

ses and the bases are computed as follows:

(ρ, θ) =

n−m

∑

s=0

(−1)

(n − s)!ρ

n−2s



n+m

− s





n−m

− s



cos

θ : m ≥ 0

sin

θ : m < 0

(1)

where ρ and θ give the log-polar coordinates repre-

sentation of the 2D image. Through this base, the op-

tical aberration W (X,Y ) at point (X,Y ) is represented

as follows:

W (X,Y ) =

∑

n=0

∑

m=−n

(ρ, θ) (2)

where B

is Zernike coefﬁcient. ∇W can be compu-

ted by partial differentiation of W with respect to X

and Y as follows:

∇W =







∂W (X,Y )

∂X

∂W (X,Y )

∂Y







(3)

The ∇W represents the extent of the light rays re-

fraction by the water drops directly.

Figure 6: Zernike bases.

Figure 7: Examples of rendered images with different Zer-

nike coefﬁcients.

Figure 6 shows Zernike bases and they correspond

to speciﬁc optical aberrations such as spherical aber-

rations. Coefﬁcients of this equation represent the de-

gree of each aberration. In general, ordinary optical

aberration can be represented by the combination of a

few bases; thereafter, we can describe the behavior of

the light rays from water drops by using a few coefﬁ-

cients.

Figure 7 shows the examples of rendered ima-

ges by our proposed model. In these ﬁgures, diffe-

rent Zernike coefﬁcients are used for rendering the

images. These ﬁgure show that the rendered images

change drastically by just changing the Zernike coef-

ﬁcients.

3 CALIBRATION OF CAMERA

Next, we consider the calibration of our proposed ca-

mera model, i.e., the estimation of the Zernike coef-

ﬁcients is discussed in this section. In general, a wa-

vefront sensor is utilized for measuring optical aber-

rations. The sensor is a type of light ﬁeld camera and

it measures the behavior of the wave directly. Howe-

ver, this sensor cannot be used in our case because the

aberrated wave should be observed directly for mea-

suring the aberration. To be precise, the sensor should

be placed between the water drops and a main lens. It

is not realistic a set up. Therefore, we estimate the

coefﬁcients by minimizing the image residual of ren-

Natural Stereo Camera Array using Waterdrops for Single Shot 3D Reconstruction

903

dered images.

In this estimation, it is assumed that the informa-

tion of the input scene such as scene shape and texture

information is known. In this case, the input image

can be virtually rendered again when Zernike coefﬁ-

cients B are provided. Let I

(B) denote the rendered

image by coefﬁcients B and I denote an input image.

In this case, image residual R is computed as follows:

R = I − I

(B) (4)

When a parameter B is equivalent to the correct pa-

rameter

B, the residual R should become small. The-

refore, the Zernike coefﬁcient

Bcan be estimated by

minimizing the residual R as follows:

B = argmin

kRk

= argmin

kI − I

(B)k

(5)

Note that, in general, point light sources that emit

spherical waves or plane waves are used for estima-

ting the aberration of the lens. In this case, optical

aberration can be measured directly; thereafter, aber-

ration parameters can be easily estimated. In our met-

hod, we can estimate the aberrations under the light

source easily. In addition, our method can estimate

the coefﬁcients even if general light rays are input to

the camera because our method focuses on the con-

sistency of the whole input image.

4 SCENE RECONSTRUCTION

Here, we explain the 3D scene reconstruction by

using a calibrated camera model. In an ordinary ste-

reo method, the correspondences of feature points

such as SIFT (Lowe, 1999) and SURF (Bay et al.,

2006) are used for the reconstruction. In this case,

the feature points are extracted from the input images

at ﬁrst. Thereafter, correspondences are determined

from the feature points. Finally, these corresponden-

ces are reconstructed under epipolar constraints.

However, we cannot use the gold standard algo-

rithm in our camera model because images for each

camera, i.e., images by water drops do not have

enough resolution for extracting feature points. Fi-

gure 8 shows the example of an input image. In

this image, although a water drop provides images

taken from different viewpoints, the provided image

does not have enough resolution for extracting feature

points.

To overcome this problem, we do not focus on fe-

ature points, but rather on whole sub-images provided

by the water drop, similar to the calibration process.

In this method, whole input images are backprojected

to a 3D scene S and the scene is texture mapped by a

sub image. Next, the 3D scene is reprojected to our

Figure 8: Example of input image with water drops.

camera model. Here, if the 3D scene S corresponds

to a real scene, the reprojected image corresponds to

the input image as well. Therefore, the 3D scene can

be reconstructed by minimizing the difference of the

input image and reprojected image. That is to say, the

3D scene

S can be estimated as follows:

S = argmin

kI − P(T (I, S, B), S, B)k

(6)

where P and T represent the projection and backpro-

jection processes of the input image I with shape S

and camera parameters B, respectively.

In order to realize this estimation, the 3D scene S

should be represented by a few parameters. For ex-

ample, the Bezier curve is a representative parame-

tric shape model. In this model, curves in the scene

are determined by control points and the curves repre-

sent various 3D shapes by moving the control points.

When the Bezier curves are used for scene represen-

tation, the 3D scene S can be described as follows:

S(u, v) =

∑

i=0

∑

j=0

(u)B

(v)q

i j

0 ≤ u ≤ 1, 0 ≤ v ≤ 1 (7)

where q is the control point and B are Bernstein basis

functions. The function is computed as follows:

(u) =

(1 − u)

n−i

(8)

i!(n − i)!

(9)

By using the Bezier curves, whole 3D scenes can

be represented and estimated by estimating the 3D po-

sition of the control points alone. For example, the

5-th order curve can be estimated by the estimation

of 36 control points. Especially, only 36 parameters

should be estimated when only the depth of the con-

trol points are changed. Figure 9 shows an example

of the 5-th order Bezier curve. The curve can be ea-

sily changed by changing the position of the control

points.

Note that the backprojection of an input image to

the 3D scene is not very complicated in our model.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

904

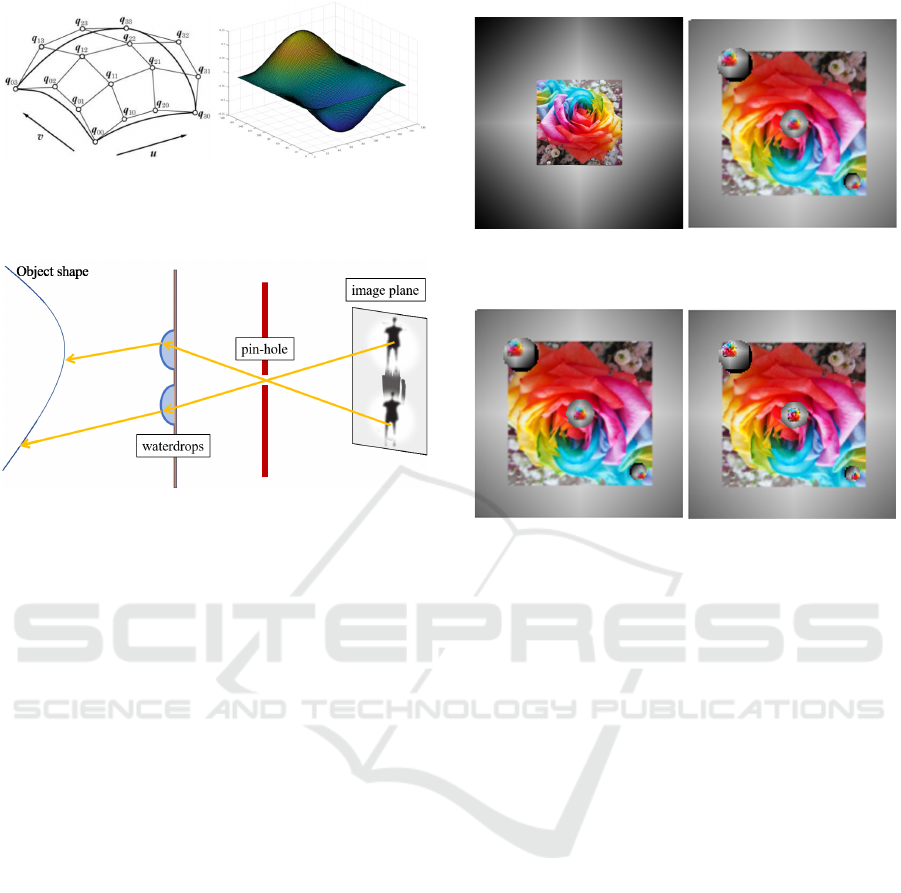
(a) control points (b) Bezier curves

Figure 9: Representation of control points and example of

Bezier curves.

Figure 10: Backprojection of an input image.

As described in the previous section, the main camera

of our camera model has a pin-hole, and only a sin-

gle light ray is received by each pixel. Therefore, the

light ray can be backtraced easily as shown in Fig.10.

In addition, since the optical aberration model is used

for the representation of light ray refractions, the re-

fraction of the traced light ray can be computed di-

rectly compared to ordinary light refraction models.

5 EXPERIMENTAL RESULTS

In this section, we present several experimental re-

sults by our proposed method. We ﬁrst explain the

experimental environment. In all the experiments, a

simulation environment was used for obtaining accu-

rate ground truth. In the computer, an experimen-

tal environment was set up and several images were

taken by a virtual camera. In front of the camera,

a transparent plane was positioned and water drops

were placed on the plane. The shape of the each water

drop was different from each other. Therefore, light

ray inputs to the drops had different behaviors. In the

input image synthesis process, each light ray to the

image plane was traced based on not our proposed

model, but rather the physics rules for validating our

proposed model.

In the estimation process, the refractions by water

drops were represented by ﬁve Zernike coefﬁcients.

In front of the camera, a planar surface was placed,

and several textures were mapped onto the plane. The

(a) Target image

(b) Input image

Figure 11: Target image and example of input image.

(a) input image

(b) calibrated result

Figure 12: Input image and camera calibration result by

using Zernike polynomials.

plane was taken by the camera. Figure 11 shows the

examples of input images and its target object. By

using the images, the camera parameters and 3D sce-

nes were estimated respectively.

We ﬁrst show the camera parameters, i.e. Zernike

coefﬁcients estimation results. As mentioned above,

the input images were synthesized based on physics

rules, and then, the validation of our camera model

was evaluated in this experiment.

We ﬁrst extract the region of the water drop by

using Hough transformation roughly. After that, Zer-

nike coefﬁcients were estimated for each detected wa-

ter drop respectively. In order to evaluate valida-

tion of our model, the target scene was projected to

the image plane by using estimated coefﬁcients. Fi-

gure 12 shows an example of the pair of input image

and reprojected image using calibrated camera para-

meters. As shown in this ﬁgure, our camera model

can synthesize images similar to the input image alt-

hough they were based on different rules. The results

indicate that our proposed camera model can repre-

sent the refraction of light rays effectively. In addi-

tion, our proposed calibration method can estimate

camera parameters from ordinary input images.

We now present scene reconstruction results by

using the calibrated parameters. In this estimation,

only the depth of the target plane was estimated from

a single input image. In order to evaluate the vali-

Natural Stereo Camera Array using Waterdrops for Single Shot 3D Reconstruction

905

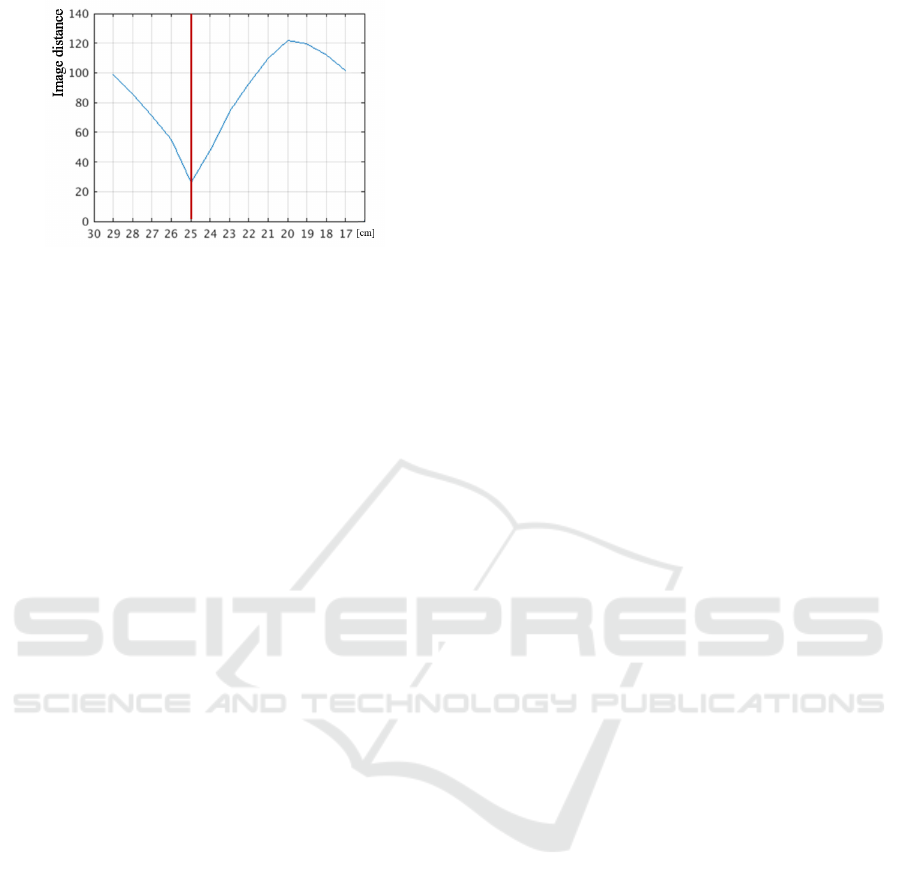
Figure 13: Depth estimation result.

dation of the estimation, we compute the difference

of a reprojection image and an input image for each

depth. Figure 13 shows the distance of the images at

each depth. In this graph, the vertical axis indicates

the distance of the images and the horizontal axis in-

dicates the estimated depth. The red line in the ﬁgure

shows correct depth. In this graph, the distance of

the image becomes local minimum at the true depth.

This, in fact, indicates that the distance between the

reprojection image and input image represents the va-

lidation of the estimated depth. Therefore, our met-

hod can estimate the depth from a single image.

These experimental results indicate our proposed

model can describe the behavior of the light rays ef-

ﬁciently and effectively. In addition, the calibration

and reconstruction methods based on the model work

efﬁciently.

6 SIMULTANEOUS ESTIMATION

OF CAMERA PARAMETERS

AND 3D SCENE

We ﬁnally discuss the simultaneous estimation of 3D

shape and camera parameters from an input image. In

an ordinary stereo method, simultaneous estimation

of these parameters, known as bundle adjustment, can

be achieved by minimizing the reprojection error of

the correspondences. In fact, bundle adjustment in

our framework can be achieved in a manner similar

to the ordinary method. In our framework, instead

of point reprojection error, image reprojection error

should be minimized for 3D reconstruction and cali-

bration. Therefore, simultaneous estimation can also

be achieved by minimizing the same error.

In this simultaneous estimation, in addition to the

parameters of the 3D shape, camera parameters are

estimated as well. When the 3D scene is represented

by an N-th order Bezier, (N + 1)

parameters are re-

quired. In addition, L water drops require L ×M (M is

the number of coefﬁcients) parameters for estimating

the camera model. Totally, (N + 1)

+LM parameters

should be estimated for the simultaneous estimation.

This, in fact, indicates that (N + 1)

+ LM or more

than (N + 1)

+LM constraints are necessary for esti-

mating these parameters. In our proposed estimation,

all pixels are used for this estimation, and then, suf-

ﬁcient number of constraints are obtained when the

number of pixels are larger than (N + 1)

+ LM.

7 CONCLUSION

In this paper, we propose 3D scene reconstruction

from a single image using water drops. In our propo-

sed method, water drops in the images are regarded as

virtual cameras and the 3D shape is reconstructed by

using the virtual cameras. For the efﬁcient description

of the virtual cameras, we utilize an optical aberra-

tion model by Zernike basis. By using the aberration

model, complicated light ray refractions can be des-

cribed via few coefﬁcients. Furthermore, parametric

3D scene description is employed for estimating the

3D scene effectively. We show experimental results

in the simulation environment and the results demon-

strate the potential of our proposed method. In future

work, we extend our proposed method to the simul-

taneous estimation of camera parameters and 3D sce-

nes.

REFERENCES

Arvind V. Iyer, J. B. (2018). Depth variation and stereo

processing tasks in natural scenes. J. Vis, 18(6).

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:

Speeded up robust features. In Computer vision–

ECCV 2006, pages 404–417. Springer.

Chen, C., Lin, H., Yu, Z., Kang, S. B., and Yu, J. (2014).

Light ﬁeld stereo matching using bilateral statistics of

surface cameras. In IEEE Conference on Computer

Vision and Pattern Recognition (CVPR).

Cheung, G. K., Kanade, T., Bouguet, J.-Y., and Holler, M.

(2000). A real time system for robust 3d voxel recon-

struction of human motions. In Computer Vision and

Pattern Recognition, 2000. Proceedings. IEEE Confe-

rence on, volume 2, pages 714–720. IEEE.

Geary, J. M. (1995). Introduction to Wavefront Sensors.

Society of Photo Optical.

Klein, G. and Murray, D. (2009). Parallel tracking and map-

ping on a camera phone. In Proc. Eigth IEEE and

ACM International Symposium on Mixed and Aug-

mented Reality (ISMAR’09), Orlando.

Kolmogorov, V. and Zabih, R. (2002). Multi-camera scene

reconstruction via graph cuts. In Computer Vision

ECCV 2002, pages 82–96. Springer.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

906

Levoy, M. and Hanrahan, P. (1996). Light ﬁeld rende-

ring. In Proceedings of the 23rd Annual Conference

on Computer Graphics and Interactive Techniques,

SIGGRAPH ’96, pages 31–42.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. In Computer vision, 1999. The pro-

ceedings of the seventh IEEE international conference

on, volume 2, pages 1150–1157. Ieee.

Newcombe, R. A., Lovegrove, S. J., and Davison, A. J.

(2011). Dtam: Dense tracking and mapping in real-

time. In Proceedings of the 2011 International Confe-

rence on Computer Vision, pages 2320–2327.

Posdamer, J. and Altschuler, M. (1982). Surface mea-

surement by space-encoded projected beam systems.

Computer graphics and image processing, 18(1):1–

17.

Roddier, F. (2004). Adaptive Optics in Astronomy. Cam-

bridge University Press.

Tyson, R. K. (2010). Principles of Adaptive Optics. CRC

Press.

You, S., Tan, R. T., Kawakami, R., Mukaigawa, Y., and

Ikeuchi, K. (2016). Waterdrop stereo. In arXiv.

Natural Stereo Camera Array using Waterdrops for Single Shot 3D Reconstruction

907