A Modiﬁed Self-training Method for Adapting Domains in the Task of

Food Classiﬁcation

Elnaz Jahani Heravi

, Hamed H. Aghdam

and Domenec Puig

Department of Computer Engineering and Mathematics, University Rovira i Virgili, Spain

The Computer Vision Center, University Autonoma Barcelona, Spain

Keywords:

Domain Adaptation, Deep Learning, Food Recognition.

Abstract:

Food trackers are tools that recognize foods using their images. In the core of these tools there is usually

a neural network that performs the classiﬁcation. Neural networks are highly expressive models that need a

large dataset to generalize well. Since it is hard to collect a training set that captures most of realistic situations

in real world, there is usually a shift between the training set and the actual test set. This potentially reduces

the performance of the network. In this paper, we propose a method based on self-training to perform unsu-

pervised domain adaptation in the task of food classiﬁcation. Our method takes into account the uncertainty

of predictions instead of probability scores to assign pseudo-labels. Our experiments on the Food-101 and the

UPMC-101 datasets show that the proposed method produces more accurate results compared to Tri-training

method which had previously surpassed other domain adaptation methods.

1 INTRODUCTION

In the past few years, methods based on deep neu-

ral networks have the signiﬁcantly improved perfor-

mance of different computer vision tasks such as clas-

siﬁcation, detection, and segmentation. This progress

became possible mainly for three reasons. First, pa-

rallel computing hardware and related software libra-

ries were emerged and made it possible to imple-

ment heavily computational models on these devices

in which running a large network on medium size

image takes less than a second. Second, large data-

sets such as ImageNet became available which were

composed of diverse samples. Using these large data-

sets, we were able to train larger networks with mil-

lions of parameters. Third, neural networks were ra-

pidly improved by the advent of ideas such as weight

sharing, initialization, micro-architectures, activation

functions, normalization, regularization, and optimi-

zation algorithms.

In general, the success of deep learning based met-

hods has been limited to applications where there is a

large dataset of diverse samples. However, neural net-

works might not generalize properly when they are

trained on datasets of few samples. This is due to

the fact that a neural network is a highly nonlinear

function and it is usually formulated using thousands

or millions of parameters. When there is not an ade-

quate amount of samples in a database, current trai-

ning algorithms cause the network to overﬁt on data

and it is very likely not to generalize well on test data.

Even if a network is trained using a large dataset,

it is probable that the network is overﬁtted on the da-

taset and it might not generalize well on the test set.

This is due to a phenomenon called database shift.

The aim of domain adaptation techniques is to train

models that are tolerant to shift in databases. In con-

tinuous domain adaptation setting, the classiﬁcation

model is trained on a source dataset. Then, it is de-

ployed and eventually, new unlabeled data is added to

the database. The newly added samples (or some of

them) might be retained for the future, or they might

be removed from the database.

In order to do continuous domain adaptation, we

ﬁrst need to study domain adaptation techniques in a

non-continuous setting in which there is a source da-

tabase and an unlabeled target database. This way,

we will be able to have a better understanding of the

advantages and disadvantages of each technique ta-

king into account the continuous domain adaptation

setting.

In this paper, we will formally explain the domain

adaptation problem in Section 2 and review state-of-

the-art methods in Section 3. Then, we propose a new

method in Section 4 by modifying the self-training

method and taking into account the uncertainty of pre-

Heravi, E., Aghdam, H. and Puig, D.

A Modiﬁed Self-training Method for Adapting Domains in the Task of Food Classiﬁcation.

DOI: 10.5220/0007688801430154

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 143-154

ISBN: 978-989-758-354-4

143

diction rather than the probability scores. This makes

our method more tolerant to error reinforcement. Our

experiments on the Food-101 and the UPMC-101 da-

tasetts in Section 5 show that our method is able to

produce superior results compared to the recently pro-

posed approach based on tri-training.

2 FORMULATION

Assume the problem of training a neural network

for classifying some foods worldwide. To this end,

we need to collect a database of foods and manu-

ally label them. Denoting the database by X

{(x

, y

), . . . , (x

, y

)}, our aim is to train the classi-

ﬁcation model

g(x

) : R

H×W

→ R (1)

to predict the label of the input image. The database

could be created by only collecting images of food

from the Internet. Also, online users tend to decorate

a food and take the best shot. The database could be

collected considering different environmental condi-

tions, variations of the same food from one country to

another and the imaging devices.

Our goal is to train a food classiﬁcation network

using these images. Then, we will deploy our mo-

del on a device which is designed to classify image

foods captured by the device. In other words, there is

another database called X

= {(x

, y

), . . . , (x

, y

)}

indicating the samples captured by the device. Here,

our dataset collected from the Internet is the source

domain and the dataset collected by the device is the

target domain where the actual test will take place.

Collecting X

using the ﬁrst approach can be done

quickly and efﬁciently. In contrast, collecting X

using the second approach is hard and it is almost in

fact impractical. However, samples in the second ap-

proach will be diverse as opposed to the samples in

the ﬁrst approach. Consequently, the model trained

on the second approach is likely to be more accurate

than the ﬁrst approach. (Torralba and Efros, 2011)

showed in most cases there is a shift between X

and

even when X

is collected using the second appro-

ach. This shift between the databases negatively af-

fects the classiﬁcation accuracy on X

More formally, the classiﬁcation model g(x

) can

be formulated by the composite function g(x

) =

f (h(x

)) where h : R

H×W

→ X

is a function that

maps the input image into a D-dimensional space cal-

led feature space. The joint probability of vectors

in the feature space and their corresponding labels

are denoted by p

(h(x

), y

), and p

(h(x

), y

) for the

source domain and target domain, respectively.

Domain adaptation refers to the problem of trai-

ning the model f (h(x

)) when p

(h(X

)) 6= p

(h(X

))

but y

, y

∈ L where L is the label space. In other

words, domain adaptation assumes that the labels y

and y

are drawn from the common label space L and

h(x

) and h(x

) are also drawn from the common fea-

ture space X

. However, distribution of feature vec-

tors in the source domain is different from the distri-

bution of feature vectors in the target domain. This is

called covariate shift.

This is different from knowledge adaptation

where the basic assumption is that p

(h(X

)) '

(h(X

)) but y

∈ L and y

∈ L

are two different la-

bel spaces. Here, we have only focused on methods

for dealing with the covariate shift problem.

2.1 Domain Adaptation Types

Domain adaptation can be further divided into su-

pervised, unsupervised and semi-supervised domain

adaptation. In supervised domain adaptation, both X

and X

are labeled. In contrary, unsupervised dom-

ain adaptation deals with situations where the source

domain is labeled but the target domain is only com-

posed of h(x

) and y

is unknown for all target sam-

ples. Finally, semi-supervised domain adaptation re-

fers to problems where the target dataset is partially

labeled. However, the number of labeled target sam-

ples is very low. Figure 1 shows these three problems

schematically.

Unsupervised and semi-supervised domain adap-

tation has important practical applications. We ex-

plain one of these applications using an example. In

order to collect X

in our application, we can simply

rely on online images instead of collecting a diverse

range of food images from wall-mounted cameras in

real-world. This way, we can collect a considerable

amount of food images in a reasonable time.

Then, we can collect many images from a wall-

mounted camera in real-world without annotating

their labels and create the X

dataset. Finally, our mo-

del can be trained using both X

and X

. Using X

the model will learn essential visual clues that are re-

quired for classifying foods. Then, it will reﬁne its

knowledge using the images in X

3 RELATED WORK

In this section, we will explain state-of-the-art domain

adaptation techniques that are applicable to the neu-

ral networks. Generally speaking, domain adaptation

techniques break down to feature space alignment, re-

construction based, generative adversarial networks

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

144

Figure 1: First to the third rows: supervised, semi-

supervised and unsupervised domain adaptation problems.

and semi-supervised learning.

3.1 Feature Space Alignment

Feature space alignment methods (Fernando et al.,

2013) directly manipulate the feature spaces such that

they are both aligned. The correlation alignment (Sun

et al., 2015; Wang et al., 2017; Morerio et al., 2017)

ﬁnds a linear transformation matrix A such that Ah(x

)

is aligned with h(x

). The transformation matrix A is

found by minimizing:

argmin

k A

A −C

(2)

where C

and C

are correlation matrices of the source

and target domains, respectively. Denoting mean sub-

tracted representation matrices with H

and H

, the

above equation will be equal to:

argmin

k A

A − H

. (3)

The advantage of the above formulation is that it is

a convex optimization problem. However, the main

drawback of this method is that all layers in the model

f (h(x)) are ﬁxed during minimization of the above

objective function. To overcome this problem, (Bou-

smalis et al., 2016b) proposed to directly adapt all lay-

ers in h(x) by minimizing:

argmin

k H

− H

. (4)

where θ denotes all parameters of h(x). On the one

hand, a neural network is normally trained using mini-

batches. On the other hand, h(x) is normally a high

dimensional vector. Consequently, small number of

samples in a mini-batch might not be able to accu-

rately approximate the correlation matrices. As the

result, the feature spaces will not be aligned properly.

3.1.1 Maximum Mean Discrepancy

Maximum Mean Discrepancy (MMD) is a method for

comparing two probability distributions (Tzeng et al.,

2014; Csurka et al., 2017; Shaham et al., 2016). It

achieves this goal by computing:

MMD(X

, X

) =

∑

∈X

K (x

, x

) − 2

∑

∈X

∑

∈X

K (x

, x

) +

∑

∈X

K (x

, x

)

(5)

where K is the kernel function. The above function

will be zero for perfectly aligned feature spaces. More

speciﬁcally, feature space represented by h(x) con-

stantly changes during training of a neural network

or aligning feature spaces by minimizing the above

objective function. Figure 2 shows the schematic dia-

gram of domain adaptation by minimizing the MMD

loss. The overall loss function is:

E = crossentropy(X

) + λMMD(X

, X

) (6)

It ﬁrst starts with training the neural network using

only the cross-entropy loss (ie. λ = 0) on the source

domain for n iterations. Then, the network is minimi-

zed using both losses. (Long et al., 2015; Long et al.,

2016) computed MMD for different layers in addition

to the last layer. For example, Figure 3 shows how to

align feature spaces by minimizing MMD of two dif-

ferent layers.

Figure 2: Schematic diagram of domain adaptation

using MMD. Dashed circles show parameters of a layer.

Green/purple rectangles are analogous to convolution-

pooling/fully-connected layers.

A Modiﬁed Self-training Method for Adapting Domains in the Task of Food Classiﬁcation

145

Figure 3: Schematic diagram of domain adaptation by com-

puting MMD for different layers.

3.1.2 Adversarial

Both Correlation Alignment and MMD methods di-

rectly align feature spaces. Domains can be also alig-

ned using an adversarial training technique. (Ganin

and Lempitsky, 2014; Ganin et al., 2015) ﬁrst trained

a classiﬁer to discriminate h(x

) from h(x

). Then,

they adapted h(x) by using the modiﬁed loss function

of the domain classiﬁer. Figure 4 illustrates the sche-

matic diagram of domain adaptation using adversarial

training. Formally, the network is trained by minimi-

Figure 4: Schematic diagram of domain adaptation using

adversarial training.

zing the following objective functions (Tzeng et al.,

2017):

argmin

,θ

crossentropy( f (h(X

)))

argmin

−log



d(h(X

))



− log



1 − d(h(X

))



argmin

−log



d(h(X

)



(7)

The ﬁrst loss function is the common cross entropy

loss function. The second loss function is the logistic

loss for training the domain classiﬁer. The third loss

function is the adversarial loss which adjusts parame-

ters of h() such that h(x

) is indistinguishable from

h(x

) by the domain classiﬁer D(.). Instead of this

adversarial loss, (Tzeng et al., 2015) proposed cross

entropy loss using the uniform distribution. Advers-

arial domain adaptation has some challenges of Ge-

nerative Adversarial Networks (GANs) (Goodfellow

et al., 2014).

3.2 Reconstruction Based

In this approach, a decoder is attached to the encoder

of the neural network and the network tries to classify

source samples X

and reconstruct target samples X

Figure 5 shows the schematic diagram of this method.

Figure 5: Schematic diagram of domain adaptation using

reconstruction based methods.

In this method, the network is adapted by minimi-

zing:

argmin

,θ

crossentropy( f (h(X

))) + (1 − λ)||

− r(h(

))||

(8)

where

is degraded version of X

and r(h(

)) is the

reconstructed image (Ghifary et al., 2016). The net-

work is ﬁrst trained using only the cross entropy loss

function for n

iterations. Then, it is trained using

only the second term in the above loss function for

iterations. This process is repeated until meeting

the stopping criteria. The basic idea behind this met-

hod is that the reconstruction function r(h(

)) learns

to reconstruct a degraded input. This way, given the

source sample x

, it will try to reconstruct h(

) such

that it looks like a sample from X

3.3 Generative Adversarial Networks

Methods based on feature space alignment has an

important issue. Speciﬁcally, they try to minimize

the distance between marginal distributions p(X

) and

p(X

) ignoring the inﬂuence of the labels on these dis-

tributions.

The idea behind domain adaptation using Ge-

nerative Adversarial Networks (GANs) (Goodfellow

et al., 2014; Creswell et al., 2017) is to reduce the

divergence between X

and X

in image domain rat-

her than feature space. We explain the general idea

in Figure 6. In this method, we ﬁrst train a GAN

to transform the given sample x

∈ X

to x

such that

possess similar visual properties of samples in X

which makes it indistinguishable from samples in X

(Bousmalis et al., 2016a). This transformation is done

using function G : R

H×W

→ R

H×W

After training the function G, a new dataset is

generated by applying this function to every sample

in X

. Then, the classiﬁcation model is trained on

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

146

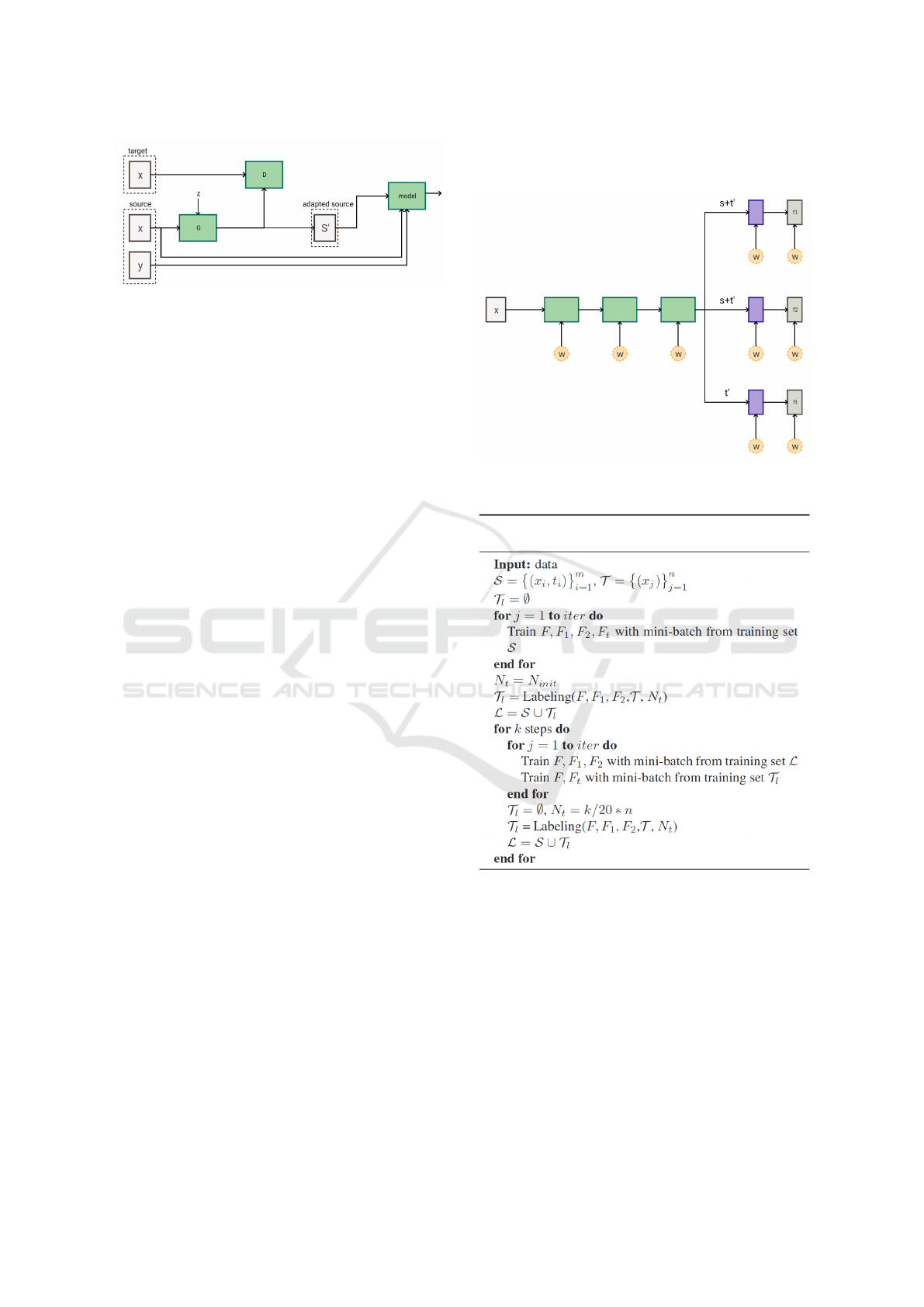
Figure 6: General idea behind domain adaptation using

GANs.

the adapted samples. Instead of training one GAN,

(Liu and Tuzel, 2016) trained two separate GANs

with shared weights on X

and X

. Also, (Hoffman

et al., 2017) trained a GAN using cycle consistent loss

which is able to adapt low-level visual cues as well.

This approach is intuitive and it decouples domain

adaptation from classiﬁcation. The main challenge in

this approach is to design and train a GAN which is

able to accurately adapt samples from X

to X

3.4 Semi-supervised

Co-training is an approach in which two different

classiﬁers F

and F

with the common feature trans-

formation function h are trained on X

(Saito et al.,

2017). This way, there are two classiﬁers F

(h(x

))

and F

(h(x

)) which are both able to correctly clas-

sify x

but each of them has a different view on the

transformed feature h(x

). These two different views

are used for labeling some samples in X

based on a

few criteria. Then, the pseudo-labeled samples from

are combined with X

, and they are used for re-

ﬁning F

and F

. This process is repeated until the

algorithm converges.

In contrast to reconstruction based methods or fe-

ature space alignment methods, this approach aligns

the feature spaces using pseudo labeled target sam-

ples. This actually aligns classes as opposed to the

adversarial domain adaptation methods. In addition,

this method does is easy to implement and train. Fi-

nally, it has also an analogy to the methods in (Haeus-

ser et al., 2017) which has proposed a loss function

based on the random walk on the bipartite graph.

Tri-training (Saito et al., 2017) is a variant of co-

training and it is a branch of a broader topic called

Multiview learning. In addition to F

and F

that we

explained above, Tri-training includes additional clas-

siﬁer F

which is explicitly trained to perform well on

the target dataset. In fact, the pseudo-labeled dataset

produced using the above approach is used for trai-

ning the target classiﬁer F

(h( ¯x

)). Figure 7 illustra-

tes the schematic diagram of this approach. Further-

more, Algorithm 1 explains the training algorithm of

Tri-training.

Figure 7: Schematic diagram of domain adaptation using

tri-training.

Algorithm 1: Tri-training algorithm for domain adaptation

(Saito et al., 2017).

The labeling step in this algorithm, assign pseudo

labels to target samples. A pseudo-label is assigned

to the unlabeled target sample x

if:

• argmax( f

(h(x

))) = argmax( f

(h(x

)))

• f

(h(x

)) > T or f

(h(x

)) > T

hold true. In other words, if both classiﬁers agree on

the class label of x

and conﬁdence of one of them is

greater than T , a pseudo-label is assigned to the tar-

get sample x

. The conﬁdence threshold value could

be set to 0.9 or 0.95. At each labeling operation, all

previously pseudo-labeled samples are removed from

the training. Then, N

samples are selected randomly

A Modiﬁed Self-training Method for Adapting Domains in the Task of Food Classiﬁcation

147

from the target dataset and they are labeled according

to the above procedure. The number of selected sam-

ples N

is increased at each cycle of adaptation.

One important step in tri-training is to encourage

(h(x

)) and F

(h(x

)) to learn different representa-

tions. Denoting the weights of F

by w

and the weig-

hts of F

by w

, tri-training adds |w

· w

| to the loss

function to encourage the weights of the two bran-

ches to be orthogonal. The trivial solution for this

regularization term is that at least one of the weights

to be zero. However, the cross entropy loss attached

to each of these branches prevent the trivial solution.

Consequently, this term encourages the two branches

to learn different representations.

Tri-training has shown superior results in some

tasks compared to other methods explained in this pa-

per (Saito et al., 2017). However, this comes with the

cost of training two more branches. In addition, set-

ting the weak penalization of the regularization term

· w

| will result in two classiﬁers which are not

basically different. In contrast, strong penalization

may encourage the trivial solution for the regulariza-

tion term |w

·w

|. This issue becomes more challen-

ging if we would like to train a network on a source

and target domain with a great divergence.

4 PROPOSED METHOD

Tri-training and co-training are in fact a variant of

another method called self-training. In self-training

(Ruder and Plank, 2018), instead of training two or

three different branches, we train a network with only

one classiﬁcation branch and assign pseudo-labels to

the target samples if the prediction probability is gre-

ater than a threshold.

Self-training is faster to perform compared to Tri-

training. Yet, it suffers from a phenomenon called

error reinforcement. To be more speciﬁc, if the di-

vergence between the two domains is high, it is likely

that some target samples are incorrectly classiﬁed by

the network. This will cause that wrong labels are as-

signed to these samples. When they are added to the

training set, the number of samples with noisy labels

will increase in the training set.

This may potentially cause the network to learn

incorrect mapping. When the network is applied to

the target samples again, it may classify more samples

incorrectly. Hence, the error is likely to be reinforced

as more cycles of pseudo-labeling are performed.

Tri-training reduces this effect using two classi-

ﬁers with different views. Then, it selects samples

that both models agree with the class of the sample

and at least one of them produces a high probability.

From another perspective, Tri-training could be

seen as an ensemble of two models in which pseudo

labels are assigned by analyzing the ensemble. We

can combine the characteristics of the self-training

and tri-training and come up with a method that is

fast to perform and it is more tolerant against error

reinforcement. To this end, we propose the variant of

self-training indicated in Algorithm 2.

Algorithm 2: Proposed variant of self-training using pool of

multi-crop samples.

Θ: A neural network

: The source dataset

: The target dataset

K: An integer showing the number of samples for

evaluation at each cycle

Train Θ on X

for t = 1 : T do

: Select K samples randomly from X

= X

for x

∈ X

Evaluate x

using multi-scale multi-crop

validation with ﬂipping

mi = Compute the mutual information x

if mi < threshold then

= X

Update Θ using X

K = αK (α > 1)

The algorithm starts with training the network on

the source domain. Then, it performs T cycles of

pseudo labeling. At each cycle, it randomly selects

K unlabeled samples from the target domain and eva-

luate each sample using the multi-crop, multi-scale

evaluation with ﬂipping.

To be more speciﬁc, we set the size of each crop

to (s

×H, s

×W ) for an image of size H ×W where

, s

∈ [0, 1]. The ﬁrst crop is obtained by placing

the cropping rectangle in the top left corner. Simi-

larly, the three other crops are obtained by placing the

cropping rectangle on the other four corners. The last

crop is obtained by placing the crop window at the

center. This way, ﬁve crops are generated. We gene-

rate a pool of 15 crops using crop sizes (0.9H, 0.9W ),

(0.8H, 0.8W ) and (0.7H, 0.7W ). Then, we add their

mirrored version to the pool. This way, the size of

the pool increases to 30 crops. Finally, we add the

original image and its mirrored version to the pool.

The Tri-training method assign pseudo labels to

the unlabeled samples and update the models using

them. However, the criteria of pseudo labeling de-

pends only on the classiﬁcation score. If the network

classiﬁes a samples incorrectly with a high probabi-

lity, a wrong label will be assigned to the sample.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

148

We tackle this problem by taking into account the

uncertainty of prediction rather than probability sco-

res. The idea is that if the network is conﬁdent about

its prediction, it must produce comparable probabi-

lities to all the crops in the pool. In contrast, if the

prediction is uncertain the probability scores of crops

would be different. The mutual information is a score

that computed how different is the average prediction

from each predictions in the pool. Formally, the mu-

tual information of T crops is equal to:

MI = H( ˆp(y|x)) − E

ˆx∈pool



H(p(y| ˆx))



. (9)

ˆp(y|x) =

∑

t=1

p(y| ˆx

) (10)

where ˆx

is a samples from the pool of crops. We com-

pute the mutual information of each sample. Then, a

pseudo-label is assigned to a sample if its mutual in-

formation is less than a threshold. This means the

model the label is assigned to a sample if it is conﬁ-

dent about its prediction. It is worth mentioning that

we remove all pseudo-labeled samples from the data-

set at the end of each cycle. This reduces the effect of

error reinforcement.

5 EXPERIMENTS

The UPMC-101 dataset (Wang et al., 2015) is the

twin dataset for the Food-101 dataset (Bossard et al.,

2014). That said, these two datasets share exactly the

same labels, but they have been collected from diffe-

rent online sources. We will train the network on the

Food-101 dataset but our goal is to get a high clas-

siﬁcation accuracy on the test set of the UPMC-101

dataset. In this paper, we use the Inception V3 (Sze-

gedy et al., 2016) trained on the ImageNet dataset as

the main network architecture. We ﬁnetuned the net-

work on the Food-101 dataset and evaluated it using

single crop and multicrop evaluation. Table 1 shows

the results on the test set of the Food-101 dataset.

Table 1: Top-1 and Top-5 validation accuracy using diffe-

rent multi-crop evaluation techniques.

Evaluation method Top-1 Top-5

No crop, no ﬂip 87.49% 97.06%

No crop, ﬂip 88.34% 97.27%

30 crops, ﬂip 89.41% 97.65%

Then, we assessed the network the test set of the

UPMC-101 dataset. Surprisingly, the accuracy of

the network dropped from to 58.6% on the UPMC-

1011 dataset when we only trained the network on the

Food-101 dataset and evaluated it on the UPMC-101

dataset. We have presented ﬁve major hypotheses in

Figure 8 to explain why the accuracy drops dramati-

cally on the UPMC-101 dataset. Assuming the source

dataset X

(blue) and the target dataset X

(magenta),

each sample in these ﬁgures belongs to one of these

datasets. Also, each dataset is represented using a dif-

ferent color.

Figure 8: Five major hypotheses for explaining the accuracy

drop on the UPMC-101 dataset. Samples with similar color

belong to the same dataset.

In the ﬁrst plot, samples of the two datasets are

perfectly separable using a linear classiﬁer. Samples

of X

partially cover the input space where there is not

any sample from X

in this part of the feature space.

Consequently, if we train the model on X

the model

is unlikely to generalize on samples from X

since this

part of the feature space is completely novel to the

model. In the second plot, the two regions slightly

overlap. In this scenario, the model might be able to

correctly classify some samples from X

. In the third

scenario, the two datasets occupy a common region in

the feature space. Nonetheless, there are some parts

in this region which are only covered by one of the

datasets. Therefore, the network may make mistake

in classifying samples belonging to these regions.

In the fourth plot, the two datasets form two dis-

tinct clusters that are non-linearly separable. This

may also cause the network to incorrectly classify

samples of X

. In the ﬁfth plot, the two datasets are

aligned properly and distribution of samples in X

are

very similar to X

. It is worth mentioning that we can

deﬁne other hypotheses but, here, we only explained

these ﬁve hypotheses.

5.1 Domain Divergence

One way to estimate the divergence between the two

domains in the ﬁrst and second scenarios is to train a

linear classiﬁer to discriminate the samples of X

from

the samples of X

. Clearly, this is a binary classiﬁca-

tion problem where samples coming from X

could be

labeled as “positive” or 1 and samples coming from X

could be labeled as “negative” or 0. Here, X

and X

include the feature vector extracted by the network. In

the case of the Inception V3, this is analogous to the

A Modiﬁed Self-training Method for Adapting Domains in the Task of Food Classiﬁcation

149

output of the global average pooling layer which is

a 2048-dimensional vector. X

is created by entering

the samples from the Food-101 dataset to the network

and collecting their feature vectors. Likewise, X

created by entering the samples from the UPMC-101

dataset to the network and collecting their feature vec-

tors.

The classiﬁcation accuracy in the ﬁrst scenario

would be 100% and it would be less than 100% in the

second scenario depending on the amount of overlap.

The linear classiﬁer in the remaining scenarios will

not be able to discriminate the two domains. Howe-

ver, a non-linear classiﬁer is potentially able to discri-

minate the two domains in some of these scenarios.

We could design different networks with various

degrees of non-linearity and train them to discrimi-

nate X

and X

. Then, based on the accuracy of each

network we could infer the scenario that describes the

divergence between X

and X

. Instead of designing

different architectures for each of these situations, we

designed the network illustrated in 9.

Figure 9: Architecture of the domain classiﬁer. The num-

ber in rectangles show the number of neurons in that layer.

In the case of input x, the number indicates the number of

elements of the input. Here, FC denote a fully connected

layer.

Formally, our network is deﬁned as:

Θ(x) = relu(w

f c

· x) + x

p(x) = σ(w

cls

· Θ(x))

(11)

where w

f c

is the weight vector of the fully connected

layer and w

cls

is the weight vector of the classiﬁcation

layer. We train the network by minimizing:

E = H(y

, p(x)) + γ||w

f c

+ λ||w

cls

. (12)

where y

is the binary label and H is the binary cross

entropy loss. The binary label y

is 1 for samples

coming from the Food-101 datasets and it is set to

0 for samples coming from the UPMC-101 dataset.

We regularize the classiﬁer different from the non-

linear transformation layer. Speciﬁcally, if we are in-

terested in a classiﬁer which acts similar to a linear

classiﬁer, we set γ to a large number in order to en-

courage the weights of this layer (w

f c

) to be very

close to zero. When w

f c

is zero or very close to

zero, |relu(w

f c

· x)| = ε will become zero or close to

zero. In other words, the input of the classiﬁer will be

Θ(x) = ε + x showing that the input enters the classi-

ﬁer almost without any modiﬁcation. In this case, the

whole network will be actually a linear classiﬁer.

Conversely, by reducing the value of γ, we let the

network to learn nonlinear boundaries with a higher

degree of non-linearity. To be more speciﬁc, this will

cause the weight vector w

f c

to have non-zero ele-

ments. This will cause that relu(w

f c

· x) to have non-

zero elements. As the result, the input x will be modi-

ﬁed non-linearly which will make the whole network

a non-linear classiﬁer.

We collected X

and X

as we mentioned above af-

ter adapting the knowledge of the Inception V3 on the

Food-101 dataset. Then, we ﬁxed λ to 1e− 5 and trai-

ned the network using different values for γ. Finally,

we trained the classiﬁer to discriminate the training

set of the Food-101 dataset from the test set of the

UPMC-101 dataset. Table 2 shows the results.

Table 2: Classiﬁcation accuracy of the domain classiﬁer for

different values of γ trained to classify the training set of the

Food-101 and the test set of the UPMC-101 datasets.

γ Accuracy (%) Precision(%) Recall (%)

linear 69.06 67.35 74.01

1 71.94 69.98 76.83

0.1 88.19 87.01 89.80

0.01 96.50 96.19 96.82

0.001 99.99 1.00 99.99

Surprisingly, a linear classiﬁer is able to discrimi-

nate 69.06% of the samples from these two datasets,

correctly. Then, we increased the non-linearity of the

network by reducing the value of γ. As the value of

γ reduces, the network becomes more ﬂexible and it

is able to discriminate the two domains more accura-

tely. We observe that by setting γ to 0.01, the network

is able to differentiate 96.50% of Food-101 samples

from the UPMC-101 samples. In addition, by setting

γ to 0.001 the network is able to discriminate 99.99%

of Food-101 samples from the UPMC-101 samples

correctly. This analysis suggests that the second and

fourth hypotheses might be true on the Food101 and

UPMC-101 datasets. In other words, the two data-

sets have diverged and this is one of the reasons that

our network performs poorly when it is trained on the

Food-101 dataset and tested on the UPMC-101 data-

set.

5.2 Modiﬁed Self-training

Next, we utilized our modiﬁed self-training approach

for adapting the domain from the Food-101 to the

UPMC-101. We assume that labels of the UPMC-

101 dataset are not available during training. In other

words, we perform unsupervised domain adaptation.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

150

We applied the domain classiﬁer from the previous

section to discriminate the training and test sets of the

UPMC-101 dataset. Table 3 shows the results.

Table 3: Classiﬁcation accuracy of the domain classiﬁer for

different values of γ trained to classify the training set and

the test set of the UPMC-101 datasets.

γ Accuracy (%) Precision(%) Recall (%)

linear 54.39 54.35 54.90

1 54.83 54.80 55.21

0.1 55.44 55.31 56.68

0.01 55.64 55.48 57.11

0.001 83.00 81.76 84.96

0.0001 90.81 88.31 94.08

Compared to Table 2, we realize that the linear

classiﬁer is only able to discriminate 54.39% of sam-

ples correctly which is 14.67% is less than the same

classiﬁer in Table 2. Also, we notice that the accuracy

of the domain classiﬁer is less than 56% when the va-

lue of γ is greater than or equal to 0.01. However, the

accuracy jumps considerably by setting γ to 0.001 or

lower. These results suggest that divergence between

the training and test sets of the UPMC-101 dataset is

potentially less than the divergence between the test

of the UPMC-101 dataset and the training set of the

Food-101 dataset.

From another perspective, if the network is trained

on the training set of the UPMC-101 dataset and tes-

ted on the test set of the UPMC-101 dataset, it is likely

to perform better than training the network using the

Food-101 dataset and assessing them on the UPMC-

101 dataset. In order to estimate what could be the lo-

wer bound of the error on the UPMC-101 dataset, we

adapted the knowledge of the network to the training

set of the UPMC-101 dataset. Table 4 compares our

results with the results obtained by the UPMC Team

As our analysis using the domain classiﬁer sugge-

sted, training the network using the UPMC-101 data-

set provides more accurate results. Since the Food-

101 dataset is more diverged from the test set of

the UPMC-101 compared to the training set of the

UPMC-101, the classiﬁcation accuracy after adapting

the domain (not knowledge) of the Food-101 to the

UPMC-101 might not be greater than 71.05% in the

best case scenario using single image validation. In

other words, denoting the classiﬁcation accuracy of

our model on the UPMC-101 dataset by acc

upmc

, we

suppose that acc

upmc

is bounded within

58.61% ≤ acc

upmc

≤ 71.05% (13)

when it utilizes the Food-101 dataset for training and

the unlabeled training set of the UPMC-101 dataset

blog.heuritech.com

for adapting the domain of the model. Next, we ap-

plied our proposed self-training approach for adap-

ting the domain of the network to the UPMC-101 da-

taset. Speciﬁcally, we used our network trained on

the Food-101 dataset and used the training set of the

UPMC-101 dataset as the unlabeled target dataset.

Then, we performed domain adaptation and assessed

the results on the test set of the UPMC-101 dataset.

Table 4 shows the results.

According to the results, Tri-training increases

the classiﬁcation accuracy to 60.81% and our modi-

ﬁed self-training approach improves the results up to

62.66%. It is worth mentioning that our method is

faster to run and setting its hyperparameters is fairly

trivial. Also, we did not compare our method with ot-

hers methods because Tri-Training approach has sur-

passed the performance of other methods in literature

(Saito et al., 2017). Figure 10 and Figure 11 shows

the precision and recall before and after performing

self-training.

We notice that the mean precision, minimum pre-

cision, and the maximum precision have been impro-

ved after adapting the domain. The recall also shows

a similar behavior and mean recall, minimum recall,

and maximum recall have been improved using our

method. This is due to the fact that our method select

samples whose prediction uncertainty is low. We ana-

lyzed the network before and after adaptation using

the class activation mapping (CAM) technique (Zhou

et al., 2015). Figure 12 shows a few samples from the

UPMC dataset.

The ﬁrst row in this ﬁgure shows the query image.

All images in this ﬁgure are incorrectly classiﬁed be-

fore adapting the domain and all of them are classiﬁed

correctly after applying our proposed method. The

second row is the CAM of actual class before adap-

ting the domain. The third row shows the CAM of the

predicted class before adapting the domain. The last

row illustrates the CAM of the predicted class after

adapting the domain. We observe that the CAM of

the network has been changed and moved after adap-

tation.

For example, the second column shows the image

of a “cannoli”. However, it is classiﬁed as “Peking

duck” before adaptation. After applying our propo-

sed self-training approach, the network shifts the at-

tention to another part of the image. After adapting

the attention, the network is able to predict the image

correctly.

A Modiﬁed Self-training Method for Adapting Domains in the Task of Food Classiﬁcation

151

Table 4: Classiﬁcation accuracy of the UPMC-101 dataset when the network is trained on different training sets.

Model Method Training set Accuracy Top-1 (%) Accuracy Top-5(%) evaluation

our KA Food-101 60.02 77.57 multi-crop

our KA Food-101 58.61 76.61 single image

our KA UPMC-101 73 87.29 multi-crop

our KA UPMC-101 71.05 86 single image

UPMC Team KA UPMC-101 66.83 NA NA

UPMC Team scratch UPMC-101 53.62 NA NA

Table 5: Classiﬁcation accuracy on the UPMC-101 dataset after adapting the knowledge of the network.

Method Accuracy Top-1 (%) Accuracy Top-5(%) evaluation

Tri-training 60.81 77.86 single

Modiﬁed self-training (our) 62.66 78.81 single

Figure 10: Precision of the network on the UPMC dataset before (top) and after (bottom) applying our modiﬁed self-training

approach (best viewed electronically).

6 CONCLUSION

In this paper, we proposed a new method based on

self-training in which we assign pseudo-labels to tar-

get samples taking into account the uncertainty of pre-

diction rather than their probability scores. To es-

timate the uncertainty, we utilized multi-crop multi-

scale evaluation with ﬂipping and computed the mu-

tual information of predictions.

Next, we applied our network trained on the Food-

101 dataset to the UPMC-101 dataset and showed that

the accuracy drops to 58.61%. We further analyzed

this behavior using a domain classiﬁer. To be more

speciﬁc, we designed a domain classiﬁer with adapta-

ble nonlinearity and trained it to discriminate samples

of the Food-101 dataset from the UPMC-101 dataset.

We showed that a linear classiﬁer is able to classify

69.06% of these samples correctly. This suggests that

there is a divergence between the two datasets even

though their label spaces are identical. We applied

our proposed method as well as the tri-training met-

hod to this problem. Our experiments showed that the

proposed method is able to produce superior results.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

152

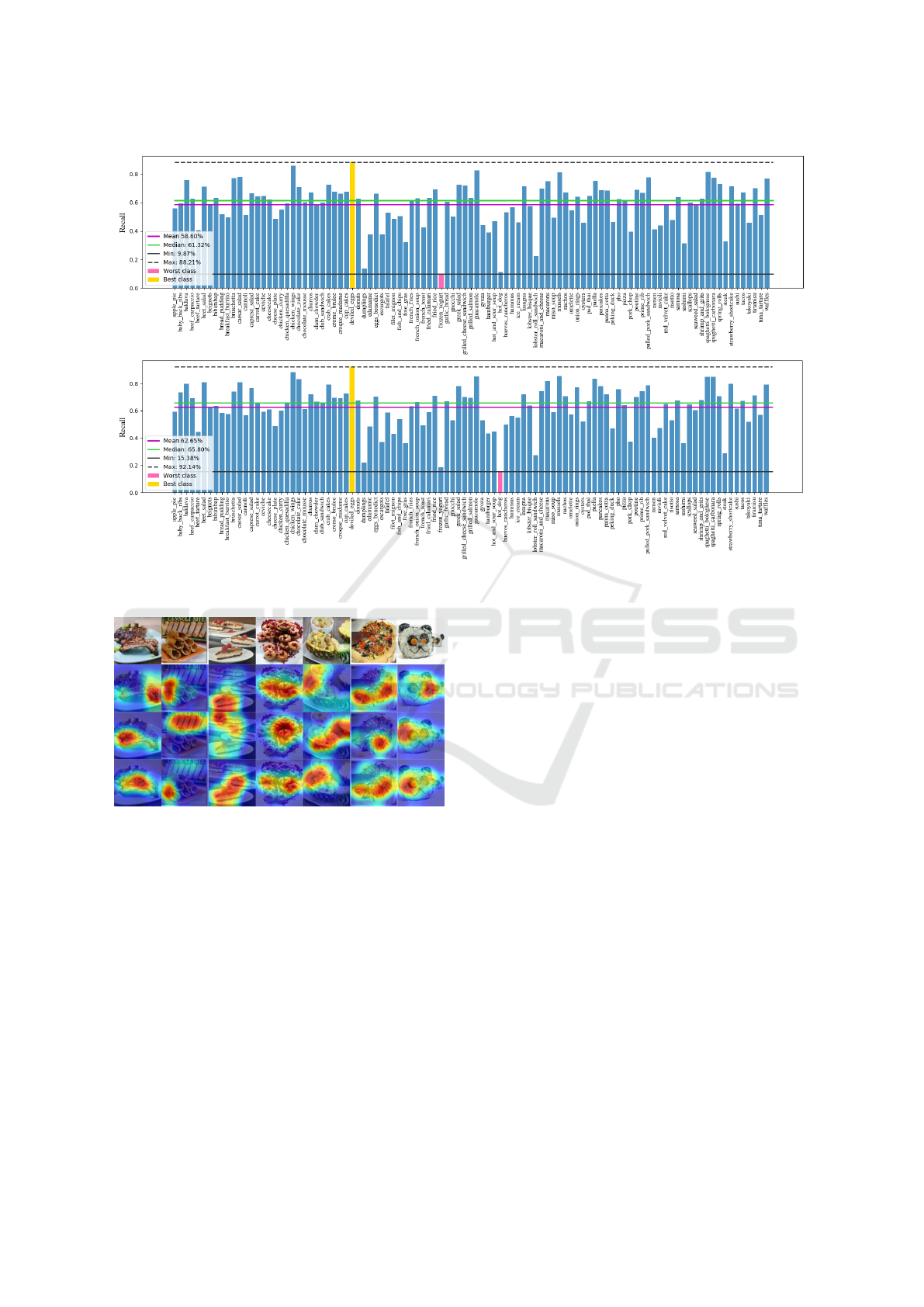
Figure 11: Recall of the network on the UPMC dataset before (top) and after (bottom) applying our modiﬁed self-training

approach (best viewed electronically).

Figure 12: Visualizing the network using CAM before and

after adaptation on a few samples from the UPMC dataset.

REFERENCES

Bossard, L., Guillaumin, M., and Van Gool, L. (2014).

Food-101 – Mining Discriminative Components with

Random Forests, pages 446–461. Springer Internatio-

nal Publishing.

Bousmalis, K., Silberman, N., Dohan, D., Erhan, D.,

and Krishnan, D. (2016a). Unsupervised Pixel-Level

Domain Adaptation with Generative Adversarial Net-

works.

Bousmalis, K., Trigeorgis, G., Silberman, N., Krishnan, D.,

and Erhan, D. (2016b). Domain Separation Networks.

(NIPS).

Creswell, A., White, T., Dumoulin, V., Arulkumaran, K.,

Sengupta, B., and Bharath, A. A. (2017). Generative

Adversarial Networks: An Overview. (April):1–14.

Csurka, G., Baradel, F., and Chidlovskii, B. (2017).

Discrepancy-based networks for unsupervised domain

adaptation : a comparative study. International Con-

ference on Computer Vision (ICCV), (1):2630–2636.

Fernando, B., Habrard, A., Sebban, M., and Tuytelaars, T.

(2013). Unsupervised visual domain adaptation using

subspace alignment. Proceedings of the IEEE Interna-

tional Conference on Computer Vision, pages 2960–

2967.

Ganin, Y. and Lempitsky, V. (2014). Unsupervised Domain

Adaptation by Backpropagation. (i).

Ganin, Y., Ustinova, E., Ajakan, H., Germain, P., Laro-

chelle, H., Laviolette, F., Marchand, M., and Lem-

pitsky, V. (2015). Domain-Adversarial Training of

Neural Networks. 17:1–35.

Ghifary, M., Kleijn, W. B., Zhang, M., Balduzzi, D., and

Li, W. (2016). Deep reconstruction-classiﬁcation net-

works for unsupervised domain adaptation. Lecture

Notes in Computer Science (including subseries Lec-

ture Notes in Artiﬁcial Intelligence and Lecture Notes

in Bioinformatics), 9908 LNCS:597–613.

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative Adversarial Networks. pa-

ges 1–9.

Haeusser, P., Frerix, T., Mordvintsev, A., and Cremers, D.

(2017). Associative Domain Adaptation.

Hoffman, J., Tzeng, E., Park, T., Zhu, J.-Y., Isola, P., Sa-

enko, K., Efros, A. A., and Darrell, T. (2017). Cy-

A Modiﬁed Self-training Method for Adapting Domains in the Task of Food Classiﬁcation

153

CADA: Cycle-Consistent Adversarial Domain Adap-

tation. pages 1–12.

Liu, M.-Y. and Tuzel, O. (2016). Coupled Generative Ad-

versarial Networks. (NIPS).

Long, M., Cao, Y., Wang, J., and Jordan, M. I. (2015). Lear-

ning Transferable Features with Deep Adaptation Net-

works. 37.

Long, M., Zhu, H., Wang, J., and Jordan, M. I.

(2016). Unsupervised Domain Adaptation with Re-

sidual Transfer Networks. (Nips).

Morerio, P., Cavazza, J., and Murino, V. (2017). Minimal-

Entropy Correlation Alignment for Unsupervised

Deep Domain Adaptation. (2011):1–14.

Ruder, S. and Plank, B. (2018). Strong baselines for neural

semi-supervised learning under domain shift. CoRR,

abs/1804.09530.

Saito, K., Ushiku, Y., and Harada, T. (2017). Asymmetric

Tri-training for Unsupervised Domain Adaptation.

Shaham, U., Stanton, K. P., Zhao, J., Li, H., Raddassi, K.,

Montgomery, R., and Kluger, Y. (2016). Removal of

Batch Effects using Distribution-Matching Residual

Networks.

Sun, B., Feng, J., and Saenko, K. (2015). Return of Frustra-

tingly Easy Domain Adaptation. (Figure 1).

Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna,

Z. (2016). Rethinking the inception architecture for

computer vision. In IEEE Conference on Computer

Vision and Pattern Recognition, (CVPR), pages 2818–

2826.

Torralba, A. and Efros, A. A. (2011). Unbiased Look at

Dataset Bias.

Tzeng, E., Hoffman, J., Darrell, T., Saenko, K., and Lowell,

U. (2015). Simultaneous Deep Transfer Across Dom-

ains and Tasks. International Conference on Compu-

ter Vision (ICCV).

Tzeng, E., Hoffman, J., Saenko, K., and Darrell, T. (2017).

Adversarial Discriminative Domain Adaptation.

Tzeng, E., Hoffman, J., Zhang, N., Saenko, K., and Darrell,

T. (2014). Deep Domain Confusion: Maximizing for

Domain Invariance.

Wang, X., Kumar, D., Thome, N., Cord, M., and Precioso,

F. (2015). Recipe recognition with large multimodal

food dataset. 2015 IEEE International Conference

on Multimedia and Expo Workshops, ICMEW 2015,

(1):2–7.

Wang, Y., Li, W., Dai, D., and Van Gool, L. (2017). Deep

Domain Adaptation by Geodesic Distance Minimiza-

tion.

Zhou, B., Khosla, A., Lapedriza,

A., Oliva, A., and

Torralba, A. (2015). Learning deep features for dis-

criminative localization. CoRR, abs/1512.04150.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

154