A Proposal for a Language Combining Biochemical Rules and

Topological Structure for Systems Biology

Anasthasie Joelle Compaore

1 a

and Pascale Le Gall

2 b

Ecole Supérieure d’Informatique, Université Nazi Boni, Bobo-Dioulasso, Burkina Faso

Laboratoire MISC, CentraleSupélec, Université Paris Saclay, Gif-Sur-Yvette, France

Keywords:

Rule-Based Modelling, Biochemical Rules, Compartments, Topology-Based Modelling.

Abstract:

For about twenty years, rule-based modelling has been widely used for Systems Biology issues. Most existing

languages focus on biochemical reactions primarily, and to a lest extent, on the cell structure in compartments.

BIOCHAM and Pathway Logic Assistant (PLA) are representative examples of such rule-based languages.

They are equipped with tools providing great analysis capabilities. We propose to provide such biochemical

languages with annotations relating to the compartments in which the biochemical reactions take place. We

will make sure that biochemical rules always indicate the nature of the compartments involved and the neigh-

bourhood relations between them. At the end, it sufﬁces to specialize the generic rules according to a particular

topological structure in order to obtain sets of localized rules. Thus, resulting models can be analysed by using

either BIOCHAM or PLA.

1 INTRODUCTION

Systems biology concerns the study of molecular in-

teraction networks at the cellular level by using differ-

ent disciplinary ﬁelds such as biochemistry, cell biol-

ogy, computer science, mathematics or systems en-

gineering. Cellular biological mechanisms are con-

sidered as natural complex systems (Ma’ayan, 2017)

mainly characterized by unpredictability, context de-

pendency, emergence and stochasticity (Chen and

Crilly, 2016). A lot of aspects participate to this com-

plexity: the dynamic rearrangements of the compart-

ments, related to the movements of membranes; the

kinetic parameters characterizing each reaction; the

combinatorial complexity due to the possible great

numbers of the states of the molecules knowing that

for a given molecule M, different states of M can

induce different functionalities and thus different re-

actions involving M. Because of this intrinsic com-

plexity, elucidating or predicting the functioning of

biological systems generally proceeds by modelling.

This modelling aims at interconnecting the different

underlying cellular processes - at the cellular level

- and integrating different hierarchies of cells - at a

cells population level. In this effort, a lot of modelling

https://orcid.org/0000-0003-3045-9579

https://orcid.org/0000-0002-8955-6835

approaches, based on a diversity of formalisms (Bar-

tocci and Lio, 2016)) have been deﬁned and used in

the study of some phenomenons such as signal trans-

duction (Talcott, 2016; Riesco et al., 2017), gene reg-

ulation (Faeder et al., 2009), metabolism and protein-

protein interactions (Fages et al., 2004).

The way the coupling between biochemical reac-

tions and compartmentalization is made differs from

one approach to another: while the spatio-temporal

dynamics-oriented approaches explain the interested

phenomenon only by the dynamic of the system’s ge-

ometry (Regev et al., 2004; Cardelli, 2004; Gian-

nakis and Andronikos, 2017), some others such as

BIOCHAM (Fages et al., 2004), pathway Logic (Eker

et al., 2002), the ﬁrst version of BioNetGen (Faeder

et al., 2005) focus on the biochemical reactions in an

implicit static compartmentalization. The majority of

the ﬁrst models are equation-based and permit quan-

titative analysis. However, these modellings can be

limited by the number of equations to be deﬁned (due

to the combinatorial complexity) and the difﬁculties

in the estimation of kinetics. Therefore, other for-

malisms, inspired by computer science such as pro-

cess calculi, cellular automata, agents and rule-based

languages have been used, and the so designed mod-

elling tools permit quantitative and/or qualitative sim-

ulations and analysis (Machado et al., 2011; Pedersen

et al., 2015).

310

Compaore, A. and Gall, P.

A Proposal for a Language Combining Biochemical Rules and Topological Structure for Systems Biology.

DOI: 10.5220/0007689303100317

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 310-317

ISBN: 978-989-758-353-7

We chose to focus on rule-based modelling of bio-

chemical reactions in a static compartmentalization

for the following main reason: a rule-based modelling

formalism is generally considered as relatively sim-

ple and intuitive: a reaction results in changes in the

contents - in terms of present molecules and/or their

quantities or concentrations - of some compartments

of the considered system. Rules, representing reac-

tions, are then of the form Le f t Hand → Right Hand

to materialize this transition of states. Le ft Hand

and Right Hand respectively represent the needed

molecules for the reaction to occur and the molecules

resulting from this occurrence. This form of rules

is familiar to biologists because inspired of classi-

cal chemical equations. To simplify modelling a lit-

tle more, molecules are often abstracted by identi-

ﬁers and if necessary, mechanisms are added to spec-

ify sites. For a very classical example, the reac-

tion of water dislocation can be expressed by the rule

2A −→ B +C where A, B et C respectively stand for

molecules H

O, H

and HO

−

. In the context of bi-

ology, the localization of the involved molecules is a

key information to be added to this rule. In (Hlavacek

et al., 2006), one can ﬁnd other advantages of rule-

based languages for the modelling of biological cells.

The remainder of the paper is organized as follows: in

Section 2, we present in more details our motivations

in the context of rule-based languages for systems bi-

ology. In Section 3, we outline our approach empha-

sizing the role of compartmentalization and the inter-

est of systematically locating biomolecules in com-

partments in a generic way. In Section 4, we illustrate

our approach on some examples issued from the liter-

ature. Section 5 gives some concluding remarks.

2 MOTIVATIONS

2.1 Context

Rule-based modelling is widely used in Systems Bi-

ology as evidenced by the important number of tools

such as Kappa (Danos and Laneve, 2004; Boutil-

lier et al., 2018), Virtual Cell (VCell) (Blinov et al.,

2017) and BioNetGen (Faeder et al., 2009) issued

from studies dealing with the explicitation of biolog-

ical phenomena by the mean of this formalism. The

rule-based languages underlying these three tools are

designed for the deﬁnition of models that especially

track biomolecular sites dynamics. Generally, the ex-

pressible reactions are reversible and consist in the

synthesis of a molecule, the binding of two molecules

and the modiﬁcation of the form of a molecule. Those

of the languages that take into account compartments

can express the transport of a molecule from one com-

partment to another and species spanning multiple

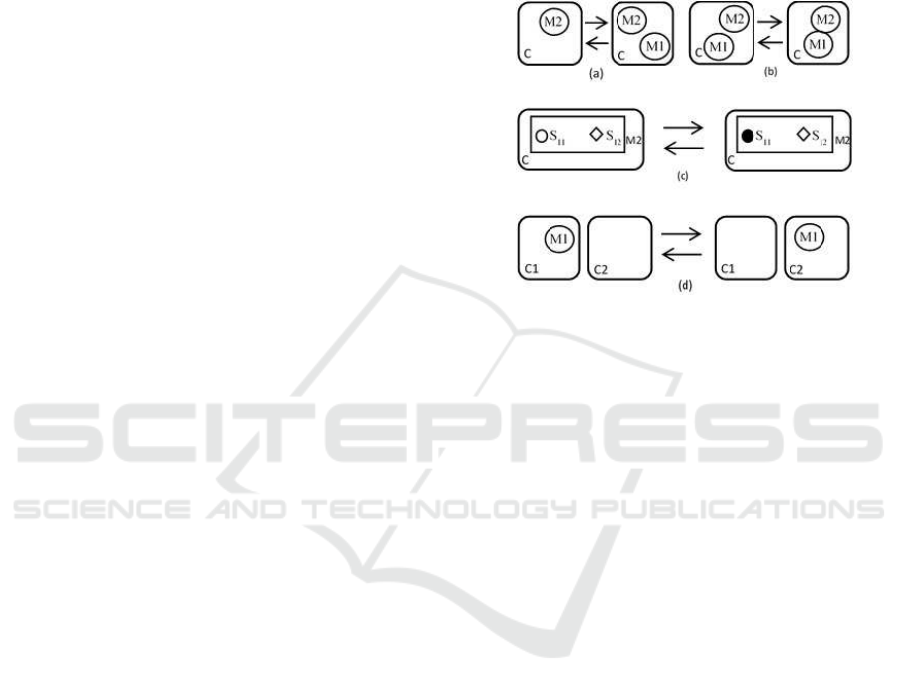
compartments. Figure 1 gives a schematic representa-

tion of some localized reactions. More or less similar

schematics can be found in the literature of most of

the aforementioned languages and their understand-

ing is intuitive.

Figure 1: Representation of some rules. (a): Synthesis (→)

and Degradation (←) of M1 catalysed by M2 in C. (b):

Binding (→) and Unbinding (←) of M1 and M2 in C. (c):

Phosphorylation (→) and Dephosphorylation (←) of M2 on

site S

in C. (d): Transport of M1 from C1 to C2 (→) and

from C2 to C1 (←).

Each of the tool-sets provide capabilities to simulate,

analyse and visualize networks generated from the

models and the graphs issued from simulation. Cur-

rently, more and more initiatives are working to en-

able modellers to easily take advantage of the func-

tionality of different tools. That results either in trans-

lators like the Kappa-BioNetGen one introduced by

(Suderman and Hlavacek, 2017) that enables transla-

tion in the two senses or in provided capabilities of

inferring from a given model, another model based

on a different formalism.

Most of the rule-based approaches ﬁrst focused on

biochemical reactions before proposing extensions to

highlight the topology a little more. BioNetGen Lan-

guage (BNGL) has therefore been extended, result-

ing in compartmental BNGL (cBNGL) (Harris et al.,

2009) that makes it possible to explicit topology as an

inclusion graph. Similarly, the modeling of compart-

ments and space within the cell is possible in Virtual

Cell (VCell) since the extension presented in (Blinov

et al., 2017).

The approach we propose in this paper depends on

BIOCHAM (Fages and Soliman, 2008) and Path-

way Logic (PL) (Eker et al., 2002; Talcott, 2016).

BIOCHAM is an environment to modelling biochem-

ical interactions which provides a rule-based lan-

guage for the deﬁnition of the models and a tempo-

A Proposal for a Language Combining Biochemical Rules and Topological Structure for Systems Biology

311

ral logic based language to express properties that are

supposed to be checked by the system. It offers differ-

ent semantics, the boolean one being based on rewrit-

ing logic, and the carrying out of both qualitative and

quantitative analysis. It also enables the checking

(and the learning (Calzone et al., 2005)) of the prop-

erties of the models by the using of NuSMV model-

checker. BIOCHAM has been extended to provide the

capability of infering rule-based models from ODE-

based one (Fages et al., 2015). This is useful when

kinetics parameters value are not totally deﬁned. PL

is another rule-based approach to modelling cellular

processes, that uses the rewriting language MAUDE

(Clavel et al., 2000) to write the algebraic speciﬁca-

tion underlying its models. It queries its models by

using Pathway Logic Assistant (PLA) (Talcott and

Dill, 2005) that offers a graphical interface and ac-

cesses to some formal tools such as Pathanalyser (Dill

et al., 2005) and the simulation and model-checking

features of MAUDE. These tools materialize localiza-

tions by attaching simple labels to molecules, with a

difference for PL that can write models from which

one can deduce the hierarchical organization of cells

found in Biomodels (Li et al., 2010). A model in these

languages is not explicitly guaranteed to be coherent

with a speciﬁc topology. It is this aspect of combin-

ing rules with formal topological structure that we ad-

dress in this paper.

2.2 Motivations

Living organisms are highly compartmentalized bio-

logical systems whose functioning depends on the co-

ordination of the isolated behaviours of each compart-

ment. Then, topology, i.e the nature of compartments

composing the system and their relative position in

the system, as well as biochemical reactions are de-

terminant for the life of the system. The importance

of topology is directly related to the role of compart-

mentalization. On one hand, compartments of same

nature are entities sharing the same functionalities and

the same behaviour. On the other hand, by group-

ing in each compartment the appropriate molecules

(due to the selective permeability of membranes),

it improves systems efﬁciency by speeding up the

molecular interactions given that their occurrences

are location-dependant. This role of compartmen-

talization is highlighted by (Harris et al., 2009) that

presents a compartmental model of an eukaryotic cell

in which a signalling process results from interactions

between molecules from four distinct compartments

each containing speciﬁc molecules and transport re-

actions concerning neighbouring compartments.

Despite its importance, a relative weakness in the tak-

ing into account of the topology can be noticed in

most formalisms for rule-based modelling of biolog-

ical processes. Our motivation is then to reinforce

in these modellings, the place of the topology by en-

abling its separate representation. A particular regard

is put on the neighbouring relationships to take into

account the location-dependency of reactions, and on

the types of compartments to respect the speciﬁc po-

tential behaviour of each compartment. Moreover, the

organels are not abstracted by a generic one (if a sys-

tem has n compartments of type T , all the n compart-

ments are represented), to make possible the simul-

taneous occurrences of concurrent reactions. The re-

sulted models are guaranteed to be coherent with the

static topological structure of the system under con-

sideration: all the rules are contextualized with regard

to the compartments. Then, our models can be used

through existing tools. We have chosen BIOCHAM

and PL as privileged target tools because they have a

lot of similarities.

3 THE MODELLING APPROACH

3.1 General Overview

Classically, in rule-based modelling of biological pro-

cesses, topology and biochemical reactions are taken

into account in an integrated manner. Unlike these ap-

proaches, our rule-based modelling approach focuses

on an explicit speciﬁcation of the topological struc-

ture. We propose to separate the two following com-

plementary aspects: a static topology of the system

and biochemical reactions. Our approach can then be

considered as a topology-driven rule-based modelling

approach as shown in Figure 2. We propose to take

as input data ﬁrstly a graph, that we call as exchange

graph and that abstracts the topology of the system

and secondly, a set of generic rules that describe the

biochemical reactions that can occur in the system

provided that there is some correspondence between

compartments mentioned in the topological structure

and indications of localization w.r.t types of compart-

ments given in the rules. Then, we automatically elab-

orate a concrete model which can be translated in such

a way that it can be handled by the target tool chosen

by the modeller.

3.2 The Exchange Graph

Generally speaking, a compartment of a biological

system is of a certain type and is delimited by a

double-layered membrane. Molecules may be local-

ized more precisely in one of the four locations related

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

312

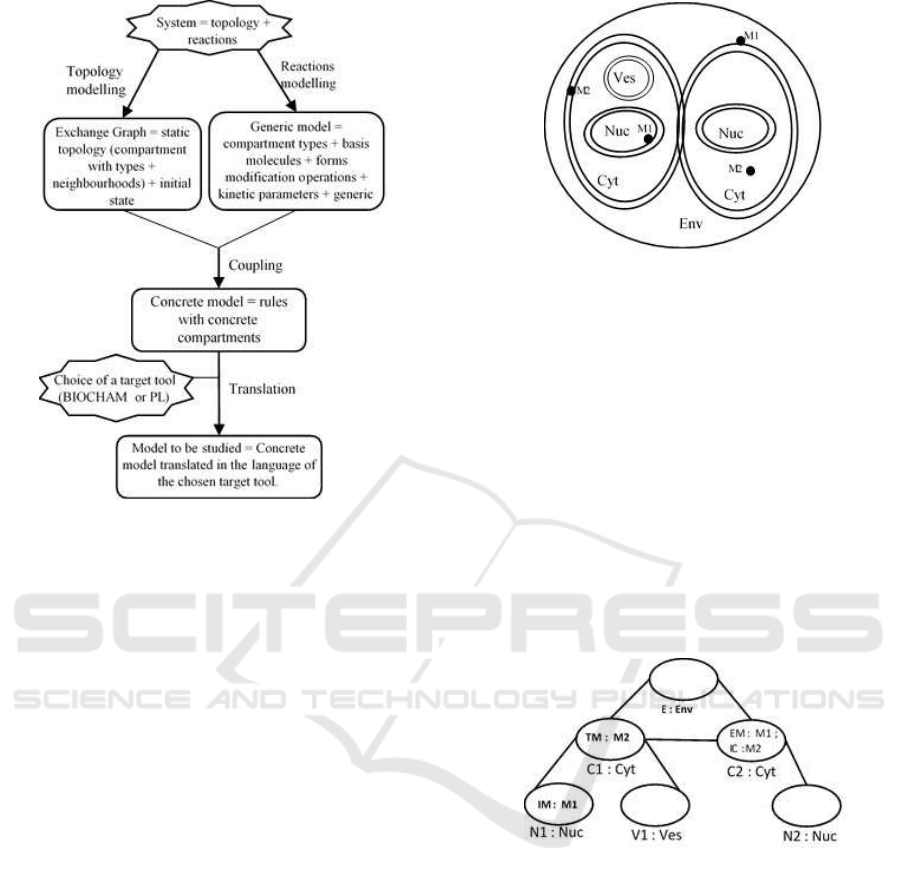
Figure 2: Schematic representation of the approach.

to a given compartment: from the most external to the

most internal, we name these locations EM (molecule

is tethered to the external membrane), T M (molecule

is in the trans-membrane space), IM (molecule is teth-

ered to the internal membrane) and IC (molecule is in-

side the compartment). IC is the default location for

a given compartment. Two kinds of neighbourhoods

for localisations are considered: the neighbourhood

by inclusion in which one compartment is included

in another one and the neighbourhood by adjacency

in which two compartments stuck each other by por-

tions of their membranes. Figure 3 is an example of

such a topology. The particular compartment of type

Env stands for the outer compartment of any system.

Its role is to delimit the system of interest. Gener-

ally speaking, the rules will bring into play molecules

that are in localities connected by neighbourhood re-

lations.

The exchange graph of a biological system S captures

all the neighbourhood relations between the compart-

ments of S and only these ones. It will also store the

contents of these compartments. We note V

the set of

the compartments of S, T

the set of the types of the

compartments of S and E the unique external com-

partment of type Env. The exchange graph GE

as-

sociated to S is an undirected graph in which a ver-

tex represents an element of V

∪ E and an edge

represents either the adjacency between two compart-

ments, or the inclusion of a compartment in another

one. Each compartment is associated with its type,

an element of T

∪ Env and its content in terms of

Figure 3: A topological structure S

. It has two adjacent

compartments of type Cyt: each of them contain a com-

partment of type Nuc while only one of them contains in

addition a compartment of type Ves (for vesicle). The local-

izations of molecules are T M for the ﬁrst compartment of

type Cyt, EC and IC for the second one and IM for the ﬁrst

compartment of type Nuc.

molecules. To sum up, we impose the following con-

ditions on the exchange graphs: i) exactly one com-

partment is of type Env and ii) for each element t of

, there is at least one element of V

whose type is

t. For example, when considering the topology S

(Figure 3), we have V

= {C1,C2, N1, N2,V 1} and

= {Cyt, Nuc,Ves} by naming C

and C

. . . the

compartments of S

. Figure 4 gives the schematic rep-

resentation of GE

Figure 4: Exchange Graph GE

for to S

(Figure 3).

In practice, there are essentially two ways for obtain-

ing an exchange graph: the ﬁrst one is to directly

construct it by manually designing it while respect-

ing basic topological and biological conditions. This

method is clearly sufﬁcient when the topology to be

abstracted is simple enough not to be mistaken.

The second way consists in extracting the graph from

geometric models, called the bio-geometric mod-

els and handled by some geometric 3D-modellers.

For our part, we build bio-geometric models us-

ing a specialization of MOKA (Vidil et al., 2002),

a topology-based geometric modeller implementing

3-Generalized-Maps. For modelling an object as

Generalized-Map, the topology of the object is ﬁrst

modelled by as a set of darts (obtained by decompos-

ing the objects along their topological structure until

A Proposal for a Language Combining Biochemical Rules and Topological Structure for Systems Biology

313

getting elements of smaller dimensions, called darts).

Then embeddings, that is pieces of information such

as forms, colors, dimensions or molecule concentra-

tions, . . . are associated to main elements (such as vol-

umes, faces, vertices) composing the topology in or-

der to obtain a full geometric object.

In our specialization of MOKA, we represent com-

partments as double-cubes (representing respectively

the inner membrane and the outer membrane of the

compartment) linked by a 3-dimensional neighbour-

hood relation. A compartment has then forty-eight

darts (eight for each face). In our setting, the embed-

dings consist in the name, the type and the content of

compartment attached to the 3-cells (volumes) of the

topology. In addition to the creation of the environ-

ment, we offer two other creation operations: i) the

creation of a compartment C1 in a compartment C2 :

the name C2 is associated to the outer membrane of

C1; ii) the creation of a compartment C1 stuck to a

compartment C2 : the bonding surface on C2 must be

deﬁned and 3-dimensional links are established be-

tween corresponding surfaces of C1 and C2. An il-

lustration of the bonding surface is given by Figure 5

where the 3-dimensional links are the horizontal black

lines between two darts (points).

Figure 5: Bonding surface of two volumes.

Figure 6 represents the bio-geometric model of S

(Figure 3). Five compartments are visible and we use

colors for distinguishing compartments.

Figure 6: Bio-Geometric model of S

(Figure 3).

Using geometric modellers becomes particularly con-

venient for situations involving a signiﬁcant number

of compartments (e.g. Figure 7)

The extraction of the exchange graph is done by

browsing the darts of the bio-geometric model. For a

compartment C1, the set of its neighbours contains all

Figure 7: Bio-Geometric model of a system that has a com-

partment (the central one) which has no direct neighbour-

hood with its container, because it is adjacent on all its faces

to another compartment.

the compartments which have at least one dart linked

with a dart of C1 by an 3-dimensional link.

3.3 The Generic Model

The generic model is the transcription in our rule-

based language, of the reactions. As shown by Listing

1 that gives an extract of the grammar of the language,

a generic model (GM) is organized in ﬁve sections

(line 1) each delimited by BEGIN_section-name and

END_section-name.

The ﬁrst section CTypes that lists the compartment

types is original to our approach while the others re-

spectively listing the basis molecules (BMols), the

molecules forms transformations (Modifs), the kinetic

parameters identiﬁers (KPS) and the generic reaction

rules (GRS ) are classically found in the other lan-

guages. The syntax allows association of particular

sites to a basis molecule (lines 8 and 9) and kinetic

parameters are valued (line 16).

Listing 1: Syntax of generic model.

1 GM : : = CTypes BMols Modifs KPS GRS

3 CTypes : : = BEGIN_CTypes LCT END_CTypes

4 LCT : : = idCT | idCT ;LCT

6 BMols : : = BEGIN_BMols LBM END_BMols

7 LBM : : = BM | BM; LBM

8 BM : : = idBM | idBM ( L S i t e s )

9 L S i t e s : : = i d S i t e | i d S i t e , L S i t e s

11 Modifs : : = BEGIN_Modifs LMod END_Modifs

12 LMod : : = idMod | idMod , LMod

14 KPS : : = BEGIN_KPS LKP END_KPS

15 LKP : : = KP | KP , LKP

16 KP : : = idKP ( r e e l )

18 GRS : : = BEGIN_GRS LGR END_GRS

19 LGR : : = GR | GR LGR

21 GR : : = idGR : PREC KParam

22 S t a t e => S t a t e

23 CondMolVar .

24 S t a t e : : = [ ] @CVar | LocSol

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

314

25 LocSol : : = [ MolSet ]@CVar |

26 [ MolSet ]@CVar & LocSol

27 MolSet : : = Molec | Molec + MolSet

28 Molec : : = idBM | ( Molec : Modif ) |

29 Molec−Molec

30 Modif : : = idMod < LS it es > | idMod

31 CVar : : = idCV : idCT TCPart | idCV |

32 idCT TCPart | AnyW

33 TCPart : : = (EM) | (TM) | ( IM) | ( IC ) | _

34 PREC : : = [ PreC : LCond ]

35 LCond : : = {CVar , CVar} | {CVar , CVar}LCond

The generic rules language is widely inspired from

BIOCHAM and PL in the sense that it has been de-

signed to be able to express what is expressible in

the rule-based languages of these environments. List-

ing 1 gives from line 21 the syntax of (the transition

part of) a generic rule which consists in two manda-

tory components (rule identiﬁer (idGR) and transition

part (line 22)), the others being optional. A molecule

(Molec is a basis one, an altered form of a molecule

or a complex). The localizations of molecules are

expressed using @ (line 24 to 26) that attaches a

compartment variable (CVar) to a set of molecules

(solution, MolSet ) or to [] (empty solution). The

compartment-variable gives the type of compartment

in which the molecules are localized. It can be ab-

breviated (line 30, options 2 and 3) when there is no

possibility of confusion and AnyW is used to express

that all the types of compartment can be concerned.

Concerning the optional components of a rule, a

speciﬁcity of our language is the neighbourhood pre-

conditions (PREC) that give the possibility to make

explicit some conditions to the occurrence of a re-

action. They consists in a list of pairs of compart-

ment variables to signify that instances of these vari-

ables must have a direct neighbourhood. Kinetic pa-

rameters (KParam) are inspired of BIOCHAM. They

consist in some arithmetic terms ranging from con-

stant values to more complex expressions based on

the identiﬁers given in the KPS section and the con-

centrations of molecules.

3.4 The Target Model

Once an exchange graph and a generic model have

been designed, the next step consists in instantiating

the generic reaction rules with topological informa-

tions given by the exchange graph in order to build

a concrete model. This last one is deﬁned by all

valid instances of generic rules, obtained by replacing

compartment variables by compartments of the ex-

change graph, provided that conditions on compart-

ment types and compartments neighbourhoods are

satisﬁed in the exchange graph. For an exchange

graph EG = (V

, E

), a concrete rule cr is valid

if the three following conditions are met where SL

and SR

represent the sets of compartments appear-

ing in respectively the left hand and the right hand of

cr: i) the neighbourhood preconditions associated to

the rule are veriﬁed ; ii) the sub-graph resulting from

the restriction of EG to SL

is connex or reduced to

one vertex ; and iii) each element SR

is an element

of SR

or has a direct neighbour in SL

. For exam-

ple, the instantiation of

: [M1 + M2]@Cyt => [M1]@Cyt&[M2]@Nuc.

relatively to GE

(Figure 4) gives two concrete

rules cr

and cr

, instances of gr

in which the

couple (Cyt, Nuc) has been respectively replaced by

(C1, N1) and (C2, N2).

The concrete model can then be exploited for simu-

lation and/or analysis issues, by using features pro-

vided by BIOCHAM and/or Pathway Logic. It suf-

ﬁces to translate the concrete model in the concrete

syntax used by the targeted tool.

4 CASE STUDIES

In this section, we apply our approach on two pro-

cesses that have already been modelled in the lan-

guages of BIOCHAM or PL. The application pro-

ceeds in three steps: considering the model from

BIOCHAM or PL, we ﬁrstly infer from it information

about the involved localizations and the modelled re-

actions. This information is used to elaborate the ex-

change graph and the generic model to be used in the

coupling process. Then, we proceed to the coupling

and ﬁnally, the resulted concrete model is translated

in BIOCHAM and PL and the obtained target models

can be compared to the initial one. The models we

have chosen to consider are the model of the simpli-

ﬁed cell cycle of Tyson (Model

) and the the model of

the delta-notch signalization pathway (Model

). They

are issued from BIOCHAM.

From Model

that contains ten reaction rules and no

mention of localization, we infer that the process is

concerned by ten different reactions, occurring in the

system seen as a whole. This information induce a

one-vertex (namely E of type Env) exchange graph

and a generic model whose rules are the transcription

in generic rules language of the ten reactions.

Model

contains one hundred and forty-four (abbrevi-

ated in seventy-two) reaction rules implicating thirty

six cells arranged in a 6x6 matrix, each cell being

identiﬁed by using its line and column numbers (C

... C

). Each of the rules of the model concerns

the synthesis or the degradation of one the two in-

volved molecules, Delta and Notch. That allows that

the system is about four biochemical reactions occur-

ring in a population cells of of thirty six (36) the same

A Proposal for a Language Combining Biochemical Rules and Topological Structure for Systems Biology

315

type. Conditions attached to the rules show that the

synthesis of Notch is juxtacrine (the occurrence of the

reaction in a given compartment depends on the con-

tents of the juxtaposed compartments) When adopting

the same topology as BIOCHAM, we can elaborate

the bio-geometric model of Figure 8. The exchange

graph extracted from this geometric model exactly

conforms what was expected : Except the neighbour-

ing with E, all the cells have between two and four

neighbours. The generic model contains four rules

corresponding to the transcription of the four reac-

tions in the generic rules language.

Figure 8: Bio-geometric model of a system consisting in a

population of thirty six (36) cells arranged in a 6x6 matrix.

The coupling step in the case of Model

consists in

just eliminating the information about localization,

because it’s the default compartment Env. The con-

crete model is then equivalent to the generic one when

considering the number of rules. The target model,

obtained by syntax adaptation, conserves the seman-

tic and have the same number of rules.

The coupling of the generic model and the exchange

graph issued from the decoupling of Model

gener-

ates a concrete model with one hundred and forty four

(144) rules: four rules by cell. That means that each

generic rule has been instanciated for each cell, re-

gardless of the number of the neighbouring cells it

has. latter. The translation of the concrete model in

BIOCHAM conserves the semantic.

The presented approach intends to model processes in

BIOCHAM and PL languages with the guarantee that

the obtained models are respectful from the topology

of the system. Such models can be directly deﬁned

in the targeted tools considering an implicit topology.

However, applying the proposed approach presents

some advantages: It allows the modeller to have a

directory of generic models and another of topology

speciﬁcations. As a consequence it is possible to him

to easily study a set of biochemical reactions mod-

elled as a set of generic rules relatively to different

topologies and inversely: any combination of an ex-

change graph and a generic model deﬁnes a model.

The generic rules, by characterizing the types of com-

partments involved, contribute to inform a little more

on the role of the different types of compartment. An-

other advantage of the approach is the provided capa-

bility to study the same model thought the two target

tools: even if these tools presents a lot of similari-

ties, the analysis they carry out are not exactly the

same. Different analysis results may be interesting.

Naturally, because generic models are concise, they

are easier to edit.

Based on the cases presented above, we can say that

these interests are diversely relevant according to the

considered topology. For a system with just one com-

partment like Model

, just the second point is relevant

because the topology cannot change in any way. For

cases like Model

which concerns a topology char-

acterized by an important number of compartments

of the same type, and reactions largely depending on

neighbourhoods, all the interests are relevant.

5 CONCLUSION

In this paper, we have introduced an approach to mod-

elling biological processes by decoupling the topol-

ogy of the system and the biochemical reactions oc-

curring in the system. The topology is abstracted by

an exchange graph that contains the relevant informa-

tion on each compartment of the system : its name,

its type, its content and its neighbourhoods. The re-

actions in turn are modelled as rules characterizing

the types of compartments involved. Our approach

can be considered generic at tow levels. First of all,

it is generic with regard to the topology: a generic

model can be declined according to several graphs

of exchange, giving rise to as many concrete models.

These concrete models can then be studied through

different analysis tools (two in our case: BIOCHAM

and PL): this constitutes the second aspect of generic-

ity of our approach.

The use of geometric modelling to represent topolog-

ical pieces of information is a second trait of original-

ity of our approach. This allows us to design generic

models that are at least as concise as resulting con-

crete models and that are consistent models from a

topological point of view.

REFERENCES

Bartocci, E. and Lio, P. (2016). Computational modeling,

formal analysis, and tools for systems biology. PLOS

Computational Biology, 12(1):1–22.

Blinov, M. L., Schaff, J. C., Vasilescu, D., Moraru, I. I.,

Bloom, J. E., and Loew, L. M. (2017). Compartmen-

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

316

tal and spatial rule-based modelling with virtual cell.

Biophysical Journal, 113(8):1365–1372.

Boutillier, P., Maasha, M., Li, X., Medina-Abarca, H. F.,

Krivine, J., Feret, J., Cristescu, I., Forbes, A. G., and

Fontana, W. (2018). The kappa platform for rule-

based modeling. Bioinformatics.

Calzone, L., Chabrier-Rivier, N., Fages, F., and Soliman, S.

(2005). Apprentissage de règles de réactions biochim-

iques à partir de propriétés en logique temporelle. In

Guy Perrière, A. G. e. C. G., editor, Actes de JO-

BIM’05, pages 183–192, Lyon.

Cardelli, L. (2004). Brane calculi. In Computational

Methods in Systems Biology, International Confer-

ence, CMSB 2004, volume 3082 of Lecture Notes in

Computer Science, pages 257–278. Springer.

Chen, C.-C. and Crilly, N. (2016). Describing complex de-

sign practices with a cross-domain framework : learn-

ing from synthetic biology and swarm robotics. Res

Eng Design, 27:291–305. 10.1007/s00163-016-0219-

Clavel, M., Duran, F., Eker, S., Lincoln, P., Marti-Oliet,

N., Meseguer, J., and Quesada, J. (2000). Towards

Maude 2.0. In 3rd International Workshop on Rewrit-

ing Logic and its Applications (WRLA’00), volume 36

of Electronic Notes in Theoretical Computer Science.

Elsevier.

Danos, V. and Laneve, C. (2004). Formal molecular biol-

ogy. Theoretical Computer Sciences, 325(1):69–110.

Dill, D. L., Merrill, K. A., Pamela, G., Talcott, C. L., Lader-

oute, K., and Lincoln, P. (2005). The pathalyzer:

A tool for analysis of signal transduction pathways.

In Proceedings of the First Annual Recomb Satellite

Workshop on Systems Biology, pages 11–22.

Eker, S., Knapp, M., Laderoute, K., Lincoln, P., and Tal-

cott, C. (2002). Pathway Logic: Executable models of

biological networks. In Proceedings of Fourth Inter-

national Workshop on Rewriting Logic and Its Appli-

cations (WRLA).

Faeder, J. R., Blinov, M. L., Goldstein, B., and Hlavacek,

W. S. (2005). Rule-based modeling of biochemical

networks. Complexity, 10(4):22–41.

Faeder, J. R., Blinov, M. L., and Hlavacek, W. S. (2009).

Rule-based modeling of biochemical systems with

bionetgen. Systems Biology, 10(4).

Fages, F., Gay, S., and Soliman, S. (2015). Inferring re-

action systems from ordinary differential equations.

Theoretical Computer Science, 599:64 – 78. Ad-

vances in Computational Methods in Systems Biol-

ogy.

Fages, F. and Soliman, S. (2008). Formal cell biology

in biocham. In Formal Methods for Computational

Systems Biology, 8th International School on Formal

Methods for the Design of Computer, Communication,

and Software Systems, SFM 2008, Bertinoro, Italy,

Advanced Lectures, volume 5016 of Lecture Notes in

Computer Science, pages 54–80. Springer.

Fages, F., Soliman, S., and Chabrier-Rivier, N. (2004).

Modelling and querying interaction networks in the

biochemical abstract machine biocham.

Giannakis, K. and Andronikos, T. (2017). Membrane au-

tomata for modeling biomolecular processes. Natural

Computing, 16(1):151–163.

Harris, L. A., Hogg, J. S., and Faeder, J. R. (2009). Com-

portmental rule-based modeling of biochemical sys-

tems. In Proceedings of the 2009 Winter Simulation

Conference. M. D. Rossetti, R. R. Hill, B. Johansson,

A. Dunkin, and R. G; Ingalls, eds.

Hlavacek, W. S., Faeder, J. R., Blinov, M. L., Posner, R. G.,

Hucka, M., and Fontana, W. (2006). Rules for mod-

eling signal-transduction systems. Sciences STKE,

344(6).

Li, C., Donizelli, M., Rodriguez, N., Dharuri, H., Endler,

L., Chelliah, V., Li, L., He, E., Henry, A., Stefan, M.,

Snoep, J., Hucka, M., NovÃ¨re, N. L., and Laibe, C.

(2010). Biomodels database: An enhanced, curated

and annotated resource for published quantitative ki-

netic models. BMC Syst Biol, 4(92).

Ma’ayan, A. (2017). complex systems biology. J. R. Soc

Interface, 14(20170391).

Machado, D., Costa, R. S., Rocha, M., Ferreira, E. C.,

Tidor, B., and Rocha, I. (2011). Modeling formalisms

in systems biology. AMB Express a SpringerOpen

Journal.

Pedersen, M., P.hillips, A., and Plotkin, G. D. (2015).

A high-level language for rule-based modelling.

PLoSONE10(6):e0114296.doi:10.1371/journal.

pone.0114296.

Regev, A., Panina, E. M., Silverman, W., Cardelli, L., and

Shapiro, E. Y. (2004). Bioambients: an abstraction

for biological compartments. Theor. Comput. Sci.,

325(1):141–167.

Riesco, A., Santos-Buitrago, B., Rivas, J. D. L., Knapp, M.,

Santos-Garcia, G., and Talcott, C. (2017). Epidermal

growth factor signaling towards proliferation: Model-

ing and logic inference using forward and backward

search. BioMed Research International, 2017:11.

https://doi.org/10.1155/2017/1809513.

Suderman, R. and Hlavacek, W. S. (2017). Truml: A

translator for rule-based modeling languages. In Pro-

ceedings of the 8th ACM International Conference

on Bioinformatics, Computational Biology,and Health

Informatics, ACM-BCB ’17, pages 372–377, New

York, NY, USA. ACM.

Talcott, C. (2016). The pathway logic formal modeling sys-

tem: Diverse views of a formal representation of sig-

nal transduction. In Workshop on Formal Methods in

Bioinformatics and Biomedicine.

Talcott, C. and Dill, D. L. (2005). The pathway logic assis-

tant. In Proceedings of the Workshop Computational

Methods in Systems Biology (CMSB, G. Plotkin, Ed.,

2005, pages 228–239.

Vidil, F., Damiand, G., Dexet-Guiard, M., Guiard, N.,

Ledoux, F., Fousse, A., Fradin, D., Liang, Y., Men-

eveaux, D., and Bertrand, Y. (2002). Moka: 3d topo-

logical modeler.

A Proposal for a Language Combining Biochemical Rules and Topological Structure for Systems Biology

317