Constraint Maximal Inter-molecular Helix Lengths within RNA-RNA

Interaction Prediction Improves Bacterial sRNA Target Prediction

Rick Gelhausen

, Sebastian Will

, Ivo L. Hofacker

, Rolf Backofen

1,3

and Martin Raden

Bioinformatics Group, University of Freiburg, Georges-Koehler-Allee 106, 79110 Freiburg, Germany

Institute for Theoretical Chemistry, University of Vienna, Waehringer Strasse 17, 1090 Wien, Austria

Centre for Biological Signalling Studies (BIOSS), University of Freiburg, Schaenzlestr. 18, 79104 Freiburg, Germany

Keywords:

RNA-RNA Interaction Prediction, Steric Constraints, Constrained Helix Length, Canonical Helix, Seed.

Abstract:

Efﬁcient computational tools for the identiﬁcation of putative target RNAs regulated by prokaryotic sRNAs

rely on thermodynamic models of RNA secondary structures. While they typically predict RNA–RNA in-

teraction complexes accurately, they yield many highly-ranked false positives in target screens. One obvious

source of this low speciﬁcity appears to be the disability of current secondary-structure-based models to reﬂect

steric constraints, which nevertheless govern the kinetic formation of RNA–RNA interactions. For example,

often—even thermodynamically favorable—extensions of short initial kissing hairpin interactions are kineti-

cally prohibited, since this would require unwinding of intra-molecular helices as well as sterically impossible

bending of the interaction helix. In consequence, the efﬁcient prediction methods, which do not consider such

effects, predict over-long helices. To increase the prediction accuracy, we devise a dynamic programming

algorithm that length-restricts the runs of consecutive inter-molecular base pairs (perfect canonical stackings),

which we hypothesize to implicitely model the steric and kinetic effects. The novel method is implemented by

extending the state-of-the-art tool INTARNA. Our comprehensive bacterial sRNA target prediction benchmark

demonstrates signiﬁcant improvements of the prediction accuracy and enables 3-4 times faster computations.

These results indicate—supporting our hypothesis—that length-limitations on inter-molecular subhelices in-

crease the accuracy of interaction prediction models compared to the current state-of-the-art approach.

1 INTRODUCTION

Small RNAs (sRNAs) are central regulators in

prokaryotic cells (Storz et al., 2011). For instance,

they can trigger mRNA decay (Lalaouna et al., 2013)

or modulate translation (Hoe et al., 2013) via di-

rect inter-molecular base pairing. Different mech-

anisms are known (detailed e.g. in (Nitzan et al.,

2017)) like the blocking of the ribosomal binding site

causing translation inhibition or the (de-)stabilization

of mRNAs by covering (or providing) binding sites

of RNAases. The sRNA–RNA interactions typically

contain a small nearly perfect subinteraction of about

7 base pairs (known as seed region) (K

unne et al.,

2014) and have been shown to be located at acces-

sible regions that are mainly unpaired (Richter and

Backofen, 2012). Thus, beside general RNA–RNA

interaction prediction approaches (reviewed e.g. in

(Wright et al., 2018)), dedicated prediction tools like

INTARNA (Busch et al., 2008) or RNAPREDATOR

(Eggenhofer et al., 2011) have been developed and

applied (Li et al., 2012). Recently, fast heuristics

for genome-wide screens have been implemented,

e.g. RIBLAST (Fukunaga and Hamada, 2017) and

RISEARCH2 (Alkan et al., 2017).

For elucidating the regulatory network of sRNAs,

target prediction is applied (Backofen et al., 2014)

to guide experimental validation. While the essen-

tial bioinformatics machinery for this task is avail-

able (Backofen et al., 2017), computational meth-

ods still predict a high number of false positive tar-

gets. The latter can be reduced when individual tar-

get predictions of homologous sequences (Lott et al.,

2018) are combined in comparative approaches like

COPRARNA (Wright et al., 2014). Unfortunately,

this technique is only applicable for the identiﬁcation

of evolutionary conserved targets. Another option is

to incorporate experimental structure probing data to

emend the RNAs’ accessibility information (Miladi

et al., 2019). Integrating probing data, which can be

obtained from high-throughput experiments (Choud-

hary et al., 2017), can signiﬁcantly alleviate the prob-

Gelhausen, R., Will, S., Hofacker, I., Backofen, R. and Raden, M.

Constraint Maximal Inter-molecular Helix Lengths within RNA-RNA Interaction Prediction Improves Bacterial sRNA Target Prediction.

DOI: 10.5220/0007689701310140

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 131-140

ISBN: 978-989-758-353-7

131

lem of inaccurate accessibility prediction. However, it

does not touch—and is even orthogonal to—the here

discussed issues of target prediction.

In this work, we study means to efﬁciently im-

prove sRNA target prediction by restricting the ad-

missible interaction patterns. This is hypothesized to

incorporate steric and kinetic aspects going beyond

the thermodynamic secondary structure-based mod-

els. Speciﬁcally, our method is motivated by the ob-

servation that interacting sites of sRNAs are either

not enclosed by any base pairing (exterior) or located

within loop regions. For loop regions, the forma-

tion of (long) inter-molecular helices (i.e. the entan-

gling of the RNA molecules) requires the ‘unwinding’

of intra-molecular helices, which imposes additional

constraints on the substantial steric rearrangements

(rotating large parts of the molecules through space)

while the interaction grows. Consequently, the forma-

tion of long inter-molecular duplexes seems to be pro-

hibited, even if it would be expected in the currently

used thermodynamic models due to high hybridiza-

tion stability and sufﬁcient accessibility. This well-

known phenomenon has been studied in the context

of other loop-initiated RNA–RNA interactions (Kolb

et al., 2000; Brunel et al., 2002).

Concretely, we test whether interaction predic-

tion can be improved by explicitly constraining the

maximal length of inter-molecular helices, which—

as we conjecture—indirectly considers steric and ki-

netic constraints. While preserving tractability, limit-

ing this length ensures that long helices must be in-

terrupted by interior loops—which is thought to re-

lax the ‘winding tension’. We provide efﬁcient dy-

namic programming algorithms both for exact as well

as heuristic interaction prediction, incorporating the

new helix-length constraint (in addition to the well-

established seed constraint of previous approaches).

The approach is incorporated into INTARNA (Mann

et al., 2017), a state-of-the-art RNA–RNA interaction

prediction tool (Umu and Gardner, 2017). Finally,

we assess the effect of the helix-length constraints on

a large prokaryotic sRNA target prediction data set

extending (Wright et al., 2013). In this benchmark,

the helix length limitation reduces the overall runtime

and, supporting our conjecture, improves the predic-

tion quality.

2 METHODS

In the following, we will ﬁrst present the recursions

used by the current state-of-the-art prediction ap-

proaches like RNAUP (M

uckstein et al., 2006) or IN-

TARNA (Mann et al., 2017). Subsequently, we in-

troduce the new recursions for helix-length restricted

prediction. First, all recursions are given for ex-

haustive/optimal interaction prediction, followed with

a discussion how they can be turned into efﬁcient

heuristic variants. To ease readability, we provide

graphical recursion depictions and provide respective

formulas in the Appendix.

2.1 Accessibility-based Interaction

Prediction

Given two RNAs S

of length n,m, resp., we want

to ﬁnd the interaction sites i..k ∈ [1,n] of S

and

j..l ∈ [1, m] of S

that minimize the interaction en-

ergy E(i, j,k, l). That is, we are interested in the most

stable interaction of an sRNA with a given putative

target. This interaction energy can then be used for

target ranking and the selection of the most promis-

ing candidates.

The interaction sites are considered free of intra-

molecular base pairs and can only form inter-

molecular base pairs. Two positions of the RNAs

can form a base pair if the respective nucleotides

are complementary (i.e. AU, GC, or GU). We con-

sider only sites where the boundaries are forming two

inter-molecular base pairs (i, j),(k,l). No two inter-

molecular base pairs (x, y),(x

) ∈ [1, n] × [1, m] are

allowed to be crossing, i.e. it holds x ≤ x

↔ y ≤

, nor allowed to share a position within the same

RNA. Following the Nearest Neighbor energy model

(Tinoco Jr et al., 1973), the hybridization or du-

plex formation energy of a site is thus given by

the sum of the loop energies (Turner and Mathews,

2010) deﬁned by consecutive base pairs. Here, we

distinguish between directly neighbored base pairs,

scored by E

terms, and neighbored base pairs that

enclose unpaired positions, evaluated by E

terms.

The hybridization energy also contains a general en-

ergy penalty term E

init

that, to some extent, reﬂects

the probability of interaction initiation. The optimal

(minimal) hybridization energy among all possible in-

teractions of the sites is given by H(i, j,k, l). The en-

ergy penalty ED needed to break all intra-molecular

base pairs within the individual sites is used to incor-

porate the sites’ accessibility for interaction forma-

tion. The overall energy of a site is thus given by

E(i, j,k, l) = H(i, j, k,l) + ED(i..k)+ ED( j..l). (1)

All energy terms presented in the following are given

in kcal/mol unit and are computed using the Vienna

RNA package (Lorenz et al., 2011) version 2.4.4. For

simplicity, we exclude dangling-end and helix-end

contributions within Eq. 1. For formalisms, we refer

to the detailed introduction provided in (Raden et al.,

2018).

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

132

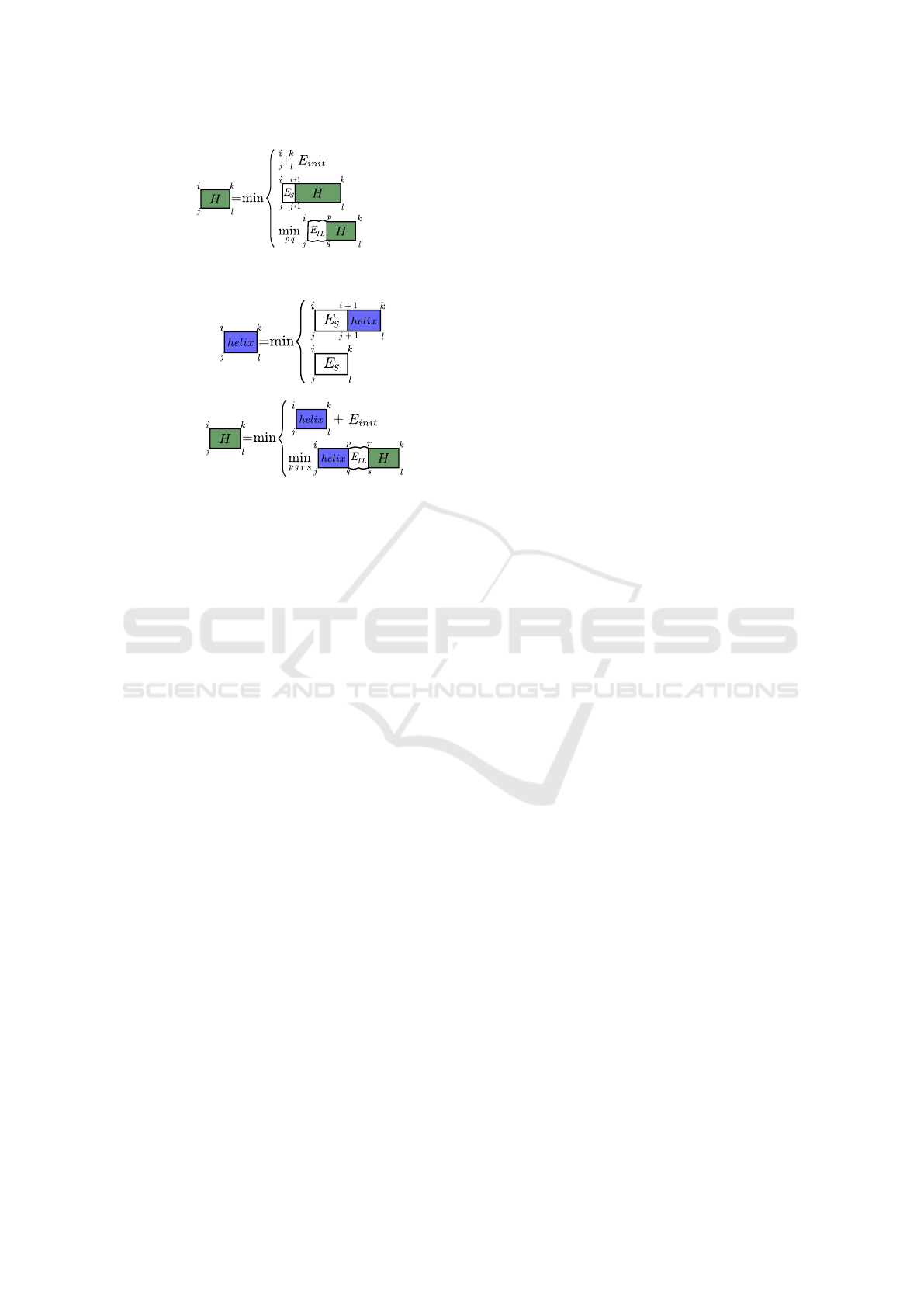
Figure 1: Sketch of the state-of-the-art recursion to compute

the optimal interaction energy without further constraints.

Figure 2: Recursion depictions to compute canonical helix

energies helix (top) using energy terms E

for stacked base

pairs and the optimal energy H (bottom) for a given inter-

action site using the energy terms E

for interior loops.

ED terms can be efﬁciently computed via dy-

namic programming (Bernhart et al., 2011). This

leaves the computation of the optimal interaction en-

ergy H, also accessible via dynamic programming

uckstein et al., 2006). Figure 1 visualizes the cen-

tral recursion that either scores an initial base pair

init

) or extends a shorter optimal interaction with

a stacked base pair (E

) or an interior loop contribu-

tion (E

). All individual energy contributions E

init

and E

are +∞ if the respective boundary indices

are non-complementary, i.e. can not form a base pair.

Note, interior loop sizes (p-r and q-s) are typically re-

stricted to a ﬁxed maximal length w  n, m, which re-

sults in a runtime complexity of O(n

). A heuristic

variant of this recursion available in INTARNA with

O(nm) runtime was introduced in (Busch et al., 2008).

The base pairs of an optimal interaction with energy

H(i, j,k, l) can be obtained via traceback if of interest.

2.2 Helix-length Restricted Prediction

In order to restrict the length of inter-molecular he-

lices to a predeﬁned constant c

≥ 2, referred to as he-

lix length, we decompose the prediction process into

two steps: (a) the energy pre-computation of possi-

ble helices composed of at most c

base pairs, and (b)

their assembly in order to ﬁnd the optimal interaction

energy for a given site.

For simplicity, we ﬁrst consider canonical he-

lices, i.e. perfect helices composed of stacked base

pairs only. Adaptions to non-canonical helices con-

taining small bulges and interior loops are discussed

in a subsequent section. Figure 2 shows the recur-

sion to compute the energy of canonical helices with

the left-/right-most inter-molecular base pair (i, j) <

(k, l), resp., stored in helix(i, j,k,l). The length con-

straint c

is ensured for canonical helices by set-

ting all entries to +∞ if the helix is too long, i.e.

max(k − i, l − j) ≥ c

. Note, for non-canonical he-

lices, helix(i, j,k,l) will contain the optimal energy

of any helix fulﬁlling the relaxed constraints.

Given this, the optimal hybridization energy

H(i, j,k, l) for the given interaction sites i..k and j..l

can be computed via the recursion depicted in Fig. 2.

That is, we either consider a full helix (if possible for

the given boundaries) or compose an interaction via

the addition of a new helix (on the left) to extend a

smaller optimal interaction. The composition inserts

an interior loop between the helix and the next inter-

action to ensure that no two helices are combined into

a longer one. Thus, the interior loop has to span at

least one unpaired position, i.e. (p − r ) + (q − s) > 2,

and is constrained in length as for the recursions dis-

cussed before. Since both helix length as well as in-

terior loop length are constrained by respective con-

stants c

and w, the overall runtime complexity is still

O(n

2.3 Enforcing Seed Constraints in

Helix-length Restricted Prediction

As already discussed, seed-constraints are a central

tool to reduce false positive sRNA target predictions

(Tjaden et al., 2006; Bouvier et al., 2008). Within IN-

TARNA, possible seed interactions and respective en-

ergies are efﬁciently computed via dynamic program-

ming analogously to the presented helix energy pre-

processing; please refer to (Busch et al., 2008) for de-

tails. In the following, the optimal energy for the seed

with left-/right-most base pairs (i, j),(k,l), resp., are

stored in seed(i, j, k, l).

In order to ensure that a reported interaction con-

tains a seed region, we follow the approach presented

in (Busch et al., 2008). Therein, a second dynamic

programming table H

is computed based on H that

provides the optimal energy for a site given that the

considered interaction contains a seed region. The op-

timal energy of a site with seed is then given by

E(i, j,k, l) = H

(i, j, k, l) + ED(i..k) + ED( j..l) (2)

replacing Eq. 1.

Since seeds are valid parts of helices, which are

the building blocks for our introduced H computation,

we use a second auxiliary matrix helix

that provides

the optimal helix energy given that the helix contains

Constraint Maximal Inter-molecular Helix Lengths within RNA-RNA Interaction Prediction Improves Bacterial sRNA Target Prediction

133

Figure 3: Depiction of the decomposition strategy for the

computation of the optimal energy of a helix containing a

seed helix

(top) and the best hybridization energy H

(bot-

tom) enforcing both the helix and seed constraint.

a seed. If the region contains no valid seed or this

would lead to too many base pairs, the energy is set

to +∞. Figure 3 depicts the recursion in order to ﬁll

helix

based on the already introduced helix informa-

tion that is combined with the seed energy. To this

end, all possible locations of a seed combined with

ﬂanking helices are evaluated. Due to the indepen-

dence of the seed and helix constraints, it is possible

to allow unpaired bases in the seed, even when not

allowing unpaired bases in the helix constraints and

vice versa.

Given this, the optimal hybridization energy H

for a given site containing a seed and only helices

with at most c

base pairs, can be computed using

a recursion as depicted in Fig. 3. That is, either (i)

the site can be ﬁlled with a single helix containing a

seed (plus accounting for interaction initiation), or (ii)

a helix-length-constrained interaction site is extended

with a seed-containing helix, or (iii) we extend an in-

teraction that contains already a seed with a helix that

is not constrained to contain a seed.

2.4 Enforcing a Minimal Helix Stability

Given our focus on helices, we can easily enforce ad-

ditional constraints on the helices that are considered

for interaction composition. As the ﬁrst step, we in-

troduce a minimal stability notion via an upper hy-

bridization energy bound E

helix

max

for individual helices.

Since energy is inversely related to stability, our ap-

proach will produce interaction patterns of stable sub-

helices connected by interior loop regions.

The energy threshold can be easily incorporated

into the presented recursions by extending the com-

putation of H and H

from Fig. 2 and 3, resp., with

side conditions. That is, entries from helix or helix

are only considered, if the respective energy value is

below the given threshold E

helix

max

Figure 4: Recursion depiction to compute the optimal hy-

bridization energy helix

(i, j,k,l,B) for non-canonical he-

lices with exactly B base pairs and interior loops containing

at most c

unpaired bases, i.e. (p − i) + (q − j) ≤ c

+ 2

and analogously for the second case.

2.5 Consideration of Non-canonical

Helices

So far, we only considered canonical helices for the

computation of helix. While this models the most sta-

ble helices that can be formed, minor variance of this

ideal, i.e. allowing for bulges or interior loops span-

ning only single or very few unpaired bases, will still

resemble a stable helix. But considering stable helices

only (using E

helix

max

) would likely exclude such helices

if the canonical subhelices are too short. Thus, we

next discuss how the hybridization energy helix for

helices including minor bulges of at most c

unpaired

bases can be computed. We consider an interior loop

as minor if c

≤ 2.

To this end, we introduce the auxiliary matrix

helix

(i, j, k, l,B) that provides the optimal helix hy-

bridization energy for the given site boundaries and

the number of base pairs B while allowing minor

bulges of size c

. Figure 4 depicts the respective re-

cursion. Note, the boundaries p,q considered for inte-

rior loops are constrained to (p−i)+(q− j) ≤ c

+2.

The optimal helix hybridization energy helix(i, j,k, l)

is thus given by helix

(i, j, k, l,c

). Note, enforcing

the helices to be stable (via E

helix

max

) will without further

constraints exclude helices composed of bulges only.

In addition to the altered helix computation, we

also have to ensure that the helices assembled within

the H and H

computation are spaced by interior

loops exceeding c

. That is, it holds for Fig. 2 and 3

that (r − p) + (s − q) > c

+ 2. Note that setting

= 0 will provide the same results as if using canon-

ical helices only.

2.6 Heuristic Helix-length Restricted

Prediction

Due to the high time and space complexity of the ex-

act approach, we implemented heuristic variants of

the recursions following the ideas from (Busch et al.,

2008) introduced for INTARNA. That is, instead of

considering all interaction ranges for a given left-most

base pair (i, j), only the optimal right boundary (k,l)

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

134

together with the respective hybridization energy is

stored in H and H

. Thus, for a given left-most base

pair (i, j), the recursions from above are not conﬁned

to a speciﬁc right k, l bound but use the right end of

the respective optimal recursion case. Please refer to

(Busch et al., 2008) for further details. This heuris-

tic reduces the space and time complexity to O(nm),

provides almost the same prediction quality (Umu and

Gardner, 2017), and makes the approach feasible for

the needed large-scale target screens also discussed in

the Result section.

Here, we apply this strategy not only to H and H

but also to the helix and helix

matrices. That is, we

only memorize the best helix energy (and right bound-

ary) for each left-most helix base pair (i, j). Note,

both matrices have to be computed using small aux-

iliary matrices that replace the respective recursions.

Note further, the computation of H and H

becomes

more simple, since we do not consider different helix

lengths (via p and q) but only use the right-most base

pair of the best helix with left-most base pair (i, j).

3 RESULTS

To evaluate our introduced predictors concerning their

sRNA target prediction performance, we introduce

the manually curated benchmark data used subse-

quently.

3.1 Data Set for sRNA Target

Prediction Benchmark

We investigate whether a restriction on inter-

molecular helix lengths could improve the overall pre-

diction accuracy of INTARNA. To this end, we cre-

ated an sRNA target prediction benchmark extending

the ideas and data from (Wright et al., 2013). The

whole benchmark data set including respective scripts

is available at:

https://github.com/BackofenLab/IntaRNA-benchmark.

The benchmark consists of a large set of bacterial

sRNA queries and potential target sequences. We re-

strict our analysis to sRNA regulation based on the

blocking of the ribosomal binding site (see (Nitzan

et al., 2017) for a discussion). Thus, the targets

are genomic sub-regions around the start codon of

the respective mRNA including 200 nucleotides up-

stream and 100 nucleotides downstream, since many

sRNAs that regulate translation bind their target in

a region around the start codon. Sequences are ex-

tracted from the GenBank database of the National

Centre for Biotechnology Information (NCBI) (Ben-

son et al., 2008). The dataset comprises 4,319 target

regions from the E.coli genome (GenBank accession

number NC 000913) and 4,552 target regions from

the Salmonella typhimurium genome (NC 003197).

The query data set consists of 15 sRNAs from E. coli

and 15 from Salmonella, which have been shown ex-

perimentally to act as post-transcriptional regulators

by base-pairing to at least one of the target mRNAs.

To evaluate the performance, we follow the ap-

proach from (Tjaden et al., 2006). To this end, we

extracted 149 sRNA-mRNA pairs from the literature

that have been experimentally veriﬁed to interact.

Within the benchmark, we test how well these veri-

ﬁed pairs can be separated from all possible sRNA-

mRNAs pairs. That is, we predict the optimal interac-

tion energy E for each of the 15 sRNAs in E.coli with

any of the 4,319 putative target regions. The same is

done for the Salmonella data set. As a result, there are

in total 133,065 potential sRNA-target interactions

and respective interaction energy estimates. From

these, only the mentioned 149 query-target pairs are

supported, leaving 132,916 unsupported pairs. Fi-

nally, we test whether interactions of the veriﬁed pairs

have lower optimal energy estimates compared to the

unsupported interactions. In other words, we evalu-

ate the ranks of the supported pairs within the energy

score distribution over all putative targets. That is, the

more veriﬁed interactions are predicted with low rank,

the more precise is the target prediction approach. A

detailed description of the technical part is available

in the Appendix.

3.2 Helix-length Constraints Enable

Faster Predictions and Improve

Prediction Quality

As reference and ”gold standard” for the evaluation of

our helix-length restricted approach, we use the pre-

diction performance of INTARNA version 2.2.0 us-

ing default values (i.e. heuristic predictions including

seeds) on the introduced benchmark data set using a

seed of length 7 for all predictions. In the following,

we refer to this version with ”original”.

Effect of Maximal Helix Length

We have extended INTARNA with implementations

of our heuristic recursions, which enables clean com-

parisons for both prediction quality as well as space

and runtime requirement of the computations. Fig-

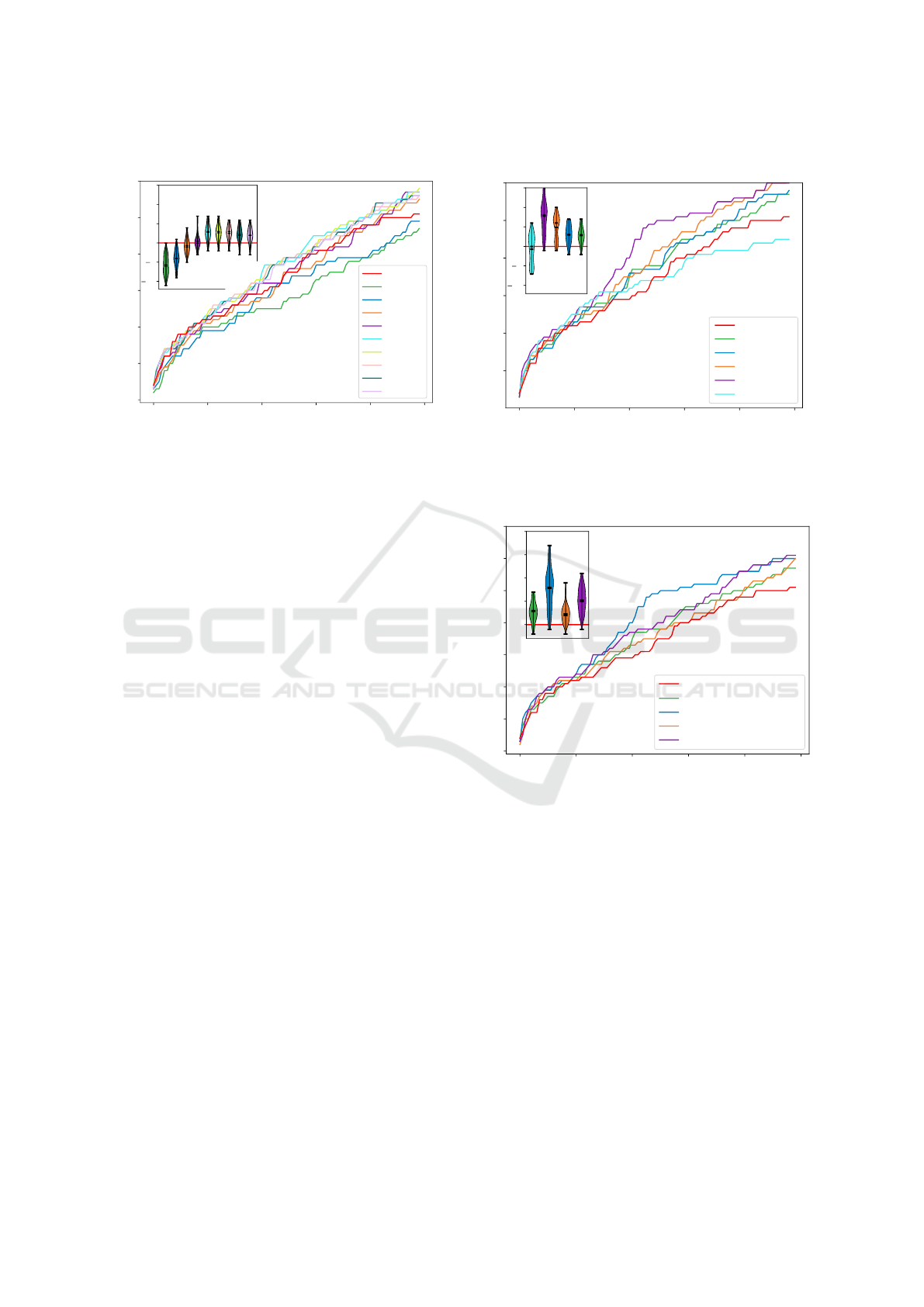
ure 5 compares the results for different maximal helix

length values c

with the original predictions. The

Constraint Maximal Inter-molecular Helix Lengths within RNA-RNA Interaction Prediction Improves Bacterial sRNA Target Prediction

135

# top-ranked targets per sRNA

0 20 40 60 80 100

sum of veriﬁed sRNA-target pairs

original

deviation

Performance for length-limited canonical stacks

containing a seed

=10

=11

=12

=13

=14

=15

Figure 5: Effect of different maximal canonical helix

lengths c

in terms of the recovery of veriﬁed sRNA-target

pairs among the top ranked predictions compared to the

original INTARNA results (red curve). The inset shows the

differences to the original results (red).

curves visualize the total number of veriﬁed sRNA-

target pairs within the respective top-ranked predic-

tions for each sRNA. That is the higher the curve the

better the recovery rate of the veriﬁed targets. To ease

comparisons, the inset shows the difference between

the results of the original version (red curve) and the

respective helix-length constrained predictions.

For low c

values, we observe a reduced predic-

tion accuracy compared to the original recursions. In

contrast, maximal helix lengths of 11-13 show much

improved recovery rates and provide the overall best

results. For c

= 11, we observe the highest recov-

ery improvement of additional 2.7 veriﬁed targets on

average. Higher c

values have a lower prediction ac-

curacy that will eventually converge towards the un-

constrained original prediction results. These obser-

vations apply to all tested variants.

In addition to the higher prediction accuracy, the

constrained version is about 3-4 times faster com-

pared to the original version, while maintaining the

same memory consumption.

Effect of Minimal Helix Stability

Next, we investigate whether the restriction to stable

helices can further improve the prediction quality. To

this end, we ﬁxed the maximal helix length to c

= 11,

given the results from above, and tested different he-

lix hybridization energy thresholds E

helix

max

. Figure 6

summarizes the results. E

helix

max

= −7.5 shows best

performance with a recovery improvement of about

8 veriﬁed targets on average, which is about three-

times higher compared to c

= 11 results without sta-

0 20 40 60 80 100

maxE=0

maxE=-2.5

maxE=-5

maxE=-7.5

maxE=-10

original

deviation

Performance for stable length-limited canonical

stacks containing a seed

# top-ranked targets per sRNA

sum of verified sRNA-target pairs

Figure 6: Effect of different maximal helix energies E

helix

max

(maxE in the plot) on the prediction performance (maximal

canonical helix length c

= 11) analogously to Fig. 5.

0 20 40 60 80 100

can. c

=11

can. c

=11 maxE=-7.5

=2 c

=13

=2 c

=13 maxE=-7.5

original

Best performing parameterizations

deviation

# top-ranked targets per sRNA

sum of veriﬁed sRNA-target pairs

Figure 7: Overview of the best prediction performance for

canonical (can.) (maximal canonical helix length c

11) and non-canonical (c

= 2) (maximal canonical helix

length c

= 13) and the overall best E

helix

max

= −7.5 for both

methods. Plot analogously to Fig. 5.

bility constraint (see above). Note, all tested E

helix

max

values above −7.5 provide improved prediction per-

formance. Too low thresholds (E

helix

max

= −10) exclude

too many helices to enable better target prediction.

Effect of Non-canonical Helices

When relaxing the helix deﬁnition to non-canonical

helices that are allowed to contain minor bulges or in-

terior loops with up to c

unpaired bases, the overall

prediction performance is not exceeding the canonical

helix variant. Here, best results are observed for c

2 and a maximal helix length c

= 13 while c

values

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

136

of 11-13 still show the best results (data not shown).

Figure 7 provides a comparison of the best parameter-

izations for the canonical and non-canonical approach

with and without E

helix

max

= −7.5 constraint. From this

it is obvious that a relaxation of the helix deﬁnition

does not improve the prediction quality compared to

stable canonical helices.

4 DISCUSSION & CONCLUSION

Predictions of helix-length constrained interactions

can be done with the same time and space complexity

as known for unconstrained RNA–RNA interaction

prediction. In fact, the helix-length constraint signiﬁ-

cantly reduces the search space such that we observe

on average a 3-4 times faster target prediction for our

benchmark data set. The reduced runtime results from

the following: compared to the current state-of-the-art

recursion from Fig. 1, the helix-length constrained ap-

proach from Fig. 2 faces the same search space for the

interior loop sizes but appends full helices instead of

individual base pairs. This becomes even more strik-

ing for the heuristic variant, which does not consid-

ered all possible helix lengths but only the optimal

helix for the left-most base pair (i, j).

Furthermore, we observe enriched target predic-

tion accuracy measured in terms of increased recov-

ery rates of veriﬁed sRNA-target pairs known from

the literature. Maximal helix lengths c

of 11-13

base pairs show the best prediction quality, while

shorter drastically reduced the recovery rate. This

is mainly achieved by disregarding low-energy inter-

actions composed of many bulge and interior loops

(putative false positives) rather than altering the inter-

action details of the veriﬁed sRNA-target pairs. Re-

sults can be further improved when only stable he-

lices with an energy below a given threshold E

helix

max

are considered for prediction. For helices of a maxi-

mal length of 11-13 base pairs, an upper energy bound

of −7.5kcal/mol provides the best target prediction

performance. Notably, the consideration of a relaxed

helix deﬁnition allowing for small bulge or interior

loops does not signiﬁcantly improve the results com-

pared to perfect canonical helices but has slightly

higher runtime requirements.

Our observations support our hypothesis that long

inter-molecular helices are less likely due to steric and

kinetic constraint of the interaction formation process.

That is, we think the ’decomposed helix interaction

model’, where short stable helices are interrupted by

ﬂexible interior loops, a more realistic model com-

pared to unconstrained predictions.

One way to further improve the model would be

to conﬁne helix-length constrained predictions to re-

gions mainly unpaired in loop regions while applying

the unconstrained approach for exterior unpaired re-

gions. This can be efﬁciently distinguished during ED

computation from the underlying partition functions

uckstein et al., 2006; Bernhart et al., 2011). An-

other planned direction is to apply further constraints

on the helices considered within the prediction. For

instance, we will further investigate the correlation of

helix base pair number c

and optimal upper energy

bounds E

helix

max

, since they are most likely linked by the

average stacking energy or similar terms.

Even though we exempliﬁed our new approach by

extending INTARNA, the concept is a generic one.

We therefore expect also other RNA–RNA interaction

prediction methods to proﬁt from a restriction of inter-

molecular helix lengths.

ACKNOWLEDGEMENTS

This work was supported by the German Research

Foundation (DFG) [BA2168/16-1] and the Austrian

Science Fund (FWF) [I 2874-N28].

REFERENCES

Alkan, F., Wenzel, A., Palasca, O., Kerpedjiev, P., Rude-

beck, A., Stadler, P. F., Hofacker, I. L., and Gorodkin,

J. (2017). RIsearch2: sufﬁx array-based large-scale

prediction of RNARNA interactions and siRNA off-

targets. Nucleic Acids Research, 45(8):e60.

Backofen, R., Amman, F., Costa, F., Findeiss, S., Richter,

A. S., and Stadler, P. F. (2014). Bioinformatics of

prokaryotic RNAs. RNA Biol, 11(5).

Backofen, R., Engelhardt, J., Erxleben, A., Fallmann, J.,

uning, B., Ohler, U., Rajewsky, N., and Stadler,

P. F. (2017). RNA-bioinformatics: Tools, services and

databases for the analysis of RNA-based regulation. J

Biotechnol, 261:76–84.

Benson, D. A., Karsch-Mizrachi, I., Lipman, D. J., Ostell,

J., and Wheeler, D. L. (2008). GenBank. Nucleic

Acids Res., 36(Database issue):25–30.

Bernhart, S. H., M

uckstein, U., and Hofacker, I. L. (2011).

RNA accessibility in cubic time. Algorithms for

Molecular Biology, 6(1):3.

Bouvier, M., Sharma, C. M., Mika, F., Nierhaus, K. H., and

Vogel, J. (2008). Small RNA binding to 5’ mRNA

coding region inhibits translational initiation. Mol.

Cell, 32(6):827–837.

Brunel, C., Marquet, R., Romby, P., and Ehresmann, C.

(2002). RNA loop–loop interactions as dynamic func-

tional motifs. Biochimie, 84(9):925 – 944.

Busch, A., Richter, A. S., and Backofen, R. (2008). In-

taRNA: efﬁcient prediction of bacterial sRNA tar-

gets incorporating target site accessibility and seed re-

gions. Bioinformatics, 24(24):2849–56.

Constraint Maximal Inter-molecular Helix Lengths within RNA-RNA Interaction Prediction Improves Bacterial sRNA Target Prediction

137

Choudhary, K., Deng, F., and Aviran, S. (2017). Compar-

ative and integrative analysis of RNA structural pro-

ﬁling data: current practices and emerging questions.

Quantitative Biology, 5(1):3–24.

Eggenhofer, F., Tafer, H., Stadler, P. F., and Hofacker, I. L.

(2011). RNApredator: fast accessibility-based pre-

diction of sRNA targets. Nucleic Acids Res, 39(Web

Server issue):W149–54.

Fukunaga, T. and Hamada, M. (2017). RIblast: an ul-

trafast RNARNA interaction prediction system based

on a seed-and-extension approach. Bioinformatics,

33(17):2666–2674.

Hoe, C.-H., Raabe, C. A., Rozhdestvensky, T. S., and

Tang, T.-H. (2013). Bacterial sRNAs: Regulation in

stress. International Journal of Medical Microbiol-

ogy, 303(5):217 – 229.

Kolb, F. A., Malmgren, C., Westhof, E., Ehresmann, C.,

Ehresmann, B., Wagner, E. G., and Romby, P. (2000).

An unusual structure formed by antisense-target RNA

binding involves an extended kissing complex with

a four-way junction and a side-by-side helical align-

ment. RNA, 6(3):311–324.

unne, T., Swarts, D. C., and Brouns, S. J. (2014). Plant-

ing the seed: target recognition of short guide RNAs.

Trends in Microbiology, 22(2):74 – 83.

Lalaouna, D., Simoneau-Roy, M., Lafontaine, D., and

Mass, E. (2013). Regulatory RNAs and target mRNA

decay in prokaryotes. Biochimica et Biophysica Acta

(BBA) - Gene Regulatory Mechanisms, 1829(6):742 –

747. RNA Decay Mechanisms.

Li, W., Ying, X., Lu, Q., and Chen, L. (2012). Predicting

sRNAs and their targets in bacteria. Genomics, Pro-

teomics & Bioinformatics, 10(5):276 – 284.

Lorenz, R., Bernhart, S. H., H

oner zu Siederdissen, C.,

Tafer, H., Flamm, C., Stadler, P. F., and Hofacker,

I. L. (2011). ViennaRNA Package 2.0. Algorithms

for Molecular Biology, 6(1):26.

Lott, S. C., Sch

afer, R. A., Mann, M., Backofen, R., Hess,

W. R., Voss, B., and Georg, J. (2018). GLASSgo -

automated and reliable detection of sRNA homologs

from a single input sequences. Frontiers in Genetics,

9:124.

Mann, M., Wright, P. R., and Backofen, R. (2017). In-

taRNA 2.0: enhanced and customizable prediction

of RNA-RNA interactions. Nucleic Acids Res.,

45(W1):W435–W439.

Miladi, M., Montaseri, S., Backofen, R., and Raden, M.

(2019). Integration of accessibility data from structure

probing into RNA-RNA interaction prediction. Bioin-

formatics, (epub ahead of print).

uckstein, U., Tafer, H., Hackerm

uller, J., Bernhart, S. H.,

Stadler, P. F., and Hofacker, I. L. (2006). Thermo-

dynamics of RNA–RNA binding. Bioinformatics,

22(10):1177–1182.

Nitzan, M., Rehani, R., and Margalit, H. (2017). Integra-

tion of bacterial small RNAs in regulatory networks.

Annual Review of Biophysics, 46(1):131–148.

Raden, M., Mohamed, M. M., Ali, S. M., and

Backofen, R. (2018). Interactive implementa-

tions of thermodynamics-based RNA structure and

RNA-RNA interaction prediction approaches for

example-driven teaching. PLOS Comput. Biol,

14(8):e1006341.

Richter, A. S. and Backofen, R. (2012). Accessibility

and conservation: General features of bacterial small

RNA-mRNA interactions? RNA Biol, 9(7):954–65.

Storz, G., Vogel, J., and Wassarman, K. (2011). Regula-

tion by small RNAs in bacteria: Expanding frontiers.

Molecular Cell, 43(6):880 – 891.

Tinoco Jr, I., Borer, P., Dengler, B., Levin, M., Uhlenbeck,

O., Crothers, D., and Bralla, J. (1973). Improved es-

timation of secondary structure in ribonucleic acids.

Nature New Biology, 246(150):40–41.

Tjaden, B., Goodwin, S. S., Opdyke, J. A., Guillier, M.,

Fu, D. X., Gottesman, S., and Storz, G. (2006). Tar-

get prediction for small, noncoding RNAs in bacteria.

Nucleic Acids Res., 34(9):2791–2802.

Turner, D. H. and Mathews, D. H. (2010). NNDB: the near-

est neighbor parameter database for predicting stabil-

ity of nucleic acid secondary structure. Nucleic Acids

Res, 38(Database issue):D280–2.

Umu, S. U. and Gardner, P. P. (2017). A comprehensive

benchmark of RNA-RNA interaction prediction tools

for all domains of life. Bioinformatics, 33(7):988–

996.

Wright, P. R., Georg, J., Mann, M., Sorescu, D. A., Richter,

A. S., Lott, S., Kleinkauf, R., Hess, W. R., and Back-

ofen, R. (2014). CopraRNA and IntaRNA: predicting

small RNA targets, networks and interaction domains.

Nucleic Acids Res., 42(Web Server issue):W119–23.

Wright, P. R., Mann, M., and Backofen, R. (2018). Struc-

ture and interaction prediction in prokaryotic RNA bi-

ology. Microbiol Spectrum, 6(2).

Wright, P. R., Richter, A. S., Papenfort, K., Mann, M.,

Vogel, J., Hess, W. R., Backofen, R., and Georg, J.

(2013). Comparative genomics boosts target predic-

tion for bacterial small RNAs. Proceedings of the Na-

tional Academy of Sciences, 110(37):E3487–96.

APPENDIX

A Benchmarking Workﬂow

The benchmark workﬂow used for the creation of the

prediction accuracy plots is shown in Figure 8. First,

for each sRNA query, optimal interactions with all

mRNA targets are predicted using INTARNA with a

certain parameter set. Then the resulting interactions

are sorted according to their energy values, from the

most favourable, i.e. those with the lowest values, to

the least favourable. Finally, we identify the rank of

each veriﬁed target (considered a supported predic-

tion). For each maximal rank value (later plotted on

the x-axis), we count the number of veriﬁed targets for

all sRNA queries that show a rank smaller or equal to

this.

This process is repeated for each benchmarked pa-

rameter set. The data collected is then plotted. The

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

138

x-axis of the plot represents the maximal rank we

consider for each result ﬁle, e.g. a number of target

predictions of 20 means that we consider the 20 ﬁrst

lines of each result ﬁle and count how many veriﬁed

targets appear. This is covered by the y-axis, which

represents how many veriﬁed targets were among the

considered top-ranked target predictions. The violin

plots are generated by calculating the difference of a

certain parameterization of INTARNA e.g. c

= 11 to

the original predictor. This reveals general trends of

the different methods compared to the curve plot.

mRNA

targets

sRNA 1

IntaRNA

Result

ﬁle 1

sort

energy

sorted

ﬁle 1

mRNA

targets

sRNA 2

IntaRNA

Result

ﬁle 2

sort

energy

sorted

ﬁle 2

rank 7

rank 15

rank 202

veriﬁed

targets

Figure 8: Depiction of the benchmarking process.

Constraint Maximal Inter-molecular Helix Lengths within RNA-RNA Interaction Prediction Improves Bacterial sRNA Target Prediction

139

B Formal Recursions

(i, j, k, l) =











energy contribution for

stacking base pairs (i, j), (k, l)

: if k − i = 1 and l − j = 1,

+∞ : otherwise

(3)

(i, j, k, l) =











energy contribution for

stack or interior loop (i, j), (k, l)

: if i < k and j < l,

+∞ : otherwise

(4)

helix(i, j,k,l) =











min

(

(i, j, i + 1, j + 1) + helix(i + 1, j + 1,k,l)

(i, j, k, l)

: if canonical helix

helix

(i, j, k, l;c

) : otherwise

(5)

helix

(i, j, k, l;U,B) = min











min

p,q with

min(k−p,l−q)≥B−1

(p−i)+(q− j)≤U +2

(i, j, p,q)

+helix

(p, q,k,l;U, B − 1)

: if B > 2,

(i, j, k, l) : otherwise.

(6)

helix

(i, j, k, l) = min

p,r

q,s



helix(i, j, p,q) + seed(p,q,r,s) + helix(r,s,k,l)



(7)

H(i, j,k, l) = min











helix(i, j,k,l) + E

init

min

p,r,q,s with

(r−p)+(s−q)>c

helix(i, j,k,l)≤E

helix

max



helix(i, j, p,q) + E

(p, q,r,s) + H(r,s,k,l)



(8)

(i, j, k, l) = min











helix

(i, j, k, l) + E

init

min

p,r,q,s with

(r−p)+(s−q)>c

helix

(i, j,k,l)≤E

helix

max



helix

(i, j, p,q) + E

(p, q,r,s) + H(r,s,k,l)



min

p,r,q,s with

(r−p)+(s−q)>c

helix(i, j,k,l)≤E

helix

max



helix(i, j, p,q) + E

(p, q,r,s) + H

(r, s,k,l)



(9)

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

140