
Singularity Analysis for Redundant Manipulators of Arbitrary
Kinematic Structure
Ahmad A. Almarkhi
a
and Anthony A. Maciejewski
b
Department of Electrical and Computer Engineering, Colorado State University, Fort Collins, CO 80523-1373, U.S.A.
Keywords:
Redundant Robots, Singularities, Kinematics.
Abstract:
This paper presents a technique to identify singularities of any rank for a robot of any kinematic structure.
The technique is based on computing the gradient of singular values of the robot Jacobian. The algorithm
deals with the situations when two or more singular values become nearly equal and their corresponding
singular vectors are ill-defined. Also, an algorithm is developed to identify the physically meaningful singular
directions from the high dimensional singular subspaces of high-rank singularities. The suggested technique
is applied to a 4-DoF and a 7-DoF robot to show its efficacy at identifying robot singularities of all ranks and
dealing with the ill-defined singular directions.
1 INTRODUCTION
A robot singular configuration is a configuration in
which the robot’s end effector loses the ability to
move in one (or more) direction(s), i.e., singular
direction(s). Such singular configurations are usu-
ally called singularities (Baker and Wampler, 1988).
Robot singularities are also called critical points
(Burdick, 1989) or special configurations (Hunt,
1986). At a singularity, there is no joint velocity that
can result in an end-effector velocity in a singular di-
rection(s). Singularities result from having the cor-
responding Jacobian (J) columns be linearly depen-
dent. The singular value decomposition (SVD) of J
can reveal immediate information about singularities.
At a singularity, one (or more) singular value(s) of
the robot Jacobian are zero. Robot singularities can
offer mechanical advantages (Kieffer and Lenarcic,
1994), however, they require more sophisticated in-
verse kinematics solutions (Nakamura and Hanafusa,
1986).
Identifying robot singularities has been exten-
sively studied. For non-redundant manipulators,
where J is square, singularities can be found by sym-
bolically solving for conditions when the determinant
of J equals zero (|J|= 0) (Waldron et al., 1985). For
redundant manipulators, where |J| does not exist, the
conditions that make |JJ
>
| = 0 can be computed,
a
https://orcid.org/0000-0002-5767-6103
b
https://orcid.org/0000-0002-1376-5825
but this is usually difficult to solve. In this case, one
viable approach is to solve for conditions that make
all the 6 ×6 sub-Jacobians singular, i.e., the determi-
nants of all sub-Jacobians equal zero (Litvin et al.,
1986), but this also becomes infeasible for robots with
a large number of degrees of freedom (DoF). For ex-
ample, an 8-DoF manipulator requires computing the
determinants of 28 sub-Jacobians. In addition, these
techniques typically lack the ability to provide infor-
mation about the singular vector(s) associated with a
singularity.
To more easily identify singularities and find sin-
gular directions, (Sugimoto et al., 1982) suggested
using the fact that at a singularity, there must be
a screw reciprocal to all screws that represent the
columns of the robot Jacobian. This technique has
been used to identify the rank-1 singularity condi-
tions and the singular directions for 7-DoF manip-
ulators (Boudreau and Podhorodeski, 2010). The
reciprocity-based methodology has also been used to
find the rank-1 singularities of an 8-DoF manipula-
tor (Nokleby and Podhorodeski, 2004b). In addition,
it was extended to identify the rank-2 singularities
of a 7-DoF manipulator (Nokleby and Podhorodeski,
2004a). This technique shows its merit of being rel-
atively easy and extendable, but it is highly depen-
dent on selecting a reference frame that simplifies
the computation of J. Building on the reciprocity-
based approach, researchers have suggested further
simplifications of the Jacobian by performing elemen-
tary transformations on the Jacobian before solving
42
Almarkhi, A. and Maciejewski, A.
Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure.
DOI: 10.5220/0007833100420049
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 42-49
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

for the singularity conditions as in (Xu et al., 2013).
This approach has been further employed in perform-
ing singularity avoidance for manipulators with non-
spherical wrists (Xu et al., 2016). All these techniques
work well for simple classes of kinematically redun-
dant manipulators and for rank-1 singularities. Such
manipulators have their successive joint axes either
perpendicular or parallel, which makes computing J
relatively easy.
In this paper we suggest a technique to find the
singularities of a manipulator with an arbitrary degree
of redundancy and arbitrary kinematic structure. This
can be achieved by driving a certain singular value,
σ
i
, of J to zero by following the gradient descent of
that singular value, i.e., −∇σ
i
. The complexity of this
technique is independent of the rank of the singularity.
In addition, we present an algorithm to identify the
singular directions at high-rank singularities.
The rest of this paper is organized as follows.
Methodologies to identify robot singularities and their
corresponding singular directions are presented in
section 2. In section 3, the results of applying the
methodologies to a 4-DoF robot and a 7-DoF robot
are discussed. Finally, the conclusions of this work
are presented in section 4.
2 SINGULARITY ANALYSIS
2.1 Background
The forward kinematics of an n-DoF robot that is act-
ing in an m-dimensional workspace can be written as
˙x = J
˙
θ (1)
where ˙x is an m ×1 vector representing the end-
effector velocity, J is the m ×n robot Jacobian, and
˙
θ
is an n ×1 vector that represents the joint angle rates.
For redundant robots, n > m, where n −m is the de-
gree of redundancy. For a redundant manipulator, J is
not a square matrix, and thus not invertible, however,
an inverse kinematics solution can be found using
˙
θ = J
+
˙x + n
J
(2)
where J
+
is the pseudoinverse of J and n
J
is an ar-
bitrary vector in the null space of the Jacobian.
The singular value decomposition of J can be rep-
resented as
J =
r
∑
i=1
σ
i
u
i
v
>
i
(3)
where r is the rank of J, the σ
i
’s are the ordered sin-
gular values, i.e., σ
1
≥ σ
2
≥ ··· ≥ σ
m
≥ 0, the unit
vectors u
i
represent the output singular vectors, and
v
i
are the input singular vectors. For a robot at a
rank-n singularity, there are n singular values, σ
i
’s,
that become zero. Thus, employing a technique that
minimizes singular values of J can be used to identify
robot singular configurations.
2.2 Identifying Robot Singularities
In this section, we explain how to employ the gradient
descent of a singular value of J to drive a robot of
an arbitrary kinematic structure to a singularity. This
technique is not limited by the rank of the singularity.
The singular value σ
i
in (3) can be expressed as
σ
i
= u
>
i
Jv
i
. (4)
Differentiating (4) with respect to time results in
˙
σ
i
= ˙u
>
i
Jv
i
+ u
>
i
˙
Jv
i
+ u
>
i
J ˙v
i
. (5)
One can note that u
>
i
u
j
and v
>
i
v
j
are zero for i 6= j
and that the derivative of a unit vector is orthogonal to
that vector. So, (5) can be further simplified to (Ma-
ciejewski, 1988)
˙
σ
i
= u
>
i
˙
Jv
i
. (6)
The partial derivative of σ
i
with respect to some θ
k
can be expressed as
∂σ
i
∂θ
k
= u
>
i
∂J
∂θ
k
v
i
(7)
where
∂J
∂θ
k
=
∂j
1
∂θ
k
,
∂j
2
∂θ
k
,··· ,
∂j
n
∂θ
k
. (8)
The partial derivative of the i
th
column of the Jaco-
bian is given by (Klein and Chu, 1997), (Groom et al.,
1999)
∂j
i
∂θ
k
=
"
(z
>
k
p
i
)z
i
−(z
>
k
z
i
)p
k
z
k
×z
i
#
, k < i
"
(z
>
i
p
k
)z
k
−(z
>
k
z
i
)p
k
0
#
, k ≥i
(9)
Then, the gradient of σ
i
for any J can be simply com-
puted from (7), (8), and (9), as
∇σ
i
=
∂σ
i
∂θ
1
,
∂σ
i
∂θ
2
,··· ,
∂σ
i
∂θ
n
. (10)
Now that one can compute ∇σ
i
, it is possible to
employ the gradient descent technique to locate a
minima for any singular value σ
i
. In the following, we
explain an algorithm to find rank-1 and higher rank
singularities.
Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure
43

2.2.1 Identifying Rank-1 Singularities
For rank-1 singularities, one can employ the general
equation
θ
(k+1)
= θ
(k)
−α
k
∇σ
(k)
i
(11)
where, θ
(k+1)
is a vector that represents the new joint
angles of a robot, the vector θ
(k)
is the current joint
angles, α
k
is an adaptive step size, and ∇σ
(k)
i
is the
gradient of σ
i
(σ
i
= σ
m
for rank-1 singularities). In
order to identify all rank-1 robot singular configura-
tions, one can start by generating random configura-
tions that span the robot joint space. Then, from each
random configuration, one can move the robot along
the gradient descent of σ
m
as in (11). For faster con-
vergence to a singularity, one can use the steepest de-
scent method, in which α
k
needs to be adaptive, i.e., it
is chosen at each iteration to achieve a maximum de-
crease in σ
m
. This can be done by conducting a one-
dimensional search along the −∇σ
(k)
m
direction until a
minimizer, θ
(k+1)
, is found.
2.2.2 Identifying Rank-2 Singularities
A robot is said to be in a rank-2 singularity if ε >
σ
m−1
≥ σ
m
, where ε is a small threshold (virtually
zero). To identify rank-2 singularities, one can start
with a population of random joint configurations and
employ (11) by moving along the −∇σ
(k)
m−1
direction
until the σ
m−1
< ε condition is satisfied. However,
it is not uncommon for an undesirable behavior to
occur, that results from having the two singular val-
ues σ
m−1
and σ
m
become nearly equal before they
reach zero, i.e., σ
m−1
≈ σ
m
> ε. In this case, the
two singular values are not distinct, which means that
their corresponding singular vectors are ill-defined. In
other words, any singular vectors (u and v) in the
{u
m−1
,u
m
} and {v
m−1
,v
m
} subspaces are valid for
solving (6). Figure 1, shows the behavior of the algo-
rithm when the two smaller singular values become
nearly equal through the process of driving a robot
into a rank-2 singularity. In this case, σ
5
≈ σ
6
(at
around iteration 600), which makes them indistinct
and their corresponding singular vectors ill-defined.
The direction of ∇σ
5
can completely change direc-
tion from one iteration to another, which affects the
rate of convergence.
To overcome this unwanted effect, one can start
with moving the robot along the −∇σ
(k)
m−1
direction
until σ
5
and σ
6
become very close in value. Then,
a combination between the two gradients is com-
puted. Because the singular value decomposition is
not unique in these cases, any singular vectors u and
v in the subspace associated with the equal singular
Figure 1: In subplot (a), the evolution of σ
5
and σ
6
is shown
as the standard gradient descent algorithm is employed. The
singular value σ
5
is minimized until σ
5
≈ σ
6
at around it-
eration 600. When they become nearly equal, the angle be-
tween the gradients in successive iterations becomes large.
These angles are plotted in (b), where the change in the an-
gles reaches 180
◦
. It is clear that the convergence requires
a long time (about 3000 iterations) due to the large change
in the gradient direction. In this case, the convergence time
is approximately 40 seconds. The threshold, ε = 10
−6
, is
indicated with a red horizontal line.
values are valid. One can rotate the singular subspace
such that the angle between ∇σ
(k)
5
and ∇σ
(k)
6
is mini-
mized, i.e.,
u
5(new)
= u
5
cosφ + u
6
sinφ
u
6(new)
= u
6
cosφ −u
5
sinφ
v
5(new)
= v
5
cosφ + v
6
sinφ
v
6(new)
= v
6
cosφ −v
5
sinφ
(12)
where φ is the angle of rotation. It should be noted
that the angle between the gradients of σ
5
and σ
6
can
vary from 0 to π based on the angle of rotation φ. A
suitable selection of the rotation angle for the singu-
lar subspaces is crucial in minimizing the change in
the gradient direction from one iteration to another.
Once the ∇σ
(k)
5
and ∇σ
(k)
6
that have the minimum an-
gle between them are computed, a combination that
minimizes σ
5
can be found
∇σ
(k)
= γ∇σ
(k)
5
+ (1 −γ)∇σ
(k)
6
(13)
where ∇σ
(k)
is the desired gradient and γ is a posi-
tive scalar where 0 ≤ γ ≤ 1. This linear search will
minimize the change in the gradient direction from
one iteration to another. After ∇σ
(k)
is computed, the
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
44

steepest descent method is applied to find an optimal
value of α
k
in (11) that minimizes σ
5
. An analogous
process can be employed for identifying higher rank
singularities.
2.2.3 Identifying High-rank Singularities
To identify high-rank singularities, i.e., where three
or more singular values become zero, one can em-
ploy a similar approach to that applied for identifying
rank-2 singularities. For a robot in a singular config-
uration, J is of rank r if σ
i
= 0 for i > r, which also
means the robot is in a rank-(m −r) singularity. To
find high-rank singularities, one can move the robot
by iteratively solving (11) until a desired σ
i
reaches
zero. While moving along the −∇σ
i
direction, it is
possible that σ
i
and σ
i+1
become nearly equal. In this
case, the procedure in the previous section can be ap-
plied.
In some cases, more than two singular values be-
come nearly equal but larger than the threshold, i.e.,
σ
i
≈ σ
i+1
≈ ··· ≈ σ
m
> ε. For the purpose of illus-
tration, we will consider the case where a robot is be-
ing driven to a rank-3 singularity when the situation
σ
4
≈ σ
5
≈ σ
6
> ε occurs, as illustrated in Figure 2.
One can note that around iteration 186 in Figure 2
all three singular values became very close in value.
At this point, the angle between the gradient of σ
4
in successive iterations (the angles between ∇σ
(k−1)
4
and ∇σ
(k)
4
) became 170
◦
, which resulted from having
the singular values indistinct and their correspond-
ing singular vectors ill-defined. This also contributed
to an unwanted increase in σ
4
because the gradients
switched direction. In this case, one can rotate their
corresponding singular subspaces to find a suitable ro-
tation that minimizes the sum of the angles between
the three gradients. The solution is to minimize an
objective function H, where
H =
m
∑
(i=r+1)
m
∑
( j=i+1)
θ
i, j
(14)
and θ
i, j
is the angle between ∇σ
i
and ∇σ
j
. The ro-
tation of the singular subspaces can be done by iter-
atively employing (12). That is, because the singular
subspaces are three-dimensional (or higher), one can
iteratively rotate one plane at a time, i.e., in this case,
{u
4
,u
5
} and {v
4
,v
5
}, then {u
5
,u
6
} and {v
5
,v
6
},
and so on. This iterative rotation should be done until
the sum of the angles between all gradients is mini-
mized. After finding the gradients of the singular val-
ues, one can use (13) to compute a combination be-
tween the first two gradients,∇σ
4
and ∇σ
5
, that min-
imize σ
4
. Then, using (13) again to compute a com-
bination between the resulting gradient and ∇σ
6
that
Figure 2: In (a), the singular value σ
4
is minimized until it-
eration 106, where (σ
4
≈σ
5
). At iterations 135 and 186 the
singular values σ
4
, σ
5
, and σ
6
become nearly equal. Subfig-
ure (b) shows the change in the angle between the gradients
in successive iterations. The change of angle reaches 170
◦
when the three singular values become nearly equal. In this
case, the singular values σ
4
, σ
5
, and σ
6
never converge to
zero. The threshold, ε = 10
−6
, is indicated with a red hori-
zontal line.
minimizes σ
4
. This approach guarantees achieving
a minimum amount of gradient direction change and
thus a shorter convergence time.
This process can continue until the algorithm can-
not converge to any higher rank singularities. This al-
gorithm, along with an adaptive step size, was applied
to the same robot that resulted in Figure 2 and the re-
sults are shown in Figure 3. It is clear that the conver-
gence is faster and the change in the gradient angle is
smaller. The average convergence time was improved
from 40 seconds to less than 2 seconds when the pro-
posed technique is employed.
If one applies the above algorithm to an initial
population of random configurations then one can
identify all the singular configurations of various
ranks. It is then possible to analyze the resulting sin-
gularities to determine the singularity conditions for
the robot. Some singularity conditions depend on the
values of a few joints while other joints can take any
value. One may observe that a singularity can be sat-
isfied by an infinite number of joint configurations. In
the next section, we discuss a mathematical approach
to identify singular directions associated with the sin-
gularities that are physically meaningful.
Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure
45

Figure 3: This figure shows the behavior of the singular
values when the proposed algorithm is applied to a robot to
find a rank-3 singularity. This is the same robot as shown
in Figure 2. Subfigure (a) shows the values of the three
smaller singular values, σ
4
, σ
5
, and σ
6
, while applying the
algorithm with an adaptive step size α
k
. In subfigure (b),
the angles between the gradients in successive iterations are
shown. The angles average around 120
◦
. The algorithm
converges in 16 iterations. The convergence time in this
case is less than two seconds. The threshold, ε = 10
−6
, is
indicated with a red horizontal line.
2.3 Identifying Singular Directions
For a robot Jacobian J with rank r, the last m −r out-
put singular vectors, i.e., u
i
’s, span the directions of
lost end-effector motion. For spatial manipulators,
these singular vectors are 6-dimensional and repre-
sent a simultaneous translational and rotational ve-
locity. For rank-1 singularities, there is only one
unique singular direction, u
m
, and it is easy to vi-
sualize. At higher rank singularities, the singular
value decomposition is not unique. Thus, the singu-
lar vectors corresponding to the zero singular values
(σ
r+1
,σ
r+2
,··· ,σ
m
) are ill defined and will likely not
be well aligned with the world (or task) frame of the
robot. However, one can apply Givens rotations to
these vectors in order to identify an intuitive repre-
sentation for the lost end effector motion. Consider
Figure 4, that shows a 7-DoF robot in a rank-3 singu-
larity, where both subfigures correspond to the same
robot in the same singular configuration. The origi-
nal singular vectors, identified by employing the sin-
gular value decomposition, can be rotated to a more
1
Figure 4, 6, 7, 8, and 9 are produced using the Robotics
Toolbox (Corke, 2017).
Figure 4: A 7-DoF robot in the same rank-3 singularity is
presented.
1
In subfigure (a), the three SVD-generated singu-
lar directions are indicated. In subfigure (b), the singular di-
rections are plotted after they are properly rotated. The sin-
gular directions, u
4
, u
5
, and u
6
are represented by green,
red, and blue respectively. Dotted arrows represent rota-
tional velocity and solid arrows represent translational ve-
locity.
intuitive set that is aligned with the world coordinate
frame as follows:
[u
4
u
5
u
6
]=
0 0 0
−0.27 0.62 −0.61
0.74 −0.17 −0.50
−0.50 −0.71 −0.50
−0.33 0.08 0.23
−0.12 0.28 −0.27
⇒
0 0 0
0 −0.91 0
0 0 0.91
−1 0 0
0 0 −0.41
0 −0.41 0
Using the rotated subspace above (shown in Fig-
ure 4(b)), one can easily determine that there is no
joint velocity that can generate any rotational veloc-
ity around the −X direction (green). In addition, the
robot cannot have a simultaneous velocity with the il-
lustrated components of −Y translational motion with
−Z rotational motion (red). Likewise, there are no
joint rates that can generate a simultaneous velocity
with the illustrated components of Y translational mo-
tion with −Z rotational motion (blue). In the next sec-
tion, we illustrate the results of applying the proposed
algorithms to robots of different kinematic structures.
3 CASE STUDIES
3.1 Introduction
Our algorithm to identify robot singularities is neither
limited by the kinematic structure of the robot, nor
by the rank of the singularity. We employed it on
several 4-DoF regional and 7-DoF spatial robots and
present the results of one 4-DoF and one 7-DoF robot
here. For each robot we start with 10, 000 random
configurations in the joint space. From each point, we
apply the gradient-based algorithm to find rank-1 and
all higher rank singularities. The resulting singular
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
46

vectors are then rotated to the most intuitive
representation of the lost directions of motion.
3.2 4-DoF Regional Robot
We study a locally optimal fault-tolerant 4-DoF robot
presented in (Ben-Gharbia et al., 2013) with the DH
parameters given in Table 1. This robot is a spa-
tial positioning (regional) manipulator, i.e., it has a
3-dimensional workspace. Our focus is on identify-
ing the singular configurations of this manipulator.
Table 1: DH parameters of an example 4-DoF manipulator.
Link
i
α
i
[radians] a
i
[m] d
i
[m] θ
i
[radians]
1 π/2
√
2 0 θ
1
2 -π/2
√
2 1 θ
2
3 π/2
√
2 -1 θ
3
4 0
p
3/2 1/2 θ
4
It was found that this robot has only rank-1 singu-
larities as presented in Figure 5. These singularities
are arranged along continuous manifolds in the joint
space. This means that the robot can continuously
move while staying in a singular configuration. Note
that these are not the same as the self-motion mani-
folds.
Because the robot does not have any high-rank
singularities, the presentation of the singular direc-
tions is straightforward. The singular direction, u
3
,
gives the actual direction of the loss of the end-
effector velocity. Figure 6 shows the 4-DoF robot in
two different rank-1 singularities along with the sin-
gular directions with respect to the world frame.
3.3 Mitsubishi PA-10 Robot
3.3.1 Introduction
The Mitsubishi PA-10 is a 7-DoF manipulator with a
6-dimensional work space. Its kinematic structure is
similar to the human arm with three spherical joints in
the shoulder, one joint in the elbow, and three spher-
ical joints in the wrist. The DH parameters of the
PA-10 are listed in Table 2. The singularity analy-
sis on the PA-10 resulted in rank-1, rank-2, and rank-
3 singularities being identified. We were able to find
singularity conditions for each singularity rank. The
singular directions, u
i
’s, were also identified and ap-
propriately rotated. In all figures, loss of directional
velocity is indicated with a solid arrow, while the loss
of rotational velocity is indicated with a dotted arrow.
Blue arrows indicate u
6
, red arrows indicate u
5
, and
green arrows indicate u
4
.
Figure 5: This figure illustrates the 4-DoF robot rank-1 sin-
gularities. In (a) the singular configurations are shown us-
ing a 2-D projection in [θ
2
,θ
3
]. In (b) a 3-D projection in
[θ
2
,θ
3
,θ
4
] is shown.
Figure 6: This figure shows the 4-DoF robot in two dif-
ferent rank-1 singular configurations. In (a) the robot is
shown in the configuration θ = [−3.11,3.02,−1.53,0.15]
rad. The singular direction corresponding to the singularity
is u
3
= [0,1,0]
>
, which indicates that the singular direction
is aligned with the Y direction. In (b) the robot is shown in
the configuration θ = [−1.76,−1.85,−1.39, 0.02] rad. The
singular direction is u
3
= [−1,0, 0]
>
, which indicates that
the singular direction is aligned with the −X direction.
Table 2: DH parameters of the PA-10 robot.
Link
i
α
i
[radians] a
i
[m] d
i
[m] θ
i
[radians]
1 -π/2 0 0 θ
1
2 π/2 0 0 θ
2
3 -π/2 0 0.45 θ
3
4 π/2 0 0 θ
4
5 -π/2 0 0.50 θ
5
6 π/2 0 0 θ
6
7 0 0 0.45 θ
7
3.3.2 Rank-1 Singularities
All rank-1 singularities are summarized in Table 3.
Joint 4 is critical in that the robot will be singular if
θ
4
is equal to ±π or 0. One can observe that joint 4
is the only joint that can change the distance between
the shoulder and the wrist.
The robot singular directions that indicate the loss
of the end-effector velocity are all shown in Figure 7.
Because these are rank-1 singularities, their corre-
sponding singular directions are well defined.
Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure
47
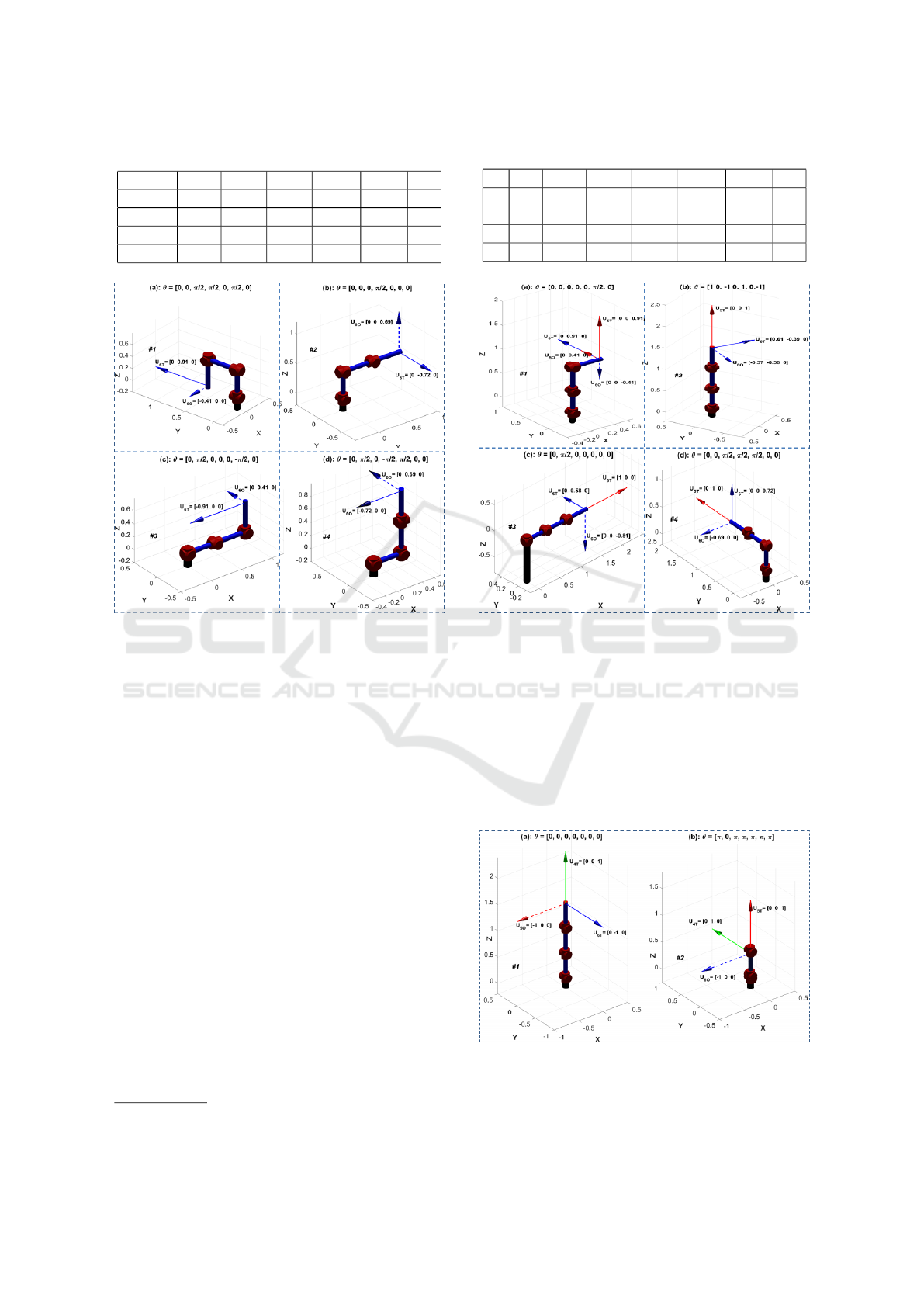
Table 3: PA-10 robot’s rank-1 singular configurations
2
.
i θ
1
θ
2
θ
3
θ
4
θ
5
θ
6
θ
7
1 x ±π,0 ±π/2 x x x x
2 x ±π,0 x x x ±π,0 x
3 x x x ±π,0 x x x
4 x x x x ±π/2 ±π, 0 x
Figure 7: The PA-10 robot is shown in rank-1 singular con-
figurations. The singular direction, u
6
, is also plotted for
each singularity. The singularity conditions, 1, 2, 3, and 4,
in Table 3 are satisfied in subfigures (a), (b), (c), and (d),
respectively.
3.3.3 Rank-2 Singularities
The PA-10’s rank-2 singularity conditions are shown
in Table 4. The common feature between these condi-
tions is that they do not depend on the value of θ
1
or
θ
7
. We employed Givens rotation to make sure that
the two singular vectors, u
5
and u
6
, are rotated to
represent the most intuitive set of singular directions.
Figure 8 shows the four singular conditions listed in
Table 4.
3.3.4 Rank-3 Singularities
It was found that the PA-10 robot can have rank-3 sin-
gularities by aligning the axes of joints 1, 3, 5, and
7 so that their columns of the Jacobian are linearly
dependent. The conditions for these rank-3 singular-
ity configurations are listed in Table 5. As before,
we have used Givens rotations to make the singular
vectors, u
4
, u
5
, u
6
as intuitive as possible. Figure 9
shows the manipulator in two different rank-3 singu-
2
In all tables, “x” means the angle value does not matter.
Table 4: PA-10 robot’s rank-2 singular configurations.
i θ
1
θ
2
θ
3
θ
4
θ
5
θ
6
θ
7
1 x ±π,0 ±π,0 ±π, 0 x x x
2 x ±π,0 x ±π,0 x ±π, 0 x
3 x x x ±π,0 ±π, 0 ±π,0 x
4 x ±π,0 ±π/2 x ±π/2 ±π,0 x
Figure 8: The PA-10 robot is shown in rank-2 singular con-
figurations. The singular directions u
5
and u
6
are plotted
for each singularity condition. The singularity conditions,
1, 2, 3, and 4, in Table 4 are represented in the subfigues (a),
(b), (c), and (d), respectively.
lar configurations. One can observe that the rank-
3 singularities occur for the PA-10 when it is com-
pletely stretched out (workspace boundary singular-
ity) or when it is folded back on itself.
In general, our approach for identifying robot sin-
gularities does not consider physical joint limits. One
Figure 9: The PA-10 robot is shown in rank-3 singular con-
figurations. The singular directions, u
4
, u
5
, and u
6
are in-
dicted in green, red, and blue respectively. In (a), the robot
is in configuration θ = [0, 0,0,0, 0, 0,0] and in (b) the robot
is in θ = [π, 0,π,π, π, π,π].
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
48

Table 5: PA-10 robot’s rank-3 singular configurations.
i θ
1
θ
2
θ
3
θ
4
θ
5
θ
6
θ
7
1 x ±π,0 ±π,0 ±π, 0 ±π, 0 ±π,0 x
can employ our technique to find any robot singular
configuration but one must exclude infeasible angles
due to mechanical limits.
4 CONCLUSIONS
This work has proposed a procedure based on com-
puting the gradient of a singular value to drive a robot
into a singular configuration. This algorithm is able
to: (1) identify the singularities of any rank for any
robot and (2) deal with ill-defined singular vectors
when their corresponding singular values are equal.
A second algorithm was presented to obtain the most
intuitive representation of the singular vectors associ-
ated with configurations that correspond to high-rank
singularities. Both algorithms are applicable to robots
with an arbitrary number of degrees of freedom and of
arbitrary kinematic structure These algorithms were
illustrated on a 4-DoF redundant positioning robot
and on a 7-DoF redundant PA-10 robot.
REFERENCES
Baker, D. R. and Wampler, C. W. (1988). On the inverse
kinematics of redundant manipulators. The Interna-
tional Journal of Robotics Research, 7(2):3–21.
Ben-Gharbia, K. M., Maciejewski, A. A., and Roberts,
R. G. (2013). Kinematic design of redundant robotic
manipulators for spatial positioning that are opti-
mally fault tolerant. IEEE Transactions on Robotics,
29(5):1300–1307.
Boudreau, R. and Podhorodeski, R. P. (2010). Singularity
analysis of a kinematically simple class of 7-jointed
revolute manipulators. Transactions of the Canadian
Society for Mechanical Engineering, 34(1):105–117.
Burdick, J. W. (1989). On the inverse kinematics of re-
dundant manipulators: Characterization of the self-
motion manifolds. International Conference on
Robotics and Automation, 1(2):264–270.
Corke, P. (2017). Robotics, vision and control: Fundamen-
tal algorithms in MATLAB
R
, volume 118. Springer.
Groom, K. N., Maciejewski, A. A., and Balakrishnan, V.
(1999). Real-time failure-tolerant control of kinemat-
ically redundant manipulators. IEEE Transactions on
Robotics and Automation, 15(6):1109–1115.
Hunt, K. H. (1986). Special configurations of robot-arms
via screw theory. Robotica, 4(3):171–179.
Kieffer, J. and Lenarcic, J. (1994). On the exploitation of
mechanical advantage near robot singularities. Infor-
matica, 18(3):315–323.
Klein, C. A. and Chu, L.-C. (1997). Comparison of ex-
tended Jacobian and Lagrange multiplier based meth-
ods for resolving kinematic redundancy. Journal of
Intelligent & Robotic Systems, 19(1):39–54.
Litvin, F., Yi, Z., Castelli, V. P., and Innocenti, C. (1986).
Singularities, configurations, and displacement func-
tions for manipulators. The International Journal of
Robotics Research, 5(2):52–65.
Maciejewski, A. A. (1988). The analysis and control of
robotic manipulators operating at or near kinemati-
cally singular configurations. PhD thesis, The Ohio
State University.
Nakamura, Y. and Hanafusa, H. (1986). Inverse kinematic
solutions with singularity robustness for robot manip-
ulator control. Journal of Dynamic Systems, Measure-
ment, and Control, 108(3):163–171.
Nokleby, S. B. and Podhorodeski, R. P. (2004a). Iden-
tifying multi-DOF-loss velocity degeneracies in
kinematically-redundant manipulators. Mechanism
and Machine Theory, 39(2):201–213.
Nokleby, S. B. and Podhorodeski, R. P. (2004b). Identi-
fying the 1-DOF-loss velocity-degenerate (singular)
configurations of an 8-joint manipulator. Transactions
of the Canadian Society for Mechanical Engineering,
28(2A):109–124.
Sugimoto, K., Duffy, J., and Hunt, K. (1982). Special
configurations of spatial mechanisms and robot arms.
Mechanism and Machine Theory, 17(2):119–132.
Waldron, K., Wang, S.-L., and Bolin, S. (1985). A study of
the Jacobian matrix of serial manipulators. Journal of
Mechanisms, Transmissions, and Automation in De-
sign, 107(2):230–237.
Xu, W., Zhang, J., Liang, B., and Li, B. (2016). Singular-
ity analysis and avoidance for robot manipulators with
nonspherical wrists. IEEE Transactions on Industrial
Electronics, 63(1):277–290.
Xu, W., Zhang, J., Qian, H., Chen, Y., and Xu, Y.
(2013). Identifying the singularity conditions of
Canadarm2 based on elementary Jacobian transforma-
tion. 2013 IEEE/RSJ International Conference on In-
telligent Robots and Systems, pages 795–800.
Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure
49
