
Distributed Multi-objective Particle Swarm Optimization using
Time-delayed Virtual Global Best Method
Yuji Sato, Shota Ueno and Toshio Hirotsu
Department of Computer and Information Sciences, Hosei University, Tokyo, Japan
Keywords: Particle Swarm Optimization, Parallel and Distributed System, Performance Improvement, Multi-objective
Optimization.
Abstract: To reduce the computational cost of particle swarm optimization (PSO) methods, research has begun on the
use of Graphics Processing Units (GPUs) to achieve faster processing speeds. However, since PSO methods
search based on a global best value, they are hampered by the frequent need for communication with global
memory. Even using a standard PSO that uses a local best value does not solve this problem. In this paper,
we propose a virtual global best method that speeds up computations by defining a time-delayed global best
as a virtual global best in order to reduce the frequency of communication with low-speed global memory.
We also propose a method that combines decomposition-based multi-objective PSO (MOPSO/D) with a
virtual global best method to speed up multi-objective particle swarm optimization by running it in parallel
while maintaining search accuracy, and we demonstrate the effectiveness of this approach by using a number
of unimodal/multimodal single objective benchmark test functions and three classical benchmark test
functions with two objectives.
1 INTRODUCTION
Particle swarm optimization (PSO) is an optimization
algorithm that models the behavior of flocks of birds
and schools of fish (Kennedy, 1995), and which is one
of the population based non-deterministic
optimization algorithms. There is a personal best and
global best and both affect the direction in which
particles are moving. PSO has attracted attention as a
useful optimization tool due to its simple algorithm
and other attributes. However, a problem with this
algorithm is that when the number of particles is
increased in order to deal with a more complex
objective function, the computational cost also
increases, resulting in longer search times. There have
already been studies aimed at preventing this issue of
increased search times by using GPUs to distribute
the computational load (Zhou, 2009; Souza, 2011;
Hussain, 2016). A study that uses parallel
acceleration of PSO on a GPU based on a master-
slave model to solve multi-objective problems has
also been reported (Cao, 2017; Hussain, 2018).
However, since these previous studies use global
memory to store particle swarm data, they are unable
to achieve adequate speed increases even when
running many cores in parallel. Alternatively, if
attempts are made to speed up processing based on a
master-slave model, the efficiency of processing
speed improvements is liable to deteriorate as the
number of cores increases. To address these issues,
this paper proposes a method that can improve
computation speeds by defining a time-delayed
global best as a virtual global best for each streaming
multiprocessor (SM) in order to reduce the frequency
of communication with low-speed global memory.
Next, compared with single-objective optimization
where it is important to converge on just one optimal
solution, in multi-objective optimization it is
necessary to increase the speed of computation while
maintaining diversity in the search process as well as
convergence on the Pareto front. However, there is
often a trade-off between convergence on the Pareto
front and maintenance of diversity, and this problem
cannot be solved simply by operating the proposed
method in parallel. Therefore, we propose running a
multi-objective particle swarm optimization method
in parallel by combining a virtual global best method
and decomposition-based multi-objective PSO
(MOPSO/D) (Peng, 2008), which is capable of global
searching, and we use benchmark problems to
demonstrate the effectiveness of this approach.
Sato, Y., Ueno, S. and Hirotsu, T.
Distributed Multi-objective Particle Swarm Optimization using Time-delayed Virtual Global Best Method.
DOI: 10.5220/0007955200210030
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 21-30
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
21

2 OVERVIEW OF PARTICLE
SWARM OPTIMIZATION
2.1 Original PSO
In original PSO, each particle has a position vector
and a velocity vector that are used to calculate the
evaluation values and the positions to which these
particles move. After using the position vectors to
calculate the evaluation value at the current position
of each particle, the velocity vectors and position
vectors are updated according to the following
formula:
(1)
(2)
where v(t) and v(t+1) are the velocity vectors in
generations t and t+1 respectively, and x(t) and x(t+1)
are the corresponding position vectors. P
bestx
represents the personal best which is the best solution
found by each particle up to generation t. G
bestx
is the
global best, which is the current best position found
by the whole group. The coefficients c
1
and c
2
are
positive constants, and rand1 and rand2 are random
variables in the range from 0 to 1. After each particle
has been moved, the calculation of evaluation values
and the updating of vectors are repeated until the end
condition is satisfied in order to find an
approximation to the optimal solution.
2.2 Standard PSO
Standard particle swarm optimization (SPSO)
(Bratton, 2007) is an algorithm that extends the
original PSO algorithm described above. Based on
the topology of the particle group defined by the
designer, the best position from among each particle
and its neighbors is used as a local best instead of
using a global best.
In SPSO, changing the topology changes the
search motion of the entire particle group. A
simplified diagram of the ring topology that is
generally used as the topology for SPSO is shown in
Fig. 1. In a ring topology, a particle shares
information with its neighbors on both sides. This is
because convergence on the optimal solution is
impaired if the particles are split into completely
independent groups. In this case, with a reduced
amount of shared information, the convergence is
slightly worse compared with the original PSO, but
the global search performance is maintained for a
longer time. SPSO is therefore able to search for
better solutions to problems that converge to a local
solution in PSO.
Figure 1: Ring topology example.
Furthermore, particle groups in PSO may fail to
converge due to an excessive increase in velocity.
Therefore, in order to guarantee that the particle
group converges as the search proceeds, SPSO uses
the following calculation formula taking the inertia
weight χ into consideration. Here, L
bestx
represents the
local best.
(3)
(4)
When a search is performed using the above
formula, the movement of the entire particle group
changes according to the value of φ. When φ is less
than 4, the particle groups repeatedly converge and
diverge. When it is greater than 4, the particle groups
are guaranteed to converge. Therefore, a combination
of c
1
= c
2
= 2.05 is generally used in SPSO.
3 RUNNING PSO IN PARALLEL
3.1 Parallel PSO in Earlier Research
In a GPU-based parallel implementation of PSO, the
computational load is distributed by allocating each
particle to a CUDA core. The GPU can be used to
parallelize parts that exist independently for each
particle, such as calculating its evaluation value and
updating its vectors. However, the global best
calculation requires the collection of information on
the whole particle group, which reduces the degree of
parallelism. In previous studies by Zhou et al. (Zhou,
2009) and Hussain et al. (Hussain, 2016), SPSO was
run in parallel by using a ring topology. Hussain et al.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
22
also sought to achieve greater speed by using coreless
access, which is an access technique for efficient
communication with global memory.
In the methods proposed in these previous studies,
there remains a problem in that the frequency of
communication with global memory increases. In
parallel SPSO, neighboring particles may exist in
another SM. When using a topology where there is no
sharing between particles in different SMs, it is not
possible to perform searches using a global best, the
overall convergence of the particle group is impaired,
and it is not possible to search efficiently. Therefore,
when SPSO is run in parallel, it must use global
memory to share information between SMs. For these
reasons, the previous studies basically used global
memory to store data. This results in frequent
communication with global memory while
performing search calculations. When implementing
parallel processing on a GPU, this communication
with low-speed memory becomes a bottleneck,
making it hard to improve the effective execution
speed no matter how great the degree of parallelism.
3.2 Parallelization using Virtual Global
Best
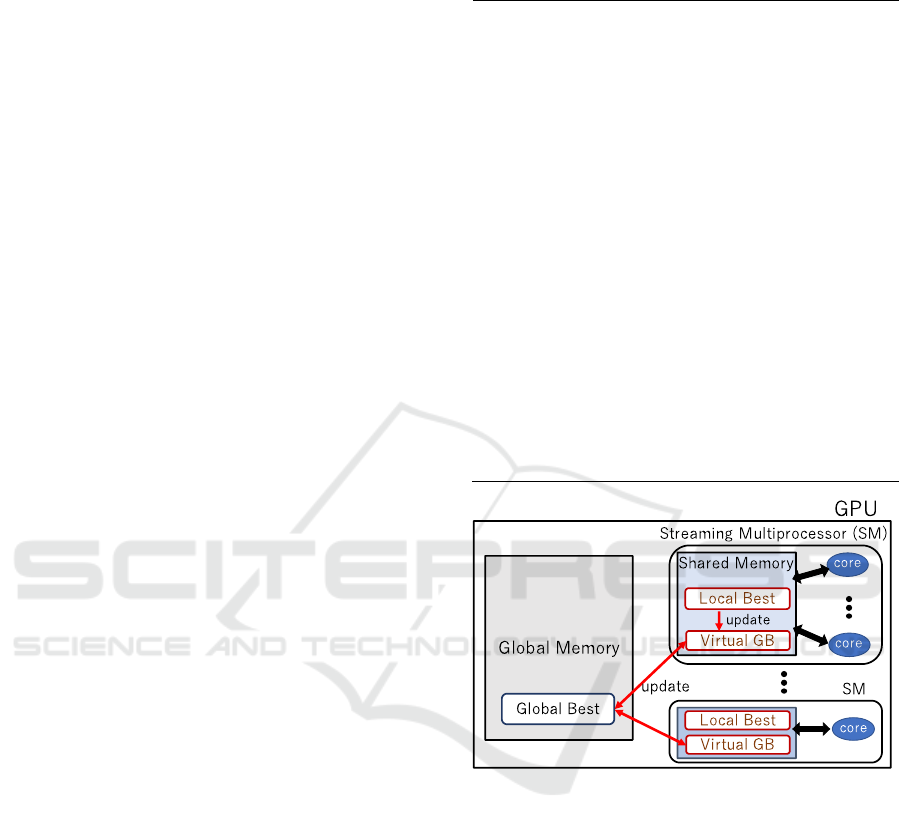
Figure 2 shows an outline of our proposed
parallelization using virtual global best. The virtual
global best method reduces the frequency of
communication with global memory. First, the
population (particle swarm) in PSO is separated into
several new swarms. These new swarms are
associated with each SM, with information such as
the particle coordinates being stored in registers or
shared memory. In order to minimize the number of
data transfers between SMs, each particle searches
using a virtual global best instead of the current global
best. The initial value of the virtual global best is
allocated to each SM as the global best of the particle
swarm in the initial state before separation. The local
best of each SM is compared with the virtual global
best, and when the local best is better than the virtual
global best, the virtual global best is updated and is
simultaneously compared with the global best stored
in global memory. When necessary, the global best
and virtual global best are updated. In this way, it is
no longer necessary to communicate with global
memory when particle information is required. This
can reduce the memory communication bottleneck,
making parallel processing more effective. When the
global best is updated in global memory, the timing
of this event is delayed in each sub-swarm to prevent
loss of data.
The virtual global best search algorithm
(Algorithm 1) is as follows:
1 let N = the number of particles in the sub swarm
2 let s = the index of sub swarm
3 let B = the number of sub swarms
4 let T = the number of migration interval
5 store global best in global memory
6 store virtual global best in shared memory
7 if the index of thread is N+1 then
8 for j = 1 to iterations do
9 if (j%(B*T)) is (s*T) then
10 update global best and virtual global best
11 end if
12 end for
13 end if
14 else
15 for j = 1 to iterations do
16 update velocity and position
17 calculate fitness, personal best, and virtual global
best
18 end for
19 end else
Figure 2: Outline of virtual global best method.
4 PARALLEL MOPSO USING
VIRTUAL GLOBAL BEST
4.1 Multi-objective Optimization
Multi-objective optimization is a method that
simultaneously optimizes multiple objective
functions in a trade-off relationship. Figure 3 shows a
conceptual illustration of the optimization of two
objectives. In multi-objective optimization, one of the
currently known solutions that has a good evaluation
value for any particular objective function is called a
non-inferior solution and is regarded as an optimal
solution. As shown in Fig. 3, there are usually
Distributed Multi-objective Particle Swarm Optimization using Time-delayed Virtual Global Best Method
23
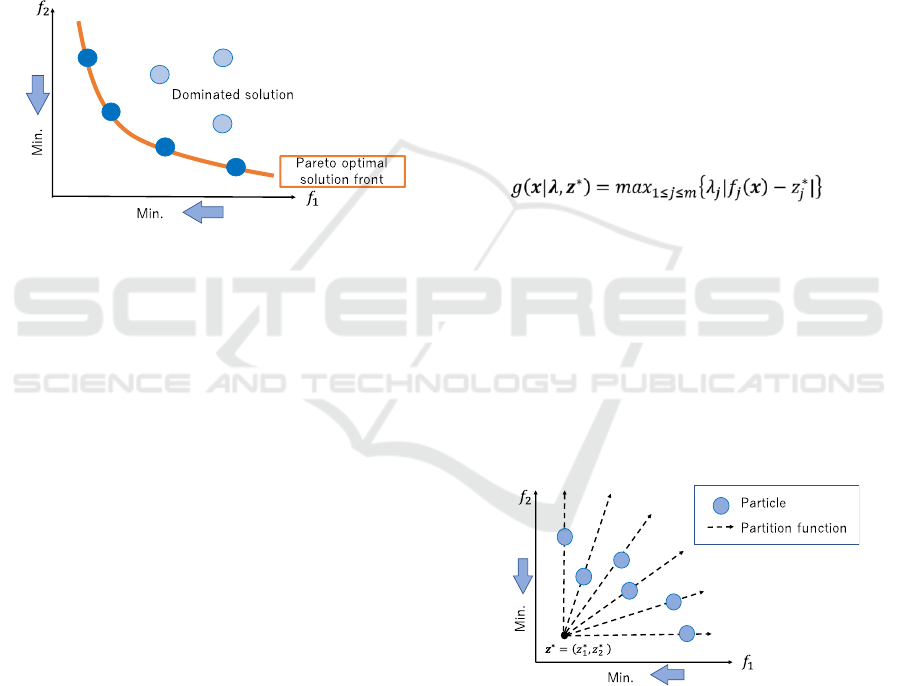
multiple non-inferior solutions. The set of non-
inferior solutions is called the Pareto optimal
solution. The surface formed by the Pareto optimal
solution is called the Pareto front, and the purpose of
a search algorithm such as evolutionary computation
is to conduct searches so that the Pareto front takes a
form that better satisfies the criteria of the objective
function. Basically, PSO is a population based non-
deterministic optimization algorithms as a single
objective optimizer. On the other hand, research on
PSO strategy for solving multi-objective problems
(Multi-Objective PSO, MOPSO) has already began
(Moore, 1999; Hussain, 2018).
Figure 3: Conceptual illustration of the optimization of two
objectives.
4.2 Proposal of Parallel MOPSO/D
using Virtual Global Best
In MOPSO, the global best cannot be updated in the
same way as in single-objective PSO because the
optimal solution of the whole particle swarm is not
uniquely determined. Thus, when the virtual global
best algorithm is simply implemented as parallel
MOPSO, we can consider a method that uses an
archive. The archive stores the coordinates of
multiple candidate best solutions out of the personal
best solutions of each particle. A particle updates its
velocity by using the coordinates of one candidate
selected from the archive as the virtual global best.
In MOPSO using an archive, when selecting a
solution stored in the archive or a global best, it is
possible to improve diversity by considering
parameters such as the particle congestion factor.
However, if this solution requires complex
computations, it will increase the computational load
and adversely affect the execution time. Furthermore,
to prevent the loss of information stored in memory,
the addition of information to the archive must be
performed sequentially for each particle, making it
difficult to conceal the added computational load in
parallel processing. Accordingly, the above trade-off
relationship cannot be resolved in the virtual global
best method using an archive. Therefore, in the
proposed method, we use a combination of
MOPSO/D, which is capable of performing global
searches, and a virtual global best approach that
effectively operates at high speed in parallel by
avoiding communication with low-speed memory.
This not only ensures the diversity of solutions, but
can also reduce the execution time.
4.2.1 MOPSO/D
In MOPSO/D, a partition function is uniformly
distributed in evaluation value space based on the
objective function, and the particles optimize this
partition function. In this way, by having each particle
optimize a single objective function, the overall
particle swarm find uniform and diverse solutions in
evaluation value space by optimizing a single
objective function. The Tchebycheff function
(Zhang, 2007) is used as a partition function. This
function is calculated as follows,
(5)
where j represents the number of objective
functions, λ is a weighting vector corresponding to
each partition function, and the search direction
changes according to its value. z* is a reference point,
and the coordinates of this point are determined by
the values of the whole particle swarm. An overview
of MOPSO/D is shown in Fig. 4. When the reference
point is set as the minimum value of the particle
swarm in a minimization problem as shown in Fig. 4,
the optimal solution can be obtained by determining
the minimum value of the partition function.
Figure 4: Outline of MOPSO/D.
The difference between this method and ordinary
PSO lies in the way in which the global best solution
is updated. Since MOPSO/D uses a different function
for the evaluation of each particle, it is not possible to
compare each of these calculated evaluation values
directly. Therefore, each particle calculates an
evaluation value by inputting the coordinates of its
neighboring particles into its own partition function.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
24

When the evaluation value is better than the current
global best, the coordinates of the referenced particle
are set as the new global best coordinates. In
MOPSO/D, adjustment of parameters is required in
order to influence the solution accuracy and execution
speed of neighboring particles that are referenced
when updating the global best and the number of
partition functions.
4.2.2 Proposed Parallelization of MOPSO/D
using Virtual Global Best
Figure 5 shows an outline of the distributed
MOPSO/D with virtual global best method. In the
proposed method, the particle swarm is partitioned
between each SM as in the virtual global best method.
This makes it possible to perform the calculations to
update coordinates and personal best solutions
without using global memory. Furthermore, the
number of partition functions is assumed to be equal
to the number of particles in an SM, and the
distribution of partition functions is assumed to be the
same for any sub-swarm. Therefore, in SM there is a
one-to-one correspondence between particles and
partition functions, and in the overall particle swarm,
a single partition function is searched by the number
of particles allocated to an SM. By sharing the global
best with particles searching for the same partition
function, it is thought that this will improve the
convergence so that an optimal solution can be found
in fewer generations. Furthermore, by storing each
particle's virtual global best solution in a register, the
frequency of communication with global memory can
be reduced. By delaying the global best update time
for each sub-swarm, we can expect to maintain the
global search performance in each partition function.
Figure 5: Outline of the distributed MOPSO/D with virtual
global best method.
The basic algorithm is the same as in the virtual
global best method, but with two main changes. The
first is that a different method is used to update the
virtual global best. In MOPSO/D, the coordinates of
neighboring particles are required when updating the
global best. Essentially, storing the coordinates in
shared memory allows the operations related to these
particles to be completed inside the SM. However,
due to shared memory capacity limits, it is not
possible to store the coordinates of sub-swarms.
Therefore, in the proposed method, the particle
coordinates are stored in global memory for the
purpose of sharing information, and are retrieved
when updating the virtual global best. In this way,
communication with the global memory takes place
at each generation, which is liable to adversely affect
the execution speed.
The second change is that there is no thread
responsible for updating the global best solution
(thread N+1 in Algorithm 1). In MOPSO/D, the
global best is stored individually by each particle, so
when one thread communicates with global memory,
the amount of communication is large, and the
execution time becomes longer. Therefore, the global
best is updated by the thread that updates each
particle.
5 EVALUATIONS
5.1 Evaluation Method
Table 1 shows the environment used in the
experiment. In this study, we performed three types
of comparative experiments. First, we solved the five
benchmark problems of previous studies shown in the
appendix in the same environment (Zhou, 2009;
Hussain, 2016), and we compared the execution times
and solution accuracy by solving five benchmark
problems with three global best methods. The results
shown here are the average values from 20 runs of
this experiment with 7,936 particles, a 100-
dimensional sphere function, and other functions with
50 dimensions, and 2,000 generations.
Table 1: Experimental environment.
CPU
Intel core i7-6700 3.40 GHz
RAM
16.00 GB
GPU
NVIDIA GeForce GTX 960
OS
Windows 10 Home
Second, by comparing the execution speeds and
solution distributions of MOPSO/D using a virtual
global best method when implemented on a CPU and
when implemented in parallel on a GPU, we verified
that it maintains the same level of accuracy while
reducing the execution time. The benchmark
problems with two objectives used in this experiment
were ZDT1, ZDT2 and ZDT3 (Zitzler, 2000) shown
below. The experiments related to execution speed
Distributed Multi-objective Particle Swarm Optimization using Time-delayed Virtual Global Best Method
25
were conducted with 4,096 particles, 30 dimensions
and 250 generations, and the experiments related to
distribution were conducted with the number of
dimensions changed to 200.
[ZDT1 function]
min f
1
(x) = x
1
min f
2
(x) = g・h
where,
,
,
x
i
[0, 1]
[ZDT2 function]
min f
1
(x) = x
1
min f
2
(x) = g・h
where,
,
,
x
i
[0, 1]
[ZDT3 function]
min f
1
(x) = x
1
min f
2
(x) = g・h
where,
,
,
x
i
[0, 1]
Third, we imposed a time limit on the CPU
execution, and compared the resulting distribution
with the results obtained by running on a GPU. In the
limited time experiment, the GPU execution was set
to either the time taken to reach the set number of
generations, or the time taken for all the particles to
reach the Pareto front of the benchmark problem. The
number of particles was 4,096, and the number of
generations was 250. We used the same benchmark
problem as in the second experiment, with the number
of dimensions set to 30.
5.2 Experimental Comparison of
Virtual Global Best Method with
Previous Studies
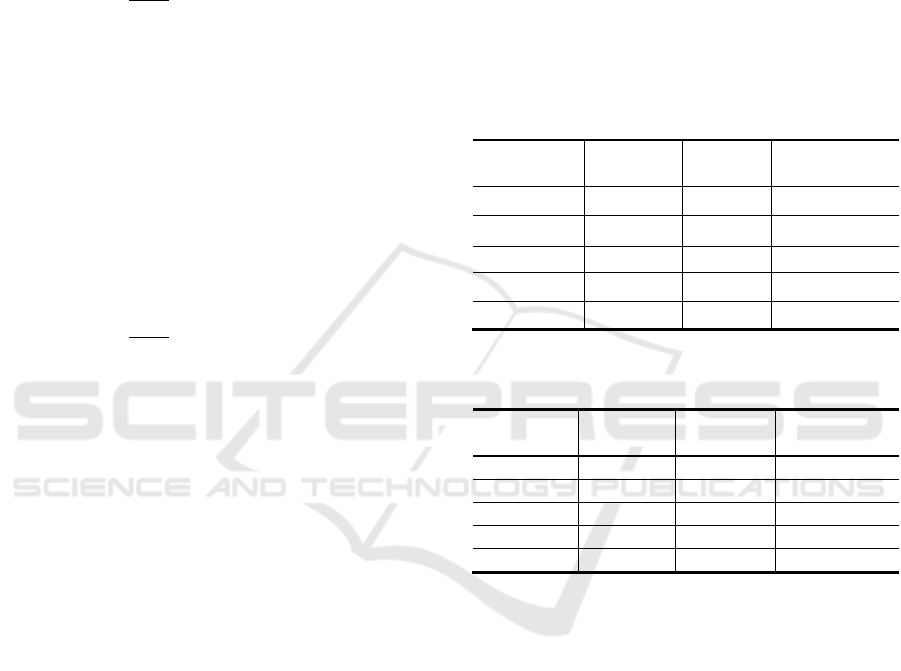
As shown in Table 2, the virtual global best method
yields much more accurate solutions for the Sphere
function and Griewank function than the parallel PSO
method used in previous studies. This is thought to be
because the virtual global best method achieves the
same high level of convergence as the original PSO
method. The Sphere function is a unimodal function
without any local solutions, while the Griewank
function is similar to a unimodal function in that it
features a large global gradient. Since a highly
convergent search algorithm is effective for searching
unimodal functions, the proposed method was able to
find better solutions. It also found very similar
solutions for other multimodal functions. This is
thought to be because the division of the particle
swarm into sub-swarms allows greater global search
performance to be maintained than with ordinary
PSO. Also, according to Table 3, the virtual global
best method is about four times faster than the
conventional parallel PSO, except for the Sphere
function. This is due to the effect of using virtual
global memory to reduce the frequency of
communication with global memory.
Table 2: Comparison of the accuracy of previous studies
and the proposed method.
Function
Zhou,
2009
Hussain,
2016
Proposed
method
Sphere
1.06e-01
1.32e-01
4.51e-29
Rosenbrock
2.11e+01
2.11e+01
2.22e+01
Rastrigin
1.45e+02
1.38e+02
8.42e+01
Griewank
8.32e-10
1.29e-09
1.40e-45
Ackley
9.44e-05
1.17e-04
3.81e-06
Table 3: Comparison of the execution time of previous
studies and the proposed method.
Function
Zhou,
2009 [ms]
Hussain,
2016 [ms]
Proposed
method [ms]
Sphere
9463.55
2767.95
1148.17
Rosenbrock
2758.78
1495.40
314.77
Rastrigin
2898.74
1579.15
409.13
Griewank
2927.17
1599.27
445.46
Ackley
2891.06
1596.29
414.08
5.3 Experimental Comparison with
Parallel MOPSO/D
Tables 4 through 6 show the average execution times
for 20 trials of each benchmark problem when the
number of generations is 250 and dimension size is
30. According to these tables, we achieved a speed
improvement factor of at least 14 for every function.
It shows an average higher performance improvement
rate than related work (Hussain, 2018). When
implemented on a CPU, the execution speed varies
with the function parameters, whereas on a GPU there
is almost no variation. This is because the evaluation
values have to be calculated sequentially on a CPU,
which has a direct effect on the function's
computation time. On the other hand, since the GPU
performs the function calculations in parallel, the
variation of computation time with the difficulty of
the function can be concealed.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
26
In addition, when implemented on a GPU, the
acceleration effects of parallel processing do not vary
greatly with the number of cores. This can be attributed
to various factors, including the proposed algorithm's
higher proportion of computations involving
neighboring particles, the use of global memory when
updating the virtual global best solutions, and the fact
that the global best is not updated in parallel.
Furthermore, the execution time increases in
proportion to the number of particles. This is thought
to be due to the large number of registers used by a
single thread. The number of threads that are run in
parallel by the GPU is scheduled according to how
much each thread occupies memory resources such as
shared memory and registers. Therefore, when a single
thread requires more memory, fewer threads can be
processed at a time, and the overall execution becomes
sequential. Since parallel MOPSO/D stores virtual
global best coordinates in addition to the particle
coordinates and personal best coordinates, each thread
requires a large number of registers. As the number of
particles increases, the number of threads that are
executed sequentially also increases by a
corresponding amount, so it is thought that the
execution time increases in proportion to the number
of particles.
Table 4: Speed improvement factors for ZDT1.
Num. of
particles
CPU
GPU
Speed improvement
factor
1024
144.9
9.8
14.71
2048
288.1
16.7
17.27
4096
650.0
32.5
17.38
8192
1133.2
68.7
16.50
Table 5: Speed improvement factors for ZDT2.
Num. of
particles
CPU
GPU
Speed improvement
factor
1024
159.3
9.6
16.51
2048
263.0
16.8
15.67
4096
504.6
31.7
15.94
8192
1001.7
67.4
14.86
Table 6: Speed improvement factors for ZDT3.
Num. of
particles
CPU
GPU
Speed improvement
factor
1024
167.0
10.3
16.23
2048
331.9
17.4
19.09
4096
650.0
33.2
19.58
8192
1283.6
70.7
18.15
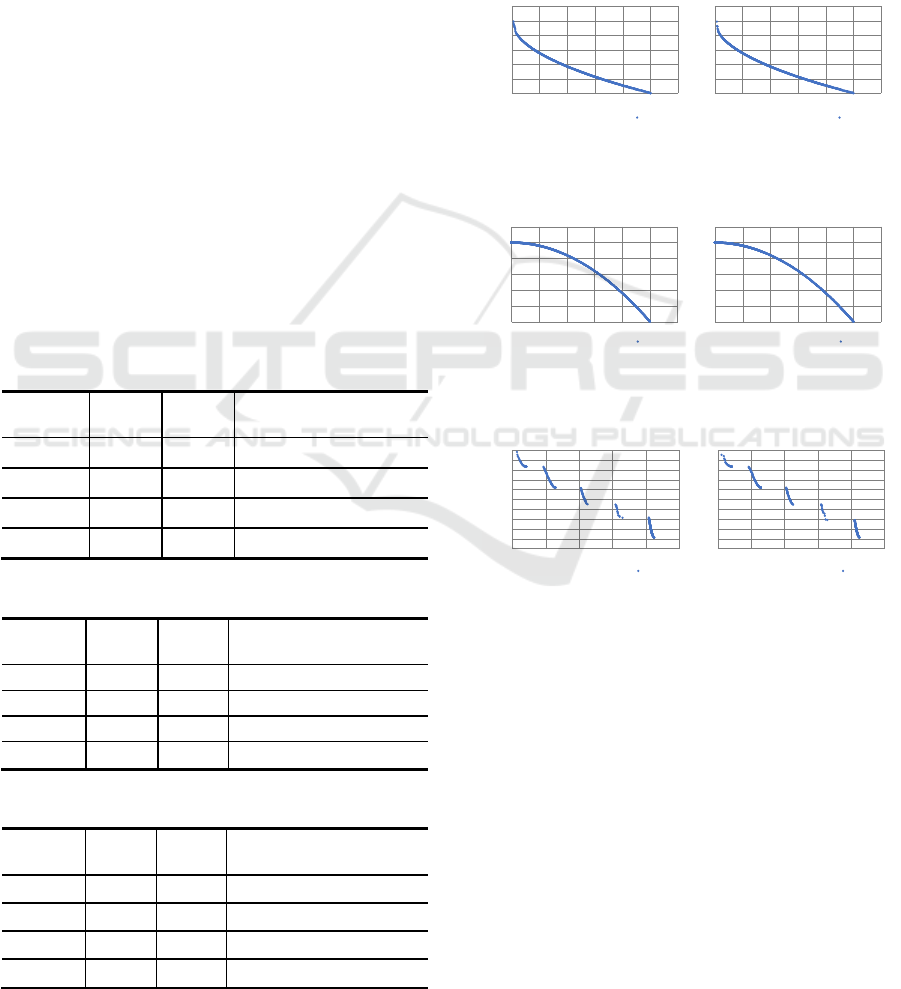
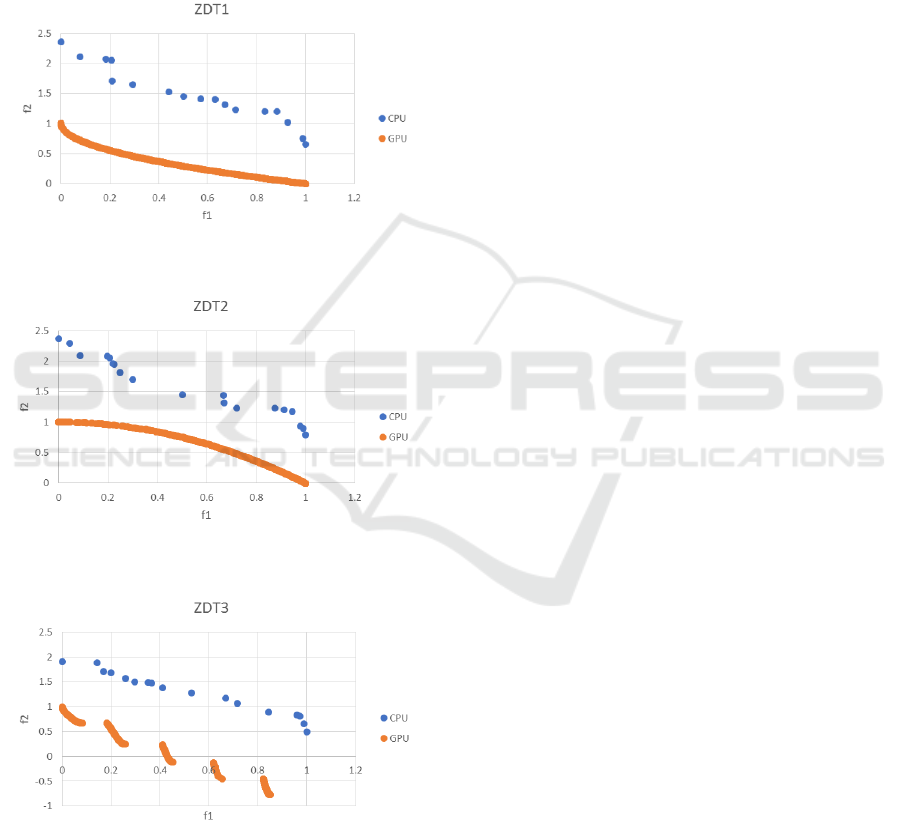
Figures 6 through 8 compare the Pareto fronts of
the solution distributions obtained when optimizing
each problem on a CPU and on a GPU. The accuracy
is almost the same for any function, but in the solution
distributions of problems ZDT1 and ZDT3, there are
slight differences in uniformity and solution
accuracy. This seems to be due to minute calculation
discrepancies between the CPU and the GPU that are
amplified when the search process is repeatedly
iterated.
Figure 6: Comparison of ZDT1 solutions on a distribution
chart.
Figure 7: Comparison of ZDT2 solutions on a distribution
chart.
Figure 8: Comparison of ZDT3 solutions on a distribution
chart.
5.4 Comparison with the Case Where
Time Limits Are Imposed
Figures 9 through 11 compare the distributions of
solutions obtained by the CPU and GPU
implementations when subject to time constraints.
Although the GPU implementation converges on the
Pareto front of the benchmark problems, the CPU
version found few Pareto solutions and yielded
similar solution distributions for any function. This is
because the CPU version can only process about 10
generations in the time it takes for the GPU version to
process 250 generations, so it was not possible to
perform sufficient searching to be able to ascertain
ZDT1
0
0.2
0.4
0.6
0.8
1
1.2
0 0.2 0.4 0.6 0.8 1 1.2
f2
f1
CPU
0
0.2
0.4
0.6
0.8
1
1.2
0 0.2 0.4 0.6 0.8 1 1.2
f2
f1
GPU
0
0.2
0.4
0.6
0.8
1
1.2
0 0.2 0.4 0.6 0.8 1 1.2
f2
f1
CPU
ZDT2
0
0.2
0.4
0.6
0.8
1
1.2
0 0.2 0.4 0.6 0.8 1 1.2
f2
f1
GPU
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0 0.2 0.4 0.6 0.8 1
f2
f1
GPU
ZDT3
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0 0.2 0.4 0.6 0.8 1
f2
f1
CPU
Distributed Multi-objective Particle Swarm Optimization using Time-delayed Virtual Global Best Method
27
the shape of the Pareto front. These results suggest
that parallelization by the proposed method is
effective even for real-time applications.
We experimented by assigning the same
execution parameter settings to different algorithms
this time. In the future, we think that the comparison
in the case of performing parameter adjustment for
each algorithm is also necessary. It is also necessary
to compare the execution time and the search
accuracy when the number of dimensions is changed.
Figure 9: Comparison of ZDT1 solutions on a distribution
chart.
Figure 10: Comparison of ZDT2 solutions on a distribution
chart.
Figure 11: Comparison of ZDT3 solutions on a distribution
chart.
6 CONCLUSION
In this study, we have shown that the proposed virtual
global method can reduce processing time by up to
90% and perform searches at least with the same level
of accuracy as the parallel processing methods of
previous studies.
We have also proposed a parallel MOPSO
algorithm that runs quickly while maintaining the
diversity of solutions by performing parallel
distributed processing based on a virtual global best
method for MOPSO/D where multiple particles
search a single partition function when performing
multi-objective optimization using virtual global best
solutions. We performed experiments to compare the
performance of the proposed method when
implemented on a CPU and on a GPU, and showed
that the proposed method can adapt to changes in the
Pareto front and can improve the processing speed by
a factor of at least 14 without loss of precision when
run in parallel.
ACKNOWLEDGEMENTS
The authors would like to thank Dr. Minami
Miyakawa from Sinshu University and Dr. Mikiko
Sato from Tokai University for their feedback. This
work was supported by JSPS KAKENHI Grant
Numbers JP19K12162.
REFERENCES
Bratton, D., and Kennedy, J., 2007. Defining a Standard for
Particle Swarm Optimization. In Proceedings of the
2007 IEEE Swarm Intelligence Symposium, pp. 120–
127.
Cao, B., Zhou, Y., and Lv, Y., Liu, X., Yang, S., and Kang,
X., Kang, K., 2017. Distributed Parallel Particle Swarm
Optimization for Multi-Objective and Many-Objective
Large-Scale Optimization. IEEE Access, vol.5, pp.
8214-8221.
Hussain, Md. M., Hattori, H., and Fujimoto, N., 2016. A
CUDA Implementation of the Standard Particle Swarm
Optimization. In Proceedings of the 18th International
Symposium on Symbolic and Numeric Algorithms for
Scientific Computing, pp. 219–226.
Hussain, Md. M., and Fujimoto, N., 2018. Parallel Multi-
Objective Particle Swarm Optimization for Large
Swarm and High Dimensional Problems, In
Proceedings of the 2018 IEEE Congress on
Evolutionary Computation (CEC-2018), pp. 1-10.
Kennedy, J., and Eberbart, R., 1995. Particle Swarm
Optimization. In Proceedings of IEEE International
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
28
Conference on Neural Networks. Perth, WA, Australia,
pp. 1942–1048.
Moore, J., and Chapman, R., 1999. Application of particle
swarm to multi-objective optimization, in an
unpublished manuscript, department of Computer
Science and Software Engineering, Auburn University.
Peng, W., and Zhan, Q., 2008. A Decomposition-based
Multi-Objective Particle Swarm Optimization
Algorithm for Continuous Optimization Problem, In
Proceedings of IEEE International Conference on
Granular Computing, pp. 534–537.
Souza, D. L., Martins, T. C., Dmitriev, V. A., and Monteiro,
G. D., 2011. PSO-GPU: Accelerating Particle Swarm
Optimization in CUDA Based Graphics Processing
Unit. In Proceedings of the 2011 ACM/SIGEVO
Genetic and Evolutionary Computation Conference
(GECCO’11), pp. 837-838.
Wikipedia: Test function for optimization., 2019,
https://en.wikipedia.org/wiki/Test_functions_for_opti
mization (cited 2019.07.06)
Zhang, Q., and Li, H., 2007. MOEA/D: A Multiobjective
Evolutionary Algorithm Based on Decomposition. In
IEEE Trans. Evolutionary Computation, Vol. 11, No. 6,
pp. 712–731.
Zhou, Y., and Tan, Y., 2009. GPU-based Parallel Particle
Swarm Optimization. In Proceedings of the 2009 IEEE
Congress on Evolutionary Computation, pp. 1493–
1500.
Zitzler, E., Deb, K., and Thiele, L., 2000. Comparison of
Multiobjective Evolutionary Algorithms: Empirical
Results. In IEEE Trans. Evolutionary Computation 8,
pp. 173–195.
APPENDIX
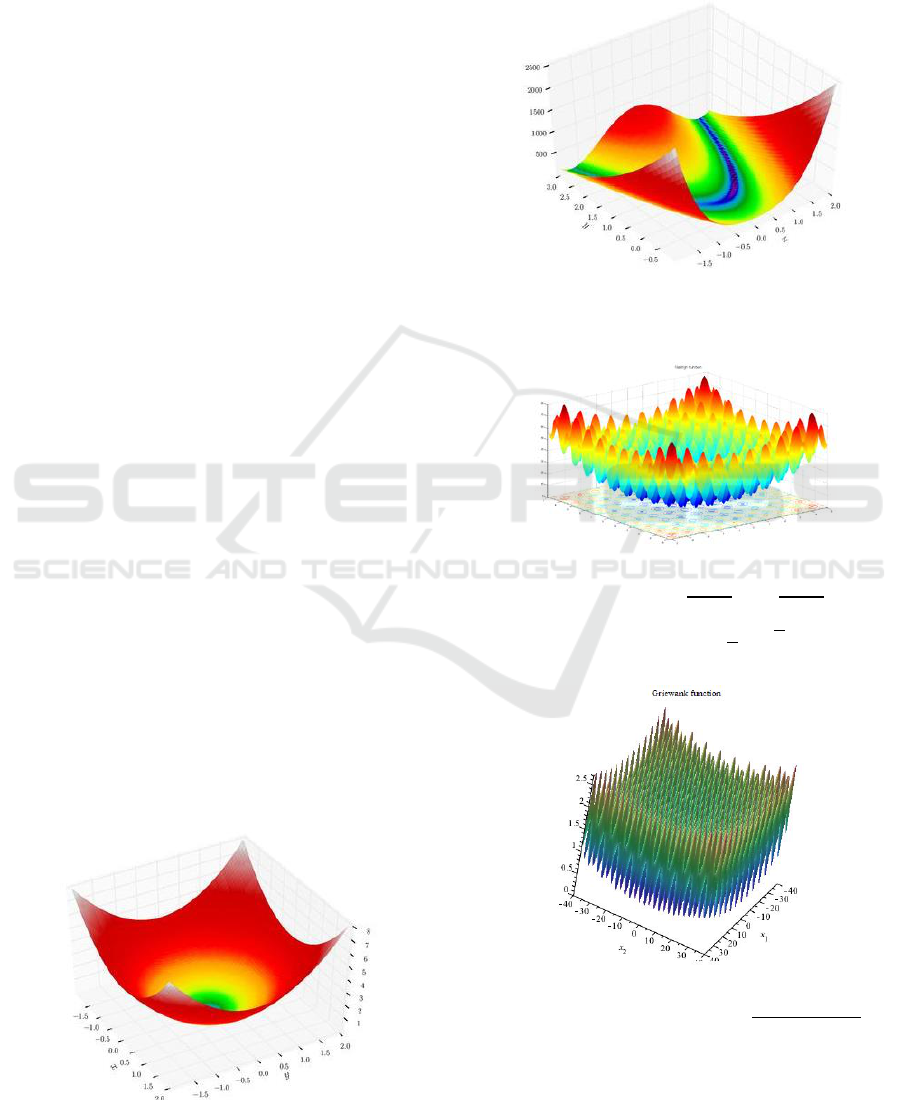
The five benchmark functions for single-objective
optimization (Wikipedia: Test functions for
optimization, 2019) for compare with previous
studies (Zhou, 2009; Hussain, 2016).
[Sphere function]
[Rosenbrock function]
[Rastrigin function]
,
[Griewank function]
[Ackley function]
Distributed Multi-objective Particle Swarm Optimization using Time-delayed Virtual Global Best Method
29

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
30
