Risk-sensitive Markov Decision Processes with Risk Constraints of

Coherent Risk Measures in Fuzzy and Stochastic Environment

Yuji Yoshida

Faculty of Economics and Business Administration, The University of Kitakyushu,

4-2-1 Kitagata, Kokuraminami, Kitakyushu 802-8577, Japan

Keywords:

Rrisk-sensitive Reward, Risk Constraint, Coherent Risk Measure, Weighted Average Value-at-Risk, Risk

Averse Utility, Fuzzy Random Variable, Perception-based Extension.

Abstract:

Risk-sensitive decision making with constraints of coherent risk measures is discussed in Markov decision

processes. Risk-sensitive expected rewards under utility functions are approximated by weighted average

value-at-risks, and risk constraints are described by coherent risk measures. In this paper, coherent risk mea-

sures are represented as weighted average value-at-risks with the best risk spectrum derived from decision

maker’s risk averse utility, and the risk spectrum can inherit the risk averse property of the decision maker’s

utility as weighting. By perception-based extension for fuzzy random variables, a dynamic portfolio model

with coherent risk measures is introduced. To ﬁnd feasible regions, ﬁrstly a dynamic risk-minimizing prob-

lem is discussed by mathematical programming. Next a risk-sensitive reward maximization problem under

the feasible coherent risk constraints is demonstrated. A few numerical examples are given to understand the

obtained results.

1 INTRODUCTION

Risk-sensitive decision making is one of most impor-

tant themes in management sciences and so on. Risk-

sensitive expected rewards and risk measures are rea-

sonable and effective tools in risk-sensitive decision

making. Risk-sensitive expectation, which was intro-

duced by (Howard and Matheson, 1972), is given by

−1

(E( f (·))), (1)

where f and f

−1

are decision maker’s utility func-

tion and its inverse function and E(·) is an expecta-

tion. Risk-sensitive expectation is a method to es-

timate random risks through utility functions, and it

is studied by several authors. (B

auerle and Rieder,

2014). However this criterion with non-linear utility

functions f has computational complexity in general.

For example, let {X

} is a sequence of random vari-

ables. Then

∑

E( f (X

)) implies a sum of decision

maker’s expected utility values and it is non-sense.

While f

−1

(E( f (X

))) belongs to a space of values

where random variables X

take, and their sum with

respect to t has meaning. Therefore in dynamic opti-

mization problems we need to compute a sum of val-

ues with criterion (1) with the inverse function f

−1

by Bellman equations. When f are non-linear utility

functions, it is difﬁcult to compute the optimal values

immediately (B

auerle and Rieder, 2014).

In decision making, several risk measures have

been proposed for economic theory, ﬁnancial analy-

sis, asset management and engineering. The variance

was classically used as a risk measure in decision

processes, and the risk measure has been improved

from both practical and theoretical aspects. Nowa-

days drastic declines of asset prices are studied, and

value-at-risk (VaR) is used widely to estimate the risk

of asset price decline in practical management (Jo-

rion, 2006). VaR is deﬁned by percentiles at a speci-

ﬁed probability, however it does not have coherency.

Coherent risk measures have been studied to improve

the criterion of risks with worst scenarios (Artzner et

al., 1999). Several improved risk measures based on

VaR are proposed: for example, conditional value-at-

risks, expected shortfall, entropic value-at-risk (Rock-

afellar and Uryasev, 2000), (Tasche, 2002). Recently

(Kusuoka, 2001) gave a spectral representation for co-

herent risk measures, and (Acerbi, 2002) and (Adam

et al., 2008) discussed its applications to portfolio se-

lection and so on. Further (Yoshida, 2018) has intro-

duced a spectral weighted average value-at-risk as the

best coherent risk measure derived from utility func-

tions. Using this derived coherent risk measure, the

risk measure can inherit the risk averse property of

the decision maker’s utility function as risk spectrum

Yoshida, Y.

Risk-sensitive Markov Decision Processes with Risk Constraints of Coherent Risk Measures in Fuzzy and Stochastic Environment.

DOI: 10.5220/0007957502690277

In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 269-277

ISBN: 978-989-758-384-1

269

weighting. This paper adopts the spectral weighted

average value-at-risks to estimate risk-sensitive re-

wards under constraints, which is also a kind of risk-

sensitive extended model of (Yoshida, 2017).

Fuzzy random variables, which were introduced

by (Kwakernaak, 1978), are applied to decision mak-

ing under uncertainty with fuzziness such as linguistic

data in engineering, economics et al.. To represent un-

certainty, we use fuzzy random variables which have

two kinds of uncertainties, i.e. randomness and fuzzi-

ness. In this paper, randomness is used to repre-

sent the uncertainty regarding the belief degree of fre-

quency, and fuzziness is applied to linguistic impre-

cision of data because of a lack of information about

the current stock market. In this paper, using fuzzy

random variables, we deal with optimization of port-

folio allocation in an environment with both random-

ness and fuzziness. We extend coherent risk measures

and a risk-sensitive estimation for real-valued random

variables to one regarding fuzzy random variables

from the viewpoint of perception-based method in

(Yoshida, 2007), and we apply the perception-based

criteria to estimate the uncertainties. (Yoshida, 2006)

introduced the mean, the variance and the covariances

of fuzzy random variables, using evaluation weights

and θ-mean functions. This paper estimates fuzzy

numbers and fuzzy random variables by probabilis-

tic expectation and these criteria, which are charac-

terized by possibility and necessity criteria for sub-

jective estimation and pessimistic-optimistic indexes

for subjective decision.

In Section 2, we introduce coherent risk mea-

sures and their spectral representation for coherent

risk measures based on (Kusuoka, 2001), and a co-

herent risk measure is given with the best risk spec-

trum derived from decision maker’s utility. In Section

3, we introduce coherent risk measures and a risk-

sensitive estimation for fuzzy random variables by

perception-based extension, and we give estimation

tools with evaluation weights and θ-mean functions

in order to evaluate the randomness and fuzziness for

fuzzy random variables. In Section 4, we discuss a

risk-sensitive decision problem under risk constraints

by use of coherent risk measures. Then risk-sensitive

rewards are approximated by weighted average value-

at-risks with the risk spectrum derived from the util-

ity, and the risk constraints are described by coherent

risk measures which are represented by weighted av-

erage value-at-risks. In Section 5 we investigate the

lower bound of risk values to ﬁnd feasible regions of

the constraints. In Section 6 we discuss maximiza-

tion of risk-sensitive rewards under risk conditions.

In Section 7, we give a few numerical examples to

understand the obtained results.

2 COHERENT RISK MEASURES

DERIVED FROM RISK AVERSE

UTILITY

Let R = (−∞,∞) and let P be a non-atomic probabil-

ity on a sample space Ω. Let X be the family of all

integrable real-valued random variables X on Ω with

a continuous distribution x 7→ F

(x) = P(X < x) for

which there exists a non-empty open interval I such

that F

(·) : I → (0,1) is strictly increasing and onto.

Then there exists a strictly increasing and continuous

inverse function F

−1

: (0,1) → I. For a probability

p ∈ (0,1), value-at-risk (VaR) is given by the per-

centile of the distribution F

, i.e.

VaR

(X) = F

−1

(p). (2)

Then average value-at-risk (AVaR) at a probability

p ∈ (0, 1] is given by

AVaR

(X) =

VaR

(X) dq. (3)

The following fundamental concepts are well-known

(Artzner et al., 1999, Kusuoka, 2001).

Deﬁnition 1. Let a map ρ : X 7→ R.

(i) Random variables X(∈ X ) and Y(∈ X ) are called

comonotonic if (X(ω)−X(ω

))(Y (ω) −Y (ω

)) ≥

0 holds for almost all ω,ω

∈ Ω.

(ii) ρ is called comonotonically additive if ρ(X +Y ) =

ρ(X) + ρ(Y ) holds for all comonotonic X,Y ∈X .

(iii) ρ is called law invariant if ρ(X) = ρ(Y ) holds for

all X,Y ∈X satisfying P(X < ·) = P(Y < ·).

(iv) ρ is called continuous if lim

n→∞

ρ(X

) = ρ(X)

holds for {X

} ⊂ X and X ∈ X such that

lim

n→∞

= X almost surely.

Hence the following deﬁnition characterizes co-

herent risk measures (Artzner at al., 1999).

Deﬁnition 2. A map ρ : X 7→ R is called a coherent

risk measure if it satisﬁes the following (i) – (iv):

(i) ρ(X) ≥ ρ(Y ) for X,Y ∈ X satisfying X ≤ Y .

(monotonicity)

(ii) ρ(cX) = cρ(X) for X ∈ X and c ∈ R satisfying

c ≥ 0. (positive homogeneity)

(iii) ρ(X +c) = ρ(X) −c for X ∈ X and c ∈R. (trans-

lation invariance)

(iv) ρ(X + Y ) ≤ ρ(X) + ρ(Y ) for X,Y ∈ X . (sub-

additivity)

It is known in (Artzner et al., 1999) that

−AVaR

(·) is a coherent risk measure however

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

270

−VaR

(·) is not coherent because sub-additivity (iv)

does not hold, where − means the minus singature.

Conditional value-at-risks and expected shortfall are

also famous coherent risk measures (Rockafellar and

Uryasev, 2000, Tasche, 2002). Now, for a probability

p ∈(0,1] and a non-increasing right-continuous func-

tion λ on [0, 1] satisfying

λ(q)dq = 1, we deﬁne a

weighted average value-at-risk with weighting λ on

(0, p) by

AVaR

(X) =

VaR

(X) λ(q) dq



λ(q)dq.

(4)

Then λ is called a risk spectrum, and −AVaR

be-

comes a coherent risk measure. Further recently

(Kusuoka, 2001) proved coherent risk measures are

represented by weighted average value-at-risks in the

following spectral representation (Yoshida, 2018).

Lemma 1. Let ρ : X 7→R be a law invariant, comono-

tonically additive, continuous coherent risk measure.

Then there exists a risk spectrum λ such that

ρ(X) = −AVaR

(X) (5)

for X ∈ X . Further, −AVaR

is a coherent risk mea-

sure on X for p ∈(0,1).

In this paper we use a law invariant, comonoton-

ically additive, continuous coherent risk measure ρ,

and we also deal with a case when value-at-risks are

represented as

VaR

(X) = E(X ) + κ(p) ·σ(X ) (6)

with the mean E(X) and the standard deviation σ(X )

of random variables X ∈X , where κ : (0,1) 7→R is an

increasing function. From (4) and (6) we have

AVaR

(X) = E(X) + κ

(p) ·σ(X), (7)

where

(p) =

κ(q)λ(q)dq



λ(q)dq. (8)

Let f : I 7→ R be a C

-class risk averse utility function

satisfying f

> 0 and f

≤ 0 on I, where I is an open

interval. For a probability p ∈ (0,1] and a random

variable X ∈ X , a non-linear risk-sensitive form

−1



f (VaR

(X)) dq



(9)

is an average value-at-risk of X on the downside (0, p)

under utility f . We note that (9) is reduced to (3) if

f is risk-neutral, i.e. it is a linear increasing function.

Hence we have the following lemma from (Yoshida,

2018).

Lemma 2. A risk spectrum λ which minimizes the

distance between (9) and (4):

∑

X∈X



−1



f (VaR

(X)) dq



−AVaR

(X)



(10)

for p ∈ (0, 1] is given by

λ(p) = e

−

C(q) dq

C(p) (11)

with a component function C in (Yoshida, 2018) if λ

is non-increasing.

For exponential utility function f , the correspond-

ing component function C is given concretely in Ex-

ample 2. The component functions C for several

utilities f are also investigated in (Yoshida, 2018).

In Lemma 2 the coherent risk measure −AVaR

has

a kind of semi-linear property such as Deﬁnition

2(ii)(iii) and it brings us effective computation, and

the risk spectrum λ can also inherit the risk averse

property of the non-linear utility function f as weight-

ing on (0, p). Regarding risk-sensitive rewards (1),

in the sequel we use the risk spectrum λ in Lemma

2 because −AVaR

is the best coherent risk measure

derived from risk averse utility f .

3 FUZZINESS AND EXTENDED

CRITERIA

A fuzzy number is represented by its membership

function ˜n : R → [0,1] which is normal, upper-

semicontinuous, fuzzy convex and has a compact sup-

port (Zadeh, 1965). Let N be the set of all fuzzy num-

bers. For a fuzzy number ˜n ∈N , its α-cuts are given

by closed intervals ˜n

= {x ∈R | ˜n(x) ≥α}= [˜n

−

, ˜n

]

for α ∈ (0,1]. An addition and a scalar multiplica-

tion for fuzzy numbers are deﬁned by their α-cuts.

For fuzzy numbers ˜n, ˜m ∈ N , fuzzy max order ˜n  ˜m

means that ˜n

≥ ˜m

for all α ∈ (0,1]. A fuzzy-

number-valued map

X : Ω → N is called a fuzzy ran-

dom variable if

∈ X for all α ∈ (0,1], where

(ω) = {x ∈ R |

X(ω)(x) ≥ α} = [

−

(ω),

(ω)]

for ω ∈ Ω. Let

X be the family of all fuzzy random

variables on Ω. (Kruse and Meyer, 1987) gave the ex-

pectation of fuzzy random variables

X ∈

X in the fol-

lowing perception-based deﬁnition based on Zadeh’s

extension principle:

X)(x) = sup

X∈X :E(X )=x

inf

ω∈Ω

X(ω)(X (ω)) (12)

for x ∈ R, where E(·) is the expectation for real-

valued random variables. Then, the expectation

Risk-sensitive Markov Decision Processes with Risk Constraints of Coherent Risk Measures in Fuzzy and Stochastic Environment

271

X) is a fuzzy number with α-cut

[E(

−

),E(

)]. Deﬁne criterion (1) by

ϕ(X) = f

−1

(E( f (X))) (13)

for X ∈ X . For a weighted average value-at-risk

AVaR

, the criterion ϕ and a coherent risk measure

ρ, their extensions for a fuzzy random variable

X ∈

are also fuzzy numbers:

AVaR

(

X)(x) = sup

X∈X :AVaR

(X)=x

inf

ω∈Ω

X(ω)(X (ω)),

(14)

ϕ(

X)(x) = sup

X∈X :ϕ(X)=x

inf

ω∈Ω

X(ω)(X (ω)), (15)

ρ(

X)(x) = sup

X∈X :ρ(X)=x

inf

ω∈Ω

X(ω)(X (ω)) (16)

for x ∈ R. Then their α-cuts are given respec-

tively by

ϕ(

= [ϕ(

−

),ϕ(

)] and

ρ(

[ρ(

),ρ(

−

)], and the extended measure

ρ(·) has

the following properties similarly to Deﬁnition 2

(Yoshida, 2008).

Lemma 3.

ρ(·) is monotonically decreasing, pos-

itively homogeneous, translation invariant and sub-

additive.

In the latter sections we use a coherent risk mea-

sure ρ in Lemma 1 and its extension

ρ in (16) to esti-

mate risks in a ﬁnancial model. We also need defuzzi-

ﬁcation methods. A defuzziﬁcation of a fuzzy number

˜n ∈N with a θ-mean and an evaluation weight w(α)

is given by

( ˜n) =

(θ · ˜n

−

+ (1 −θ) · ˜n

)w(α)dα

w(α)dα

, (17)

where ˜n

= [ ˜n

−

, ˜n

]. Here θ is called decision

maker’s pessimistic index if θ = 1, and it is also called

the optimistic index if θ = 0. w(α) is called the pos-

sibility evaluation if w(α) = 1 for α ∈ [0, 1], and it is

also called the necessity evaluation if w(α) = 1 −α

for α ∈ [0,1] (Yoshida, 2006, 2008). Then E

(·) has

the following properties.

Lemma 4. For θ ∈[0, 1], E

(·) is positively homoge-

neous, additive and monotonically increasing.

The randomness of fuzzy random variables is

evaluated by probabilistic expectation, and its fuzzi-

ness is estimated by the θ-mean and the weight w(α)

as follows: For a fuzzy random variable

X ∈

X , the

mean of the expectation E(E

(

X)) is a real number

E(E

(

X)) = E







(θ ·

−

+ (1 −θ) ·

)w(α)dα

w(α)dα







(18)

From Lemma 4, we obtain the following results

(Yoshida, 2006, 2007).

Lemma 5. For θ ∈[0, 1], E(E

(·)) is positively homo-

geneous, additive and monotonically increasing, and

it has the following properties (i) and (ii):

(i) E(E

(·)) = E

(

E(·)).

(ii) E(E

( ˜n)) = E

( ˜n) and E(E

(X)) = E(X) for ˜n ∈

N and X ∈ X .

Let

be a family of fuzzy random variables

X ∈

X for which there exist a random variable X ∈ X and

a fuzzy number ˜n ∈N such that

X(ω)(x) = 1

{X(ω)}

(x) + ˜n(x) (19)

for ω ∈ Ω and x ∈ R, where 1

{·}

denotes the charac-

teristic function of a singleton. Then we can easily

check the following proposition for the weighted av-

erage value-at-risks AVaR

, coherent risk measures ρ

and their extensions

AVaR

and

ρ (Yoshida, 2008).

Proposition 1. For θ ∈ [0, 1], it holds that

(

AVaR

(

X)) = AVaR

(

X)), (20)

1−θ

(

ρ(

X)) = ρ(E

(

X)) (21)

for fuzzy random variables

X ∈

4 RISK ALLOCATION WITH

COHERENT RISK MEASURES

Let a state space by S = R and an action space by

A = {(x

,···,x

) ∈R

∑

i=1

= 1 and x

≥0 (i =

1,2,···,n)}, where n is a positive integer. In this

paper we focus on risk-sensitive expected rewards

to choose alternatives consisting of n assets. Let a

positive integer T be a terminal time, and let time

t = 1, 2, ··· ,T . Let

(∈

X ) be a fuzzy reward for as-

set i (= 1,2, ··· ,n). Hence we put their expectations

and covariances respectively by µ

= E

(

)) =

E(E

(

)) and σ

i j

= E((E

(

) −µ

)(E

(

) −µ

))

for i, j = 1, 2, ··· ,n. We give Markov policies by

π = {π

}

t=1

where mappings π

= (π

,π

,···,π

) :

Ω 7→A for t = 1, 2,··· ,T , and then π

is called a strat-

egy. They are chosen depending only on the current

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

272

state X

t−1

. Put a collection of all Markov policies by

Π. A reward with a strategy π

= (π

,π

,···,π

) is

given by

∑

i=1

. (22)

Let a probability p ∈ (0,1) and let a positive con-

stant δ. Let f be a C

-class risk averse utility function

which is given in Section 2. While let ρ be a coherent

risk measure for risk constraints. Let β be a positive

constant. Hence we focus on the following optimiza-

tion problem with (13), (15) and (16).

Problem (P1). Maximize the risk-sensitive estima-

tion

∑

t=1

t−1

−1

(E( f (E

(

)))) (23)

with respect to strategies π

∈ Π under risk constraint

1−θ

(

ρ(

)) ≤ δ (24)

for time t = 1, 2, ··· ,T .

From the results of Lemma 2, f

−1

(E( f (·))) =

−1

(

VaR

( f (·))dq) is approximated by AVaR

(·)

with a risk spectrum λ. While by Lemma 1 there ex-

ists a risk spectrum ν such that ρ = −AVaR

. Hence

we estimate the downside risks on (0, p). By Proposi-

tion 1 this paper discusses the following optimization

instead of Problem (P1).

Problem (P2). Maximize the risk-sensitive estima-

tion

∑

t=1

t−1

AVaR

(

)) (25)

with respect to strategies π

∈ Π under risk constraint

−AVaR

(

)) ≤ δ (26)

for time t = 1,2,··· , T .

In (25) and (26), risk spectra λ and ν are different

in general, however we can select same risk spectrum,

i.e. λ = ν. Hence from (22) the expectation and the

standard deviation of reward

are

E(E

(

)) =

∑

i=1

(27)

and

σ(E

(

)) =

∑

i=1

∑

j=1

i j

. (28)

Together with (7), we also have weighted average

value-at-risk

AVaR

(

)) =

∑

i=1

+ κ

(p)

∑

i=1

∑

j=1

i j

(29)

where

(p) =

κ(q)ν(q)dq



ν(q)dq. (30)

In this paper we assume κ

(1) ≤ 0 and κ

(p) < 0.

Let Π

(δ) be the collection of strategies π

satisfy-

ing risk constraint (26), and let Π

= sup

δ>0

(δ). In

the rest of this section we investigate the lower bound

of −AVaR

(

)) for the feasibility of constraint

(26) in Problem (P2), i.e. Π

(δ) 6=

0. From (29),

we ﬁrstly discuss the following maximization prob-

lem for AVaR

(

)).

Problem (P3). Maximize weighted average value-at-

risk

AVaR

(

)) =

∑

i=1

+ κ

(p)

∑

i=1

∑

j=1

i j

(31)

with respect to strategies π

= (π

,π

,···,π

Let γ ∈ R. From (27), under a constraint

E(E

(

)) =

∑

i=1

= γ, (32)

Problem (P3) is solved by quadratic programming and

then the corresponding value (31) is

γ + κ

(p)

−2B

γ +C

∆

, (33)

where

µ=













,Σ=







··· σ



















= 1

−1

1,B

= 1

−1

= µ

−1

,∆

= A

−

and T denotes the transpose of a vector. If A

0, ∆

> 0 and κ

(p) < −

∆

are satisﬁed, we

can easily check the real-valued function (19) of γ

is concave and it has the maximum

−

√

(p)

−∆

at γ =

∆

√

(p)

−∆

. Since sup

∈Π

(31) =

sup

{sup

∈Π:

∑

i=1

=γ

(31)}, we obtain the follow-

ing analytical solutions for Problem (P3).

Theorem 1. Let A

> 0, ∆

> 0 and κ

(p) <

−

∆

. Then the following (i) and (ii) hold.

(i) The maximum weighted average value-at-risk of

Problem (P3) is

−

(p)

−∆

(34)

Risk-sensitive Markov Decision Processes with Risk Constraints of Coherent Risk Measures in Fuzzy and Stochastic Environment

273

at the expected reward

γ =

∆

(p)

−∆

. (35)

The corresponding strategy is given by

◦

= ξ

◦

−1

1 + η

◦

−1

(36)

if π

◦

≥ 0

0, where ξ

◦

−B

∆

and η

◦

γ−B

∆

(ii) If Σ

−1

1 ≥0

0, Σ

−1

≥ 0

0 and κ

(p) ≥C

, then the

strategy (36) satisﬁes π

◦

≥ 0

5 RISK-SENSITIVE REWARD

MAXIMIZATION UNDER

FEASIBLE RISK

CONSTRAINTS

Let p ∈(0,1) be a probability and let ν be a risk spec-

trum which are given in Section 4. From Theorem 1,

we deﬁne the lower bound of −AVaR

(

)) by a

constant δ

(p):

(p) = inf

∈Π

(−AVaR

(

)))

= − sup

∈Π

AVaR

(

))

= −

(p)

−∆

. (37)

Thus the feasible range of δ in risk constraint (26) is

{δ |Π

(δ) 6=

0}= [δ

(p),∞). Now we take a risk level

δ ∈ [δ

(p),∞), and then we have sup

∈Π

(δ)

(31) =

sup

{sup

∈Π

(δ):

∑

i=1

=γ

(31)}. Thus, from the view

point of (33), Problem (P2) is reduced to the following

problem with constraint (32), i.e.

∑

i=1

= γ.

Problem (P4). Maximize the risk-sensitive estima-

tion

+ κ

(1)

−2B

∆

(38)

with respect to γ ∈ R under risk constraint

+ κ

(p)

−2B

∆

≥ −δ. (39)

Hence (39) is equivalent to γ

∈ [γ

−

,γ

], where

(p)

+ ∆

(p)

−∆

∓

√

∆

(p)

+ 2B

δ +C

−κ

(p)

−∆

. (40)

By solving concave maximization (38) within con-

straint [γ

−

,γ

] in Problem (P4), we easily obtain the

following results for Problem (P2).

Theorem 2. Let A

> 0, ∆

> 0, κ

(p) ≤ κ

(1) ≤

0 and κ

(p) < −

∆

. Then the maximum risk-

sensitive estimation in Problem (P2) is

∗











−

(1)

−∆

at γ

∗

∆

(1)

−∆

if δ

≤ δ and κ

(1) < −

∆

−

(1)

(p)

(δ + γ

)

at γ

∗

= γ

otherwise,

(41)

where δ

= −

(1)κ

(p) −∆

(1)

−∆

6 DYNAMIC MAXIMUM

RISK-SENSITIVE REWARD

UNDER FEASIBLE RISK

CONSTRAINTS

Let the initial state be a real number X

= x

. Then

E(X

) = γ

= x

and σ(X

)

= 0. For a Markov pol-

icy π = {π

}

t=1

∈Π, the expectation and the standard

deviation of terminal rewards X

= x

∑

t=1

are

Problem (P5). Maximize the total risk-sensitive ex-

pected immediate reward

∑

t=1

t−1





+ κ

(1)

−2B

∆





(42)

with respect to (γ

,γ

,···γ

) ∈ R

under risk con-

straint

∈ [γ

−

,γ

] (43)

for all t = 1,2,··· , T .

Lemma 6. Let {v

} be a sequence given by the fol-

lowing optimality equations

= sup

∈[γ

−

,γ

]







+ κ

(1)

−2B

∆







+βv

t+1

(44)

for t = 1,2,··· , T and v

T +1

= 0. Then v

is the max-

imum total risk-sensitive expected immediate reward

for Problem (P5).

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

274

From Theorem 2, we have the following results.

Theorem 3. Let A

> 0, ∆

> 0, κ

(p) ≤ κ

(1) ≤ 0

and κ

(p) < −

∆

for t = 1,2,··· , T .

(i) Let {v

} be a sequence given by the following op-

timality equations

= ϕ

∗

+ β v

t+1

(45)

for t = 1,2,··· , T and v

T +1

= 0. Then v

is the

maximum of the total risk-sensitive expected re-

wards in Problem (P5).

(ii) Further the optimal portfolios of (44) in Lemma

6 are given by

∗

= ξ

∗

−1

1 + η

∗

−1

(46)

for t = 1, 2, ··· ,T , where γ

∗

is given by (41), ξ

∗

−B

∗

∆

and η

∗

−B

∆

(iii) Further, one of sufﬁcient condition for w

∗

≥ 0

is the followings: κ

(1)

≥C

, C

(p)

≥ (C

δ)

, A

(p)

≥ (A

δ + B

)

, Σ

−1

1 ≥ 0

0 and

−1

≥ 0

0 for t = 1,2,...,T .

7 NUMERICAL EXAMPLES

We give a few examples to understand the results in

the previous sections.

Example 1. Let a domain I = R and let f be a risk

neutral utility function f (x) = ax + b for x ∈ R with

constants a(> 0) and b(∈ R). Then its risk spectrum

in Lemma 2 is given by λ(p) = 1. The corresponding

weighted average value-at-risk (4) is reduced to the

average value-at-risk (3), and we have

−1

(E( f (X))) = E(X) = AVaR

(X) (47)

for X ∈ X (Yoshida, 2018).

Example 2. Let a domain I = R and let a risk averse

exponential utility function

f (x) =

1 −e

−τx

(48)

for x ∈R with a positive constant τ. Then −

= τ is

the degree of decision maker’s absolute risk aversity

(Arrow, 1971). Fig.1 illustrates utility functions f (x).

Let X be a family of random variables X which have

normal distribution functions. Deﬁne the cumulative

distribution function G : R → (0,1) of the standard

normal distribution by

G(x) =

√

2π

−∞

−

dz (49)

for x ∈ R, and deﬁne an increasing function κ :

(0,1) 7→ R by its inverse function κ(p) = G

−1

(p) for

probabilities p ∈ (0,1). Then we have value-at-risk

VaR

(X) = µ + κ(p) ·σ for X ∈ X with mean µ and

standard deviation σ. Suppose there exists a distri-

bution ψ : R × (0, ∞) 7→ [0,∞) such that ψ(µ,σ) =

φ(µ) ·

1−n/2

Γ(n/2)

n−1

−

for (µ,σ) ∈ R ×[0,∞), where

φ(µ) is some probability distribution, Γ(·) is a gamma

function and

1−n/2

Γ(n/2)

n−1

−

is a chi distribution with

degree of freedom n. We take a utility f (x) =

1−e

−0.05x

0.05

with τ = 0.05 in (48), and by Lemma 2 there exists a

risk spectrum λ satisfying f

−1

(E( f (·))) ≈ AVaR

(·).

Then, by (Yoshida, 2018), the best risk spectrum in

Lemma 2 is given by

λ(p) = e

−

C(q) dq

C(p) (50)

for p ∈ (0, 1] with the component function

C(p)=

∞

1 −

τσ(κ(p)−κ(q))

−

dσ

∞

log



τσ(κ(p)−κ(q))



−

dσ

(51)

with τ = 0.05. From (49) and (50), we have κ

(1) =

κ(q)λ(q)dq

λ(q)dq = −0.03. On the other

hand for risk measures ρ we use another utility g(x) =

1−e

−x

with τ = 1 in (48). Then by Lemma 1 there ex-

ists a risk spectrum ν such that ρ(·) = −AVaR

(·). We

discuss a case of risk probability 5%, i.e. p = 0.05, in

the normal distribution, and then similarly we can cal-

culate κ

(0.05) =

0.05

κ(q)ν(q)dq

0.05

ν(q)dq =

−2.29701. We give fuzzy rewards by fuzzy random

variables

∈

(i = 1, 2, . ..,n) as follows:

(ω)(·) = 1

(ω)}

(·) + ˜a

(·) (52)

for ω ∈ Ω, where X

(∈ X ) and ˜a

is a fuzzy num-

ber ˜a

(x) = max{1 − |x|/c

,0} for x ∈ R with a

positive number c

, which is a fuzzy factor. Let

n = 4 be the number of assets. Hence we put

the expectations µ

of rewards X

and fuzzy fac-

tors c

by Table 1, and we let the covariances σ

i j

of rewards X

by Table 2. We deal with an opti-

mistic and possibility case, i.e. θ = 0 and w(α) =

1 for α ∈ [0,1]. Hence we have A

= 15.1405 >

0 and ∆

= 0.003449 > 0. And we can easily

check κ

(0.05) < κ

(1) < −

∆

= −0.0150931.

From (37) we also have δ

(p) = 0.495737. There-

fore now we take a risk level δ = 0.55 in the fea-

sible range [0.495737,∞). From Theorem 2, we

obtain the maximum risk-sensitive estimation ϕ

∗

Risk-sensitive Markov Decision Processes with Risk Constraints of Coherent Risk Measures in Fuzzy and Stochastic Environment

275

Table 1: Expectations µ

and fuzzy factors c

i = 1 0.098 0.008

i = 2 0.084 0.008

i = 3 0.091 0.007

i = 4 0.088 0.006

Table 2: Variance-covariances σ

i j

j = 1 j = 2 j = 3 j = 4

i = 1 0.38 −0.09 −0.07 0.05

i = 2 −0.09 0.39 −0.08 0.06

i = 3 −0.07 −0.08 0.38 −0.06

i = 4 0.05 0.06 −0.06 0.37

0.0879143 at the expected reward γ

∗

= 0.0968356

for Problem (P2) with an optimal strategy π

∗

(0.453443,0.159892,0.313565,0.0731002). Hence

the difference between the real expected reward γ

∗

0.0968356 and the decision maker’s maximum risk-

sensitive estimation ϕ

∗

= 0.0879143 comes from de-

cision maker’s risk averse feeling.

1 2 3 4 5

1.0

0.5

1.0

Example 1

Example 2

Example 1

Example 2

$!!%

Figure 1: Utility functions f (x).

We can also use a pessimistic and necessity case,

i.e. θ = 1 and w(α) = 1 −α for α ∈ [0,1]. From

Tables 1 and 2, we ﬁnd the maximum risk-sensitive

estimation is in 0.0785810 ≤ϕ

∗

≤0.0874494, and the

expected reward is in 0.0875022 ≤γ

∗

≤ 0.0968356.

Fig.2 illustrates the maximum risk-sensitive es-

timation ϕ

∗

for δ in Theorem 2, and we see the

two lines are cut and connected at δ

. Fig.3 illus-

trates the maximum risk-sensitive estimation ϕ

∗

and

the expected reward γ

∗

for δ. We see ϕ

∗

is smaller

than γ

∗

because γ

∗

implies actual expected rewards

and ϕ

∗

contains decision maker’s risk aversity un-

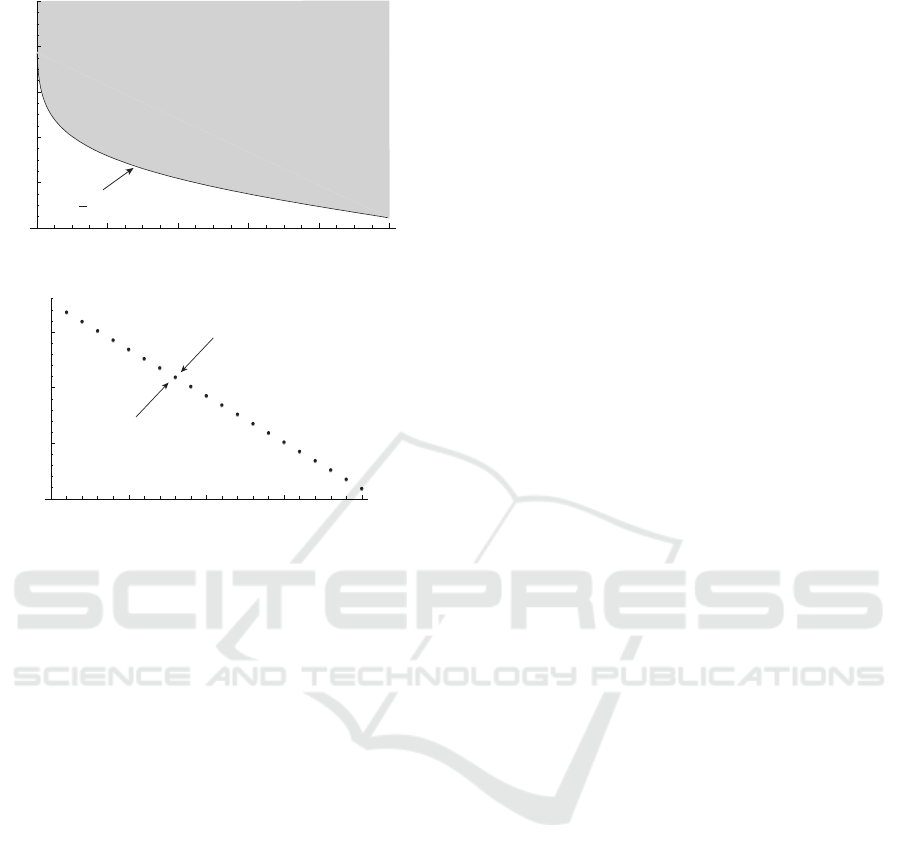
der his utility. Fig.4 also shows the feasible range

{(p,δ) |Π

(δ) 6=

0}= {(p, δ) |δ

(p) ≤δ} in Example

2 (τ = 1).

We discuss a dynamic case with an expiration date

T = 20 and a discount rate β = 0.95. Then by The-

Table 3: Risk-sensitive estimation ϕ

∗

and expected reward

∗

Pess. & Nec. Opti. & Poss.

∗

0.0875022 0.0968356

∗

0.0785810 0.0879143

( )

Max risk-sensitive expectation

0.55 0.60 0.65 0.70

0.086

0.087

0.088

0.089

0.090

Figure 2: The max. risk-sensitive estimation ϕ

∗

Max risk-sensitive expectation

Expected reward

( )

0.55

0.60

0.65

0.70

0.085

0.090

0.095

0.100

Figure 3: The max. risk-sensitive estimation ϕ

∗

and the ex-

pected reward γ

∗

orem 3 we obtain the optimal total weighted average

value-at-risk v

= 1.67037 for Problem (P4) and we

can observe the sequence {v

} of sub-total weighted

average value-at-risks after time t in Theorem 3.

Concluding Remarks. Using Lemma 2, we can in-

corporate the decision maker’s risk averse attitude

into coherent risk measures as weighting for average

value-at-risks. As we have seen in Examples 1 and 2,

risk-sensitive estimations with utility f are approxi-

mated by weighted average risks with a spectrum λ in

(50) and (51), and the coherent risk measures ρ with

fuzzy factors is given by weighted average risks with

a spectrum ν. The proposed method brings us reason-

able and computable risk-sensitive optimization mod-

els under risk constraints, and it is useful for other

subjective optimization in management sciences. We

can reply immediately risk values ρ = −AVaR

from

(7) when we prepare constants (8), and this approach

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

276

0.0 0.2 0.4 0.6 0.8 1.0

0.2

0.4

0.6

0.8

1.0

0.0

( )

Feasible range of Example 2

( )

= 1

Figure 4: Feasible region for risk levels δ.

Example 1

Example 2



0.5

1.0

1.5

Figure 5: Sequences {v

} for Example 1 and Example 2

(τ = 1) (p = 0.05).

will be applicable to timely and quick risk-sensitive

decision making together with AI computing, for ex-

ample, stock trading, auto driving and so on (Yoshida,

to appear).

ACKNOWLEDGEMENTS

This research is supported from JSPS KAKENHI

Grant Number JP 16K05282.

REFERENCES

Acerbi, C., Spectral measures of risk: A coherent represen-

tation of subjective risk aversion, Journal of Banking

& Finance, vol.26, pp.1505-1518, 2002.

Adam, A., Houkari, M., Laurent, J.-P., Spectral risk mea-

sures and portfolio selection, Journal of Banking &

Finance, vol.32, pp.1870-1882, 2008.

Arrow, K.J., Essays in the Theory of Risk-Bearing,

Markham, Chicago, 1971.

Artzner, P., Delbaen, F., Eber, J.-M., Heath, D., Coher-

ent measures of risk, Mathematical Finance, vol.9,

pp.203-228, 1999.

auerle, N., Rieder, U., More risk-sensitive Markov deci-

sion processes, Math. Oper. Res., vol.39, pp.105-120,

2014.

Howard, R., Matheson, J., Risk-sensitive Markov decision

processes, Management Science, vol.18, pp.356-369,

1972.

Jorion, P., Value at Risk: The New Benchmark for Managing

Financial Risk, McGraw-Hill, New York, 2006.

Kruse, R., Meyer, K.D., Statistics with Vague Data, Riedel

Publ. Co., Dortrecht, 1987.

Kusuoka, S., On law-invariant coherent risk measures, Ad-

vances in Mathematical Economics, vol.3, pp.83-95,

2001.

Kwakernaak, H., Fuzzy random variables – I. Deﬁnitions

and theorem, Inform. Sci., vol.15, pp.1-29, 1978.

Rockafellar, R.T., Uryasev, S., Optimization of conditional

value-at-risk, J. of Risk, vol.2, pp.21-41, 2000.

Rockafellar, R.T., Uryasev, S., Conditional value-at-risk for

general loss distribution functions, J. of Banking and

Finance, vol.26, pp.1443-1471, 2002.

Tasche, D., Expected shortfall and beyond, J. of Banking

and Finance, vol.26, pp.1519-1533, 2002.

Yoshida, Y., Mean values, measurement of fuzziness and

variance of fuzzy random variables for fuzzy opti-

mization, Proceedings of SCIS & ISIS 2006, pp.2277-

2282, Sept. 2006.

Yoshida, Y., Fuzzy extension of estimations with random-

ness: The perception-based approach, in: P.Melin

et al. eds., IFSA2007, LNAI 4617, pp.381-391,

Springer, Sept. 2007.

Yoshida, Y., Perception-based estimations of fuzzy random

variables: Linearity and convexity, International Jour-

nal of Uncertainty, Fuzziness and Knowledge-Based

Systems, vol.16, suppl., pp.71-87, 2008.

Yoshida, Y., Maximization of returns under an average

value-at-risk constraint in fuzzy asset management,

Procedia Computer Science, Vol.112, pp.11-20, 2017.

Yoshida, Y., Coherent risk measures derived from utility

functions, in: V.Torra and Y.Narukawa eds., Model-

ing Decisions for Artiﬁcial Intelligence - MDAI 2018,

LNAI 11144, Springer, pp.15-26, 2018.

Yoshida, Y., Portfolio optimization in fuzzy asset manage-

ment with coherent risk measures derived from risk

averse utility, Neural Computing and Applications, to

appear, https://doi.org/10.1007/s00521-018-3683-y.

Zadeh, L.A., Fuzzy sets, Inform. and Control, vol.8,

pp.338-353, 1965.

Risk-sensitive Markov Decision Processes with Risk Constraints of Coherent Risk Measures in Fuzzy and Stochastic Environment

277