
Applying Feature Selection to Rule Evolution for Dynamic Flexible Job
Shop Scheduling
Yahia Zakaria, Ahmed BahaaElDin and Mayada Hadhoud
Computer Engineering Department, Faculty of Engineering, Cairo University, Giza, Egypt
Keywords:
Feature Selection, Flexible Job Shop Scheduling, Dynamic Scheduling, Genetic Programming.
Abstract:
Dynamic flexible job shop scheduling is an optimization problem concerned with job assignment in dynamic
production environments where future job arrivals are unknown. Job scheduling systems employ a pair of
rules: a routing rule which assigns a machine to process an operation and a sequencing rule which determines
the order of operation processing. Since hand-crafted rules can be time and effort-consuming, many papers
employ genetic programming to generate optimum rule trees from a set of terminals and operators. Since the
terminal set can be large, the search space can be huge and inefficient to explore. Feature selection techniques
can reduce the terminal set size without discarding important information and they have shown to be effective
for improving rule generation for dynamic job shop scheduling. In this paper, we extend a niching-based
feature selection technique to fit the requirements of dynamic flexible job shop scheduling. The results show
that our method can generate rules that achieves significantly better performance compared to ones generated
from the full feature set.
1 INTRODUCTION
Job Shop Scheduling (JSS) (Brucker and Schlie,
1990) is a popular optimization problem with many
practical applications in multiple fields such as cloud
computing and manufacturing. JSS aims to assign job
operations to machines where each job contains a se-
quence of operations that can only be processed in
a certain order and each operation can only be pro-
cessed on a certain machine. Since static job shop as-
sumes that all jobs are known before the scheduling
starts, it is inapplicable to many realistic use-cases
where job arrival times are unknown. Dynamic Job
Shop Scheduling (DJSS) is an extension of JSS where
jobs can arrive at any point in time and the sched-
uler has no information about future jobs. JSS also
assumes that each operation is processable on only
one machine. This assumption is not always true es-
pecially in large production environments. Flexible
Job Shop Scheduling (FJSS) relaxes the aforemen-
tioned assumption by allowing each operation to be
processed on any member from a subset of the ma-
chines. In this paper, we are only concerned with Dy-
namic Flexible Job Shop Scheduling (DFJSS).
Due to the scalability and speed requirements in
practical DJSS applications, Dispatching Rules (DR)
are popular due to their simplicity and scalability
(Blackstone et al., 1982). Dispatching rules are
heuristics that compute a priority for each operation in
the machine queue. In DFJSS, Scheduling is operated
by a pair of rules (Dauzere-Peres and Paulli, 1997): A
Routing Rule (RR) that routes each operation to a ma-
chine queue and A Sequencing Rule (SR) that assigns
a priority to each operation in the queue. Scheduling
rules can be handcrafted by experts but different en-
vironments require customized rules so manual rule
design tend to be time and effort-consuming.
Genetic Programming (GP) (Koza, 1992) has been
adopted by many recent works for automated rule
generation. GP encodes the rules as trees where
leaves denote features holding information about the
decision situation, and inner nodes denote operators
connected via edges to its operands. To search for op-
timum rules, GP starts from a random tree population
and applies a sequence of selection, crossover and
mutation operators to generate offspring. However,
the probability of finding a good rule degrades with
the expansion of the search space. Since adding more
features will exponentially expand the search space,
irrelevant features should be discarded. In DJSS, fea-
ture selection (Mei et al., 2017) was applied to opt out
features deemed irrelevant to the rule fitness. To our
knowledge, the feature selection method proposed by
(Mei et al., 2017) is yet to be applied for DFJSS.
Zakaria, Y., BahaaElDin, A. and Hadhoud, M.
Applying Feature Selection to Rule Evolution for Dynamic Flexible Job Shop Scheduling.
DOI: 10.5220/0007957801390146
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 139-146
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
139

To address the issue of irrelevant features, this pa-
per has the following objectives:
• Extend feature selection to routing and sequenc-
ing rule generation for DFJSS.
• Analyze the feature selection results and compare
the results before and after feature selection.
The rest of the paper is organized as follows: Sec-
tion 2 briefly reviews the related work. Section 3 ex-
plains the proposed method. Section 4 details the ex-
perimental setup then Section 5 shows and discusses
the experimental results. Finally, conclusions and fu-
ture work are given in Section 6.
2 RELATED WORK
2.1 Routing and Sequencing Rules
In DJSS, dispatching rules are used exhaustively due
to their computational efficiency. At decision time, a
dispatching rule calculates a priority for each avail-
able operation and the operation with the highest pri-
ority is selected for processing. Non-delay dispatch-
ing rules are applied whenever the machine is idle and
its queue is nonempty. Non-delay rules were proved
to perform better than active rules (Nguyen et al.,
2013) where decisions can be delayed. Early studies
focused on manually-designed rules but these rules
failed to generalize so attention was shifted to auto-
matically generated hyper-heuristics. Application of
Genetic Programming (GP) for DJSS rule generation
was explored in many recent works (Nguyen et al.,
2013; Yska et al., 2018).
Unlike DJSS, each operation in DFJSS is pro-
cessable on multiple machines, so a DFJSS sched-
uler has two tasks: routing operations to machines
(Routing) and ordering the operations in the machine
queue (Sequencing). To fit DFJSS, GP has been ex-
panded to generate routing and sequencing rule pairs.
To evolve two rules at the same time, Cooperative Co-
evolution GP (CCGP) was proposed in (Yska et al.,
2018) where separate populations were used for rout-
ing and sequencing rules. During evaluation, CCGP
pairs every rule with the most fit rule from the other
type. To evolve routing and dispatching rules in one
population, a multi-tree representation for the chro-
mosome was proposed by (Zhang et al., 2018) in ad-
dition to a swapping crossover operator where one
pair of corresponding rules is mated and the other is
swapped. The swapping operator should allow for a
more diverse offspring without easily breaking useful
blocks.
2.2 Feature Selection
With the latest advances in AI and Machine Learning,
Feature Selection was proven to be significant (Guyon
and Elisseeff, 2003). As features can be irrelevant
and misleading, they may deteriorate the model’s per-
formance, therefore properly selected features signifi-
cantly decrease the search space thus improve perfor-
mance. Feature Selection techniques are divided into
3 categories (Liu and Yu, 2005): Wrapper techniques
that pick features with high variance, Filter techniques
that greedily search for feature subsets that improve
performance and Embedded techniques that combine
the advantages of the aforementioned techniques.
GP exhibits embedded feature selection so rele-
vant features will tend to show up in good individuals.
However, using the feature frequency in good individ-
uals as a relevance measure has two main drawbacks.
First, it might be biased to a local optima thus fail to
generalize. Second, the occurrence might have no ef-
fect in the rule such as (X − X ) or (X /X ). Later in
(Mei et al., 2016), feature contribution to fitness was
introduced and features were ranked then selected ac-
cording to these contributions. The drawback of this
method is that GP must be run many times (30 times
in their experiments) to generate a diverse rule set
without bias to a singular local optima. To overcome
this drawback, A Niching-GP method was proposed
in (Mei et al., 2017) to generate a set with diverse
phenotypes in a single run using a clearing method.
3 PROPOSED METHOD
3.1 Problem Formulation
In DFJSS, a scenario can be formulated as follows:
• Each scenario S contains a set of Jobs J =
{J
1
,J
2
,...,J
n
}.
• Each job J
j
has an arrival time t
a
(J
j
) and a due
time t
d
(J
j
) and a weight W (J
j
).
• Each scenario S contains a set of machines M =
{M
i
,M
2
,..., M
m
}.
• Each job J
j
contains a sequence of operations
O(J
j
) = (O
j1
,O
j2
,..., O
jl
j
).
• Each operation O
ji
can only be processed by a
machine M
k
∈ π(O
ji
) ⊂ M where the processing
time on machine M
k
is δ(O
ji
,M
k
). Unlike Clas-
sical JSS which assume that |π(O
ji
)| = 1, FJSS
relaxes the assumption to |π(O
ji
)| ≥ 1.
• At any given time, each machine can only process
up to one operation.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
140

• Operation processing is non-preemptive, so if a
machine M
k
starts to process an operation O
ji
at
time t
s
(O
ji
), it is ensured that the processing will
end at time t
e
(O
ji
) = t
s
(O
ji
) + δ(O
ji
,M
k
).
• In any job J
j
, processing of any operation O
ji
can
only start after operation O
j(i−1)
has been finished
and processing of operation O
j1
can only start af-
ter its job arrival time t
a
(J
j
).
During the simulation, the scheduler is responsi-
ble for applying two rules: routing rule r
r
(O
ji
,M
k
)
and sequencing rule r
s
(O
ji
,M
k
). When a new opera-
tion O
ji
becomes available for processing, it is routed
to the machine M
k
= argmin r
r
(O
ji
,M), M ∈ π(O
ji
)
then it is added to the machine’s queue Q(M
k
). When-
ever a machine M
k
is idle and its queue Q(M
k
) is
not empty, the operation O
ji
= arg min r
s
(O,M
k
),O ∈
Q(M
k
) is assigned to the machine M
k
and removed
from its queue Q(M
k
).
The goal of genetic programming is to find a
pair of routing and sequencing rules that minimizes
a given fitness function f (r) where r = (r
r
,r
s
). The
work in this paper will only focus on minimizing
the maximum ( f (r) = maxF(J
j
)), mean ( f (r) =
E[F(J
j
)]) and weighted mean ( f (r) = E[W (J
j
) ×
F(J
j
)]) of the objective function F(J
j
) across all jobs
J
j
∈ J in any given scenario S . The objective func-
tions, used in this paper, are:
• Tardiness T (J
j
) = t
e
(O
jl
j
) − t
d
(J
j
) which is the
delay in finishing the job beyond its due time.
• Flow-time C(J
j
) = t
e
(O
jl
j
) − t
a
(J
j
) which is the
total amount of time that the job spends in the sys-
tem.
3.2 Multi-tree Genetic Programming
In this paper, we use the multi-tree chromosome and
the swapping multi-tree crossover operator proposed
in (Zhang et al., 2018). Each multi-tree chromosome
contains a pair of trees: routing rule tree and sequenc-
ing rule tree. Figure 1 shows an example of a rule
tree. The swapping multi-tree crossover operator is
described in Algorithm 1. As a method for bloat con-
trol, the crossover operator is followed by static limit
check to replace any offspring that exceeds the height
limit with one of their parents (Koza, 1992).
Algorithm 1: Swapping Multi-Tree Crossover.
Input: Chromosomes C1, C2
1: Randomly pick r ∼ {0,1} with probability 50%
2: C1[r],C2[r] ← TreeCrossover(C1[r],C2[r])
3: C1[1 − r],C2[1 − r] ← C2[1 − r],C1[1 − r]
×
+
−
PT
W
JT
Figure 1: Rule Tree Example (PT +W ) × (−JT ).
3.3 Niching-GP Feature Selection
We use the Niching-GP Feature Selection Framework
(NiSuFS) proposed in (Mei et al., 2017) which con-
sists of four main steps:
1. Apply Genetic Programming with clearing ap-
plied after every generation to prevent the popu-
lation from converging to a single phenotype.
2. Extract the best diverse set from the final popula-
tion.
3. Calculate the performance degradation of each
rule after opting out each feature, then vote for
features whose absence cause a significant degra-
dation.
4. Filter features based on votes to create the final
feature subset.
Step 3 follows the assumption that a feature’s sig-
nificance is proportional to the rule fitness degrada-
tion after opting out the feature. Since DFJSS con-
tains two rules, step 3 and 4 are extended so that it is
applied once to sequencing rules without modifying
routing rules and vice versa. The result will be two
feature subsets: significant features for routing and
significant features for sequencing.
There are four components in NiSuFS which are
as follows:
3.3.1 Phenotype Similarity
In order to measure a chromosome phenotype, a set
of discriminative situations are required. The set of
situations are randomly sampled from multiple simu-
lations which are scheduled by a benchmark rule-pair
(Least-Work-in-Queue for routing and Maximum-
Operation-Waiting-Time for Sequencing). Situations
that contain options (machines or operations) fewer
than a certain threshold are filtered out due to their
low discriminative properties. Two sets of situations
are sampled: Routing Situations and Sequencing Sit-
uations. In each situation, the options are sorted by
their benchmark priorities and stored for later use in
the clearing method. To calculate the chromosome
phenotype, its rules are applied to each situation, then
Applying Feature Selection to Rule Evolution for Dynamic Flexible Job Shop Scheduling
141

a phenotype vector is composed of the new ranks for
the options which was given rank-1 by the benchmark
rules. The distance between any two chromosomes is
the euclidean distance between their phenotype vec-
tors. The phenotype calculation steps are shown in
Algorithm 2.
Algorithm 2: Calculate Phenotype.
Input: Rule r, Benchmark-Sorted Situation Set S
Output: Phenotype P
1: for i = 0 to length(S) do
2: priorites ← ApplyRule(r,S[i])
3: indices ← ArgSort(priorities)
4: P[i] ← FindIndex(indices,0)
5: end for
3.3.2 Clearing Method
Clearing is a niching technique applied after each
generation to prevent crowding. First, the chromo-
somes are sorted by fitness (best fitness first). Then,
each chromosome will iterate through weaker siblings
within a certain phenotype distance σ, keep the best
k siblings and set the fitness of the rest to ∞. The
cleared chromosomes stay in the population but will
have a very low chance of being picked by selection.
The steps are shown in Algorithm 3.
Algorithm 3: Clearing Method.
Input: Population P
1: SortByFitness(P)
2: for i = 0 to length(P) − 1 do
3: if P[i]. f itness = ∞: Continue
4: size = 1
5: for j = i + 1 to length(P) − 1 do
6: if Distance(P[i],P[ j]) ≤ σ then
7: if size = k then
8: P[ j]. f itness ← ∞
9: else
10: size = size + 1
11: end if
12: end if
13: end for
14: end for
3.3.3 Best Diverse Set
The best diverse set algorithm is exactly the same as
the clearing method except that only the best R rule
pairs are kept. The best diverse set is picked from the
final population in order to supply the feature selec-
tion with the best generated rule pairs from different
phenotypic proximities.
3.3.4 Voting for Features
Each feature’s significance to a rule is assumed to
be proportional to the rule fitness degradation after
the feature has been set to a fixed value. If the fit-
ness degradation exceed a certain threshold ε, the rule
votes for the feature. The fitness of the rule pair f (r)
is measured as the mean fitness on a set of reference
scenarios which are randomly generated once before
the feature selection. Each rule has a different vot-
ing weight from 0 to 1 based on its fitness as shown
in Equation 1. Any feature, that collect votes greater
than a certain ratio α of the total weights, is added to
the selected subset.
w(r
0
) =
max
r
( f (r)) − f (r
0
)
max
r
( f (r)) − min
r
( f (r))
(1)
During degradation calculation, The feature t
is set to 1 for either the routing rule or the se-
quencing rule. After that, the degraded fitness of
the rule pair f
n
(r|t = 1) is measured where n ∈
{routing,sequencing}. The significance ζ
n
(r,t) is cal-
culated as shown in Equation 2. Based on the signif-
icance, the feature selection algorithm is applied as
shown in Algorithm 4. The fixed feature is set to
1 since it is the multiplicative and divisive identity
value. Although 1 is not the additive or subtractive
identity, it will not affect the overall ranking.
ζ
n
(r,t) = f (r) − f (r|t = 1) (2)
Since the scenario lengths in our experiments are
short, the fitness function tends to be noisy, thus some
insignificant features may be selected by some diverse
sets. To increase the quality of the selected feature,
we run the experiments multiple times and select only
the features that has selected by a certain number of
diverse sets.
Algorithm 4: Feature Selection.
Input: Rule Pairs R, Features T, Rule type n
Output: Selected Feature
˜
T
1: W ← CalculateWeights(R)
2: w
threshold
← α
∑
w∈W
w
3:
˜
T ← {}
4: for t in T do
5: v ← 0
6: for r in R do
7: if ζ
n
(r,t) ≥ ε then
8: v ← v +W [r]
9: end if
10: end for
11: if v ≥ w
threshold
then
12:
˜
T ←
˜
T ∪ {t}
13: end if
14: end for
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
142

4 EXPERIMENTAL SETUP
This section details the experimental steps and the
configuration for each step. The experiments were
conducted 6 times; once for each objective: maxi-
mum, mean and weighted mean of tardiness and flow-
time. We do not clamp the tardiness of early-finished
jobs to zero in order to reward the rules that finish as
early as possible. Before running the feature selec-
tion, we generate and store 20 situations for each rule
type (routing and sequencing) and each situation must
have at least 5 options available. We also generate 5
reference scenarios for feature selection and 21 test
scenarios for performance comparison. All the sce-
narios used for situation generation, training, feature
selection and testing have the same configuration. For
each objective, The NiSuFS algorithm is run 5 times
followed by feature aggregation to generate an aggre-
gated feature set. The significance threshold ε is set
to 0.0001 and the voting threshold ratio α is set to
0.25. Setting the voting threshold ratio to 0.5 as in
(Mei et al., 2017) led to selecting only one or two fea-
tures per run. We hypothesize that fixing the feature in
only one rule from the pair undermines its perceived
significance. Any feature that has been selected less
than 2 times are removed by the aggregation step. The
regular Multi-tree GP without niching is run twice per
objective: once with full feature set and once with se-
lected features only.
4.1 Scenario Generation Configuration
Due to time and parsimonious constraints, the sce-
nario length is set to be very short. Since short sce-
narios will rarely contain situations that discriminate
between rules, we added a short spike in the job ar-
rival schedule at the start of the simulation and set the
warm up jobs to zero. The scenario generation con-
figuration is detailed in Table 1.
Table 1: Scenario Generation Configuration.
Parameter Value
#Machines 10
#Jobs 50 + (10 with t
a
(J
j
) = 0)
#Ops per job U(1,10)
#Machines per op U(1,5)
Op processing time U(1,99) ∈ Z
Utilization 0.99
Job arrival Poisson process
Due time factor U(1,1.3)
Job weight 1(20%), 2(60%), 4(20%)
4.2 GP Configuration
The Niche-GP configuration is based on a combina-
tion of the configurations in (Mei et al., 2017; Zhang
et al., 2018) with some settings toned down to fit our
resource constraints. The configuration is detailed in
table 2. The operators used in our experiments are
{+,−, ×,÷, negative,mininmum, maximum}. All the
operators are binary except negative which is unary.
Each feature has a corresponding terminal as shown
in Table 3. The feature set include the features used
by (Zhang et al., 2018) in addition to time-invariant
versions of some features used by (Mei et al., 2017).
The Regular GP configuration is based on the con-
figuration in (Zhang et al., 2018) with toned-down set-
tings to fit our resource constraints. The configuration
is detailed in table 2. The same operators and termi-
nals as in Niche-GP are used in Regular-GP.
4.3 Rule Comparison
To compare two rule pairs, each pair is applied to
the 21 test scenarios and the fitness is supplied to
Wilcoxon signed-rank test at 5% level. The fitness
of the rule pair for each scenario f (r,s) is normal-
ized relative to the benchmark rule-pair fitness for
the same scenario f
b
(s) before applying the Wilcoxon
test. In our implementation, tardiness can be nega-
tive so dividing by the benchmark tardiness can flip
the objective from minimization to maximization. To
solve this problem, we subtract a lower-bound fitness
f
l
(s), that can never exceed the fitness of any rule,
from the rule-pair and benchmark fitness before nor-
malization. The lower bound is calculated by assum-
ing that each operation will be processed as soon as it
is available and that it will be assigned to the machine
with the least processing time. The normalized fitness
ˆ
f (r,s) is calculated as shown in Equation 3.
ˆ
f (r,s) =
f (r,s) − f
l
(s)
f
b
(s) − f
l
(s)
(3)
5 RESULTS AND ANALYSIS
Figure 2 shows the results of feature selection. The
horizontal axis denotes the terminals and the vertical
axis denotes the Niche-GP run. From the figure, we
can conclude the following:
• PT was selected in nearly every routing and se-
quencing rule which shows that it has great sig-
nificance in the rules’ performance.
• WIQ is selected in every routing rule since it is
a significant indicator of the expected operation
Applying Feature Selection to Rule Evolution for Dynamic Flexible Job Shop Scheduling
143

Table 2: GP Configuration.
Parameter Niche-GP Regular-GP
#Generation 51 51
Population Size 512 512
Selection Method Tournament of Size 7 Tournament of Size 7
Crossover Probability 0.8 0.8
Mutation Probability 0.15 0.15
#Elites - 32
Generated Tree Size U(1,2) U(1,2)
Maximum Tree Size 8 8
#Simulation Replication per Evaluation 1 1
Clearing Distance σ 5 -
Clearing Set Size k 1 -
Best Diverse Set Size R 32 -
Table 3: Feature Set.
Feature Description
NIQ Number of Operations in Machine Queue
WIQ Current Work in Machine Queue
MWT Machine Waiting Time
NMWT Median Waiting Time for Next Operation Machines
NINQ Median Operation Count in Next Operation Machines Queues
WINQ Median Work in Next Operation Machines Queues
PT Operation Processing Time
OWT Operation Waiting Time
NPT Next Operation Median Processing Time
WKR Sum of Median Processing Time for Remaining Operations
JT Current Delay After Job Due Time
NOR Number of Remaining Operations in Job
W Job Weight
TIS Time Spent by Job in System
waiting time and aids in load balancing. However,
NIQ is rarely selected, probably due to its redun-
dancy with the more informative feature WIQ.
• OWT is highly relevant to sequencing and mostly
irrelevant to routing.
• MWT is sometimes important for routing rules
and never relevant to sequencing.
• JT is relevant in most sequencing rules but its sig-
nificance is fluctuating in routing rules.
• W is heavily selected by sequencing rules in Mean
Weighted Flow-time and Tardiness but it is rarely
selected otherwise, which is intuitively expected.
• TIS is very relevant to sequencing for Maximum
Flow-time only, otherwise, it is rarely selected.
• NPT, NOR, NINQ and WINQ are mostly deemed
to be irrelevant as they were rarely selected.
NMWT barely passed the threshold for sequenc-
ing in mean weighted and maximum flow-time.
It is noteworthy that the selected features after
aggregation do not exceed 6 features for sequencing
rules and 4 features for routing rules. Since the num-
ber of selected features is always below half the full
feature set, we can expect that the search space will
be much smaller and efficient to explore. Table 4
shows the comparison results between using the se-
lected feature set and using the full feature set. In
half the tests, using the selected features yields sig-
nificantly better results and in the remaining cases, it
is either insignificantly better or worse. Applying GP
in a smaller search space should increase the proba-
bility of converging to good rules. However, opting
out important features will create a search space with
no good rules and GP will only converge to weak so-
lutions. Since the results show that our method has a
higher probability of finding good rules, we can con-
clude that the feature selection does keep important
features while tightening the search space.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
144

NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(a) Mean Flow-time Sequencing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(b) Mean Flow-time Routing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(c) Mean Weighted Flow-time Sequencing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(d) Mean Weighted Flow-time Routing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(e) Maximum Flow-time Sequencing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(f) Maximum Flow-time Routing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(g) Mean Tardiness Sequencing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(h) Mean Tardiness Routing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(i) Mean Weighted Tardiness Sequencing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(j) Mean Weighted Tardiness Routing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(k) Maximum Tardiness Sequencing
NIQ
WIQ
MWT
NMWT
WINQ
NINQ
PT
OWT
NPT
WKR
JT
NOR
W
TIS
0
1
2
3
4
5
(l) Maximum Tardiness Routing
Figure 2: Selected Features.
Applying Feature Selection to Rule Evolution for Dynamic Flexible Job Shop Scheduling
145
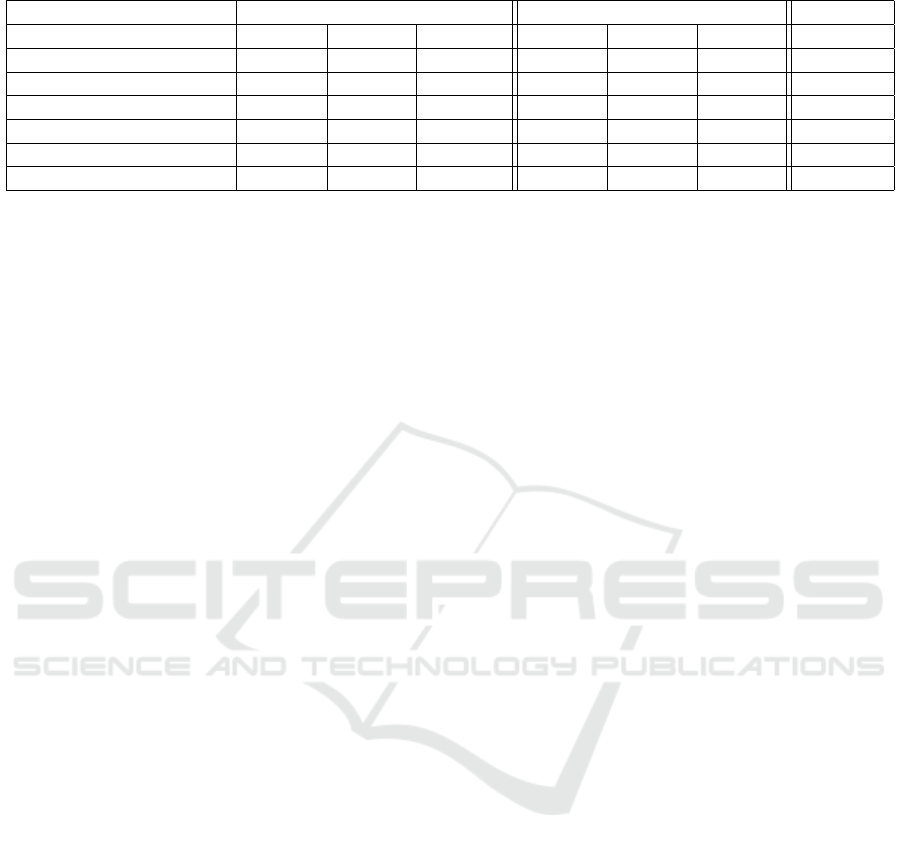
Table 4: Performance Comparison Results.
Using The Selected Feature Set Using The Full Feature Set Wilcoxon
Objective Average Min Max Average Min Max p-value
Mean flow-time 0.28238 0.18709 0.36727 0.31201 0.20618 0.41312 00.10%
Mean weighted flow-time 0.28278 0.19737 0.44225 0.29387 0.20499 0.43446 05.82%
Maximum flow-time 0.58983 0.47137 0.72148 0.67963 0.54417 0.83272 00.02%
Mean tardiness 0.28217 0.19048 0.38080 0.28607 0.20464 0.38240 35.70%
Mean weighted tardiness 0.30408 0.18893 0.47572 0.29339 0.20966 0.42190 16.97%
Maximum tardiness 0.55338 0.44895 0.70544 0.60615 0.41829 0.81957 00.19%
6 CONCLUSION AND FUTURE
WORK
This paper proposed an extension to Niching-GP Fea-
ture selection (NiSuFS) to be compatible with multi-
tree genetic programming for Dynamic Flexible Job
Shop Scheduling. NiSuFS was applied to DJSS in
(Mei et al., 2017) and the results proved its effective-
ness in improving rule generation. However, it was
not applied to DFJSS in other works. The results in
this paper showed that the extended NiSuFS can en-
hance the rule generation in multi-tree genetic pro-
gramming. The improvement was significant in 50%
of our tests and the generated rules were never sig-
nificantly worse than the baseline. For future work,
we plan to investigate the assumption that feature sig-
nificance can be measured on routing and sequenc-
ing separately despite the rule pair interaction. We
also plan to study information redundancy in features
and the applicability of feature reduction techniques
such as PCA. Since situation sampling for phenotype
measurement is completely random, different compo-
nents of the phenotype may be dependent, so pheno-
types with orthogonal components is worth exploring.
Moreover, other discriminative phenotype measure-
ment methods will be investigated in future work.
REFERENCES
Blackstone, J. H., Phillips, D. T., and Hogg, G. L. (1982).
A state-of-the-art survey of dispatching rules for man-
ufacturing job shop operations. In International Jour-
nal of Production Research, pages 27–45.
Brucker, P. and Schlie, R. (1990). Job-shop scheduling with
multi-purpose machines. Computing, 45:369–375.
Dauzere-Peres, S. and Paulli, J. (1997). An integrated ap-
proach for modeling and solving the general multipro-
cessor job-shop scheduling problem using tabu search.
In Ann. Oper. Res, pages 281–306.
Guyon, I. and Elisseeff, A. (2003). An introduction to vari-
able and feature selection. Journal of Machine Learn-
ing Research, 3:1157–1182.
Koza, J. (1992). Genetic programming: on the program-
ming of computers by means of natural selection. In
MIT press, volume volume 1.
Liu, H. and Yu, L. (2005). Toward integrating feature selec-
tion algorithms for classification and clustering. IEEE
Transactions on Knowledge and Data Engineering,
17(4):491–502.
Mei, Y., Nguyen, S., Xue, B., and Zhang, M. (2017).
An efficient feature selection algorithm for evolving
job shop scheduling rules with genetic programming.
IEEE Transactions on Emerging Topics in Computa-
tional Intelligence, 1(5):339–353.
Mei, Y., Zhang, M., and Nyugen, S. (2016). Feature selec-
tion in evolving job shop dispatching rules with ge-
netic programming. In GECCO.
Nguyen, S., Zhang, M., Johnston, M., and Tan, K. (2013).
A computational study of representations in genetic
programming to evolve dispatching rules for the job
shop scheduling problem. IEEE Transactions on Evo-
lutionary Computation, 17(5):621–639.
Yska, D., Mei, Y., and Zhang, M. (2018). Genetic pro-
gramming hyper-heuristic with cooperative coevolu-
tion for dynamic flexible job shop scheduling. In Pro-
ceedings of the European Conference on Genetic Pro-
gramming, pages 306–321. Springer.
Zhang, F., Mei, Y., and Zhang, M. (2018). Genetic pro-
gramming with multi-tree representation for dynamic
flexible job shop scheduling. In Australasian Joint
Conference on Artificial Intelligence, pages 472–484.
Springer.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
146
