
A Decomposition-based Approach for Constrained Large-Scale
Global Optimization
Evgenii Sopov
a
and Alexey Vakhnin
b
Reshetnev Siberian State University of Science and Technology, Krasnoyarsk, Russia
Keywords: Large-Scale Global Optimization, Constrained Optimization, Differential Evolution.
Abstract: Many real-world global optimization problems are too complex for comprehensive analysis and are viewed
as “black-box” (BB) optimization problems. Modern BB optimization has to deal with growing
dimensionality. Large-scale global optimization (LSGO) is known as a hard problem for many optimization
techniques. Nevertheless, many efficient approaches have been proposed for solving LSGO problems. At the
same time, LSGO does not take into account such features of real-world optimization problems as constraints.
The majority of state-of-the-art techniques for LSGO are based on problem decomposition and use
evolutionary algorithms as the core optimizer. In this study, we have investigated the performance of a novel
decomposition-based approach for constrained LSGO (cLSGO), which combines cooperative coevolution of
SHADE algorithms with the ε-constraint handling technique for differential evolution. We have introduced
some benchmark problems for cLSGO, based on scalable separable and non-separable problems from IEEE
CEC 2017 benchmark for constrained real parameter optimization. We have tested SHADE with the penalty
approach, regular ε-SHADE and ε-SHADE with problem decomposition. The results of numerical
experiments are presented and discussed.
1 INTRODUCTION
Many global optimization problems are too complex
for comprehensive analysis. For some problems, we
cannot discover any useful features for choosing a
proper optimization approach and tuning its
parameters, even the objective function is defined
analytically. For many real-world optimization
problems, the objective function is defined
algorithmically or its value is assigned as a result of
experiments. Such problems usually are viewed as
“black-box” (BB) optimization problems. There exist
many efficient techniques for different classes of
global BB optimization, and, today, nature-inspired
stochastic population-based algorithms have become
very popular in this field.
Evolutionary algorithms (EAs) have proved their
efficiency at solving many complex real-world
optimization problems. However, their performance
usually decreases when the dimensionality of the
search space increases. Global BB optimization
problems with many hundreds or thousands of
a
https://orcid.org/0000-0003-4410-7996
b
https://orcid.org/0000-0002-4176-1506
objective variables are called large-scale global
optimization (LGSO) problems. There exist many
efficient LSGO techniques (Mahdavi et al., 2015),
and the majority of them are based on the problem
decomposition concept using cooperative
coevolution (CC). At the same time, LSGO does not
take into account many features of real-world
optimization problems. In this study, we will expand
the concept of LSGO with constraint handling.
At the present time, constrained LSGO (cLSGO)
is not studied. In this paper, we will introduce new
test problems for cLSGO, which are based on scalable
separable and non-separable problems from IEEE
CEC 2017 benchmark for constrained real parameter
optimization. We will investigate the performance of
solving cLSGO problems using one of the best self-
adaptive differential evolution (DE) algorithm,
namely Success-History Based Parameter Adaptation
for Differential Evolution (SHADE). We will
combine SHADE with the ε-constraint handling
technique for DE. We will compare the performance
of the standard SHADE and SHADE with
decomposition-based CC. Our hypothesis is that such
Sopov, E. and Vakhnin, A.
A Decomposition-based Approach for Constrained Large-Scale Global Optimization.
DOI: 10.5220/0007966901470154
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 147-154
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
147

a combination of the constraint handling and LSGO
approaches can deal with cLSGO problems and can
improve the performance of the standard constraint
handling techniques.
The rest of the paper is organized as follows.
Section 2 describes related work. Section 3 describes
the proposed approach and experimental setups. In
Section 4, the experimental results are presented and
discussed. In the conclusion, the results and further
research are discussed.
2 RELATED WORK
There exist a great variety of different LSGO
techniques that can be combined in two main groups:
non-decomposition methods and cooperative
coevolution algorithms. The best results and the
majority of approaches are presented by the second
group. The CC methods decompose LSGO problems
into low dimensional sub-problems by grouping the
problem subcomponents. CC consists of three general
steps: problem decomposition, subcomponent
optimization and subcomponent coadaptation
(merging solutions of all subcomponents to construct
the complete solution) (Mahdavi et al., 2015; Potter
and De Jong, 2000; Yang et al., 2008).
DE is an evolutionary algorithm proposed for
solving complex continuous optimization problems
(Storn and Price, 2002). DE is also used for solving
LSGO problems (Yang et al., 2007). Many modern
DE-based approaches use different schemes for self-
adaptation of parameters. In (Tanabe and Fukuna,
2013), authors have proposed a new self-adaptive DE
with success-history titled as SHADE. SHADE is
able to tune scale-factor F and crossover rate CR
parameters using information from previous
generations. SHADE also uses an external archive for
saving improved solutions, which are used for
maintaining diversity in the population. SHADE has
demonstrated high performance for many hard BB
optimization problems.
There exist many well-studied techniques for
handling constraints (Coello, 2002). In (Takahama et
al., 2006), a new DE-based approach for constrained
optimization has been proposed. The approach
applies the ε-level comparison that compares search
points based on the constraint violation. ε-DE
outperforms many standard penalty-based and other
techniques for constrained optimization.
3 PROPOSED APPROACH AND
EXPERIMENTAL SETUPS
3.1 Test Functions for cLSGO
In this paper, the following constrained optimization
problem is discussed:
(1)
where is an objective function,
is a candidate solution to the problem,
is the feasible search space defined by the following
inequality and equality constraints:
(2)
(3)
Because of the problem of rounding in computer
calculations, a solution is regarded as feasible if all
inequality constraints are satisfied and
. We do not use any assumption on properties of the
objective function and constraints, thus they are
viewed as BB models.
There exist popular benchmarks for LSGO and
for constrained real parameter optimization, proposed
within special sessions and competitions of the IEEE
CEC conference. The combination of constrained and
large-scale global optimization problems proposed in
the paper is not studied, and a benchmark for cLSGO
is not proposed yet.
The IEEE CEC 2013 LSGO benchmark contains
1000-dimensional single-objective non-constrained
problems (Li et al., 2013). Introducing constraints for
these problems needs performing analysis of feasible
and infeasible domains of the search space.
Unfortunately, CEC LSGO problems are defined
algorithmically, thus we cannot perform
comprehensive mathematical analysis. Experimental
analysis is also almost impossible because fitness
evaluations need huge computational efforts.
In this study, we will design new test problems for
cLSGO based on the benchmark, proposed for the
IEEE CEC Competition on Constrained Real
Parameter Optimization in 2017 (Wu et al., 2016).
The benchmark contains 28 constrained optimization
problems. Although the problems have been
developed as scalable, 14 problems use
transformation matrixes, which are defined only for
10, 30, 50 and 100 dimensions. All problems that
don’t use a transformation matrix, are included in our
set of cLSGO problems with 1000 dimensions. Some
details on the problems are presented in Table 1.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
148

Table 1: Test functions for cLSGO.
cLSGO
problem
Original constrained
problem
Objective type
The number and a type of constraints
Equality
Inequality
cLSGO01
С01
Non-separable
0
1, Separable
cLSGO02
С02
Non-separable
0
1, Non-separable
cLSGO03
С04
Separable
0
2, Separable
cLSGO04
С06
Separable
6, Separable
0
cLSGO05
С08
Separable
2, Non-separable
0
cLSGO06
С12
Separable
0
2, Separable
cLSGO07
С13
Non-separable
0
3, Separable
cLSGO08
С14
Non-separable
1, Separable
1, Separable
cLSGO09
С15
Separable
1
1
cLSGO10
С16
Separable
1, Non-separable
1, Separable
cLSGO11
С17
Non-separable
1, Non-separable
1, Separable
cLSGO12
С18
Separable
1
2, Non-separable
cLSGO13
С19
Separable
0
2, Non-separable
cLSGO14
С20
Non-separable
0
2
The performance evaluation criteria are the same
as in the rules of the Competition on Constrained Real
Parameter Optimization.
Maximum function evaluations in a run are set to
3E+06 as in the rules of the IEEE CEC 2010 and 2013
LSGO benchmarks. The dimensionality is equal to
1000 as in the IEEE CEC LSGO Competitions.
The tolerance threshold for all equality
constraints is equal to 0.0001.
For each test problem, the following performance
criteria are evaluated over 25 independent runs:
1. best, median, worst solutions, mean value and
standard deviation;
2. the mean violations at the median solution
(denoted as );
3. the mean constraint violation value of all the
solutions of 25 run (denoted as
);
4. the feasibility rate of the solutions obtained in 25
runs (denoted as ).
The mean violations for a solution is calculated
using (4).
(4)
where
(5)
(6)
All estimations of the performance are based on
the idea that feasible solutions are preferable than
infeasible solutions. For sorting obtained solutions
we will use the following scheme:
1. Sort feasible solutions in front of infeasible
solutions;
2. Sort feasible solutions according to their objective
function values;
3. Sort infeasible solutions according to their mean
value of the violations of all constraints.
3.2 Decomposition-based Approach for
cLSGO
In this study, we will develop and investigate the
following approach for solving cLSGO problems.
We will apply the problem decomposition
concept using CC. The problem decomposition is
applied for dealing with the high dimensionality of
LSGO. The number of subcomponents (groups of
objective variables) is the controlled parameter of the
proposed algorithm.
Each subcomponent in CC will be optimized
using SHADE algorithm. SHADE is a self-adaptive
approach, thus its only controlled parameter is the
population size. We will apply the ԑ constrained DE
technique for constraint handling. The technique
modifies the selection stage in DE in the following
way:
(7)
The parameter in this study is defined using the
following scheme. On each iteration after fitness and
constraint violations evaluations, we sort all in
ascending order, and apply the formula (8).
A Decomposition-based Approach for Constrained Large-Scale Global Optimization
149
(8)
where is a counter of fitness evaluations,
is the maximum number of fitness
evaluations,
is a violation value for
solution with index
after sorting,
is the population size, and is equal to 0.8.
Thus, is decreased at the final iterations and the
search process is being concentrated in the feasible
domain of the search space.
We will perform all experiments with population
size equal to 50. This number is chosen in order to
supply each adaption period in CC with enough
fitness evaluations. The number of subcomponents in
experiments is equal to 2, 4, 8, 10 and 20 (denoted as
ԑ-CC-SHADE( ), where is the number of
subcomponents). Also we will evaluate the
performance for SHADE without problem
decomposition (denoted as ԑ-SHADE).
4 EXPERIMENTAL RESULTS
AND DISCUSSION
We have performed experiments for all algorithms
using the proposed cLSGO benchmark. First, we have
compared algorithms by the measure. The
experimental results have shown that feasibility rate
varies for test functions. The hardest problems for
investigated algorithms are 4, 5, 7 and 11-13. We
have averaged all values over all problems, the
average and median results are presented in Figure 1.
The best results are obtained by ԑ-CC-SHADE with
problem decomposition and the number of
subcomponents equal to 4, 8 and 10. Thus, the
decomposition-based algorithms outperform the
standard approach.
We have analysed convergence graphs for the
average fitness and violation in the runs. As we have
found in the figures, the proposed approach is able to
improve constraint violations and fitness value
simultaneously almost for all functions. An example
of the dynamic for cLSGO07 is presented in Figures
2 and 3. For some problems (for instance, cLSGO04)
searching for feasible solutions is more difficult, and
the fitness value changes slower than constraint
violations do.
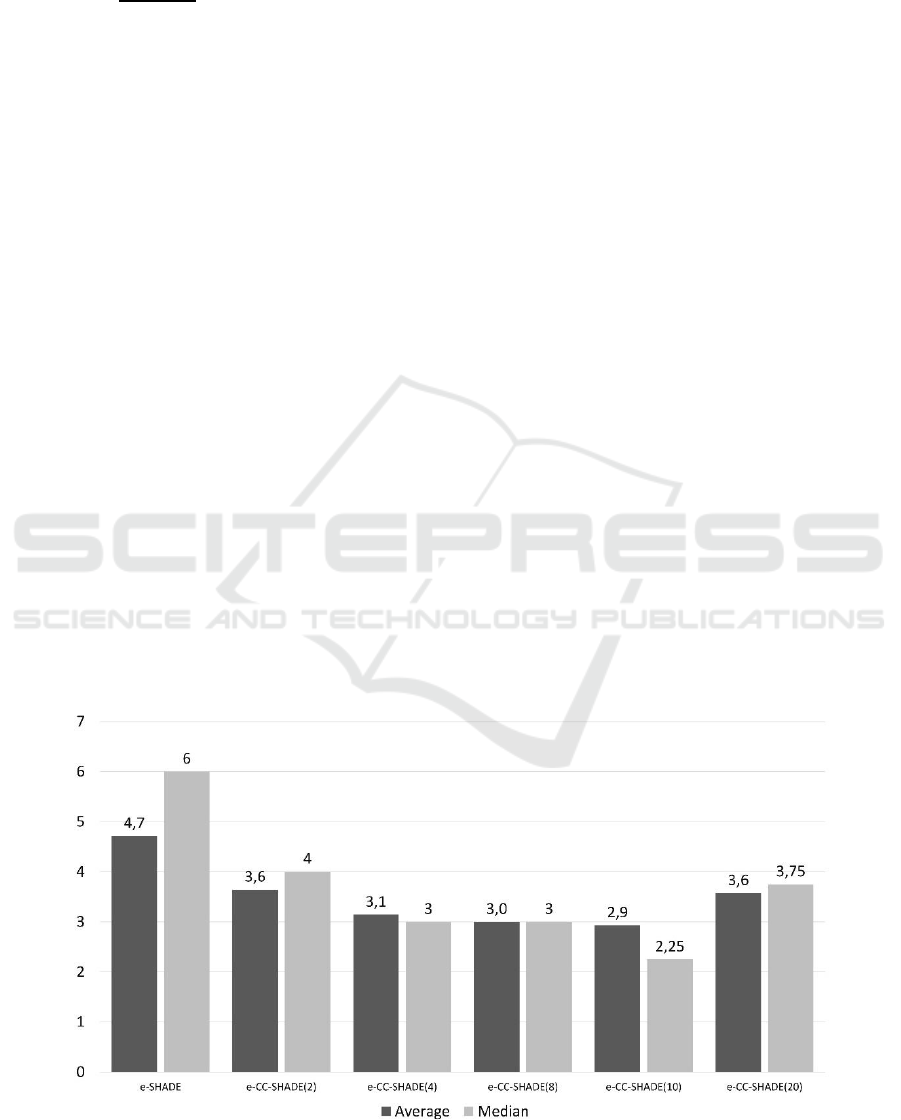
Next, we have ranked all algorithms by the
median best-found objective value and its
corresponding mean violations (). We have applied
the ranking scheme discussed in the previous section.
Distributions of ranks and the average ranks are
presented in Figures 4 and 5.
As we can see in figures, ԑ-CC-SHADE
algorithms with the number of subcomponents equal
to 4, 8 and 10 outperform other algorithms and
demonstrate more stable results in the runs.
We have also estimated is there a statistically
significant difference in the results. We have applied
the Wilcoxon-Mann-Whitney test with the
significance level equal to 0.05. Tables 2 and 3
present the results of performing the test.
Figure 1: Algorithms comparison by feasibility rate SR.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
150
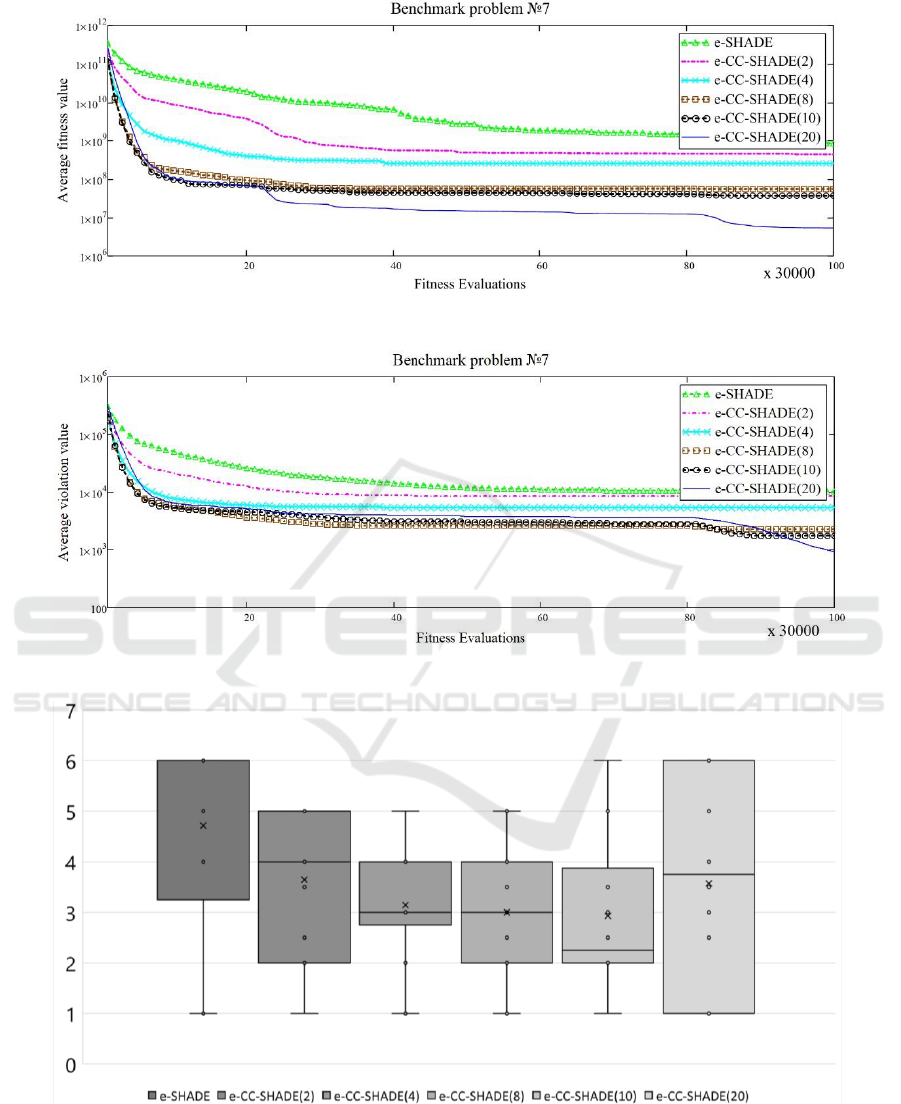
Figure 2: Average fitness convergence for cLSGO07.
Figure 3: Mean violations convergence for cLSGO07.
Figure 4: Distributions of ranks.
A Decomposition-based Approach for Constrained Large-Scale Global Optimization
151
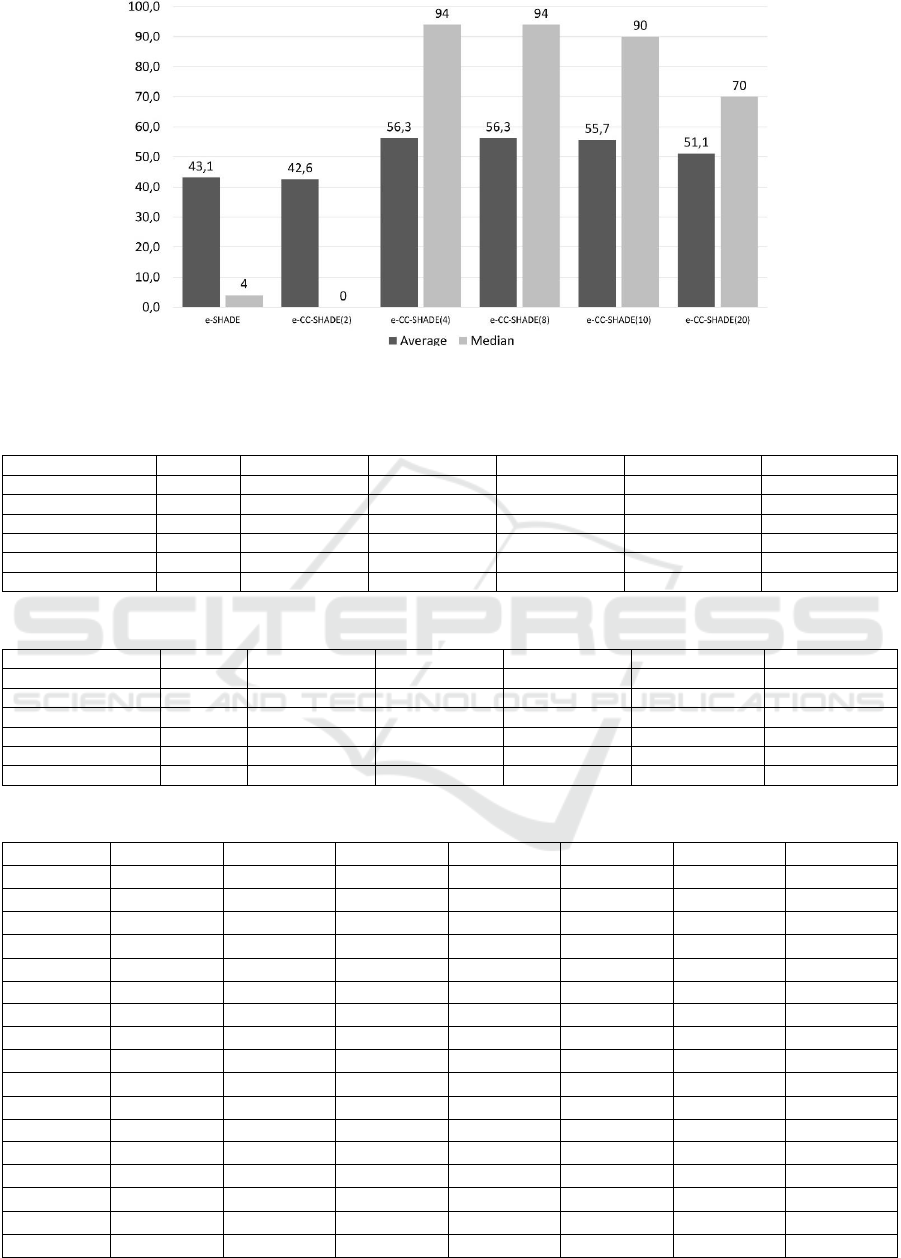
Figure 5: Algorithms comparison by ranks.
Table 2: The number of test problems, for which the performance of an algorithm in a row is significantly better than the
performance of an algorithm in a column.
ԑ-SHADE
ԑ-CC-SHADE(2)
ԑ-CC-SHADE(4)
ԑ-CC-SHADE(8)
ԑ-CC-SHADE(10)
ԑ-CC-SHADE(20)
ԑ-SHADE
-
3
3
3
3
5
ԑ-CC-SHADE(2)
10
-
4
5
4
6
ԑ-CC-SHADE(4)
10
9
-
4
4
7
ԑ-CC-SHADE(8)
10
8
8
-
2
8
ԑ-CC-SHADE(10)
9
8
7
4
-
7
ԑ-CC-SHADE(20)
8
6
3
3
3
-
Table 3: The number of test problems, for which there is no statistically significant difference in the algorithms performance.
ԑ-SHADE
ԑ-CC-SHADE(2)
ԑ-CC-SHADE(4)
ԑ-CC-SHADE(8)
ԑ-CC-SHADE(10)
ԑ-CC-SHADE(20)
ԑ-SHADE
-
-
-
-
-
-
ԑ-CC-SHADE(2)
1
-
-
-
-
-
ԑ-CC-SHADE(4)
1
1
-
-
-
-
ԑ-CC-SHADE(8)
1
1
2
-
-
-
ԑ-CC-SHADE(10)
2
2
3
8
-
-
ԑ-CC-SHADE(20)
1
2
4
3
4
-
Table 4: The experimental results for ԑ-CC-SHADE(8).
Function
1
2
3
4
5
6
7
Best
4.88E+04
8.28E+07
4.98E+03
1.82E+05
1.01E+02
2.82E+00
2.48E+07
Median
8.20E+04
1.91E+08
5.43E+03
1.63E+05
1.52E+02
3.22E+00
7.03E+07
0.00E+00
0.00E+00
0.00E+00
9.75E-02
1.39E+05
0.00E+00
2.28E+03
Mean
8.41E+04
2.26E+08
5.39E+03
1.78E+05
1.32E+02
3.95E+00
5.49E+07
Worst
0.00E+00
0.00E+00
0.00E+00
9.75E-02
1.39E+05
0.00E+00
2.28E+03
std
8.41E+04
2.26E+08
5.39E+03
1.78E+05
1.32E+02
3.95E+00
5.49E+07
SR, %
100
96
100
0
0
100
0
0.00E+00
3.08E-06
0.00E+00
9.77E-02
7.32E+05
0.00E+00
2.28E+03
Function
8
9
10
11
12
13
14
Best
2.68E-01
3.06E+01
6.87E+03
2.00E+00
5.58E+02
3.88E+02
2.26E+02
Median
2.72E-01
4.95E+01
7.09E+03
2.00E+00
1.18E+03
5.65E+02
2.29E+02
0.00E+00
0.00E+00
0.00E+00
5.01E+02
2.57E+02
4.91E+05
0.00E+00
Mean
2.73E-01
4.85E+01
7.08E+03
2.00E+00
1.37E+03
5.80E+02
2.29E+02
Worst
2.81E-01
3.38E+01
7.35E+03
2.00E+00
3.77E+03
1.04E+03
2.33E+02
std
3.33E-03
1.14E+01
1.23E+02
1.25E-04
5.92E+02
1.29E+02
2.02E+00
SR, %
100
92
100
0
0
0
100
0.00E+00
3.40E-06
0.00E+00
5.01E+02
2.63E+02
4.91E+05
0.00E+00
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
152

Table 5: The experimental results for ԑ-CC-SHADE(10).
Function
1
2
3
4
5
6
7
Best
3.81E+04
6.04E+07
4.43E+03
1.78E+05
1.03E+02
2.81E+00
1.69E+07
Median
6.02E+04
1.34E+08
4.70E+03
1.78E+05
1.37E+02
3.32E+00
2.19E+07
0.00E+00
0.00E+00
0.00E+00
1.02E-01
2.67E+05
0.00E+00
1.75E+03
Mean
6.58E+04
1.40E+08
4.71E+03
1.78E+05
1.51E+02
6.65E+00
3.71E+07
Worst
1.19E+05
1.26E+08
5.04E+03
1.79E+05
1.81E+02
2.26E+01
8.86E+07
std
1.89E+04
6.90E+07
1.51E+02
9.18E+03
2.85E+01
6.99E+00
1.88E+07
SR, %
100
92
100
0
0
100
0
0.00E+00
4.05E-06
0.00E+00
1.11E-01
2.36E+06
0.00E+00
1.75E+03
Function
8
9
10
11
12
13
14
Best
2.72E-01
3.06E+01
6.79E+03
2.00E+00
5.59E+02
4.20E+02
2.25E+02
Median
2.77E-01
4.01E+01
7.11E+03
2.00E+00
9.60E+02
6.24E+02
2.31E+02
0.00E+00
0.00E+00
0.00E+00
5.01E+02
1.88E+02
4.91E+05
0.00E+00
Mean
2.77E-01
3.98E+01
7.09E+03
2.00E+00
1.10E+03
6.92E+02
2.30E+02
Worst
2.80E-01
3.06E+01
7.39E+03
2.00E+00
4.38E+03
1.53E+03
2.35E+02
std
1.91E-03
6.21E+00
1.26E+02
3.17E-05
7.42E+02
2.47E+02
2.86E+00
SR, %
100
88
100
0
0
0
100
0.00E+00
9.92E-06
0.00E+00
5.01E+02
1.91E+02
4.91E+05
0.00E+00
0.00E+00
0.00E+00
0.00E+00
5.01E+02
1.88E+02
4.91E+05
0.00E+00
Mean
2.77E-01
3.98E+01
7.09E+03
2.00E+00
1.10E+03
6.92E+02
2.30E+02
Worst
2.80E-01
3.06E+01
7.39E+03
2.00E+00
4.38E+03
1.53E+03
2.35E+02
std
1.91E-03
6.21E+00
1.26E+02
3.17E-05
7.42E+02
2.47E+02
2.86E+00
SR, %
100
88
100
0
0
0
100
0.00E+00
9.92E-06
0.00E+00
5.01E+02
1.91E+02
4.91E+05
0.00E+00
In comparisons of ԑ-SHADE with all other CC
algorithms, all differences in the results are
significant except one function. Thus we can
conclude that the problem decomposition using CC
improves the performance of DE when solving
cLSGO problems.
ԑ-CC-SHADE(2) and ԑ-CC-SHADE(20) have
demonstrated the worst results. They have the equal
number of wins, and there are only two functions with
not significant differences in the performance.
The best performance has been demonstrated by
ԑ-CC-SHADE(8) and ԑ-CC-SHADE(10). We cannot
conclude which one is better because there are 8
functions from 14 for which differences in the
performance are not significant. Full experimental
results for these algorithms are presented in Tables 4
and 5.
Finally, we have compared ԑ-CC-SHADE with
the best settings and SHADE using the dynamic
penalty function approach (Coello, 2002). The
penalty function is the well-studied and widely used
approach by many researchers and applied specialists,
thus we can use it as a baseline approach for cLSGO.
In our experiments, SHADE with the penalty function
has demonstrated the worst performance. The
feasibility rate was equal to zero for all test
problems, except 3rd (=32) and 14th (=8). For
these two problems, all decomposition-based
algorithms have demonstrated =100.
5 CONCLUSIONS
In this paper, we have presented the experimental
results of investigating a new class of complex global
BB optimization problems that combines high
dimensionality and constraint handling. We have
developed new test functions based on the popular
benchmark for constrained optimization. We have
proposed a novel decomposition-based approach,
which uses SHADE algorithm with CC and the ε level
comparison of constraint violations.
The experimental results have shown that the
proposed approach is able to efficiently solve cLSGO
problems, and CC with problem decomposition
improves the performance of applying search
algorithms with constraint handling.
In further work, we will investigate more
advanced CC approaches with adaptive grouping.
A Decomposition-based Approach for Constrained Large-Scale Global Optimization
153

ACKNOWLEDGEMENTS
This research is supported by the Ministry of
Education and Science of Russian Federation within
State Assignment № 2.1676.2017/ПЧ.
REFERENCES
Coello, A.C., 2002. Theoretical and Numerical Constraint-
Handling Techniques Used with Evolutionary
Algorithms: A Survey of the State of the Art. Comput.
Methods Appl. Mech. Engrg. 191(11-12), pp. 1245-
1287.
Li, X., Tang, K., Omidvar, M.N., Yang, Zh., Qin, K., 2013.
Benchmark functions for the CEC 2013 special session
and competition on large-scale global optimization.
Technical Report, Evolutionary Computation and
Machine Learning Group, RMIT University, Australia.
Mahdavi, S., Shiri, M.E., Rahnamayan, Sh., 2015.
Metaheuristics in large-scale global continues
optimization: A survey. Information Sciences, Vol.
295. pp. 407–428.
Potter, M.A., De Jong, K.A., 2000. Cooperative
coevolution: an architecture for evolving coadapted
subcomponents. Evolutionary computation, vol. 8, no.
1, pp. 1–29.
Storn, R., Price, K., 2002. Differential Evolution - A Simple
and Efficient Adaptive Scheme for Global
Optimization over Continuous Spaces. Technical
Report.
Takahama, T., Sakai, S., Iwane, N., 2006. Solving
Nonlinear Constrained Optimization Problems by the E
Constrained Differential Evolution. Systems, Man and
Cybernetics, 2006. SMC '06. IEEE International
Conference, vol.3, pp. 2322-2327.
Tanabe, R., Fukunaga, A., 2013. Success-history based
parameter adaptation for Differential Evolution. In
2013 IEEE Congress on Evolutionary Computation,
CEC 2013, pp. 71-78.
Wu, G., Mallipeddi, R., Suganthan, P., 2016. Problem
Definitions and Evaluation Criteria for the CEC 2017
Competition and Special Session on Constrained Single
Objective Real-Parameter Optimization. Technical
Report, Nanyang Technological University, Singapore.
Yang, Zh., Tang, K., Yao, X., 2008. Large scale
evolutionary optimization using cooperative
coevolution. Information Sciences, vol. 178, no. 15, pp.
2985–2999.
Yang, Zh., Tang, K., Yao, X.,2007. Differential evolution
for high-dimensional function optimization. IEEE
Congress on Evolutionary Computation, CEC 2007, pp.
3523–3530.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
154
