Online Encoder-decoder Anomaly Detection using Encoder-decoder

Architecture with Novel Self-conﬁguring Neural Networks & Pure

Linear Genetic Programming for Embedded Systems

Gabriel

e Kasparavi

1,2

, Malin Thelin

, Peter Nordin

1,3

, Per S

oderstam

, Christian Magnusson

and Mattias Almljung

Chalmers University of Technology, Chalmersplatsen 4, Gothenburg, Sweden

University of Gothenburg, R

annv

agen 6B, Gothenburg, Sweden

Semcon AB, Lindholmsall

en 2, Gothenburg, Sweden

Mattias.Almljung}@semcon.com

Keywords:

Encoder-decoder, Anomaly Detection, Linear Genetic Programming, Evolutionary Algorithm, Genetic

Algorithm, Embedded, Self-conﬁguring, Neural Network.

Abstract:

Recent anomaly detection techniques focus on the use of neural networks and an encoder-decoder architec-

ture. However, these techniques lead to trade offs if implemented in an embedded environment such as high

heat management, power consumption and hardware costs. This paper presents two related new methods for

anomaly detection within data sets gathered from an autonomous mini-vehicle with a CAN bus. The ﬁrst

method which to the best of our knowledge is the ﬁrst use of encoder-decoder architecture for anomaly de-

tection using linear genetic programming (LGP). Second method uses self-conﬁguring neural network that

is created using evolutionary algorithm paradigm learning both architecture and weights suitable for embed-

ded systems. Both approaches have the following advantages: it is inexpensive regarding resource use, can

be run on almost any embedded board due to linear register machine advantages in computation. The pro-

posed methods are also faster by at least one order of magnitude, and it includes both inference and complete

training.

1 INTRODUCTION

The complexity of modern embedded systems such as

vehicle systems have increased over the past decade,

in part due to the increasing amount of sensors (Hegde

et al., 2011). As a consequence, computational effort

of the control network of vehicle systems has become

a problem, with implications on battery management,

weight, price etc. Furthermore it has become difﬁcult

to be able to keep track of the total number of system

errors or anomalies, which tend to accumulate with

additional complexity. Thus, there is a risk that an

embedded system such as a vehicle deviates from its

expected values without alarms being raised. Further-

more, current methods of anomaly detection are both

time and power consuming processes and/or restricted

in the anomalies they can detect.

Unexpected behaviours are often interchange-

ably called errors, anomalies, outliers, or exceptions.

Anomaly detection is the act of detecting a deviation

from the anticipated value; many times referred to as

the data mean behaviour (Chandola et al., 2009). It

is used in different ﬁelds (and with slightly different

meanings) in, e.g., network intrusion detection (Tay-

lor et al., 2015), motor abnormalities in unmanned

vehicles (Lu et al., 2018), fraud detection (Ahmed

et al., 2016), medical anomaly detection (Pachauri

and Sharma, 2015), and the controller area network

bus interference (Hangal and Lam, 2002). It is im-

portant to clarify that none of these examples use an

encoder-decoder architecture.

There is a wide variety of techniques to discover

anomalies. Some of these techniques have been de-

veloped for certain domains. Lately a technique with

a wide applicability has become popular: deep neu-

ral networks (Sabokrou et al., 2017). More specif-

ically an encoder-decoder anomaly detection system

(EncDecAD) using deep neural networks. However,

there are some major issues with the use of this tech-

nique. For example, within the automotive industry,

Kasparavi

e, G., Thelin, M., Nordin, P., Söderstam, P., Magnusson, C. and Almljung, M.

Online Encoder-decoder Anomaly Detection using Encoder-decoder Architecture with Novel Self-conﬁguring Neural Networks Pure Linear Genetic Programming for Embedded Systems.

DOI: 10.5220/0008064401630171

In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 163-171

ISBN: 978-989-758-384-1

163

Figure 1: Crossover example in linear genetic program-

ming.

to be able to have a capable deep neural network ar-

chitecture in a vehicle requires high power consump-

tion and thus, creates a heating, price and efﬁciency

issue.

As a result, this paper introduces the ﬁrst encoder-

decoder anomaly detection system (EncDecAD) us-

ing linear genetic programming (LGP) where the

trained model is run on an embedded device. Ad-

ditionally, this paper showcases an embryo of evolu-

tionary technique in self-conﬁguring neural networks

and simultaneous training as a variant of the ﬁrst lin-

ear genetic programming method. Vehicle data for

both experiments was obtained from an autonomous

mini-vehicle that was run on different tracks; the ﬁrst

time the mini-vehicle had no abnormalities, the sec-

ond time the suspension was loosened on the vehicle

to create an anomaly in the data; the third time the ve-

hicle had a resistor soldered in series with the battery

of the vehicle. The results show promising potential

for the presented techniques.

2 RELATED WORK

2.1 Linear Genetic Programming

Linear genetic programming (LGP) is an artiﬁcial in-

telligence technique that uses a sequence of simple

instructions to solve a problem (Banzhaf et al., 1998).

The problem with this solution is ﬁnding the best

function that represents the given data. The ability

to ﬁnd the correct function to solve the problem de-

pends on the expressiveness of the instructions and

the evolutionary methods. LGP has a wide applica-

tion domain, e.g., it has been used in prediction of

hydrological processes (Mehr et al., 2013), software

optimization (Langdon and Harman, 2015), feature

learning for image classiﬁcation (Shao et al., 2014),

and miniature robot behaviours(Nordin and Banzhaf,

1995).

LGP is built on Darwin’s principle of natural se-

lection and evolution (Banzhaf et al., 1998). A popu-

lation is created with random individuals that compete

against each other by applying a chosen ﬁtness func-

tion. It has been an established practice to use a stan-

dard ﬁtness function. This means that the closer the

ﬁtness value is to zero, the better an individual scores

among the population. The evolutionary concepts in

LGP include selection, mutation, and crossover, and

are deﬁned as follows:

Representation: LGP utilizes an imperative program-

ming concept which is composed of a set of registers

and basic instructions. Execution of the individual re-

spects the order of instructions. The basic example

of such an instruction is a = b + c, where a, b, and c

are all variables. In this case, a is the register that is

being written to, b and c are operands that are sepa-

rated by an operator +. In genetic algorithm terms,

one instruction is called a gene. This example shows

a 3-register (a, b, c) instruction, where it operates on

two arbitrary variables (b and c). Operands can be

swapped with constants, e.g., a = 5 + c. These con-

stants belong to what is known as the terminal set.

The collection of operators that can be selected is

known as the function set. Chromosome or individual

is a number of instructions followed one after another,

e.g., (a = b + c,b = a − c,a = 2 ∗ a).

Initialization: The number of initialized individuals

is chosen by the population size. Each individual has

a set length. Individuals (usually) consist of ineffec-

tive instructions that have no impact on the end ﬁtness

value, e.g., a = a + 0. Such instructions are called in-

trons.

Selection Operators: One of the most popular se-

lection operator is called the steady-state tournament

selection. In this selection usually four tournament

members are chosen randomly from the population.

They compete among each other and the two best

individuals are retained and taken to the crossover

and mutation methods. The children received after

the previously discussed methods overwrite the losers

in the tournament and take their respective positions

in the population. The advantage of the steady-state

tournament selection is that it does not require indi-

vidual comparison among all individuals in a popula-

tion. The experiment ran for EncDecAD utilizes this

tournament selection.

Variation Operators: There are a few variation opera-

tors. In crossover, two individuals (sometimes called

parents) are chosen and portions of each individual

are exchanged. Figure 1 shows an example of a one

point crossover. The idea behind mutation is that

any component of the instruction (destination register,

operands, and operator) can be changed for another

alternative. If the operator is changed into one of the

possible alternatives, then these substitutes are called

function sets. The most basic function sets include

multiplication, summation, division, and subtraction.

For example, in the following instruction a = a + b,

the operator can be randomly assigned to division,

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

164

Figure 2: An example of encoder-decoder architecture

based on (Cho et al., 2014).

thus the instruction becomes a = a/b. The probabil-

ities of both, crossover and mutation, are distinct pa-

rameters often called pCross and pMut respectively.

2.2 Encoder-decoder Anomaly

Detection

The proposed anomaly detection techniques are based

on an autoencoder (see ﬁg. 2). It has two parts: en-

coder and decoder, which are used to learn and recon-

struct the behaviour of the chosen system and later use

the reconstructed error to expose an anomaly (Malho-

tra et al., 2016). In some literature this is also referred

to as a deviation based anomaly detection (An and

Cho, 2015). The input data of an autoencoder is also

the target data. Therefore, at ﬁrst an autoencoder is

run on normal data sequences that have no anomalies.

Later on, when the model has learned the normal be-

haviour of the system, the same model is run on data

that has anomalous sequences. Thus, an autoencoder

is trained by unsupervised learning.

There are different techniques to perform anomaly

detection, one being neural networks (Xu et al., 2015;

An and Cho, 2015; Tsai et al., 2009).

2.3 Neural Network Architecture

Evolution

Neural network architecture is deﬁned by the design

of how many neurons (circles) are connected together

by synapses (lines) (see ﬁg. 3). The function f is an

activation function. For example, ReLu is an activa-

tion function, where y = max(0,x). This means that

any value below zero will be zero after running activa-

tion function and any number above zero is returned.

Weights are described as a unit that determine the

strength of each connected synapse. Bias is an addi-

tional unit that modiﬁes the output. Different type of

neural network usage brought strong results in various

Figure 3: An example of a traditional neural network, based

on (Hsu et al., 1995).

disciplines such as diagnosis of myocardial infarc-

tion (Baxt, 1991), speech recognition (Mikolov et al.,

2010), engine fault detection (Ahmed et al., 2015).

Other researchers have evolved the architecture of

neural networks with promising outcome (Rawal and

Miikkulainen, 2018; Assunc¸

ao et al., 2018; Miikku-

lainen et al., 2019; Dabhi and Chaudhary, 2015). A

portion of these papers show recent work on train-

ing the weights and biases with evolutionary systems

(Tsai et al., 2006; Zhang and Suganthan, 2016). An-

other research shows examples of evolving neural net-

work architecture (Such et al., 2017). Finally, some

authors have achieved successful showcases of using

evolutionary approaches to ﬁnd both architectures and

weights (Schaffer et al., 1992; Koza and Rice, 1991).

3 EXPERIMENTAL VALIDATION

This paper studies two EncDecAD methods that uti-

lize evolutionary techniques. The ﬁrst method uses

LGP and was executed both ofﬂine and online while

the second method uses self-conﬁguring neural net-

work that is created using evolutionary paradigms.

The ofﬂine training means that the training has been

conducted on a laptop while the validation has been

run on the embedded device. Online training means

that both the training and the validation have been per-

formed on the embedded device.

The suggested method for anomaly detection is

much faster than a conventional tuned neural network

alternative. The neural network with autoencoder ar-

chitecture was chosen to solve the same issue. It had

the following dimensionality of hidden layers: [19,

15, 11, 7, 3, 7, 11, 15, 19]. The neural network was

created using Tensorﬂow. Its parameters are as fol-

lows: ReLu activation function, loss function RMSE,

learning rate 0.01, with enabled dropout. This neural

network’s architecture requires 1187 calculations to

evaluate a new input, while our proposed method re-

quires maximum 50 (after the introns were removed).

Thus our proposed anomaly detection method is at

Online Encoder-decoder Anomaly Detection using Encoder-decoder Architecture with Novel Self-conﬁguring Neural Networks Pure

Linear Genetic Programming for Embedded Systems

165

least 20 times faster.

Furthermore, one of the motivations to use the

combination of encoder-decoder architecture and lin-

ear genetic programming is that it does not require

a high power supply, costly computer, labeling of

the data, nor it produces heating problems due to it’s

speed.

Authors of this paper propose a method to evolve

weights and the architecture using a self-conﬁguring

neural network. As the results later in this paper show,

the proposed technique is efﬁcient to execute due to

the use of simple instructions compared to running

advanced structures like lists in computer systems that

take long time. The parameters for the experiments

have been chosen after a comparison within a few

runs.

The online (i.e., on-board) experiments were run

on a single board computer called STM32-F407.

This development board has the following features;

STM32F407ZGT6 Cortex-M4 210 DMIPS, 1MB

Flash, and 196KB RAM (Olimex, 2018).

3.1 Collection of Data

The data used for training and testing of the proposed

anomaly detection model was gathered from a self-

driving mini-vehicle. The used mini-vehicle was fully

equipped with sensors and a CAN bus (a vehicle bus

standard) just like its real-size counterpart (Di Natale,

2000). The vehicle completed a total of 12 runs, each

time with a randomized route where the vehicle ex-

hibited both different speeds and various sharp and

wide turns.

Twelve runs of approximately 3 min duration each

were done with an induced anomaly. The anomaly

data consists of two data sets: one where the designed

error was produced by loosened suspension on one of

the front wheels, and another with a resistor soldered

in series with the battery of the vehicle.

The collected data included the following vari-

ables: temperature, battery current, motor current,

battery voltage, speed, roll, pitch, yaw, three ac-

celerometer values, three gyroscope values, three

magnetometer values, tachometer, and commanded

steering angle.

3.2 Validation through Ofﬂine Training

This subsection describes the settings used in the ini-

tial experiment validation, where the training has been

applied ofﬂine. This step has been done as a proof of

concept.

The ﬁrst step to designing an autoencoder with

LGP is to choose the common parameters for the

model. Table 1 lists the parameters for all the runs.

The ﬁtness function chosen for the autoencoder can

be followed in equations 1, 2, and 3. The individ-

ual length size is divided into two parts: encoder and

decoder. Hereby the ﬁrst half of the individual, i.e.,

1500 instructions, is used to ﬁnd the proper encoder

values while the other half of the individual utilizes

the previously found encoder values with the goal to

reconstruct the original input-values.

= α

∑

i=1

EncoderValue

(1)

∑

i=1

− X

)

+ ES

(2)

Fitness =

∑

i=1

(3)

where:

- ES is the encoder-sum.

- p is the number of encoder registers.

- α is the chosen number which provides a weight

to the feature vector.

- EncoderValue

is the element in the feature vec-

tor (see ﬁg.2).

- RE is the row error, where row is the input array.

k is the number of decoder registers.

- X

is the decoder register i.

- X

is the groundtruth value of the register i.

- n is the number of input rows/arrays.

In other words, when an individual receives the

ﬁrst row of the input array, it only executes half of

instructions of one individual. Since the chosen en-

coder register number in the presented example is 3,

the encoder-sum adds the ﬁrst 3 values of the output

which is equal to the ﬁrst equation. Then these ﬁrst

three values are saved and the other register values

are set to zero (in the presented example this becomes

the decoder register’s array). This allows the second

half of the individual to ﬁll the rest of the values itself.

When this is done, the second equation is used where

it calculates the root mean squared error of the cal-

culated decoder register’s value and the input value,

i.e., groundtruth value. The addition of the encoder-

sum in the second equation plays a role. By provid-

ing the encoder-sum to this equation, it indicates to

the ﬁtness function that the encoder values need to

be signiﬁcant. If this was not be added, the autoen-

coder would not work, since the feature vector would

be random numbers that do not provide anything to

the ﬁtness function. Finally, when all row errors have

been calculated the total ﬁtness for the individual is

the average of these errors, see equation 3. This im-

plies that the closer the output values are to the input

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

166

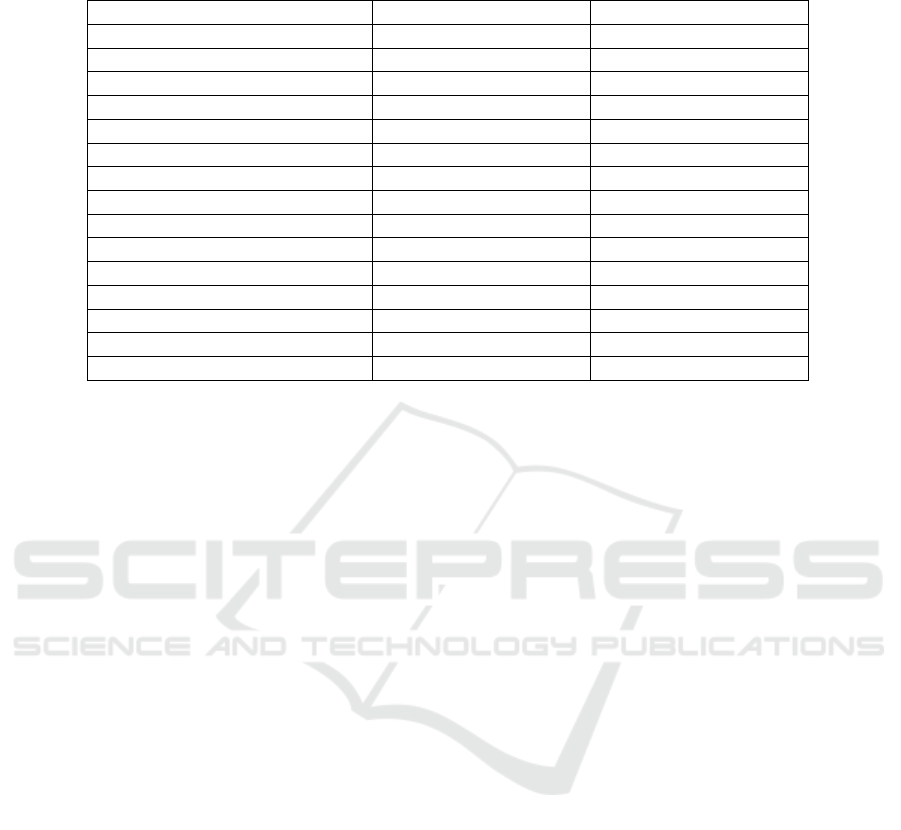
Table 1: LGP parameters used in two scenarios: the validation through ofﬂine training and validation through an online

(on-board) embedded training.

Parameter Ofﬂine training settings Online training settings

Fitness function Standardized, RMSE Standardized, RMSE

Terminal set [-5, 5] [-1, 1]

Function set +, -, *, / +, -, *

Safe division enabled? Yes No

Number of encoder registers 3 3

Number of decoder registers 19 19

Population size 50 50

Crossover probability 0.6 0.6

Mutation probability 0.05 0.05

Selection Steady-state tournament Steady-state tournament

Number of tournament members 4 4

Termination criteria None None

Individual length 3000 50

Undeﬁned constant 1000000 None

Alpha 0.01 0.01

values the closer the autoencoder ﬁtness value will be

to zero.

The function set included a safe division

(Brameier and Banzhaf, 2007). This means that if

an instruction includes a division by zero, it sets the

source register to an undeﬁned constant. In this ex-

periment’s case that constant is 1000000.

Termination criteria is set to none as the algorithm

was allowed to run the set number of generations in-

stead of stopping it when it reached some value of

ﬁtness function. This enabled the algorithm to reach

its best ﬁtness function without making any assump-

tions.

The training part of the initial anomaly detection

system was executed on a computer with the fol-

lowing speciﬁcations: Intel(R) Core(TM) i7-6820HQ

CPU @ 2.70GHz, 16.0 GB installed memory (RAM),

64-bit Operating System, Windows 10 OS. The train-

ing model was written in Python 3.6. It was trained

on half of the gathered data. The other half of the

data was left for validation.

3.3 Validation through On-board

Embedded Training

After the initial experiment was demonstrated to up-

hold the concept behind EncDecAD using evolution-

ary programming, the next step was to enable not only

the testing part, but also the training part on the em-

bedded device.

The ﬁtness function is the same as used in the val-

idation through the ofﬂine training experiment. How-

ever, there are some substantial differences in the cho-

sen LGP parameters for this experiment (see table 1).

To start with, the individual was trained on a

smaller set of data, i.e., 2000 input rows of data, since

the on-board ﬂash memory has a total storage space

of 1MB, and the space that was allocated for train-

ing data was 384KB. Secondly, the function set does

not include division. The reason for this approach is

that division requires 2-12 cycles on a Cortex-M pro-

cessor, while the other mathematical operations only

require 1 cycle. Lastly, the individual length has been

reduced to hold between 10 to 50 instructions.

The algorithm was developed in the C++ program-

ming language. The algorithm was trained on the

70% of non-faulty data and validated on the other

30% of unseen non-faulty data. The data arrays were

chosen randomly from a large pool of non-faulty data.

3.4 Validation through On-board

Embedded Training using

Evolutionary Approach to Neural

Networks

This paper proposes a novel solution to anomaly de-

tection. The idea behind it is to use an evolution-

ary approach to neural networks on the embedded

device. The concept follows the familiar encoder-

decoder anomaly detection architecture but this last

experiment employs virtual neural network compo-

nents in it. The evolutionary neural network is con-

structed as a restrained register machine and shares

the advantages with the unconstrained LGP method

but in addition generates a pure deep neural network

which may be more easily integrated in some data

science environments. What we do is that we re-

strain the functions set and grammar of the LGP in

Online Encoder-decoder Anomaly Detection using Encoder-decoder Architecture with Novel Self-conﬁguring Neural Networks Pure

Linear Genetic Programming for Embedded Systems

167

such a way that everything that is produced is isomor-

phic to a standard neural network. Similarly any neu-

ral network can be expressed using this ”register ma-

chine syntax”. The motivation is twofold; ﬁrst, many

data-scientists are more comfortable using what can

be shown to be equivalent to a neural network, and

second, there may be advantages in the learning time

of this constrained model as compared to the general

linear genetic programming approach (Brameier and

Banzhaf, 2001). The advantage of the neural model is

pure speculation based on information-theoretic rea-

soning and some early runs but are by no means

proven in this paper. The neural network approach

is more of a teaser in need of further investigation.

The differences of this neural network approach

as compared to the previous LGP approaches in this

paper are as follows: to start with, instead of using

the linear genetic programming instructions that are

generic on the form a = b − c, the proposed method

employs a different set of more constrained instruc-

tions. The instances are shown in the example instruc-

tions below.

= S

+ S

(4)

= ReLu(S

) ∗ w

+ b

(5)

= w

+ w

(6)

= w

∗ w

(7)

= b

+ b

(8)

= b

∗ b

(9)

where:

- S is a weighted sum.

- w is a weight.

- b is a bias.

- ReLu is an activation function, where y =

max(0,x).

The weighted sum simply takes a register and adds

it to another, see instruction 4. The instruction in 5

employs the activation function called rectiﬁer, mul-

tiplies it by a randomly chosen weight and adds a

bias. The last two instruction examples (see 8 and 9)

show the manipulation of weights, where the function

set consists of only multiplication and summation and

one of the weights has the possibility to change into

a terminal set (a constant that belongs to the chosen

range, e.g., see ”Terminal set” in table 1).

Second difference compared to the online train-

ing settings experiment is that the individual size is

increased from 50 to 200 where the ﬁrst half manipu-

lates the encoder-related data and the other half han-

dles the decoder data.

Thirdly, self-conﬁguring neural network approach

initializes another vector with weights and biases.

The usual number for weights is 3 and the values are

chosen between [−1,1]. Biases are initialized in the

same way. Lastly, the new approach was tested while

running for 100 000 generations.

The neural network starts with the required vec-

tors (weight and bias) initialization. The next step is

to run an activation function on all of the starting reg-

isters in order to progress from the input layer to the

hidden layer. After that any instruction takes place as

described before. If an instruction employs the acti-

vation function, this is a very similar step to creating

a new hidden layer in the neural networks (see ﬁg. 3).

When 100 instructions have been run, only the ﬁrst

three registers are kept and others are set to zero. This

way the neural network keeps the same EncDecAD

architecture. The last step in the decoder part is to run

an activation function again just as it is done on a tra-

ditional neural network. An example of this approach

is provided in the ﬁgure 4.

Given the provided weights and biases in the ﬁg-

ure 4, the proposed evolutionary neural network fol-

lows the instructions on the right side of the ﬁgure.

The numbers next to the instructions show their ex-

ecution order in the ﬁgure. Let’s assume the input

layer consists of variables 3, 20, and -5. Due to sim-

pliﬁcation all weights are set to value 1 and bias is

set to a value 0.1 (see the top blue box on the right of

ﬁgure 4). The ﬁrst three instructions ((1) -(3)) in the

example are for running the activation function which

resembles adding another neural network layer in the

Figure 4: An example of a proposed evolutionary approach to neural network.

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

168

Table 2: Conﬁdence intervals.

Experiment Data set

Sample

mean

Standard

deviation

Sample

size

Population mean

with 95% conﬁdence

Online training

Validation data 2031 713 1000 [1987, 2076]

Resistance testing data 2406 715 1000 [2362, 2450]

Suspension testing data 2469 575 1000 [2433, 2504]

Online training with

self-conﬁguring

neural network

Validation data 1153.72 486.84 1000 [120, 1180]

Resistance testing data 1513.12 397.81 1000 [1490, 1540]

Suspension testing data 1638.24 1180.20 1000 [1570, 1710]

Figure 5: Fitness scores for loosen suspension data in of-

ﬂine training.

traditional scenario. Thus the input layer shown in

blue color progresses to the ﬁrst hidden layer 1 in the

green color. For example, if the input variable is 3,

then after executing the ﬁrst instruction (1), the result

is 3.1 (ReLu(3) retrieves value 3, which multiplied by

1 and added to 0.1, gives the result 3.1). Instruction

(5) executes a multiplication using a neuron S

from

the hidden layer 1. The only way to create another

neural network layer is by running the activation func-

tion which is achieved by the last instruction (6).

4 RESULTS AND DISCUSSION

The data was processed as follows: when the best in-

dividual for the anomaly detection has been found, it

has been stripped off the introns. This resulted in the

individual that has been reduced in its size by over

120 times (from 3000 to 50). The next step was to

do a validation test and run the individual on unseen

non-faulty data. In the following step, the best indi-

vidual is tested on the faulty unseen data (right side of

the ﬁgures 5, 6, 7). This allows us to determine if the

algorithm managed to ﬁnd the anomaly. This step is

executed on the embedded system (see section 3).

The initial step to check the validity of the re-

sults in ofﬂine training included displaying boxplots

of both results: normal (validation) data and the faulty

data (testing) of the loosened suspension data set.

The non-overlapping notches indicate that the sam-

ples come from populations with different medians

Figure 6: Fitness scores in online training.

(µValidation = 23382, µTesting = 85367). With a

95% conﬁdence the validation population mean is be-

tween 23000 and 23800 while with the same 95%

conﬁdence the testing population mean is between

84600 and 86100 (see table 2).

The anomaly detection method presented in the

online training made an assumption that the two data

sets (faulty and normal) were adequately different

from each other to be able to detect the anomaly.

Furthermore, the distributions of all acquired data in

this step followed a normal distribution. Therefore,

Welch’s t-test for independent samples following the

normal distribution data was applied.

The hypothesis is that ﬁtness scores obtained in

the validation and testing differ signiﬁcantly. The

mean of suspension fault (testing) differed signiﬁ-

cantly to the mean of the normal validation data ac-

cording to a Welch’s t-test, t(1911.20) = -15.069, p

< .001, n = 1000. The mean between validation

(µ = 2031.7) and suspension fault data (µ = 2468.77)

is signiﬁcant (see table 2).

The identical hypothesis was tested on the valida-

tion and resistance faulty data. The mean resistance

fault differed signiﬁcantly to the mean of normal val-

idation data according to a Welch’s t-test, t(1997.99)

= -11.72, p < .001, n = 1000. The mean between nor-

mal validation (µ = 2031.7) and suspension fault data

(µ = 2406.44) is signiﬁcant.

Conﬁdence intervals are also shown in ﬁgure 6.

Since notches in all boxplots do not overlap, this con-

cludes that the data in all three sets belong to different

distributions.

Online Encoder-decoder Anomaly Detection using Encoder-decoder Architecture with Novel Self-conﬁguring Neural Networks Pure

Linear Genetic Programming for Embedded Systems

169

Figure 7: Fitness scores in online training using self-

conﬁguring neural network.

The proposed evolving neural network architec-

ture uses the same assumptions as above. The indi-

vidual was trained for 100 000 generations. The re-

sults are as follows: the Welch’s t-test between vali-

dation and suspension showed that t(1329) = 12.0014,

p < .001, n = 1000. The mean between normal

validation (µ = 1153.72) and suspension fault data

(µ = 1638.24) is signiﬁcant. The results between val-

idation and resistance show similar outcome: t(1921)

= 18.0772, p < .001, n = 1000. The mean of resis-

tance data is µ = 1513.12 (see table 2). By conven-

tional criteria, this difference is considered to be ex-

tremely statistically signiﬁcant.

Therefore the proposed EncDecAD using linear

genetic programming veriﬁes these anomalies.

5 CONCLUSION AND FUTURE

WORK

This paper presents two approaches to detect anoma-

lies using encoder-decoder architecture while utiliz-

ing linear genetic programming. This is an improve-

ment compared to the conventional neural network

approach: ﬁrstly, the proposed method is faster by

at least one order of magnitude, and secondly, it can

be easily run on an embedded device. The ﬁrst ap-

proach includes encoder-decoder anomaly detection

using linear genetic programming on an embedded

device. The second ”teaser” approach presented sug-

gests an approach using a self-evolving neural net-

work employing genetic algorithm to simultaneously

evolve the architecture, weights and bias.

The suggested approaches have been evaluated by

applying data from an autonomous multisensor mini-

vehicle with 19 features and a CAN-bus. The vehicle

has been run repeatedly on different paths to gather

data with induced anomalies, such as loosened sus-

pension and soldered resistor in series with the bat-

tery.

The experiments were carried out on an embedded

device, STM32-F407. The results included compar-

ing the distributions of the acquired ﬁtness scores be-

tween the validation (normal) data and testing (faulty)

data. The proposed encoder-decoder anomaly de-

tection using linear genetic programming veriﬁes

anomalies by applying Welch’s t-test on the two data

sets.

To our knowledge there is no previous research

where an encoder-decoder anomaly detection has

been performed using linear genetic programming.

The framework presented for detecting anomalies can

be applied to a broader class of problems including

sequence problems. This can open new opportunities

of having an anomaly detection system in any vehicle,

e.g., placing such a device in an electric vehicle and

allowing it to develop a model for the precise car or

driver.

Further experimental investigations include grad-

uating from encoder-decoder anomaly detection to

adversarial neural networks which may improve the

ability to identify which anomaly has been triggered.

REFERENCES

Ahmed, M., Mahmood, A. N., and Islam, M. R. (2016).

A survey of anomaly detection techniques in ﬁnan-

cial domain. Future Generation Computer Systems,

55:278–288.

Ahmed, R., El Sayed, M., Gadsden, S. A., Tjong, J., and

Habibi, S. (2015). Automotive internal-combustion-

engine fault detection and classiﬁcation using artiﬁ-

cial neural network techniques. IEEE Transactions on

vehicular technology, 64(1):21–33.

An, J. and Cho, S. (2015). Variational autoencoder based

anomaly detection using reconstruction probability.

Special Lecture on IE, 2:1–18.

Assunc¸

ao, F., Lourenc¸o, N., Machado, P., and Ribeiro, B.

(2018). Evolving the topology of large scale deep

neural networks. In European Conference on Genetic

Programming, pages 19–34. Springer.

Banzhaf, W., Nordin, P., Keller, R. E., and Francone, F. D.

(1998). Genetic programming: an introduction, vol-

ume 1. Morgan Kaufmann San Francisco.

Baxt, W. G. (1991). Use of an artiﬁcial neural network for

the diagnosis of myocardial infarction. Annals of in-

ternal medicine, 115(11):843–848.

Brameier, M. and Banzhaf, W. (2001). A comparison of lin-

ear genetic programming and neural networks in med-

ical data mining. IEEE Transactions on Evolutionary

Computation, 5(1):17–26.

Brameier, M. F. and Banzhaf, W. (2007). Basic concepts

of linear genetic programming. Linear Genetic Pro-

gramming, pages 13–34.

Chandola, V., Banerjee, A., and Kumar, V. (2009).

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

170

Anomaly detection: A survey. ACM computing sur-

veys (CSUR), 41(3):15.

Cho, K., Van Merri

enboer, B., Bahdanau, D., and Bengio,

Y. (2014). On the properties of neural machine trans-

lation: Encoder-decoder approaches. arXiv preprint

arXiv:1409.1259.

Dabhi, V. K. and Chaudhary, S. (2015). Empirical modeling

using genetic programming: a survey of issues and

approaches. Natural Computing, 14(2):303–330.

Di Natale, M. (2000). Scheduling the can bus with earliest

deadline techniques. In Proceedings 21st IEEE Real-

Time Systems Symposium, pages 259–268. IEEE.

Hangal, S. and Lam, M. S. (2002). Tracking down soft-

ware bugs using automatic anomaly detection. In Soft-

ware Engineering, 2002. ICSE 2002. Proceedings of

the 24rd International Conference on, pages 291–301.

IEEE.

Hegde, R., Mishra, G., and Gurumurthy, K. (2011). An

insight into the hardware and software complexity

of ecus in vehicles. In International Conference on

Advances in Computing and Information Technology,

pages 99–106. Springer.

Hsu, K.-l., Gupta, H. V., and Sorooshian, S. (1995). Arti-

ﬁcial neural network modeling of the rainfall-runoff

process. Water resources research, 31(10):2517–

2530.

Koza, J. R. and Rice, J. P. (1991). Genetic generation of

both the weights and architecture for a neural network.

In Neural Networks, 1991., IJCNN-91-Seattle Inter-

national Joint Conference on, volume 2, pages 397–

404. IEEE.

Langdon, W. B. and Harman, M. (2015). Optimizing exist-

ing software with genetic programming. IEEE Trans-

actions on Evolutionary Computation, 19(1):118–

135.

Lu, H., Li, Y., Mu, S., Wang, D., Kim, H., and Serikawa, S.

(2018). Motor anomaly detection for unmanned aerial

vehicles using reinforcement learning. IEEE internet

of things journal, 5(4):2315–2322.

Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agar-

wal, P., and Shroff, G. (2016). Lstm-based encoder-

decoder for multi-sensor anomaly detection. arXiv

preprint arXiv:1607.00148.

Mehr, A. D., Kahya, E., and Olyaie, E. (2013). Streamﬂow

prediction using linear genetic programming in com-

parison with a neuro-wavelet technique. Journal of

Hydrology, 505:240–249.

Miikkulainen, R., Liang, J., Meyerson, E., Rawal, A., Fink,

D., Francon, O., Raju, B., Shahrzad, H., Navruzyan,

A., Duffy, N., et al. (2019). Evolving deep neural net-

works. In Artiﬁcial Intelligence in the Age of Neural

Networks and Brain Computing, pages 293–312. El-

sevier.

Mikolov, T., Karaﬁ

at, M., Burget, L.,

Cernock

y, J., and

Khudanpur, S. (2010). Recurrent neural network

based language model. In Eleventh Annual Confer-

ence of the International Speech Communication As-

sociation.

Nordin, P. and Banzhaf, W. (1995). A genetic programming

system learning obstacle avoiding behavior and con-

trolling a miniature robot in real time. Univ., Systems

Analysis Research Group.

Olimex, L. (September, 2018). STM32-E407 development

board USER’S MANUAL. Olimex LTD.

Pachauri, G. and Sharma, S. (2015). Anomaly detec-

tion in medical wireless sensor networks using ma-

chine learning algorithms. Procedia Computer Sci-

ence, 70:325–333.

Rawal, A. and Miikkulainen, R. (2018). From nodes to

networks: Evolving recurrent neural networks. arXiv

preprint arXiv:1803.04439.

Sabokrou, M., Fayyaz, M., Fathy, M., and Klette, R. (2017).

Deep-cascade: Cascading 3d deep neural networks for

fast anomaly detection and localization in crowded

scenes. IEEE Transactions on Image Processing,

26(4):1992–2004.

Schaffer, J. D., Whitley, D., and Eshelman, L. J. (1992).

Combinations of genetic algorithms and neural net-

works: A survey of the state of the art. In Com-

binations of Genetic Algorithms and Neural Net-

works, 1992., COGANN-92. International Workshop

on, pages 1–37. IEEE.

Shao, L., Liu, L., and Li, X. (2014). Feature learning for im-

age classiﬁcation via multiobjective genetic program-

ming. IEEE Transactions on Neural Networks and

Learning Systems, 25(7):1359–1371.

Such, F. P., Madhavan, V., Conti, E., Lehman, J., Stanley,

K. O., and Clune, J. (2017). Deep neuroevolution: ge-

netic algorithms are a competitive alternative for train-

ing deep neural networks for reinforcement learning.

arXiv preprint arXiv:1712.06567.

Taylor, A., Japkowicz, N., and Leblanc, S. (2015).

Frequency-based anomaly detection for the automo-

tive can bus. In WCICSS, pages 45–49.

Tsai, C.-F., Hsu, Y.-F., Lin, C.-Y., and Lin, W.-Y. (2009). In-

trusion detection by machine learning: A review. Ex-

pert Systems with Applications, 36(10):11994–12000.

Tsai, J.-T., Chou, J.-H., and Liu, T.-K. (2006). Tuning the

structure and parameters of a neural network by using

hybrid taguchi-genetic algorithm. IEEE Transactions

on Neural Networks, 17(1):69–80.

Xu, D., Ricci, E., Yan, Y., Song, J., and Sebe, N. (2015).

Learning deep representations of appearance and mo-

tion for anomalous event detection. arXiv preprint

arXiv:1510.01553.

Zhang, L. and Suganthan, P. N. (2016). A survey of ran-

domized algorithms for training neural networks. In-

formation Sciences, 364:146–155.

Online Encoder-decoder Anomaly Detection using Encoder-decoder Architecture with Novel Self-conﬁguring Neural Networks Pure

Linear Genetic Programming for Embedded Systems

171