
A Novel Method for Evaluating Records from a Dataset using
Interval Type-2 Fuzzy Sets
Miljan Vučetić
and Aleksej Makarov
Vlatacom Institute of High Technologies, 5 Milutina Milankovića Blvd, Belgrade, Serbia
Keywords: Interval Type-2 Fuzzy Sets, Conformance Measure, Record Ranking, Interval-valued Aggregation.
Abstract: In this paper, we describe a method for evaluating suitable records from heterogeneous datasets based on
interval type-2 fuzzy sets (IT2FSs). Retrieving records from a dataset including numerical, categorical, binary
and fuzzy data in accordance with diverse user’s preferences is still a challenging task. The main challenge is
how to deal with heterogeneity present when data in attribute values and user’s preferences are different by
nature, e.g. when users explain their interests in linguistic term(s), whereas the attribute value is stored as a
number and vice versa. Furthermore, a user may have different interests among desired preferences expressed
with different data types. Using fuzzy theory can effectively help in handling heterogeneity in building robust
query engines. This efficacy is mitigated when two or more values belong to an ordinary (type-1) fuzzy set
with the same membership degree. We propose a solution based on IT2FSs, which are capable to better
represent uncertainty in data and preferences. It efficiently improves the ranking of suitable records retrieved
from datasets. The connection with aggregation of interval-valued data is also discussed.
1 INTRODUCTION
Nowadays, large datasets are characterized by a
variety of data types. When retrieving suitable
records from such datasets (cars, flats, hotels, etc.) we
need a robust tool to match user’s needs with the most
suitable items. Querying data in heterogeneous
datasets is still a challenging task. Users expect a
query process to provide them with results close to
the desired ones, even when no record ideally
matches the query conditions. In addition, user’s
preferences may vary in their nature (e.g. equal
preferences, weights, constraints and wishes, etc.),
(Vučetić and Hudec, 2018a).
In heterogeneous datasets, we distinguish the
following scenarios related to data heterogeneity: (a)
different attributes may be represented by different
data types including numerical, categorical, binary or
fuzzy data and (b) an attribute may be described using
different data types at the same time (Bashon et al.,
2013). Furthermore, an attribute data type in the
query conditions may not collide with attribute data
types in a dataset. This raises an issue regarding the
appropriateness of data querying mechanisms.
A method presented in (Vučetic and Hudec,
2018b), based on aggregation of fuzzy conformances,
may be used to tackle these issues. In this approach,
the transformation of the data context to a fuzzy
environment is proposed in order to calculate the
similarity between user’s preferences and the values
stored in a dataset. The matching score of fuzzy
conformances is then calculated by different
aggregation operators in order to handle diverse
preferences among attributes. Using type-1 fuzzy sets
(T1FSs) (Zadeh, 1965) for calculating fuzzy
conformance as a measure of closeness does not
provide a means for distinguishing between values
belonging to the same fuzzy set with the same
membership degree (although the difference can be
perceived intuitively). Fig. 1 shows a situation with
Short distance between a hotel and the city centre,
where x
1
=50m and x
2
=200m have the same
membership value (i.e. µ
Short
(50) = µ
Short
(200)=1).
User may require the expected walking distance from
a hotel to the city centre to be less than 100m, but in
a dataset real numbers stored as walking distance of
120m and 200m are identically treated. As Klein
states (Klein, 1980), the natural order of real numbers
can be lost in fuzzy semantic. However, by using
general type-2 fuzzy sets (Wagner and Hagras, 2010)
we can interpret the difference between x
1
and x
2
. This
might be useful when retrieving the most suitable
items from a dataset and sorting them in accordance
with the users’ requirements. In order to improve data
Vu
ˇ
ceti
´
c, M. and Makarov, A.
A Novel Method for Evaluating Records from a Dataset using Interval Type-2 Fuzzy Sets.
DOI: 10.5220/0008068403090316
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 309-316
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
309

ranking, we have extended our approach by using
interval type-2 fuzzy sets (IT2FSs) (Liu and Mendel,
2008). In the past, IT2FSs were proposed for their
computational efficiency with respect to other general
type-2 fuzzy sets (Mendel, 2001).
Distance [m]
Short
1
0
µ(x)
300x
1
=50 x
2
=200
Figure 1: Issue with T1FS in fuzzy conformance
calculation.
The rest of this paper is organized as follows.
Section 2 introduces the interval-valued conformance
measure. Section 3 presents aggregation of interval-
valued conformances and provides an illustrative
example. The discussion is presented in Section 4.
Finally, Section 5 draws concluding remarks.
2 INTERVAL-VALUED
CONFORMANCE MEASURE
The similarity among heterogeneous attributes’
values is a complicated task, because user perception
is a relative concept. This work proposes a new
understanding of matching user’s preferences with
records (items) in a dataset.
2.1 Basics of Fuzzy Sets
Fuzzy theory introduced by (Zadeh, 1965) has been
successfully applied to many data mining tasks
(Marsala and Bouchon-Meunier, 2015). A T1FS
shown in Fig. 2 can be represented as
where the numerators are the
membership degrees to the fuzzy set A of the numbers
in the denominators. The membership degree of each
element belongs to the [0, 1] interval. The degree that
fuzzy number B is in the fuzzy concept (or family of
fuzzy concepts) is calculated by the possibility
measure (Galindo, 2008; Zadeh, 1978):
(1)
where X is a universe of discourse and t is a t-norm.
In practice, the minimum t-norm is used. Eq. (1) is
applicable when we want to match two fuzzy sets,
where the one appears in the user’s requirements and
the other in the attribute values.
1
0
µ
A
(x)
5020 40
A
60
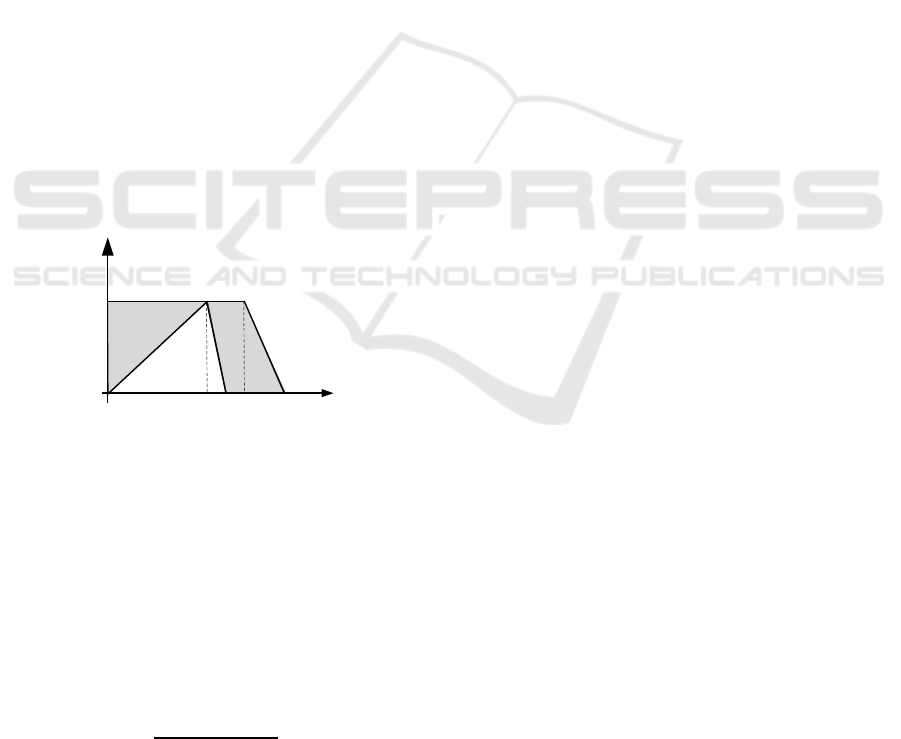
Figure 2: Type-1 fuzzy set.
Although introduced to model uncertainty,
research has shown some limitations of T1FSs
(Mendel, 2001). The membership grades of T1FSs
are crisp values. In the previous section we illustrated
a potential problem with retrieving suitable records
when two values belong to the same fuzzy set with
the same membership degrees. In this work, we show
how IT2FSs can be applied for matching the user’s
preferences with records (items) in a dataset. Unlike
a T1FS, whose membership degree for x from
universe of discourse X is a number, the membership
degree of IT2FS is an interval (e.g. number 30 has a
membership degree [0.20, 1] and number 50 [0.75,
1]). Say an IT2FS
is bounded by two fuzzy sets A
U
and A
L
, characterised by upper and lower membership
functions, µ
A
U
(x) and µ
A
L
(x), respectively (Mendel et
al., 2006). The area between the upper and lower
fuzzy sets is called the footprint of uncertainty (FOU)
as shown in Fig. 3.
x
FOU
0
µ
5020 40 60
0.75
A
U
A
L
1
Figure 3: An interval type-2 fuzzy set.
2.2 Fuzzy Conformance based on
Interval Type-2 Fuzzy Sets
Retrieving records from a dataset can be complicated
when matching complex user’s requirements to
records in a dataset with heterogeneous (mixed) data
types. Furthermore, a record (item) may be a
candidate if it is close to the desired values per
observed attributes (conditions). A method based on
fuzzy conformance and aggregation functions
(Vučetić and Hudec, 2018b) is proposed to that effect.
Our results suggest that fuzzy conformance can be
applied in calculating similarity among the attribute
and the expected values for an item in a dataset. The
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
310
matching score is a crisp value from the unit interval
indicating how items (records) are conformant with
the desired ones on observed attributes A
i
(i = 1,...,n).
Fuzzy conformance, based on type-1 fuzzy sets and
proximity relations, enables straightforward handling
of heterogeneous data types and is calculated as
(Vučetić, 2013):
(2)
where C is the fuzzy conformance of an attribute A
i
defined on domain D
i
between the user requirement t
u
and a record t
j
in a dataset, s is a proximity relation
and
tu
(A
i
) and
tj
(A
i
) are the membership degrees of
the user preferred value and of the j
th
value in a dataset
mapped to T1FSs on fuzzified domain, respectively.
Thus, by using T1FSs in the fuzzy conformance
measure of observed attributes (Eq. (2)), semantic
relations in the user’s perception can be lost (e.g. a
user sets the preferred distance from a hotel to the city
centre to be around 200m; hence the distances of
180m and 220m have the same membership degrees
µ
Short
(180) = µ
Short
(220) = 1 to the trapezoidal fuzzy
set Short distance, although the user would prefer a
shorter distance). One of the ways of approaching this
problem is to use IT2FSs (Bustince, 2000; Wu et al.,
2012) as illustrated on Fig. 4:
Distance [m]
Short
1
0
µ
300
250
200
Around 200
500
Figure 4: Fuzzy conformance of the attribute Distance with
IT2FS.
As previously, the IT2FS representation can be
defined as µ(x) = [µ
A
L
(x), µ
A
U
(x)]. Following this, we
calculate the membership degrees of 180m and 200m
as µ(180) = [0.9, 1] and µ(220) = [0.6, 1]. Intuitively,
we can perceive the difference between the two
values although the interval-valued membership
degree handles higher level of uncertainty than the
crisp membership degree. In addition, an IT2FS has a
crisp output as follows:
(3)
Eq. (3) also confirms the user’s preferences of the
distance value of 180m (y
= 0.95) over 220m (y
=
0.80).
This allows for developing a robust query engine
for manipulating heterogeneous data and ranking
items (records) in accordance with the user’s
preferences. We can now formulate the fuzzy
conformance measure based on IT2FS as:
(4)
where
is an interval-valued fuzzy conformance of
attribute A
i,
and
are the interval-
valued membership degrees of the user’s desired
feature and of a value in a dataset at the observed
attribute A
i,
, respectively, and is a proximity relation
which also may be an interval. Note that the min
function is straightforwardly applied on intervals,
simply by putting min ([x
1
, y
1
], …,[x
n
, y
n
]) = [min(x
1,
…,
x
n
), min(y
1, …,
y
n
)] (Mesiar et al., 2018).
In order to model the user’s requirements and to
match them with items in a dataset with
heterogeneous data types, we need to transform all
data to a fuzzy domain. Domains of numeric
attributes are fuzzified into appropriate fuzzy sets,
while categorical and binary data types are treated as
fuzzy singletons. For example, the domain of the
attribute Distance related to the hotel distance from
the city centre is fuzzified into three fuzzy sets: short,
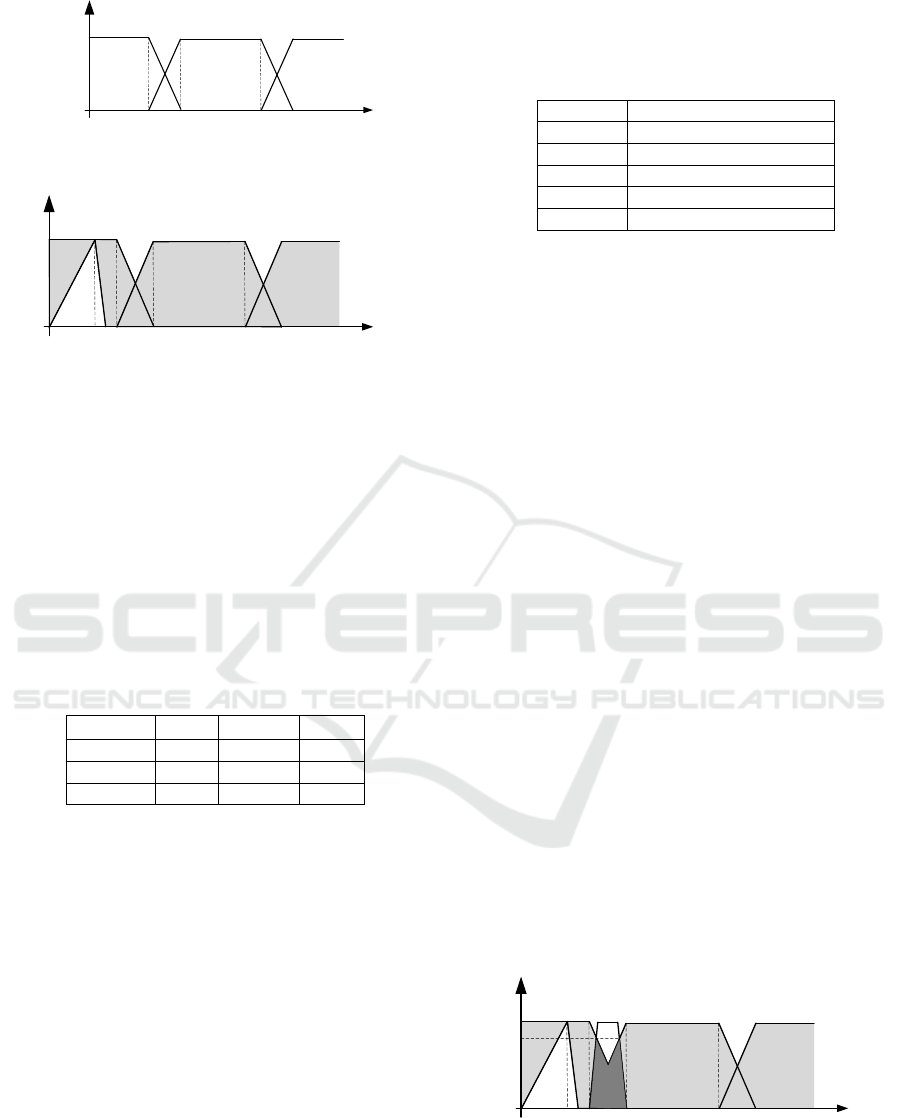
medium and long, as shown in Fig. 5. From the user’s
perspective, T1FSs are useful for modelling different
opinions from different individuals regarding their
preferences. Regardless of the data type in which the
user expresses their preferences (e.g. the user prefers
the distance from the city centre to the hotel to be
200m as depicted in Fig. 6), a T1FS-based model is
used (the triangular fuzzy set (0, 200, 250) in the
example depicted by Fig. 6) because an item from
datasets may be a possible solution even if it is similar
to the desired one. An IT2FS is defined by combining
the fuzzified attribute domain with fuzzy sets
representing users’ preferences, as shown in Fig. 6.
This IT2FS is dynamically changing due to different
requirements of different users. Hence, IT2FS is
accompanied by atomic conditions in a query when
retrieving records from a dataset.
A proximity relation is used for calculating fuzzy
conformances at the observed attributes. This relation
is reflexive and symmetric without limitation caused
by the transitivity property of similarity relation
(Shenoi and Melton, 1999). The proximity relation
introduces a closeness measure over the scalar
attribute domains such as those illustrated in Table 1
A Novel Method for Evaluating Records from a Dataset using Interval Type-2 Fuzzy Sets
311
Distance [m]
Short
1
0
µ(x)
500
300
1000 1200
Medium
Long
200
Figure 5: Fuzzified domain over the attribute Distance.
Distance [m]
Short
1
0
500
300
1000 1200
Medium
Long
200
t
u
=200m
Figure 6: The IT2FS of the attribute Distance for matching
user’s preferences with records in a dataset.
for the attribute Distance. This work offers a way to
define the proximity relation between the fuzzy
domain partitions as an interval that generalizes the
ones valued on [0, 1] (Gonzales del Campo et al.,
2009). Sometimes it is easier for an expert to provide
a proximity interval rather than a value from a unit
interval. The benefit of the interval-valued proximity
relations in selecting the best option from a set of
solutions is addressed in (Bentkowska et al., 2015).
Table 1: The proximity relation over the fuzzified domain
of the attribute Distance.
Distance
short
medium
long
short
1
0.75
0
medium
1
0.60
long
1
The interval-valued proximity relation maps into
an interval [x, y]. In many applications we set x = y,
i.e. the proximity relation becomes a crisp number as
shown in Table 1. In this work we assume that a fuzzy
number belonging to two fuzzy sets is defined on the
domain of an attribute whose proximity is represented
by an interval. For example, if a user prefers the
distance from a hotel to the city centre between 350m
and 450m, then in accordance with Fig. 6, the
proximity is an interval [0.75, 1] (see Table 1.).
By way of illustration, let us consider the selection
of a hotel in a city. Every customer has requirements
related to the price, the distance from the centre, the
category, the quality of service or the availability of a
swimming pool. We illustrate the calculation of fuzzy
conformances on the attribute Distance from the city
centre. The user’s expectation about the distance is
t
u
(Distance) = 200m. Dataset details, given in Table
2, contain information about the distance of hotels
from the city centre.
Table 2: Distance of a hotel from the city centre.
Record
Distance (A
1
)
t
1
190m
t
2
less than 400m
t
3
between 350m and 450m
t
4
1340m
t
5
around 600m
Using Eq. (4), the fuzzy sets for the user’s
preference and the domain of the attribute A
1
shown
in Fig. 6 as well as the proximity relation defined in
Table 1, the interval-valued fuzzy conformances are
obtained as follows:
(see Fig. 7)
For the interval-valued fuzzy conformances we
compute crisp outputs: 0.975, 0.875, 0.4, 0, and
0.375, respectively. Consequently, the ranking of the
records related to the attribute A
1
(t
1
– t
2
– t
3 –
t
5
– t
4
)
is in accordance with the user expectation. This is a
beneficial contribution regarding ranking (sorting by
relevance) items from datasets in order to provide
better selection of suitable records.
Distance [m]
Short
1
0
500
300
1000 1200
Medium
Long
200
t
u
=200m
0.8
b/w 250m-350m
Figure 7: Interval-valued fuzzy conformance of the
attribute Distance between t
u
and t
3
.
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
312

Similarly, we compute fuzzy conformances for
other attributes. Say the attribute A
2
is categorical,
describing the quality of service. The user expresses
their preference as {good, excellent}, while
t
4
(Quality_of_Service) = {good} and
QoS
(good,
excellent) = 0.80. Fuzzy conformance is computed as
follows:
The presence of swimming pool in a hotel can be
expressed by a binary attribute, say A
4
. In such a case,
the interval-valued conformance usually takes values
[0, 0] or [1, 1]. In theory, however, the proximity
between two binary values can be greater than 0
unlike in the presented example.
The computed interval-valued fuzzy
conformances for attributes A
1
– A
4
between the user
preferences expressed by the vector of ideal values tu
and records t
1
to t
5
are shown in Table 4.
3 AGGREGATING
INTERVAL-VALUED FUZZY
CONFORMANCES
This section examines the most expected cases of
aggregation of interval-valued conformances among
attributes which might be raised by users. These
aggregations are able to cover a variety of needs for
aggregating conformances (Hudec and Vučetić,
2019). The proposed aggregations for the main
classes of problems based on the observations
(Dujmovic, 2018) are summarized in Table 3.
The aggregation of intervals is covered by (Mesiar
et al., 2018). Theoretically, we can consider an
interval as a pair of numbers (the lower and upper
bounds). Thus, we can straightforwardly apply the
usual aggregation functions by putting A([x
1
, y
1
],
…,[x
n
, y
n
]) = [A(x
1
, …,x
n
), A(y
1
, …,y
n
)].
When all conditions are equally important and
should be at least partially met, we should apply
conjunction, usually expressed through t-norms. The
minimum t-norm, adjusted for the interval-valued
fuzzy conformance (4), for a record t
j
is computed as:
(5)
(where n is the number of atomic conditions). The
solution is shown in Table 5 where the lower bound
Table 3: Type of aggregation and suggested operators.
Type of aggregation
Suggested operators
Conjunction of equally
important atomic
conditions
For smaller number of
atomic conditions, a non-
idempotent t-norm
Weak conjunction of
equally important atomic
conditions
Averaging functions of the
ANDNESS measure
greater than 0.5, e.g. the
geometric or harmonic
mean.
Weak disjunction of
atomic conditions
(conditions considered as
alternatives)
Averaging functions of the
ORNESS measure greater
than 0.5, e.g., the
quadratic mean.
At least majority of
conditions should be
satisfied
Quantified query
condition
At least majority of
conditions should be
satisfied, but some of
them should be
imperatively met
Aggregation of a
quantified query condition
with a non-idempotent t-
norm.
Coalitions of atomic
conditions
Choquet integral
is minimum of the lower bounds of all atomic
interval-valued fuzzy conformances, whereas the
upper bound is the minimum of their upper bounds.
Other t-norms have not been considered due to the
downward reinforcement (Beliakov et al., 2007)
which becomes more pronounced with a higher
number of either common or interval-valued atomic
conformances. Just for illustrative purposes, the
product t-norm is given by:
(6)
The t-norm functions map their inputs into the unit
interval, i.e. [0, 1]
n
→ [0, 1], where 1 is the ideal case,
i.e. the perfect match. Non-idempotent t-norms may
result in poor record match scores and mislead the user
to conclude that the records poorly match their
preferences. On the other hand, due to ignoring values
greater than the minimal one, Eq. (5) makes no
distinction between a tuple having interval-valued
fuzzy conformances of e.g. say [0, 0.2] and [0.1, 0.3]
and another with conformances of say [0, 0.2] and [0.8,
0.9].
The weak or full disjunctions are not solutions for
this class of tasks because one significant conformance
substitutes (all) other weak conformances.
Thus, an alternative could be uni-norm. This class
of functions meets the property of full reinforcement
(Beliakov et al., 2007). The 3-∏ function (Yager and
A Novel Method for Evaluating Records from a Dataset using Interval Type-2 Fuzzy Sets
313

Table 4: Interval-valued fuzzy conformances of attributes A
1
to A
4
between user preferences and records t
1
to t
5
.
Record
C(A
1
[t
u
, t
j
])
C(A
2
[t
u
, t
j
])
C(A
3
[t
u
, t
j
])
C(A
4
[t
u
, t
j
])
t
1
[0.95, 1]
[0.85, 0.95]
[0.85, 0.85]
[1, 1]
t
2
[0.75, 1]
[0.25, 0.35]
[0.26, 0.37]
[1, 1]
t
3
[0, 0.8]
[0.65, 0.75]
[0.46, 0.56]
[0, 0]
t
4
[0, 0]
[0.8, 1]
[0.88, 0.92]
[1, 1]
t
5
[0, 0.75]
[1, 1]
[1, 1]
[1, 1]
Table 5: Aggregation of interval-valued fuzzy conformances by different suggested operators.
Record
min t-norm (5)
product t-norm (6)
uni-norm (7)
geom. mean (8)
quantified (9)
t
1
[0.85, 0,85]
[0.687, 0.807]
[1, 1]
[0.910, 0.948]
[1, 1]
t
2
[0.25, 0.35]
[0.049, 0.129]
[1, 1]
[0.470, 0.600]
[0.162, 0.45]
t
3
[0, 0]
[0, 0]
[0, 0]
[0, 0]
[0, 0.069]
t
4
[0, 0]
[0, 0]
[0, 0]
[0, 0]
[0.425,0.575]
t
5
[0, 0.75]
[0, 0.75]
[0, 1]
[0, 0.931]
[0.625, 1]
Rybalov, 1996) is adjusted to calculate the interval-
valued fuzzy conformance (4) of a record t
j
as:
(7)
The product in the numerator (7) ensures that only
the records (items) at least partially satisfying all the
specified conditions are considered, i.e. the value 0 is
annihilator. Due the disjunction used in the
denominator in the mixed aggregation function (7),
the value 1 is the neutral element. Consequently, the
uni-norm has the desired behaviour when
conformances are in the open interval (0, 1).
Applying (7) on the data shown in Table 4 results in
records either fully meeting or fully rejecting the user
preferences, except for record t
5
. The main problem is
annihilator 0 for the conjunctive part and neutral
element 1 for the disjunctive part. Therefore, we
should be careful when considering the uni-norm.
Another option is to use averaging aggregation
functions, which are suitable since small values are
compensated by high values. In (Vučetic and Hudec,
2018b), it was shown that the geometric mean is a
suitable option. The same holds for the aggregation of
interval-valued fuzzy conformances:
(8)
Furthermore, there are cases when it suffices that
the majority of interval-valued fuzzy conformances is
greater than 0. The corresponding aggregation is
calculated as:
(9)
where is the interval-valued validity or the
matching degree for item t
j
to a quantified condition,
n is the number of conformances and µ
Q
is the
function of relative quantifier most of in the sense of
Zadeh (1983), expressed as the increasing linear
function with parameters (interval bounds) 0.5 and
0.9. However, this approach is suitable when all
atomic conditions are weak, i.e. when there is no
particular conformance which should be imperatively
greater than zero.
The results of the aggregation operators
considered above are intervals of numbers. However,
for ranking purposes, one needs to provide a single
value. The conversion to a single number can be
realized by selecting the mid-point of the interval (Eq.
(3)). This selection is also compatible with
defuzzification of interval when the interval is
considered as a symmetric triangular fuzzy set whose
most expected value is in its middle and whose
support is its length. Therefore, defuzzification can be
simplified as (Bojadziev and Bojadziev, 2007):
(10)
where a is the lower bound of an interval, m is its mid-
point or its most expected value, b is its upper bound
and s is a coefficient from the set of natural numbers
regulating the prominence of the modal point. In a
case of a symmetric fuzzy set, any value of s provides
the same result. For instance, the solution for tuples
in Table 5 evaluated by uni-norm (7) is 1, 1, 0, 0 and
0.5 for tuples t
1
, t
2
, t
3
, t
4
and t
5
, respectively. The
defuzzified results are shown in Table 6.
Expectedly, the ranking of records depends on the
aggregated function. The quantified aggregation for
the tuple t
4
gives a significantly higher score. The
main reason is that 0 and 1 are neither annihilators nor
neutral elements, therefore these values contribute in
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
314

Table 6: Defuzzified scores from (10) for data in Table 5.
Rec.
(5)
(6)
(7)
(8)
(9)
t
1
0.85
0.747
1
0.929
1
t
2
0.30
0.089
1
0.535
0.306
t
3
0
0
0
0
0.034
t
4
0
0
0
0
0.50
t
5
0.375
0.375
0.5
0.465
0.812
satisfying the majority of fuzzy conformances. Users
should be careful when selecting a particular
aggregation. Guidance can be inferred from Table 3.
The aggregation of coalitions can be realized by the
Choquet integral-based aggregation (Choquet, 1954).
While an attribute can be less important per se, its
importance increases when combined with other
attributes (e.g. attributes A
1
and A
3
have equal weights
of 0.4, but their combined weight is 0.7 as shown in
Fig. 8). A modified expression for the Choquet integral
(Beliakov et al., 2007) in which crisp numbers are
replaced by the interval-valued fuzzy conformance is:
(11)
where conformances are expressed as
(A
i
[t
u,
t
j
])=
i
(t
j
) as in (4),
0
(t
j
) = 0 by convention,
is a non-decreasing permutation of
conformances for tuple t
j
and v is a fuzzy measure of
H
i
= {(i), …, (n)}. The fuzzy measure v is a set function
(Wang and Klir. 1992):
which is
monotonic and satisfies
and
,
. For the sake of illustration, let the
weights of coalitions among attributes A
1
to A
4
be those
shown in Fig. 8. The Choquet discrete integral is an
averaging function, resulting in an interval defuzzified
to a crisp number inside the interval bounds, as shown
in Table 7.
v(N)
1
v({A
1
, A
2
, A
3
})
0.80
v({A
1
, A
2
, A
4
})
0.70
v({A
1
, A
3
, A
4
})
0.50
v({A
2
, A
3
, A
4
})
0.70
v({A
1
, A
2
})
0.60
v({A
1
, A
3
})
0.70
v({A
1
, A
4
})
0.30
v({A
2
, A
3
})
0.45
v({A
2
, A
4
})
0.30
v({A
3
, A
4
})
0.30
v({A
1
})
0.40
v({A
2
})
0.45
v({A
3
})
0.40
v({A
4
})
0.25
v(0)
0
Figure 8: The set function v for attributes A
1
, A
2
, A
3
and A
4
.
Table 7: Solution of the Choquet integral equation (11) for
data from Table 5.
Record
solution
defuzzified value
t
1
[0.892, 0.935]
0.913
t
2
[0.464, 0.549]
0.506
t
3
[0.292, 0.582]
0.437
t
4
[0.614, 0.668]
0.641
t
5
[0.7, 0.925]
0.812
4 DISCUSSION
This work was inspired by difficulties in resolving
uncertainties in ordinal fuzzy sets (Gaussian,
trapezoidal or triangular). The collected data may be
of mixed data types, i.e. numerical, categorical or
fuzzy for the same attribute. In addition, in many
tasks, the user may define a wide range of
preferences, modalities and interdependencies among
attributes. In this paper we propose a novel method
for improved ranking of the most suitable records
(items) from datasets when uncertainty cannot be
ignored. Let us consider the following tuples in the
hotel selection problem (the selection criteria are: the
distance from the city center, the quality of service,
the price and the availability of swimming poll): the
vector of user preferences t
u
=(200m, {good,
excellent}, about 45 EUR, Yes) and records from a
dataset t
1
=(180m, {good, excellent}, about 45 EUR,
Yes) and t
2
=(220m, {good, excellent}, about 45
EUR, Yes). When retrieving the most suitable records
using the conformance measure, t
1
and t
2
have the
same matching scores when obtained by ordinary
fuzzy sets, due to µ
Short
(200) = µ
Short
(180)= µ
Short
(220)
= 1 (Fig. 5). The proposed method uses IT2FSs to
better handle the uncertainty caused by the data
heterogeneity and improves selection and sorting of
the most suitable item increasing the discriminating
power of matching scores (µ(180) = [0.9, 1] (dfz =
0.95), and µ(220) = [0.6, 1] (dfz = 0.80) as shown in
Fig. 4). When aggregating these conformances, the
record t
1
will be better ranked, in accordance with the
user’s expectation due to the shorter distance.
In addition, we examined conjunctive (including
non t-norms), averaging and hybrid aggregation
functions in order to cover diverse preferences among
atomic conditions demanded by users. These
aggregations are made to act on intervals. We
considered the most frequent cases. From practical
point of view, selecting a suitable aggregation
function is not a trivial task. Hence, more research is
needed in this direction.
5 CONCLUDING REMARKS
Data heterogeneity cannot be ignored in real-world
problems. Ranking of the most suitable records is a
challenging issue in such datasets. Our work
highlights the impact of IT2FSs in improving the
matching of complex user requirements with records
(items) in a dataset when heterogeneous data are
considered. The goal is to improve the ranking of
A Novel Method for Evaluating Records from a Dataset using Interval Type-2 Fuzzy Sets
315

records in data retrieval tasks. We have discussed
several aggregation operators applied to [0, 1]
interval in order to cope with diversity of attributes in
users’ preferences. We believe that this study may
help software engineers and practitioners in building
robust frameworks for data retrieval tasks and
recommendation problems when dealing with
uncertain data. Also, this task is interesting from a
machine learning perspective. Namely, machine
learning might help in selecting appropriate
aggregation functions and fitting their parameters.
REFERENCES
Bashon, Y., Neagu, D., Ridley, M. J. 2013. A framework
for comparing heterogeneous objects: on the similarity
measurements for fuzzy, numerical and categorical
attributes. Soft Computing, 17(9): 1595-1615.
Beliakov, G., Bustince, H., Calvo, T. 2016. A Practical
Guide to Averaging Functions, Springer, Berlin.
Beliakov, G., Pradera, A., Calvo, T. 2007. Aggregation
Functions: A Guide for Practitioners, Springer, Berlin.
Bentkowska, U., Bustince, H., Jurio, A., Pagola, M.,
Pekala, P. 2015. Decision making with an interval-
valued fuzzy preference relation and admissible orders.
Applied Soft Computing, 35:792-801.
Bojadziev, G., Bojadziev, M. 2007. Fuzzy Logic for
Business, Finance and Management, World Scientific
Publishing Co., London.
Bustince, H. 2000. Indicator of inclusion grade for interval-
valued fuzzy sets. Application to approximate
reasoning based on interval-valued fuzzy sets.
International Journal of Approximate Reasoning,
23(3):137–209.
Choquet, G. 1954. Theory of capacities. Ann. Inst. Fourier,
5:131-192.
Dujmovic, J. 2018. Soft computing evaluation logic, Wiley-
IEEE, Hoboken.
Galindo, J. 2008. Introduction and Trends to Fuzzy Logic
and Fuzzy Databases. In Handbook of Research on
Fuzzy Information Processing in Databases, pages. 1-
33. Information Science Reference, Hershey.
Gonzáles del Campo, R., Garmendia, L., Recasens, J. 2009.
Transitive closure of interval-valued relations. In IFSA-
EUFSLAT 2009, Lisbon.
Hudec, M., Vučetić, M. 2019. Aggregation of fuzzy
conformances. In Halaš, R., Gagolewski, M., Mesiar,
R. (Eds.), New Trends in Aggregation Theory, Springer.
Klein, E. 1980. A semantics for positive and comparative
adjectives. Linguistics and Philosophy, 4(1):1-45.
Liu, F., Mendel, J.M. 2008. Encoding words into interval
type-2 fuzzy sets using an Interval Approach. IEEE
Trans. on Fuzzy Systems, 16(6): 1503–1521.
Marsala, C., Bouchon-Meunier, B. 2015. Fuzzy data
mining and management of interpretable and subjective
information. Fuzzy Sets and Systems. 281:252-259.
Mendel, J. M. 2001. Uncertain Rule-Based Fuzzy Logic
Systems: Introduction and New Directions, Upper
Saddle River, New Jersey, Prentice-Hall.
Mendel, J.M., John, R., Liu, R. 2006. Interval type-2 fuzzy
logic systems made simple. IEEE Trans. on Fuzzy
Systems, 14(6):808–821.
Mesiar, R., Borkotokey, S., Jin, L., Kalina, M. 2018.
Aggregation Under Uncertainty. IEEE Trans. on Fuzzy
Systems, 26(4):2475-2478.
Shenoi, S., Melton, A. 1999. Proximity relations in the
fuzzy relational database model. Fuzzy Sets and
Systems, 100:51-62.
Vučetić, M. 2013. Analysis of functional dependencies in
relational databases using fuzzy logic. PhD thesis,
University of Belgrade, Serbia.
Vučetić, M., Hudec, M. 2018 (a). A fuzzy query engine for
suggesting the products based on conformance and
asymmetric conjunction. Expert Systems with
Applications, 101:143-158.
Vučetić M., Hudec, M. 2018 (b). A Flexible Approach to
Matching User Preferences with Records in Datasets
Based on the Conformance Measure and Aggregation
Functions. In 10
th
International Joint Conference on
Computational Intelligence (IJCCI 2018), Seville.
Wagner, C., Hagras, H. 2010. Toward general type-2 fuzzy
logic systems. IEEE Trans. on Fuzzy Systems, 18(4):
637-660.
Wang, Z., Klir, G. 1992. Fuzzy Measure Theory, Plenum
Press, New York.
Wu, D., Mendel, J.M., Coupland, S. 2012. Enhanced
Interval Approach for encoding words into interval
type-2 fuzzy sets and its convergence analysis. IEEE
Trans. on Fuzzy Systems, 20(3): 499-513.
Yager, R., Rybalov, A. 1996. Uninorm aggregation
operators. Fuzzy Sets and Systems, 80:111–120.
Zadeh, L.A. 1965. Fuzzy sets. Information and Control, 8:
338–353.
Zadeh, L.A. 1978. Fuzzy sets as a basis for a theory of
possibility. Fuzzy Sets and Systems, 1:3-28.
Zadeh, L.A. 1983. A computational approach to fuzzy
quantifiers in natural languages. Computers &
Mathematics with Applications, 9:149–184.
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
316
