Past-future Mutual Information Estimation in Sparse Information

Conditions

Yuval Shalev

and Irad Ben-Gal

Laboratory for AI, Machine Learning, Business & Data Analytics, Department of Industrial Engineering,

Keywords:

Past-future Mutual Information, Context Tree, Transfer Entropy, Time Series Analysis.

Abstract:

We introduce the CT-PFMI, a context tree based algorithm that estimates the past-future mutual information

(PFMI) between different time series. By applying a pruning phase of the context tree algorithm, uninfor-

mative past sequences are removed from PFMI estimation along with their false contributions. In situations

where most of the past data is uninformative, the CT-PFMI shows better estimates to the true PFMI than other

benchmark methods as demonstrated in a simulated study. By implementing CT-PFMI on real stock prices

data we also demonstrate how the algorithm provides useful insights when analyzing the interactions between

ﬁnancial time series.

1 INTRODUCTION

Accurate estimation of the mutual information be-

tween the past of one time series and the future of

another is an important task in time series analysis.

For instance, the transfer entropy (Schreiber, 2000),

that measures the conditional past-future mutual in-

formation (PFMI) between the past of one or more

time series and an output time series that are condi-

tioned on the past of the output time series, has been

widely explored in the past two decades in various do-

mains such as neural-science and economics (Bosso-

maier et al., 2016). However, a difﬁculty arises when

PFMI needs to be estimated from data observations.

The number of possible sequences that potentially

contributes to the mutual information increases expo-

nentially with the number of time lags. When most

realized past sequences are uninformative about the

future, a condition we call sparse PFMI, large num-

ber of false contributors could lead to overestimation

of PFMI, hence associating predictive power to unin-

formative sequences.

The methods that are used to estimate PFMI, usu-

ally in the context of transfer entropy estimation,

are based on commonly used MI estimation meth-

ods ranging from naive binning (also called the Plug-

in method) to bias and variance corrections such as

the nearest neighbors method (Montalto et al., 2014;

https://orcid.org/0000-0003-2125-9735

https://orcid.org/0000-0003-2411-5518

Runge et al., 2012). When applied to time series,

these methods resolve the time dimensionality prob-

lem by removing uninformative time lags entirely.

Nevertheless, to the best of our knowledge, none of

these methods apply estimation correction at a real-

ization level, which has a greater potential for dimen-

sionality reduction and can provide an insightful per-

spective on the nature of the underlying interactions.

We provide such a solution by estimating the

PFMI using an expansion of the context tree (CT) al-

gorithm which is called the input/output context tree

(I/O CT) algorithm (Ben-Gal et al., 2005; Brice and

Jiang, 2009). This algorithm parses the input time

series into a tree of contexts (sequences), where in

each node, the conditional probability of the out-

put given the context is assigned. Next, only nodes

with conditional probabilities that are signiﬁcantly

different from those of their parent nodes (often mea-

sured by the Kullback-Liebler divergence) are kept,

and the others are pruned. This algorithm, as well

as other algorithms from the Variable Order Markov

Models family, were proposed to overcome overﬁt-

ting in learning tasks such as classiﬁcation and pre-

diction (Ben-Gal et al., 2005; Begleiter et al., 2004;

Shmilovici and Ben-Gal, 2012; Yang et al., 2014). Es-

timating the information between a time series’ past

and future was usually not one of the tasks these al-

gorithms were used for. We show how to estimate

PFMI between time series as the sum of the Kullback-

Leibler divergence (Kullback and Leibler, 1951) be-

Shalev, Y. and Ben-Gal, I.

Past-future Mutual Information Estimation in Sparse Information Conditions.

DOI: 10.5220/0008069300650071

In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 65-71

ISBN: 978-989-758-382-7

tween the root node and the leaves of I/O CT. The

proposed procedure is implemented by a proposed

context tree past-future mutual information algorithm

(CT-PFMI): First, a full I/O CT is built. Second, the

PFMI is calculated for descending values of the prun-

ing constant c, a positive parameter which deﬁnes the

number of pruned sequences(Ben-Gal et al., 2003).

Third, by identifying the threshold at which redun-

dant information is removed, a value of c is chosen to

obtain an estimate for the "ﬁltered" PFMI as well as

most of the informative sequences.

In the results section it is shown that in simulated

sparse PFMI condition, the CT-PFMI estimates the

PFMI more accurately than benchmark methods. The

proposed CT-PFMI is also implemented on real time

series of stock prices returns, that due to market efﬁ-

ciency, follow the sparse PFMI condition (Shmilovici

and Ben-Gal, 2012). The outcome of the CT-PFMI

algorithm can also be exploited to gain important in-

sights by performing a higher-resolution analysis of

the PFMI contributors as demonstrated by real time

series data.

To conclude, the ﬁrst contribution of this paper is

to demonstrate the extraction of PFMI from an I/O CT

constructed from input and output time series. The

second contribution is the introduction of a novel al-

gorithm, called the CT-PFMI. This algorithm, is used

for PFMI estimation, while offering a new method of

identifying the value of the pruning constant that gov-

erns the compression rate. The third contribution is

showing how the CT-PFMI algorithm can be used for

in-depth analysis of interaction’s insights in the data.

2 RELATED WORK

In the previous section we mentioned the works on

transfer entropy (Schreiber, 2000; Bossomaier et al.,

2016) as an important source for discussion on esti-

mating the information ﬂow between the past and the

future of time series.

Researchers such as (Runge et al., 2012; Montalto

et al., 2014) used standard methods of MI estimation,

such as binning (Cover and Thomas, 2012) or nearest-

neighbours (Kraskov et al., 2004), to estimate TE. Ac-

cording to those methods, when a speciﬁc time lag is

found to be informative in some speciﬁc realizations,

all its realizations, including the uninformative ones,

are included in the estimation. In sequential data,

where the number of different realizations is poten-

tially large, this drawback can be crucial by adding

many uninformative sequences to the estimation af-

fecting both the TE accuracy as well as the extracted

insights from the data.

To overcome this challenge, we utilize the CT

algorithm, a member of the family of Variable Or-

der Markov Models that were originally constructed

for compression of a single time series, and found

it to be well-suited to the prediction task of discrete

time series (Weinberger et al., 1995; Begleiter et al.,

2004; Shmilovici and Ben-Gal, 2012). Variable Or-

der Markov Models and their usage have been exten-

sively explored (Begleiter et al., 2004; Shmilovici and

Ben-Gal, 2012; Yang et al., 2014; Slonim et al., 2003;

Largeron-Leténo, 2003; Society et al., 2014; Chim

and Deng, 2007; Ben-Gal et al., 2003; Begleiter et al.,

2013; Ben-Gal et al., 2005; Kusters and Ignatenko,

2015). Two works were found that incorporated Vari-

able Order models and information or entropy (Schür-

mann and Grassberger, 1996; Slonim et al., 2003), yet

none of them used these models for PFMI estimation.

Ben-Gal et al (Ben-Gal et al., 2005) and later

Brice et al (Brice and Jiang, 2009) proposed an in-

put/output formulation of the context tree algorithm

(I/O CT), where the branches of the context tree be-

long to one time series and the leaves belong to an-

other time series. In this way, the researchers could

incorporate data from different time series for learn-

ing tasks, such as structure learning and anomaly de-

tection within the CT framework.

Let us also note that the CT-PFMI algorithm is

scalable using methods presented in (Satish et al.,

2014; Kaniwa et al., 2017; Tiwari and Arya, 2018;

Satish et al., 2014; Tiwari and Arya, 2018).

3 PRELIMINARIES AND

MATHEMATICAL

BACKGROUND

Henceforth, unless stated otherwise, random vari-

ables are represented by capital letters, while their

realizations are denoted by lower-case letters; multi-

dimensional variables and arrays are denoted by bold

letters.

Mutual Information(Cover and Thomas, 2012):

Given two discrete random variables X and Y, the

Mutual Information between them is deﬁned as

IpX ;Y q “

xPX

yPY

Ppx, yqlog

Ppx, yq

PpxqPpyq

. (1)

IpX ;Y q is a positive symmetrical measure. The

Kullback-Liebler divergence (D

) between arbitrary

probability functions Qp¨q and Pp¨q is given by

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

pQpX, Y q k PpX, Y qq “

xPX

yPY

Qpx, yq log

Qpx, yq

Ppx, yq

(2)

Following Eq.(2), the IpX ;Y q can be written as

IpX ;Y q “ xD

pPpY |X q k PpY qqy

PpXq

, (3)

where x¨y

Pp¨q

is the expectation with respect to the

subscript distribution.

The Past-future Mutual Information: To explain

PFMI, we use the notation in (Bialek et al., 2001;

Still, 2014) whom introduce a similar measure to

PFMI called the predictive information (PI), that is

the mutual information between two random vectors,

one representing the past τ

time lags,

ÐÝ

and an-

other representing time series values from the future

time lags,

ÝÑ

. Following Eq.(3), the PI can be

deﬁned by using D

PIp

ÐÝ

;

ÝÑ

q “

pPp

ÝÑ

ÐÝ

q k Pp

ÝÑ

qqy

ÐÝ

(4)

and,

PIp

ÐÝ

;

ÝÑ

f “1

q “ PFMIp

ÐÝ

;

ÝÑ

Y q. (5)

Context Tree (CT) Algorithm (Weinberger et al.,

1995; Ben-Gal et al., 2003): Given a sequence of

length N, x

, generated from a tree source X , the CT

algorithm ﬁnds a ﬁnite set S of size |S | of contexts

S px

q. S satisﬁes the requirement that the conditional

probability to obtain a symbol given the whole se-

quence preceding that symbol is close enough to the

Table 1: Optimal contexts of the I/O CT of Deutsche Bank

(input) to HSBC (output) as obtained with the CT-PFMI

algorithm and the pruning constant tuning algorithms (see

Section 5). The returns are discretized to "1" for positive

return, "0" for zero return and "-1" for negative return with

respect to the previous minute.

Optimal Context

Context

Probability Conditional probability

root - (0.42, 0.16, 0.42)

("-1") 0.369 (0.45, 0.15, 0.40)

("0") 0.111 (0.40, 0.20, 0.40)

("1") 0.370 (0.40, 0.15, 0.45)

("-1", "0") 0.057 (0.43, 0.20, 0.37)

("1", "0") 0.058 (0.37, 0.20, 0.43)

("0", "0") 0.011 (0.37, 0.27, 0.36)

("0", "0", "1") 0.011 (0.36, 0.25, 0.39)

("0", "0", "0", "-1") 0.003 (0.35, 0.30, 0.35)

("0", "0", "0", "1") 0.003 (0.33, 0.30, 0.37)

("0", "0", "0", "0") 0.002 (0.32, 0.33, 0.35)

("0", "0", "0", "0", "0") 0.005 (0.06, 0.87, 0.07)

conditional probability of obtaining the symbol given

a context, i.e.,

Ppx|x

q – Ppx|S px

qq. (6)

Given Eq.(6), when |S | sequences are informative, the

number of conditional probability parameters that are

required to describe x

equals |S |(d-1), where d is the

alphabet size of X.

To obtain S , the learning algorithm constructs a

context tree where each node holds a set of ordered

counters that represent the distribution of symbols

that follow that context, which is deﬁned by the path

to that node (Ben-Gal et al., 2003). At the next step,

a pruning procedure is performed to leave only those

contexts in S (called optimal contexts (Ben-Gal et al.,

2003)) - with corresponding nodes in the tree that rep-

resent the conditional distribution of the output vari-

able conditioned on the context which is different

from the distributions of the output variable condi-

tioned only on part of the context (represented by the

path from the tree root to the parent node). Table 1

shows all the optimal contexts and their correspond-

ing conditional probabilities in a I/O context tree ob-

tained in stock returns data that will be discussed in

the result section. Fig. 1 shows in a context tree for-

mation some of the optimal contexts obtained in this

table.

Descriptions of the main principles of the CT Al-

gorithm, including how to obtain S and a numerical

example appear in (Ben-Gal et al., 2003).

The I/O CT (Ben-Gal et al., 2005; Brice and Jiang,

2009) algorithm is a generalization of the CT algo-

rithm where the tree’s contexts are from the input se-

quence and the leaves represent counters of the output

sequence, in contrast to Eq.(6), where the input and

the output are from the same time series

Ppy|x

q – Ppy|S px

qq. (7)

4 THE CONTEXT TREE

PAST-FUTURE MUTUAL

INFORMATION ALGORITHM

Let t

ÐÝ

x ;

ÐÝ

x u P

ÐÝ

represent the informative and un-

informative contexts respectively from the input time

series,

ÝÑ

y represents the symbols from the output

time series and

{

PFMIp

ÐÝ

;

ÝÑ

y q represent the esti-

mated PFMI. We deﬁne the uninformative sequences

as those with conditioning probability with respect to

the output that do not result in a conditional distribu-

tion of the output time series, which is signiﬁcantly

different from unconditional marginal distribution of

Past-future Mutual Information Estimation in Sparse Information Conditions

Figure 1: The I/O CT representation of some of the optimal contexts in Table 1 as obtained from HSBC (input) to Deutsche

Bank (output) stock prices time series. Each edge represents a single context realizations. Consecutive edges represent

contexts (sequences) in reverse order. The nodes represent the conditional probabilities of the output time series given the

input context between the root to that node of the tree. The root (at the top of the tree) contains the marginal distribution of

the output time series.

the output. Formally, t

ÐÝ

x : D

pPp

ÝÑ

y |

ÐÝ

x q k Pp

ÝÑ

y qq “

0u. Due to the ﬁnite size of the data, often the empiri-

cal measurement leads to D

ÝÑ

y |

ÐÝ

x q k

ÝÑ

y q ą 0,

so positive bias can occur. In the sparse PFMI condi-

tion, where

ÐÝ

x |

ÐÝ

x |

ăă 1, removing these contexts can

signiﬁcantly decrease

{

PFMI estimation error and en-

hance better understanding of the "source of informa-

tion" (Tishby et al., 2000).

To achieve this goal, we apply some of the prin-

ciples implemented in (Slonim et al., 2003), to intro-

duce a novel method for

{

PFMI estimation using the

I/O CT. Let X

and Y

be the input and the output

time series of length N respectively. As discussed

in Section 3, the root node of the I/O CT represents

the marginal (unconditioned) distribution of Y

(the

symbols’ frequency in Y

). The estimated PFMI be-

tween the input and the output time series is the sum

of the D

between the root node and the conditional

probabilities given the contexts in S , weighted by the

probabilities of these contexts, following Eqs.(4) and

(5) is

{

PFMI

“ xD

ÝÑ

y |S

ÐÝ

x q k

ÝÑ

y qqy

PpS

ÐÝ

x q

(8)

where

{

PFMI

is the empirical PFMI obtained from

the I/O CT algorithm with a pruning constant c and

ÐÝ

x q is its corresponding optimal contexts set. To

continue with the running example of stocks returns

data, we use Table 1 that represents the obtained con-

text tree. using Eq.(8),

{

PFMI with c “ 1 can be cal-

culated as follows

{

PFMI

“

0.369 ¨ D

p0.45, 0.15, 0.40q||p0.42, 0.16, 0.42q`

0.111 ¨ D

p0.40, 0.20, 0.40q||p0.42, 0.16, 0.42q`

. . . `

0.005 ¨ D

p0.06, 0.87, 0.07q||p0.42, 0.16, 0.42q “

0.016 bits.

(9)

So far, the extraction of

{

PFMI from CT with a

given c value has been described. A tuning method

for ﬁnding the value of c that results in a good sep-

aration between informative and uninformative con-

texts is now proposed by utilizing the statistics gained

by the ﬁrst stage in the CT algorithm. Consider the

vector c of indexed pruning constant values c

. The

empirical second derivative of

{

PFMI

with respect

to |S

| can be obtained by

{

PFMI

B|S

“

{

PFMI

i`1

{

PFMI

i´1

´ 2

{

PFMI

p|S

i`1

| ´ |S

i´1

(10)

When the absolute value of Eq.(10) reaches a greater

value than a threshold ε, the correspondent pruning

constant is chosen. The second derivative is used to

enable the detection of changes from higher than a lin-

ear order (e.g, a curved shaped changes) in the

{

PFMI.

Linear decrease is expected to happen when uninfor-

mative contexts are removed. The reason for this be-

haviour lies in the pruning threshold of the CT algo-

rithm. This threshold equals to the probability of a

context times a parent-child D

measure. In the un-

informative case, incrementally increasing the prun-

ing constant will result in the pruning of all the leaves

in the same tree level in a reverse order. Hence, in

each incremental increase in the pruning constant c,

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

the same size of

{

PFMI is subtracted. When one of the

contexts contains a signiﬁcant amount of information,

its pruning will result in a higher order change in the

empirical PFMI.

{

PFMI extraction and the tuning of the pruning

constant c constitute the CT-PFMI algorithm (see Al-

gorithm 1). First, the estimated PFMI is extracted

iteratively from the I/O CT for decreasing values of

c. When the second derivative condition is satisﬁed,

the algorithm stops and returns the values of c and

the PFMI of the last iteration. Note that the full I/O

CT is constructed only once in the ﬁrst iteration, so

the complexity of this algorithm is dominated by this

construction with complexity of OpNlogN) (Ben-Gal

et al., 2003).

Considering the

{

PFMI randomness, we need to

reject the null hypothesis that

{

PFMI = 0, especially

in sparse PFMI condition. Here, we adopt the ap-

proach of (Vicente et al., 2011) by setting the stopping

threshold ε to be higher than the 95 percentile value

{

PFMI obtained by repeatedly reshufﬂing the time

series and measuring the resulting

{

PFMI.

Algorithm 1: Context Tree Past-Future Mutual Information.

1: Input: x

, y

, c, ε

2: Implement on x

, y

the ﬁrst stage of the I/O CT algo-

rithm to obtain a full I/O context tree

3: for i in 1 to |c|-1 do

4: Implement the following stages of the I/O CT algo-

rithm

5: with c

i´1

, c

i`1

, and obtain S

i´1

, S

i`1

6: Calculate

{

PFMI

i´1

{

PFMI

{

PFMI

i`1

7: if |S

i´1

| = |S

i`1

| then

8: dv2 Ð 0

9: else

10: dv2 Ð |

{

PFMI

B|S

11: end if

12: if dv2 ą ε then

13: return c

14: end if

15: end for

16: return 0

5 EMPIRICAL RESULTS

This section shows the results of a simulation setup

with a known ground truth, which is used to measure

the performance of the CT-PFMI algorithm compared

to benchmark methods in sparse PFMI environment.

Later, a real ﬁnancial time series is used as an exam-

ple for the CT-PFMI algorithm usage for PFMI esti-

mation and a high-resolution data analysis.

5.1 PFMI Estimation in Sparse PFMI

Conditions, a Simulated Study

In this example,

{

PFMI is measured between an input

time series with alphabet size starting from 20 to 90

symbols and the output binary time series. The time

series length is 5000 discrete time steps. The sparse

PFMI condition is achieved by randomly choosing

two of the alphabet symbols to be informative with

the following conditional probability:

ÝÑ

y “ 1|

ÐÝ

q “ 0.95

ÝÑ

y “ 0|

ÐÝ

q “ 0.05

ÝÑ

y “ 1|

ÐÝ

q “ 0.05

ÝÑ

y “ 0|

ÐÝ

q “ 0.95.

One hundred simulation runs were performed per

each alphabet size. When the size of the alpha-

bet increases, the sparse PFMI condition becomes

more signiﬁcant. The CT-PFMI performances were

compared to the commonly used plug-in (Cover

and Thomas, 2012) method and the K-NN method

(Kraskov et al., 2004) which is used in many recent

studies on TE (Runge et al., 2012; Vicente et al.,

2011; Montalto et al., 2014). The PFMI estimation

error of CT-PFMI and the benchmark methods rela-

tively to the true theoretical PFMI is shown in Fig.2,

as a function of the dictionary (alphabet) size. Three

values of K in the K-NN method where used, testing

different bias-variance trade-offs. Fig.2 demonstrates

the robustness of CT-PFMI estimations to increasing

size of uninformative sequences, showing relatively

small increase in estimation error while the bench-

mark methods that show signiﬁcant increase with the

plug-in method that is the most sensitive to increas-

ing alphabet size. K-NN method with k “ 10 shows

the best results for this method. The fact that CT-

PFMI can remove uninformative sequences, and not

only assign to them a small contribution, supports this

robustness.

5.2 The CT-PFMI Algorithm - Example

of Real Stock Prices Data

Stock market time series analysis is an example of a

real-world application of the CT-PFMI algorithm. In

this case, the sparse PFMI condition is a reasonable

assumption because of market efﬁciency (Shmilovici

and Ben-Gal, 2012). That is, in an efﬁcient market

only few historical pattern or contexts exist that can be

used for predictions, while most of these patterns are

insigniﬁcant (Shmilovici and Ben-Gal, 2012). The

dataset comprises minute-by-minute time series of

stock prices of eight large banks in the U.S. for the

Past-future Mutual Information Estimation in Sparse Information Conditions

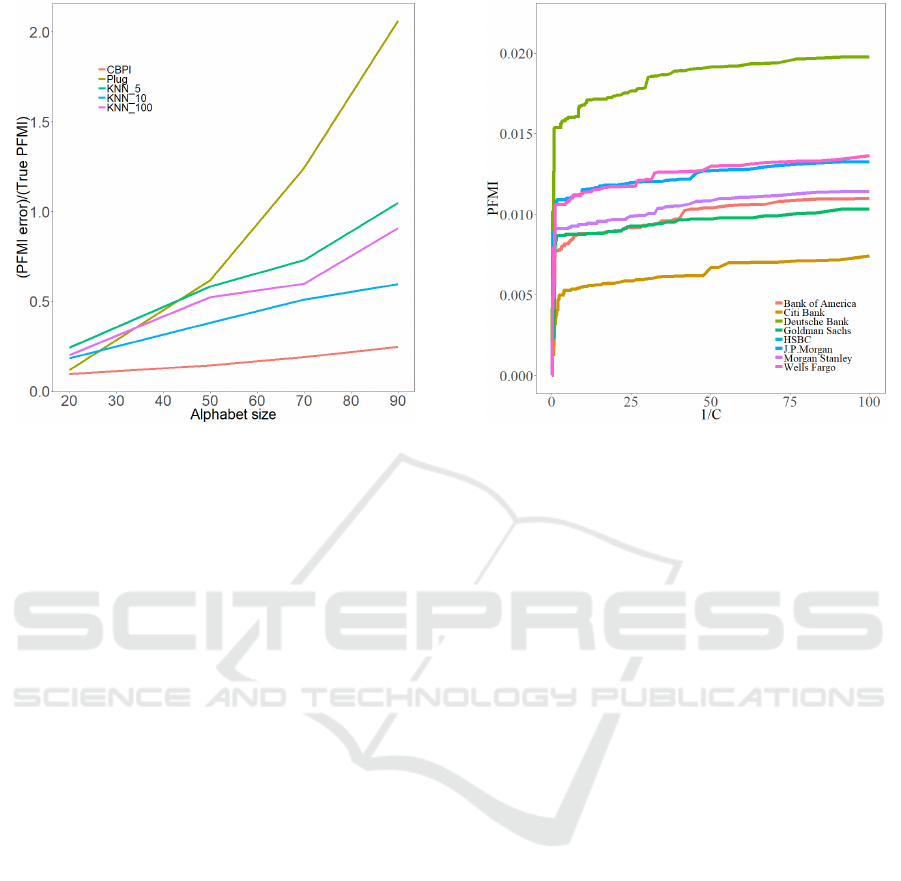
Figure 2: Average PFMI estimation error of the CT-PFMI

algorithm and the benchmark methods with respect to the

true PFMI theoretical value in different values of alphabet

size. The K-NN with different number of neighbors (k) was

calculated using the Parmigene R package (Sales and Ro-

mualdi, 2011).

period of 1.2008-1.2010 that because of the banking

crisis within these years, has a potential of nonzero

{

PFMI in between banks (Dimpﬂ and Peter, 2014).

The length of the time series was 197,000, hence, a

distributed I/O CT algorithm was implemented.

Stock prices were discretized to `1, 0 and ´1

for positive, zero and negative changes, respectively,

relatively to the price of the previous minute. For

each bank, the PFMI was obtained by implementing

the algorithm of Section 4 for various values of 1{c

(see Fig.3). All curves exhibit a similar behavior of

a phase where uninformative sequences are removed

followed by a steep drop in PFMI after crossing a

certain pruning constant threshold that corresponded

to pruning of sequences from S . The Pruning con-

stant obtained from the CT-PFMI algorithm ranged

between 0.13 to 1.33, depending on the input/output

pair. These values corresponds to ﬁltering 96 percent

of sequences.

Using the descriptive power of the CT-PFMI al-

gorithm, hierarchical analysis can be obtained. For

example, in the higher level, a geographic orientation

can be identiﬁed when looking at Fig.3. The esti-

mated PFMI between the European banks HSBC and

DB is higher than the estimated PFMI between these

banks and the American banks.

Moving to lower hierarchies of the interactions,

the conditional probabilities of the output sequences

given the contexts in S differ from the marginal distri-

Figure 3: Estimated PFMI of large banks’ stock prices in the

Wall Street stock exchange (input) with respect to the stock

prices of HSBC bank (output), calculated as a function of

the inverse of the pruning constant c. Shufﬂed input time

series showed maximum PFMI values of « 5 ¨ 10

´5

bution of the output in the probabilities of each sym-

bol, but the symmetry between ´1 and `1 is rela-

tively preserved. For example, see the contexts ob-

tained with the I/O CT of DB to HSBC in Table 1.

Hence, for trading purposes, additional information is

needed.

Another conclusion can be drawn from the con-

texts’ length. The average memory of the process

is 1.5 symbols, as calculated by multiplication of all

contexts’ lengths by their respective probabilities (see

Table 1). This observation implies that most of the

information within τ

“ 2.

6 CONCLUSIONS

We showed how the Input/Output context tree algo-

rithm can be utilized to measure the past-future mu-

tual information between time series. Using that,

we demonstrated how the pruning constant param-

eter of the I/O CT algorithm can be calibrated in

a way that separates informative versus uninforma-

tive sequences. This approach constitutes the CT-

PFMI algorithm for PFMI estimation. We used sparse

past-future predictive information (sparse PFMI) sim-

ulated data with a known theoretical PFMI values

to benchmark the CT-PFMI algorithm against other

common PFMI estimation methods. This comparison

shows the advantages of the CT-PFMI algorithm over

the benchmark methods under sparse PFMI condi-

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

tions. The CT-PFMI algorithm was also implemented

on real stock prices data to show the sparse PFMI ef-

fect between pairs of real-world time series. It was

also demonstrated how the CT-PFMI algorithm can

be used for in-depth analyses of interactions between

time series.

ACKNOWLEDGEMENTS

This research was funded by the Koret foundation

grant for Smart Cities and Digital Living 2030.

REFERENCES

Begleiter, R., El-Yaniv, R., and Yona, G. (2004). On predic-

tion using variable order markov models. Journal of

Artiﬁcial Intelligence Research, 22:385–421.

Begleiter, R., Elovici, Y., Hollander, Y., Mendelson, O.,

Rokach, L., and Saltzman, R. (2013). A fast and

scalable method for threat detection in large-scale dns

logs. In Big Data, 2013 IEEE International Confer-

ence on, pages 738–741. IEEE.

Ben-Gal, I., Morag, G., and Shmilovici, A. (2003). Context-

based statistical process control: A monitoring pro-

cedure for state-dependent processes. Technometrics,

45(4):293–311.

Ben-Gal, I., Shani, A., Gohr, A., Grau, J., Arviv, S.,

Shmilovici, A., Posch, S., and Grosse, I. (2005). Iden-

tiﬁcation of transcription factor binding sites with

variable-order bayesian networks. Bioinformatics,

21(11):2657–2666.

Bialek, W., Nemenman, I., and Tishby, N. (2001). Pre-

dictability, complexity, and learning. Neural compu-

tation, 13(11):2409–2463.

Bossomaier, T., Barnett, L., Harré, M., and Lizier, J. T.

(2016). An introduction to transfer entropy. Springer.

Brice, P. and Jiang, W. (2009). A context tree method for

multistage fault detection and isolation with applica-

tions to commercial video broadcasting systems. IIE

Transactions, 41(9):776–789.

Chim, H. and Deng, X. (2007). A new sufﬁx tree similarity

measure for document clustering. In Proceedings of

the 16th international conference on World Wide Web,

pages 121–130. ACM.

Cover, T. M. and Thomas, J. A. (2012). Elements of infor-

mation theory. John Wiley & Sons.

Dimpﬂ, T. and Peter, F. J. (2014). The impact of the ﬁ-

nancial crisis on transatlantic information ﬂows: An

intraday analysis. Journal of International Financial

Markets, Institutions and Money, 31:1–13.

Kaniwa, F., Kuthadi, V. M., Dinakenyane, O., and

Schroeder, H. (2017). Alphabet-dependent parallel al-

gorithm for sufﬁx tree construction for pattern search-

ing. arXiv preprint arXiv:1704.05660.

Kraskov, A., Stögbauer, H., and Grassberger, P. (2004).

Estimating mutual information. Physical review E,

69(6):066138.

Kullback, S. and Leibler, R. A. (1951). On information

and sufﬁciency. The annals of mathematical statistics,

22(1):79–86.

Kusters, C. and Ignatenko, T. (2015). Dna sequence model-

ing based on context trees. In Proc. 5th Jt. WIC/IEEE

Symp. Inf. Theory Signal Process. Benelux, pages 96–

103.

Largeron-Leténo, C. (2003). Prediction sufﬁx trees for su-

pervised classiﬁcation of sequences. Pattern Recogni-

tion Letters, 24(16):3153–3164.

Montalto, A., Faes, L., and Marinazzo, D. (2014). Mute: a

matlab toolbox to compare established and novel esti-

mators of the multivariate transfer entropy. PloS one,

9(10):e109462.

Runge, J., Heitzig, J., Petoukhov, V., and Kurths, J. (2012).

Escaping the curse of dimensionality in estimating

multivariate transfer entropy. Physical review letters,

108(25):258701.

Sales, G. and Romualdi, C. (2011). parmigene—a par-

allel r package for mutual information estimation

and gene network reconstruction. Bioinformatics,

27(13):1876–1877.

Satish, U. C., Kondikoppa, P., Park, S.-J., Patil, M., and

Shah, R. (2014). Mapreduce based parallel sufﬁx tree

construction for human genome. In Parallel and Dis-

tributed Systems (ICPADS), 2014 20th IEEE Interna-

tional Conference on, pages 664–670. IEEE.

Schreiber, T. (2000). Measuring information transfer. Phys-

ical review letters, 85(2):461.

Schürmann, T. and Grassberger, P. (1996). Entropy esti-

mation of symbol sequences. Chaos: An Interdisci-

plinary Journal of Nonlinear Science, 6(3):414–427.

Shmilovici, A. and Ben-Gal, I. (2012). Predicting stock re-

turns using a variable order markov tree model. Stud-

ies in Nonlinear Dynamics & Econometrics, 16(5).

Slonim, N., Bejerano, G., Fine, S., and Tishby, N. (2003).

Discriminative feature selection via multiclass vari-

able memory markov model. EURASIP Journal on

Applied Signal Processing, 2003:93–102.

Society, T. X., Wang, S., Jiang, Q., and Huang, J. Z. (2014).

A novel variable-order markov model for clustering

categorical sequences. IEEE Transactions on Knowl-

edge and Data Engineering, 26(10):2339–2353.

Still, S. (2014). Information bottleneck approach to predic-

tive inference. Entropy, 16(2):968–989.

Tishby, N., Pereira, F. C., and Bialek, W. (2000). The

information bottleneck method. arXiv preprint

physics/0004057.

Tiwari, V. S. and Arya, A. (2018). Distributed context tree

weighting (ctw) for route prediction. Open Geospatial

Data, Software and Standards, 3(1):10.

Vicente, R., Wibral, M., Lindner, M., and Pipa, G. (2011).

Transfer entropy—a model-free measure of effective

connectivity for the neurosciences. Journal of compu-

tational neuroscience, 30(1):45–67.

Weinberger, M. J., Rissanen, J. J., and Feder, M. (1995). A

universal ﬁnite memory source. IEEE Transactions on

Information Theory, 41(3):643–652.

Yang, J., Xu, J., Xu, M., Zheng, N., and Chen, Y. (2014).

Predicting next location using a variable order markov

model. In Proceedings of the 5th ACM SIGSPATIAL

International Workshop on GeoStreaming, pages 37–

42. ACM.

Past-future Mutual Information Estimation in Sparse Information Conditions