
On the Time Complexity of Simple Cartesian Genetic Programming
Roman Kalkreuth and Andre Droschinsky
Department of Computer Science, TU Dortmund University, Otto-Hahn-Straße 14, Dortmund, Germany
Keywords:
Cartesian Genetic Programming, Runtime Analysis, Theory.
Abstract:
Since its introduction, Cartesian Genetic Programming has been mostly analyzed on an experimental level with
boolean function problems. Consequently, there is still little theoretical understanding of Cartesian Genetic
Programming. In this paper, we present a first time complexity analysis of Cartesian Genetic Programming.
We introduce and analyze a simple mathematical problem and a simple logical boolean problem called SUM
and AND. The results of our analysis show that simple CGP is able to solve SUM efficiently in time Θ(n logn).
However, our analysis of the AND problem shows that simple CGP is not able to solve AND efficiently.
1 INTRODUCTION
Genetic programming (GP) can be described as a
paradigm which opens the automatic derivation of
programs for problem-solving. First work on GP
has been done by Forsyth (1981), Cramer (1985)
and Hicklin (1986). Later work by Koza (1990,
1992, 1994) significantly popularized the field of GP.
GP traditionally uses trees as program representation.
Just over two decades ago Miller, Thompson, Kal-
ganova, and Fogarty presented first publications on
Cartesian Genetic Programming (CGP) —an encod-
ing model inspired by the two-dimensional array of
functional nodes connected by feed-forward wires of
an FPGA device (Miller et al., 1997; Kalganova and
Miller, 1997; Miller, 1999). CGP offers a graph-
based representation which in addition to standard
GP problem domains, makes it easy to be applied to
many graph-based applications. Furthermore, CGP
has been found for beneficial for the training of com-
putational methods such as neural networks. CGP
has been mostly analyzed and investigated on an ex-
perimental level with boolean function problems to
investigate and proof important dogmas of the CGP
functionality such as Redundancy, Computational Ef-
ficiency and Neutrality.
For instance, Miller and Smith (2006) showed
that the most evolvable representations occur when
the genotype is extremely large and in which over
95% of the genes are inactive. The best performance
was found to employ extremely high levels of redun-
dancy. Another example is the work of Yu and Miller
(2001) which sheds light on the significance of neu-
trality in CGP. Experimental analysis of CGP also
gave answers to the question why the candidate pro-
grams in CGP doesn’t bloat during the evolutionary
search Turner and Miller (2014). Despite the fact that
those publications significantly contribute to the fun-
damental understanding of the behavior and compu-
tational efficiency of CGP on an experimental level,
there is only little theoretical understanding in the
field of CGP. Theoretical analyses of CGP have been
mainly unattended in the past. Moreover, even if CGP
has been found as an efficient approach for solving
several problems which can be represented as graphs,
there is a significant lack of runtime analysis of the
most used CGP algorithms. The amount of experi-
mental results in the field of CGP opens the question
if the findings can be reproduced and approved from
a theoretical point of view. Furthermore, we feel that
the current state of knowledge of CGP is one-sided
and has to be balanced by more theoretical work. In
this paper, we present a first time complexity analysis
of a simple (1 + 1)-CGP algorithm and make one step
towards fundamental theoretical knowledge of CGP.
Another purpose of this paper is the introduction
of an analysis setup including two simple problems
called SUM and AND. Section 2 of this paper de-
scribes CGP and the multiplicative drift analysis. Rel-
evant previous theoretical works of GP and CGP are
surveyed in Section 3. In Section 4 we introduce two
simple test problems for CGP. In Section 5 and 6 we
analyze the runtime of the (1 + 1)-CGP algorithm. In
Section 7 we discuss the results of our analyses. Fi-
nally, Section 8 gives a conclusion and outlines future
work.
172
Kalkreuth, R. and Droschinsky, A.
On the Time Complexity of Simple Cartesian Genetic Programming.
DOI: 10.5220/0008070201720179
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 172-179
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORK
2.1 Cartesian Genetic Programming
Cartesian Genetic Programming is a form of Genetic
Programming which offers a graph-based representa-
tion. In contrast to tree-based GP, CGP represents a
genetic program via genotype-phenotype mapping as
an indexed, acyclic, and directed graph. Originally
the structure of the graphs was a rectangular grid of
N
r
rows and N
c
columns, but later work also focused
on a representation with one row. The genes in the
genotype are grouped, and each group refers to a node
of the graph, except the last one which represents the
outputs of the phenotype. Each node is represented
by two types of genes which index the function num-
ber in the GP function set and the node inputs. The
first gene of each node represents the function num-
ber and the following genes represent the arity input
connections of the node. These nodes are called func-
tion nodes and execute functions on the input values.
The number of input genes depends on the maximum
arity N
a
of the function set. The last group in the
genotype represents the indexes of the nodes which
lead to the outputs. Since the output nodes can be
connected to any previous function node, the repre-
sentation of CGP allows inactive function nodes. A
backward search is used to decode the correspond-
ing phenotype. The backward search starts from the
outputs and processes the linked nodes in the geno-
type. In this way, only active nodes are processed
during the evaluation procedure. The number of in-
puts N
i
, outputs N
o
, and the length of the genotype is
fixed. Every candidate program is represented with
N
r
∗N
c
∗(N
a
+1)+N
o
integers. Even when the length
of the genotype is fixed for every candidate program,
the length of the corresponding phenotype in CGP is
variable which can be considered as a significant ad-
vantage of the CGP representation. An example of the
decoding from genotype to phenotype is illustrated in
Figure 1.
CGP is traditionally used with a (1+λ) evolution-
ary algorithm. The new population in each generation
consists of the best individual of the previous popula-
tion and the λ created offspring. The breeding proce-
dure is mostly done by a point mutation which swaps
genes in the genotype of an individual in the valid
range by chance. In this way, connection genes can
be connected to other previous function or input nodes
and function genes can be mutated to other function
numbers.
Genotype
0 1 0 1 2 1 2 2 3
3
Phenotype
+
/
-
OP
IP1
IP2
Function
Lookup Table
Index Function
0
1
2
Addition
Subtraction
Division
Decode
Node
Number
2 3
4
OP
432
0
1
Figure 1: Exemplification of the decoding procedure of a
CGP genotype to its corresponding phenotype. The nodes
are represented by two types of numbers which index the
number in the function lookup table (underlined) and the in-
puts (non-underlined) for the node. Inactive function nodes
are shown in gray color.
2.2 Drift Analysis
Drift analysis is one of the state-of-the-art techniques
to analyze the runtime of randomized search heuris-
tics such as evolutionary algorithms. Furthermore,
drift analysis is a powerful tool to analyze the opti-
mization behavior of a randomized search algorithm
over a search space by measuring the progress of the
algorithm with respect to a potential function. Such
a function maps each search point to a non-negative
real number, where a potential of zero indicates that
the search point is optimal. Drift analysis has signif-
icantly contributed to the analysis of meta-heuristics.
Many important results about the optimization time of
meta-heuristics were achieved with drift analysis.
Multiplicative Drift Analysis.
Multiplicative Drift Analysis as introduced by
Doerr et. al. (Doerr et al., 2010, 2012) is based on
Additive Drift Analysis which has been proposed
by He et al. (He and Yao, 2004, 2001). The mul-
tiplicative drift theorem can be considered as the
multiplicative version of the additive drift theorem.
Theorem 2.1 (Additive Drift (He and Yao, 2004)).
Let S ⊆ R be a finite set of positive numbers and let
(X
(t)
)
t∈N
over S be a sequence of random variables
over S ∪ {0}. Let T be the random variable that de-
notes the first point in time t ∈ N for which X
(t)
= 0.
Suppose that there exists a constant δ > 0 such that
E[X
(t)
− X
(t+1)
|T > t] ≥ δ (1)
holds. Then
On the Time Complexity of Simple Cartesian Genetic Programming
173

E[T ] ≤
X
(0)
δ
(2)
The additive drift theorem describes how to com-
bine the expected time at which the potential function
reaches zero to the first time at which the expected
value of the potential reaches zero. If the potential de-
creases in each step and in expectation by δ then after
X
(0)
/δ steps the expected potential is zero. In order
to apply the previous theorem to the analysis of ran-
domized search heuristics over a finite search space S,
the defined potential function h : S → R maps all op-
timal search points to zero and all non-optimal search
points to values which are larger than zero. The ran-
dom variable X
(t)
is defined as the potential h(x
(t)
) of
a search point x
(t)
in the t-th iteration of the algorithm.
The random variable T is defined as the optimization
time of the algorithm which is the number of itera-
tions until the algorithm finds an optimum.
When applying Theorem 2.1, the expected differ-
ence between h(x
(t)
) and h(x
(t+1)
) is called the drift of
the random process {x
(t)
}
t∈N
with respect to h. This
drift is additive if condition (1) holds.
The multiplicative method allows easier analyses
in those settings where the optimization progress is
roughly proportional to the current distance to the op-
timum. This method requires a progress which mul-
tiplicatively depends on the current potential value.
That is the reason why the method was named mul-
tiplicative drift analysis. It has been found that for
a number of problems such potential functions are a
natural choice (Doerr et al., 2010, 2012). However,
since multiplicative drift analysis is derived from the
original additive result, it is clear that the multiplica-
tive version cannot be stronger than the original theo-
rem.
Theorem 2.2 (Multiplicative Drift (Doerr et al.,
2010)). Let S ⊆ R be a finite set of positive num-
bers with minimum s
min
. Let (X
(t)
)
t∈N
over S be a
sequence of random variables over S ∪ {0}. Let T
be the random variable that denotes the first point in
time t ∈ N for which X
(t)
= 0. If there exists δ, c
max
,
c
min
> 0 such that
E[X
(t)
− X
(t+1)
|X
(t)
] ≥ δ · X
(t)
(3)
and
c
min
≤ X
(t)
≤ c
max
(4)
for all t < T , then
E[T ] ≤
2
δ
· ln(1 +
c
max
c
min
) (5)
The drift of a random process with respect to a
potential function g is multiplicative if condition (3)
holds for the affiliated random variables. The advan-
tage of the multiplicative approach is that it allows
using potential functions which are more natural. The
most natural potential function can be considered as
the distance of the objective value of the current so-
lution to the optimum. This condition has been found
to be a good choice in the analysis of combinatorial
optimization problems (Doerr et al., 2010, 2012).
2.3 Single Active Gene Mutation
Strategy
The single active gene mutational strategy as pro-
posed by Goldman and Punch (2013) mutates at least
one active gene of an individual in one generation.
This means that all genes of active function nodes and
the output nodes can be selected for mutation. The ac-
tive gene is selected by random. The mutation itself is
done by a bit flip in the legal range of a certain gene.
This procedure is equal to the standard probabilistic
CGP mutation. The single active gene strategy has
been found as highly beneficial for the performance
of CGP. Another benefit of this strategy is the fact
that no parameter for the strength of the mutation is
necessary.
3 PREVIOUS THEORETICAL
WORK ON GP AND CGP
A major theoretical contribution to the understanding
of GP behaviour has been made by applying schema
theory (Langdon and Poli, 2002), (Poli et al., 2004).
However, the results of these works do not contribute
to the runtime analysis of GP.
According to Mambrini and Oliveto (2016), first
studies of runtime analysis in GP focused on two
functions which are called ORDER and MAJORITY.
For these types of problems, the fitness of an individ-
ual depends on the structure of the syntax tree and
not on its execution. However, these types of prob-
lems can be considered as very simple compared to
the problems to which GP is usually applied. How-
ever, according to Neumann et al. (2011), the results
for the mentioned problems show that GP is able to
optimize both functions efficiently.
In their work, Mambrini and Oliveto (2016) re-
ported that a recent study analyzed the same simple
GP systems on the MAX Problem. The analysis in-
cluded a set of functions, a set of terminals and a
bound D on the maximum depth of the solution, the
goal is to evolve a tree that returns the maximum
value given any combination of functions and termi-
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
174

nals (Koetzing et al., 2014). The results of the analy-
sis show that simple GP systems can efficiently evolve
MAX with a function set F=[+; ∗] and one constant as
the terminal set. Compared to the previous functions,
MAX is more similar to those evolved by GP in prac-
tical applications since the fitness indeed depends on
the behavior of the computed function on the input.
Still, dependence is not very strong, since the space
of possible inputs can be partitioned into just two sub-
sets such that for every input in a subset, the optimal
solution to the problem is the same.
Two more theoretical results were obtained by
Moraglio et al. (2013) and Moraglio and Mambrini
(2013) with the runtime analysis of mutation-based
Geometric Semantic Genetic Programming for evolv-
ing boolean and basic regression functions. Recently,
Mambrini and Oliveto (2016) presented a theoret-
ical analysis of two simple GP algorithms on two
boolean problems called AND and XOR. Both al-
gorithms were equipped with a minimal function set
with a maximum of two functions. It has been rig-
orously proved that both algorithms can solve both
easy problems with minimal sets efficiently. How-
ever, Mambrini and Oliveto (2016) concluded that:
“If an extra function (i.e. NOT) is added to
the function set, the algorithms require at least
exponential time to evolve the conjunction of
n variables. ”
Recently, Lissovoi and Oliveto (2018) presented re-
sults on the time and space complexity of GP for
evolving boolean conjunctions. The authors present
a performance analysis that sheds light on the be-
haviour of simple GP systems for evolving conjunc-
tions of n variables (AND
n
). On one hand the analysis
of a random local search GP with minimal terminal
and function sets with minimal terminal and function
sets revealed the relationship between the number of
iterations and the expected error of the evolved pro-
gram on the complete training set. The authors also
considered a more realistic GP system equipped with
a global mutation operator and proved that it can ef-
ficiently solve AND
n
by producing programs of lin-
ear size that fit a training set to optimality and with
high probability generalise well. Based on the results
of Lissovoi and Oliveto (2018), Doerr et al. (2019)
made a considerable step forward by analyzing the be-
haviour and performance of the GP system for evolv-
ing a Boolean function with unknown components,
i.e., the function may consist of both conjunctions and
disjunctions. In their work Doerr et al. rigorously
proved that if the target function is the conjunction of
n variables, then the RLS-GP using the complete truth
table to evaluate program quality evolves the exact
target function in O(`log2n) iterations in expectation,
where ` ≥ n is a limit on the size of any accepted tree.
Regarding the theoretical knowledge of CGP, Wood-
ward (2006) investigated the functional complexity in
CGP. To our best knowledge, the work of Woodward
seems to be the only theoretical work which has been
contributed to the understanding of CGP behavior.
Furthermore, Woodward’s work does not contribute
to the understanding of the runtime complexity by ob-
taining upper and lower runtime bounds of the CGP
algorithm itself. This significant lack of theoretical
knowledge in CGP has been the motivation for our
work.
4 PRELIMINARIES
We will analyze a (1+1)-CGP algorithm on test prob-
lems called SUM and AND. We say that an algorithm
solves a problem efficiently if it can evolve a solution
in expected polynomial time, where time is defined as
the number of fitness function evaluations. As a ge-
netic operator, the single-active-gene mutation strat-
egy is in use. We will analyze two scenarios. For the
SUM problem, the runtime analysis of the algorithm
depends on the number of n arity connections of a
function node which are represented by the connec-
tion genes of the CGP genotypes. On the other hand,
the runtime analysis of the algorithm depends on the
number of n boolean inputs (terminals) for the given
AND problem. We define Artificial Fitness Levels for
the analysis of the SUM and AND problem. For our
analysis, we utilize the Multiplicative Drift Theorem
which has been described in Section 2. For the anal-
ysis of the SUM problem, the CGP is equipped with
a function set consisting of three mathematical func-
tions, SUM, MIN, and AVG. For the analysis of the
AND problem, the function set only consists of the
logical AND function.
4.1 The SUM Problem
The SUM problem is a very simple mathematical test
problem for the theoretical analysis of CGP behavior.
With the SUM problem, we will analyze the (1+1)-
CGP algorithm depending on the number n of arity
connections of a function node. For the analysis of
this problem, the number of function nodes in the
genotype is limited to 1 and the genotype has two
input nodes. The first input node is a terminal with
a constant value of x = 0 and the second input is a
constant with a value of y = 1. The goal of this prob-
lem is to connect all arity connections of the function
node to the second input and to add up the ”1” values.
The genotype has one output which is connected to
On the Time Complexity of Simple Cartesian Genetic Programming
175
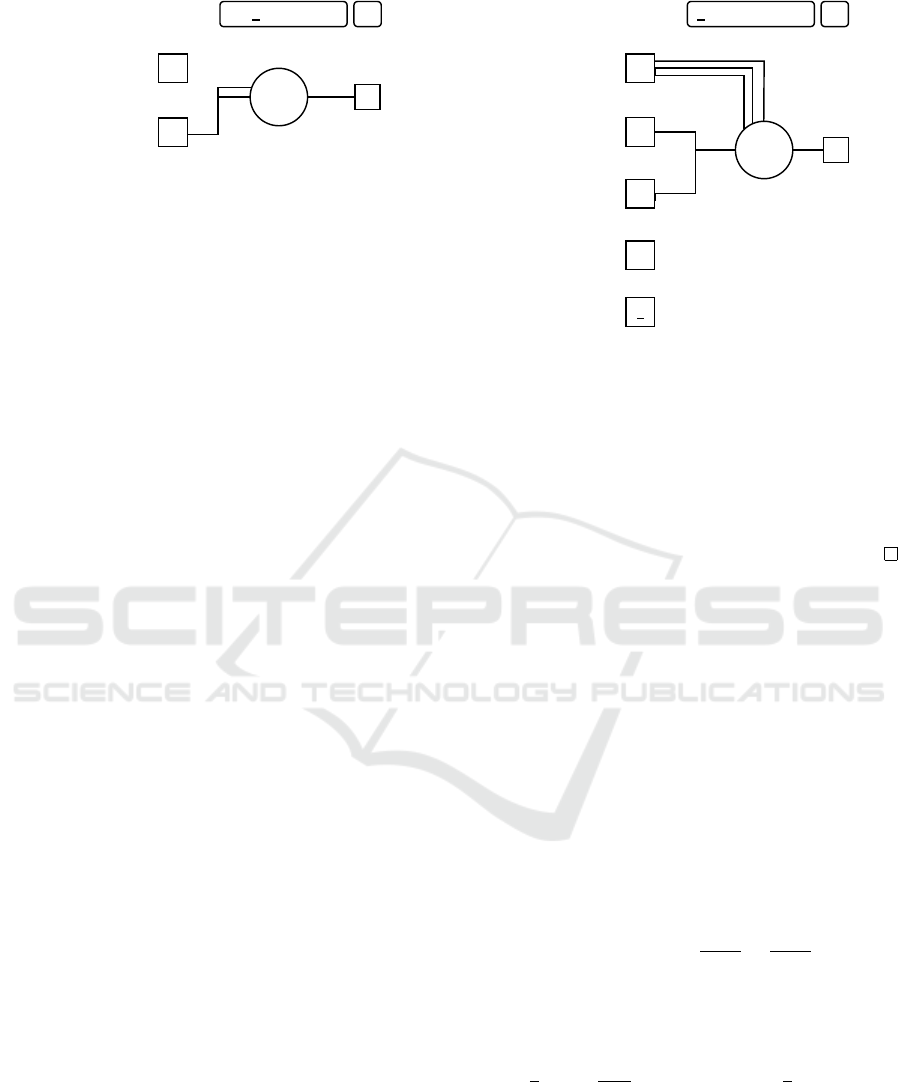
x
y
SUM
OP
0 1 1
2
0
1
Genotype
Phenotype
2
2 OP
Node number
Figure 2: An example of the SUM problem which is used
for the analysis. In the example, the function node has two
arity connections and adds the input value of the second
input node. The sum of this value is then given to the output.
the function node. The function set consists of three
functions. In the first place, we have a function SUM
which simply adds up all values of the connected in-
puts of the function node. The function set also con-
sists of a function MIN which calculates the minimum
of the given input values. The third function of the
function set is a function AVG which calculates the
average of the input values. An example of the SUM
problem is shown in Figure 2.
4.2 The AND Problem
The AND problem is a simple logical problem with
boolean values. With the AND problem we will an-
alyze the (1 + 1)-CGP algorithm depending on the
length of n input nodes which represent the boolean
inputs. The number of function nodes in the genotype
is set to 1. The AND problem represents a simple
boolean problem which has the goal to build up and
correct valid logical AND connections between the
input nodes.
For both problems, the number of function nodes
is fixed and set to 1. The reason for this is that we
will focus more on the theoretical analysis of the mu-
tational abilities of CGP to build and reconnect arity
connections. This behavior has been found as one of
the key features of CGP and is considered highly ben-
eficial for the efficiency of CGP. The output node is
connected to the function node which represents a set-
ting of the levels back parameter witha value of 1. An
example of the AND problem is shown in Figure 3.
5 ANALYSIS OF THE SUM
PROBLEM
Theorem 5.1. The (1+1)-CGP using n arity function
node connections with a function set F={ SUM, MIN,
AVG } of size m := |F| solves SUM in expected time
Θ(nlogn).
Proof. First, we prove the upper bound using multi-
x
y
AND
OP
0 0 0 0 1 2 5
0
1
Genotype
Phenotype
5
5 OP
Node number
z
h
2
3
k
4
Figure 3: An example of the AND problem which is used
for the analysis. In the example, the function node has five
arity connections and builds logical AND connections be-
tween the five boolean inputs of the inputs nodes.
plicative drift analysis, cf. Proposition 5.2. Second,
we prove the lower bound by estimating the prob-
ability that at least one connection to the first node
does not switch to the second after a certain amount
of steps, cf. Proposition 5.3.
Proposition 5.2. The expected upper time bound for
the SUM problem as defined above is O(n logn).
Proof. Let i be the number of arity connections which
have not been connected to the second input node with
the constant. The fitness of the individuals is defined
by the value of the output. The fitness value depends
on the respective function of the function node and
the amount of arity connections which have been con-
nected to the second input. A single connection gene
is chosen with probability 1/(n + 1). Therefore, the
probability to achieve a higher fitness in a certain gen-
eration is i/(n+1). The negative drift is 0 since solu-
tions with fewer connections to the second input will
not be accepted. We have
E[X
(t)
− X
(t+1)
|X
(t)
] ≥
i
n + 1
=
1
n + 1
· X
(t)
.
Choosing δ = 1/(n+1), c
min
= 1, and c
max
= n fulfills
the requirements of Theorem 2.2. From it we obtain
E[T ] ≤
2
δ
·ln(1+
c
max
c
min
) = 2·(n+1)·ln(1+
n
1
) = O(n logn).
For now we did not consider the function gene.
We analyze the expected time independently from the
connection genes. With probability 1/(n + 1) the
function node is chosen for mutation. If SUM is
not the current function operator and at least one ar-
ity connection is connected to the second input, then
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
176

with probability
1
2
the function operator is mutated to
SUM. The probability that at least one arity connec-
tion is connected to the second input is at least 1 −
1
2
n
.
If SUM is the current operator, the function SUM is
kept as executing function. The reason for this is that
neither the use of the MIN function nor the use of the
AVG function can achieve a higher fitness value than
the SUM function. Assuming the SUM operator has
not yet been chosen, then the probability to mutate to
SUM is at least
1
n+1
·
1
2
·(1−
1
2
n
), which implies an up-
per bound for the expected number of turns to mutate
to the SUM operator of O(n).
Proposition 5.3. The expected lower time bound for
the SUM problem as defined above is Ω(n log n).
Proof. We assume the function node is set to SUM
during initialization; the expected running time with
random initialization of the function node cannot be
lower. A given connection flips with probability p :=
1/(n + 1). It does not flip in t steps with probability
(1 − p)
t
. Therefore, each of n/2 inputs switch at least
once in t steps with probability (1−(1− p)
t
)
n/2
. With
p as above and t := n log n we have
1 − (1 − p)
t
n
2
=
1 −
1 −
1
n + 1
nlog n
!
n
2
≤
1 −
1
e
logn
!
n
2
=
1 −
1
n
n·
1
2
≤
1
e
1
2
< 0.61
Therefore, with constant probability c > 1 −
0.61 = 0.39 at least one of n/2 inputs does not switch
after t steps.
With probability at least 1/2 at least n/2 con-
nections are initialized to the first input. This fol-
lows from the binomial distribution. With the results
above we obtain the following estimation on the lower
bound.
E(T ) =
∞
∑
t=1
t · p(t) ≥ nlogn ·
1
2
· 0.39 = Ω(n logn)
6 ANALYSIS OF THE AND
PROBLEM
Theorem 6.1. The (1+1)-CGP using n input nodes
and F = { AND } solves the AND in expected time
O(n
2
logn).
Proof. Let i be the number of input nodes which have
not been connected the function node of the genotype.
The fitness of the individuals depend on the boolean
value of the output. Consequently, we merely achieve
TRUE or FALSE as fitness values. To classify the fit-
ness of an individuals more precisely, we define Arti-
ficial Fitness Levels (A
1
,A
2
,A
j
...,A
n
), where j is the
number of input nodes which have been connected
to the function node. We observe that in level A
j
at
least i + 1 connections share another connection to
the same input node. In level A
n
, all n input connec-
tions have been connected to the function node and
the AND problem is solved. A higher artificial fit-
ness level is achieved, if and only if such a connection
is mutated to an unconnected input. The probability
to mutate to an unconnected input is i/(n − 1). We
again use multiplicative drift analysis to prove the up-
per bound. The negative drift is 0 since solutions with
more unconnected nodes will not be accepted. We
have
E[X
(t)
− X
(t+1)
|X
(t)
] ≥
i + 1
n
·
i
n − 1
=
i + 1
n(n − 1)
· i ≥
2
n
2
· i =
2
n
2
· X
(t)
.
Choosing δ = 2/n
2
, c
min
= 1, and c
max
= n − 1 fulfills
the requirements of Theorem 2.2. From it we obtain
E[T ] ≤
2
δ
· ln(1 +
c
max
c
min
) = n
2
· ln(1 +
n − 1
1
) = O(n
2
logn).
Theorem 6.2. The (1+1)-CGP using n input nodes
and F = { AND } solves the AND in expected time
Ω(n
2
).
Proof. The lower bound of Ω(n
2
) is obvious. The
probability to start in fitness level A
n−1
is at most 1/2,
if n > 1. The probability to proceed from fitness level
A
n−1
to A
n
is 2/n · 1/n, therefore the expected time is
Ω(n
2
).
7 DISCUSSION
The results of our time complexity analysis show
that CGP is able to solve the simple SUM problem
in expected time Θ(n log n). For the AND problem
we proved an upper bound O(n
2
logn) and a lower
bound Ω(n
2
). If a function is part of the function
set which cannot lead to the correct solution, CGP
can efficiently solve the SUM problem. Compared to
the conventional tree representation of GP, the graph-
based representation enables multiple connections be-
tween former nodes and the inputs. Consequently, the
probabilities that beneficial mutations are performed
On the Time Complexity of Simple Cartesian Genetic Programming
177

and the algorithm proceeds towards the global op-
timum can be quite low. Therefore, the result for
the SUM problem when the function set includes
functions which do not contribute to the evolutionary
search is quite interesting. Regarding the analysis of
Mambrini and Oliveto (2016) which found that if an
extra function was added to the function set, the algo-
rithms require at least exponential time to evolve the
simple boolean problems, our result sheds more light
on the behavior of CGP when such function sets are
in use.
One point which should be discussed is the use of
the single active gene mutational strategy. This strat-
egy has been found as more beneficial for the search
performance of CGP as the use of classical mutational
probabilities on a practical level. However, flipping
merely one bit may reduce the probability that a muta-
tion is performed which hopefully processes the algo-
rithm towards the global optimum. Moreover, the use
of the single active gene mutational strategy has only
been investigated and compared on an experimental
level. Therefore, we think a theoretical analysis of a
(1+1)-CGP algorithm with classical mutational prob-
abilities is needed and should be considered in future
work.
Another point which should be discussed is the
fact that both test problems only include one func-
tion node. As a first step towards, we focused on the
behavior and efficiency of the point mutation opera-
tor. Especially in terms of building and reconnecting
connections between input nodes and arity connection
genes. This behavior has been considered highly im-
portant for the search performance of CGP but has
never been investigated on a theoretical level. The
next step towards profound theoretical knowledge of
CGP is the analysis of the mutational behavior of
function nodes.
For the AND problem we proved a higher upper
bound as for the SUM problem. The results indicate
that the expected time of CGP can significantly in-
crease when the given problem enables a high number
of combinatorial possibilities.
The last point which should be discussed is the
complexity of the test problems itself. From a prac-
tical point of view, these problems can be considered
as toy problems which have the limitation of being
very simple and with characteristics of regularity that
make them rather different from any real-life appli-
cation or practical problem. Furthermore, compared
to the state of theoretical knowledge in tree-based GP,
our analysis with the introduced test problems is quite
simple. For instance Mambrini et al. also investigated
incomplete training sets. Nevertheless, as a first step
forward we focused more on the development of suit-
able test problems and studied the feasibility of run-
time complexity analysis in CGP. The complexity of
our problem can easily be increased for further analy-
ses. For instance, the AND problem can be extended
to a boolean NAND problem. To solve this problem,
two functions (AND & NOT) are necessary and at
least two function nodes are needed to find the cor-
rect solution. Therefore, we think that the analysis of
the NAND problem would be a good step forward.
8 CONCLUSION AND FUTURE
WORK
A first time complexity analysis for CGP has been
presented. We introduced a simple mathematical test
problem and a simple boolean test problem for CGP
which can be used for the drift analysis of the (1 + 1)-
CGP algorithm. Our analysis has shown that CGP is
able to solve the mathematical SUM problem in time
Θ(nlogn). Furthermore, adding functions to the func-
tion set which do not contribute to the evolution of the
correct solution does not degrade the time complex-
ity of the (1 + 1)-CGP for this problem. However,
for the AND problem we proved an upper bound of
O(n
2
logn) and a lower bound of Ω(n
2
). Our result
clearly shows that even a simple boolean problem can
lead to a significant level of complexity in CGP which
makes it difficult to find the ideal solution in polyno-
mial time. In the future, we will focus on a more the-
oretical understanding of CGP behavior when larger
genotypes are in use. In particular, we will create
and analyze problems with a higher number of func-
tion nodes. Furthermore, since our obtained results
are strongly problem dependent, other problems have
to be studied in order to make more general state-
ments about the runtime of CGP. Another big ques-
tion which arises from our analyses is in which way
former experimental results in the field of CGP can
be verified and proved on a theoretical level. We also
have to investigate the question of the results of our
study can be replicated for problems that are more
complex. As a next step forward we will analyze the
discussed NAND problem.
REFERENCES
Cramer, N. L. (1985). A representation for the adaptive gen-
eration of simple sequential programs. In Proceedings
of the 1st International Conference on Genetic Algo-
rithms, pages 183–187, Hillsdale, NJ, USA. L. Erl-
baum Associates Inc.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
178

Doerr, B., Johannsen, D., and Winzen, C. (2010). Multi-
plicative drift analysis. In Proceedings of the 12th An-
nual Conference on Genetic and Evolutionary Com-
putation, GECCO ’10, pages 1449–1456, New York,
NY, USA. ACM.
Doerr, B., Johannsen, D., and Winzen, C. (2012). Multi-
plicative drift analysis. Algorithmica, 64(4):673–697.
Doerr, B., Lissovoi, A., and Oliveto, P. S. (2019). Evolv-
ing boolean functions with conjunctions and disjunc-
tions via genetic programming. In Proceedings of the
Genetic and Evolutionary Computation Conference,
GECCO 2019, Prague, Czech Republic, July 13-17,
2019, pages 1003–1011.
Forsyth, R. (1981). BEAGLE a Darwinian approach to pat-
tern recognition. Kybernetes, 10(3):159–166.
Goldman, B. W. and Punch, W. F. (2013). Reducing
Wasted Evaluations in Cartesian Genetic Program-
ming, pages 61–72. Springer Berlin Heidelberg,
Berlin, Heidelberg.
He, J. and Yao, X. (2001). Drift analysis and average time
complexity of evolutionary algorithms. Artificial In-
telligence, 127(1):57 – 85.
He, J. and Yao, X. (2004). A study of drift analysis for esti-
mating computation time of evolutionary algorithms.
Natural Computing, 3(1):21–35.
Hicklin, J. (1986). Application of the genetic algorithm to
automatic program generation. Master’s thesis.
Kalganova, T. and Miller, J. F. (1997). Evolutionary Ap-
proach to Design Multiple-valued Combinational Cir-
cuits. In Proc. Intl. Conf. Applications of Computer
Systems (ACS).
Koetzing, T., Sutton, A. M., Neumann, F., and O’Reilly,
U.-M. (2014). The max problem revisited: The im-
portance of mutation in genetic programming. Theo-
retical Computer Science, 545:94–107.
Koza, J. (1990). Genetic Programming: A paradigm for ge-
netically breeding populations of computer programs
to solve problems. Technical Report STAN-CS-90-
1314, Dept. of Computer Science, Stanford Univer-
sity.
Koza, J. R. (1992). Genetic Programming: On the Pro-
gramming of Computers by Means of Natural Selec-
tion. MIT Press, Cambridge, MA, USA.
Koza, J. R. (1994). Genetic Programming II: Automatic
Discovery of Reusable Programs. MIT Press, Cam-
bridge Massachusetts.
Langdon, W. B. and Poli, R. (2002). Foundations of Genetic
Programming. Springer-Verlag.
Lissovoi, A. and Oliveto, P. S. (2018). On the time and
space complexity of genetic programming for evolv-
ing boolean conjunctions. In Proceedings of the
Thirty-Second AAAI Conference on Artificial Intelli-
gence, (AAAI-18), the 30th innovative Applications
of Artificial Intelligence (IAAI-18), and the 8th AAAI
Symposium on Educational Advances in Artificial In-
telligence (EAAI-18), New Orleans, Louisiana, USA,
February 2-7, 2018, pages 1363–1370.
Mambrini, A. and Oliveto, P. S. (2016). On the Analysis
of Simple Genetic Programming for Evolving Boolean
Functions, pages 99–114. Springer International Pub-
lishing, Cham.
Miller, J. F. (1999). An empirical study of the efficiency
of learning boolean functions using a cartesian ge-
netic programming approach. In Proceedings of the
Genetic and Evolutionary Computation Conference,
volume 2, pages 1135–1142, Orlando, Florida, USA.
Morgan Kaufmann.
Miller, J. F. and Smith, S. L. (2006). Redundancy and com-
putational efficiency in cartesian genetic program-
ming. IEEE Transactions on Evolutionary Computa-
tion, 10(2):167–174.
Miller, J. F., Thomson, P., and Fogarty, T. (1997). De-
signing Electronic Circuits Using Evolutionary Algo-
rithms. Arithmetic Circuits: A Case Study.
Moraglio, A. and Mambrini, A. (2013). Runtime analysis of
mutation-based geometric semantic genetic program-
ming for basis functions regression. In GECCO ’13:
Proceeding of the fifteenth annual conference on Ge-
netic and evolutionary computation conference, pages
989–996, Amsterdam, The Netherlands. ACM.
Moraglio, A., Mambrini, A., and Manzoni, L. (2013). Run-
time analysis of mutation-based geometric semantic
genetic programming on boolean functions. In Pro-
ceedings of the Twelfth Workshop on Foundations of
Genetic Algorithms XII, FOGA XII ’13, pages 119–
132, New York, NY, USA. ACM.
Neumann, F., O’Reilly, U.-M., and Wagner, M. (2011).
Computational Complexity Analysis of Genetic Pro-
gramming - Initial Results and Future Directions,
pages 113–128. Springer New York, New York, NY.
Poli, R., McPhee, N. F., and Rowe, J. E. (2004). Exact
schema theory and markov chain models for genetic
programming and variable-length genetic algorithms
with homologous crossover. Genetic Programming
and Evolvable Machines, 5(1):31–70.
Turner, A. and Miller, J. (2014). Cartesian genetic pro-
gramming: Why no bloat? In Nicolau, M., Kraw-
iec, K., Heywood, M. I., Castelli, M., Garcia-Sanchez,
P., Merelo, J. J., Rivas Santos, V. M., and Sim, K.,
editors, 17th European Conference on Genetic Pro-
gramming, volume 8599 of LNCS, pages 222–233,
Granada, Spain. Springer.
Woodward, J. R. (2006). Complexity and Cartesian Ge-
netic Programming, pages 260–269. Springer Berlin
Heidelberg, Berlin, Heidelberg.
Yu, T. and Miller, J. (2001). Neutrality and the evolvability
of Boolean function landscape. In Genetic Program-
ming, Proceedings of EuroGP’2001, volume 2038 of
LNCS, pages 204–217, Lake Como, Italy. Springer-
Verlag.
On the Time Complexity of Simple Cartesian Genetic Programming
179
