On the Time Complexity of Simple Cartesian Genetic Programming

Roman Kalkreuth and Andre Droschinsky

Department of Computer Science, TU Dortmund University, Otto-Hahn-Straße 14, Dortmund, Germany

Keywords:

Cartesian Genetic Programming, Runtime Analysis, Theory.

Abstract:

Since its introduction, Cartesian Genetic Programming has been mostly analyzed on an experimental level with

boolean function problems. Consequently, there is still little theoretical understanding of Cartesian Genetic

Programming. In this paper, we present a ﬁrst time complexity analysis of Cartesian Genetic Programming.

We introduce and analyze a simple mathematical problem and a simple logical boolean problem called SUM

and AND. The results of our analysis show that simple CGP is able to solve SUM efﬁciently in time Θ(n logn).

However, our analysis of the AND problem shows that simple CGP is not able to solve AND efﬁciently.

1 INTRODUCTION

Genetic programming (GP) can be described as a

paradigm which opens the automatic derivation of

programs for problem-solving. First work on GP

has been done by Forsyth (1981), Cramer (1985)

and Hicklin (1986). Later work by Koza (1990,

1992, 1994) signiﬁcantly popularized the ﬁeld of GP.

GP traditionally uses trees as program representation.

Just over two decades ago Miller, Thompson, Kal-

ganova, and Fogarty presented ﬁrst publications on

Cartesian Genetic Programming (CGP) —an encod-

ing model inspired by the two-dimensional array of

functional nodes connected by feed-forward wires of

an FPGA device (Miller et al., 1997; Kalganova and

Miller, 1997; Miller, 1999). CGP offers a graph-

based representation which in addition to standard

GP problem domains, makes it easy to be applied to

many graph-based applications. Furthermore, CGP

has been found for beneﬁcial for the training of com-

putational methods such as neural networks. CGP

has been mostly analyzed and investigated on an ex-

perimental level with boolean function problems to

investigate and proof important dogmas of the CGP

functionality such as Redundancy, Computational Ef-

ﬁciency and Neutrality.

For instance, Miller and Smith (2006) showed

that the most evolvable representations occur when

the genotype is extremely large and in which over

95% of the genes are inactive. The best performance

was found to employ extremely high levels of redun-

dancy. Another example is the work of Yu and Miller

(2001) which sheds light on the signiﬁcance of neu-

trality in CGP. Experimental analysis of CGP also

gave answers to the question why the candidate pro-

grams in CGP doesn’t bloat during the evolutionary

search Turner and Miller (2014). Despite the fact that

those publications signiﬁcantly contribute to the fun-

damental understanding of the behavior and compu-

tational efﬁciency of CGP on an experimental level,

there is only little theoretical understanding in the

ﬁeld of CGP. Theoretical analyses of CGP have been

mainly unattended in the past. Moreover, even if CGP

has been found as an efﬁcient approach for solving

several problems which can be represented as graphs,

there is a signiﬁcant lack of runtime analysis of the

most used CGP algorithms. The amount of experi-

mental results in the ﬁeld of CGP opens the question

if the ﬁndings can be reproduced and approved from

a theoretical point of view. Furthermore, we feel that

the current state of knowledge of CGP is one-sided

and has to be balanced by more theoretical work. In

this paper, we present a ﬁrst time complexity analysis

of a simple (1 + 1)-CGP algorithm and make one step

towards fundamental theoretical knowledge of CGP.

Another purpose of this paper is the introduction

of an analysis setup including two simple problems

called SUM and AND. Section 2 of this paper de-

scribes CGP and the multiplicative drift analysis. Rel-

evant previous theoretical works of GP and CGP are

surveyed in Section 3. In Section 4 we introduce two

simple test problems for CGP. In Section 5 and 6 we

analyze the runtime of the (1 + 1)-CGP algorithm. In

Section 7 we discuss the results of our analyses. Fi-

nally, Section 8 gives a conclusion and outlines future

work.

172

Kalkreuth, R. and Droschinsky, A.

On the Time Complexity of Simple Cartesian Genetic Programming.

DOI: 10.5220/0008070201720179

In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 172-179

ISBN: 978-989-758-384-1

2 RELATED WORK

2.1 Cartesian Genetic Programming

Cartesian Genetic Programming is a form of Genetic

Programming which offers a graph-based representa-

tion. In contrast to tree-based GP, CGP represents a

genetic program via genotype-phenotype mapping as

an indexed, acyclic, and directed graph. Originally

the structure of the graphs was a rectangular grid of

rows and N

columns, but later work also focused

on a representation with one row. The genes in the

genotype are grouped, and each group refers to a node

of the graph, except the last one which represents the

outputs of the phenotype. Each node is represented

by two types of genes which index the function num-

ber in the GP function set and the node inputs. The

ﬁrst gene of each node represents the function num-

ber and the following genes represent the arity input

connections of the node. These nodes are called func-

tion nodes and execute functions on the input values.

The number of input genes depends on the maximum

arity N

of the function set. The last group in the

genotype represents the indexes of the nodes which

lead to the outputs. Since the output nodes can be

connected to any previous function node, the repre-

sentation of CGP allows inactive function nodes. A

backward search is used to decode the correspond-

ing phenotype. The backward search starts from the

outputs and processes the linked nodes in the geno-

type. In this way, only active nodes are processed

during the evaluation procedure. The number of in-

puts N

, outputs N

, and the length of the genotype is

ﬁxed. Every candidate program is represented with

∗N

∗(N

+1)+N

integers. Even when the length

of the genotype is ﬁxed for every candidate program,

the length of the corresponding phenotype in CGP is

variable which can be considered as a signiﬁcant ad-

vantage of the CGP representation. An example of the

decoding from genotype to phenotype is illustrated in

Figure 1.

CGP is traditionally used with a (1+λ) evolution-

ary algorithm. The new population in each generation

consists of the best individual of the previous popula-

tion and the λ created offspring. The breeding proce-

dure is mostly done by a point mutation which swaps

genes in the genotype of an individual in the valid

range by chance. In this way, connection genes can

be connected to other previous function or input nodes

and function genes can be mutated to other function

numbers.

Genotype

0 1  0 1 2 1 2 2  3

Phenotype

IP1

IP2

Function

Lookup Table

Index Function

Addition

Subtraction

Division

Decode

Node

Number

2 3

432

Figure 1: Exempliﬁcation of the decoding procedure of a

CGP genotype to its corresponding phenotype. The nodes

are represented by two types of numbers which index the

number in the function lookup table (underlined) and the in-

puts (non-underlined) for the node. Inactive function nodes

are shown in gray color.

2.2 Drift Analysis

Drift analysis is one of the state-of-the-art techniques

to analyze the runtime of randomized search heuris-

tics such as evolutionary algorithms. Furthermore,

drift analysis is a powerful tool to analyze the opti-

mization behavior of a randomized search algorithm

over a search space by measuring the progress of the

algorithm with respect to a potential function. Such

a function maps each search point to a non-negative

real number, where a potential of zero indicates that

the search point is optimal. Drift analysis has signif-

icantly contributed to the analysis of meta-heuristics.

Many important results about the optimization time of

meta-heuristics were achieved with drift analysis.

Multiplicative Drift Analysis.

Multiplicative Drift Analysis as introduced by

Doerr et. al. (Doerr et al., 2010, 2012) is based on

Additive Drift Analysis which has been proposed

by He et al. (He and Yao, 2004, 2001). The mul-

tiplicative drift theorem can be considered as the

multiplicative version of the additive drift theorem.

Theorem 2.1 (Additive Drift (He and Yao, 2004)).

Let S ⊆ R be a ﬁnite set of positive numbers and let

(t)

)

t∈N

over S be a sequence of random variables

over S ∪ {0}. Let T be the random variable that de-

notes the ﬁrst point in time t ∈ N for which X

(t)

= 0.

Suppose that there exists a constant δ > 0 such that

E[X

(t)

− X

(t+1)

|T > t] ≥ δ (1)

holds. Then

On the Time Complexity of Simple Cartesian Genetic Programming

173

E[T ] ≤

(0)

(2)

The additive drift theorem describes how to com-

bine the expected time at which the potential function

reaches zero to the ﬁrst time at which the expected

value of the potential reaches zero. If the potential de-

creases in each step and in expectation by δ then after

(0)

/δ steps the expected potential is zero. In order

to apply the previous theorem to the analysis of ran-

domized search heuristics over a ﬁnite search space S,

the deﬁned potential function h : S → R maps all op-

timal search points to zero and all non-optimal search

points to values which are larger than zero. The ran-

dom variable X

(t)

is deﬁned as the potential h(x

(t)

) of

a search point x

(t)

in the t-th iteration of the algorithm.

The random variable T is deﬁned as the optimization

time of the algorithm which is the number of itera-

tions until the algorithm ﬁnds an optimum.

When applying Theorem 2.1, the expected differ-

ence between h(x

(t)

) and h(x

(t+1)

) is called the drift of

the random process {x

(t)

}

t∈N

with respect to h. This

drift is additive if condition (1) holds.

The multiplicative method allows easier analyses

in those settings where the optimization progress is

roughly proportional to the current distance to the op-

timum. This method requires a progress which mul-

tiplicatively depends on the current potential value.

That is the reason why the method was named mul-

tiplicative drift analysis. It has been found that for

a number of problems such potential functions are a

natural choice (Doerr et al., 2010, 2012). However,

since multiplicative drift analysis is derived from the

original additive result, it is clear that the multiplica-

tive version cannot be stronger than the original theo-

rem.

Theorem 2.2 (Multiplicative Drift (Doerr et al.,

2010)). Let S ⊆ R be a ﬁnite set of positive num-

bers with minimum s

min

. Let (X

(t)

)

t∈N

over S be a

sequence of random variables over S ∪ {0}. Let T

be the random variable that denotes the ﬁrst point in

time t ∈ N for which X

(t)

= 0. If there exists δ, c

max

min

> 0 such that

E[X

(t)

− X

(t+1)

(t)

] ≥ δ · X

(t)

(3)

and

min

≤ X

(t)

≤ c

max

(4)

for all t < T , then

E[T ] ≤

· ln(1 +

max

min

) (5)

The drift of a random process with respect to a

potential function g is multiplicative if condition (3)

holds for the afﬁliated random variables. The advan-

tage of the multiplicative approach is that it allows

using potential functions which are more natural. The

most natural potential function can be considered as

the distance of the objective value of the current so-

lution to the optimum. This condition has been found

to be a good choice in the analysis of combinatorial

optimization problems (Doerr et al., 2010, 2012).

2.3 Single Active Gene Mutation

Strategy

The single active gene mutational strategy as pro-

posed by Goldman and Punch (2013) mutates at least

one active gene of an individual in one generation.

This means that all genes of active function nodes and

the output nodes can be selected for mutation. The ac-

tive gene is selected by random. The mutation itself is

done by a bit ﬂip in the legal range of a certain gene.

This procedure is equal to the standard probabilistic

CGP mutation. The single active gene strategy has

been found as highly beneﬁcial for the performance

of CGP. Another beneﬁt of this strategy is the fact

that no parameter for the strength of the mutation is

necessary.

3 PREVIOUS THEORETICAL

WORK ON GP AND CGP

A major theoretical contribution to the understanding

of GP behaviour has been made by applying schema

theory (Langdon and Poli, 2002), (Poli et al., 2004).

However, the results of these works do not contribute

to the runtime analysis of GP.

According to Mambrini and Oliveto (2016), ﬁrst

studies of runtime analysis in GP focused on two

functions which are called ORDER and MAJORITY.

For these types of problems, the ﬁtness of an individ-

ual depends on the structure of the syntax tree and

not on its execution. However, these types of prob-

lems can be considered as very simple compared to

the problems to which GP is usually applied. How-

ever, according to Neumann et al. (2011), the results

for the mentioned problems show that GP is able to

optimize both functions efﬁciently.

In their work, Mambrini and Oliveto (2016) re-

ported that a recent study analyzed the same simple

GP systems on the MAX Problem. The analysis in-

cluded a set of functions, a set of terminals and a

bound D on the maximum depth of the solution, the

goal is to evolve a tree that returns the maximum

value given any combination of functions and termi-

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

174

nals (Koetzing et al., 2014). The results of the analy-

sis show that simple GP systems can efﬁciently evolve

MAX with a function set F=[+; ∗] and one constant as

the terminal set. Compared to the previous functions,

MAX is more similar to those evolved by GP in prac-

tical applications since the ﬁtness indeed depends on

the behavior of the computed function on the input.

Still, dependence is not very strong, since the space

of possible inputs can be partitioned into just two sub-

sets such that for every input in a subset, the optimal

solution to the problem is the same.

Two more theoretical results were obtained by

Moraglio et al. (2013) and Moraglio and Mambrini

(2013) with the runtime analysis of mutation-based

Geometric Semantic Genetic Programming for evolv-

ing boolean and basic regression functions. Recently,

Mambrini and Oliveto (2016) presented a theoret-

ical analysis of two simple GP algorithms on two

boolean problems called AND and XOR. Both al-

gorithms were equipped with a minimal function set

with a maximum of two functions. It has been rig-

orously proved that both algorithms can solve both

easy problems with minimal sets efﬁciently. How-

ever, Mambrini and Oliveto (2016) concluded that:

“If an extra function (i.e. NOT) is added to

the function set, the algorithms require at least

exponential time to evolve the conjunction of

n variables. ”

Recently, Lissovoi and Oliveto (2018) presented re-

sults on the time and space complexity of GP for

evolving boolean conjunctions. The authors present

a performance analysis that sheds light on the be-

haviour of simple GP systems for evolving conjunc-

tions of n variables (AND

). On one hand the analysis

of a random local search GP with minimal terminal

and function sets with minimal terminal and function

sets revealed the relationship between the number of

iterations and the expected error of the evolved pro-

gram on the complete training set. The authors also

considered a more realistic GP system equipped with

a global mutation operator and proved that it can ef-

ﬁciently solve AND

by producing programs of lin-

ear size that ﬁt a training set to optimality and with

high probability generalise well. Based on the results

of Lissovoi and Oliveto (2018), Doerr et al. (2019)

made a considerable step forward by analyzing the be-

haviour and performance of the GP system for evolv-

ing a Boolean function with unknown components,

i.e., the function may consist of both conjunctions and

disjunctions. In their work Doerr et al. rigorously

proved that if the target function is the conjunction of

n variables, then the RLS-GP using the complete truth

table to evaluate program quality evolves the exact

target function in O(`log2n) iterations in expectation,

where ` ≥ n is a limit on the size of any accepted tree.

Regarding the theoretical knowledge of CGP, Wood-

ward (2006) investigated the functional complexity in

CGP. To our best knowledge, the work of Woodward

seems to be the only theoretical work which has been

contributed to the understanding of CGP behavior.

Furthermore, Woodward’s work does not contribute

to the understanding of the runtime complexity by ob-

taining upper and lower runtime bounds of the CGP

algorithm itself. This signiﬁcant lack of theoretical

knowledge in CGP has been the motivation for our

work.

4 PRELIMINARIES

We will analyze a (1+1)-CGP algorithm on test prob-

lems called SUM and AND. We say that an algorithm

solves a problem efﬁciently if it can evolve a solution

in expected polynomial time, where time is deﬁned as

the number of ﬁtness function evaluations. As a ge-

netic operator, the single-active-gene mutation strat-

egy is in use. We will analyze two scenarios. For the

SUM problem, the runtime analysis of the algorithm

depends on the number of n arity connections of a

function node which are represented by the connec-

tion genes of the CGP genotypes. On the other hand,

the runtime analysis of the algorithm depends on the

number of n boolean inputs (terminals) for the given

AND problem. We deﬁne Artiﬁcial Fitness Levels for

the analysis of the SUM and AND problem. For our

analysis, we utilize the Multiplicative Drift Theorem

which has been described in Section 2. For the anal-

ysis of the SUM problem, the CGP is equipped with

a function set consisting of three mathematical func-

tions, SUM, MIN, and AVG. For the analysis of the

AND problem, the function set only consists of the

logical AND function.

4.1 The SUM Problem

The SUM problem is a very simple mathematical test

problem for the theoretical analysis of CGP behavior.

With the SUM problem, we will analyze the (1+1)-

CGP algorithm depending on the number n of arity

connections of a function node. For the analysis of

this problem, the number of function nodes in the

genotype is limited to 1 and the genotype has two

input nodes. The ﬁrst input node is a terminal with

a constant value of x = 0 and the second input is a

constant with a value of y = 1. The goal of this prob-

lem is to connect all arity connections of the function

node to the second input and to add up the ”1” values.

The genotype has one output which is connected to

On the Time Complexity of Simple Cartesian Genetic Programming

175

SUM

0  1 1

Genotype

Phenotype

2 OP

Node number

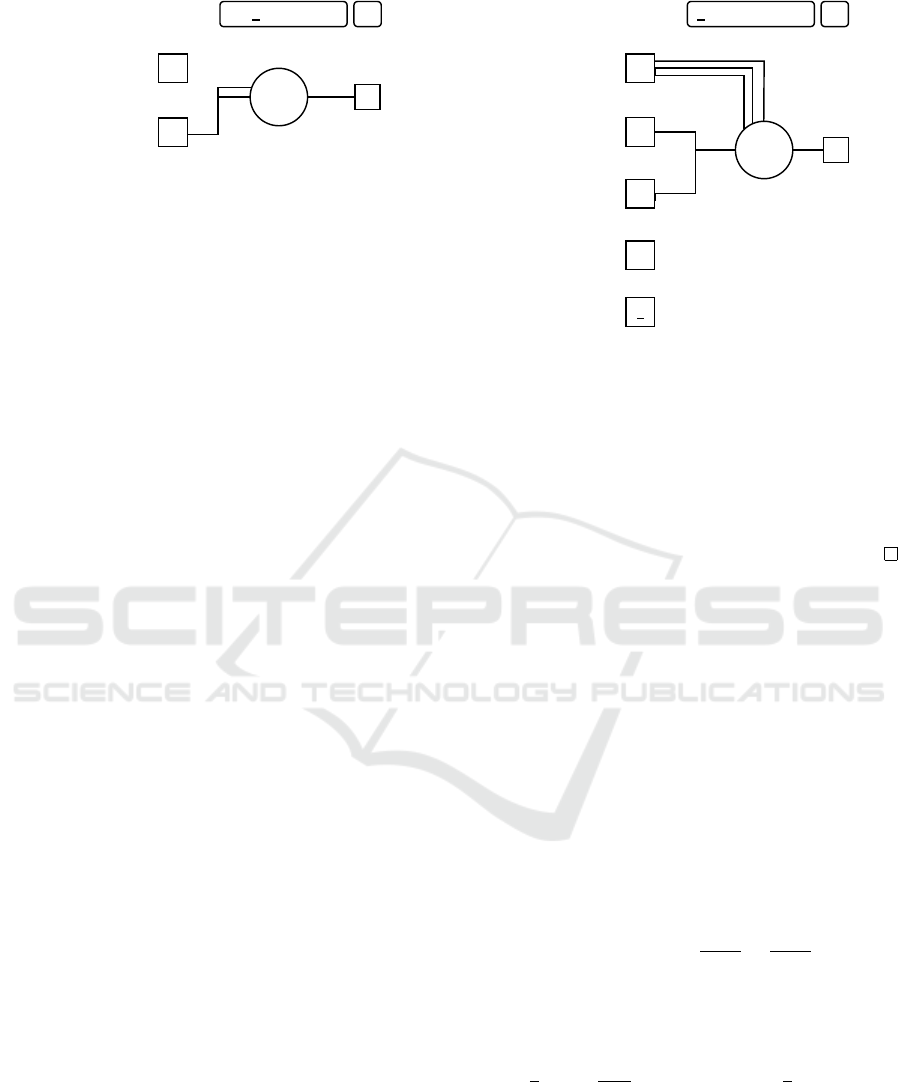
Figure 2: An example of the SUM problem which is used

for the analysis. In the example, the function node has two

arity connections and adds the input value of the second

input node. The sum of this value is then given to the output.

the function node. The function set consists of three

functions. In the ﬁrst place, we have a function SUM

which simply adds up all values of the connected in-

puts of the function node. The function set also con-

sists of a function MIN which calculates the minimum

of the given input values. The third function of the

function set is a function AVG which calculates the

average of the input values. An example of the SUM

problem is shown in Figure 2.

4.2 The AND Problem

The AND problem is a simple logical problem with

boolean values. With the AND problem we will an-

alyze the (1 + 1)-CGP algorithm depending on the

length of n input nodes which represent the boolean

inputs. The number of function nodes in the genotype

is set to 1. The AND problem represents a simple

boolean problem which has the goal to build up and

correct valid logical AND connections between the

input nodes.

For both problems, the number of function nodes

is ﬁxed and set to 1. The reason for this is that we

will focus more on the theoretical analysis of the mu-

tational abilities of CGP to build and reconnect arity

connections. This behavior has been found as one of

the key features of CGP and is considered highly ben-

eﬁcial for the efﬁciency of CGP. The output node is

connected to the function node which represents a set-

ting of the levels back parameter witha value of 1. An

example of the AND problem is shown in Figure 3.

5 ANALYSIS OF THE SUM

PROBLEM

Theorem 5.1. The (1+1)-CGP using n arity function

node connections with a function set F={ SUM, MIN,

AVG } of size m := |F| solves SUM in expected time

Θ(nlogn).

Proof. First, we prove the upper bound using multi-

AND

0 0 0 0  1  2 5

Genotype

Phenotype

5 OP

Node number

Figure 3: An example of the AND problem which is used

for the analysis. In the example, the function node has ﬁve

arity connections and builds logical AND connections be-

tween the ﬁve boolean inputs of the inputs nodes.

plicative drift analysis, cf. Proposition 5.2. Second,

we prove the lower bound by estimating the prob-

ability that at least one connection to the ﬁrst node

does not switch to the second after a certain amount

of steps, cf. Proposition 5.3.

Proposition 5.2. The expected upper time bound for

the SUM problem as deﬁned above is O(n logn).

Proof. Let i be the number of arity connections which

have not been connected to the second input node with

the constant. The ﬁtness of the individuals is deﬁned

by the value of the output. The ﬁtness value depends

on the respective function of the function node and

the amount of arity connections which have been con-

nected to the second input. A single connection gene

is chosen with probability 1/(n + 1). Therefore, the

probability to achieve a higher ﬁtness in a certain gen-

eration is i/(n+1). The negative drift is 0 since solu-

tions with fewer connections to the second input will

not be accepted. We have

E[X

(t)

− X

(t+1)

(t)

] ≥

n + 1

· X

(t)

Choosing δ = 1/(n+1), c

min

= 1, and c

max

= n fulﬁlls

the requirements of Theorem 2.2. From it we obtain

E[T ] ≤

·ln(1+

max

min

) = 2·(n+1)·ln(1+

) = O(n logn).

For now we did not consider the function gene.

We analyze the expected time independently from the

connection genes. With probability 1/(n + 1) the

function node is chosen for mutation. If SUM is

not the current function operator and at least one ar-

ity connection is connected to the second input, then

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

176

with probability

the function operator is mutated to

SUM. The probability that at least one arity connec-

tion is connected to the second input is at least 1 −

If SUM is the current operator, the function SUM is

kept as executing function. The reason for this is that

neither the use of the MIN function nor the use of the

AVG function can achieve a higher ﬁtness value than

the SUM function. Assuming the SUM operator has

not yet been chosen, then the probability to mutate to

SUM is at least

n+1

·(1−

), which implies an up-

per bound for the expected number of turns to mutate

to the SUM operator of O(n).

Proposition 5.3. The expected lower time bound for

the SUM problem as deﬁned above is Ω(n log n).

Proof. We assume the function node is set to SUM

during initialization; the expected running time with

random initialization of the function node cannot be

lower. A given connection ﬂips with probability p :=

1/(n + 1). It does not ﬂip in t steps with probability

(1 − p)

. Therefore, each of n/2 inputs switch at least

once in t steps with probability (1−(1− p)

)

n/2

. With

p as above and t := n log n we have



1 − (1 − p)



1 −



1 −

n + 1



nlog n

≤

1 −





logn



1 −



n·

≤





< 0.61

Therefore, with constant probability c > 1 −

0.61 = 0.39 at least one of n/2 inputs does not switch

after t steps.

With probability at least 1/2 at least n/2 con-

nections are initialized to the ﬁrst input. This fol-

lows from the binomial distribution. With the results

above we obtain the following estimation on the lower

bound.

E(T ) =

∞

∑

t=1

t · p(t) ≥ nlogn ·

· 0.39 = Ω(n logn)

6 ANALYSIS OF THE AND

PROBLEM

Theorem 6.1. The (1+1)-CGP using n input nodes

and F = { AND } solves the AND in expected time

O(n

logn).

Proof. Let i be the number of input nodes which have

not been connected the function node of the genotype.

The ﬁtness of the individuals depend on the boolean

value of the output. Consequently, we merely achieve

TRUE or FALSE as ﬁtness values. To classify the ﬁt-

ness of an individuals more precisely, we deﬁne Arti-

ﬁcial Fitness Levels (A

...,A

), where j is the

number of input nodes which have been connected

to the function node. We observe that in level A

least i + 1 connections share another connection to

the same input node. In level A

, all n input connec-

tions have been connected to the function node and

the AND problem is solved. A higher artiﬁcial ﬁt-

ness level is achieved, if and only if such a connection

is mutated to an unconnected input. The probability

to mutate to an unconnected input is i/(n − 1). We

again use multiplicative drift analysis to prove the up-

per bound. The negative drift is 0 since solutions with

more unconnected nodes will not be accepted. We

have

E[X

(t)

− X

(t+1)

(t)

] ≥

i + 1

n − 1

i + 1

n(n − 1)

· i ≥

· i =

· X

(t)

Choosing δ = 2/n

, c

min

= 1, and c

max

= n − 1 fulﬁlls

the requirements of Theorem 2.2. From it we obtain

E[T ] ≤

· ln(1 +

max

min

) = n

· ln(1 +

n − 1

) = O(n

logn).

Theorem 6.2. The (1+1)-CGP using n input nodes

and F = { AND } solves the AND in expected time

Ω(n

Proof. The lower bound of Ω(n

) is obvious. The

probability to start in ﬁtness level A

n−1

is at most 1/2,

if n > 1. The probability to proceed from ﬁtness level

n−1

to A

is 2/n · 1/n, therefore the expected time is

Ω(n

7 DISCUSSION

The results of our time complexity analysis show

that CGP is able to solve the simple SUM problem

in expected time Θ(n log n). For the AND problem

we proved an upper bound O(n

logn) and a lower

bound Ω(n

). If a function is part of the function

set which cannot lead to the correct solution, CGP

can efﬁciently solve the SUM problem. Compared to

the conventional tree representation of GP, the graph-

based representation enables multiple connections be-

tween former nodes and the inputs. Consequently, the

probabilities that beneﬁcial mutations are performed

On the Time Complexity of Simple Cartesian Genetic Programming

177

and the algorithm proceeds towards the global op-

timum can be quite low. Therefore, the result for

the SUM problem when the function set includes

functions which do not contribute to the evolutionary

search is quite interesting. Regarding the analysis of

Mambrini and Oliveto (2016) which found that if an

extra function was added to the function set, the algo-

rithms require at least exponential time to evolve the

simple boolean problems, our result sheds more light

on the behavior of CGP when such function sets are

in use.

One point which should be discussed is the use of

the single active gene mutational strategy. This strat-

egy has been found as more beneﬁcial for the search

performance of CGP as the use of classical mutational

probabilities on a practical level. However, ﬂipping

merely one bit may reduce the probability that a muta-

tion is performed which hopefully processes the algo-

rithm towards the global optimum. Moreover, the use

of the single active gene mutational strategy has only

been investigated and compared on an experimental

level. Therefore, we think a theoretical analysis of a

(1+1)-CGP algorithm with classical mutational prob-

abilities is needed and should be considered in future

work.

Another point which should be discussed is the

fact that both test problems only include one func-

tion node. As a ﬁrst step towards, we focused on the

behavior and efﬁciency of the point mutation opera-

tor. Especially in terms of building and reconnecting

connections between input nodes and arity connection

genes. This behavior has been considered highly im-

portant for the search performance of CGP but has

never been investigated on a theoretical level. The

next step towards profound theoretical knowledge of

CGP is the analysis of the mutational behavior of

function nodes.

For the AND problem we proved a higher upper

bound as for the SUM problem. The results indicate

that the expected time of CGP can signiﬁcantly in-

crease when the given problem enables a high number

of combinatorial possibilities.

The last point which should be discussed is the

complexity of the test problems itself. From a prac-

tical point of view, these problems can be considered

as toy problems which have the limitation of being

very simple and with characteristics of regularity that

make them rather different from any real-life appli-

cation or practical problem. Furthermore, compared

to the state of theoretical knowledge in tree-based GP,

our analysis with the introduced test problems is quite

simple. For instance Mambrini et al. also investigated

incomplete training sets. Nevertheless, as a ﬁrst step

forward we focused more on the development of suit-

able test problems and studied the feasibility of run-

time complexity analysis in CGP. The complexity of

our problem can easily be increased for further analy-

ses. For instance, the AND problem can be extended

to a boolean NAND problem. To solve this problem,

two functions (AND & NOT) are necessary and at

least two function nodes are needed to ﬁnd the cor-

rect solution. Therefore, we think that the analysis of

the NAND problem would be a good step forward.

8 CONCLUSION AND FUTURE

WORK

A ﬁrst time complexity analysis for CGP has been

presented. We introduced a simple mathematical test

problem and a simple boolean test problem for CGP

which can be used for the drift analysis of the (1 + 1)-

CGP algorithm. Our analysis has shown that CGP is

able to solve the mathematical SUM problem in time

Θ(nlogn). Furthermore, adding functions to the func-

tion set which do not contribute to the evolution of the

correct solution does not degrade the time complex-

ity of the (1 + 1)-CGP for this problem. However,

for the AND problem we proved an upper bound of

O(n

logn) and a lower bound of Ω(n

). Our result

clearly shows that even a simple boolean problem can

lead to a signiﬁcant level of complexity in CGP which

makes it difﬁcult to ﬁnd the ideal solution in polyno-

mial time. In the future, we will focus on a more the-

oretical understanding of CGP behavior when larger

genotypes are in use. In particular, we will create

and analyze problems with a higher number of func-

tion nodes. Furthermore, since our obtained results

are strongly problem dependent, other problems have

to be studied in order to make more general state-

ments about the runtime of CGP. Another big ques-

tion which arises from our analyses is in which way

former experimental results in the ﬁeld of CGP can

be veriﬁed and proved on a theoretical level. We also

have to investigate the question of the results of our

study can be replicated for problems that are more

complex. As a next step forward we will analyze the

discussed NAND problem.

REFERENCES

Cramer, N. L. (1985). A representation for the adaptive gen-

eration of simple sequential programs. In Proceedings

of the 1st International Conference on Genetic Algo-

rithms, pages 183–187, Hillsdale, NJ, USA. L. Erl-

baum Associates Inc.

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

178

Doerr, B., Johannsen, D., and Winzen, C. (2010). Multi-

plicative drift analysis. In Proceedings of the 12th An-

nual Conference on Genetic and Evolutionary Com-

putation, GECCO ’10, pages 1449–1456, New York,

NY, USA. ACM.

Doerr, B., Johannsen, D., and Winzen, C. (2012). Multi-

plicative drift analysis. Algorithmica, 64(4):673–697.

Doerr, B., Lissovoi, A., and Oliveto, P. S. (2019). Evolv-

ing boolean functions with conjunctions and disjunc-

tions via genetic programming. In Proceedings of the

Genetic and Evolutionary Computation Conference,

GECCO 2019, Prague, Czech Republic, July 13-17,

2019, pages 1003–1011.

Forsyth, R. (1981). BEAGLE a Darwinian approach to pat-

tern recognition. Kybernetes, 10(3):159–166.

Goldman, B. W. and Punch, W. F. (2013). Reducing

Wasted Evaluations in Cartesian Genetic Program-

ming, pages 61–72. Springer Berlin Heidelberg,

Berlin, Heidelberg.

He, J. and Yao, X. (2001). Drift analysis and average time

complexity of evolutionary algorithms. Artiﬁcial In-

telligence, 127(1):57 – 85.

He, J. and Yao, X. (2004). A study of drift analysis for esti-

mating computation time of evolutionary algorithms.

Natural Computing, 3(1):21–35.

Hicklin, J. (1986). Application of the genetic algorithm to

automatic program generation. Master’s thesis.

Kalganova, T. and Miller, J. F. (1997). Evolutionary Ap-

proach to Design Multiple-valued Combinational Cir-

cuits. In Proc. Intl. Conf. Applications of Computer

Systems (ACS).

Koetzing, T., Sutton, A. M., Neumann, F., and O’Reilly,

U.-M. (2014). The max problem revisited: The im-

portance of mutation in genetic programming. Theo-

retical Computer Science, 545:94–107.

Koza, J. (1990). Genetic Programming: A paradigm for ge-

netically breeding populations of computer programs

to solve problems. Technical Report STAN-CS-90-

1314, Dept. of Computer Science, Stanford Univer-

sity.

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion. MIT Press, Cambridge, MA, USA.

Koza, J. R. (1994). Genetic Programming II: Automatic

Discovery of Reusable Programs. MIT Press, Cam-

bridge Massachusetts.

Langdon, W. B. and Poli, R. (2002). Foundations of Genetic

Programming. Springer-Verlag.

Lissovoi, A. and Oliveto, P. S. (2018). On the time and

space complexity of genetic programming for evolv-

ing boolean conjunctions. In Proceedings of the

Thirty-Second AAAI Conference on Artiﬁcial Intelli-

gence, (AAAI-18), the 30th innovative Applications

of Artiﬁcial Intelligence (IAAI-18), and the 8th AAAI

Symposium on Educational Advances in Artiﬁcial In-

telligence (EAAI-18), New Orleans, Louisiana, USA,

February 2-7, 2018, pages 1363–1370.

Mambrini, A. and Oliveto, P. S. (2016). On the Analysis

of Simple Genetic Programming for Evolving Boolean

Functions, pages 99–114. Springer International Pub-

lishing, Cham.

Miller, J. F. (1999). An empirical study of the efﬁciency

of learning boolean functions using a cartesian ge-

netic programming approach. In Proceedings of the

Genetic and Evolutionary Computation Conference,

volume 2, pages 1135–1142, Orlando, Florida, USA.

Morgan Kaufmann.

Miller, J. F. and Smith, S. L. (2006). Redundancy and com-

putational efﬁciency in cartesian genetic program-

ming. IEEE Transactions on Evolutionary Computa-

tion, 10(2):167–174.

Miller, J. F., Thomson, P., and Fogarty, T. (1997). De-

signing Electronic Circuits Using Evolutionary Algo-

rithms. Arithmetic Circuits: A Case Study.

Moraglio, A. and Mambrini, A. (2013). Runtime analysis of

mutation-based geometric semantic genetic program-

ming for basis functions regression. In GECCO ’13:

Proceeding of the ﬁfteenth annual conference on Ge-

netic and evolutionary computation conference, pages

989–996, Amsterdam, The Netherlands. ACM.

Moraglio, A., Mambrini, A., and Manzoni, L. (2013). Run-

time analysis of mutation-based geometric semantic

genetic programming on boolean functions. In Pro-

ceedings of the Twelfth Workshop on Foundations of

Genetic Algorithms XII, FOGA XII ’13, pages 119–

132, New York, NY, USA. ACM.

Neumann, F., O’Reilly, U.-M., and Wagner, M. (2011).

Computational Complexity Analysis of Genetic Pro-

gramming - Initial Results and Future Directions,

pages 113–128. Springer New York, New York, NY.

Poli, R., McPhee, N. F., and Rowe, J. E. (2004). Exact

schema theory and markov chain models for genetic

programming and variable-length genetic algorithms

with homologous crossover. Genetic Programming

and Evolvable Machines, 5(1):31–70.

Turner, A. and Miller, J. (2014). Cartesian genetic pro-

gramming: Why no bloat? In Nicolau, M., Kraw-

iec, K., Heywood, M. I., Castelli, M., Garcia-Sanchez,

P., Merelo, J. J., Rivas Santos, V. M., and Sim, K.,

editors, 17th European Conference on Genetic Pro-

gramming, volume 8599 of LNCS, pages 222–233,

Granada, Spain. Springer.

Woodward, J. R. (2006). Complexity and Cartesian Ge-

netic Programming, pages 260–269. Springer Berlin

Heidelberg, Berlin, Heidelberg.

Yu, T. and Miller, J. (2001). Neutrality and the evolvability

of Boolean function landscape. In Genetic Program-

ming, Proceedings of EuroGP’2001, volume 2038 of

LNCS, pages 204–217, Lake Como, Italy. Springer-

Verlag.

On the Time Complexity of Simple Cartesian Genetic Programming

179