Neural Sequence Modeling in Physical Language Understanding
Avi Bleiweiss
BShalem Research, Sunnyvale, U.S.A.
Keywords: Kinematics, Recurrent Neural Networks, Long Short-term Memory, Sequence Model, Attention.
Abstract:
Automating the tasks of generating test questions and analyzing content for assessment of written student re-
sponses has been one of the more sought-after applications to support classroom educators. However, a major
impediment to algorithm advances in developing such tools is the lack of large and publicly available domain
corpora. In this paper, we explore deep learning of physics word problems performed at scale using the trans-
former, a state-of-the-art self-attention neural architecture. Our study proposes an intuitive novel approach to
a tree-based data generation that relies mainly on physical knowledge structure and defers compositionality
of natural language clauses to the terminal nodes. Applying our method to the simpler kinematics domain
that describes motion properties of an object at a uniform acceleration rate and using our neural sequence
model pretrained on a dataset of ten thousand machine-produced problems, we achieved BLEU scores of 0.54
and 0.81 for predicting derivation expressions on real-world and synthetic test sets, respectively. Notably
increasing the number of trained problems resulted in a diminishing return on performance.
1 INTRODUCTION
Science language understanding is a form of text com-
prehension and commonly involves an expression-
rich natural language that reduces to concise com-
putational semantics and grammar. Typically, a hu-
man learner interprets the text describing a problem,
follows by deriving a compact number-sentence rep-
resentation, and only then performs a calculation to
answer the problem query. Vilenius-Tuohimaa et al.
(2008) showed that performance on math word prob-
lems at primary school levels strongly relates to the
child reading comprehension skills.
Machine solving science problems remains a
long-standing challenge to natural language process-
ing (NLP) practitioners. The pilot STUDENT system
(Bobrow, 1964) that dates back over fifty years ago,
finds a solution to a large class of algebra problems,
but had no machine learning component. Then only in
recent years, automatically solving math word prob-
lems attracted considerable attention in the research
community. Models proposed use both feature engi-
neered machine learning (Hosseini et al., 2014; Kush-
man et al., 2014; Roy and Roth, 2015; Shi et al., 2015;
Zhou et al., 2015; Huang et al., 2016; Huang et al.,
2017; Matsuzaki et al., 2017) and deep learning (Ling
et al., 2017; Wang et al., 2017; Huang et al., 2018;
Wong, 2018; Wang et al., 2018). In practice, the broad
Table 1: Key kinematic variables with their corresponding
notation symbols and SI units of measurement (m for meters
and s for seconds).
Variable Symbol Units
Time t s
Acceleration a or g m/s/s
Initial Displacement x
0
or y
0
m
Final Displacement x or y m
Initial Velocity v
0
m/s
Final Velocity v m/s
output space of math solvers is often constrained, as
our study maps a problem to a single equation, either
linear or non-linear, of one unknown variable.
Despite the extensive interest in physical language
understanding by artificial intelligence (AI) scientists,
a sustainable research to develop tools purposed to
read physical word problems and output algebraic ex-
pressions has been fairly sparse. The earliest known
machine-comprehension based work by Suppes et al.
(1998) uses an equational language of well-defined
grammar and semantics to formulate one-dimensional
kinematic problems. Their model associates terms oc-
curring in the natural language statement of the prob-
lem with an equation, but note that learning a fixed
list of words and phrases that refer to qualitative se-
mantics of physical concepts are more effective when
drawn directly from the structure of natural language.
Recently, Leszczynski and Moreira (2016) intro-
464
Bleiweiss, A.
Neural Sequence Modeling in Physical Language Understanding.
DOI: 10.5220/0008071104640472
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 464-472
ISBN: 978-989-758-384-1
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 2: Derivation templates with a {4,5,5} split across missing variables {x,v,t}, respectively.
x v t
v = v0 +a ∗t x = x0 + v0 ∗t + 0.5 ∗a ∗t
2
v = sqrt(v0
2
+ 2 ∗a ∗(x −x0))
v0 = v −a ∗t x0 = x −v0 ∗t −0.5 ∗a ∗t
2
v0 = sqrt(v
2
−2 ∗a ∗(x −x0))
a = (v −v0)/t v0 = (x −x0 −0.5 ∗a ∗t
2
)/t a = (v
2
−v0
2
)/(2 ∗(x −x0))
t = (v −v0)/a t = sqrt(v0
2
+ 2 ∗a ∗(x0 −x)) x0 = (v
2
−v0
2
−2 ∗a ∗x)/(−2 ∗a)
a = (x −x0 −v0 ∗t)/(0.5 ∗t
2
) x = (v
2
−v0
2
+ 2 ∗a ∗x0)/(2 ∗a)
duced a machine solver of word problems that de-
scribe a free falling object due to standard gravity in a
two-dimensional space. Their model consists of two
long short-term memory (LSTM) networks (Hochre-
iter and Schmidhuber, 1997) that are tasked to extract
from the word problem key physical parameters and
the type of question asked, which are then fed to a nu-
merical integrator for calculating the answer. Given
the natural language question that is sampled from
a fixed grammar, their relative small train set might
limit coverage of the query space.
On the other hand, sequence-to-sequence neural
networks (Sutskever et al., 2014; Cho et al., 2014)
have enjoyed great success in a variety of NLP tasks
such as machine translation, speech recognition, and
text summarization. Motivated by the results of Wang
et al. (2017) for solving math word problems, our
work uses an encoder-decoder architecture to trans-
late natural language queries to kinematic equation
derivations in plain text that subsequently feed a neu-
ral expression encoder rather than a discrete evaluator.
Moreover, instead of word, we use character embed-
dings (Pennington et al., 2014) end-to-end to achieve
a compact vocabulary that effectively expresses ab-
breviated units of measurement, math operator to-
kens, and positive and negative decimal numbers with
variable digits assigned to symbolic variables.
The best performing sequence models connect the
encoder and decoder through an attention mechanism.
Attention allows at each timestep to model position-
less dependencies for variable length input and output
sequences. The standard and most widespread atten-
tion technique is additive based that is used in con-
junction with a recurrent neural network (RNN) (Bah-
danau et al., 2015). However, recurrent models main-
tain hidden state of the entire past and their inher-
ent sequential nature of computations limits scalabil-
ity. Attempting to address this shortcoming, ConvS2S
(Elbayad et al., 2018) uses convolutional neural net-
works (CNN) as a basic building block to compute
hidden representations in parallel for all input and
output positions. Aimed toward very long sequences,
the transformer (Vaswani et al., 2017) uses a net-
work with no recurrence and relies entirely on a self-
attention mechanism to draw global dependencies be-
tween input and output sequences. Attention is finely
distributed in independent layers for each the encoder
and decoder stack modules. Outperforming ConvS2S,
the transformer considerably improves on language
translation quality and significantly reduces computa-
tion runtime by exploiting concurrency. In our work,
we chose the additive attention form as a baseline
to contrast performance with the self-attended trans-
former while iterating our kinematics corpus size.
Our main contributions are (1) a tool to construct
kinematic word problems from a high level of ab-
straction and emit summarized queries that are mostly
stripped out of reasoning and thus allow us to focus on
the task of translation, and (2) motivate a neural ex-
pression evaluator to compute rough problem results
and report quantifiable results on how scalable the
neural sequence models we chose are, as we increase
the train dataset, using both synthetic and real-world
test sets. We hypothesize that dissimilarities between
word problems originate primarily from randomized
numerical values assigned to kinematic variables, and
hence expect translation performance to tail-off as the
number of problems exceeds a reasonable threshold.
Our first dataset version has 50,000 contrived prob-
lems to train and evaluate our sequence models
1
.
The rest of this paper is structured as follows.
In Section 2, we overview our two-step process for
constructing machine-synthesized kinematic word-
problems. In Section 3, we introduce the architecture
of our neural model that involves an attention-based
encoder-decoder for natural to mathematical language
translation, and follows with a character-level expres-
sion encoder to calculate a rough problem solution.
Section 4 highlights field definitions of a word prob-
lem object, of which our synthesized corpus is built
on and further contrasted with a baseline real-world
test data, and provides initial data analyzes and de-
tails of our training methodology. In Section 5, we re-
port extensive quantitative results over our scalability
studies. Discussion, summary and identified avenues
for prospective work are provided in Section 6.
1
https://github.com/bshalem/kwp
Neural Sequence Modeling in Physical Language Understanding
465

Table 3: Field definitions of a kinematics word-problem object with corresponding sample values.
Field Value
problem id 5
missing t
equation vˆ2 = v
0
ˆ2 + 2 ∗a ∗(x −x
0
)
asked x
0
known v, v
0
,a,x
values 7830 m/s,5530 m/s,5297 m/s/s,7892 m
derivation x
0
= (5530ˆ2 −7830ˆ2 −2 ∗5297 ∗7892)/(−2 ∗5297)
solution 10792.51 m
question
a car has a final velocity of 7830 m/s, initial velocity of 5530 m/s, acceleration of 5297 m/s/s, final
displacement of 7892 m . what is the initial displacement ?
2 DATA
There are three major equations that are used to de-
scribe motion of an object under constant accelera-
tion. They determine the following mathematical re-
lationship between the formal kinematic parameters
and involve addition, subtraction, multiplication, and
square operators
v = v
0
+ a ∗t (x)
x = x
0
+ v
0
∗t + 0.5 ∗a ∗t
2
(v)
v
2
= v
2
0
+ 2 ∗a ∗(x −x
0
), (t)
where variable symbols are linked by their name and
quantity units as shown in Table 1. Our word prob-
lem grammar uses the tokens identified with two out
of the seven base units that are outlined in the modern
International System of Units (SI) for physical mea-
surements, namely m for displacement in meters and s
for time in seconds. The motion equations have the at-
tractive quality that identifies each by a distinct miss-
ing variable listed as a tag to the right of the formulas.
Missing
Variable
Equation
Asked
Variable
Known
Variables
Derivation
Values
template number list
Figure 1: Visualization of our tree-based process for the first
stage to machine-generated kinematic word-problems.
Our dataset comprises a list of problem objects,
each in a data structure we synthesize following a
two-stage task. In the first step, a tree-based process
progresses in several levels as illustrated graphically
in Figure 1. At the root node, we randomly select a
missing variable ∈{x,v,t} and that leads to the equa-
tion node, where the scope of problem generation is
narrowed to one of the three kinematic formulations.
Each equation defines a close set of n kinematic vari-
ables, of which we randomly choose an asked vari-
able, and let the remaining (n −1) variables become
the known variables. Following at the derivation leaf
node, we chose one of fourteen template classes (Ta-
ble 2), each representing an assignment statement that
has the asked variable on its left-hand-side (lhs), and
the right-hand-side (rhs) is an expression composed of
the known variables linked together by arithmetic op-
eration symbols. At the sibling leaf node, we built an
(n −1)-size list of randomly chosen numeric values
that are ordered by the sequence of known physical
parameters.
Sequence
to
Sequence
Transformer
Expression
Evaluator
numeric
solution
arithmetic
statement
natural
language
query
Figure 2: Architecture overview of our neural model. The
model input is the natural language query and the output
is a numeric solution computed off an intermediate math
statement.
In the second stage, we use both the template and
the number list produced in the former phase to gener-
ate the natural language query of the kinematics prob-
lem. Our simply interpreted query comprises a brief
preamble stating the moving object, a list of short-text
phrases, each expanding on a known physical quantity
with its value and SI unit, and concludes with a ‘what
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
466

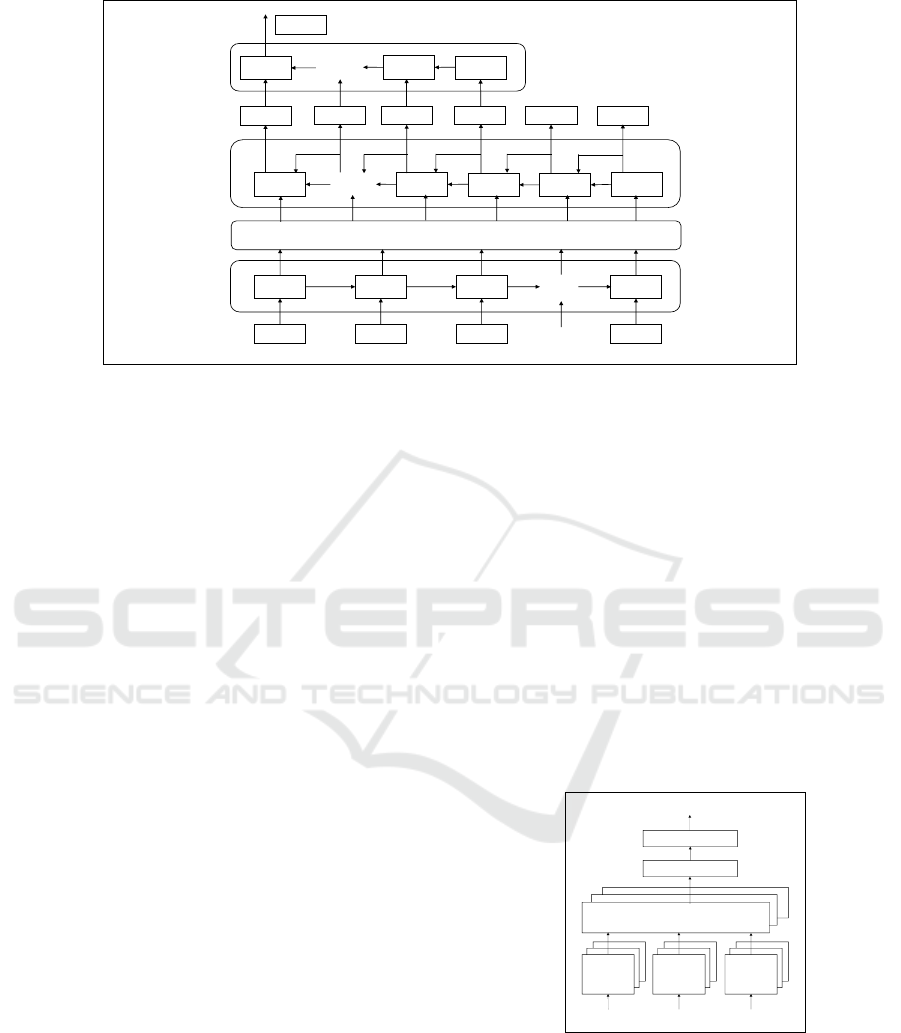
lstm lstm lstm lstm
⋯
b ca
3
⋯
Rough
Solution
Assignment
lstm
lstmlstm
lstm
⋯
Derivation
Decoder
lstm
v
=
+
?
*
13
Character
Embeddings
lstmlstm
⋯
lstm
Query
Encoder
Expression
Encoder
5
Attention
Figure 3: End-to-end architecture of our recurrent neural model: we let character embeddings representing the natural-
language problem question feed at the bottom of our query encoder that connects to the derivation decoder via an additive-
based attention mechanism. The derivation decoder outputs an assignment statement comprised of the asked symbolic vari-
able, math operator tokens, and decimal numbers. Then, the statement rhs enters a character-based expression encoder that
calculates a rough numerical solution to the problem. Model components are built of unidirectional LSTM units.
is asked for’ question clause, as illustrated in Table 3.
Uniformly all tokens of the query are lowercased. Ad-
ditionally, we compute a gold problem solution that
is used as a reference label in training, by providing
a value-substituted template rhs to a string-based ex-
pression evaluator (R Core Team, 2013).
3 MODEL
Our proposed model to evaluate physical language
understanding is shown in Figure 2. The model com-
prises a pair of neural network components, a trans-
lation frontend that feeds forward an arithmetic ex-
pression evaluator. In our experiments, the translation
module is configured with either an additive attention
in the context of a recurrent LSTM-based sequence-
to-sequence network, or the self-attended transformer
architecture (Vaswani et al., 2017).
Our end-to-end LSTM-based neural model is out-
lined in Figure 3. In succession, the model consists of
a query encoder, a derivation decoder, and an expres-
sion encoder. The first two stages make up the stan-
dard sequence-to-sequence network that is fed with
the problem query represented in character embed-
dings, and outputs a derivation statement of which
kinematic variables are already assigned numerical
values. The statement rhs part, a blend of numbers
and math operator tokens, is then passed to the neu-
ral expression evaluator that calculates a rough prob-
lem answer. Our recurrent translation module aligns
sequence positions to steps in computation time, and
uses additive attention (Bahdanau et al., 2015) that
computes the compatibility function c
i
over a feed-
forward neural network with a single hidden layer us-
ing the weighted sum
c
i
=
T
∑
j=1
α
i j
h
j
,
where T is the input sequence length, to score how
well the inputs around position j and the output at
position i match using a probability weight α
i j
and
hidden state h
j
.
Scaled Dot-Product Attention
Project Project Project
Q
K V
Concatenate
Project
O
Figure 4: Transformer: multi-head attention.
To ameliorate the limitations rooted in a serialized
recurrent layer, the transformer introduces multi-head
attention (Figure 4). By restating the definition of an
attention function, the transformer maps a query com-
bined with a set of key-value pairs to an output. Let-
ting each the query and key be a d
k
-dimensional vec-
tor, the transformer computes dot-products of a query
Neural Sequence Modeling in Physical Language Understanding
467

with all the keys, divides each by
√
d
k
, and applies a
softmax function to obtain the weights on the value
vectors of dimensionality d
v
. To compute a set of out-
puts simultaneously, the transformer uses an efficient
matrix representation of queries Q, keys K, and values
V in the formulation of scaled dot-product attention
attention(Q,K,V ) = softmax(
QK
T
√
d
k
)V.
Instead of performing a single attention function, the
transformer linearly projects queries, keys, and val-
ues h times, with h the number of heads, each with
distinctly learned hyperparameters in the form of pro-
jection matrices. Scaled dot-product attention is com-
puted then for each version of the projected inputs and
further concatenated and projected once more to pro-
duce final values (Figure 4). Multi-head attention thus
benefits attending jointly to relevant information from
non-aligned sequence positions.
Given n the sequence length and d the represen-
tation dimension, the theoretical computational com-
plexity per layer of the transformer is O(n
2
·d) com-
pared to O(n ·d
2
) for the recurrent model. In our task,
n  d and thus the transformer is performing faster
than the recurrent model.
4 EXPERIMENTAL SETUP
We measured answer quality of a problem by compar-
ing decoded to reference target derivation, and chose
to report unigram BLEU ∈ {0,1} at the corpus level
for our performance metric (Papineni et al., 2002).
Accuracy, the share of problems that generated a nu-
merical result within ±10% margin of a gold solution-
cluster center was used for offline model tuning.
4.1 Corpus
To address model scalability, we constructed a suffi-
ciently large synthetic dataset of fifty thousand word
problems with the provision to load any subset thereof
for experimentation. Loaded data was partitioned into
train, validation, and test split sets using an 8:1:1 ra-
tio. In Table 3, we show the field definitions of a kine-
matics word-problem object with their corresponding
string values. The first instructive fields include a run-
ning problem ID for object indexing followed by the
missing variable, and thereafter the implied one-of-
three kinematic equations to use. Next in the object
data-structure are the asked variable and a key-value
ordered lists of the known variables. The lists facili-
tate a dictionary to look up a pair of a numeric value
and an SI unit of measurement from a symbolic vari-
able. In our current implementation, variable assigned
values are numbers randomly sampled from a wide
range of 1 to 10,000. Succeeding in the object records
are the gold elements that include the target derivation
statement and the problem numeric solution we used
in training our model. Lastly, the composition of the
summarized natural-language query is shown.
a
t
v
v0
x
x0
t v x
Missing Variable
Asked Variable
Figure 5: Visualization of grid-based distribution of the
asked variable over missing variables using a 50,000 prob-
lem dataset.
−60
−30
0
30
60
−60 −30 0 30 60
X
Y
a
t
v
v0
x
x0
Figure 6: Visualization of problem solution clusters for
each asked variable using a 50,000 problem dataset. Clus-
ters are used to determine rough problem answers.
We conducted initial analysis on our synthesized
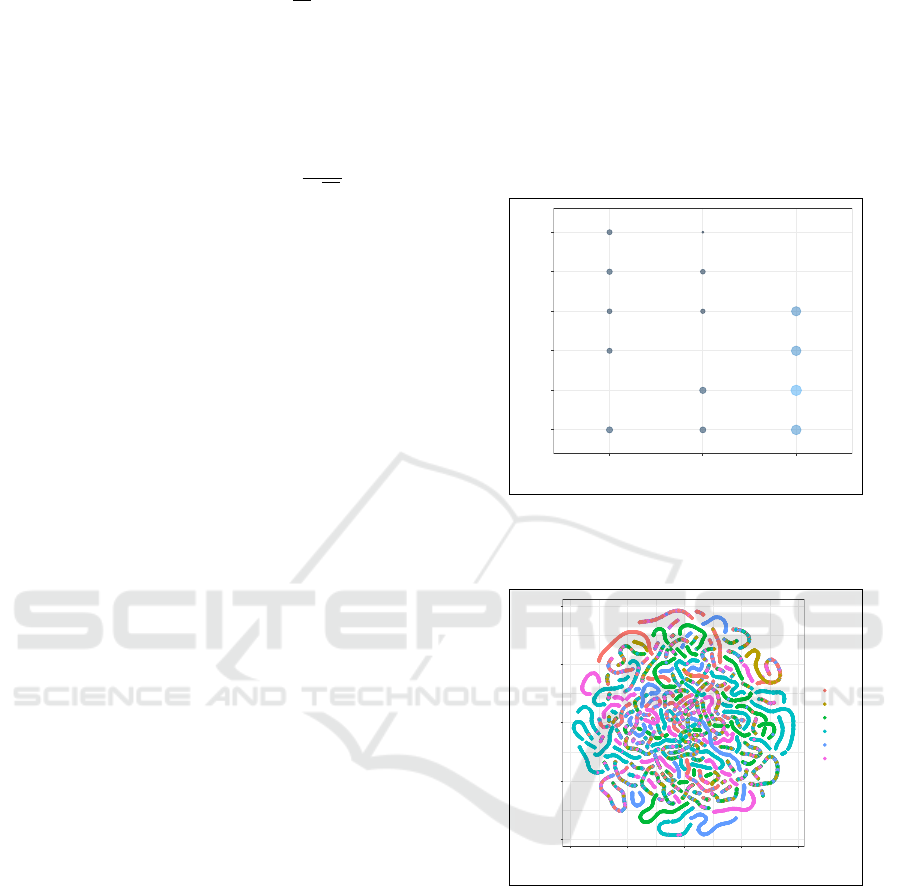
problem data. In Figure 5, we show grid-based dis-
tribution of asked variables across missing variables.
At each asked-missing variable intersection we draw
the count of occurrences using a distinct color. As ex-
pected, the number of total observations for the kine-
matics equation identified with the missing variable x
and described by four variables is larger than for the
other two equations that are each represented by five
variables. Given a missing variable, asked variables
consistently render a relatively even distribution. In
Figure 6, we show problem solution clusters arranged
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
468

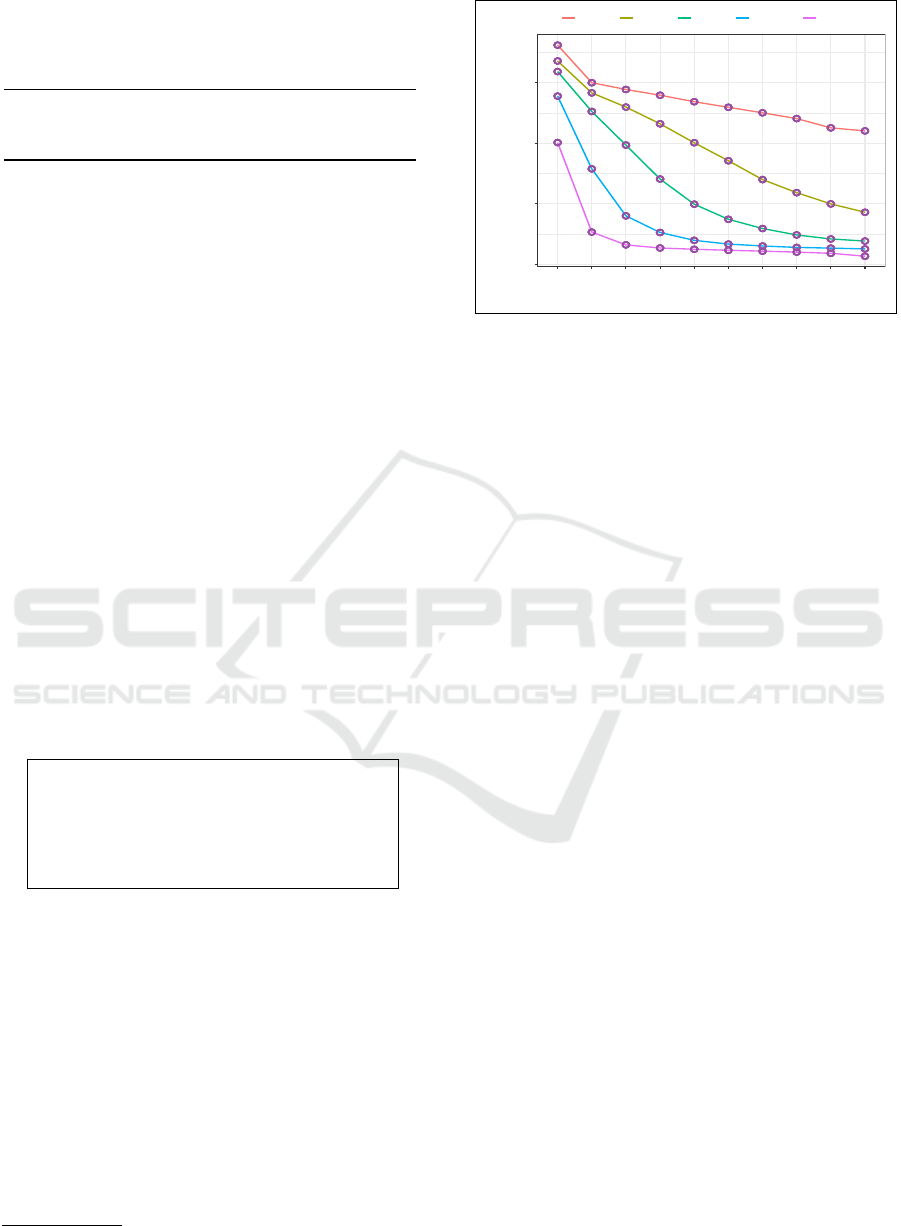
Table 4: Number of character tokens and longest sequence
size used for each the input and output of the translation
module. Shown across the synthesized and real-world data.
Synthesized Real-World
tokens sequence tokens sequence
Encoder 35 171 47 303
Decoder 26 40 27 40
for each asked variables. We use t-distributed stochas-
tic neighbor embedding (t-SNE) (van der Maaten and
Hinton, 2008) to project the large solution space of
50,000 word problems onto a two-dimensional extent.
Numerical solutions to our synthesized problems ap-
pear overall well behaved with no apparent outliers.
To contrast model performance on our machine-
made data, we have extracted real-world kinematic
world problems from the open Web. Unlike the broad
selection for math, and to the extent of our knowl-
edge, we found no large word-problem repositories
in the domain of physics that are publicly available.
We conducted manual searches and managed to ob-
tain one hundred of high-quality kinematic problems
we used as our real-world test set. Real-world queries
were pre-processed to abide by the SI units of phys-
ical measurements, and lowercased for consistency
with our synthesized data. Figure 7 shows a typi-
cal real-world query sampled from an open grammar.
While in Table 4, we show the number of tokens and
the longest sequence in our concise character vocab-
ulary that applies to both the input and output of the
translation module. On the encoder side, figures are
considerably larger for the real-world test set.
a pitcher throws a fastball with a velocity of 43.5
m/s. it is determined that during the windup and
delivery the ball covers a displacement of 2.5 m.
this is from the point behind the body when the
ball is at rest to the point of release. calculate the
acceleration during his throwing motion.
Figure 7: A typical real-world word problem sampled from
an open grammar.
4.2 Training
In our work, we used both Keras (Chollet et al.,
2015) and PyTorch (Paszke et al., 2017) as our deep
learning research platforms for training and evaluat-
ing the sequence-to-sequence and transformer trans-
lation models, respectively.
Keras is a high-level deep learning interface that
runs on top of the TensorFlow
2
software library.
We trained our model using the RMSProp optimizer
2
https://www.tensorflow.org/
0.9
1.2
1.5
1.8
1 2 3 4 5 6 7 8 9 10
Epoch
Loss
1000 2500 5000 10000 25000
Figure 8: Epoch loss progression of sequence-to-sequence
model training parameterized by the number of contrived
kinematic problems.
(Tieleman and Hinton, 2012) with an initial learn-
ing rate of 0.1 and a variable mini-batch size that is
based on the loaded number of word problems. Uni-
formly over both the encoder and decoder compo-
nents, we used 100 dimensional character vectors, and
set the LSTM hidden state to a 256 element vector. To
overcome train data overfitting we used a dropout of
0.2, and a patience of two epochs in early train stop-
ping. In Figure 8, we show our sequence-to-sequence
loss behavior in model training that is parameterized
by five discrete choices of number of dataset prob-
lems ∈ {1,000,2,500,5,000,10,000,25,000}. As evi-
denced by the plot, starting from about the fifth epoch
onward the loss curves of 10,000 and 25,000 pro-
grammatic problems draw exceedingly close.
PyTorch is a Python-based scientific computing
package that provides for tensor computation and effi-
cient parallel execution in building deep neural archi-
tectures. We incorporated the annotated PyTorch im-
plementation of the transformer (Rush, 2018) in our
software framework and modified it to suit our task
and datasets. The transformer was trained on the CPU
performing modest runtime concurrency, as we used
a two-layer stack for each the encoder and decoder
components, rather than the six-layer default. Multi-
head attention was configured with h = 8 and model
size d
model
= 512, and each the query, key, and value
vectors set to d
k
= d
v
= d
model
/h = 64. The inner
layer of the encoder and decoder had dimensionality
d
f f
= 2048. We used the Adam optimizer (Kingma
and Ba, 2014) and followed the transformer method
for increasing the learning rate in the first warmup
epochs of training and then decreasing it proportion-
ally to the inverse square-root of the epoch number.
To avoid train overfitting we used a dropout of 0.1.
We trained the expression encoder separately us-
ing a dataset of compact problem objects, each com-
Neural Sequence Modeling in Physical Language Understanding
469

0.2
0.3
0.4
0.5
0 5000 10000 15000 20000 25000
Word Problems
BLEU Score
realworld synthetic
Figure 9: Sequence-to-sequence model scalability. Show-
ing BLEU scores for real-world baseline and synthesized
test problems as a function of a non-descending number of
trained word problems.
0.5
0.6
0.7
0.8
0 2500 5000 7500 10000
Word Problems
BLEU Score
realworld synthetic
Figure 10: Transformer model scalability. Showing BLEU
scores for real-world baseline and synthesized test problems
as a function of a non-descending number of trained word
problems.
posed of a pair of derivation and solution fields (Ta-
ble 3). Due to the large evaluation space of signed
floating-point numeric quantities, we expected the ex-
pression train set to be considerably larger than the
translation set, and hence the motivation to chose the
concept of computing rough problem results. We used
k-means to bin gold solutions and used the cluster
centers as the reference to compare against decoded
rough solutions. The number of clusters is a user set-
table hyperparameter to tune system accuracy.
5 EXPERIMENTAL RESULTS
In this section, we report quality of kinematic problem
answers for both the sequence-to-sequence and trans-
former neural models. Our rendered BLEU scores for
sequence-to-sequence scalability are shown in Figure
9 on both the reat-world and synthesized test data, as
a function of an increasing number of loaded word
problems. Initially rates climb precipitously up about
2,500 problems, then on to a more moderate upslope,
or a decline for real-world data, and end in a fairly
flat course starting at about 10,000 problems. On av-
erage, machine-made data performance is higher than
on real-world baseline by about 0.12 BLEU.
In Figure 10, we show performance of our trans-
former model at scale. Upon first observation, BLEU
rates advance in a pattern that resembles for the
most part the behavior of our neural recurrent model.
Notably however, the transformer quality flattens at
around 5,000 problems, and moreover, with BLEU
scores of 0.54 and 0.81, it outperforms our recur-
rent model by a factor of 1.45 and 1.65 on real-
world and synthesized data, respectively. Markedly
the transformer encountered diminishing returns in
performance with relative modest amounts of data and
saturated rather quickly in contrast to the recurrent
model. We hypothesize this is mostly owing to a sim-
pler transformer architecture (Zhu et al., 2015).
Results of our comparative analysis of quality as
performed by neural models purposed for science lan-
guage understanding are shown in Table 5. The prob-
lem data type used in the studies listed ranges from
purely real-world or machine-generated to a merger
of the two, while the dataset dimensionality varies
from tens to one hundred thousand word problems.
The data-average performance of our recurrent model
at (0.49 + 0.37)/2 = 0.43 BLEU is on a par with the
0.48 BLEU score reported by Wong et al. (2018).
Their work pertains to the math domain and uses a
similar sequence-to-sequence model to ours. We note
that their approach concatenates both word and char-
acter level embeddings and uses the Python based
SymPy, a symbolic mathematical library to evaluate
a text expression, unlike our model that applies for
this task a dedicated neural network. At the rate of
0.54 BLEU on the real-world test set, the translation
quality of our transformer model tops the rest of the
neural models.
Using our synthesized data, we chose twenty hu-
man experts that include high school students to as-
sess their written response to randomly selected ques-
tions from a set of 10,000 problems. Labeled queries
were uniformly sampled from each of the derivation
templates (Table 2), as each participant in this experi-
ment was asked to solve fourteen problems, leading to
a total of 280 queries for the entire group. The aver-
age score of expert users was about 0.93 BLEU com-
pared to 0.81 BLEU for our transformer based model
(Table 5). Remarkably the most challenging task we
observed for the students was reasoning the selection
of one of the three kinematic equations, while devel-
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
470

Table 5: Comparative model quality of science language understanding. Human expert performance provided for reference.
Model Domain Data Type Word Problems BLEU
Ling et al. (2017) Math Real-World, Synthetic 100,000 0.27
Wong et al. (2018) Math Real-World, Synthetic 18,000 0.48
Our Model (recurrent) Physics
Real-world 25,000 0.37
Synthetic 25,000 0.49
Our Model (transformer) Physics
Real-world 10,000 0.54
Synthetic 10,000 0.81
Our Data (human expert) Physics Synthetic 10,000 0.93
oping the derivation statement was of little effort.
Although the broader scope of attention scalabil-
ity is outside the extent of this paper, the concept
of pointer networks (Vinyals et al., 2015; See et al.,
2017) warrants a brief discussion. These networks use
attention as a pointer to select a member of the input
sequence as the output. They target problems whose
outputs are a sequence of discrete tokens that corre-
spond to positions in the input. Our model maps sum-
marized natural language queries onto an equation
derivation comprised of distinct symbols, and hence
pointer networks are likely to boost answer quality.
6 CONCLUSIONS
In this work, we proposed to extend the encoder-
decoder based sequence translation architecture by
a neural expression evaluator that computes a rough
problem solution to effectively learn kinematic word
problems. Counter to a common intuition, we showed
that performance of both a recurrent and self-attended
sequence models may not scale as the dataset size in-
creases, a statement we proved for both synthesized
and real-world content. We contend that analyzing the
data scale pattern for science language understanding
is key to advance learning algorithms in the underly-
ing network foundation, and prove continued gains in
answer quality by efficiently using large datasets.
We showed that the problem answer quality of
the multi-head self-attended transformer significantly
outperformed our recurrent sequence-to-sequence ar-
chitecture by at least over fifteen percentage points.
Combined with its outstanding training efficiency,
this positions the transformer as the more compelling
solution for our task.
Given a neural model with an output that corre-
sponds to positions in the query sequence, using self-
attention rules evidenced in the transformer archi-
tecture is our natural progression to improve answer
quality. We envision our neural expression evaluator
to take part not just in a backward path with the ob-
jective of assisting the training of the translation sub-
system, but also involved more directly in inference
to quantify the correctness of the problem numeri-
cal solution. Separating the formal variables from the
question clause in the query is a plausible approach to
explore a more effective mapping to a derivation tem-
plate by simulating human expert reasoning. Lastly,
our framework is generic and easily extensible to aid
in learning other physics problem domains.
ACKNOWLEDGMENTS
We would like to thank the anonymous reviewers for
their insightful suggestions and feedback.
REFERENCES
Bahdanau, D., Cho, K., and Bengio, Y. (2015). Neural ma-
chine translation by jointly learning to align and trans-
late. In ICLR, San Diego, California.
Bobrow, D. G. (1964). Natural language input for a com-
puter problem solving system. Technical report, MIT,
Cambridge, MA. http://hdl.handle.net/1721.1/6903.
Cho, K., van Merrienboer, B., Gulcehre, C., Bahdanau,
D., Bougares, F., Schwenk, H., and Bengio, Y.
(2014). Learning phrase representations using RNN
encoder–decoder for statistical machine translation. In
Empirical Methods in Natural Language Processing
(EMNLP), pages 1724–1734, Doha, Qatar.
Chollet, F. et al. (2015). Keras. https://keras.io.
Elbayad, M., Besacier, L., and Verbeek, J. (2018). Per-
vasive attention: {2D} convolutional neural networks
for sequence-to-sequence prediction. In Proceedings
of the 22nd Conference on Computational Natural
Language Learning (CONLL), pages 97–107, Brus-
sels, Belgium.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural Computation, 9(8):1735–1780.
Hosseini, M. J., Hajishirzi, H., Etzioni, O., and Kushman,
N. (2014). Learning to solve arithmetic word prob-
lems with verb categorization. In Empirical Meth-
ods in Natural Language Processing (EMNLP), pages
523–533, Doha, Qatar.
Huang, D., Shi, S., Lin, C.-Y., and Yin, J. (2017). Learn-
ing fine-grained expressions to solve math word prob-
Neural Sequence Modeling in Physical Language Understanding
471

lems. In Empirical Methods in Natural Language Pro-
cessing (EMNLP), pages 805–814, Copenhagen, Den-
mark.
Huang, D., Shi, S., Lin, C.-Y., Yin, J., and Ma, W.-Y.
(2016). How well do computers solve math word
problems? large-scale dataset construction and evalu-
ation. In Annual Meeting of the Association for Com-
putational Linguistics (ACL), pages 887–896, Berlin,
Germany.
Huang, D., Yao, J.-G., Lin, C.-Y., Zhou, Q., and Yin, J.
(2018). Using intermediate representations to solve
math word problems. In Annual Meeting of the As-
sociation for Computational Linguistics (ACL), pages
419–428, Melbourne, Australia.
Kingma, D. P. and Ba, J. (2014). Adam: A method for
stochastic optimization. CoRR, abs/1412.6980. http:
//arxiv.org/abs/1412.6980.
Kushman, N., Artzi, Y., Zettlemoyer, L., and Barzilay,
R. (2014). Learning to automatically solve algebra
word problems. In Annual Meeting of the Association
for Computational Linguistics (ACL), pages 271–281,
Baltimore, Maryland.
Leszczynski, M. and Moreira, J. (2016). Machine solver for
physics word problems. In Neural Information Pro-
cessing Systems (NIPS) Intuitive Physics Workshop,
Barcelona, Spain.
Ling, W., Yogatama, D., Dyer, C., and Blunsom, P. (2017).
Program induction by rationale generation: Learn-
ing to solve and explain algebraic word problems.
In Annual Meeting of the Association for Computa-
tional Linguistics (ACL), pages 158–167, Vancouver,
Canada.
Matsuzaki, T., Ito, T., Iwane, H., Anai, H., and H. Arai,
N. (2017). Semantic parsing of pre-university math
problems. In Annual Meeting of the Association for
Computational Linguistics (ACL), pages 2131–2141,
Vancouver, Canada.
Papineni, K., Roukos, S., Ward, T., and Zhu, W.-J. (2002).
BLEU: a method for automatic evaluation of machine
translation. In Annual Meeting of the Association
for Computational Linguistics (ACL), pages 311–318,
Philadelphia, Pennsylvania.
Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E.,
DeVito, Z., Lin, Z., Desmaison, A., Antiga, L., and
Lerer, A. (2017). Automatic differentiation in py-
torch. In Workshop on Autodiff, Advances in Neu-
ral Information Processing Systems (NIPS) ), Long
Beach, California.
Pennington, J., Socher, R., and Manning, C. (2014). Glove:
Global vectors for word representation. In Empirical
Methods in Natural Language Processing (EMNLP),
pages 1532–1543, Doha, Qatar.
R Core Team (2013). R: A Language and Environment
for Statistical Computing. R Foundation for Sta-
tistical Computing, Vienna, Austria. http://www.R-
project.org/.
Roy, S. and Roth, D. (2015). Solving general arithmetic
word problems. In Empirical Methods in Natural Lan-
guage Processing (EMNLP), pages 1743–1752, Lis-
bon, Portugal.
Rush, A. (2018). The annotated transformer. In Proceedings
of Workshop for NLP Open Source Software (NLP-
OSS), pages 52–60, Melbourne, Australia.
See, A., Liu, P. J., and Manning, C. D. (2017). Get to
the point: Summarization with pointer-generator net-
works. In Annual Meeting of the Association for Com-
putational Linguistics (ACL), pages 1073–1083, Van-
couver, Canada.
Shi, S., Wang, Y., Lin, C.-Y., Liu, X., and Rui, Y. (2015).
Automatically solving number word problems by se-
mantic parsing and reasoning. In Empirical Meth-
ods in Natural Language Processing (EMNLP), pages
1132–1142, Lisbon, Portugal.
Suppes, P., B
¨
ottner, M., and Liang, L. (1998). Machine
learning of physics word problems: A preliminary re-
port. In Computing Natural Language, pages 141–
154. Stanford University, California, USA.
Sutskever, I., Vinyals, O., and Le, Q. V. (2014). Se-
quence to sequence learning with neural networks. In
Advances in Neural Information Processing Systems
(NIPS), pages 3104–3112. Curran Associates, Inc.,
Red Hook, NY.
Tieleman, T. and Hinton, G. E. (2012). Lecture 6.5-
RMSProp: Divide the gradient by a running average
of its recent magnitude. Technical report, COURS-
ERA:Neural Network for Machine Learning, 4, 26-
30.
van der Maaten, L. and Hinton, G. E. (2008). Visualizing
data using t-sne. Journal of Machine Learning Re-
search (JMLR), 9(Nov):2579–2605.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,
L., Gomez, A. N., Kaiser, L. u., and Polosukhin, I.
(2017). Attention is all you need. In Advances in
Neural Information Processing Systems (NIPS), pages
5998–6008. Curran Associates, Inc., Red Hook, NY.
Vilenius-Tuohimaa, P. M., Aunola, K., and Nurmi, J.
(2008). The association between mathematical word
problems and reading comprehension. Educational
Psychology, 28(4):409–426.
Vinyals, O., Fortunato, M., and Jaitly, N. (2015). Pointer
networks. In Advances in Neural Information Pro-
cessing Systems (NIPS), pages 2692–2700. Curran
Associates, Inc.
Wang, L., Wang, Y., Cai, D., Zhang, D., and Liu, X. (2018).
Translating a math word problem to a expression tree.
In Empirical Methods in Natural Language Process-
ing (EMNLP), pages 1064–1069, Brussels, Belgium.
Wang, Y., Liu, X., and Shi, S. (2017). Deep neural solver for
math word problems. In Empirical Methods in Natu-
ral Language Processing (EMNLP), pages 845–854,
Copenhagen, Denmark.
Wong, R. (2018). Solving math word problems. Tech-
nical report, Stanford University, Palo Alto, CA.
https://web.stanford.edu/class/archive/cs/cs224n/
cs224n.1184/reports/6866023.pdf.
Zhou, L., Dai, S., and Chen, L. (2015). Learn to solve alge-
bra word problems using quadratic programming. In
Empirical Methods in Natural Language Processing
(EMNLP), pages 817–822, Lisbon, Portugal.
Zhu, X., Vondrick, C., Fowlkes, C. C., and Ramanan, D.
(2015). Do we need more training data? CoRR,
abs/1503.01508. http://arxiv.org/abs/1503.01508.
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
472