
Engineering Smart Behavior in Evacuation Planning using Local
Cooperative Path Finding Algorithms and Agent-based Simulations
R
´
obert Selvek and Pavel Surynek
a
Faculty of Information Technology, Czech Technical University in Prague, Th
´
akurova 9, 160 00 Praha 6, Czech Republic
Keywords: Evacuation Planning, Cooperative Path-finding, Local Algorithms, Simulations, Real-life Scenarios.
Abstract:
This paper addresses evacuation problems from the perspective of cooperative path finding (CPF). The evac-
uation problem we call multi-agent evacuation (MAE) consists of an undirected graph and a set of agents.
The task is to move agents from the endangered part of the graph into the safe part as quickly as possible.
Although there exist centralized evacuation algorithms based on network flows that are optimal with respect
to various objectives, such algorithms would hardly be applicable in practice since real agents will not be
able to follow the centrally created plan. Therefore we designed a local evacuation planning algorithm called
LC-MAE based on local CPF techniques. Agent-based simulations in multiple real-life scenarios show that
LC-MAE produces solutions that are only worse than the optimum by a small factor. Moreover our approach
led to important findings about how many agents need to behave rationally to increase the speed of evacuation.
1 INTRODUCTION
Evacuation planning represents an important real-life
problem and is increasingly studied in artificial intelli-
gence (Chalmet et al., 1982; Mishra et al., 2015). The
task consists of evacuation of people or other agents
from the endangered area into the safe zone.
Various techniques have been applied to address
the problem including modeling the problem as net-
work flows (Arbib et al., 2018) or nature inspired com-
putation such as bee colony optimization.
The map where the evacuation task takes place
is often modeled as a graph where vertices represent
locations for agents, and edges model the possibil-
ity of moving between pairs of locations (Liu et al.,
2016). Hence the evacuation problem can be inter-
preted as a variant of cooperative path finding (Sil-
ver, 2005; Wang and Botea, 2011; Surynek, 2014;
Surynek, 2015) (CPF). Similarly as in CPF, the evac-
uation modeling must take into account potential col-
lisions between agents and solving techniques must
ensure proper avoidance (Foudil et al., 2009). The
collision avoidance in CPF is usually represented by
a constraint of having at most one agent per vertex. In
contrast to CPF, where agents have unique individual
goals (locations), we usually do not distinguish be-
tween individual agents in the evacuation task. That
a
https://orcid.org/0000-0001-7200-0542
is, an agent can evacuate itself to anywhere in the safe
zone (not to a specific location in the safe zone).
Another important challenge in evacuation plan-
ning is represented by the execution of a plan by real
agents. In real-life evacuation scenarios, we cannot
simply assume that all agents will want to follow the
plan. The real agent may for example prefer the near-
est exit while a centrally created plan make it go else-
where, thus not being realistic for the agent. This
differs from classical planning (Ghallab et al., 2016),
where the planning authority fully observes the envi-
ronment, actions are assumed to be deterministic, and
plans created in advance are perfectly executed
Therefore we focus on local evacuation planning
relying on local cooperative path finding techniques
and agent-based simulations. Our assumption is that
evacuation paths planned locally using information
available to the agent will be more realistic. At the
same time we do not rule out the central aspect com-
pletely as we also consider some agents to be more
informed (about alternative exits, through a commu-
nication device) than others.
This paper begins with a formal introduction to
the concept of evacuation planning, followed by a
short summary of local cooperative path finding algo-
rithms which are the base of our novel evacuation al-
gorithm called Local Cooperative Multi-agent Evacu-
ation (LC-MAE), described and experimentally eval-
uated in multiple scenarios using agent-based simu-
Selvek, R. and Surynek, P.
Engineering Smart Behavior in Evacuation Planning using Local Cooperative Path Finding Algorithms and Agent-based Simulations.
DOI: 10.5220/0008071501370143
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 137-143
ISBN: 978-989-758-382-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
137

lations. As part of the simulations, the algorithm is
compared to a network-flow based algorithm which
produces near-optimal plans.
2 BACKGROUND
The abstract multi-agent evacuation problem (MAE)
takes place in an undirected graph G = (V, E) which
has vertices divided into a set of endangered (D) ver-
tices and a set of safe (S) vertices. Agents from a set,
A = {a
1
, a
2
, ..., a
k
}, are distributed among the vertices
and the task is to evacuate them from endangered ver-
tices to safe vertices. This problem is similar to coop-
erative path finding (CPF) (Silver, 2005) from which
we took the model for movements of agents.
Each agent is placed in a vertex of G so that there
is at most one agent per vertex. The configuration of
agents in vertices of the graph at time t will be de-
noted as c
t
: A → V . Similarly as in CPF an agent can
move into a vacant adjacent vertex. Multiple agents
can move simultaneously, provided they do not col-
lide with each other (that is, no two agents enter the
same target vertex at the same time).
Definition 1. Multi-Agent evacuation (MAE) is a
5-tuple E = [G = (V, E), A, c
0
, D, S], where G repre-
sents the environment, A is a set of agents, c
0
: A → V
is the initial configuration of agents, D and S such
that D ⊆ V , S ⊆ V , V = D ∪ S with D ∩ S 6=
/
0, and
|S| ≥ k represent a set of endangered and a set of safe
vertices respectively.
The task in MAE is to find a plan that moves
all agents into the safe vertices; that is a plan π =
[c
0
, c
1
, ..., c
m
] so that c
m
(a) ∈ S ∀a ∈ A. The total time
until the last agent reaches the safe zone is called a
makespan; the makespan of π is m.
To increase chances of evacuation, the makespan
should be small. A near makespan-optimal evacua-
tion plan can be found in polynomial time using net-
work flow techniques (Yu and LaValle, 2012; Yu and
LaValle, 2015; Arbib et al., 2018). However, these al-
gorithms require a centralized approach where agents
perfectly follow the central plan which is hardly ap-
plicable in real-life evacuation scenarios (Foudil et al.,
2009; Hudziak et al., 2015).
3 COOPERATIVE PATH FINDING
ALGORITHMS
We address MAE from a local point of view inspired
by CPF algorithms like Local Repair A* (LRA*) and
Windowed Hierarchical Cooperative A* (WHCA*)
(Silver, 2005). These algorithms feature a decentral-
ized approach to multi-agent path finding. Instead of
using optimization techniques or network flow, each
agent’s path is found separately, resolving conflicts
between agents trying to enter the same vertex as they
occur.
While LRA* only resolves conflicts at the mo-
ment agent tries to enter an occupied vertex, a naive
strategy which can easily lead to deadlock, WHCA*
is more advanced. Instead of only planning their paths
in space, agents plan their paths in space-time and
share them with other agents using a data structure
called reservation table. When planning, vertices re-
served by another agent at a given time are considered
to be impassable.
If each agent planned and reserved its whole path
to destination, agents planning later would have infor-
mation about its complete route and their needs and
goals would not be taken into account, leading to self-
ish behavior and deadlocks. The fix to this behavior is
windowing, in which agents plan their paths only for
a certain, small, number of time units and the plan-
ning is staggered, so that each agent has an option of
reserving a certain vertex.
4 LOCAL MULTI-AGENT
EVACUATION (LC-MAE)
Our new local multi-agent evacuation (LC-MAE) al-
gorithm divides the evacuation task into three sub-
problems:
• Evacuation Destination Selection: The most im-
portant difference between MAE and simple CPF
is that agents’ destinations are not specified.
• Path-finding to Safety: Once an agent has picked
its destination in S, it has to find a collision-free
path to it.
• Behavior in the Safe Zone: Agents that have left
D do not disappear from the map. They must not
block other agents from entering S.
Agent movement in the last two sub-problems is
based on modified versions of WHCA* algorithm, de-
scribed in their respective sections.
4.1 Evacuation Destination Selection
The basic data structure used by LC-MAE when
choosing an evacuation destination is the frontier de-
noted F, F ⊆ S. The frontier is a set of safe vertices
which separates the endangered zone from the safe
zone. It holds that an agent must enter S by passing a
vertex from F.
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
138

In other other words, removing F from G will sep-
arate D and S into disconnected components. F is cre-
ated on algorithm initialization. It holds that an agent
must enter S by passing a vertex from F.
Destination selection uses a modified A* algo-
rithm, inspired by the RRA* algorithm (Silver, 2005).
Agent’s position is set as the path-finding goal, while
all nodes in F are added to the initial open set. Man-
hattan distance (Korf and Taylor, 1996) is used as the
heuristic.
The result is a vertex in F that is located at the
shortest true distance from the agent while, at the
same time, being reachable by the agent. With the
vertex at hand, the algorithm returns its true distance
from the agent. This matches many real-world evac-
uation scenarios in which people are being evacuated
from an area they know and thus have a mental map
of the nearest exits (Kurdi et al., 2018).
While evacuating, agents track the number of
steps they have taken to reach their destination. Since
the goal’s true distance from the starting position is
known, they can compare these two numbers. If the
number of steps taken is significantly higher than the
distance, it may indicate the agent has veered off the
optimal path. This could be, for example, because the
path to the chosen destination is congested. In that
case, the agent repeats the destination selection pro-
cess, an action that we call retargeting.
4.2 Reservation Table
In LC-MAE we use a variant of the reservation table
used in the Cooperative A* algorithm (Silver, 2005).
Every vertex in G is associated with a mapping of
time steps to reservation structures. Every reservation
structure includes a reference to the reserved vertex,
the ID of the agent that created the reservation and a
priority. Associating priority with reservations is our
primary distinguishing feature. Agents can make a
reservation for vertex v and time step t provided they
fulfill one of the following conditions:
1. No reservation exists yet for v at time t and the
vertex can be reserved at time t + 1.
2. A lower-priority reservation exists for v at time t
and the vertex can be reserved at time t + 1.
3. The agent holds a reservation for vertex v at t − 1.
Condition 3 ensures that CPF algorithms used
in LC-MAE can always perform at least one ac-
tion, staying in place, without having to dynamically
change the order in which agents’ paths are planned
or performing invalid actions, like colliding with an-
other agent.
The t +1 reservability requirement in conditions 1
and 2 prevents the creation of so-called trains - lines
or crowds of agents which move in the same direction
at the same time and which reduce the simulation re-
alism. A simple example of a train being formed is
shown in the right column of figure 1.
4.3 Path-finding To Safety
Once the agent has picked its destination vertex s in
S, it plans a path towards s using WHCA* with the
RRA* heuristic. An agent plans its path on-demand
when it has to return an action for the next time step
and fulfills any of these conditions:
• Is more than halfway through its planned path
1
• Has to retarget
• Has lost a reservation for a vertex on its planned
path
• Is making its first step
Endangered agents are prioritized relative to
agents that are in S - they are processed before agents
located in S. This ensures that endangered agents gen-
erate their plans first.
As soon as an agent enters S (even if it is not
its current destination vertex), it stops following the
planned path and switches to the behavior described
in the next section.
4.4 Safe Zone Behavior
While some parts of the behavior of an endangered
agent, e.g. on-demand planning for a specified num-
ber of steps in advance and reserving the vertices for
given times do not change once the agents enters a
safe zone, the costs for different actions that WHCA*
algorithm considers for each step are different and
more dynamic.
The major difficulty in the safe zone is that freshly
arriving agents must not impede the ongoing evacua-
tion. A simple approach is to move agents as far from
D as possible. However, knowing whether an agent is
getting away from D is not a trivial problem from the
local point of view.
The behavior agents adopt after entering S in LC-
MAE (called surfing) is based on modified WHCA*
algorithm. Costs for the passage from one vertex to
another are computed dynamically, depending on the
positions of other agents and the type of the agent’s
target vertex.
1
Only using half of the planned path before replanning is
a simple way of improving agent cooperation described in
(Silver, 2006)
Engineering Smart Behavior in Evacuation Planning using Local Cooperative Path Finding Algorithms and Agent-based Simulations
139

Algorithm 1: The algorithm for computing the number of
agents following agent a.
1 previous-reserved (E , π, a, t)
2 let π = [c
0
, c
1
, ..., c
t
]
3 V
a
← {c
t−b
(a) | b = 0, ...,
l
2
}
4 for v ∈ V
a
do
5 if reserved(v, t) then
6 r ← r + 1
7 return r
The basic idea is that an agent’s priorities should
vary according to the number of agents following be-
hind, on the same path. When no other agents are
following, it will prefer staying in place. With an in-
creasing number of agents behind, the cost of to stay
in place will increase.
The agent determines the number of following
agents by checking whether there are reservations cre-
ated for positions it has passed before. The process is
formalized in pseudo-code as Algorithm 1.
Since agents only make this check when they start
planning their next few steps, the results have to
be adjusted to account for the increasing uncertainty
about the steps that other agents will take. This is
done by subtracting the number of future time steps
from the number of following agents (see line 11 of
Algorithm 2).
Algorithm 2: Computing costs of different actions for
agents in the safe zone. Actions are considered relative to
agent a located at v at time t. t
c
specifies the time at which
the plan is generated.
1 neighbors (E , π, a, t, v, t
c
)
2 let π = [c
0
, c
1
, ..., c
t
]
3 A
p
← previous-reserved(E ,π,a,t
c
)
4 costs ← []
5 foreach u ∈ S | {v, u} ∈ E do
6 if reservable(u, t + 1)∧u ∈ S then
7 if u ∈ {c
t
(a) | t = 0, 1, ..., t} then
8 costs ← costs ∪{(u, 3)}
9 else
10 costs ← costs ∪{(u, 2)}
11 b ← max(1, |A
p
| − (t −t
c
))
12 if reservable(v, t + 1) then
13 costs ← costs ∪{(u, 1 ∗ b)}
14 else
15 costs ← costs ∪{(u, 4 ∗ b)}
16 return costs
The complete cost-calculation algorithm can be
found in Algorithm 2. With increasing back-pressure,
Figure 1: Movement of agents in ordinary MAE (left) and
in relaxed MAE (right).
moving into a reservable adjacent vertex becomes the
cheapest option. The agent keeps a list of positions
it has already visited and assigns them a higher cost.
This leads to better diffusion of agents through S as
endangered agents can ”nudge” safe agents deeper.
5 RELATED
WORK - CENTRALIZED
EVACUATION
Near optimal solutions of MAE can be found by mod-
eling an MAE instance as network flow (Arbib et al.,
2018; Yu and LaValle, 2012) and planning it centrally.
The core concept is to construct a time expanded net-
work having m copies of G in which a flow of size |A|
exists if and only if the corresponding relaxed MAE
has a solution of makespan m. In the relaxed MAE
we do not require agents to enter vacant vertices, lead-
ing to the possibility of movement similar to the right
column of figure 1.
The solution for a relaxed MAE problem ob-
tained from the network flow algorithms can be post-
processed into a solution of ordinary MAE by post-
poning moves that would violate the invariant of not
entering a vertex that has just been left by an agent.
However, postponing moves may lead to deadlocks,
so the post-processing algorithm swaps the paths
planned for deadlocked agents when a deadlock is de-
tected. We’re calling this planning algorithm based on
post-processed network flows POST-MAE.
6 EXPERIMENTAL EVALUATION
We implemented LC-MAE in Python and evaluated
it in multiple benchmark scenarios. We also imple-
mented POST-MAE on top of Push-relabel max-flow
algorithm (Goldberg and Tarjan, 1988). In order to es-
timate the difference between the makespans of plans
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
140
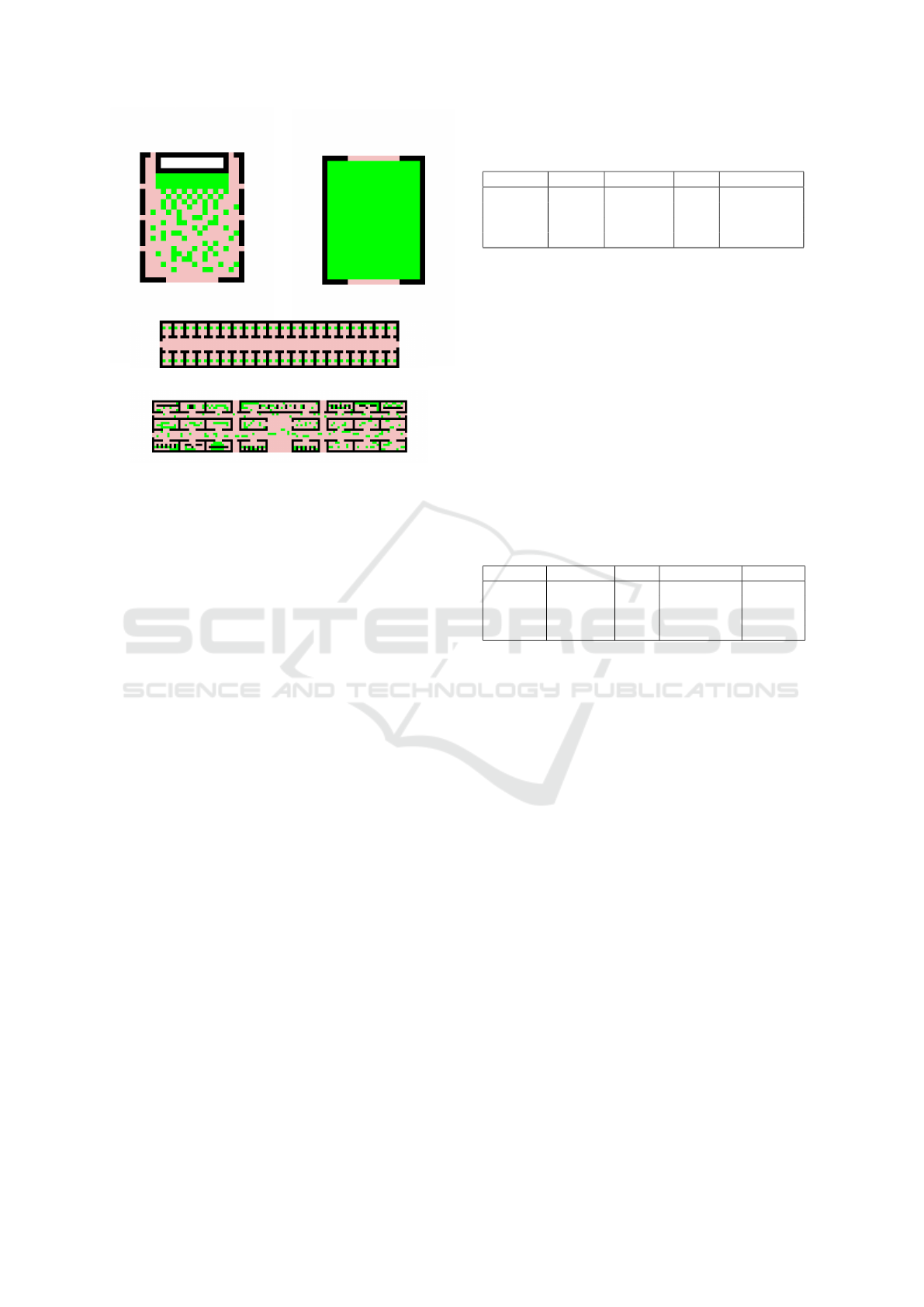
(a) Concert scenario (b) Blocker scenario
(c) Office scenario
(d) Shops scenario
Figure 2: Maps inspired by real-life evacuation scenarios.
generated by LC-MAE and makespans of optimal (if
completely unrealistic) plans, we also benchmarked
POST-MAE without the post-processing, denoted as
flow in comparison tables. Our implementation re-
lies on data structures implemented in the networkx
library (Hagberg et al., 2008). The visualization is
implemented on top of the arcade library (Craven,
2019). In the LC-MAE implementation, the look-
ahead window was set to 10 steps.
6.1 Agent Types
To simulate real-life scenarios with higher fidelity we
used agents of two types. They differ in their behav-
ior while in S all agents rely on surfing. Retargeting
agents fully implement the destination selection algo-
rithm while static agents plan a path to a vertex spec-
ified in advance.
6.2 Setup of Experiments
We used 4 different maps in our evaluations as shown
in Figure 2 - they represent 4-connected grids with
obstacles. Free and safe vertices are white (surround-
ing area), free and endangered vertices are pink. Ver-
tices occupied by agents are green. Black squares sig-
nify walls, so no vertices are present in the underlying
graph at those positions.
6.3 Experimental Results
We first compared the makespan of evacuation plans
generated by LC-MAE with optimal makespans cal-
culated by the flow-based algorithm for relaxed MAE
Table 1: Makespans for evacuation plans.
Scenario Agents LC-MAE Flow POST-MAE
Concert 118 90 17 33
Office 80 94 47 62
Shops 299 129 36 75
Blocker 414 146 23 69
and with makespans of solutions post-processed with
POST-MAE - see table 1. LC-MAE generates plans
that are only worse by a small constant factor (ranging
from 1.52 to 2.73) from those generated by POST-
MAE, which indicates that LC-MAE solutions are
close to the true optimal makespan. Moreover, plans
generated by LC-MAE are more realistic as they need
local communication only.
The performance of LC-MAE is better than the
performance of flow algorithm and than that of POST-
MAE, as demonstrated in table 2. An additional ad-
vantage is that since LC-MAE is a local algorithm and
uses windowing, the plans can be used while they are
being generated, since the steps taken by agents do
not change.
Table 2: Seconds taken by plan generation.
Scenario LC-MAE Flow POST-MAE Speedup
Concert 7 52 62 8.9×
Office 4 57 61 15.3×
Shops 20 379 403 20.2×
Blocker 27 220 243 9.0×
6.4 Agent-based Simulations
We also made a series of experiments to understand
the real process of evacuation in scenarios in which
various types of agents are mixed together, that is,
when some agents are better informed than others.
For each map, we created multiple scenarios with
some of the retargeting agents replaced by static
agents. These static agents try to exit through the
largest opening between the safe and endangered zone
(which could be described as the main exit from the
area) and ignore all other exits. With this setup, re-
targeting agents could be considered to be better in-
formed, given they take all the possible exits into ac-
count.
The percentage of agents that have reached safety
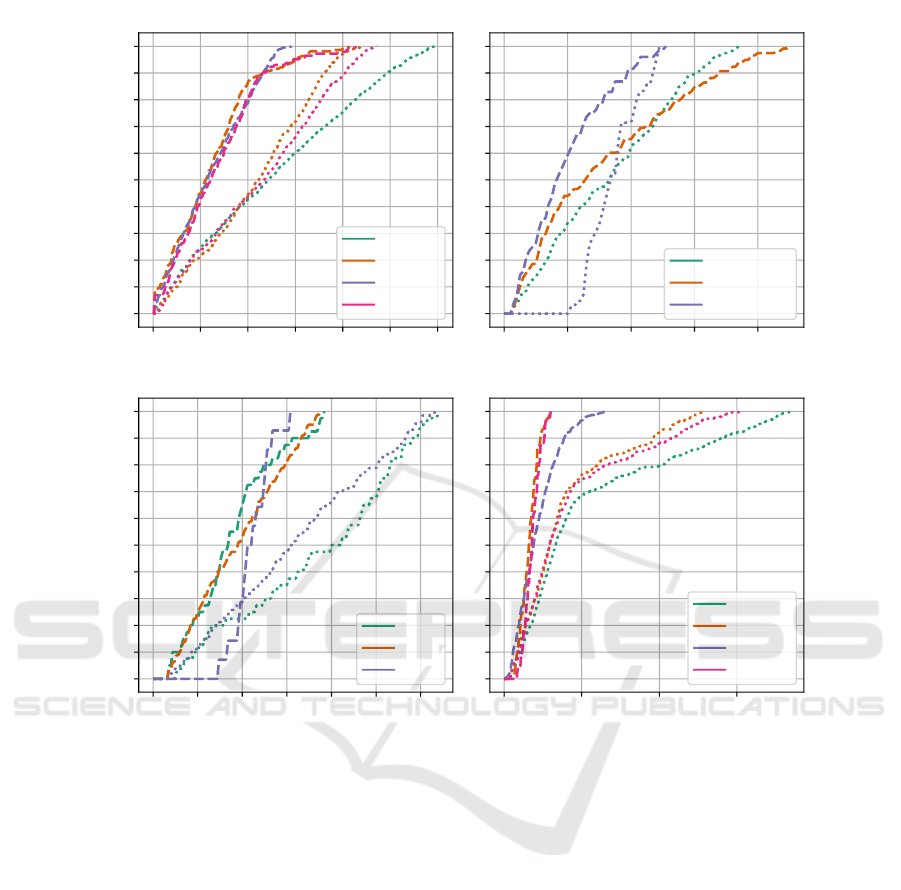
as a function of time is shown in Figure 3.
The Concert evacuation scenario is one of the sce-
narios with a large difference in the makespan be-
tween the relaxed optimum and the plan generated by
LC-MAE.
Our hypothesis is that this is caused by the fact
that the side emergency exits are very small and
the area behind them quickly becomes crowded with
agents that escaped through the emergency exit clos-
est to them.
Engineering Smart Behavior in Evacuation Planning using Local Cooperative Path Finding Algorithms and Agent-based Simulations
141
0 50 100 150 200 250 300
Time
0
10
20
30
40
50
60
70
80
90
100
Safe agents (%)
blocker
allstatic
half
r
third
0 20 40 60 80
Time
Safe agents (%)
concert
allstatic
r
staticcrowd
0 25 50 75 100 125 150
Time
0
10
20
30
40
50
60
70
80
90
100
Safe agents (%)
office
half
r
sixth
0 100 200 300
Time
Safe agents (%)
shops
allstatic
quarter
r
sixth
Figure 3: The percentage of safe agents in time. Line colors differentiate between different scenarios. Dashed lines represent
percentage of retargeting agents in S, dotted lines represent the percentage of static agents in S.
To test this hypothesis, we created two more sce-
narios. The first one is called allstatic and all the
agents are static and try escaping through the large
opening in the lower part of the map. In the second
one, called staticcrowd, only the first three rows in
front of the stage are static. The original scenario with
all retargeting agents is labeled r.
Both allstatic and the original version exhibit
relatively long makespan, although our hypothesis is
confirmed by allstatic’s being shorter. The best
makespan is exhibited by staticcrowd. Retarget-
ing agents use the side exits which do not get over-
crowded and leave most of the endangered zone free
for static agents to pass through.
In the Office scenario we tried two modified ver-
sions: half and sixth - where one half and one sixth
of the agents respectively are retargeting, while oth-
ers are static, trying to escape through the left exit.
For the Shops scenario, we created three modified ver-
sions where static agents are trying to escape through
the large exit at the bottom.
Finally, the Blocker scenario best illustrates how
static agents can impede the evacuation of retarget-
ing agents. Since exits from the endangered zone are
large and there is plenty of safe space on the map, the
shortest makespan is achieved when all of the agents
are retargeting and the longest when they are all static
and try to evacuate through a single exit.
7 CONCLUSION
We presented a new local algorithm called LC-MAE
for evacuation of agents in graphs. LC-MAE uses
a modification of WHCA* as the underlying path-
finding process but also introduces several high-level
procedures that guide agents’ behaviour depending
on whether they are in the endangered or the safe
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
142

zone. Our experimental evaluation indicates that LC-
MAE generates solutions with makespan that is only
a small factor worse than the optimum. We also stud-
ied how different ratios of less informed agents af-
fect the process of evacuation. We found that de-
pending on the scenario, the presence of some unin-
formed agents can improve the evacuation outcome
for the well-informed agents. Additionally, even large
numbers of uninformed agents don’t impede informed
agents from reaching the correct exit.
ACKNOWLEDGEMENTS
This research has been supported by GA
ˇ
CR - the
Czech Science Foundation, grant registration number
19-17966S. We would like to thank anonymous re-
viewers for their valuable comments.
REFERENCES
Arbib, C., Muccini, H., and Moghaddam, M. T. (2018). Ap-
plying a network flow model to quick and safe evacu-
ation of people from a building: a real case. In Pro-
ceedings of the GEOSAFE Workshop on Robust So-
lutions for Fire Fighting, RSFF 2018, L’Aquila, Italy,
July 19-20, 2018., pages 50–61.
Chalmet, L. G., Francis, R. L., and Saunders, P. B. (1982).
Network models for building evacuation. Fire Tech-
nology, 18(1):90–113.
Craven, P. V. (2019). The python arcade library. http://
arcade.academy.
Foudil, C., Djedi, N., Sanza, C., and Duthen, Y. (2009). Path
finding and collision avoidance in crowd simulation.
CIT, 17:217–228.
Ghallab, M., Nau, D. S., and Traverso, P. (2016). Automated
Planning and Acting. Cambridge University Press.
Goldberg, A. V. and Tarjan, R. E. (1988). A new approach
to the maximum-flow problem. J. ACM, 35(4):921–
940.
Hagberg, A. A., Schult, D. A., and Swart, P. J. (2008). Ex-
ploring network structure, dynamics, and function us-
ing networkx. In Proceedings of the 7th Python in
Science Conference, pages 11 – 15.
Hudziak, M., Pozniak-Koszalka, I., Koszalka, L., and
Kasprzak, A. (2015). Comparison of algorithms for
multi-agent pathfinding in crowded environment. In
Nguyen, N. T., Trawi
´
nski, B., and Kosala, R., editors,
Intelligent Information and Database Systems, pages
229–238. Springer International Publishing.
Korf, R. E. and Taylor, L. A. (1996). Finding optimal solu-
tions to the twenty-four puzzle. In Proceedings of the
Thirteenth National Conference on Artificial Intelli-
gence and Eighth Innovative Applications of Artificial
Intelligence Conference, AAAI 96, IAAI 96, Portland,
Oregon, USA, August 4-8, 1996, Volume 2., pages
1202–1207.
Kurdi, H. A., Al-Megren, S., Althunyan, R., and Almulifi,
A. (2018). Effect of exit placement on evacuation
plans. European Journal of Operational Research,
269(2):749–759.
Liu, C., li Mao, Z., and min Fu, Z. (2016). Emergency evac-
uation model and algorithm in the building with sev-
eral exits. Procedia Engineering, 135:12 – 18. 2015
International Conference on Performance-based Fire
and Fire Protection Engineering (ICPFFPE 2015).
Mishra, G., Mazumdar, S., and Pal, A. (2015). Improved
algorithms for the evacuation route planning prob-
lem. In Combinatorial Optimization and Applica-
tions, pages 3–19. Springer International Publishing.
Silver, D. (2005). Cooperative pathfinding. In Young, R. M.
and Laird, J. E., editors, Proceedings of the First Ar-
tificial Intelligence and Interactive Digital Entertain-
ment Conference, June 1-5, 2005, Marina del Rey,
California, USA, pages 117–122. AAAI Press.
Silver, D. (2006). Cooperative pathfinding. In AI Game
Programming Wisdom 3.
Surynek, P. (2014). Solving abstract cooperative path-
finding in densely populated environments. Compu-
tational Intelligence, 30(2):402–450.
Surynek, P. (2015). Reduced time-expansion graphs and
goal decomposition for solving cooperative path find-
ing sub-optimally. In IJCAI, pages 1916–1922.
Wang, K. and Botea, A. (2011). MAPP: a scalable multi-
agent path planning algorithm with tractability and
completeness guarantees. JAIR, 42:55–90.
Yu, J. and LaValle, S. M. (2012). Multi-agent path plan-
ning and network flow. In Algorithmic Foundations
of Robotics X - Proceedings of the Tenth Workshop on
the Algorithmic Foundations of Robotics, WAFR 2012,
pages 157–173.
Yu, J. and LaValle, S. M. (2015). Optimal multi-robot
path planning on graphs: Structure and computational
complexity. CoRR, abs/1507.03289.
Engineering Smart Behavior in Evacuation Planning using Local Cooperative Path Finding Algorithms and Agent-based Simulations
143
