A Synergistic Approach to Enhance the Accuracy-interpretability

Trade-off of the NECLASS Classiﬁer for Skewed Data Distribution

Jamileh Youseﬁ

, Andrew Hamilton-Wright

and Charlie Obimbo

Shannon School of Business, Cape Breton University, Sydney, NS, Canada

School of Computer Science, University of Guelph, Guelph, ON, Canada

Keywords:

Fuzzy, Discretization, Neuro-fuzzy, Classiﬁcation, Skewness, NEFCLASS, Rule-pruning, Adjusted residual,

EQUAL-WIDTH, MME.

Abstract:

NEFCLASS is a common example of a neuro-fuzzy system. The popular NEFCLASS classiﬁer exhibits sur-

prising behaviour when the feature values of the training and testing datasets exhibit signiﬁcant skew. This

paper presents a combined approach to improve the classiﬁcation accuracy and interpretability of the NEF-

CLASS classiﬁer, when data distribution exhibits positive skewness. The proposed model consists of two steps.

Firstly, we used an alternative discretization method to initialize fuzzy sets. Secondly, we devised a statistical

rule pruning algorithm based on adjusted residual to reduce the number of rules, thus improving interpretabil-

ity. This method improves the interpretability of NEFCLASS without signiﬁcant accuracy deterioration. More-

over, a hybrid approach combining the two approaches is developed to increase the accuracy-interpretability

trade-off of NEFCLASS.

1 INTRODUCTION

Skewness is a numerical measure which indicates

whether data distribution is symmetric or not. Skewed

feature values are commonly observed in biological

and medical datasets. Addressing skewness in medi-

cal diagnosis systems is vital for ﬁnding rare events,

such as rare diseases (Gao et al., 2010). Most ma-

chine learning algorithms perform poorly on skewed

datasets (Ben-Gal, 2010). This poses a challenge for

the classiﬁcation of medical data.

Data distributions in the majority of machine

learning algorithms, when they are discussed at all,

are generally expected to have a symmetric distribu-

tion with a central tendency, if not a normally distri-

bution (Ben-Gal, 2010; Mueller and Massaron, 2016).

For example, approaches based on Maximum Like-

lihood and Minimum Distance depend on the as-

sumption of a multivariate Gaussian distribution of a

dataset (Marapareddy et al., 2017). Neural networks

don’t have a priori assumption about the data distribu-

tion (Gupta, 2016). Support Vector Machines (SVMs)

do not assume normality assumption but the SVMs

based on smooth loss functions enjoy an asymptotic

normality (Hable, 2012). Naive Bayes classiﬁer de-

pends on the assumption of a normal distribution for

numerical variables. Another example is the NEF-

CLASS classiﬁer, which uses the EQUAL-WIDTH dis-

cretization method. The EQUAL-WIDTH discretiza-

tion method provides a feature value density indepen-

dent map of input space.

NEURO-FUZZY systems are common machine

learning approaches in the medical domain because of

their ability to learn fuzzy rules from training data and

represent the rules in an understandable way. There-

fore, addressing skewness in neuro-fuzzy systems is

a topic of interest because of their applicability in the

medical domain.

In this work, the NEFCLASS classiﬁer is ex-

tended to provide improved accuracy-interpretability

trade-off over the original NEFCLASS classiﬁer when

trained on skewed data. In order to improve accu-

racy, we used an alternative discretization method.

Additionally, we devised a statistical rule pruning

algorithm which prunes the rules based on a mea-

sure of statistical signiﬁcance when measured by ad-

justed residuals. Moreover, a hybrid approach com-

bining the two approaches is proposed to enhance the

accuracy-interpretability trade-off of NEFCLASS.

We provide a study based on an easily repro-

ducible synthetic data distributions, in order to allow

deeper insights into the data analysis. We evaluated

the accuracy of the classiﬁers using misclassiﬁcation

percentages, and the transparency of the rule-based

Youseﬁ, J., Hamilton-Wright, A. and Obimbo, C.

A Synergistic Approach to Enhance the Accuracy-interpretability Trade-off of the NECLASS Classiﬁer for Skewed Data Distribution.

DOI: 10.5220/0008072503250334

In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 325-334

ISBN: 978-989-758-384-1

325

classiﬁers using the number of rules.

The next section of this paper contains a short re-

view of the NEFCLASS classiﬁer and adjusted resid-

ual measure that will be used to modify the NEF-

CLASS classiﬁer. Section 3 describes the methodol-

ogy of our study. Section 4 presents the statistical

analysis for the results obtained. Finally, conclusions

are presented.

2 BACKGROUND

2.1 The NEFCLASS Classiﬁer

NEFCLASS (Nauck et al., 1996; Nauck and Kruse,

1998; Klose et al., 1999) is a NEURO-FUZZY classi-

ﬁer that generate fuzzy rules and tune the shape of the

membership functions to determine the correct class

label for a given input.

Fig. 1 shows a NEFCLASS model that classiﬁes

input data with two features into two output classes

by using three fuzzy sets and two fuzzy rules. In-

put features are supplied to the nodes at the bottom

of the ﬁgure. These are then fuzziﬁed, using a num-

ber of fuzzy sets. The sets used by a given rule are

indicated by linkages between input nodes and rule

nodes. If the same fuzzy set is used by multiple rules,

these links are shown passing through an oval, such as

the one marked “large” in Fig. 1. Rules directly im-

ply an output classiﬁcation, so these are shown by un-

weighted connections associating a rule with a given

class. Multiple rules may support the same class,

however that is not shown in this diagram.

In Fig. 2a, a set of initial fuzzy membership func-

tions describing regions of the input space are shown,

here for a two-dimensional problem in which the

fuzzy sets are based on the initial discretization pro-

duced by the EQUAL-WIDTH algorithm. As will be

demonstrated, NEFCLASS functions work best when

these regions describe regions speciﬁc to each in-

tended output class, as is shown here, and as is de-

scribed in the presentation of a similar ﬁgure in the

classic work describing this classiﬁer (Nauck et al.,

1996, pp. 239).

As is described in the NEFCLASS overview pa-

per (Nauck and Kruse, 1998, pp. 184), a relationship

is constructed through training data to maximize the

association of the support of a single fuzzy set with a

single outcome class. This implies both that the num-

ber of fuzzy sets must match the number of outcome

classes exactly, and in addition, that there is an as-

sumption that overlapping classes will drive the fuzzy

sets to overlap as well.

Figure 1: A NEFCLASS model with two inputs, two rules,

and two output classes. The ﬁgure extracted from (Youseﬁ

and Hamilton-Wright, 2016).

(a) Initial fuzzy set membership functions in NEFCLASS,

produced using EQUAL-WIDTH discretization

(b) Results of tuning the above membership functions to bet-

ter represent class/membership function information

Figure 2: Fuzzy membership functions before and after

training data based tuning using the NEFCLASS algorithm.

The ﬁgure extracted from (Youseﬁ and Hamilton-Wright,

2016).

Fig. 2a shows the input membership functions as

they exist before membership function tuning per-

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

326

formed by the original NEFCLASS algorithm, when

the input space is partitioned into EQUAL-WIDTH

fuzzy intervals.

Fig. 2b demonstrates that during the fuzzy set tun-

ing process, the membership function is shifted and

the support is reduced or enlarged, in order to better

match the coverage of the data points belonging to

the associated class, however as we will see later, this

process is strongly informed by the initial conditions

set up by the discretization to produce the initial fuzzy

membership functions.

There are three different modes to be used for rule

selection in NEFCLASS. These modes are based on

the performance of a rule or on the coverage of the

training data. The three options for the rule selec-

tion mode presented here are Simple, Best and Best-

PerClass. The Simple rule selection chooses the ﬁrst

generated rules until a predeﬁned maximum number

of rules is achieved. The Best rule selection is an al-

gorithm that ranks the rules based on the number of

patterns associated with each rule and select the rules

from this list. The BestPerClass option is selection of

rules by creating an equal number of rules for each

class. This method uses the Best rule selection algo-

rithm to ranks the rules.

After the construction of the fuzzy rules, a fuzzy

set learning procedure is applied to the training data,

so that the membership functions are tuned to better

match the extent of the coverage of each individual

class in the training data space (Nauck et al., 1996,

pp. 239). Fuzzy membership functions will grow or

shrink, as a result, depending on the degree of ambi-

guity between sets and the dataset coverage.

2.2 Discretization

A discretization process divides a continuous numeri-

cal range into a number of covering intervals where

data falling into each discretized interval is treated

as being describable by the same nominal value in

a reduced complexity discrete event space. In fuzzy

work, such intervals are then typically used to deﬁne

the support of fuzzy sets, and the precise placement

in the interval is mapped to the degree of membership

in such a set.

In the following discussion, we describe the

EQUAL-WIDTH and MME discretization methods.

For example, imagine a dataset formed of three over-

lapping distributions of 15 points each, as shown with

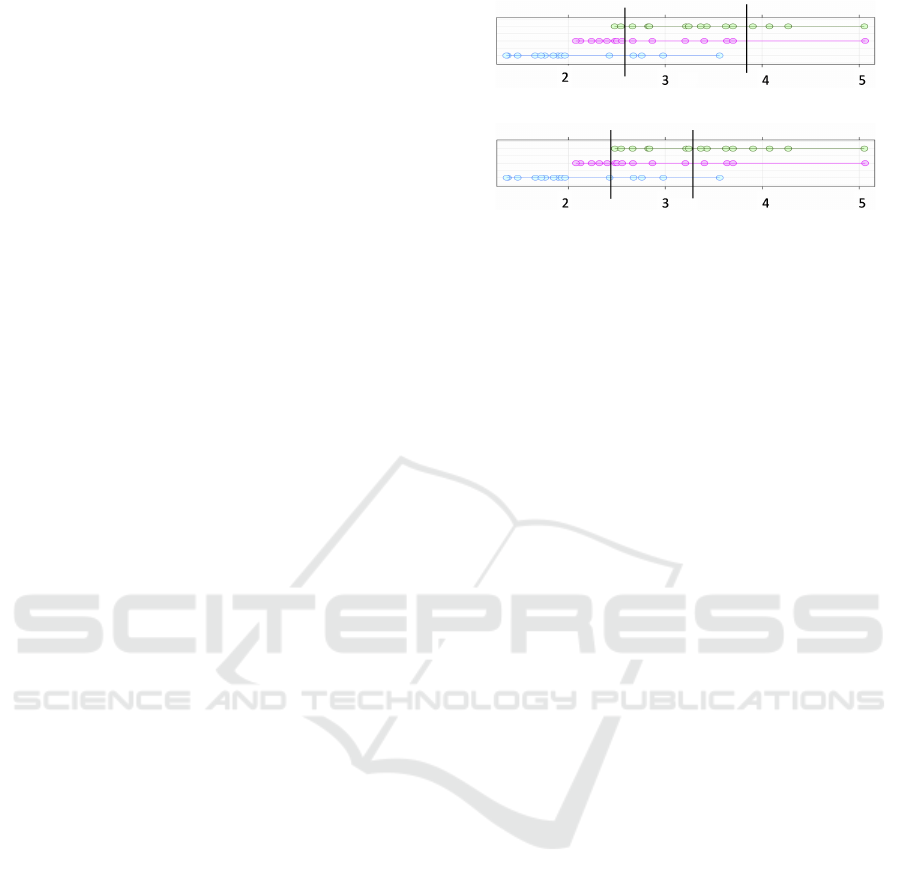
the three coloured arrangements of points in Fig. 3.

The points deﬁning each class are shown in a horizon-

tal band, and the points are connected together to indi-

cate that they are part of the same class group. In parts

3a and 3b, the results of binning these points with two

(a) EQUAL-WIDTH

(b) MME

Figure 3: Two discretization techniques result in different

intervals produced on the same three-class dataset. The ﬁg-

ure extracted from (Youseﬁ and Hamilton-Wright, 2016).

different discretization techniques are shown. The

subﬁgures within Fig. 3 each show the same data,

with the green, red and blue rows of dots (top, middle

and bottom) within each ﬁgure describing the data for

each class in the training data.

2.2.1 EQUAL-WIDTH

The EQUAL-WIDTH discretization algorithm divides

the observed range of continuous values for a given

feature into a number of equally sized intervals, pro-

viding a simple mapping of the input space that is

created independent of both the distribution of class

and of the density of feature values within the input

space (Kerber, 1992; Chemielewski and Grzymala-

Busse, 1996).

Fig. 3a demonstrates the partitioning using

EQUAL-WIDTH intervals. Note that the intervals

shown have different numbers of data points within

each (21, 19 and 5 in this case).

2.2.2 Marginal Maximum Entropy

Marginal Maximum Entropy based discretization

(MME) (Chau, 2001; Gokhale, 1999) divides the

dataset into a number of intervals for each feature,

where the number of points is made equal for all of

the intervals, under the assumption that the informa-

tion of each interval is expected to be equal. The in-

tervals generated by this method have an inverse rela-

tionship with the points’ density within them. Fig. 3b

shows the MME intervals for the example three-class

dataset. Note that the intervals in Fig. 3b do not

cover the same fraction of the range of values (i.e.,

the widths differ), being the most dense in regions

where there are more points. The same number of

points (15) occur in each interval. In both of these

discretization strategies, class identity is ignored, so

there is likely no relationship between class label dis-

tribution and discretization boundary.

A Synergistic Approach to Enhance the Accuracy-interpretability Trade-off of the NECLASS Classiﬁer for Skewed Data Distribution

327

2.3 Adjusted Residual

We use the Hebreman’s adjusted residual algorithm

(Haberman, 1973; Haberman, 1979) in our rule-

pruning model.

In statistics, a residual is deﬁned as a function

of the difference between the expected and observed

counts under the assumed model. The adjusted resid-

uals is a measure of the strength of the difference be-

tween observed and expected counts. The residual is

deﬁned as:

Deﬁnition 1. Given a training set of size n, the resid-

ual for each independent event R

is deﬁned as:

= o

−e

(1)

where o

and e

are the observed number and the

expected number of the event R

, respectively; and r

is the residual associated with R

Deﬁnition 2. The adjusted residuals is deﬁned as:

√

(2)

where z

is the standard residual and v

is the maxi-

mum likelihood estimate of the standard residual vari-

ance, and is deﬁned as:

= var(z

) = var

−e

√

= 1 −

∏

j=1,N

(3)

where o

is the number of occurrences of the pri-

mary event R

∈ R

The expected number of occurrences of R

is de-

ﬁned as:

= n

∏

j=1,n

(4)

The value of the adjusted residuals deﬁnes the rel-

ative signiﬁcance of the associated event R

The advantage of adjusted residuals is that they follow

a Gaussian frequency distribution (with mean zero

and a standard deviation one). Thus we can use a test

of signiﬁcance to determine the likelihood of certain

residual’s value being obtained by chance. The null

hypothesis is that the occurrence of each component’s

primary event is random and independent. A signif-

icance test compares the event’s observed number of

occurrences with the expected number of occurrences

under this null hypothesis. If the adjusted residual is

larger than -1.96 or smaller than 1.96 (the critical val-

ues for > .95 conﬁdence), we conclude that the differ-

ences between the observed and expected number of

occurrences of an even are signiﬁcant. A detailed ex-

position of residual analysis can be found in (Haber-

man, 1973; Haberman, 1979), where the properties of

the analysis are discussed.

3 METHODOLOGY

This paper has two objectives. The ﬁrst is to eval-

uate an alternative discretization method to counter-

act the performance problems in skewed data do-

mains which was identiﬁed in (Youseﬁ and Hamilton-

Wright, 2016). The second is to reduce the rule-base

complexity of the NEFCLASS classiﬁer without losing

accuracy.

Experiments were performed on synthesized

datasets with different levels of feature values skew-

ness. Besides, we conducted a set of experiments

to evaluate the effectiveness of our approaches for a

real-world dataset, EMG data, which contains several

highly skewed features. Results from the experiments

are presented in terms of misclassiﬁcation percent-

ages and number of rules.

In the following sections, we explain the MME

discretization method and the rule pruning algorithm

that are used in our modiﬁed NEFCLASS.

3.1 Improving Accuracy by using the

MME Discretization Methods

The NEFCLASS classiﬁer as presented in (Nauck

et al., 1996) uses an EQUAL-WIDTH discretization

method to divide the observed range of continuous

values for a given feature into fuzzy intervals as de-

scribed in Section 2.1. The fuzzy sets constructed

by the EQUAL-WIDTH discretization method only re-

ﬂect the extent of the data distribution, but do not

reﬂect the variability of density within the distribu-

tion, nor do they reﬂect class labels. This raises the

question of whether taking the distribution of sam-

ples within its extent may improve classiﬁcation per-

formance. To evaluate this question, we use skewed

distributions and the MME method of discretization.

The MME method is not part of the standard NE-

FCLASS implementation, therefore we implemented

a modiﬁed NEFCLASS classiﬁer, utilizing the MME

discretization method.

3.2 Rule Pruning by using the Adjusted

Residual Measure

In this work, we have evaluated rule pruning based

on the adjusted residual on the grounds that a statis-

tically signiﬁcant association, as encoded by a fuzzy

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

328

rule, should give a measure by which higher quality

rules may be identiﬁed. We therefore propose a rule

pruning algorithm based on the adjusted residual that

proceeds as described below.

Deﬁnition 3. Let T be a training set of n training

examples (x

, x

, . . . , x

, y

); i = 1, . . . , n. Each

training example is represented by an instance

, x

, . . . , x

} and it’s associated class label y

where

m is the dimensionality of the input space. There are

m features for each training example, x

, x

, . . . , x

;

c is the dimensionality of the output space. There are

c class labels, l

, l

, . . . , l

Let values for each feature x

, x

, . . . , x

be di-

vided into a number of s fuzzy sets.

where

Feature x

is associated with fuzzy sets F

, F

, . . . , F

;

Feature x

is associated with fuzzy sets F

, F

, . . . , F

;

And feature x

is associated with F

, F

, . . . , F

Let R be a set of k rules generated from the

training set T .

where

is a linguistic rule generated from the example

, x

, . . . , x

, y

);

is the antecedent of R

;

, . . . ,C

are the conditions for the antecedent A

Each condition C

deﬁned as “If x

is F

” ;

i = 1, . . . , m and j = 1, . . . , s;

is deﬁned as follows:

= If C

and C

and . . . and C

then l is y

(5)

Residuals for R

are calculated as follows:

= o(R

) −e(R

) (6)

where

r(R

) is the residual of rule R

;

o(R

) is the observed number of occurrences of rule

in the training set.

e(R

) is the number of occurrences of rule R

ex-

pected under an assumed model of uniform random

chance, and is calculated as follows:

e(R

) = e(A

) ×e(l is y

) (7)

e(A

) = n ×e(C

) ×e(C

) ×···×e(C

) (8)

e(C

) =

o(C

)

(9)

The rules that are statistically signiﬁcant, based on

their adjusted residual, will be selected, whereas the

insigniﬁcant rules will be removed. Finally we use

the new fuzzy rule-base for retraining the NEFCLASS

classiﬁer in order to tune the membership functions in

a way such that they match with new rules.

3.3 Modiﬁed NEFCLASS Classiﬁers

Table 1 summarizes the four NEFCLASS classiﬁers

with their respective properties and provides the

names by which they will be identiﬁed in the rest of

the paper.

3.4 Synthesized Datasets

Four synthesized datasets were used for experiments.

Three datasets were produced by randomly gener-

ating numbers following the F-DISTRIBUTION with

different degrees of freedom chosen to control skew.

The F-DISTRIBUTION (Natrella, 2003) has been cho-

sen as the synthesis model because the degree of skew

within an F-DISTRIBUTION is controlled by the pairs

of degrees of freedom speciﬁed as a pair of distribu-

tion control parameters. This allows for a spectrum of

skewed data distributions to be constructed. We de-

signed the datasets to present different levels of skew-

ness with increasing skew levels. Three pairs of de-

grees of freedom parameters have been used to gen-

erate datasets with different levels of skewness, in-

cluding low, medium, and high-skewed feature val-

ues. After initial experiments datasets with degrees of

freedom (100, 100) was chosen to provide data close

to a normal distribution, (100, 20) provides moderate

skew, and (35, 8) provides high skew.

A synthesized dataset consisting of 1000 ran-

domly generated examples consisting of four-feature

(W , X, Y , Z). F-DISTRIBUTION data for each of

three classes was created. The three classes (ClassA,

ClassB and ClassC) overlap, and are skewed in the

same direction. We have taken care to ensure that

all datasets used have a similar degree of overlap,

and same degree of variability. The size of datasets

were designed to explore the effect of skewness when

enough data is available to clearly ascertain dataset

properties. Ten-fold cross validation was used to di-

vide each dataset into training (2700) and testing (300

point) sets in which an equal number of each class is

represented. This method provides a better estimate

of median performance, as well as a measure of vari-

ability.

Another synthesized dataset was produced by

randomly generating numbers from the CIRCULAR-

UNIFORM-DISTRIBUTION. A CIRCULAR-

UNIFORM-DISTRIBUTION is a distribution within

a circle with constant probability density across the

area of the circle for all values. The CIRCULAR-

UNIFORM-DISTRIBUTION is a part of the family of

symmetric distributions, so the skewness of circular

uniform distribution is close to 0.

Fig. 4 shows the skewness of each dataset for each

A Synergistic Approach to Enhance the Accuracy-interpretability Trade-off of the NECLASS Classiﬁer for Skewed Data Distribution

329

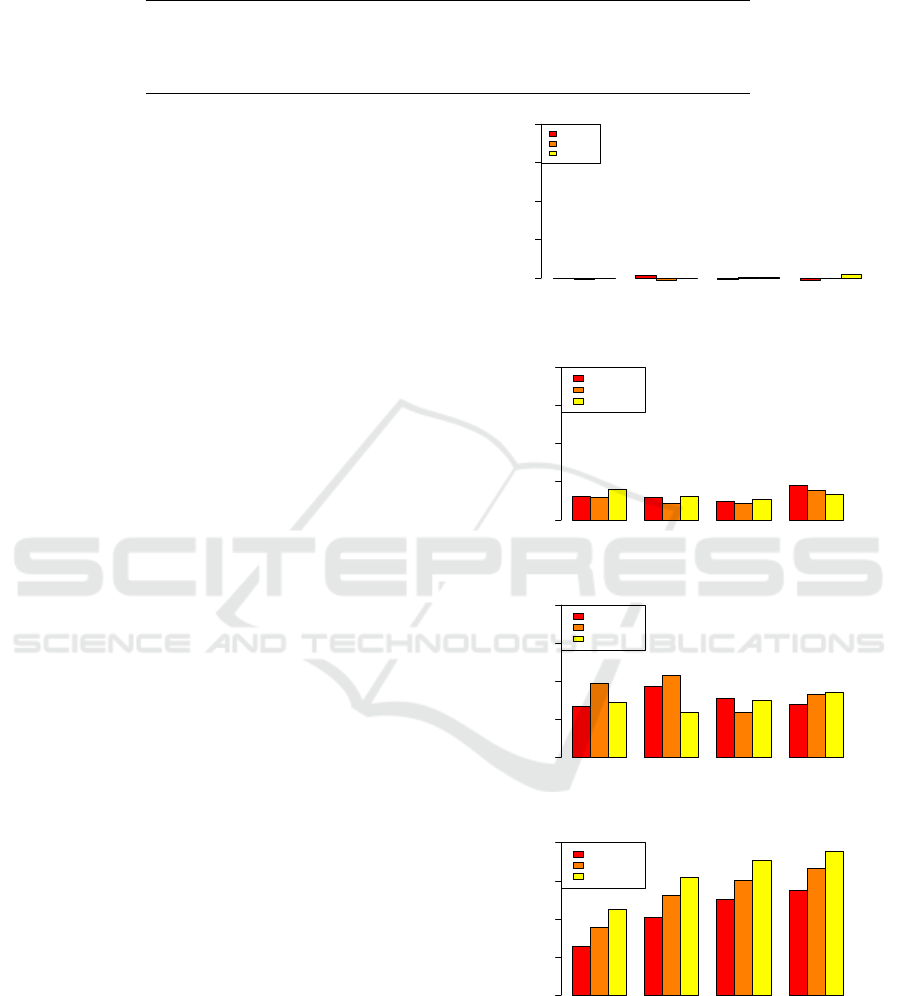
Table 1: List of all classiﬁers derived from the NEFCLASS classiﬁer.

Classiﬁer Discretization Technique Rule Pruning Technique

NEF-ORG Default (EQUAL-WIDTH) Default (BestPerClass)

NEF-MME MME Default (BestPerClass)

NEF-AR Default (EQUAL-WIDTH) Adjusted Residuals

NEF-MME-AR MME Adjusted Residuals

feature. From these ﬁgures one can see that the UNI-

FORM and LOW-100,100 data are relatively symmet-

ric, while as the skew increases as we consider the

MED-100,20 and HIGH-35,8 data show an increas-

ing, and ultimately quite dramatic, skew.

3.5 Electromyography Dataset (EMG)

To show the pertinence of this analysis to a real

world data problem, we have explored the skewness

of a dataset from the clinically applicable world of

quantitative electromyography (QEMG). QEMG is

the study of the electrical potentials observed from

contracting muscles as seen through the framework of

quantitative measurement. QEMG is used in research

and diagnostic study (Stashuk and Brown, 2002).

EMG datasets are known to contain features with

highly skewed value distributions (Enoka and Fugl-

evand, 2001).

The EMG dataset used here contains seven

features of MUP templates (Amplitude, Duration,

Phases, Turns, AAR, SizeIndex, and MeanMUVolt-

age) observed on 791 examples representing three

classes (Myopathy, Neuropathy, Healthy), collected

through a number of contractions, and used in previ-

ous work (Varga et al., 2014). Each example is based

on measuring values from a MUP template extracted

from an EMG signal, and it describes the contribution

of all observed MUs that contributed to the obtained

EMG signal.

Figure 5 shows the skewness values for all the

features with respect to each class. As is shown in

Figure 5, the distribution of values for Amplitude

and MeanMUVoltage are highly positively skewed,

particularly in Myopathy cases. In contrast, Turns

is highly skewed in Neuropathy and Normal cases.

Also, Phases, AAR, and SizeIndex demonstrate rel-

atively low skewness.

4 RESULTS AND DISCUSSIONS

We evaluate the effect of discretization methods on

the misclassiﬁcation percentages and the number of

rules obtained by a NEFCLASS based classiﬁer when

trained on skewed data. The misclassiﬁcation per-

centages obtained by the four classiﬁers are gathered

W X Y Z

Feature

Skewness Value

0 1 2 3 4

ClassA

ClassB

ClassC

(a) UNIFORM

W X Y Z

Skewness Value

0 1 2 3 4

ClassA

ClassB

ClassC

(b) LOW-100,100

W X Y Z

Skewness Value

0 1 2 3 4

ClassA

ClassB

ClassC

W X Y Z

Skewness Value

0 1 2 3 4

ClassA

ClassB

ClassC

(d) HIGH-35,8

Figure 4: Skewness by label and feature for the three syn-

thetic datasets. The ﬁgure extracted from (Youseﬁ and

Hamilton-Wright, 2016).

in Table 2, while the number of rules appears in Ta-

ble 3. The results have been calculated over the 10

cross-validation trials. Mann-Whitney-Wilcoxon was

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

330

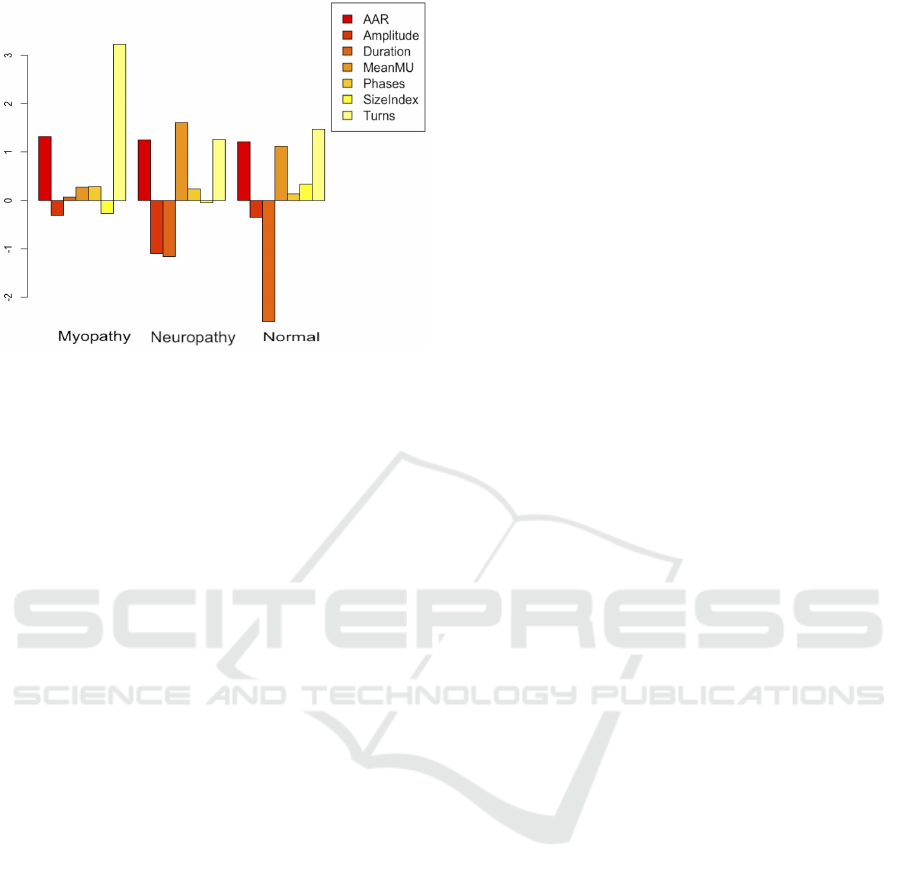
Figure 5: Degree of skewness for the EMG dataset.

used because an analysis using a Shapiro-Wilks test

indicated that a non-parametric test was appropriate.

4.1 The Effect of Discretization Method

on the Performance of NEFCLASS

The results of NEF-MME were compared with

those of NEF-ORG, which uses the default EQUAL-

WIDTH discretization strategy. The analyses were

performed using two-sided M-W-W test at a 0.05 sig-

niﬁcance level. The test identiﬁed a signiﬁcant differ-

ence in the misclassiﬁcation percentage between the

two classiﬁers for all datasets. As shown in Table 2,

NEF-MME achieved lower misclassiﬁcation percent-

ages compared to NEF-ORG using all datasets except

LOW-100,100. Additionally, the test resulted in a

signiﬁcant difference in the number of rules obtained

by NEF-ORG versus NEF-MME for all cases. As

shown in Table 3, NEF-MME constructed a higher

number of rules than did the NEF-ORG, for medium

and high skewed datasets, resulted in a higher accu-

racy. The number of rules obtained by NEF-ORG de-

creased with increase of data skewness level. This is

an underlying cause for the increase in misclassiﬁca-

tion percentages trained on skewed datasets. The de-

creasing trend in the number of rules constructed by

the NEF-ORG classiﬁer conﬁrms that less informa-

tion is being captured about the dataset as the skew-

ness increases.

This study indicated that the choice of initial dis-

cretization method affected the classiﬁcation accu-

racy of the NEFCLASS classiﬁer and that this effect

was very strong in skewed datasets. Utilizing MME

discretization method in the NEFCLASS classiﬁer sig-

niﬁcantly improved classiﬁcation accuracy for highly

skewed data.

4.2 The Effect of the Rule Pruning

Algorithm on the Performance of

NEFCLASS

To assess the effect of the rule pruning algorithm,

we compared each pair of classiﬁers to determine

whether the application of the rule pruning algorithm

signiﬁcantly reduced the number of rules. Addi-

tionally, the misclassiﬁcation percentages were com-

pared to determine whether a reduction in the num-

ber of rules signiﬁcantly increase the misclassiﬁca-

tion percentage. Comparisons between classiﬁers

were performed as follows: for each discretization

method and each dataset, results obtained by AR-

PRUNING algorithm were compared with those of the

NEFCLASS DEFAULT RULE-PRUNING . Hence, we

examined two comparisons: (i) classiﬁers with the

EQUAL-WIDTH discretization method, i.e., NEF-AR

versus NEF-ORG, (ii) classiﬁers with the MME dis-

cretization method, i.e., NEF-MME-AR versus NE-

F-MME. Additionally, we compared the ﬁnal com-

bined classiﬁer, i.e., NEF-MME-AR versus NEF-

ORG.

The analyses were performed using one-way M-

W-W test at a 0.05 signiﬁcance level. Tables 4 and

5 report the M-W-W test results for comparison of

the misclassiﬁcation percentages and the number of

rules, respectively. Comparisons between classiﬁers

were performed as follows:

• NEF-AR versus NEF-ORG:

As shown in Table 5, the test yielded a signiﬁcant

decrease in the number of rules by application of

AR-PRUNING for all datasets. The test results

shown in Table 4 revealed that this reduction

of rules did not increase the misclassiﬁcation

percentages. This reduction in the rule-base

size without reducing accuracy means that the

use of AR-PRUNING raised the efﬁciency of the

classiﬁer.

• NEF-MME-AR versus NEF-MME:

As shown in Table 5, the test determined that

NEF-MME-AR constructed a signiﬁcantly

lower number of rules for all datasets, except

for UNIFORM. Also, the test results shown in

Table 4 revealed that there was no signiﬁcant

increase in misclassiﬁcation percentages. As

shown in Table 5, NEF-MME-AR signiﬁcantly

reduced the number of rules for medium and high

skewed datasets without signiﬁcantly decreasing

accuracy.

A Synergistic Approach to Enhance the Accuracy-interpretability Trade-off of the NECLASS Classiﬁer for Skewed Data Distribution

331

Table 2: Misclassiﬁcation percentages (Median ± IQR) based on the rule pruning algorithm.

Classiﬁer Dataset

UNIFORM LOW-100,100 MED-100,20 HIGH-35,8

NEF-ORG 30.16 ± 3.50 22.66 ± 1.33 65.00 ± 5.51 66.67 ± 3.26

NEF-AR 30.16 ±0.75 23.00 ±0.75 71.83 ±0.00 66.67 ±1.00

NEF-MME 16.66 ± 2.00 26.00 ± 1.50 34.16 ± 1.00 42.50 ± 1.00

NEF-MME-AR 17.50 ±1.75 23.33 ±1.75 32.33 ±0.00 41.50 ±0.75

Table 3: Number of fuzzy rules (Median ± IQR) based on the rule pruning algorithm.

Classiﬁer Dataset

UNIFORM LOW-100,100 MED-100,20 HIGH-35,8

NEF-ORG 55.50 ± 1.00 49.00 ± 0.00 34.50 ± 2.00 15.00 ± 1.00

NEF-AR 49.50 ±1.00 42.50 ±1.75 19.00 ±0.00 10.00 ±1.00

NEF-MME 43.00 ± 2.00 44.00 ± 1.50 50.00 ± 1.00 46.00 ± 1.00

NEF-MME-AR 43.50 ±1.75 40.00 ±1.75 29.00 ±0.00 21.00 ±0.75

Table 4: Results of the one-tailed M-W-W test for comparison of the misclassiﬁcation percentages between classiﬁers using

different rule pruning algorithms.

Classiﬁer Dataset

UNIFORM LOW-100,100 MED-100,20 HIGH-35,8

NEF-AR vs. NEF-ORG .60 .80 .99 .69

NEF-MME-AR vs. NEF-MME .45 .94 .93 .75

NEF-MME-AR vs. NEF-ORG *** .97 *** ***

*** signiﬁcant at 95% conﬁdence (p < .05)

Table 5: Results of one-tailed M-W-W test for comparison of the number of rules between classiﬁers using different rule

pruning algorithms.

Classiﬁer Dataset

UNIFORM LOW-100,100 MED-100,20 HIGH-35,8

NEF-AR vs. NEF-ORG *** *** *** ***

NEF-MME-AR vs. NEF-MME .10 *** *** ***

NEF-MME-AR vs. NEF-ORG *** *** *** .99

*** signiﬁcant at 95% conﬁdence (p < .05)

• NEF-MME-AR versus NEF-ORG:

M-W-W identiﬁed a signiﬁcant decrease in the

number of rules obtained by NEF-MME-AR

compared to NEF-ORG for all datasets, except

for high-skewed data. The results shown in Ta-

ble 3 suggest that, in the case of HIGH-35,8, the

number of rules increased due to the effect of

the discretization method. However, some of the

rules were pruned later after the AR-PRUNING

process took place. At the end of training, the ﬁ-

nal number of rules obtained by NEF-MME-AR

was more than that of NEF-ORG but less than

those of NEF-MME. For example, the number

of rules obtained by NEF-ORG using the HIGH-

35,8 data was 15. Then, the application of the

MME discretization method increased the num-

ber of rules to 45. Finally, pruning the rules us-

ing AR-PRUNING decreased the number of rules

to 21. Furthermore, the test indicated a signiﬁ-

cant decrease in the misclassiﬁcation percentages

for all comparisons except in the case of LOW-

100,100.

The ﬁndings of this analysis revealed that the

combination of the MME discretization method with

the AR-PRUNING algorithm not only led to a signiﬁ-

cant reduction in the number of rules but also improve

the accuracy using medium and high skewed data.

4.3 Experiments using Real-world Data

Table 6 depicts the misclassiﬁcation percentages and

the number of rules. Table 7 gives the test results.

As shown in the table, the test revealed a signiﬁ-

cant decrease in the misclassiﬁcation percentages ob-

tained by NEF-MME compared to NEF-ORG. The

results of this experiment once again conﬁrmed that

using the MME method improved accuracy. Addi-

tionally, the test indicated a signiﬁcant decrease in

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

332

Table 6: Misclassiﬁcation percentages (Median ±IQR) and number of rules (Median ±IQR) obtained from classiﬁers trained

on the EMG dataset.

Classiﬁer Misclassiﬁcation Percentage Number Of rules

NEF-ORG 54.18 ± 28.00 149.00 ± 4.00

NEF-MME 41.00 ± 22.00 90.00 ± 14.00

NEF-MME-AR 21.00 ±25.00 33.00 ±16.00

*** signiﬁcant at 95% conﬁdence (p < .05)

Table 7: Results of one-tailed M-W-W to compare the rule pruning methods for the EMG dataset.

Classiﬁer Misclassiﬁcation Percentage Number Of rules

NEF-ORG vs. NEF-MME .03 .84

NEF-ORG vs. NEF-MME-AR *** ***

*** signiﬁcant at 95% conﬁdence (p < .05)

the misclassiﬁcation percentages and the number of

rules obtained by NEF-MME-AR compared to NEF-

ORG. In light of the above ﬁndings, it is concluded

that using a simpliﬁed rule-base obtained by the ap-

plication of AR-PRUNING not only reduced the num-

ber of rules but also reduced the confusion in the

decision-making process.

5 CONCLUSIONS

The results of our last study indicated that the NE-

FCLASS classiﬁer performs increasingly poorly as

data feature value skewness increases. Also, the

study indicated that the choice of initial discretization

method affected the classiﬁcation accuracy of the NE-

FCLASS classiﬁer and that this effect was very strong

in skewed datasets. This study revealed that utilizing

MME discretization method in the NEFCLASS classi-

ﬁer signiﬁcantly improved classiﬁcation accuracy for

the medium and high skewed data. Furhter, the ﬁnd-

ings of this study showed that the combination of the

MME discretization method with the AR-PRUNING

algorithm not only led to a signiﬁcant reduction in the

number of rules but also improve the accuracy in the

majority of cases. Hence, the NEF-MME-AR clas-

siﬁer produced a compelling combination of the dis-

cretization method and the rule pruning algorithm for

skewed datasets.

The proposed model-based strategy can be use-

ful in medical diagnosis systems because it not only

provides more accurate results but, by reducing the

number of rules, will likely make interpretation of the

system simpler. Other domains where skewed data

is common are likely additional areas of application,

and include fraud detection, computer security, and

ﬁnance. Finally, it should be noted that while it has

been evaluated using NEFCLASS, the adjusted resid-

uals rule pruning system introduced here can be used

in any rule based system, and is likely to have simi-

lar beneﬁts, as there is nothing speciﬁc to the fuzzy

domain.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the support of

NSERC, the National Sciences and Engineering Re-

search Council of Canada, for ongoing grant support.

REFERENCES

Ben-Gal, I. (2010). Outlier detection. In Maimon, O. and

Rokach, L., editors, Data Mining and Knowledge Dis-

covery Handbook, chapter 7, pages 131–146. Springer

Science & Business Media.

Chau, T. (2001). Marginal maximum entropy partition-

ing yields asymptotically consistent probability den-

sity functions. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 23(4):414–417.

Chemielewski, M. R. and Grzymala-Busse, J. W. (1996).

Global discretization of continuous attributes as pre-

processing for machine learning. International Jour-

nal of Approximate Reasoning, 15:319–331.

Enoka, R. and Fuglevand, A. (2001). Motor unit physiol-

ogy: some unresolved issues. Muscle & Nerve, 24:4–

17.

Gao, J., Hu, W., Li, W., Zhang, Z., and Wu, O. (2010).

Local outlier detection based on kernel regression.

In Proceedings of the 10th International Conference

on Pattern Recognition, pages 585–588, Washington,

DC, USA. EEE Computer Society.

Gokhale, D. V. (1999). On joint and conditional entropies.

Entropy, 1(2):21–24.

Gupta, A. (2016). Neural networks in data processing. In-

ternational Journal of Advanced Research in Com-

puter Engineering & Technology (IJARCET), 5(5):1–

13.

Haberman, S. J. (1973). The analysis of residuals in cross-

classiﬁed tables. Biometrics, 29(1):205–220.

A Synergistic Approach to Enhance the Accuracy-interpretability Trade-off of the NECLASS Classiﬁer for Skewed Data Distribution

333

Haberman, S. J. (1979). Analysis of Qualitative Data,

volume 1 of Springer Series in Statistics, pages 78–

79,82–83. Academic Press, Toronto.

Hable, R. (2012). Asymptotic normality of support vector

machine variants and other regularized kernel meth-

ods. Journal of Multivariate Analysis, 106:92–117.

Kerber, R. (1992). ChiMerge discretization of numeric at-

tributes. In Proceedings of AAAI-92, pages 123–128,

San Jose Convention Center, San Jose, California.

Klose, A., N

urnberger, A., and Nauck, D. (1999). Im-

proved NEFCLASS pruning techniques applied to a

real world domain. In Proceedings Neuronale Netze

in der Anwendung, University of Magdeburg. NN’99.

Marapareddy, R., Aanstoos, J. V., and Younan, N. H.

(2017). Accuracy analysis comparison of supervised

classiﬁcation methods for anomaly detection on lev-

ees using SAR imagery. Electronics – Open Access

Journal, 68(6):1–13.

Mueller, J. P. and Massaron, L. (2016). Machine Learning

For Dummies. For Dummies.

Natrella, M. (2003). NIST SEMATECH eHandbook of Sta-

tistical Methods. NIST.

Nauck, D., Klawonn, F., and Kruse, R. (1996). Neuro-Fuzzy

Systems. Wiley.

Nauck, D. and Kruse, R. (1998). NEFCLASS-X – a soft

computing tool to build readable fuzzy classiﬁers. BT

Technology Journal, 16(3):180–190.

Stashuk, D. W. and Brown, W. F. (2002). Quantitative elec-

tromyography. In Brown, W. F., Bolton, C. F., and

Aminoff, M. J., editors, Neuromuscular Function and

Disease, volume 1, pages 311–348. W.B. Saunders,

Philadelphia.

Varga, R., Matheson, S. M., and Hamilton-Wright, A.

(2014). Aggregate features in multi-sample classiﬁ-

cation problems. IEEE Trans. Biomed. Health Inf.,

99:1.

Youseﬁ, J. and Hamilton-Wright, A. (2016). Classiﬁ-

cation confusion within nefclass caused by feature

value skewness in multi-dimensional datasets. In Pro-

ceedings of the 8th International Joint Conference on

Computational Intelligence (IJCCI 2016) - Volume 2:

FCTA, pages 21–29.

FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications

334