On the Design of a Heuristic based on Artiﬁcial Neural Networks for the

Near Optimal Solving of the (N

–1)-puzzle

Vojt

ech Cahl

ık and Pavel Surynek

Faculty of Information Technology, Czech Technical University in Prague, Th

akurova 9, 160 00 Praha 6, Czech Republic

Keywords:

−1)-puzzle, Heuristic Design, Artiﬁcial Neural Networks, Deep Learning, Near Optimal Solutions.

Abstract:

This paper addresses optimal and near-optimal solving of the (N

–1)-puzzle using the A* search algorithm.

We develop a novel heuristic based on artiﬁcial neural networks (ANNs) called ANN-distance that attempts to

estimate the minimum number of moves necessary to reach the goal conﬁguration of the puzzle. With a well

trained ANN-distance heuristic, whose inputs are just the positions of the pebbles, we are able to achieve better

accuracy of predictions than with conventional heuristics such as those derived from the Manhattan distance

or pattern database heuristics. Though we cannot guarantee admissibility of ANN-distance, an experimental

evaluation on random 15-puzzles shows that in most cases ANN-distance calculates the true minimum distance

from the goal, and furthermore, A* search with the ANN-distance heuristic usually ﬁnds an optimal solution

or a solution that is very close to the optimum. Moreover, the underlying neural network in ANN-distance

consumes much less memory than a comparable pattern database.

1 INTRODUCTION

The (N

–1)-puzzle (Wilson, 1974; Korf and Taylor,

1996; Slocum and Sonneveld, 2006) represents an im-

portant benchmark problem for a variety of heuris-

tic search algorithms (Culberson and Schaeffer, 1994;

Korf, 1999). The task in the (N

–1)-puzzle is to rear-

range N

−1 square tiles on a square board of size

N ×N into a conﬁguration where tiles ore ordered

from 1 to N −1 (see Figure 1 for an illustration of

the 8-puzzle). One blank position on the board allows

tiles to move; that is, a tile can be moved to the blank

position in one step.

It is well known that ﬁnding an optimal solu-

tion of the (N

–1)-puzzle, that is, ﬁnding the shortest

possible sequence of moves that reach the goal con-

ﬁguration, is an NP-hard problem (Ratner and War-

muth, 1986; Ratner and Warmuth, 1990; Demaine

and Rudoy, 2018). Hence the problem is considered

to be a challenging benchmark for a variety of search-

based solving algorithms.

Various approaches have been adopted to ad-

dress the problem using search-based and other tech-

niques. They include heuristics built on top of pat-

tern databases (Felner and Adler, 2005; Felner et al.,

2007) that are applicable inside A* to obtain optimal

https://orcid.org/0000-0001-7200-0542

solutions. Another approach is represented by solving

the puzzle sub-optimally using rule-based algorithms

such as those of Parberry (Parberry, 1995). The ad-

vantage of these algorithms is that they are fast and

can be used in an online mode.

Various attempts have been also made to combine

good quality of solutions with fast solving. Improve-

ments of sub-optimal solutions by using macro op-

erations, where instead of moving single tile to its

goal position, multiple tiles form a snake and move

together, were introduced in (Surynek and Michal

ık,

2017). Moving tiles together consumes fewer moves

than if tiles are moved individually. Another approach

is to design better tile rearrangement rules that by

themselves lead to shorter solutions as suggested in

(Parberry, 2015a). In the average case, these rule-

based algorithms can generate solutions that are re-

liably effective (Parberry, 2015b).

In this short paper, we present an attempt to solve

the (N

–1)-puzzle near-optimally or optimally with

high probability using a heuristic based on artiﬁcial

neural networks (ANNs) (Haykin, 1999). Our heuris-

tic is intended to be integrated into the A* algorithm

(Hart et al., 1968).

We try to directly calculate the estimation of

the number of moves remaining to reach the goal

conﬁguration using ANN. Our experimentation with

the 15-puzzle shows that our heuristic called ANN-

Cahlík, V. and Surynek, P.

On the Design of a Heuristic based on Artiﬁcial Neural Networks for the Near Optimal Solving of the (N2–1)-puzzle.

DOI: 10.5220/0008163104730478

In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 473-478

ISBN: 978-989-758-384-1

473





































   



 















={1,2,…,8}

Solution sequence:

    

Less efficient solution

sequence:





     

Figure 1: An illustration of an initial and a goal conﬁgura-

tion of the 8-puzzle.

distance yields better estimations than the compara-

ble 7/8 pattern database (Felner et al., 2004). More-

over, although the ANN-heuristic is inadmissible,

sub-optimal solutions are produced by A* with ANN-

heuristic only rarely.

The paper is organized as follows; We ﬁrst intro-

duce the (N

–1)-puzzle formally and put it in the con-

text of related works. Then, we describe the design

of the ANN-distance and ﬁnally, we experimentally

evaluate the ANN-distance as part of the A* algo-

rithm and compare it with A* using the 7/8 pattern

database on random instances of the 15-puzzle.

2 BACKGROUND

The (N

–1)-puzzle consists of a set of tiles T =

{1,2,...,N −1} placed in a non-overlapping way on

a square board of the size N ×N where positions are

numbered from 1 to N. One position on the board

remains empty. Then a conﬁguration (placement)

of tiles can be expressed as an assignment c : T →

{1,2,...,N}.

Deﬁnition 1. The (N

–1)-puzzle is a quadruple

−1

= [N,T,c

], where c

: T → {1,2,..., N}

is an initial conﬁguration of tiles and c

: T →

{1,2,...,N} is a goal conﬁguration (usually an iden-

tity with c

(t) = t for t = 1,2, ...,N −1.

The movements of tiles are always possible into

blank neighboring positions; that is, one move at a

time. The task in the (N

–1)-puzzle is to rearrange

tiles into desired goal conﬁguration c

using allowed

moves. The solution sequence can be expressed as

σ = [m

,...,m

] where m

∈ {L,R,U, D} repre-

sents: Left, Right, Up, Down movements for i =

1,2,...,l and l is the length of solution. We call so-

lution σ optimal if l is as small as possible.

3 RELATED WORK

The (N

–1)-puzzle represents a special case of a prob-

lem known as multi-agent path ﬁnding (MAPF) on

graphs, where instead of the N × N-board we are

given a graph G = (V,E) with so called agents oc-

cupying its vertices. There is at most one agent per

vertex, and similarly to the N ×N-board we can move

an agent into the empty neighboring position (vertex).

The task is to move agents so that each agent reaches

its unique goal position (vertex). Hence in the terms

of MAPF, the (N

–1)-puzzle is a MAPF instance on

a 4-connected grid of size N ×N with one empty ver-

tex where goals of agents are set according to the goal

conﬁguration of the puzzle.

There are currently many solving algorithms for

MAPF and consequently for the (N

–1)-puzzle. Op-

timal A*-based algorithms include independence de-

tection - operator decomposition ID-OD (Standley,

2010) that tries to make use of not fully occupied

graph by dividing the set of agents into multiple in-

dependent groups that are solved separately.

ICTS (Sharon et al., 2013; Sharon et al., 2011) and

CBS (Sharon et al., 2015; Boyarski et al., 2015) on the

other hand view the search space differently not as a

graph of states. ICTS searches through various dis-

tributions of costs among multiple individual agents.

CBS searches the tree of conﬂicts between agents and

resolutions of these conﬂicts.

Besides search-based algorithms there are also

polynomial-time rule-based algorithms like BIBOX

(Surynek, 2009) and Push-and-Swap (Luna and

Bekris, 2011). They use predeﬁned macro-operations

to reach the goal conﬁguration. Solutions generated

by rule-based algorithms are sub-optimal.

Generally all MAPF algorithms rely on the fact

that the environment is typically not fully occupied

by agents in MAPF. Hence these algorithms cannot

beneﬁt from their advantages in case of the (N

–1)-

puzzle as their is only one empty position.

As for the state-space search approach,

(M. Samadi, 2008) successfully used an artiﬁ-

cial neural network as a heuristic function to predict

the optimal solution costs of the 15-puzzle. They

used the estimates of several pattern database heuris-

tics as inputs to their neural network. They used a

custom error function in order to penalise overshot

predictions, biasing the heuristic’s estimates towards

admissibility.

(M. Ernandes, 2004) also used an artiﬁcial neural

network to predict the optimal solution costs of the

15-puzzle, using only pebble positions as the input

features. However, they used a very small network

with only a single hidden layer of neurons, which re-

sulted in optimal solutions being obtained by IDA* in

only about 50% of cases.

(S. Arfaee, 2011) used a bootstrapping procedure

which allowed them to eventually solve random 24-

puzzle instances even without starting with a sufﬁ-

NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications

474

ciently strong heuristic. They started with an un-

trained artiﬁcial neural network, which they used as

a heuristic to solve a number of 24-puzzle instances.

Even though this procedure failed to solve most of the

instances within time limit, they used the handful of

solved instances to train the neural heuristic. Repeat-

ing this procedure several times resulted in obtaining

a very powerful heuristic.

4 DESIGNING A NEW

HEURISTIC

The heuristic search algorithm A* maintains the

OPEN list in which it stores candidate conﬁgura-

tions for further exploration. The algorithm always

chooses conﬁguration c from OPEN with the mini-

mum g(c) + h(c) for the next expansion, where g(c)

is the number of steps taken to reach c from c

and

h(c) is the (lower) estimate of the number of remain-

ing steps from c to c

. In general, the closer h (from

below) is to the true number of steps remaining the

fewer total number of nodes the algorithm expands.

4.1 Artiﬁcial Neural Networks

In our attempt to design a heuristic that gives very

precise estimations we made use of a feed-forward

artiﬁcial neural network (ANN). The ANN consists

of multiple computational units called artiﬁcial neu-

rons that perform simple computations on their input

vectors~x ∈R

as follows: y(~x) = ξ(

∑

i=0

) where

~w ∈ R

is vector of weights, w

∈ R is a bias and

ξ is an activation function, for example a sigmoid

ξ(z) =

1+e

−λz

, where λ determines the shape of the

sigmoid.

Neurons in ANN are arranged in layers. Neurons

in the ﬁrst layer represent the input vector. Neurons

in the second layer get the outputs of neurons in the

ﬁrst layer as their input, and so on. So at every layer

neurons are fully interconnected with neurons from

the previous layer. Outputs of neurons in the last layer

form the output vector.

Usually we want an ANN to respond to given in-

puts in a particular way. This is achieved through the

process of learning (Rumelhart et al., 1986; Schmid-

huber, 2014) that sets the weight vectors ~w and biases

in individual neurons so that for a given input~x

the

network responds with an output ~y

in the last layer.

The network is trained for a data-set which contains

pairs of input ~x

and desired output ~y

. If the ANN

is designed well, that is if it has the proper number

of neurons in layers and if the data-set is representa-

tive enough, then the ANN can appropriately respond

even to inputs that are outside the training data-set.

We then say that the ANN generalizes well: this is

the goal in our design as it is unrealistic to train the

network for all possible conﬁgurations c of the (N

–

1)-puzzle that are as many as N! (N!/2 solvable ones).

4.2 Our Design

We tried various designs of ANNs for estimating the

number of remaining steps and eventually ended up

with the following topology. The underlying ANN for

the ANN-distance is a deep and fully-connected feed-

forward network composed of an input layer with 256

neurons, ﬁve hidden layers with 1024, 1024, 512, 128

and 64 neurons, and an output layer composed of a

single neuron.

The input layer corresponds to encoding of a puz-

zle conﬁguration, that is we have 16 indexes of tiles

(one for the empty pebble), with each index one-hot

encoded resulting in a 256-dimensional input vector.

The output value is the estimate for the number of

steps required to reach the goal conﬁguration in an op-

timal manner. The loss function we used is the mean

squared error of this estimate.

We used several state-of-the-art techniques to en-

hance the performance of the neural network. These

techniques include the Adam optimizer, ELU activa-

tion function, dropout regularization, and batch nor-

malization (Geron, 2017). Layer weights were ini-

tialized by He initialization (Geron, 2017).

4.3 Training Data and Training

Training was performed by Gradient Descent using

reverse-mode autodiff, a process also known as back-

propagation (E. Rumelhart, 1985). The neural net-

work was trained on a dataset of roughly 6 million

conﬁgurations and respective optimal solutions, with

the distribution corresponding to randomly permuting

the tiles on the board (unsolvable conﬁgurations were

discarded). The training data were obtained by the A*

algorithm with the 7/8 pattern database heuristic. All

algorithms and tests were implemented in Python

It is known that conﬁgurations corresponding to

odd permutations of tiles are unsolvable (Wilson,

1974). Therefore, half out of 15! conﬁgurations are

unsolvable. That is, the training conﬁgurations cov-

ers approximately

100000

of solvable conﬁgurations -

a very sparse covering yet leading to satisfactory re-

sults. The distribution of length of solutions in the

dataset used for training is shown in Figure 2 - it can

All experiments were run on an i7 CPU with 30 GB

of RAM and a NVIDIA Quadro P4000 graphics card under

Debian Linux.

On the Design of a Heuristic based on Artiﬁcial Neural Networks for the Near Optimal Solving of the (N2–1)-puzzle

475

35 40 45 50 55 60 65

optimal solution length

100

200

300

400

500

Distribution of boards in dataset (histogram)

Figure 2: The distribution of lengths of solutions of in-

stances used for training.

be seen that the average length of a solution is roughly

about 52-53 moves.

The implementation of ANN and its training has

been carried out using the Keras library with Ten-

sorFlow backend (Chollet et al., 2015) and Numpy

(van der Walt et al., 2011) libraries.

5 EXPERIMENTAL EVALUATION

Our experimental evaluation was focused on competi-

tive comparison of ANN-distance against the 7/8 pat-

tern database. The 7/8 pattern database divides the

board into two disjoint parts: one consisting of 7 po-

sitions on the board and the other consisting of re-

maining 8 positions. For each conﬁguration of 7 or 8

tiles we have a record in the database containing the

optimal solution length for a relaxed version of the

puzzle, where only 7 or 8 tiles respectively must be

placed in their goal positions. The relaxation ignores

the goal positions of the remaining tiles and hence

it is easier to solve. The value of the 7/8-heuristics

for a given conﬁguration c is calculated as the sum of

lengths of optimal solutions for c|7 and c|8 from the

database (c|7 and c|8 denote c restricted on respective

disjoint part of the board). Such heuristic is admissi-

ble as shown in (Felner et al., 2004).

The tests were run on a test set of 1600 instances

obtained as random permutations. We focused on

measuring the performance of the heuristics sepa-

rately and when they are used as part of the A* al-

gorithm.

5.1 Competitive Comparison

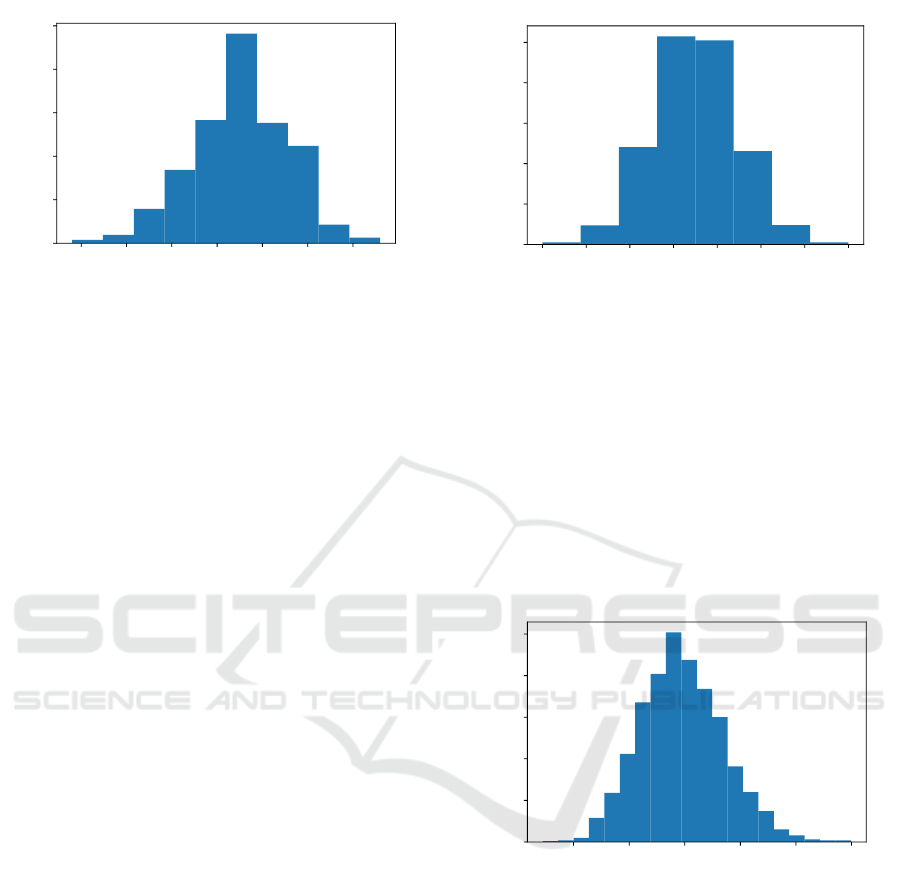
The ﬁrst series of tests show how closely the true dis-

tance from the goal conﬁguration has been estimated

by the 7/8-heuristic and by the ANN-distance. Re-

−14 −12 −10 −8 −6 −4 −2 0

heuristic prediction error

100

200

300

400

500

PDB 7-8 Heuristic: distribution of errors on single predictions

Figure 3: The distribution of error of the 7/8-heuristic.

sults are shown in Figures 3 and 4 as the distributions

of errors with respect to the true minimal distances.

Clearly the ANN-distance is an inadmissible

heuristic according to the test. However the vari-

ance is greater in case of 7/8-heuristic. In other

words, the ANN-heuristic gives more precise estima-

tions of the true distance to the goal, yet it sometimes

overestimates. The question hence is whether over-

estimations of ANN-distance lead to signiﬁcant devi-

ations from the optimal solutions when ANN-distance

is used as part of A*.

−4 −2 0 2 4 6

heuristic prediction error

100

150

200

250

ANN Heuristic: distribution of errors on single predictions

Figure 4: The distribution of error of the ANN-distance.

The positive result is that A* with ANN-distance

usually returns an optimal solution as shown in Fig-

ure 5. Only in a minority of cases it happens that the

solution length is slightly higher than the optimum.

Moreover the most important beneﬁt of using

ANN-distance is that A* expands signiﬁcantly fewer

nodes with this heuristic. The number of expanded

nodes as shown in Figure 6 and Table 1 is signiﬁcantly

lower in case of A* with the ANN-distance heuristic

compared to A* with 7/8-heuristic.

Another important advantage of the ANN-

distance is the fact that it consumes much less space

than comparable pattern databases. A relatively good

performance can be achieved with just a small ANN,

NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications

476

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0

solution length difference from optimal solution length

200

400

600

800

1000

1200

ANN Heuristic: distribution of solution length errors (A*)

Figure 5: The distribution of differences of lengths of so-

lutions returned by A* with ANN-distance from their true

optimas.

Table 1: The number of expanded nodes.

Instance A*(ANN) A*(PDB 7-8)

Easy 2517 4791

Medium 6392 15645

Hard 15756 45135

Extreme 384139 3367519

which consumes very little memory. On the other

hand, the pattern database must store all relevant

instances, which consumes a signiﬁcant amount of

memory.

Altogether A* with the ANN-distance heuristic

represents a promising alternative to common admis-

sible heuristics.

0 20000 40000 60000 80000 100000

expanded nodes

100

200

300

400

500

600

700

A*: Distribution of number of expanded nodes

ANN

PDB 7-8

Figure 6: The distribution of the number of expanded nodes

in A* with ANN-distance and A* with the 7/8-heuristic.

In addition to above experiments, we made mea-

surements of runtime, which is still higher for A* with

ANN-distance than in A* with 7/8-heuristic despite

the fact that ANN-distance is consulted much fewer

times than the 7/8-heuristic. There is however still

great room for improvement of the computation of the

output of ANN as it can be strongly paralleled or im-

plemented on a faster GPU.

6 DISCUSSION AND

CONCLUSION

This paper highly recommends the use of artiﬁcial

neural networks as the underlying paradigm for the

design of heuristics for the (N

–1)-puzzle. We de-

signed a heuristic called ANN-distance that estimates

for a given conﬁguration the distance from the goal

conﬁguration (the number of steps). Although the

heuristic is not admissible, it is relatively accurate and

does not signiﬁcantly overestimate the true distance.

As a result, the ANN-distance usually yields an opti-

mal solution when used as a part of A*. Moreover,

since ANN-distance is relatively precise in its esti-

mations, the A* with ANN-distance expands much

fewer nodes than with other heuristics like 7/8 pattern

database. Another advantage of the ANN-distance is

that it consumes much less space than a comparable

pattern database.

We also considered the heuristic design that does

not compute exact distance towards the goal conﬁg-

uration but rather orders conﬁgurations in the OPEN

list relatively. That is, the ANN will only compare

two conﬁgurations and say which one out of the two

is better. Preliminary tests revealed that determining

the best node for further expansion is quite expensive

as it requires to evaluate the ANN’s output multiple

times.

As we continue our work, we plan to improve the

implementation of ANN-distance so that it will be

able to respond faster than pattern database heuris-

tics. We also plan to implement the bootstrapping

algorithm (S. Arfaee, 2011) and use it to solve 24-

puzzle instances.

ACKNOWLEDGEMENTS

This research has been supported by GA

CR - the

Czech Science Foundation, grant registration number

19-17966S. We would like to thank anonymous re-

viewers for their valuable comments.

REFERENCES

Boyarski, E., Felner, A., Stern, R., Sharon, G., Tolpin,

D., Betzalel, O., and Shimony, S. (2015). ICBS:

improved conﬂict-based search algorithm for multi-

agent pathﬁnding. In IJCAI, pages 740–746.

Chollet, F. et al. (2015). Keras. https://keras.io.

Culberson, J. C. and Schaeffer, J. (1994). Efﬁciently search-

ing the 15-puzzle. Technical report, Department of

Computer Science, University of Alberta.

On the Design of a Heuristic based on Artiﬁcial Neural Networks for the Near Optimal Solving of the (N2–1)-puzzle

477

Demaine, E. D. and Rudoy, M. (2018). A simple proof

that the (n2-1)-puzzle is hard. Theor. Comput. Sci.,

732:80–84.

E. Rumelhart, G. Hinton, R. W. (1985). Learning internal

representations by error propagation.

Felner, A. and Adler, A. (2005). Solving the 24-puzzle with

instance dependent pattern databases. In SARA-05,

pages 248–260.

Felner, A., Korf, R. E., and Hanan, S. (2004). Additive

pattern database heuristics. Journal of Artiﬁcial Intel-

ligence Research, 22:279–318.

Felner, A., Korf, R. E., Meshulam, R., and Holte, R. C.

(2007). Compressed pattern databases. J. Artif. Intell.

Res., 30:213–247.

Geron, A. (2017). Hands-On Machine Learning with Scikit-

Learn and TensorFlow, pages 275–312. First edition.

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-

mal basis for the heuristic determination of minimum

cost paths. IEEE Transactions on Systems Science and

Cybernetics, SSC-4(2):100–107.

Haykin, S. (1999). Neural Networks: A Comprehensive

Foundation. Prentice Hall.

Korf, R. E. (1999). Sliding-tile puzzles and Rubik’s Cube

in AI research. IEEE Intelligent Systems, 14:8–12.

Korf, R. E. and Taylor, L. A. (1996). Finding optimal solu-

tions to the twenty-four puzzle. In Proceedings of the

Thirteenth National Conference on Artiﬁcial Intelli-

gence and Eighth Innovative Applications of Artiﬁcial

Intelligence Conference, AAAI 96, IAAI 96, Portland,

Oregon, USA, August 4-8, 1996, Volume 2., pages

1202–1207.

Luna, R. and Bekris, K. (2011). Efﬁcient and complete

centralized multi-robot path planning. In IROS, pages

3268–3275.

M. Ernandes, M. G. (2004). Likely-admissible and sub-

symbolic heuristics.

M. Samadi, A. Felner, J. S. (2008). Learning from multiple

heuristics.

Parberry, I. (1995). A real-time algorithm for the (n

-1)-

puzzle. Inf. Process. Lett., 56(1):23–28.

Parberry, I. (2015a). Memory-efﬁcient method for fast com-

putation of short 15-puzzle solutions. IEEE Trans.

Comput. Intellig. and AI in Games, 7(2):200–203.

Parberry, I. (2015b). Solving the (n2 - 1)-puzzle with 8/3 n3

expected moves. Algorithms, 8(3):459–465.

Ratner, D. and Warmuth, M. K. (1986). Finding a shortest

solution for the N x N extension of the 15-puzzle is

intractable. In AAAI, pages 168–172.

Ratner, D. and Warmuth, M. K. (1990). Nxn puzzle

and related relocation problem. J. Symb. Comput.,

10(2):111–138.

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986).

Learning representations by back-propagating errors.

Nature, 323:533–.

S. Arfaee, S. Zilles, R. H. (2011). Learning heuristic func-

tions for large state spaces.

Schmidhuber, J. (2014). Deep learning in neural networks:

An overview. CoRR, abs/1404.7828.

Sharon, G., Stern, R., Felner, A., and Sturtevant, N. R.

(2015). Conﬂict-based search for optimal multi-agent

pathﬁnding. Artif. Intell., 219:40–66.

Sharon, G., Stern, R., Goldenberg, M., and Felner, A.

(2011). Pruning techniques for the increasing cost tree

search for optimal multi-agent pathﬁnding. In Sympo-

sium on Combinatorial Search (SOCS).

Sharon, G., Stern, R., Goldenberg, M., and Felner, A.

(2013). The increasing cost tree search for optimal

multi-agent pathﬁnding. Artif. Intell., 195:470–495.

Slocum, J. and Sonneveld, D. (2006). The 15 Puzzle.

Slocum Puzzle Foundation.

Standley, T. (2010). Finding optimal solutions to coopera-

tive pathﬁnding problems. In AAAI, pages 173–178.

Surynek, P. (2009). A novel approach to path planning for

multiple robots in bi-connected graphs. In ICRA 2009,

pages 3613–3619.

Surynek, P. and Michal

ık, P. (2017). The joint movement

of pebbles in solving the ( n

- 1 )-puzzle subopti-

mally and its applications in rule-based cooperative

path-ﬁnding. Autonomous Agents and Multi-Agent

Systems, 31(3):715–763.

van der Walt, S., Colbert, S. C., and Varoquaux, G. (2011).

The numpy array: A structure for efﬁcient numerical

computation. Computing in Science and Engineering,

13(2):22–30.

Wilson, R. M. (1974). Graph puzzles, homotopy, and the

alternating group. Journal of Combinatorial Theory,

Series B, 16(1):86 – 96.

NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications

478