
Detect the Unexpected: Novelty Detection in Large Astrophysical
Surveys using Fisher Vectors
Michael Rotman
1
, Itamar Reis
2
, Dovi Poznanski
2
and Lior Wolf
1,3
1
School of Computer Science, Tel-Aviv University, Israel
2
School of Physics and Astronomy, Tel-Aviv University, Israel
3
Facebook AI Research, Israel
Keywords:
Anomaly Detection, Galaxies Spectra, Fisher Vectors.
Abstract:
Finding novelties in an untagged high dimensional dataset poses an open question. In this work, we present
an innovative method for detecting such novelties using Fisher Vectors. Our dataset distribution is modeled
using a Gaussian Mixture Model. An anomaly score that stems from the theory of Fisher Vector is computed
for each of the samples. We compute the anomaly score on the SDSS galaxies spectra dataset and present the
different types of novelties found. We compare our findings with other outlier detection algorithms from the
literature, and demonstrate the ability of our method to distinguish between samples taken from intersecting
probability distributions.
1 INTRODUCTION
The detection of outliers in real-world datasets is
a key component in the analysis of unfamiliar pro-
cesses. Historically, many discoveries in astronomy
were made serendipitously by encountering unique
unexpected observations while examining the skies.
Two famous examples of this exhausting search are
the Cosmic Microwave Background and Uranus. To-
day, when large amounts of astronomical information
are available, visual inspection of data is a daunt-
ing task. Current astronomical surveys datasets may
contain millions of instances each, from a variety of
different sources, and are usually categorized by fit-
ting physical models. The emergence of new ob-
jects throughout astronomical surveys, without a clear
physical understanding of their origins, may not be
explained by any of these models.
The Sloan Digital Sky Survey (SDSS; Eisenstein
et al., 2011) is one of the most successful astronomi-
cal surveys. The SDSS spectroscopic dataset consists
3 million optical spectra. These include ∼ 2 million
galaxy spectra, with which we will work, and an ad-
ditional ∼ 1 million spectra of quasars and stars. The
SDSS also contains imaging data covering 14,055
square degrees of sky, which is about one third of
the sky. Despite its size, large fractions of the SDSS
were in fact visually inspected. Hall et al. (2013), for
example, visually inspected 100,000 quasar spectra,
covering all objects in the relevant redshift range with
good signal to noise ratio, in the search of a specific
phenomena. Another large scale visual inspection
campaign, in this case targeting imaging data, is the
Galaxy Zoo (Lintott et al., 2008). Citizen scientists
inspected various SDSS catalogs and detected a broad
range of objects. It is worthwhile noting that this ini-
tiative led to the detection of a previously unknown
category of galaxies, named the green pea galaxies
(Cardamone et al., 2009).
Upcoming surveys lead us to a new era where a
complete visual analysis of the data would not be fea-
sible. For example, the Dark Energy Spectroscopic
Instrument (DESI, Levi et al., 2013) will include
spectra of 25 million galaxies. This is about an order
of magnitude more objects than in SDSS. The DESI
dataset will contain unique galaxies with occurrence
rate of one in tens of millions. Detecting such galaxies
would require the employment of anomaly detection
algorithms.
A desirable outcome of processing a large scale
survey would be to separate the wheat from the chaff,
by dividing the instances into two or more sets. One
set should contain the frequent instances and the out-
liers that obey an extreme behaviour of a commonly
known pattern. The other sets should contain only the
proposed novelties, instances without a clear physical
model that describes them. The sorting of instances
to these sets may be achieved by assigning each an
124
Rotman, M., Reis, I., Poznanski, D. and Wolf, L.
Detect the Unexpected: Novelty Detection in Large Astrophysical Surveys using Fisher Vectors.
DOI: 10.5220/0008163301240134
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 124-134
ISBN: 978-989-758-382-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

anomaly score. Many solutions to this task have
been proposed. Each solution usually falls into one
of the following three approaches: Reconstruction-
based anomaly detection, distance-based anomaly de-
tection, and probabilistic-based anomaly detection.
For further reading, refer to Pimentel et al. (2014).
Similar anomaly detection techniques are com-
monly applied in many research areas. However, each
area may possess distinct motivations. As a conse-
quence, measuring the success a proposed algorithm
may vary between different fields. When searching
for bank frauds, the criteria for success could be the
fraction of detected frauds. In scientific application,
however, our ultimate goal is to detect previously un-
seen phenomena. Such phenomena might manifest
only once in the entire dataset. It is reasonable to
think that in order to increase our chances of detect-
ing such objects, the applied methods should be sen-
sitive to a wide range of unusual behaviours. For this
reason, in scientific applications the criteria for suc-
cess could be the range of different types of detected
anomalies. In physics, most of the unusual objects de-
tected by any method had previously been known and
discussed in the literature. The detection of an object
whose properties are unknown is an extremely rare
event that has a considerable element of luck, making
it an unreasonable measure of success.
In this paper we present an anomaly detection
method that can also be refined for novelty detection.
Our proposed approach first estimates a model of the
galaxy’s spectra distribution by utilizing a Gaussian
Mixture Model (GMM). Next, we show that by using
Fisher Vectors as a basic building block, an appropri-
ate anomaly score emerges. We show our results on a
1D and 2D toy problems, and present unique findings
of our method on the SDSS dataset.
2 RELATED WORK
Applications of anomaly detection in astronomy
include Boroson and Lauer (2010) who detected
anomalies in SDSS quasar spectra using Principal
component Analysis (PCA). After applying PCA to
their dataset they detected anomalies using three dif-
ferent scores; PCA reconstruction error, PCA coef-
ficients magnitude, and isolation in the PCA coeffi-
cients space. They noted that all three scores were
able to detect interesting anomalies, and did not find
a strong distinction between the types of anomalies
detected by the different methods.
Distance-based anomaly detection was applied to
SDSS galaxy spectra in Baron and Poznanski (2017),
using the unsupervised Random Forest distance (Shi
and Horvath, 2006). Notably, Baron and Poznanski
(2017) were able to detect many types of interesting
galaxies, most notably a post starburst galaxy with ev-
idence for outflows, which were followed up on in
Baron et al. (2018). A similar method was applied in
Reis et al. (2018) to infrared stellar spectra. Distance
based anomaly detection was also used for light-curve
data in Protopapas et al. (2006) and Richards et al.
(2012). In order to work with raw light-curve data,
a translational invariant distance measure is required,
and indeed, Protopapas et al. (2006) used the cross
correlation distance. Another popular approach for
handling light-curve data is representing them with a
set of extracted features. Richards et al. (2012) used
extracted features for a distance-based anomaly de-
tection. Similarly to Baron et al. (2018); Reis et al.
(2018), they used Random Forest distance, with the
difference that Richards et al. (2012) used a super-
vised Random Forest, pre-trained on labeled data.
Meusinger et al. (2012) used self-organizing maps
(Kohonen, 1982, SOM,) for anomaly detection in
SDSS quasar spectra. Their unusual quasars were
found by visually inspecting the spectra of objects re-
siding in low density regions of the SOM. This is an
example of anomaly detection by dimensionality re-
duction in which the anomalies are detected in the low
dimensional embedding of the data. The advantage of
such a method is that in the low dimension it is easy to
detect the anomalies. In Meusinger et al. (2012) this
was done by simple visual inspection.
Supervised anomaly detection was performed in
Nun et al. (2014), where a Random Forest was trained
on labeled data consisting of variable objects light-
curve features. Using the Random Forest to predict
the class of unlabeled objects, anomalies are detected
according to their obtained Random Forest voting dis-
tribution. This algorithm was applied to 20 million
light-curves from the MACHO survey, in two itera-
tions aimed at reducing the fraction of detected ob-
servational artifacts. Artifacts detected as anomalies
in the first iteration were added to the labeled data of
the second iteration.
Nun et al. (2016) detected anomalies in astronom-
ical light-curves using an ensemble of anomaly de-
tection methods. Their ensemble included 5 meth-
ods. Two k-Nearest Neighbors approaches, Random
Forest and Joint Probability (Nun et al., 2014), Local
Correlation Integral, and Learned Probability Distri-
bution. They have also created an online tool for the
inspection of the detected anomalies by the commu-
nity
1
.
In this paper, we compare our results on SDSS
galaxy spectra with the following methods: (i) un-
1
Catalog of astronomical outliers
Detect the Unexpected: Novelty Detection in Large Astrophysical Surveys using Fisher Vectors
125

supervised Random Forest as applied in Baron and
Poznanski (2017); Reis et al. (2018), (ii) PCA-
reconstruction similarly to Boroson and Lauer (2010)
(we only use the reconstruction error score), and (iii)
isolation forest (Liu et al., 2008), a baseline method
often used in anomaly detection. Isolation forest de-
tects anomalies directly without modeling the entire
dataset. This is done by detecting objects that are
most frequently isolated by randomly partitioning the
data. We used scikit learn Pedregosa et al. (2011)
in the implementation of all three methods.
3 BACKGROUND
This work presents an anomaly detection method that
is based on Fisher Vectors. Before delving into the
method itself, we review the relevant mathematical
foundations.
Gaussian Mixture Model. The first step of our
method is creating a generative statistical model of the
dataset. The chosen model for this task is the Gaus-
sian Mixture Model (GMM) for its simplicity and its
ability to perform well on a variety of tasks.
GMM is a parametric probability density function
represented as a weighted sum of multivariate Gaus-
sians. The multivariate Gaussian itself represents a
distribution over vectors in x ∈ R
D
. The probability
density function of a mixture of K multivariate Gaus-
sian is:
p(x
|
π
k
,µ
k
,Σ
k
) =
K
∑
k=1
π
k
q
(2π)
D
det
|
Σ
k
|
e
−
1
2
(x−µ
k
)
T
Σ
−1
k
(x−µ
k
)
. (1)
The model parameters, π
k
,µ
k
∈ R
D
,Σ
k
∈ R
D
×
R
D
, for a given dataset X =
{
x
1
,x
2
,.. .,x
n
}
are
learned by maximizing the log-likelihood, L, of the
data:
L (π
k
,µ
k
,Σ
k
;X) =
1
n
n
∑
i=1
log
K
∑
k=1
p( x
i
|
π
k
,µ
k
,Σ
k
) (2)
using the Expectation Maximization (EM) algo-
rithm (Dempster et al., 1977).
Fisher Information Matrix. The Fisher Informa-
tion Matrix is a measurement for the amount of in-
formation present for the model’s parameters, λ
α
∈
θ, that is available in the data (Cover and Thomas,
2012). It is defined as
F
λ
α
λ
β
= E
x∼p(x|θ)
h
∂
λ
α
log p (x|θ)∂
λ
β
log p (x|θ)
i
.
(3)
For the case where p(x|θ) is GMM distribution,
and under the assumption that there is no correlation
between the different parameters of the mixture, Σ
k
is diagonal, and can be expressed as a one-dimension
vector, σ
k
∈ R
D
. Under this assumption, F is also di-
agonal and can be written as a vector (Perronnin et al.,
2010),
F
µ
k j
=
π
k
σ
2
k j
F
σ
k j
=
π
k
2σ
4
k j
. (4)
The contribution of a sample to each of the compo-
nents of F is
∆F
λ
α
= p(x|θ)
∂
λ
α
log p (x|θ)
2
. (5)
Fisher Vectors. Fisher Vectors (FV) were first in-
troduced by Perronnin and Dance (2007) as an effi-
cient way to classify images. The FV is proportional
to the derivatives of the GMM’s log-likelihood w.r.t
its parameters, λ =
{
π
k
,µ
k
,σ
k
}
, for a given vector,
x
i
∈ R
D
. The derivatives of the log-likelihood is
∂L
∂µ
k
x
i
=
p(x
|
λ
k
)
K
∑
k
0
=1
p(x
|
λ
k
0
)
x
i
−µ
k
σ
2
k
, (6)
∂L
∂σ
k
x
i
=
p(x
|
λ
k
)
N
∑
k
0
=1
p
x
λ
0
k
(x
i
−µ
k
)
2
σ
2
k
−σ
2
k
!
. (7)
The derivatives w.r.t the priors, π
k
, are ignored as they
usually bring very little information (Perronnin et al.,
2010). Whitening the different dimensions is accom-
plished by normalizing the derivatives by using the
diagonal Fisher Information Matrix. The normalized
gradients are
"
∂L
∂µ
k
x
i
#
N
=
p(x
|
λ
k
)
K
∑
k
0
=1
p
x
λ
0
k
1
√
π
k
x
i
−µ
k
σ
k
, (8)
"
∂L
∂σ
k
x
i
#
N
=
p(x
|
λ
k
)
N
∑
k
0
=1
p
x
λ
0
k
1
√
2π
k
x
i
−µ
k
σ
2
k
2
−1
!
. (9)
The Fisher Vector, F V
~
λ
k
(x
i
) ∈ R
D
, is the vector ob-
tained by a concatenation of all the normalized gra-
dients. An empirical observation by Perronnin et al.
(2010) was that the FV become sparse as the number
of Gaussians in the mixture increases.
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
126

4 FV-BASED ANOMALY
DETECTION
In this section, we utilize the FVs derived from a diag-
onal covariance GMM and present a prescription for
creating an anomaly scores. Let X =
{
x
1
,x
2
,.. .,x
n
}
,
x
i
∈R
D
be a set of samples from an unknown distribu-
tion. A set of GMM parameters, θ =
{
π
k
,µ
k
,σ
k
}
K
k=1
is estimated from a fit to X.
To establish an anomaly score, we need to iden-
tify samples that are unlikely to be generated by our
probability distribution. Anomalies can be described
by a probability distribution function, which is a sum
of two or more components, broad and narrow ones.
In such case, the regions of low probability consist of
extreme samples from the class of regular objects and
do not include any samples from the anomaly class.
Given a shift, ε, to the Gaussian parameters, λ, the
difference in the log-likelihood of generating a given
sample x
i
∈ R
D
is
∆
p
= log p (x
i
,λ + ε) − log p(x
i
,λ) . (10)
When ε 1, Eq. (10) can be expanded to first order
in ε,
∆
p
= ε∂
λ
log p (x,λ) + O
ε
2
. (11)
As the probability of each Gaussian to generate x
i
de-
cays exponentially with the distance from x
i
, most
samples rely only on a small number of Gaussians.
Up to a scaling, Eq. (11) is equal to F V (x
i
). The
contribution for each single sample, x
i
to the estima-
tion of the distribution’s parameters is apparent in Eq.
(3). The higher the estimated probability is to gener-
ate x
i
, the more it contributed to information content
of the model. By assuming that the different features
of x
i
, x
i, j
are independent, we can reduce the depen-
dency of the probability only on the jth feature.
Denote by p
j
(x
i
|λ) the probability density func-
tion over the estimated GMM after integrating out all
the features
{
m
}
D
m=1
in x
i
besides for the j th feature,
p
j
(x
i
|λ
k
) =
Z
∞
−∞
p(x
i, j
|λ)dx
i, j
···dx
i, j−1
dx
i, j+1
···dx
i,D
=
1
q
2πσ
2
k
e
−
(
x
i, j
−µ
k, j
)
2
2σ
2
k, j
. (12)
Eq. (5) presents the contribution of each sample
x
i
to Eq. (3). Our proposed anomaly score is the one-
dimensional contribution of each sample x
i
to Eq. (3),
A
sc
(x
i
) =
max
k
"
∑
j
p
j
x
i
|
~
λ
k
F V
λ
k j
(x
i
)F V
λ
k j
(x
i
)
#
. (13)
This score achieves two competing criteria. It
awards a low score for samples with a low probability
of appearing, thus focusing on the higher probability
regions of the estimated distribution, p (x|λ), as the
integrated probability decays with the distance of the
features from the estimated Gaussian means. On the
other hand it awards a higher score to samples that
contain a large FV component.
The proposed anomaly score can also be normal-
ized before searching for the maximum FV compo-
nent,
¯
A
sc
(x
i
) =
max
k
∑
j
p
j
x
i
|
~
λ
k
F V
λ
k j
(x
i
)F V
λ
k j
(x
i
)
σ
2
A
k
sc
−
µ
A
k
sc
σ
2
A
k
sc
#
(14)
Where µ
A
k
sc
,σ
A
k
sc
are the expectation value and stan-
dard deviation,
µ
A
k
sc
=
E
x
i
∼p(x|λ)
"
∑
j
p
j
x
i
|
~
λ
k
F V
λ
k j
(x
i
)F V
λ
k j
(x
i
)
#
,
(15)
σ
2
A
k
sc
=
E
x
i
∼p(x|λ)
∑
j
p
j
x
i
|
~
λ
k
F V
λ
k j
(x
i
)F V
λ
k j
(x
i
)
!
2
−µ
2
A
k
sc
. (16)
This adaptation to the score enhances the contribution
of FV originated from low probability clusters, and
thus, enables the detection of outliers in low probabil-
ity clusters.
The use of FV assists with detecting anomalies
generated by localized probabilities of small clusters
of objects that may exist in the dataset.
5 RESULTS
We present our results on two sets of problems. We
first show how our method performs on a toy-problem
Detect the Unexpected: Novelty Detection in Large Astrophysical Surveys using Fisher Vectors
127
in section 5.1, and then compare various anomaly de-
tection methods on the SDSS dataset in section 5.2.
In both cases we found out that using the FVs of the
σ parameters Eq. (9) performed better.
The VLFeat (Vedaldi and Fulkerson, 2008) pack-
age was employed for GMM estimation and for the
FVs extraction.
5.1 Toy Problem
In this section we evaluate our method under a set-
ting of randomly generated 1D and 2D samples as
seen in Fig. 1. The 1D toy dataset contains 10000
points sampled from an 1D gaussian, N (0,1), and a
set of 100 novelties sampled from another 1D gaus-
sian, N
2.5,10
−5
. The 2D toy dataset is com-
posed of 100000 points sampled from a 2D Gaus-
sian, N (0, 1) ×N (0, 1) and a set of 5000 novelties
sampled from another 2D gaussian, N
2.5,10
−5
×
N
1.4,10
−5
.
In order to show that our method is able to detect
non-trivial outliers, we compare the given anomaly
score to the associated log-likelihood of each sam-
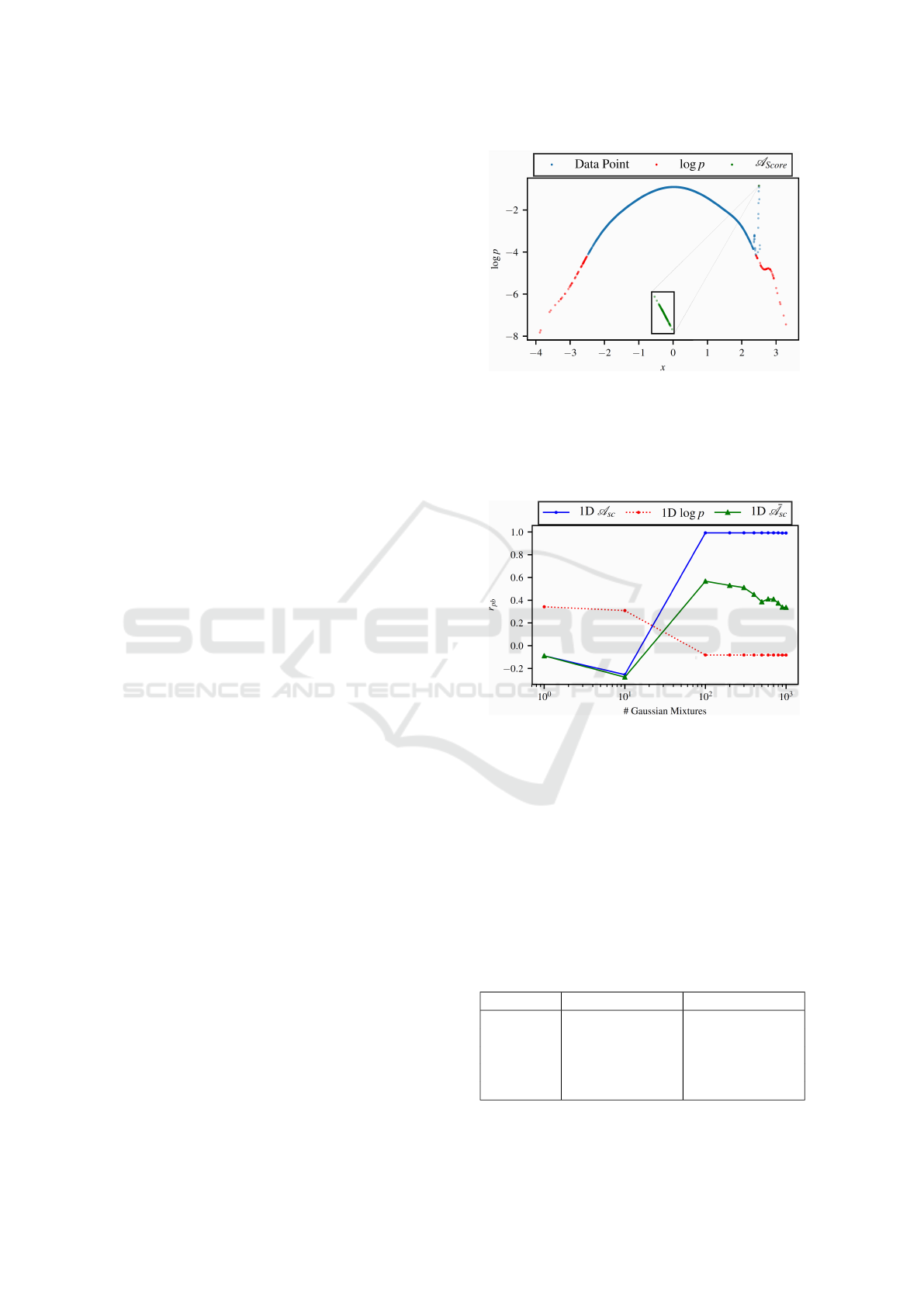
ple in Fig. 1. As expected, the log-likelihood is
highly correlated with the distance to the to the non-
anomalous gaussian center. Unlike the log-likelihood,
our anomaly score is able to overcome this, and grants
samples near the anomalous gaussian higher scores.
As a quantitative measurement for comparison to
other algorithms, we use the Point-biserial correlation
coefficient r
pb
(Which is mathematically equivalent
to the Pearson coefficient for the cases of a continu-
ous and a binary variable). Figures 2 and 3 show r
pb
as a function of the number of Gaussians in the mix-
ture utilized by our method. Clearly, as this number
rises, our method classifies samples from the anoma-
lous gaussian better. We further tested the kth-nearest-
neighbours (k-NN), Isolation Forest (IF), Local Out-
lier Factor (LOF) and Unsupervised Random Forest
(U-RF) algorithms, and report their appropriate cor-
relation coefficient on the toy problems in Table 1.
5.2 SDSS Galaxies
The galaxy spectra were obtained from the publicly
available SDSS DR14 (Abolfathi et al., 2017) dataset.
We filter samples that do not contain the Class =
GALAXY from the SpecObj table. This criterion re-
moves objects that were not classified as galaxies via
SDSS spectral fitting pipeline. We take only galaxies
for which the rest frame spectrum contains flux val-
ues in the wavelength range: 3700
˚
A < λ < 8000
˚
A.
Out of these galaxy objects we select the 150,000 with
the highest signal to noise ratio (according to the SN-
Figure 1: The distribution of samples in the 1D toy prob-
lem. The blue points represent the log-probability of each
sample when fitted using 1000 Gaussians in the mixture.
The red points represent the 100 highest ranking data points
with respect to the log p of the sample. The green points
represent the 100 highest ranking data points with respect
to our score.
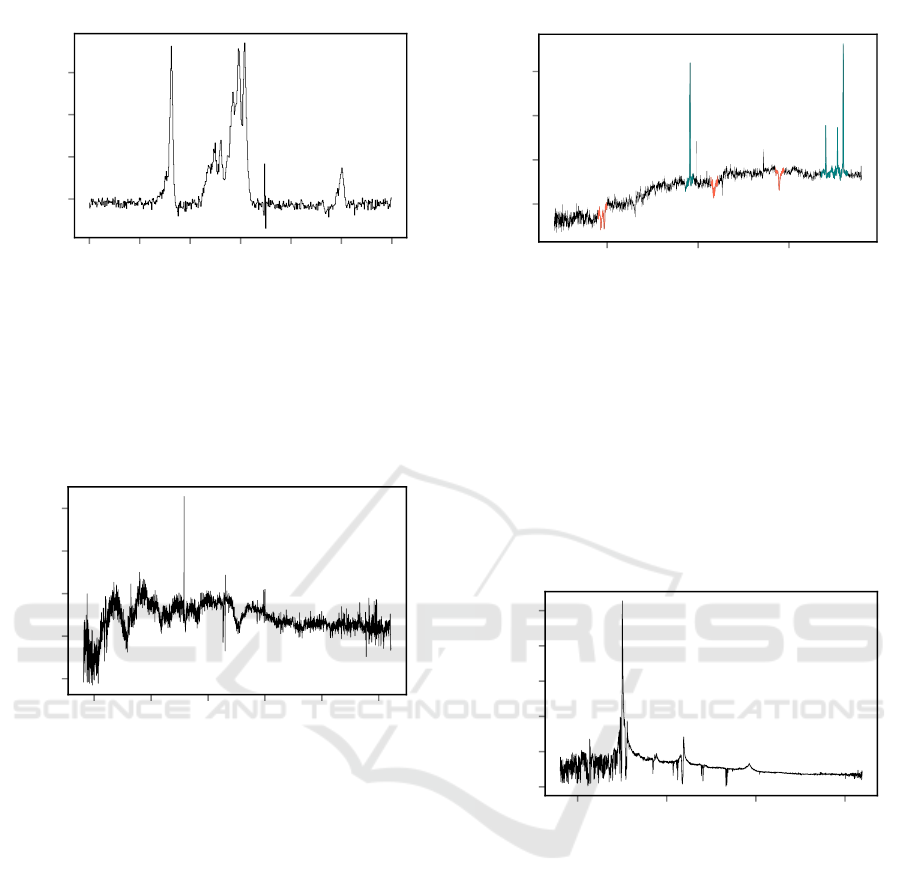
Figure 2: The correlation coefficient, r
pb
, for the different
number of clusters in the GMM for the toy problems in 1D.
As the number of gaussians in the mixture increases, and
the underlying model overfits the data distribution, the score
increases as well. On the other hand, the log-probability’s
coefficient is mostly uncorrelated and does not depend on
the underlying model.
Table 1: The correlation coefficient, r
pb
, of the 1D and 2D
toy problem of various anomaly detection algorithms. U-
RF refers to Unsupervised Random Forest. r
pb
= 1, repre-
sents the case where the true anomalies are have the high-
est anomaly scores, while r
pb
= −1 represents the case
were the true anomalies are have the lowest anomaly scores.
r
pb
= 0 represents the case were the true anomalies have
random anomaly scores. The results of our method in this
table were produced using a mixture of 100 Gaussians.
Method Toy Problem 1D Toy Problem 2D
LOF −0.0004 −0.0006
k-NN −0.0140 −0.1517
IF 0.3478 0.3365
U-RF 0.0193 −0.9392
A
sc
(ours) 0.9835 0.9684
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
128

Figure 3: The correlation coefficient, r
pb
, for the different
number of clusters in the GMM for the toy problems in 2D.
As the number of gaussians in the mixture increases, and
the underlying model overfits the data distribution, the score
increases as well. On the other hand, the log-probability’s
coefficient is mostly uncorrelated and does not depend on
the underlying model.
Median field in the SpecObj table). The prominent
spectral features are well above the noise for virtually
all galaxies in this sample. The data is publicly avail-
able, see sdss.org/dr14 for more details. The SDSS
module of Astroquery can also be used to obtain the
data.
Preprocessing stage consists of removing flux val-
ues marked as bad by the SDSS pipeline (i.e., flux val-
ues with inverse variance of 0), normalizing the spec-
tra to have a median of one, shifting the spectra to the
rest frame, as well as linearly interpolating the spectra
to the same wavelength grid.
The objects in the SDSS galaxy spectra are ranked
using both our scores, A
sc
and
¯
A
sc
, using K = 30–200
gaussians in the mixture. A visual inspection was per-
formed in order to characterize the top-ranked galax-
ies in each of the experiments.
The anomaly score, A
sc
, orders the objects in
large groups of uncommon galaxies. Most of the ob-
jects in the top-175 ranked objects by our method
are exclusively starburst galaxies, galaxies that are
currently undergoing significant star formation. This
phenomenon is present in a low fraction of the galax-
ies, and is associated by the existence of prominent
emission lines (emission lines are created by hot gas
in the galaxy emitting radiation at specific wave-
lengths, where locations of the lines are determined
by the atomic levels of the atoms composing the gas,
and relative strength and profiles of the lines are deter-
mined from the kinetic properties and ionization sta-
tus of the gas). The following 40 objects contain a
large fraction of bad spectra (mainly due to sky lines).
The next group of galaxies contains two additional
populations, one of post-starburst galaxies, galaxies
of high recent interest (Goto, 2007, e.g.), and an ad-
ditional population of galaxies with old stellar popu-
lation and some Active Galactic Nuclei (AGN) signa-
tures.
Unlike A
sc
, the top-ranked objects by normalized
anomaly score,
¯
A
sc
, are a variety of unique galaxies.
Empirically this happens when K > 100. Unfortu-
nately, the set of top-ranked objects in this case is
not robust; the group of detected anomalies may vary
greatly when using a different K.
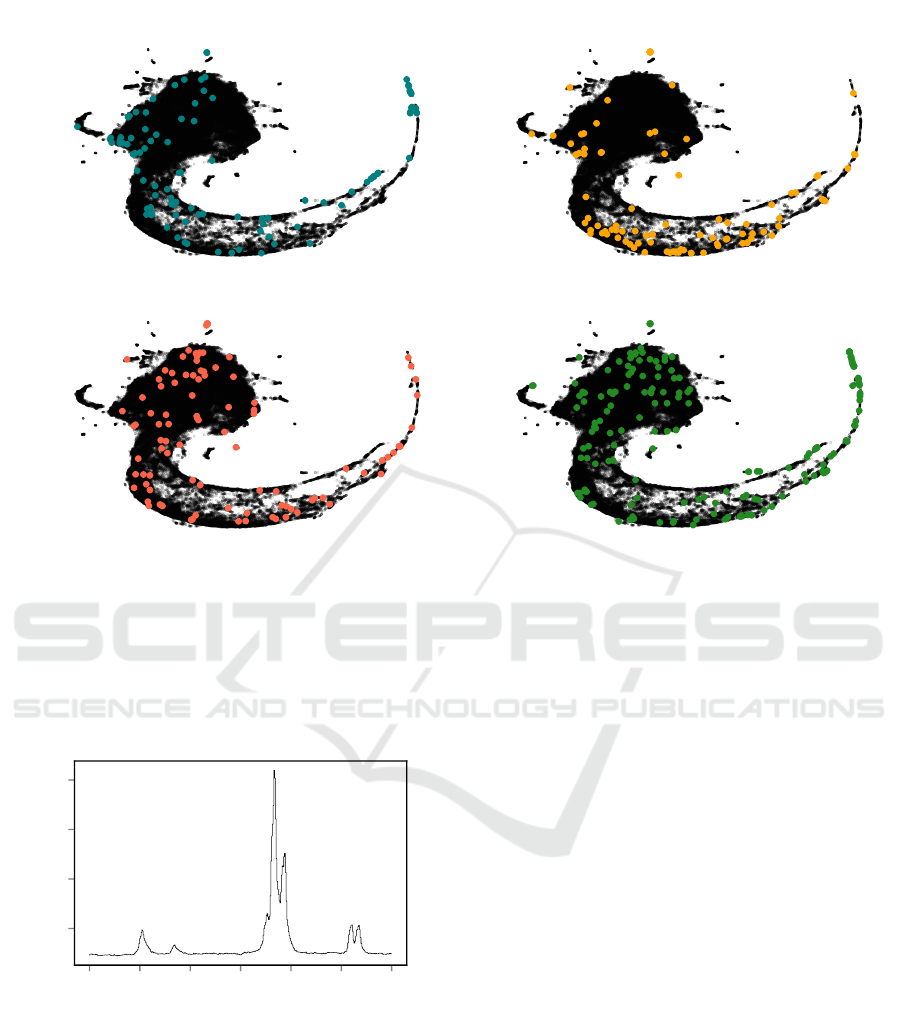
A qualitative illustration the top-ranked objects by
the two methods together with the the complete dis-
tribution is presented on a two-dimensional embed-
ding of the dataset constructed using the UMAP algo-
rithm (McInnes et al., 2018). Table 2 contains some
examples of the detected anomalies. The full list of
detected anomalies is available online. For complete-
ness, we also present the manifestation of some of the
detected anomalies on the galaxy spectra in Figures 5,
6, 7, 8 and 9.
We compared our proposed method to the fol-
lowing approaches: k-Nearest Neighbours, minimum
log-probability, Isolation Forest, Unsupervised Ran-
dom Forest, and PCA reconstruction. The 100 top-
ranked objects’ spectra proposed by each of the meth-
ods were visually inspected. Only the last three ap-
proaches detected a diverse set of objects that were
true anomalies, whereas the first two methods de-
tected only an homogeneous set of objects which had
no scientific merit. The top-ranked anomalies from
each of the methods rarely intersects, see Fig. 10.
While all three methods are successful in their desig-
nated task, they show a general disagreement as the
top-ranked anomalies sets rarely intersect, see Fig.
10. Like our normalized anomaly score, most of the
methods are not robust, and produce different can-
didates for anomalies for different hyperparameters.
Examples of the different types of objects found by
all of these methods is available in the appendix 6).
6 DISCUSSION
Novelty detection is an essential step in discovering
new phenomena in scientific datasets. In astronomy,
algorithms designed for this task are in a high demand
due to the large amount of information to be collected
in upcoming surveys.
Scientific discoveries can come in forms of out-
liers or slight deviations from a known model. Many
approaches succeed in detecting outliers, both in a
low- and a high-dimension setting, but fail at the de-
tection of a slight deviation from a known model, even
in a simple setting.
Our method is aimed at the detection of these
Detect the Unexpected: Novelty Detection in Large Astrophysical Surveys using Fisher Vectors
129

A
sc
top 175 A
sc
top 175-215
A
sc
top 215-300
¯
A
sc
top 100
Figure 4: The top-ranked objects proposed by our method on a 2D projection of the SDSS galaxy spectra dataset constructed
using the UMAP algorithm. The top, and bottom left panels show the top-ranked 175, 175-215 and 215-300 objects detected
by our method. Most of the objects detected in these panels are clustered together (top left and bottom left panels), or consist
of bad spectra (top right panel). See text for details. The bottom right panel contains the 100 top-ranked object detected by
our normalized method. The detected objects are no longer concentrated in the same region.
Table 2: Examples of anomalies detected by having a large anomaly score,
¯
A
sc
. The spectra of some of these objects are
presented in 6. It can be seen that our method is sensitive to a wide variety of unusual phenomena.
# SDSS name Comments
1 SDSS J144104.37+532008.7 Triple peaked OIII emission, rare NI λ6200 emission (double
peaked).
2 SDSS J052223.70+005916.4 Unidentified broad features and continuum shape.
3 SDSS J134423.00+193755.4 Features from two distinct galaxies at z
1
= 0.47 and z
2
= 0.11.
4 SDSS J112655.58+004046.9 Double peaked narrow emission lines.
5 SDSS J150908.75+090220.9 Emission lines with significant red wing.
6 SDSS J084715.85+315510.8 Post starburst galaxy with an active galacit nuclei.
7 SDSS J105918.12+243234.7 Velocity offset between emission and absorption lines.
8 SDSS J115023.57+281907.4 z ∼ 2 quasar mis-classified by the SDSS.
9 SDSS J095153.06+010605.8 Type Ia supernova.
slight deviations. It exploits known information met-
rics over an estimated probability distribution and
can be simply generalized to cases that contain a set
of completely different phenomenons. We give an
empirical motivation for this approach using the toy
problems which emphasize its underlying mechan-
ics. The true highlight of the method is the ability
to extract a rare set of objects from the SDSS galaxy
dataset.
ACKNOWLEDGEMENT
This work was partly funded by ISF, Israel-Singapore
grant #2541/16. The contribution of the first author is
part of a Ph.D. thesis research conducted at Tel-Aviv
University.
Funding for the Sloan Digital Sky Survey IV
has been provided by the Alfred P. Sloan Founda-
tion, the U.S. Department of Energy Office of Sci-
ence, and the Participating Institutions. SDSS-IV ac-
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
130
4700 4800 4900 5000 5100 5200 5300
rest wavelength
˚
A
40
60
80
100
flux [10
−17
erg cm
−2
s
−1
˚
A
−1
]
SDSS J144104.37+532008.7
Figure 5: Spectrum of SDSS J144104.37+532008. We
show the region of the spectrum containing the H
β
and O III
lines. The O III shows a triple peaked structure. This is
the only example of such structure we encountered. The
extremely rare N I λ6200
˚
A line is also present in the spec-
trum, and is either double peaked or has a blueshifted wing
(a wing refers to a non symmetrical line profile).
4000 5000 6000 7000 8000 9000
rest wavelength
˚
A
10
20
30
40
50
flux [10
−17
erg cm
−2
s
−1
˚
A
−1
]
SDSS J095153.06+010605.8
Figure 6: Spectrum of SDSS J095153.06+010605.8. The
spectral features of a type Ia supernova (namely broad ab-
sorption lines in specific locations) are clearly seen in this
spectrum. Indeed this object was also found by Graur and
Maoz (2013) in a dedicated search for type Ia supernova.
knowledges support and resources from the Center
for High-Performance Computing at the University of
Utah. The SDSS web site is www.sdss.org.
SDSS-IV is managed by the Astrophysical Re-
search Consortium for the Participating Institutions of
the SDSS Collaboration including the Brazilian Par-
ticipation Group, the Carnegie Institution for Science,
Carnegie Mellon University, the Chilean Participa-
tion Group, the French Participation Group, Harvard-
Smithsonian Center for Astrophysics, Instituto de As-
trof
´
ısica de Canarias, The Johns Hopkins Univer-
sity, Kavli Institute for the Physics and Mathemat-
ics of the Universe (IPMU) / University of Tokyo,
the Korean Participation Group, Lawrence Berkeley
National Laboratory, Leibniz Institut f
¨
ur Astrophysik
Potsdam (AIP), Max-Planck-Institut f
¨
ur Astronomie
(MPIA Heidelberg), Max-Planck-Institut f
¨
ur Astro-
4000 5000 6000
rest wavelength
20
40
60
80
flux [10
−17
erg cm
−2
s
−1
˚
A
−1
]
SDSS J134423.00+193755.4
Figure 7: Spectrum of SDSS J134423.00+193755.4. The
spectrum of a galaxy is shifted in wavelength according to
the relative velocity between us and the galaxy. This shift is
called redshift and marked with z. This spectrum shows fea-
tures coming an alignment of two different galaxies along
the line of sight, one at redshift of z = 0.11 (spectral fea-
tures colored in red) and the other at redshift of z = 0.47
(spectral features colored in blue). The blue spectral fea-
tures from left to right are most likely O II H
β
and the two
O III emission lines, with the rest wavelength of λ3727
˚
A ,
λ4686
˚
A , λ4960
˚
A , and λ5007
˚
A , respectively. The spec-
trum is shown in the rest frame of the z = 0.11 galaxy.
4000 6000 8000 10000
rest wavelength
˚
A
0
50
100
150
200
250
flux [10
−17
erg cm
−2
s
−1
˚
A
−1
]
SDSS J115023.57+281907.4
Figure 8: Spectrum of SDSS J115023.57+281907.4. This
is an example of a mis-classified object: This object is a
high redshift quasar mistakenly classified as a galaxy by the
SDSS pipeline. That is, this object should not have been
included in the SDSS galaxy dataset. The most prominent
line in this spectrum is the Ly
α
λ 1206
˚
A mis-classified as
an emission line at ∼ λ 5000
˚
A .
physik (MPA Garching), Max-Planck-Institut f
¨
ur Ex-
traterrestrische Physik (MPE), National Astronomi-
cal Observatories of China, New Mexico State Uni-
versity, New York University, University of Notre
Dame, Observat
´
ario Nacional / MCTI, The Ohio State
University, Pennsylvania State University, Shanghai
Astronomical Observatory, United Kingdom Partic-
ipation Group, Universidad Nacional Aut
´
onoma de
M
´
exico, University of Arizona, University of Col-
orado Boulder, University of Oxford, University of
Portsmouth, University of Utah, University of Vir-
Detect the Unexpected: Novelty Detection in Large Astrophysical Surveys using Fisher Vectors
131
Unsupervised Random Forest Isolation Forest
PCA reconstruction
¯
A
sc
Figure 10: The 100 top-ranked objects proposed by different anomaly detection methods on a 2D projection of SDSS galaxy
spectra dataset constructed using the UMAP algorithm. Different populations of galaxies reside in different regions of this
embedding. A visual inspection of all the proposed objects has revealed a high fraction of true anomalies. This plot shows that
different methods can be sensitive to different populations of galaxies. Note how one method can have a high concentration
of detected anomalies in a specific region, while another method can have zero detections in the same region. From our
experiments it appears that the difference between results obtained by a single method with different hyper parameters is
similar to the difference between completely different methods.
6200 6300 6400 6500 6600 6700 6800
rest wavelength
˚
A
100
200
300
400
flux [10
−17
erg cm
−2
s
−1
˚
A
−1
]
SDSS J150908.75+090220.9
Figure 9: Spectrum of SDSS J150908.75+090220. .The un-
usual phenomena observed in this spectra are the redshfited
wings present in all emission lines. Unlike the redshifted
wings, blueshifted wings usually represent outflowing ma-
terial. This is material that is moving towards the observer.
Redshifted wings are harder to explain, and further inves-
tigation is required to determine their source. This is an
example of the strongest redshifted wings we detected.
ginia, University of Washington, University of Wis-
consin, Vanderbilt University, and Yale University.
REFERENCES
Abolfathi, B., Aguado, D. S., Aguilar, G., Allende Prieto,
C., Almeida, A., Tasnim Ananna, T., Anders, F., An-
derson, S. F., Andrews, B. H., Anguiano, B., and et al.
(2017). The Fourteenth Data Release of the Sloan
Digital Sky Survey: First Spectroscopic Data from the
extended Baryon Oscillation Sky Survey and from the
second phase of the Apache Point Observatory Galac-
tic Evolution Experiment. ArXiv e-prints.
Baron, D., Netzer, H., Prochaska, J. X., Cai, Z., Cantalupo,
S., Martin, D. C., Matuszewski, M., Moore, A. M.,
Morrissey, P., and Neill, J. D. (2018). Direct evidence
of AGN-feedback: a post starburst galaxy stripped of
its gas by AGN-driven winds. ArXiv e-prints.
Baron, D. and Poznanski, D. (2017). The weirdest SDSS
galaxies: results from an outlier detection algorithm.
MNRAS, 465:4530–4555.
Boroson, T. A. and Lauer, T. R. (2010). Exploring the Spec-
tral Space of Low Redshift QSOs. AJ, 140:390–402.
Cardamone, C., Schawinski, K., Sarzi, M., Bamford, S. P.,
Bennert, N., Urry, C. M., Lintott, C., Keel, W. C.,
Parejko, J., Nichol, R. C., Thomas, D., Andreescu, D.,
Murray, P., Raddick, M. J., Slosar, A., Szalay, A., and
Vandenberg, J. (2009). Galaxy Zoo Green Peas: dis-
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
132

covery of a class of compact extremely star-forming
galaxies. MNRAS, 399(3):1191–1205.
Cover, T. M. and Thomas, J. A. (2012). Elements of infor-
mation theory. John Wiley & Sons.
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).
Maximum likelihood from incomplete data via the em
algorithm. Journal of the Royal Statistical Society:
Series B (Methodological), 39(1):1–22.
Eisenstein, D. J., Weinberg, D. H., Agol, E., Aihara, H.,
Allende Prieto, C., Anderson, S. F., Arns, J. A.,
Aubourg,
´
E., Bailey, S., Balbinot, E., and et al. (2011).
SDSS-III: Massive Spectroscopic Surveys of the Dis-
tant Universe, the Milky Way, and Extra-Solar Plane-
tary Systems. AJ, 142:72.
Goto, T. (2007). A catalogue of local E+A (post-starburst)
galaxies selected from the Sloan Digital Sky Survey
Data Release 5. MNRAS, 381:187–193.
Graur, O. and Maoz, D. (2013). Discovery of 90 Type Ia
supernovae among 700 000 Sloan spectra: the Type Ia
supernova rate versus galaxy mass and star formation
rate at redshift 0.1. MNRAS, 430(3):1746–1763.
Hall, P. B., Brandt, W. N., Petitjean, P., P
ˆ
aris, I., Filiz Ak,
N., Shen, Y., Gibson, R. R., Aubourg,
´
E., Anderson,
S. F., Schneider, D. P., Bizyaev, D., Brinkmann, J.,
Malanushenko, E., Malanushenko, V., Myers, A. D.,
Oravetz, D. J., Ross, N. P., Shelden, A., Simmons,
A. E., Streblyanska, A., Weaver, B. A., and York,
D. G. (2013). Broad absorption line quasars with
redshifted troughs: high-velocity infall or rotationally
dominated outflows? MNRAS, 434:222–256.
Kohonen, T. (1982). Self-organized formation of topolog-
ically correct feature maps. Biological Cybernetics,
43(1):59–69.
Levi, M., Bebek, C., Beers, T., Blum, R., Cahn, R., Eisen-
stein, D., Flaugher, B., Honscheid, K., Kron, R., La-
hav, O., McDonald, P., Roe, N., Schlegel, D., and rep-
resenting the DESI collaboration (2013). The DESI
Experiment, a whitepaper for Snowmass 2013. ArXiv
e-prints.
Lintott, C. J., Schawinski, K., Slosar, A., Land, K., Bam-
ford, S., Thomas, D., Raddick, M. J., Nichol, R. C.,
Szalay, A., Andreescu, D., Murray, P., and Vanden-
berg, J. (2008). Galaxy Zoo: morphologies derived
from visual inspection of galaxies from the Sloan Dig-
ital Sky Survey. MNRAS, 389:1179–1189.
Liu, F. T., Ting, K. M., and Zhou, Z.-H. (2008). Isolation
forest. In Proceedings of the 2008 Eighth IEEE In-
ternational Conference on Data Mining, ICDM ’08,
pages 413–422, Washington, DC, USA. IEEE Com-
puter Society.
McInnes, L., Healy, J., Saul, N., and Grossberger, L. (2018).
Umap: Uniform manifold approximation and projec-
tion. The Journal of Open Source Software, 3(29):861.
Meusinger, H., Schalldach, P., Scholz, R.-D., in der Au, A.,
Newholm, M., de Hoon, A., and Kaminsky, B. (2012).
Unusual quasars from the Sloan Digital Sky Survey
selected by means of Kohonen self-organising maps.
A&A, 541:A77.
Nun, I., Pichara, K., Protopapas, P., and Kim, D.-W. (2014).
Supervised detection of anomalous light curves in
massive astronomical catalogs. The Astrophysical
Journal, 793(1):23.
Nun, I., Protopapas, P., Sim, B., and Chen, W. (2016). En-
semble learning method for outlier detection and its
application to astronomical light curves. The Astro-
nomical Journal, 152(3):71.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer,
P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,
A., Cournapeau, D., Brucher, M., Perrot, M., and
Duchesnay, E. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research,
12:2825–2830.
Perronnin, F. and Dance, C. (2007). Fisher kernels on visual
vocabularies for image categorization. In 2007 IEEE
conference on computer vision and pattern recogni-
tion, pages 1–8. IEEE.
Perronnin, F., S
´
anchez, J., and Mensink, T. (2010). Im-
proving the fisher kernel for large-scale image classi-
fication. In European conference on computer vision,
pages 143–156. Springer.
Pimentel, M. A., Clifton, D. A., Clifton, L., and Tarassenko,
L. (2014). A review of novelty detection. Signal Pro-
cessing, 99(Supplement C):215 – 249.
Protopapas, P., Giammarco, J. M., Faccioli, L., Struble,
M. F., Dave, R., and Alcock, C. (2006). Finding
outlier light curves in catalogues of periodic variable
stars. MNRAS, 369:677–696.
Reis, I., Poznanski, D., Baron, D., Zasowski, G., and Sha-
haf, S. (2018). Detecting outliers and learning com-
plex structures with large spectroscopic surveys - a
case study with apogee stars. Monthly Notices of the
Royal Astronomical Society, page sty348.
Richards, J. W., Starr, D. L., Miller, A. A., Bloom, J. S.,
Butler, N. R., Brink, H., and Crellin-Quick, A. (2012).
Construction of a Calibrated Probabilistic Classifica-
tion Catalog: Application to 50k Variable Sources in
the All-Sky Automated Survey. ApJS, 203:32.
Shi, T. and Horvath, S. (2006). Unsupervised learning with
random forest predictors. Journal of Computational
and Graphical Statistics, 15(1):118–138.
Vedaldi, A. and Fulkerson, B. (2008). VLFeat: An open and
portable library of computer vision algorithms. http:
//www.vlfeat.org/.
APPENDIX
DSS Galaxies Anomalies
This section contains examples of the anomalies de-
tected in the SDSS galaxy dataset by the Isolation
Forest, Unsupervised Random Forest, and PCA re-
construction. These three methods were able to de-
tect diverse types of true anomalies, similarly to our
Fisher Vector based method. Examples of anoma-
lies detected by isolation forest are shown in Table 3,
Detect the Unexpected: Novelty Detection in Large Astrophysical Surveys using Fisher Vectors
133

Table 3: Examples of anomalies detected with the Isolation Forest algorithm. About 15 of the top 100 anomalies detected by
this method were chance alignments.
# SDSS name Comments
1 SDSS J001850.89-102236.6 NI λ6200 emission, unique continuum shape.
2 SDSS J153904.33+114241.6 Chance alignment with M-dwarf.
3 SDSS J052223.70+005916.4 Very unusual continuum.
4 SDSS J031248.68-010020.6 Broad unidentified features.
5 SDSS J113219.79+255012.9 Zig-zag continuum (most likely bad spectra).
6 SDSS J113219.79+255012.9 Features from two distinct redshifts.
7 SDSS J105918.12+243234.7 N I λ 6200 emission with blueshifted wing.
8 SDSS J013404.10+095703.3 Strong, blueshifted Na I λ 5895, 5889 doublet absorption.
Table 4: Examples of anomalies detected using PCA-reconstruction. 6 additional high redshift quasars are included in the top
100 anomalies detected by this method.
# SDSS name Comments
1 SDSS J235047.12+143617.5 Sodium absorption blueshifted by 850 [km/s], ionized outflows.
2 SDSS J022113.54-030539.6 high redshift quasar (mis-classified).
3 SDSS J095153.06+010605.8 Type Ia supernova.
Table 5: Examples of anomalies detected with the Unsupervised Random Forest algorithm.
# SDSS name Comments
1 SDSS J164732.08+220456.5 Unique continuum shape.
2 SDSS J115023.57+281907.4 High redshift quasar (mis-classified).
3 SDSS J154024.75+325157.2 Type Ia supernova.
4 SDSS J120432.29+220400.7 Two galaxies chance alignment.
5 SDSS J115927.68+485858.8 Multiple component emission, absorption lines redshifted from
systematic.
anomalies detected by PCA reconstruction are shown
in Table 4, and anomalies detected by Random Forest
are shown in Table 5.
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
134
