
Generalized Lehmer Mean for Success History based Adaptive
Differential Evolution
Vladimir Stanovov
1,2
a
, Shakhnaz Akhmedova
1 b
, Eugene Semenkin
2 c
and Mariia Semenkina
3 d
1
Reshetnev Siberian State University, Krasnoyarskii rabochii ave. 31, 660037, Krasnoyarsk, Russian Federation
2
Siberian Federal University, Institute of Mathematics and Computer Science,
79 Svobodny pr., 660041, Krasnoyarsk, Russian Federation
3
Heuristic and Evolutionary Algorithms Laboratory (HEAL), University of Applied Sciences Upper Austria,
Softwarepark 11, 4232 Hagenberg, Austria
Keywords:
Differential Evolution, Optimization, Parameter Control, Metaheuristic.
Abstract:
The Differential Evolution (DE) is a highly competitive numerical optimization algorithm, with a small num-
ber of control parameters. However, it is highly sensitive to the setting of these parameters, which inspired
many researchers to develop adaptation strategies. One of them is the popular Success-History based Adap-
tation (SHA) mechanism, which significantly improves the DE performance. In this study, the focus is on
the choice of the metaparameters of the SHA, namely the settings of the Lehmer mean coefficients for scaling
factor and crossover rate memory cells update. The experiments are performed on the LSHADE algorithm and
the Congress on Evolutionary Computation competition on numerical optimization functions set. The results
demonstrate that for larger dimensions the SHA mechanism with modified Lehmer mean allows a significant
improvement of the algorithm efficiency. The theoretical considerations of the generalized Lehmer mean could
be also applied to other adaptive mechanisms.
1 INTRODUCTION
In recent decades the area of Evolutionary Computa-
tion (EC) has proposed various tools to solve com-
plex optimization problems in different areas, includ-
ing engineering, technical, financial, and many more.
Most of these tools are based on various biology-
inspired heuristic approaches, but mostly follow the
evolutionary paradigm. The existing heuristic and
metaheuristic algorithms differ in problem solution
representation and operations used. One of the well-
developed areas is the area of numerical optimiza-
tion problems, in which certain success has been
made by algorithms such as real-coded Genetic Al-
gorithm (GA), Particle Swarm Optimization (PSO),
Covariance Matrix Adaptation Evolutionary Strategy
(CMA-ES) and Differential Evolution (DE).
The DE is known to be one of the most competi-
tive approaches for all types of optimization problems
a
https://orcid.org/0000-0002-1695-5798
b
https://orcid.org/0000-0003-2927-1974
c
https://orcid.org/0000-0002-3776-5707
d
https://orcid.org/0000-0002-8228-6924
and since its development (Storn and Price, 1997) has
receivedmany attention from the research community
due to its simplicity in implementation and only few
control parameters. However, the choice of optimal
parameter settings remains one of the main issues of
modern DE variants development, according to (Das
et al., 2016).
In (Al-Dabbagh et al., 2018) it is stated that one of
the most efficient parameter adaptation schemes pro-
posed for DE is the Success History based Adapta-
tion, proposed in (Tanabe and Fukunaga, 2013). This
adaptation mechanism was applied in one of the most
competitive DE variants, such as SHADE, LSHADE,
and their modifications. The SHA uses information
about previously successful values of DE parameters
to update the memory cells. To address the effect
of bias caused by the fact that smaller scaling fac-
tor and crossover rate parameter values lead to more
greedy search, the usage of Lehmer mean was pro-
posed. Some aspects of structural bias in DE have
been studied in (Caraffini et al., 2019). In this study,
the generalized variant of Lehmer mean is considered,
and the LSHADE variant is tested with various types
of Lehmer mean implementations.
Stanovov, V., Akhmedova, S., Semenkin, E. and Semenkina, M.
Generalized Lehmer Mean for Success History based Adaptive Differential Evolution.
DOI: 10.5220/0008163600930100
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 93-100
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
93

The rest of the paper is organized as follows: in
section 2 the DE state of the art is described, with the
main focus on the SHA mechanism, section 3 presents
the modified Lehmer mean and theoretical insights,
section 4 contains the experimental setup and results,
as well as discussion, and section 5 concludes the pa-
per.
2 SUCCESS HISTORY BASED
DIFFERENTIAL EVOLUTION
The Differential Evolution was originally proposed
by K. Price and R. Storn in (Storn and Price, 1997)
for real-valued optimization problems solving. DE
is a population-based algorithm, in which the popu-
lation of NP individuals is represented as x
i, j
, where
i = 1, ..., NP, j = 1, ..., D, where D is the problem di-
mension. The goal is to minimize the function f(X)
with respect to bound constraints [xmin
j
, xmax
j
].
The DE starts by initializing the population ran-
domly within the boundaries, and proceeds by per-
forming mutation, crossover and selection (replace-
ment) operations. The mutation operator is the key
component of DE, which generates new mutant vec-
tor by combining the vectors from the population.
There are several mutation strategies known, how-
ever, in this study the current − to − pbest strategy,
introduced in JADE algorithm (Zhang and Sanderson,
2009), is applied:
v
j
= x
i, j
+ F ∗ (x
pb, j
− x
i, j
) + F ∗ (x
r1, j
− x
r2, j
) (1)
where F is the scaling factor, which is a parameter
usually in range [0, 1]. The pb index is chosen from
p% best individuals in the population, while r1 and r2
are chosen randomly from the population. Next, the
crossover operation is performed, in which the trial
vector is defined as:
u
j
=
(
v
j
, if rand(0, 1) < Cr or j = jrand
x
i, j
, otherwise
where Cr is the crossover rate in range [0,1],
jrand is set to random index in [1, D] and used to
make sure that at least one variable is taken from the
mutant vector. After this, the selection procedure is
applied, and the newly generated trial vector u re-
places the target vector x
i
if it has at least as good
fitness:
x
i, j
=
(
u
j
, if f(u
j
) ≤ f(x
i, j
)
x
i, j
, otherwise
The scaling factor F, crossover rate Cr, as well as
population size NP are three main control parameters
if DE. The SHADE algorithm (Tanabe and Fukunaga,
2013) improved the adaptation procedure in JADE
(Zhang and Sanderson, 2009) by introducing several
memory cells containing best known parameter val-
ues combinations, which were then used to generate
newtrial vectors. Initially there were H memory cells,
each containing a pair M
F
, M
C
r, which are set to 0.5,
and the current memory index h was set to 1. For each
mutation and crossover the F and Cr values were gen-
erated using Cachy distribution and normal distribu-
tion with scale parameter and standard deviation of
0.1 respectively:
(
F = randc(M
F,h
, 0.1),
Cr = randn(M
Cr,h
, 0.1)
If the newly generated F or Cr is outside the [0, 1]
interval, then it is generated again until it satisfies this
condition. During the selection step, if the trial vec-
tor was successful, i.e. better then target vector, the
values of F and Cr were stored in S
F
and S
C
r, as well
as the improvement value ∆f
j
= | f (u) − f(x
i
)|. After
the end of the generation, current h-th memory cell is
updated using the weighted Lehmer mean:
mean
wL
(S) =
∑
|S|
j=1
w
j
S
2
j
∑
|S|
j=1
w
j
S
j
(2)
where S is either S
F
or S
C
r, and the weight value
w
j
=
∆f
j
∑
|S|
k=1
∆f
k
. The index of memory cell h is incre-
mented every generation and set to 1 if h = H. The
idea of using several memory cells is to provide more
robust parameter adaptation, in which the fluctuations
of F and Cr would not influence the searh signifi-
cantly. The SHA mechanism is sensitive not only to
the improvement fact, but also to the value of the im-
provement, i.e. ∆f.
3 GENERALIZED LEHMER
MEAN FOR SUCCESS
HISTORY ADAPTATION
Originally, the usage of Lehmer mean was proposed
in JADE (Zhang and Sanderson, 2009) algorithm for
the calculation of F values only. In rJADE (Peng
et al., 2009), the weighted procedure for F calcula-
tion was proposed, where the ∆f
j
values were used.
Finally, in LSHADE (Tanabe and Fukunaga, 2014)
the Lehmer mean was used for both F and Cr calcu-
lation.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
94
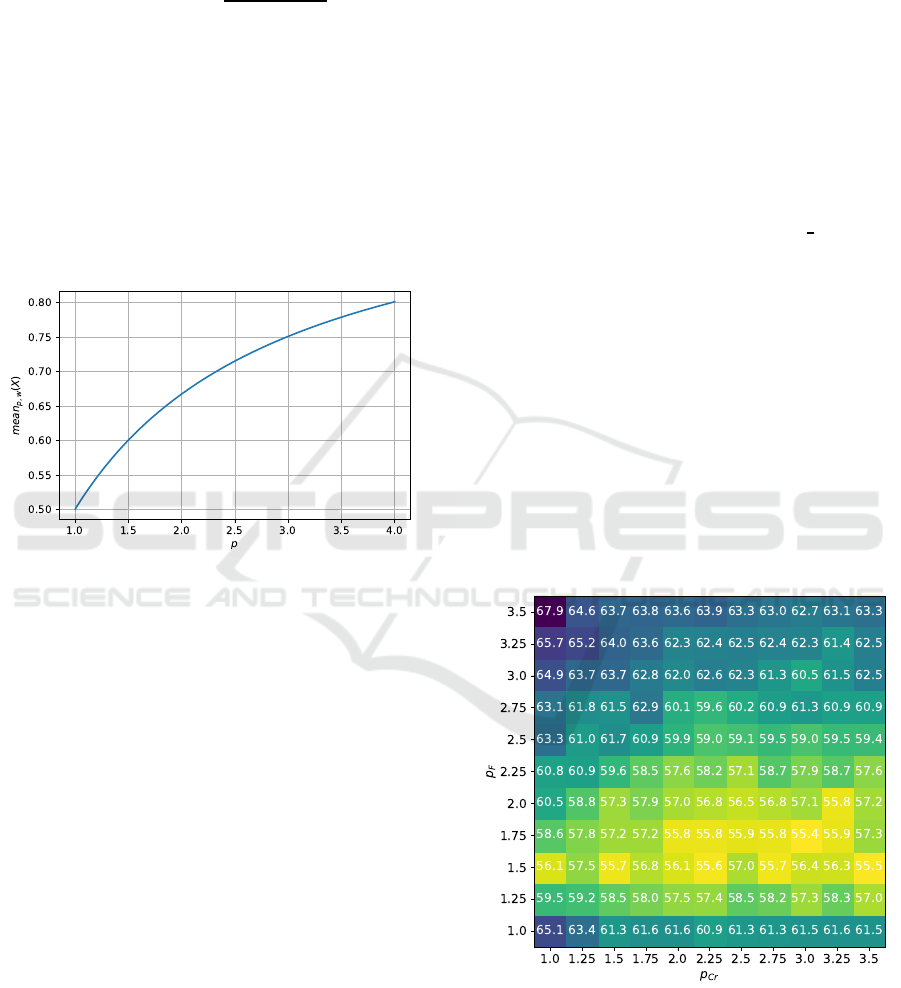
The generalized from of weighted Lehmer mean
could be written as follows (Bullen, 2003):
mean
p,w
(X) =
∑
|x|
j=1
w
j
x
p
j
∑
|x|
j=1
w
j
x
p−1
j
(3)
From this equation it could be seen that weighted
Lehmer means is a group of means, and by chang-
ing the p parameter, other means cold be obtained.
In particular, mean
0,w
(X) is the harmonic mean,
mean
1,w
(X) is arithmetic mean, and mean
2,w
(X) is
also referred to as contraharmonicmean. Other means
could be considered by changing the p value, for ex-
ample, Fig. 1 shows the means obtained by changing
p in range [1, 4] for x values uniformly distributed in
[0, 1], all w
j
= 1.
Figure 1: Dependence of generalized Lehmer mean on p
parameter.
The biased Lehmer mean with large p values
could be helpful because it tends to generate larger
M
F
and M
C
r values, which could be more preferable
on a long-term search perspective. This happens be-
cause smaller F and Cr result in more greedy search,
i.e. for most functions it is easier to generate a so-
lution close to the one at hand, which leads to local
search-like process. To determine the optimal p val-
ues, the next section contains experimental setup for
algorithm performance comparison and results.
4 EXPERIMENTAL SETUP AND
RESULTS
To evaluate the performance of LSHADE with differ-
ent settings of generalized Lehmer mean, a series of
experiments has been performed on the set of bench-
mark problems from the Congress on Evolutionary
Computation (CEC) 2017 for single-objective real-
valued bound-constrained optimization. The set of
benchmark problems consists of 30 functions defined
for dimensions 10, 30, 50 and 100. The experiments
were performed according to the competition rules,
i.e. there were 51 independent run for every function,
the total computation resource was set to 10000D, and
the best achieved fitness values were saved after NFE
= 0.01, 0.02, 0.03, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7,
0.8, 0.9 and 1.0NFE
max
, where NFE is current num-
ber of function evaluations, and NFE
max
is the total
available resource. The CEC 2017 functions defini-
tion can be found in (Wu et al., 2016).
The LSHADE algorithm used the external archive
with size NP, and index r2 in current − to − pbest
mutation strategy was generated from both population
and the archive, according to (Tanabe and Fukunaga,
2014). The population size was set to 75D
2
3
, p param-
eter in current − to− pbest strategy equal to 0.17.
To perform the comprehensive experiment, the
LSHADE algorithm was tested with different values
of p in Lehmer mean for F andCr generation. The p
F
and p
Cr
changed between 1 and 3.5 with step 0.25,
and the experiments were performed for dimensions
10, 30 and 50. The comparison was performed us-
ing two-tailed Mann-Whitney rank sum statistical test
with tie-braking and significance level p = 0.01 and
Friedman ranking procedure. Figure 2, 3 and 4 show
the Friedman ranking of different algorithms for 10D,
30D and 50D respectively. The numbers in heatmap
graphs represent the truncated to 0.1 precision final
ranking.
Figure 2: Friedman test, D = 10.
The Friedman ranking procedure performed com-
parison between all 121 algorithm variants for each
dimension. From Figures 2-4 it could be observed
that the classical LSHADE setting with p
F
= 2 and
p
Cr
= 2 is not an optimal choice for all dimensions.
Generalized Lehmer Mean for Success History based Adaptive Differential Evolution
95

Figure 3: Friedman test, D = 30.
Figure 4: Friedman test, D = 50.
Several other important conclusions could be done,
for example, for higher dimensions larger p
F
are more
preferable, probably because exploration properties
of the DE are more beneficial in this case. For all
dimensions the arithmetical mean, i.e. p = 1 is one
of the worst possible choices. As for the p
Cr
values,
the dependence on this parameter is not as significant,
however, the growth of both p
F
and p
Cr
could deliver
good search properties.
Figures 5, 6 and 7 contain the Mann-Whitney
test comparison between the case when p
F
= 2 and
p
Cr
= 2 and other cases. The numbers in heatmap
graphs represent the total score, which was defined as
the sum of wins (+1), ties (0) and losses (-1) of every
algorithm compared to baseline variant.
The comparison in Figures 5-7 shows that for
Figure 5: Mann-Whitney test, D = 10.
Figure 6: Mann-Whitney test, D = 30.
10D some of the best variants are around p
F
= 1.5
and relatively large p
Cr
. For 30D the best choice
is p
F
= 2.25 and p
Cr
= 1.75, where up to 7 signif-
icant improvements are found. For 50D, up to 17
improvements could be achieved with relatively large
p
F
= 3.0 and large p
Cr
= 2.0. From this, it can be
concluded that larger dimensional problems require
larger F values to be set for a successful search pro-
cess, while the Cr values are not so significant, al-
though, the values around p
Cr
= 2.0 appear to be a
good choice in all cases.
As for 100D problems, only a limited set of ex-
periments has been performed due to computational
complexity. The Mann-Whitney test comparison be-
tween baseline version of LSHADE and LSHADE
with variable p
F
(LSHADE-p
F
) is presented in Ta-
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
96
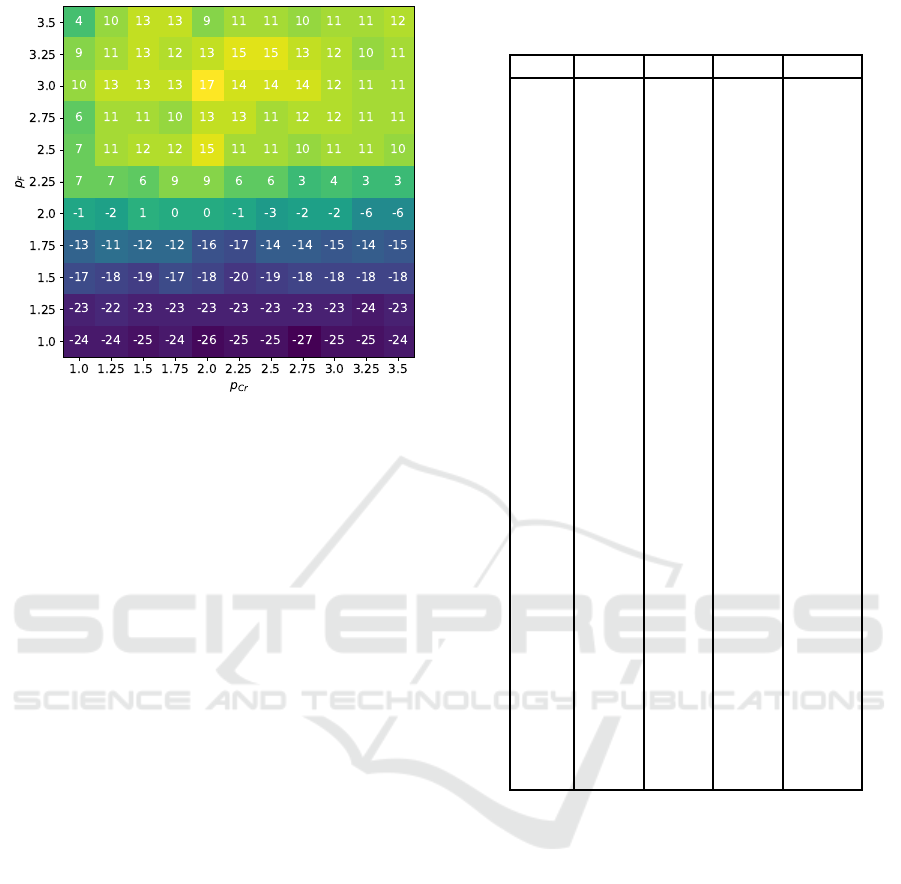
Figure 7: Mann-Whitney test, D = 50.
ble 1. For comparison on 100D the p
F
was set to
3.75, and p
Cr
= 2.0, for 10D, 30D and 50D the values
of p
F
were set to 1.5, 2.25 and 3.0 respectively, with
the same p
Cr
value. Here 1 means that LSHADE-p
F
was better for particular function, -1 means that it was
worse, and 0 means that there were no significant dif-
ference.
The results in Table 1 show that the effect on
the DE performance is observed mostly for 50D and
100D. As for different functions, there were improve-
ments for f5 and f8, as well as for f11 and f12, also
for f1, f2, f6, f15, f18, f19, f23, f25, f26 and f27.
These functions have different properties, so it can be
concluded that changingthe Lehmer mean calculation
procedure is beneficial in many scenarios.
For an additional set of experiments, one of
the best state-of-the-art LSHADE versions, namely
LSHADE-RSP (Stanovov et al., 2018) has been cho-
sen. LSHADE-RSP was ranked 2nd in CEC 2018
competition on bound-constrained numerical opti-
mization, and the best among DE variants partici-
pated. LSHADE-RSP used rank-based selective pres-
sure, and a number of parameter adaptations taken
from the jSO algorithm presented in (Brest et al.,
2017). LSHADE-RSP was modified to have the same
changing p
F
parameter as described above, resulting
in LSHADE-RSP-p
F
algorithm.
Although for 10D and 30D the LSHADE-RSP-
p
F
does not show any significant difference in per-
formance, for larger dimensions the change in mean
calculation leads to several significant improvements.
For 50D, only for f7 there was a performance loss,
while for 7 other functions improvements were found.
For 100D, the convergenceof could be slower on sim-
pler problems, such as f1-f3, however, more complex
Table 1: Mann-Whitney Statistical test results for LSHADE
and LSHADE-p
F
.
Func D=10 D=30 D=50 D=100
f1 0 0 1 1
f2 0 0 1 1
f3 0 0 0 -1
f4 0 0 0 1
f5 0 1 1 1
f6 0 0 1 1
f7 1 0 1 -1
f8 0 1 1 1
f9 0 0 0 0
f10 0 0 0 -1
f11 0 1 1 1
f12 0 1 1 1
f13 0 0 0 1
f14 0 0 0 1
f15 0 0 1 1
f16 0 0 0 -1
f17 0 0 0 0
f18 0 0 1 1
f19 0 0 1 1
f20 0 0 -1 -1
f21 0 0 1 1
f22 0 0 0 -1
f23 1 0 1 1
f24 0 0 0 1
f25 0 0 1 1
f26 0 0 1 1
f27 0 0 1 1
f28 0 0 1 0
f29 0 0 1 0
f30 0 0 0 1
Total 1 4 17 14
problems are solved better, with up to 13 significant
improvementsfrom 30. The graphs demonstrating the
convergence process for all functions and dimensions
50 and 100 are presented in the appendix. From these
graphs it can be seen that LSHADE-RSP-p
F
con-
verges slower due to larger F values and higher ex-
ploration capabilities, however eventually it gets bet-
ter solutions.
5 CONCLUSIONS
In is paper the generalized Lehmer mean was pro-
posed for calculation of control parameters in Dif-
ferential Evolution adaptation process. The general-
ized mean formulation allows different types of mean
calculation to be presented in a single equation with
one control parameter. The performed experiments
have shown that using larger p parameter in Lehmer
Generalized Lehmer Mean for Success History based Adaptive Differential Evolution
97

Table 2: Mann-Whitney Statistical test results for
LSHADE-RSP and LSHADE-RSP-p
F
.
Func D=10 D=30 D=50 D=100
f1 0 0 0 -1
f2 0 0 0 -1
f3 0 0 0 -1
f4 0 0 0 0
f5 0 0 0 0
f6 0 0 0 1
f7 0 0 -1 0
f8 0 0 0 0
f9 0 0 0 0
f10 0 0 0 -1
f11 0 0 1 1
f12 0 0 1 1
f13 0 0 0 1
f14 0 0 0 1
f15 0 0 1 1
f16 0 0 0 0
f17 0 0 0 0
f18 0 0 1 1
f19 0 0 1 1
f20 0 0 0 0
f21 0 0 0 0
f22 0 0 0 -1
f23 0 0 0 1
f24 0 0 0 1
f25 0 0 0 0
f26 0 0 1 1
f27 0 0 1 0
f28 0 0 0 1
f29 0 0 0 0
f30 0 0 0 1
Total 0 0 6 8
mean leads to an improvement in the search prop-
erties of DE, especially for larger dimensions. For
the LSHADE algorithm there were up to 17 signifi-
cant improvements according to Mann-Whitney sta-
tistical tests for 50D and up to 14 improvements for
100D. It was shown that a simple heuristic rule which
increases the p parameter for scaling factor F cal-
culation with the growth of the problem dimension
may improve even some of the best state-of-the-art
DE variants, like LSHADE-RSP. Although the pre-
sented generalization of Lehmer mean was shown be
efficient, some other mean formulation could be con-
sidered and tested.
REFERENCES
Al-Dabbagh, R. D., Neri, F., Idris, N., and Baba, M. S.
(2018). Algorithmic design issues in adaptive differ-
ential evolution schemes: Review and taxonomy. In
Swarm and Evolutionary Computation 43, pp. 284–
311.
Brest, J., Mauˇcec, M., and Boˇskovic, B. (2017). Single
objective real-parameter optimization algorithm jSO.
In Proceedings of the IEEE Congress on Evolutionary
Computation, pp. 1311–1318. IEEE Press.
Bullen, P. (2003). Handbook of Means and Their Inequali-
ties. Springer Netherlands.
Caraffini, F., Kononova, A. V., and Corne, D. (2019). In-
feasibility and structural bias in differential evolution.
Information Sciences, 496:161 – 179.
Das, S., Mullick, S., and Suganthan, P. (2016). Recent ad-
vances in differential evolution – an updated survey.
In Swarm and Evolutionary Computation, Vol. 27, pp.
1–30.
Peng, F., Tang, K., Chen, G., and Yao, X. (2009). Multi-
start jade with knowledge transfer for numerical op-
timization. In 2009 IEEE Congress on Evolutionary
Computation, pp. 1889–1895.
Stanovov, V., Akhmedova, S., and Semenkin, E. (2018).
Lshade algorithm with rank-based selective pressure
strategy for solving cec 2017 benchmark problems.
2018 IEEE Congress on Evolutionary Computation
(CEC), pages 1–8.
Storn, R. and Price, K. (1997). Differential evolution – a
simple and efficient heuristic for global optimization
over continuous spaces. In Journal of Global Opti-
mization, Vol. 11, N. 4, pp. 341-359.
Tanabe, R. and Fukunaga, A. (2013). Success-history
based parameter adaptation for differential evolution.
In IEEE Congress on Evolutionary Computation, pp.
71–78.
Tanabe, R. and Fukunaga, A. (2014). Improving the search
performance of SHADE using linear population size
reduction. In Proceedings of the IEEE Congress on
Evolutionary Computation, CEC, pp. 1658–1665.
Wu, G., R., M., and Suganthan, P. N. (2016). Problem def-
initions and evaluation criteria for the cec 2017 com-
petition and special session on constrained single ob-
jective real-parameter optimization. In Tech. rep.
Zhang, J. and Sanderson, A. C. (2009). Jade: Adaptive
differential evolution with optional external archive.
In IEEE Transactions on Evolutionary Computation
13, pp. 945–958.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
98

APPENDIX
Figure 8: Convergence of LSHADE-RSP and LSHADE-RSP-p
F
, D=50.
Generalized Lehmer Mean for Success History based Adaptive Differential Evolution
99

Figure 9: Convergence of LSHADE-RSP and LSHADE-RSP-p
F
, D=100.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
100
