Correlation Coefficient of Modal Level Operators:
An Application to Medical Diagnosis
Alex Bertei, Renata H. S. Reiser and Luciana Foss
Federal University of Pelotas (UFPEL), Centre for Technological Development (CDTEC),
Laboratory of Ubiquitous and Parallel Systems (LUPS), Street Gomes Carneiro, Pelotas, Brazil
Keywords:
Correlation Coefficient, Modal Level Operators, Intuitionistic Fuzzy Sets, Fuzzy Logic.
Abstract:
This paper studies the correlation coefficient (A-CC) related to the Atanassov’s intuitionistic fuzzy sets (A-
IFS) which are obtained as image of modal operators. Extended results from the action of A-CC over necessity
and possibility modal operators are considered, determining the A-CC of A-IFS obtained as image of the !A
and ?A modal level operators and discussing the main conditions under which the main properties related to
such fuzzy sets are preserved by conjugate and complement operations. In addition, a simulation based on the
proposal methodology using modal level operators is applied to a medical diagnosis analysis.
1 INTRODUCTION
The Atanassov‘s intuitionistic fuzzy logic (A-IFLs)
comprises a generalization of multi-valued fuzzy
logic by taking into account the membership and
non-membership degrees of the information from
Atanassov‘s intuitionistic fuzzy sets (A-IFSs) as dis-
cussed by Bustince and Burillo (Bustince and Burillo,
1995) approach and also providing the hesitation
margin of the index of intuitionist (A-IFIx), as re-
ported by Szmidt and Kacprzyk approach (Szmidt and
Kacprzyk, 2012). Many other approaches lead to a
great numbers of studies:
1. Relating similarity measure of A-IFSs to analyse
the consensus of an expert preference into a group
decision making (Gonz
´
alez-Arteaga et al., 2016);
2. Dealing with similarity measure to indicate the
similar degree between two A-IFSs (Szmidt and
Kacprzyk, 2007); and
3. Analysing the entropy of A-IFSs and describing
its fuzziness degree (Szmidt and Kacprzyk, 2001).
They are closely connected with the correlation coef-
ficient (A-CC) between two A-IFSs, which is able to
express the whole expert systems in fuzzy reasoning,
mainly those applied to decision-making processes
such as clustering analysis (Meng et al., 2016), digital
image processing, medical diagnosis and also includ-
ing pattern recognition (Huang and Guo, 2017).
A-CC should provide an expression given by real
parameters from −1, as the most negative (decreas-
ing) linear relationship to 1, as the most positive (in-
creasing) linear relationship. So, the closer an A-CC
is to either −1 or 1, the stronger the correlation be-
tween these A-IFS is.
This article mainly focusses on intuitionistic fuzzy
modal (A-IFM) operators and their algebraic proper-
ties have been studied by different authors. Extending
the results presented in (Bertei and Reiser, 2018), this
article studies A-CC to modal level operators based
on their analytical expressions, which can be applied
to fuzzy data analysis for classification in prediction
and diagnosis in decision making. By interpreting an
A-IFS as the image of modal level operators, as neces-
sity and possibility on U = [0, 1], is possible to obtain
a simple A-CC even when A-IFM are obtained by the
action of duality and conjugate operators.
This paper is organized as follows: Section2 con-
siders the related work presenting brief comparisons
performing A-CC in A-IFS. Section 3 states the foun-
dations on A-IFL reporting main concepts of modal
level operations, including the action of automor-
phisms and negation operators in order to obtain con-
jugate and complement of A-IFS. Section 4 brings the
main concepts of correlation coefficient from A-IFL.
New results in Section 5 show that dual and conju-
gate operators are preserved by modal α-level opera-
tors. In Section 6, the study includes the main results
based on A-CC obtained by modal operators. In the
Section 7 is presents an application for the medical
diagnosis. Finally, conclusions and further work are
discussed in Section 8.
278
Bertei, A., Reiser, R. and Foss, L.
Correlation Coefficient of Modal Level Operators: An Application to Medical Diagnosis.
DOI: 10.5220/0008164602780287
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 278-287
ISBN: 978-989-758-384-1
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORKS
In the following, Table 1 presents a brief description
of the main papers, summarizing aggregation oper-
ators and applied research area. The main aggrega-
tors used to construct the correlation coefficient are
identified, as well as examples of applicability, which
the great majority uses this coefficient in problems of
fuzzy multiple criteria decision making (MCDM).
In (Szmidt et al., 2012), an extension of previous
work (Szmidt and Kacprzyk, 2010) on A-CC is pre-
sented, measuring how strong an A-IFS relationship
can be, indicating the positively or negatively corre-
lated fuzzy set.
The A-CC analysis obtained as image of intuition-
istic fuzzy t-norms and t-conorms is accomplished
in (Reiser et al., 2013). They consider the action of
automorphisms and the class of strong fuzzy nega-
tions. A-CC related to conjugate and dual construc-
tions of these fuzzy connectives are studied.
Arithmetic operations on trapezoidal fuzzy in-
tuitionistic fuzzy sets (TzFIFSs) are discussed
in (Robinson and Amirtharaj, 2014) the multiattribute
decision making (MADM) model proposed, using A-
CC of TzFIFS for ranking the alternatives together
with weighted averaging (WA) and weighted geomet-
ric (WG) operators.
In (Singh, 2015), the authors propose A-CC for
picture fuzzy sets, which are extensions of A-IFS in-
cluding situations when facing human opinions in-
volving more answers (yes, abstain, no, and refusal).
In (Bertei et al., 2016) a correlation between A-
IFSs obtained as image of strong negations is pre-
sented considering the action of strong fuzzy nega-
tions verifying the conditions under which the A-CC
in A-IFS and their corresponding conjugate construc-
tions are obtained. Moreover, algebraic expressions
of A-CC are discussed by considering representable
intuitionistic automorphisms.
The membership and non-membership degrees of
A-IFS are considered in (Liu et al., 2016), providing a
new approach to measuring the A-CC degree between
the IFSs infinite sets. The method not only reflects
the symbol attribute of an A-CC degree, but also pre-
serves the integrity of related A-IFS.
In (Zhao and Xu, 2016), a new measure was ap-
plied to an algorithm for MADM, using the A-CC and
its desirable axiomatic properties to define the intu-
itionistic fuzzy ideal solution (IFIS) and the intuition-
istic fuzzy negative ideal solution (IFNIS). It is ex-
tended to the interval-valued approach (A-IvIFS).
A novel weighted A-CC formulation proposed
in (Garg, 2016) measures the relationship on the
Pythagorean fuzzy sets (PFS), which are one of the
most successful methods in terms of comprehensively
representing uncertain and vague information.
An MCDM problem is studied in (Solanki et al.,
2016). This proposal refines TOPSIS using A-CC,
characterizing an intuitionistic fuzzy decision matrix
considering criteria as incompleteness and impreci-
sion in the evaluation process. Intuitionistic fuzzy
weighted averaging (IFWA) operator aggregate each
DMs opinions for evaluating the relevance of alterna-
tives. Then positive-ideal and negative-ideal solutions
are calculated, using A-CC a relative closeness coef-
ficient of the alternatives is obtained.
The theory of neutrosophic sets presented
by (Smarandache, 1999) is a powerful technique to
handle incomplete, indeterminate and inconsistent in-
formation in the real world. A-CC between Dy-
namic single-valued neutrosophic multiset (DSVNM)
and a weighted coefficient between DSVNMs are
presented to measure the correlation degrees be-
tween DSVNMs, and their properties are investigated
by (Ye, 2017).
Huang (Huang and Guo, 2017) introduced an im-
proved A-CC of the IFSs, discussing its properties in
the IFS theory and the generalization of the coefficient
of IvIFS is also introduced.
Choquet integral is used in (Qu et al., 2017) pre-
senting a new extension of A-CC. When the weight
information about criteria represented by IFSs is in-
complete, a fuzzy measure model for the optimal
measures on the criteria set is established, which can
be used to determine the criteria fuzzy measure.
Main results in (Bertei and Reiser, 2018) extend
the studies in (Bertei et al., 2016) analyzing A-CC
obtained as the image of modal level operators. The
actions of the necessity and the possibility, are consid-
ered to verify under which conditions an A-CC pre-
serves main properties related to A-IFS.
3 PRELIMINARY
Firstly, a brief account on A-IFS is stated.
Consider a non-empty and finite universe U =
{x
1
, . . . , x
n
} an the unitary interval [0, 1] = U. Ac-
cording with (Bustince and Burillo, 1995), an Atanas-
sosv’s intutionistic fuzzy set A (A-IFS) based on U is
expressed as
A = {(x, µ
A
(x), ν
A
(x)): x ∈ U } (1)
whenever the membership and non-membership func-
tions µ
A
, ν
A
: U → U are related by the inequality
µ
A
(x
i
) + ν
A
(x
i
) ≤ 1, for all i ∈ N
n
= {1, 2, . . . , n}.
Additionally, a function π : A → U given as
π
A
(x
i
) = 1 − µ
A
(x
i
) − ν
A
(x
i
) (2)
Correlation Coefficient of Modal Level Operators: An Application to Medical Diagnosis
279

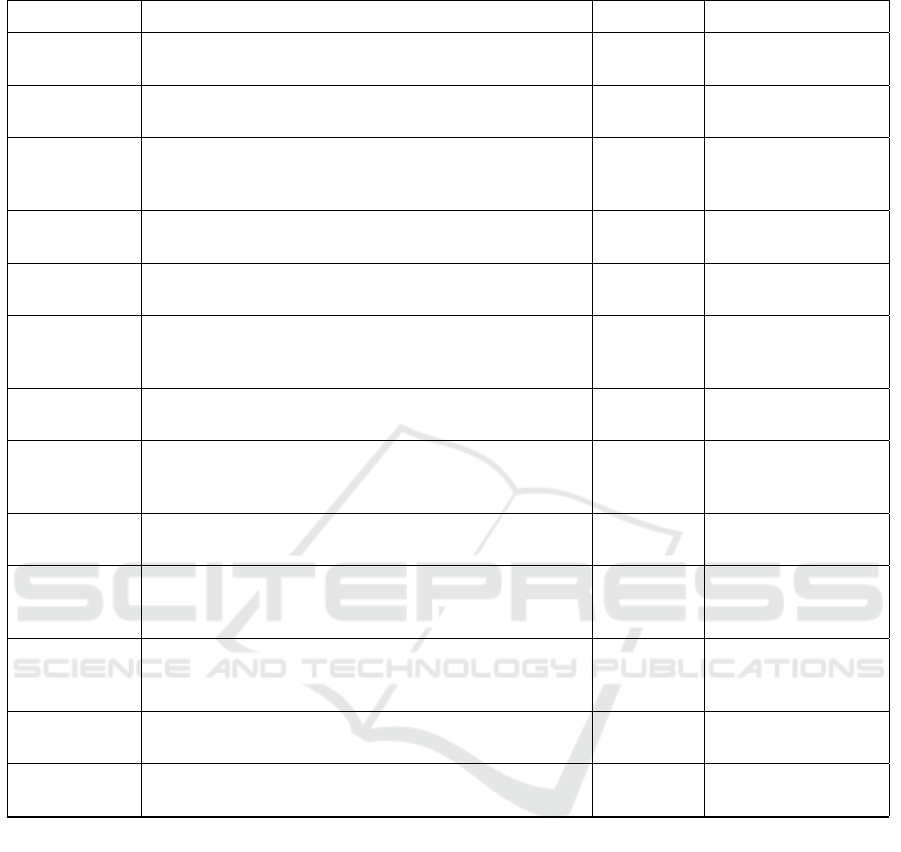
Table 1: Comparisons performing correlation coefficient in A-IFL.
Paper Title Aggregation Applied Field
(Szmidt et al.,
2012)
Correlation between intuitionistic fuzzy sets: Some
conceptual and numerical extensions
Arithmetic
mean
Data analysis and
decision making
(Reiser et al.,
2013)
Correlations from conjugate and dual intuitionistic fuzzy
triangular norms and conorms
Sum
Decision making and
similarity measure
(Robinson and
Amirtharaj,
2014)
MADM Problems with Correlation Coefficient of
Trapezoidal Fuzzy Intuitionistic Fuzzy Sets
TzFIFWA,
TzFIFWG
Ranking alternatives
(Singh, 2015) Correlation coefficients for picture fuzzy sets Sum
Clustering algorithm
for picture fuzzy sets
(Bertei et al.,
2016)
Correlation coefficient analysis based on fuzzy negations
and representable automorphisms
Arithmetic
mean
Fuzzy data analysis
and decision making
(Liu et al.,
2016)
A new correlation measure of the intuitionistic fuzzy sets
Variance
and
covariance
Medical diagnosis
(Zhao and Xu,
2016)
Intuitionistic fuzzy multi-attribute decision making with
ideal-point-based method and correlation measure
Quadratic
mean
Decision making
(Garg, 2016)
A Novel Correlation Coefficients between Pythagorean
Fuzzy Sets and Its Applications to Decision-Making
Processes
Weighted
mean
Decision making
(Solanki et al.,
2016)
A correlation based Intuitionistic fuzzy TOPSIS method on
supplier selection problem
IFWA Decision making
(Ye, 2017)
Correlation Coefficient between Dynamic Single Valued
Neutrosophic Multisets and Its Multiple Attribute
Decision-Making Method
Weighted
mean
Decision making
(Huang and
Guo, 2017)
An Improved Correlation Coefficient of Intuitionistic
Fuzzy Sets
Quasi-
arithmetic
mean
Medical diagnosis
and clustering
(Qu et al.,
2017)
Choquet integral correlation coefficient of intuitionistic
fuzzy sets and its applications
Choquet
integral
Decision making
(Bertei and
Reiser, 2018)
Correlation Coefficient Analysis Performed On Duality
And Conjugate Modal-Level Operators
Arithmetic
mean
Fuzzy data analysis
and decision making
is called the intuitionistic fuzzy index (IFIx) or hes-
itance degree of an A-IFS A. The set of all above
related A-IFSs is denoted by C (A).
Let
˜
U = { ˜x
i
= (x
i1
, x
i2
) ∈ U
2
: x
i1
+x
i2
≤ 1} be the
set of all intuitionistic fuzzy values such that ˜x
i
is a
pair of membership and non-membership degrees of
an element x
i
∈ U , i.e. (x
i1
, x
i2
) = ( µ
A
(x
i
), ν
A
(x
i
)).
And, the related IFIx is given as π
A
(x
i
) = x
i3
= 1 −
x
i1
− x
i2
, for all i ∈ N
n
= {1, 2, . . . , n}.
The projections l
˜
U
n
, r
˜
U
n
:
˜
U
n
→ U
n
are given by:
l
˜
U
n
( ˜x
1
, ˜x
2
, . . . , ˜x
n
) = (x
11
, x
21
, . . . , x
n1
) (3)
r
˜
U
n
( ˜x
1
, ˜x
2
, . . . , ˜x
n
) = (x
12
, x
22
, . . . , x
n2
) (4)
The order relation ≤
˜
U
on
˜
U is defined as: ˜x ≤
˜
U
˜y ⇔ x
1
≤ y
1
and x
2
≥ y
2
. Moreover,
˜
0 = (0, 1) ≤
˜
U
˜x ≤
˜
U
(1, 0) =
˜
1, for all ˜x ∈
˜
U.
3.1 Intuitionistic Fuzzy Negations
Intuitionistic fuzzy negations and intuitionistic auto-
morphisms are studied in the following. See more de-
tails in (Bustince et al., 2003).
An intuitionistic fuzzy negation (A-IFNs) N
I
:
˜
U →
˜
U is a function such that, for all ˜x, ˜y in
˜
U:
N
I
1 N
I
(
˜
0)=N
I
(0, 1)=
˜
1 and N
I
(
˜
1)=N
I
(1, 0) =
˜
0;
N
I
2 If ˜x≥
˜
U
˜y then N
I
( ˜x)≤
˜
U
N
I
( ˜y), ∀ ˜x, ˜y∈
˜
U.
In (Bustince et al., 2000), if an IFN N
I
also satisfies
the involutive property
N
I
3 N
I
(N
I
( ˜x)) = ˜x, ∀ ˜x ∈
˜
U,
N
I
is called a strong A-IFN.
According with (Deschrijver et al., 2004, Theo-
rem 3.6), N
I
is a strong A-IFNs iff there exists a strong
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
280

fuzzy negation N on U such that:
N
I
(x
1
, x
2
) = (N(N
S
(x
2
)), N
S
(N(x
1
))). (5)
Thus, N
I
is an example of N-representable IFN.
Moreover, if N = N
S
, equation (5) can be given as
N
S
I
( ˜x) = N
S
I
(x
1
, x
2
) = (x
2
, x
1
). (6)
By (Bustince et al., 2004), the complement of an
IFS A w.r.t. N
I
in (5) is given as
A
N
I
= {(x, N
I
(µ
A
(x), ν
A
(x))): x ∈ U }. (7)
When N = N
S
in Eq.(5), then the complement of an
IFS A with respect to N
S
I
is expressed as
A = {(x, ν
A
(x), µ
A
(x)): x ∈ U }. (8)
Let N
I
be an IFN. The function f
N
I
:
˜
U
n
→
˜
U is
the N
I
-dual operator of f :
˜
U
n
→
˜
U given as follows:
f
N
I
( ˜x
1
, . . . , ˜x
n
) = N
I
( f (N
I
(x
1
), . . . , N
I
( ˜x
n
))). (9)
For further information, see (Atanassov and Gar-
gov, 1989; Atanassov, 1986; Atanassov, 1999).
3.2 Modal Operators
Following (Atanassov, 1983), two operators are con-
sidered over the IFSs, transforming an IFS into a
fuzzy set (FS). These two operators are similar to the
logical operators of necessity (2) and possibility (3)
and their properties resemble those of Modal Logic.
Adverbial locutions as “very or absolutely” and
“more or less” are interpreted as the linguistic modi-
fiers necessity and possibility, modifying the evalua-
tion of the linguistic Boolean truth values: “true” and
“false” (Atanassov, 1986).
In deduction process, the analytic representation
of such expressions plays an important role, and the
A-CC analysis is able to identify the close correlation
related A-IFSs (Dombi, 2013).
Relevant properties are reported below:
Definition 1. (Atanassov, 1999, Def. 1.41) Let A be
an A-IFS. The related 2A-IFS and 3A-IFS obtained
by the necessity and possibility modal operators are,
respectively, given as follows:
2A = {hx, µ
A
(x), 1 − µ
A
(x)i|x ∈ U }; (10)
3A = {hx, 1 − ν
A
(x), ν
A
(x)i|x ∈ U }. (11)
Obviously, by Def. 1, if A is an ordinary fuzzy set
then 2A = A = 3A.
Proposition 2. (Atanassov, 1999, Prop. 1.42) For ev-
ery A-IFS, the following properties are verified:
2A = 3A, 3A = 2A, (12)
22A = 2A, 23A = 3A, (13)
32A = 2A, 33A = 3A. (14)
3.3 Modal α-level Operators
Initially, the operators K
α
, L
α
:
˜
U →
˜
U are defined as:
K
α
(x
1
, x
2
) =

max

1
2
, x
1

, min

1
2
, x
2

; (15)
L
α
(x
1
, x
2
) =

min

1
2
, x
1

, max

1
2
, x
2

. (16)
Further, related IFS are given in the following.
Definition 3. (Atanassov, 1999, Def. 1.99) Let A be
an A-IFS. For α ∈ U , K
α
A-IFS and L
α
A-IFS are re-
spectively given as follows:
K
α
A=
{
(x, max (α, x
1
), min (α, x
2
)) : x ∈ U
}
; (17)
L
α
A=
{
(x, min (α, x
1
), max (α, x
2
)) : x ∈ U
}
. (18)
The complementary relation K
α
A = L
α
A is ob-
tained from the pair (K
α
, L
α
) of N
S
I
-dual operators.
When α =
1
2
, we use the notation !≡K
1
2
and ?≡L
1
2
and related !A-IFS and ?A-IFS are given below:
Definition 4. (Atanassov, 1999, Def.1.96) Let A be an
A-IFS. The related two modal level operators !A-IFS
and ?A-IFS are respectively given as follows
!A=

x, max

1
2
, x
1

, min

1
2
, x
2

: x ∈ U

; (19)
?A=

x, min

1
2
, x
1

, max

1
2
, x
2

: x ∈ U

. (20)
Theorem 5. (Atanassov, 1999, Theorema 1.97) Let A
and B be IFS, the following holds:
!A = ?A, !?A =?!A, (21)
!(A ∩ B) =!A ∩ !B, !(A ∪ B) =!A ∪ !B, (22)
?(A ∩ B) =?A ∩ ?B, ?(A ∪ B) =?A ∪ ?B. (23)
Theorem 6. (Atanassov, 1999, Theorema 1.98)For
every IFSs A, the following properties are verified:
2!A =!2A, 2?A =?2A, (24)
3!A =!3A, 3?A =?3A. (25)
3.4 Conjugate Operators
In (Reiser and Bedregal, 2017, Def.1), a function
Φ :
˜
U →
˜
U is an intuitionistic fuzzy automorphism
(A-IFA) on
˜
U if Φ is a bijective and non-decreasing
function, ˜x ≤
˜
U
˜y ⇔ Φ( ˜x) ≤
˜
U
Φ( ˜y).
Aut(
˜
U) denotes the set of all A-IFA, extending the
notion of a fuzzy automorphism φ : U → U in Aut(U).
And, the action of Φ :
˜
U →
˜
U on f
I
:
˜
U
n
→
˜
U is
a function f
Φ
I
:
˜
U →
˜
U called intuitionistic conjugate
(A-IFA) of f
I
and defined as follows:
f
Φ
I
( ˜x
1
, . . . , ˜x
n
) = Φ
−1
( f
I
(Φ( ˜x
1
), . . . , Φ( ˜x
n
))). (26)
Now, the φ-representability of an A-IFA is reported:
Correlation Coefficient of Modal Level Operators: An Application to Medical Diagnosis
281

Proposition 7. (Reiser and Bedregal, 2017, Prop.
5) Let φ ∈ Aut(U ) and φ ∈ Aut(U). The a φ -
representable A-IFA Φ ∈ Aut(
˜
U) is defined as follows:
Φ(x
1
, x
2
) = (φ(x
1
), 1 − φ (1 − x
2
)). (27)
Proposition 8. (Bertei and Reiser, 2018, Propo-
sition IV.16) Consider a Φ-representable automor-
phism given by Eq.(27) and 2A-IFS and 3A-IFS
given by Eqs. (10) and (11), respectively. Then, for
all ˜x = (x
1
, x
2
) ∈
˜
U the following holds:
(2)
Φ
( ˜x) = 2(x
1
, 1 − x
1
); (28)
(3)
Φ
( ˜x) = 3(1 − x
2
, x
2
). (29)
4 CORRELATION FROM A-IFL
Using denotation related to Eqs. (2), (3)a and (3)b:
(µ
A
(x
1
), µ
A
(x
2
), . . . , µ
A
(x
n
)) = (x
11
, x
21
, . . . , x
n1
) = x
i1
;
(ν
A
(x
1
), ν
A
(x
2
), . . . , ν
A
(x
n
)) = (x
12
, x
22
, . . . , x
n2
) = x
i2
;
(π
A
(x
1
), π
A
(x
2
), . . . , π
A
(x
n
)) = (x
13
, x
23
, . . . , x
n3
) = x
i3
.
and the two corresponding classes of the quasi-
arithmetic means are reported below:
(i) the arithmetic mean related to an A-IFS A, given
as follow:
m(x
i1
)=
1
n
n
∑
i=1
x
i1
; m(x
i2
)=
1
n
n
∑
i=1
x
i2
; m(x
i3
)=
1
n
n
∑
i=1
x
i3
.
(ii) the quadratic mean, performed over the difference
between each intuitionistic fuzzy value of an A-IFS A
and the corresponding arithmetic mean of all its val-
ues are described in the following:
m
2
(x
i1
) =
v
u
u
t
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
2
;
m
2
(x
i2
) =
v
u
u
t
n
∑
i=1
x
i2
−
1
n
n
∑
i= j
x
j2
!
2
;
m
2
(x
i3
) =
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
.
Thus, the quotient between product values obtained
by taking two sums performed over such classes
of quasi-arithmetic means extending the coefficient
correlation definition to the Atanassov-intuitionistic
fuzzy approach.
Definition 9. (Szmidt and Kacprzyk, 2012) The A-CC
between A and B in C (A) is given as follows:
C(A, B) =
1
3
(C
1
(A, B) +C
2
(A, B) +C
3
(A, B)) (30)
wherever the following holds:
C
1
(A, B) =
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
y
i1
−
1
n
n
∑
j=1
y
j1
!
v
u
u
t
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
2
n
∑
i=1
y
i1
−
1
n
n
∑
j=1
y
j1
!
2
C
2
(A, B) =
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
y
i2
−
1
n
n
∑
j=1
y
j2
!
v
u
u
t
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
2
n
∑
i=1
y
i2
−
1
n
n
∑
j=1
y
j2
!
2
C
3
(A, B) =
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
y
i3
−
1
n
n
∑
j=1
y
j3
!
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
n
∑
i=1
y
i3
−
1
n
n
∑
j=1
y
j3
!
2
In (Szmidt and Kacprzyk, 2012), the correlation
coefficient C(A, B) in Eq. (30) considers both factors:
(i) the amount of information expressed by the mem-
bership and non-membership degrees expressed by
C
1
(A, B) and C
2
(A, B), respectively; and
(ii) the reliability of information expressed by the hes-
itation margins in C
3
(A, B).
Additionally, for fuzzy data, these expressions just
make sense for A-IFS variables whose values vary
and avoid zero in the denominator. Moreover, C(A, B)
fulfils the following properties:
(i) C(A, B) = C(A, B);
(ii) If A = B then C(A, B) = 1;
(iii) −1 ≤ C(A, B) ≤ 1.
Proposition 10. (Bertei et al., 2016, Prop.1) Let N
be a strong A-IFNs, A and B be A-IFSs and A and B
be their corresponding complements. The following
holds:
C
1
(A, B) = C
2
(A, B); (31)
C
2
(A, B) = C
1
(A, B); (32)
C
3
(A, B) = C
3
(A, B). (33)
Corollary 11. (Bertei et al., 2016, Corollary.1) Let N
be a strong A-IFNs, A and B are A-IFSs and A and B
be their corresponding complements. The following
holds:
C(A, B) = C(A, B). (34)
5 RESULTS ON CONJUGATE
MODAL LEVEL OPERATORS
In this section, dual and conjugate operators are pre-
served by modal α-level operators.
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
282

Proposition 12. Consider a Φ-representable auto-
morphism given by Eq. (27) and K
α
-IFS and L
α
-IFS
given by Eqs. (17) and (18), respectively. For all
˜x = (x
1
, x
2
) ∈
˜
U, the following holds:
(K
α
)
Φ
( ˜x)=
(φ
−1
(max(α, φ (x
1
))),1−φ
−1
(1−min(α, 1−φ(1−x
2
))));
(35)
(L
α
)
Φ
( ˜x)=
(φ
−1
(min(α, φ(x
1
))), 1−φ
−1
(1−max(α, 1−φ(1−x
2
)))).
(36)
Proof. For all ˜x = (x
1
, x
2
) ∈
˜
U, we have that
(K
α
)
Φ
( ˜x) =
= Φ
−1
(K
α
(Φ(x
1
, x
2
))) by Eq.(26)
= Φ
−1
(max(α, φ(x
1
)), min(α, 1−φ(1 − x
2
))) by Eq.(27)
=(φ
−1
(max(α, φ (x
1
))), 1−φ
−1
(1−min(α, 1−φ(1−x
2
))))
by Eq.(27)
Analogously, Eq.(36) can be proved. Therefore,
Proposition 12 is verified.
Corollary 13. Consider a Φ-representable automor-
phism given by Eq. (27) and !A-IFS and ?A-IFS given
by Eqs. (19) and (20), respectively. For all ˜x =
(x
1
, x
2
) ∈
˜
U, the following holds:
(!)
Φ
( ˜x)=

φ
−1

max

1
2
, φ(x
1
)

,1−φ
−1

1−min

1
2
, 1−φ(1−x
2
)

;
(?)
Φ
( ˜x)=

φ
−1

min

1
2
, φ(x
1
)

, 1−φ
−1

1−max

1
2
, 1−φ(1−x
2
)

.
Proposition 14. Consider Φ ∈ Aut(
˜
U) and K
α
-IFS
and L
α
-IFS given by Eqs. (17) and (18), respectively.
For all ˜x = (x
1
, x
2
) ∈
˜
U, the following holds:
K
Φ
α
( ˜x) = N
Φ
SI

L
Φ
α
( ˜x)

and L
Φ
α
( ˜x) = N
Φ
SI

K
Φ
α
( ˜x)

.
Proof. For all ˜x ∈
˜
U, the results below are verified:
N
Φ
SI

L
Φ
α
( ˜x)

= N
Φ
SI
(Φ
−1
(L
α
(Φ(x
1
, x
2
)))) by Eq.(26)
= Φ
−1
(N
SI
(L
α
(Φ(x
1
, x
2
)))) by Eq.(26)
= Φ
−1
(N
SI
(L
α
(φ(x
1
), 1−φ(1−x
2
)))) by Eq.(27)
= Φ
−1
(N
SI
((min(α, φ (x
1
)), max(α, 1−φ(1−x
2
))))
by Eq.(36)
= Φ
−1
(max(α, 1−φ(1−x
2
)), min(α, φ(x
1
))))
by Eq.(6)
=(φ
−1
(max(α, φ(x
1
)),1−φ
−1
(1−min(α, 1−φ (1−x
2
))))
by Eq.(27)
= K
Φ
α
( ˜x), by Eq.(35).
Since N
SI
is a strong IFN, the other equation can be
straightforward proved. So, Prop. 14 is verified.
6 RESULTS ON A-CC AND
MODAL LEVEL OPERATORS
This section studies main results of A-CC related to
A-IFS, !A-IFS, ?A-IFS, 2A-IFS and 3A-IFS. For that,
consider i ∈ N
n
, k ∈ N
3
and the notations below:
α
ik
= min

1
2
, x
ik

, β
ik
= max

1
2
, x
ik

.
Proposition 15. The A-CC between A-IFS A and ?A-
IFS is given as
C(A, ?A) =
1
3
(C
1
(A, ?A) +C
2
(A, ?A) +C
3
(A, ?A)) (37)
whenever the following holds:
C
1
(A, ?A) =
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
α
i1
−
1
n
n
∑
j=1
α
j1
!
v
u
u
t
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
2
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
2
C
2
(A, ?A) =
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
β
i2
−
1
n
n
∑
j=1
β
j2
!
v
u
u
t
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
2
n
∑
i=1
β
i2
−
1
n
n
∑
j=1
β
j2
!
2
C
3
(A, ?A) =
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
α
i1
+ β
i2
−
1
n
n
∑
j=1
α
j1
+ β
j2
!
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
n
∑
i=1
α
i1
+β
i2
−
1
n
n
∑
j=1
α
j1
+β
j2
!
2
Proof. Let A-IFS A and ?A-IFS given by Eqs.(1)
and (20), respectively. C
1
(A, ?A) and C
2
(A, ?A) fol-
low from (11) and (30). And, the related resultant
margin to C
3
is given as follows:
C
3
(A, ?A) =
=
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
1 − α
i1
− β
i2
−
1
n
n
∑
j=1
1 − α
j1
− β
j2
!
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
n
∑
i=1
1−α
i1
−β
i2
−
1
n
n
∑
j=1
1 − α
j1
− β
j2
!
2
=
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
α
i1
+ β
i2
−
1
n
n
∑
j=1
α
j1
+ β
j2
!
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
n
∑
i=1
α
i1
+ β
i2
−
1
n
n
∑
j=1
α
j1
+ β
j2
!
2
Therefore, Proposition 15 is verified.
Correlation Coefficient of Modal Level Operators: An Application to Medical Diagnosis
283

Proposition 16. The A-CC between A-IFS and ?A-
IFS is given as follows:
C(A, ?A) =
1
3

C
1
(A, ?A) +C
2
(A, ?A) +C
3
(A, ?A)

(38)
whenever the following holds
C
1
(A, ?A) =
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
β
i2
−
1
n
n
∑
j=1
β
j2
!
v
u
u
t
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
2
n
∑
i=1
β
i2
−
1
n
n
∑
j=1
β
j2
!
2
C
2
(A, ?A) =
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
α
i1
−
1
n
n
∑
j=1
α
j1
!
v
u
u
t
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
2
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
2
C
3
(A, ?A) =
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
β
i2
+ α
i1
−
1
n
n
∑
j=1
β
j2
+ α
j1
!
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
n
∑
i=1
β
i2
+α
i1
−
1
n
n
∑
j=1
β
j2
+ α
j1
!
2
Proof. C
1
(A, ?A) and C
2
(A, ?A) follows from Eqs. (1),
(8), (20) and (30). C
3
(A, ?(A)) is given as follows:
C
3
(A, ?(A)) =
=
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
1 − β
i2
− α
i1
−
1
n
n
∑
j=1
1 − β
j2
− α
j1
!
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
n
∑
i=1
1 − β
i2
− α
i1
−
1
n
n
∑
j=1
1 − β
j2
− α
j1
!
2
=
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
β
i2
+ α
i1
−
1
n
n
∑
j=1
β
j2
+ α
j1
!
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
n
∑
i=1
β
i2
+ α
i1
−
1
n
n
∑
j=1
β
j2
+ α
j1
!
2
Thus, Proposition 16 is also verified.
Proposition 17. Let ?A-IFS and !A-IFS given by
Eqs.(20) and (19), respectively. The following holds:
C(A, !A) = C(A, ?A) (39)
Proof. By Eq.(30) we have that:
C
1
(A, !A) =
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
β
i2
−
1
n
n
∑
j=1
β
j2
!
v
u
u
t
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
2
n
∑
i=1
β
i2
−
1
n
n
∑
j=1
β
j2
!
2
= C
1
(A, ?A)
C
2
(A, !A) =
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
α
i1
−
1
n
n
∑
j=1
α
j1
!
v
u
u
t
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
2
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
2
= C
2
(A, ?A)
C
3
(A, !A) =
=
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
1−β
i2
−α
i1
−
1
n
n
∑
j=1
1−β
j2
−α
j1
!
v
u
u
t
n
∑
i=1
x
i3
−
1
n
n
∑
j=1
x
j3
!
2
n
∑
i=1
1−β
i2
−α
i1
−
1
n
n
∑
j=1
1−β
j2
−α
j1
!
2
= C
3
(A, ?A)
Therefore, Proposition (17) is verified.
Corollary 18. Let A− IFS A, ?A−IFS and !A −IFS
given as Eqs. (1), (20) and (19), respectively. Based
on their NS-dual constructions, the following holds:
C(A, !A)
Eq.(34)
= C(A, !A)
Eq.(21)a
= C(A, ?A). (40)
Proof. It follows from Propositions (10) and (17) also
considering results from above propositions.
Proposition 19. Let A-IFS A, ?A-IFS and 3A-IFS
given by Eqs. (1), (20) and (11) respectively. The
following holds:
C(A, 3?A) =
1
3

C
1
(A, 3?A) +C
2
(A, 3?A)

, (41)
whenever the following holds
C
1
(A, 3?A)=(−1)
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
β
i1
−
1
n
n
∑
j=1
β
j1
!
v
u
u
t
n
∑
i=1
x
i1
−
1
n
n
∑
j=1
x
j1
!
2
n
∑
i=1
β
i1
−
1
n
n
∑
j=1
β
j1
!
2
C
2
(A, 3?A) =
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
β
i1
−
1
n
n
∑
j=1
β
j1
!
v
u
u
t
n
∑
i=1
x
i2
−
1
n
n
∑
j=1
x
j2
!
2
n
∑
i=1
β
i1
−
1
n
n
∑
j=1
β
j1
!
2
Proof. Straightforward.
Corollary 20. Let A−IFS A, ?A−IFS and 3A−IFS
given as Eqs. (1), (20) and (11), respectively. Then the
following holds:
C(A, 3?A)
Eq.(13)b
= C(A, 23?A)
Eq.(34)
= C(A, 23?A);
C(A, 3?A)
Eq.(34)
= C(A, 3?A)
Eq.(14)b
= C(A, 33?A).
Proof. It results from Propositions 2, 10 and 19.
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
284

Proposition 21. Let A be an A −IFS. The correlation
between IFS A and 2!A-IFS is given as
C(A, 2!A) = −C

A, 3?A

, (42)
Proof. Straightforward.
Corollary 22. Let A−IFS A, !A−IFS and 3A −IFS
given as Eqs. (1), (19), and (11) respectively. Then
the following holds:
C(A, 2!A)
Eq.(21)
= C(A, 2?A)
Eq.(34)
= C(A, 2?A).
(43)
C(A, 2!A)
Eq.(13)a
= C(A, 22!A)
Eq.(14)a
= C(A, 322!A).
(44)
Proof. It results from Propositions 2, 10 and 21.
Proposition 23. Let ?A-IFS, !A-IFS, 3A-IFS and
2A-IFS given by Eqs. (20), (19), (11) and (10) re-
spectively. The following holds:
C(2?A, 3!A) =
2
3
(C
1
(2?A, 3!A)), (45)
whenever the following holds
C
1
(2?A, 3!A)=(−1)
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
α
i2
−
1
n
n
∑
j=1
α
j2
!
v
u
u
t
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
2
n
∑
i=1
α
i2
−
1
n
n
∑
j=1
α
j2
!
2
Proof. By Equations. (20), (19), (11), (10) and (30)
we have the following results:
C
1
(2?A, 3!A) =
=
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
1 − α
i2
−
1
n
n
∑
j=1
1 − α
j2
!
v
u
u
t
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
2
n
∑
i=1
1 − α
i2
−
1
n
n
∑
j=1
1 − α
j2
!
2
= (−1)
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
α
i2
−
1
n
n
∑
j=1
α
j2
!
v
u
u
t
n
∑
i=1
α
i1
−
1
n
n
∑
j=1
α
j1
!
2
n
∑
i=1
α
i2
−
1
n
n
∑
j=1
α
j2
!
2
= C
2
(2?A, 3!A)
Since C
3
(2?A, 3!A) = 0, Prop. 23 is verified.
Corollary 24. Let ?A−IFS, !A−IFS, 3A−IFS and
2A − IFS given as Eqs. (20), (19), (11) and (10), re-
spectively. Then the following holds:
C(2?A, 3!A)
Eq.(21)
= C(2?A, 3?A)
Eq.(34)
= C(2?A, 3?A).
C(2?A, 3!A)
Eq.(13)a
= C(22?A, 3!A).
Proof. It follows from Propositions 10, 2 and 23.
Proposition 25. Let ?A-IFS, !A-IFS, 3A-IFS and
2A-IFS given by Eqs. (20), (19), (11) and (10) re-
spectively. The following holds:
C(2?A, 3!A) = −
2
3
(C
1
(2?A, 3!A)),
Proof. It follows from Proposition 23.
Corollary 26. Let ?A−IFS, !A−IFS, 3A−IFS and
2A − IFS given as Eqs. (20), (19), (11) and (10), re-
spectively. Then the following holds:
C(2?A, 3!A)
Eq.(34)
= C(2?A, 3!A)
Eq.(21)
= C(2?A,3?A).
Proof. It follows from Propositions 2, 10 and 25.
Proposition 27. For an A-IFS A, we have that:
C(2?A, 3!A) =
2
3
(C
1
(2?A, 3!A)). (46)
Proof. It follows from Prop. 23 and Corollary 6.
An application considering the previous theoreti-
cal results is presented in the following.
7 MADM - MEDICAL DIAGNOSIS
Previous analytical expressions of modal operator A-
CC are applied in developing a method to medical
diagnosis (MADM-MD) which is adapted from (Xu,
2006)) related to a medical knowledge base, provid-
ing a proper diagnosis D = {Viral fever (VF) , Malaria
(Ma) , Typhoid (Ty) , Stomach problem (SP) , Chest
problem (CP)} for a patient with the given symp-
toms S = {temperature (T), headache (H), stomach
pain (SPa), cough (C), chest pain (CPa)} described in
terms of A-IFSs. Two methodologies are applied:
(i) the former uses necessity and possibility modal op-
erators in MADM-MD; and
(ii) the latter extends the method in order to apply the
modal type operators ?A and !A.
The possibility modal-operator (3) in the Eq. (11)
and necessity modal-operator 2 in Eq. (10) together
with the operator (2?) are applied to values from Ta-
ble 1 (T1) in (Xu, 2006), resulting in values of Ta-
ble 2. In addition, each symptom is described by its
related membership and non-membership degrees.
The necessity modal operator (2) and possibility
modal-operator (3) along with modal-level operators
(!) and (3!) are applied to values of Table 2 (T2)
in (Xu, 2006), and symptom results are described in
Table 3. The set of patients is P = {Al, Bob, Joe,
Correlation Coefficient of Modal Level Operators: An Application to Medical Diagnosis
285

Ted}. Furthermore, we need to seek a diagnosis for
each patient p
i
, for i = 1, 2, 3, 4.
Table 2: Symptoms characteristic for the diagnoses.
Op VF Ma Ty SP CP
T
3T 1 (1,0) (1,0) (0.7,0.3) (0.3,0.7) (0.2,0.8)
2?T 1 (0.4,0.6) (0.5,0.5) (0.3,0.7) (0.1,0.9) (0.1,0.9)
H
3T 1 (0.5,0.5) (0.4,0.6) (0.9,0.1) (0.6,0.4) (0.2,0.8)
2?T 1 (0.3,0.7) (0.2,0.8) (0.5,0.5) (0.2,0.8) (0,1)
SPa
3T 1 (0.3,0.7) (0.1,0.9) (0.3,0.7) (1,0) (0.2,0.8)
2?T 1 (0.1,0.9) (0,1) (0.2,0.8) (0.5,0.5) (0.2,0.8)
C
3T 1 (0.7,0.3) (1,0) (0.4,0.6) (0.3,0.7) (0.2,0.8)
2?T 1 (0.4,0.6) (0.5,0.5) (0.2,0.8) (0.2,0.8) (0.2,0.8)
CPa
3T 1 (0.3,0.7) (0.2,0.8) (0.1,0.9) (0.3,0.7) (0.9,0.1)
2?T 1 (0.1,0.9) (0.1,0.9) (0.1,0.9) (0.2,0.8) (0.5,0.5)
Table 3: Symptoms characteristic for the patient.
Op T H SPa C CPa
Al
2T 2 (0.8,0.2) (0.6,0.4) (0.2,0.8) (0.6,0.4) (0.9,0.1)
3!T 2 (0.9,0.1) (0.9,0.1) (0.5,0.5) (0.9,0.1) (0.5,0.5)
Bob
2T 2 (0,1) (0.4,0.6) (0.6,0.4) (0.1,0.9) (0.1,0.9)
3!T 2 (0.5,0.5) (0.6,0.4) (0.9,0.1) (0.5,0.5) (0.5,0.5)
Joe
2T 2 (0.8,0.2) (0.8,0.2) (0,1) (0.2,0.8) (0,1)
3!T 2 (0.9,0.1) (0.9,0.1) (0.5,0.5) (0.5,0.5) (0.5,0.5)
Ted
2T 2 (0.6,0.4) (0.5,0.5) (0.3,0.7) (0.7,0.3) (0.3,0.7)
3!T 2 (0.9,0.1) (0.6,0.4) (0.6,0.4) (0.8,0.2) (0.6,0.4)
We calculate the A-CC in Eq. (30) between Ta-
bles 2 and 3 deriving a diagnosis for each patient
p
i
, for i = 1,2,3,4. In the first step, the method is
performed applying the A-CC between the operators
3T 1 and 2T 2. And, in the second one, the method
uses the operators 2?T 1 and 3!T 2 deriving the re-
lated A-CC. All the results for the considered patients
are listed in Table 4.
Table 4: Resulting A-CC of symptoms for each patient.
A-CC VF Ma Ty SP CP
Al
(3T 1, 2T 2) 0,610 0,568 0,538 -0,255 -0,452
(2?T 1, 3!T 2) 0,642 0,555 0,441 -0,441 -0,448
Bob
(3T 1, 2T 2) -0,430 -0,472 0,029 0,646 -0,208
(2?T 1, 3!T 2) -0,381 -0,460 0 0,634 -0,103
Joe
(3T 1, 2T 2) 0,455 0,326 0,632 -0,158 -0,327
(2?T 1, 3!T 2) 0,361 0,238 0,562 -0,361 -0,488
Ted
(3T 1, 2T 2) 0,553 0,632 0,344 -0,363 -0,375
(2?T 1, 3!T 2) 0,544 0,614 0 -0,389 -0,189
Based on the arguments in Table 4, for both meth-
ods a proper diagnosis coincides as follows: Al suf-
fers from Viral fever, Bob from a stomach problem,
Joe from Typhoid, and Ted from Malaria. Addition-
ally, one can observe that in (Xu, 2006)), the diagno-
sis is the same in two patients (Bob and Joe) and it
is reverse in other two (Al and ted). Despite the A-
CC expression used in (Xu, 2006, Definition 3.1)) is
able to preserve the property on which any two IFSs
equals one iff these two IFSs are the same, it does not
consider the action of the IFIx π providing the mea-
sure of hesitance degree. The distinct methodologies
justified the difference in the results.
8 CONCLUSION
In this paper, the analytical expressions of A-CC were
considered to pairs of modal α-level operators K
1
2
and
L
1
2
, in particular, for !A and ?A, also including their
conjugate operators. Moreover, we present an appli-
cation of the A-CC with the modal operators of ne-
cessity, possibility, and related modal-level operators
?A and !A.
Further work intends to extend these studies of A-
IFSs to other fuzzy connectives frequently applied to
making decision based on fuzzy systems.
ACKNOWLEDGEMENTS
This work was supported by CAPES/Brasil - Finance
Code 001 and PqG-FAPERGS (17/2551-0001207-0)
and Pq-CNPq (310106/2016-8).
REFERENCES
Atanassov, K. (1983). Intuitionistic fuzzy sets. vii itkr ses-
sion. sofia. Centr. Sci.-Techn. Library of Bulg. Acad.
of Sci., 1697(84).
Atanassov, K. and Gargov, G. (1989). Interval valued intu-
itionistic fuzzy sets. Fuzzy Sets Systems, 31(3):343–
349.
Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy
Sets and Systems, pages 87–96.
Atanassov, K. T. (1999). Intuitionistic Fuzzy Sets: Theory
and Applications. Studies in Fuzziness and Soft Com-
puting. Physica-Verlag HD, Heidelberg, Germany,
Germany.
Bertei, A. and Reiser, R. (2018). Correlation coefficient
analysis performed on duality and conjugate modal-
level operators. In 2018 IEEE Intl. Conf. on Fuzzy
Systems, pages 1–8.
Bertei, A., Zanotelli, R., Cardoso, W., Reiser, R., Foss, L.,
and Bedregal, B. (2016). Correlation coefficient anal-
ysis based on fuzzy negations and representable auto-
morphisms. In 2016 IEEE Intl. Conf. on Fuzzy Sys-
tems, pages 127–132.
Bustince, H., Barrenechea, E., and Mohedano, V. (2004).
Intuicionistic fuzzy implication operators - an expres-
sion and main properties. Uncertainty, Fuzziness and
Knowledge-Based Systems, 12:387–406.
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
286

Bustince, H. and Burillo, P. (1995). Correlation of interval-
valued intuitionistic fuzzy sets. Fuzzy Sets and Sys-
tems, 74(2):237 – 244.
Bustince, H., Burillo, P., and Soria, F. (2003). Automor-
phisms, negations and implication operators. Fuzzy
Sets and Systems, 134(2):209 – 229.
Bustince, H., Kacprzyk, J., and Mohedanoi, V. (2000). Tn-
tuitionistic fuzzy generators, application to intuition-
istic fuzzy complementation. Fuzzy Sets and Systems,
114:485–504.
Deschrijver, G., Cornelis, C., and Kerre, E. (2004). On
the representation of intuitionistic fuzzy t-norms and
t-conorms. IEEE Trans. Fuzzy Systems, 1(12):45–61.
Dombi, J. D. (2013). A special class of fuzzy operators
and its application in modelling effects and decision
problems. PhD thesis, University of Szeged, Szeged.
(in Portuguese).
Garg, H. (2016). A novel correlation coefficients be-
tween pythagorean fuzzy sets and its applications to
decision-making processes. Intl. Jrnl. of Intell. Sys-
tems, 31(12):1234–1252.
Gonz
´
alez-Arteaga, T., de Andr
´
es Calle, R., and Chiclana, F.
(2016). A new measure of consensus with reciprocal
preference relations: The correlation consensus de-
gree. Intl. Jrnl. of Knowledge-Based Systems, 107:104
– 116.
Huang, H.-L. and Guo, Y. (2017). An improved correlation
coefficient of intuitionistic fuzzy sets. Jrnl. of Intell.
Systems.
Liu, B., Shen, Y., Mu, L., Chen, X., and Chen, L. (2016).
A new correlation measure of the intuitionistic fuzzy
sets. Jrnl. of Intell. and Fuzzy Systems, 30:1019–1028.
Meng, F., Wang, C., Chen, X., and Zhang, Q. (2016). Cor-
relation coefficients of interval-valued hesitant fuzzy
sets and their application based on the shapley func-
tion. Intl. Jrnl. of Intell. Syst., 31(1):17–43.
Qu, G., Qu, W., Zhang, Z., and Wang, J. (2017). Choquet
integral correlation coefficient of intuitionistic fuzzy
sets and its applications. Jrnl. of Intell. and Fuzzy Sys-
tems, 33:543–553.
Reiser, R. and Bedregal, B. (2017). Correlation in interval-
valued atanassov
´
s intuitionistic fuzzy sets - conju-
gate and negation operators. Intl. Jrnl. of Un-
certainty, Fuzziness and Knowledge-Based Systems,
25(05):787–819.
Reiser, R., Visintin, L., Ben
´
ıtez, I., and Bedregal, B. (2013).
Correlations from conjugate and dual intuitionistic
fuzzy triangular norms and conorms. In 2013 Joint
IFSA World Congress and NAFIPS Annual Meeting,
pages 1394–1399.
Robinson, J. and Amirtharaj, H. (2014). Madm problems
with correlation coefficient of trapezoidal fuzzy intu-
itionistic fuzzy sets. Advances in Decision Sciences,
2014.
Singh, P. (2015). Correlation coefficients for picture fuzzy
sets. Jrnl. of Intell. and Fuzzy Systems, 28(2):591–
604.
Smarandache, F. (1999). A Unifying Field in Logics: Neu-
trosophic Logic. American Research Press.
Solanki, R., Gulati, G., Tiwari, A., and Lohani, Q. M. D.
(2016). A correlation based intuitionistic fuzzy topsis
method on supplier selection problem. In 2016 IEEE
Intl. Conf. on Fuzzy Systems (FUZZ-IEEE), pages
2106–2112.
Szmidt, E. and Kacprzyk, J. (2001). Entropy for intuition-
istic fuzzy sets. Fuzzy Sets and Systems, 118(3):467 –
477.
Szmidt, E. and Kacprzyk, J. (2007). A new similarity mea-
sure for intuitionistic fuzzy sets: Straightforward ap-
proaches may not work. In 2007 IEEE Intl. Fuzzy Sys-
tems Conf., pages 1–6.
Szmidt, E. and Kacprzyk, J. (2010). Correlation of intu-
itionistic fuzzy sets. In H
¨
ullermeier, E., Kruse, R., and
Hoffmann, F., editors, Computational Intelligence for
Knowledge-Based Systems Design, pages 169–177,
Berlin, Heidelberg. Springer Berlin Heidelberg.
Szmidt, E. and Kacprzyk, J. (2012). A new approach to
principal component analysis for intuitionistic fuzzy
data sets. In et al., S. G., editor, CCIS – IPMU 2012,
volume 298, pages 529–538. Springer.
Szmidt, E., Kacprzyk, J., and Bujnowski, P. (2012). Cor-
relation between intuitionistic fuzzy sets: Some con-
ceptual and numerical extensions. In 2012 IEEE Intl.
Conf. on Fuzzy Systems. p.1-7.
Xu, Z. (2006). On correlation measures of intuitionistic
fuzzy sets. In Intell. Data Engineering and Automated
Learning – IDEAL 2006, pages 16–24.
Ye, J. (2017). Correlation coefficient between dynamic sin-
gle valued neutrosophic multisets and its multiple at-
tribute decision-making method. Information, 8.
Zhao, H. and Xu, Z. (2016). Intuitionistic fuzzy multi-
attribute decision making with ideal-point-based
method and correlation measure. Jrnl. of Intell. and
Fuzzy Systems, 30(2):747–757.
Correlation Coefficient of Modal Level Operators: An Application to Medical Diagnosis
287