Inventing ET Rules to Improve an MI Solver on KR-logic

Tadayuki Yoshida

, Ekawit Nantajeewarawat

, Masaharu Munetomo

and Kiyoshi Akama

Tokyo Software Development Laboratory, International Business Machines Corporation, Tokyo, Japan

Computer Science Program, Sirindhorn International Institute of Technology Thammasat University,

Pathumthani, Thailand

Information Initiative Center, Hokkaido University, Sapporo, Japan

Keywords:

Logical Problem Solving Framework, Equivalent Transformation, Knowledge Representation, Computation

Rule, Query-answering Problem.

Abstract:

We understand that many logical problems cannot be solved by using logic programs. Logic programs have the

limited capability of representation. We try to overcome this limitation by adopting KR-logic, an extension

to ﬁrst-order logic. The extension includes function variables. In this paper, we take a problem which is

well-described with function variables. We rely on Logical Problem Solving Framework (LPSF) to formalize

our problem as a Model-intersection problem. Then we develop a solver for MI problems by adding ﬁve

new transformation rules concerning function variables. Correctness of each rule is proved.i.e., each rule is

an equivalent tranformation (ET) rule. Since each rule is correct, all ET rules can be used together without

modiﬁcation and combinational cost. Thus, the invented rules can be safely reused in other LPSF-based

solvers.

1 INTRODUCTION

Logic programs such as Prolog take an approach to

rely on SLDNF-resolution (Chang and Lee, 1973;

Lloyd, 1987). There are many logical problems which

cannot be solved by using conventional logic ap-

proach. The Agatha puzzle is one of such problems.

We use LPSF (Akama et al., 2019) to formalize the

Agatha puzzle as a Model-intersection (Akama and

Nantajeewarawat, 2016) problem.

Usual clauses don’t have enough expressive power

to represent and compute the Agatha puzzle. We

take an extended clause in ECLS

as a representation

space. ECLS

is a class of clauses with function vari-

ables on KR-logic(Akama et al., 2019). The objective

of this paper is to construct a solver for the Agatha

puzzle by development of equivalent transformation

(ET) rules.

We already have developed several ET rules

(Akama and Nantajeewarawat, 2011),(Akama and

Nantajeewarawat, 2015), (Akama et al., 2018a),

(Akama et al., 2018b) as well as unfolding (Akama

and Nantajeewarawat, 2013) for computation of ex-

tended clauses. However, it turned out that the solver

using these existing rules cannot give an answer to

the Agatha puzzle. This difﬁculty is due to the lack

of ET rules to handle function variables. To repre-

sent the Agatha puzzle correctly, function variables

are essential. Representation spaces without function

variables, such as conventional clauses, don’t have

enough expressive power of existential quantiﬁcation.

This paper proposes a set of ET rules which trans-

form extended clauses containing function variables.

The LPSF theory ensures the correctness of answers

to the Agatha puzzle strictly from a combination of

ET rules. The heuristic approach cannot guarantee

the correctness of the method, while LPSF can do for

ET rules. We think ET rules discovered in solving

a certain problem are usable for a general purpose.

Thus, once we invent an ET rule, such rule is reused

independently together with a variety of existing ET

rules.

We take the squeeze method to discover ET rules.

We also study to prove the correctness of rules dis-

covered. Then we state that a new ET rule is truly in-

vented. In this paper, we successfully invent ﬁve new

ET rules through iterations of the squeeze method.

The answer to the Agatha puzzle is obtained by

expanding a computation sequence through invented

rule application. This is our ﬁrst achievement to con-

struct an MI solver for the Agatha puzzle based on the

extended space on ECLS

. We also demonstrate the

fact that new ET rules contribute to an improvement

274

Yoshida, T., Nantajeewarawat, E., Munetomo, M. and Akama, K.

Inventing ET Rules to Improve an MI Solver on KR-logic.

DOI: 10.5220/0008165702740281

In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 274-281

ISBN: 978-989-758-382-7

of the solver. Due to the limited representation ca-

pability of conventional clauses with ﬁrst-order logic,

we cannot solve the Agatha puzzle by using any possi-

ble computation methods. The LPSF theory provides

a ﬁrm foundation for stepwise improvement of logical

problem solving.

The rest of this paper is organized as follows: Sec-

tion 2 discusses about how to design an MI solver

based on LPSF for the Agatha puzzle. Section 3

explains the rule invention process for a solution of

the Agatha puzzle, by iteratively squeezing applica-

ble rules from an interim transformation status as a

result of application of exiting known rules. Section 4

proves correctness of the invented ﬁve transformation

rules in this paper. Section 5 shows how a newly con-

structed MI solver works and what other LPSF param-

eters can be taken into considerations. Section 6 gives

a discussion about the comparison with existing log-

ical structures, one on the usual clausal logic and the

other is the extended clause space with constraints.

Section 7 concludes the paper.

2 DESIGN OF MI SOLVER FOR

QA PROBLEMS

We discuss a design consideration of MI solver for the

famous Agatha Puzzle.

2.1 Agatha Puzzle

Consider the “Dreadsbury Mansion Mystery” prob-

lem, which was given by Len Schubelt and can be de-

scribed as follows: 1) Someone who lives in Dreads-

bury Mansion killed Aunt Agatha. 2) Agatha, the but-

ler, and Charles live in Dreadsbury Mansion, and are

the only people who live therein. 3) A killer always

hates his victim, and 4) is never richer than his vic-

tim. 5) Charles hates no one that Aunt Agatha hates.

6) Agatha hates everyone except the butler. 7) The

butler hates everyone not richer than Aunt Agatha. 8)

The butler hates everyone Agatha hates. 9) No one

hates everyone. The Agatha QA problem is to ﬁnd all

persons who killed Agatha. The Agatha proof prob-

lem is to show that Agatha killed herself.

2.2 Formalization of the Puzzle

We take ECLS

as a logical structure. We already

know many ET rules on the space of ECLS

, how-

ever, they are not enough for complete solution of the

Agatha puzzles.

Assume that eq and neq are predeﬁned binary con-

straint predicates. For any ground usual terms t

and

, (i) eq(t

) is true iff t

= t

, and (ii) neq(t

)

is true iff t

6= t

. The background knowledge of

this mystery is formalized as the conjunction of the

ﬁrst-order formulas, where (i) the constants A, B, C,

and D denote “Agatha,” “the butler,” “Charles,” and

“Dreadsbury Mansion,” respectively, and (ii) for any

terms t

and t

, live(t

), kill(t

), hate(t

), and

richer(t

) are intended to mean “t

lives in t

,” “t

killed t

,” “t

hates t

,” “t

is richer than t

,” respec-

tively.

Let K be the conjunction of the ﬁrst-order formu-

las F

to F

and let q = kill(x, A). The Agatha puzzle

is formalized as a QA problem hK,qi. The answer

to this QA problem, denoted by answer(K,q), is the

set of all ground instances of q that follows logically

from K.

= ∃x : (l ive(x,D) ∧ k ill(x,A))

= ∀x : (live(x,D) ↔ (eq(x,A)∨eq(x, B)∨eq(x,C))

= ∀x : ∀y : (kill(x,y) → hate(x,y))

= ∀x : ∀y : (kill(x,y) → ¬richer(x, y))

= ¬∃x : (hate(C,x) ∧ hate(A, x) ∧ live(x, D))

= ∀x : ((neq(x,B)∧ live(x,D)) → hate(A,x))

= ∀x : (¬richer(x,A) ∧ live(x,D)) → hate(B,x))

= ∀x : ((hate(A,x) ∧ live(x,D)) → hate(B,x))

= ¬∃x : (live(x , D)∧∀y : (live(y,D) → hate(x,y)))

K is converted into the set Cs consisting of the

fourteen extended clauses C

to C

by applying

meaning-preserving Skolemization (Akama and Nan-

tajeewarawat, 2011) as follows: MPS(F

) = C

, C

MPS(F

) = C

, C

, MPS(F

) = C

, MPS(F

) =

, MPS(F

) = C

, MPS(F

) = C

, MPS(F

) = C

MPS(F

) = C

, and MPS(F

) = C

, C

: live(x , D) ← f unc( f

,x)

: kill(x,A) ← f unc( f

,x)

: ← live(x, D),neq(x,A),neq(x,B),neq(x,C)

: live(A, D) ←

: live(B, D) ←

: live(C, D) ←

: hate(x, y) ← kill(x,y)

: ← kill(x,y),richer(x,y)

: ← hate(A,x),hate(C,x),live(x,D)

: hate(A,x) ← neq(x,B),live(x,D)

: richer(x,A),hate(B, x) ← live(x,D)

: hate(B,x) ← hate(A,x),live(x, D)

: ← hate(x,y), f unc( f

,x,y), live(x, D)

: live(y,D) ← live(x,D), f unc( f

,x,y)

Let state S

be {C

,...,C

Inventing ET Rules to Improve an MI Solver on KR-logic

275

2.3 Answer Mapping

The QA problem hK,qi is then reformulated as a

model-intersection (MI) problem hCs, ϕi, where ϕ is

a mapping from the power set of G

to the power set

of {A,B,C}, deﬁned by ϕ(G) = {t |kill(t,A) ∈ G} for

any G ⊆ G

. In other words, we have

answer(K, q) = ϕ(

Models(Cs)).

Our plan for solving the Agatha puzzle is to sim-

plify ϕ(

Models(Cs)) mainly by transforming Cs

preserving Models(Cs) or

Models(Cs).

3 RULE INVENTION PROCESS

We introduce a process to invent transformation rules

through the squeeze method.

3.1 The Squeeze Method

Many successful research work have proposed gen-

eral ET rules applicable to a wide range of problem

domain. Based on these outcomes, we ﬁrst apply such

existing ET rules to the QA problem introduced in

2.1, and then investigate the interim set of clauses af-

ter an application process of ET rules terminates. The

iteration of the squeeze method goes as follows: 1)

add one or more rules with a proper priority control

for them, 2) run an application process of combined

ET rule set, 3) verify the interim result if it reaches

to the domain of the deﬁned answer mapping. Other-

wise, go back to 1).

3.2 Applying Existing ET Rules

By applying ET rules discussed in (Akama and Nan-

tajeewarawat, 2014) and (Akama et al., 2018b), to the

original clauses in S

, these clauses are transformed

into simple clauses where atoms like live and hate are

resolved. Then we get the clauses in state S

as the

ﬁrst interim result with which our iteration process

starts. The process of transformation to these clauses

is discussed 2.3 in (Akama and Nantajeewarawat,

2018)

= {C

,...,C

}

: ← neq(x,B), f unc( f

,B, x)

: ← f unc( f

,B, A)

: ← f unc( f

,B,C)

: ← f unc( f

,C)

: kill(x,A) ← f unc( f

,x)

: ← f unc( f

,B, x), f unc( f

,x)

: ← f unc( f

,x,A), f unc( f

,x)

: ← neq(x,A),neq(x,B),neq(x ,C), f unc( f

,x)

: ← neq(x,A),neq(x, B),neq(x ,C), f unc( f

,C, x)

: ← f unc( f

,A, A)

: ← f unc( f

,A,C)

: ← neq(x,B), f unc( f

,A, x)

3.3 Determining Development Strategy

There are many func-atoms in the body of clauses in

. In order to make further transformations, such

func-atoms need to get handled correctly. It is ob-

served that two types of func-atoms occurrences in

: a) A func-atom alone in a body and no head atoms

like C

, and b) Combination of a sin-

gle func-atom variable and a sequence of neq atoms,

and no head atoms like C

. In addition to

these types of func-atoms, we also need to remove a

clause containing a func-atom alone in a body in order

to match to the domain of the answer-mapping func-

tion deﬁned in 2.3. The answer-mapping function can

be applicable when C

is simpliﬁed to have no body

atoms. So a rule for safe func-atom clause removal is

being developed. In the rest of this paper, we invent

these types of ET rules on the LPSF and observe if an

answer to the problem can be obtained by using such

rules from S

again.

3.4 Squeeze Method Iteration

3.4.1 Side Change of neq-atoms in Body

The rule of side change of neq, denoted as

(chSide neq), is to move neq atoms from body part

into head part with altering predicate to eq. This rule

is applied and C

, C

, and C

are obtained

from C

, C

and C

respectively.

these are transformed into:

: eq(x,B) ← f unc( f

,B, x)

: eq(x,A),eq(x, B),eq(x,C) ← f unc( f

,x)

: eq(x,A),eq(x, B),eq(x,C) ← f unc( f

,C, x)

: eq(x,B) ← f unc( f

,A, x)

3.4.2 False func-atom Elimination

The rule of false func-atom elimination, denoted

as elimNegfvr, is to eliminate a clause containing

a false func-atom. According C

, f

(B) = B is

determined. So any other declarations for f

(B) must

be false. Due to this, C

and C

are deleted. Also,

(A) = B is determined by C

so any f

(A) atoms

else are false. C

and C

can be eliminated.

KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development

276

3.4.3 Candiate eq-atom Elimination

The rule of candidate eq-atom elimination, denoted

as elimPosfvr, is to remove eq atoms in head

that match with negative declaration of the same

func-atom. According to C

, f

() 6= C. This means

eq(x,C) in the head of C

can be removed and obtain

: eq(x,A),eq(x, B) ← f unc( f

,x)

3.4.4 True func-atom Elimination

The rule of true func-atom elimination, denoted as

applyPosfvr, is to eliminate func-atom evaluated as

true by referring to a clause of the same func-atom.

It is applied to C

with C

and replace C

with C

: ← f unc( f

,B)

3.4.5 Combinational Rule Application

Again, elimNegfvr and elimPosfvr several times

: kill(x,A) ← f unc( f

,x)

: ← f unc( f

,x,A), f unc( f

,x)

: eq(x,B) ← f unc( f

,B, x)

: eq(x,A),eq(x, B),eq(x,C) ← f unc( f

,C, x)

: eq(x,A) ← f unc( f

,x)

: eq(x,B) ← f unc( f

,A, x)

applyPosfvr to C

with C

and replace C

with C

, and applyPosfvr to C

with C

and

replace C

with C

: eq(x,B) ← f unc( f

,B, x)

: eq(x,A) ← f unc( f

,x)

: eq(x,A),eq(x, B),eq(x,C) ← f unc( f

,C, x)

: eq(x,B) ← f unc( f

,A, x)

: ← f unc( f

,A, A)

: kill(A,A) ←

elimNegfvr to C

: eq(x,B) ← f unc( f

,B, x)

: eq(x,A) ← f unc( f

,x)

: eq(x,A),eq(x, B),eq(x,C) ← f unc( f

,C, x)

: eq(x,B) ← f unc( f

,A, x)

: kill(A,A) ←

3.4.6 Isolated func-atom Elimination

The rule of isolated func-atom elimination, denoted

as elimIsoFunc is to remove a clause containing

a func-atom which has no uniﬁable candidates in

body atoms of other clauses. In C

, f

(B) = B is

determined and no uniﬁable pattern to f

(B) exist in

and C

. This situation makes the removal of

: eq(x,A) ← f unc( f

,x)

: eq(x,A),eq(x, B),eq(x,C) ← f unc( f

,C, x)

: eq(x,B) ← f unc( f

,A, x)

: kill(A,A) ←

In the same way, C

, C

and C

all can be

removed.

We run through four iterations of squeezing and ﬁ-

nally the clause is simpliﬁed enough to apply answer-

mapping to get an answer to the Agatha puzzle. The

process resulted in ﬁnding four new ET rules.

The next chapter, we provide a theoretical basis

for each rule so that we can make strict deﬁnitions of

newly invented rules.

4 CORRECTNESS

We give formal deﬁnitions for ﬁve new ET rules.

Each subsection starts with a formal description of

new rule, followed by its brief proof.

4.1 Correctness of Computation

The LPSF guarantees a correct computation with a

bunch of transformation rules by giving a theoreti-

cal foundation to discuss the correctness of each in-

dividual rule. This yields a stable growth of an MI

solver’s capability through adding a set of newly in-

vented transformation rules to existing rule set. We

don’t need to have any concern about the consistency

regarding the correctness of whole computation pro-

cess. It is always kept valid as long as it is based on

the LPSF.

4.2 Side Change of neq-atoms in Body

Let hCs,ϕi be a MI problem on ECLS

. Assume that

a clause C in Cs such that

C = (← Neqs(n), f unc( f , s

,..., s

,x)),

Neqs(n) = {neq(x,t

),..., neq(x,t

)}

Inventing ET Rules to Improve an MI Solver on KR-logic

277

where x is a usual variable, t

,...,t

and s

,..., s

are

ground terms, f is a function variable, n > 1, and

m >= 0. There exists at least one f unc-atom in body

of C and a set of neq-atoms which has the same occur-

rence of the variable x in the f unc-atom, where all do-

main terms in f unc-atom have been already grounded

,...s

Under this condition, a new clause C

is con-

structed from C and all neq-atoms in body of C can be

side-changed into head as eq-atoms. The rest of body

atoms in C, represented as Bs remain unchanged.

= (Eqs(n) ← f unc( f ,s

,..., s

,x))

Eqs(n) = {eq(x,t

),..., eq(x,t

)}

= (Cs − {C }) ∪ {C

}

The correctness of this rule is shown as follows:

Let σ and θ be substitutions for function variables and

usual variables, respectively. Assume that Cσθ is true.

Since C has no head atom, Neqs(n)σθ is false, while

f uncσ is true.

Neqs(n)σθ = false

⇔ (xσθ 6= t

∧ ... ∧ xσθ 6= t

) = false

⇔ ¬(xσθ = t

∨ ... ∨ xσθ = t

) = false

⇔ (xσθ = t

∨ ... ∨ xσθ = t

) = true

⇔ Eqs(n)σθ = true

If Eqs(n)σθ is true, then C

σθ is true and obvi-

ously Models(Cs) = Models(Cs

) is true.

4.3 Candidate eq-atom Elimination

Let hCs,ϕi be a MI problem on ECLS

. Assume that

a set of clauses C in Cs such that

C = (← f unc( f ,s

,...., s

,g))

where s

,..., s

,g are ground terms, f is a function

variable, and m >= 0.

If there is a func-atom f unc( f ,s

,..., s

,v) in the

right-hand side of a clause C

rather than C in Cs, and

the head atoms of C

only contains a sequence of eq-

atoms and each eq atom contains a pair of v and a

ground term,

= (Eqs(n) ← f unc( f ,s

,...., s

,v))

Eqs(n) = {eq(v,t

),..., eq(v,t

)}

then Cs

is obtained from Cs as follows:

head atom eq(v, g) can be removed from C

and C is

removed from Cs.

= (Eqs(n,i) ← f unc( f ,s

,...., s

,v))

Eqs(n,i) = Eqs(n,i) − { eq(v,t

)}

= (Cs − {C,C

}) ∪ {C

}

where t

= g.

The correctness of this rule is shown as follows:

Basically, C

constructs a set of possible range val-

ues {t

,...t

} for f . Since the negative clause C de-

clares an impossible candidate g of the range of f , if

a range candidate contains t

(= g), then it can be re-

moved. Also, C itself is no longer needed for deﬁning

the models of Cs, so C can be removed from the re-

sulting clauses. Then Models(Cs) = Models((Cs −

{C,C

}) ∪ {C

}) is true.

4.4 True func-atom Elimination

Let hCs,ϕi be a MI problem on ECLS

. Assume that

a set of clauses C ∈ Cs such that

C = (eq(x, g) ← f unc( f ,s

,...., s

,x))

where x is a usual variable, s

,..., s

,g are ground

terms, f is a function variable, and m >= 0.

If there is a func-atom f unc( f ,s

,..., s

,v) in the

right-hand side of a clause C

rather than C in Cs, then

can be specialized by applying a substitution θ =

{v/g}, and the true func-atom f unc( f , s

,..., s

,g)

can be removed from the resulting clause C

θ.

θ = (Hsθ ← Bsθ, f unc( f ,s

,...., s

,v)θ)

θ = (Hsθ ← Bsθ)

= (Cs − {C

}) ∪ {C

θ}

where Hs and Bs are a sequence of atoms.

The correctness of this rule is shown as fol-

lows: The above transformation is correct since

f unc( f , s

,..., s

,v)θ (= f unc( f ,s

,..., s

,g)) is true.

Then Models(Cs) = Models((Cs − {C

}) ∪ {C

θ})

is true.

4.5 False func-atom Elimination

Let hCs,ϕi be a MI problem on ECLS

. Assume that

a set of clauses C ∈ Cs such that

C = (Eqs(n) ← f unc( f ,s

,...., s

,x))

Eqs(n) = {eq(x,t

),..., eq(x,t

)}

where x is a usual variable, t

,...,t

,..., s

,g are

ground terms, f is a function variable, n >= 1 and

m >= 0.

If there is a ground func-atom f unc( f ,s

,..., s

,u)

in the right-hand side of a clause C

in Cs and u 6=

,...,t

}, then C

can be removed from Cs.

= (Hs ← Bs, f unc( f ,s

,...., s

,u))

= (Cs − {C

})

where Hs and Bs are a sequence of atoms.

The correctness of this rule is shown as fol-

lows: The above transformation is correct since

f unc( f , s

,..., s

,u) is false. Then Models(Cs) =

Models((Cs − {C

})) is true.

KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development

278

4.6 Isolated func-atom Elimination

Let hCs,ϕi be a MI problem on ECLS

. Assume that

a set of clauses C in Cs such that

Cs = Cs

∪ {C },

C = (Hs ← Bs, f unc( f , s

,...., s

,x))

where x is a usual variable, s

,..., s

are ground terms,

f is a function variable, Hs and Bs are a sequence of

built-in atoms, and m >= 0.

A func-atom is isolated with respect to Cs

if there

is no func-atom of the form f unc( f

,...., s

,t) in

the body of any clause in Cs

such that f

= f , m

= m,

,...s

,t are terms, and the lists of terms [s

,...s

]

and [s

,...s

] are uniﬁable. If the following conditions

are satisﬁed:

1. f unc( f ,s

,...., s

,x) is isolated with respect to

, and

2. (Hs ← Bs) contains no func atoms and satisﬁable,

then C can be eliminated and Cs

= Cs

The correctness of this rule is shown as fol-

lows: Assume that g is a ground term such that

(Hs ← Bs){x/g} is satisﬁable. Then there ex-

ists h such that f unc( f ,s

,...., s

,g){ f /h} is true.

Thus, C{x /g}{ f /h} is satisﬁable and can be elimi-

nated. The instantiation { f /h} doesn’t affect to Cs

since f unc( f ,s

,...., s

,x) is isolated with respect to

. Then the above transformation is correct since

Models(Cs

) = Models(Cs

) = Models(Cs).

5 EXPERIMENTS

We show a solution for the example Agatha puzzle by

integrating ﬁve new rules with existing ones.

5.1 Solution Improvement

We have designed and implemented an improved MI

solver with ﬁve invented ET rules. In this section we

will observe the transformation process of the original

clauses C

to C

in 2.2.

Before the introduction of ﬁve new rules, we use

seven existing rules and control of priority shown in

Section 3.2. The computation process terminated at

125th steps of transformation where (chSide) is ap-

plied 1 time, (dup) 8 times, (erase) 7 times, (neq) 6

times, (specAtom) 1 time, (subsumed) 72 times, and

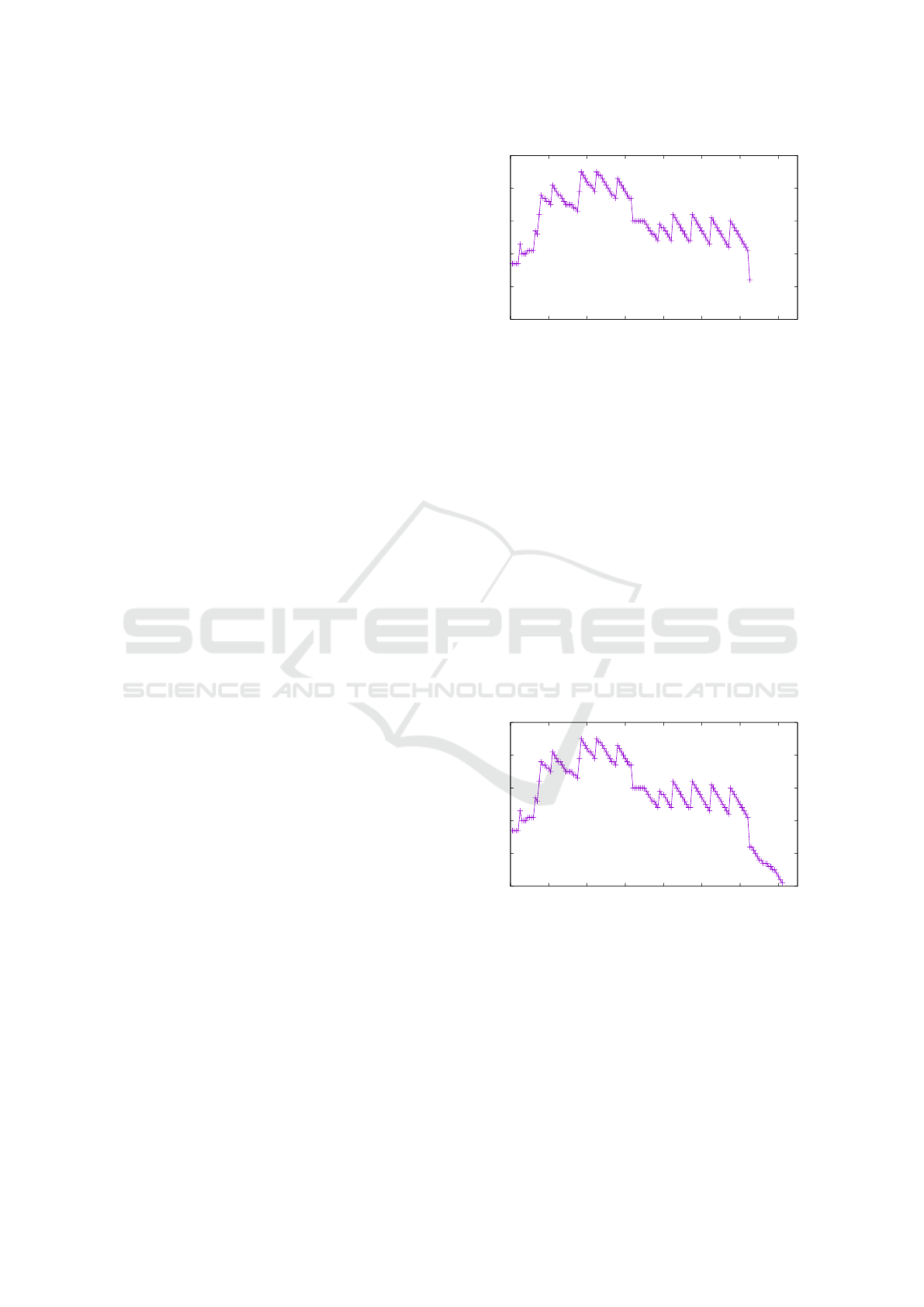
(ud) 30 times. Figure 1 shows the transition of the

number of clauses on each transformation step. The

number of clauses goes down to 11 at 125th step.

However, the answer is not obtained since the result-

ing clauses are not simple enough to apply the answer

mapping function ϕ.

0 20 40 60 80 100 120 140

numberofclauses

numberoftransforms

Figure 1: Transition of the number of clauses without new

rules.

After integration of ﬁve invented rules, we use

twelve rules in total. When we modify the rule pri-

ority as

(neq)>

(elimNegfvr)>(elimPosfvr)>

(applyPosfvr)>(elimIsoFunc)>

(subsumed)>(dup)>(erase)>

(specAtom)>(ud)>

(chSide)>(chSide neq)

then the process is stretched with 17 more steps

of transformation where (applyPosfvr) is applied 3

times, (chSide neq) 1 time, (elimNegfvr) 7 times,

(elimPosfvr) 2 times, and (elimIsoFunc) 4 times. Fig-

ure 2 shows the stretched transition of the number of

clauses. The number of clauses goes down to 1 at

142th step and it is simple enough to apply the an-

swer mapping ϕ, then the answer is obtained.

0 20 40 60 80 100 120 140

numberofclauses

numberoftransforms

Figure 2: Stretched transition of the number of clauses with

new rules.

5.2 Comprehensive Transformation

Flow

All 142 steps cannot be listed in this paper. We give

a summary of transformation for each stage where

atoms are eliminated and simplicity increases.

1. By unfolding using the deﬁnition of kill (C

), all

body atoms with the predicate kill are removed.

Inventing ET Rules to Improve an MI Solver on KR-logic

279

By deﬁnite-clause removal, the deﬁnition of kill

) is removed. By unfolding, three body atoms

with patterns hate(A, x) or hate(C, x) are removed.

2. By side-change transformation for richer, the

richer-atoms in some clauses are removed and

not richer-atoms are obtained in the other side of

these clauses.

3. By unfolding, not richer-atoms and hate-atoms

in clause bodies are removed. The deﬁnitions of

not richer and hate are removed.

4. Unfolding with respect to live-atoms has been sus-

pended since one of the deﬁnite clauses deﬁning

live introduces a new live-atom with a pure vari-

able as its ﬁrst argument. To remedy the situation,

the atom live(x,D) in the body of a clause is spe-

cialized into three clauses, which enable further

application of unfolding.

5. By unfolding live-atoms and deﬁnite-clause re-

moval, all live-atoms are removed and the clauses

to C

are obtained.

6. By side-change transformation for neq, neq-atoms

are removed from body part and eq-atoms are ob-

tained in the respective head side in four clauses.

7. By eliminating clauses whose body contain false

func-atoms, by eliminating eq-atoms for a cer-

tain func-atom which is not consistent with other

clauses of the same func-atoms in question from

a head part of a clause, and by eliminating func-

atoms which hold true regarding the settled values

declared in another clause of the same func-atom.

8. By eliminating isolated func-atom declarations

which don’t occur in any other clauses.

9. The ground atom is obtained consistently and the

answer A meaning “Agatha” is obtained by apply-

ing the answer mapping ϕ.

6 DISCUSSION

In this section, we discuss the improvement of our

approach compared with existing framework.

6.1 Failure in CLS

(The Usual Clausal

Logic)

The conventional formalization consists of the follow-

ing two steps:

• From the Agatha problem described by sentences

(Section 2.1) we obtain K in the ﬁrst-order formu-

las.

• To K we apply CSK to have a set of clauses Cs

The conventional Skolemization (CSK) is a major

hindrance to developing a general solution for proof

and QA problems on ECLS

since it does not gen-

erally preserve satisﬁability nor logical meanings by

Theorem 1 in (Akama and Nantajeewarawat, 2016),

and thus does not generally preserve the answers to

proof and QA problems.

When we transform the Agatha background

knowledge K into a set Cs

of usual clauses us-

ing the conventional Skolemization, we know that

Models(K) 6=

0 and Models(Cs

) =

0, hence neither

satisﬁability nor logical meanings is preserved in this

case, and further computation starting from Cs

to ﬁnd

answers is thus useless.

6.2 Success in ECLS

(The Extended

Clausal Logic)

In this paper, we are successful to create an MI solver

based on the LPSF with a general logical structure as

much as possible. We already have achieved another

approach to introduce constraint is one of key con-

siderations on building such a general one (Akama

and Nantajeewarawat, 2018). However, rules which

work independently from constraints would beneﬁt

MI solvers to focus on creating rules which are more

speciﬁc and effective to a certain problem.

Based on LPSF, transformation rule is a small

building block to construct an algorithm for prob-

lems which requires logical structure for representa-

tion. We proved the correctness of each individual

transformation rule. This means we can reuse safely

newly invented rules in other scenario where same

knowledge representation may ﬁt to MI-solver. When

integrating invented rules, we don’t need additional

effort to prove overall correctness as long as the rule-

by-rule correctness is given.

One of KR-logic unique approach is the existence

of func-atom using function variable and a substi-

tution σ. As shown in the computation process of

Agatha puzzle, we have rich computation algorithm

using ET rules to handling func-atom.

7 CONCLUSIONS

The conventional clauses don’t have enough expres-

sive power of existential quantiﬁcation that is required

to represent and compute the Agatha puzzle. Function

variables are essentially used for transformation of ex-

istential quantiﬁcation. We take extended clauses in

ECLS

that have function variables. Hence, we need

KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development

280

a new logic and logical computation for the extended

space.

To solve the Agatha puzzle, we discover ET rules

to handle function variables. We obtained ﬁve gen-

eral ET rules as follows: (1) side-change of neq body-

atoms to eq head-atoms, (2) elimination of candidate

eq head-atom, (3) elimination of func atom by en-

forced specialization, (4) elimination of a clause by

false func atom, and (5) elimination of a clause con-

taining an isolated func atom.

These invented rules are discovered through the

squeeze method. We also prove the correctness of

each rule strictly. Thus, we construct an MI solver

based on the extended space on ECLS

. The solver

is applied to not only the Agatha puzzle, but also

any other problems represented similarly in extended

clauses. It is shown that the proposed new ET rules

contribute to an improvement of a solver. We can

make a constant progress by adopting a suitable repre-

sentation space for the problem that cannot be solved

in the conventional clause space. Increasing the capa-

bility by accumulating properly validated ET rules is

a core research methodology of logical problem solv-

ing framework.

REFERENCES

Akama, K. and Nantajeewarawat, E. (2011). Meaning-

preserving skolemization. In Proc. 3rd international

conference on Knowledge Engineering and Ontology

Development (KEOD), pages 322–327, Paris, France.

Akama, K. and Nantajeewarawat, E. (2013). Unfolding-

based simpliﬁcation of query-answering problems in

an extended clause space. International Journal

of Innovative Computing, Information and Control

9:3515–3526.

Akama, K. and Nantajeewarawat, E. (2014). Equivalent

transformation in an extended space for solving query-

answering problems. In Proc. 6th Asian Confer-

ence on Intelligent Information and Database Sys-

tems, pages 232–241, Bangkok, Thailand.

Akama, K. and Nantajeewarawat, E. (2015). Function-

variable elimination and its limitations. In Proc. 7th

International Joint Conference on Knowledge Discov-

ery, Knowledge Engineering and Knowledge Manage-

ment, volume 2, pages 212–222, Lisbon, Portugal.

Akama, K. and Nantajeewarawat, E. (2016). Model-

intersection problems with existentially quantiﬁed

function variables: Formalization and a solution

schema. In Proc. 8th International Joint Confer-

ence on Knowledge Discovery, Knowledge Engineer-

ing and Knowledge Management, volume 2, pages

52–63, Porto, Portugal.

Akama, K. and Nantajeewarawat, E. (2018). Solving query-

answering problems with constraints for function vari-

ables. Springer International Publishing AG, part of

Springer Nature 2018, N. T. Nguyen et al. (Eds.): ACI-

IDS 2018, LNAI 10751, pages 36–47.

Akama, K., Nantajeewarawat, E., and Akama, T. (2018a).

Computation control by prioritized et rules. In

Proc. 10th International Joint Conference on Knowl-

edge Discovery, Knowledge Engineering and Knowl-

edge Management (KEOD), volume 2, pages 84–95,

Seville, Spain.

Akama, K., Nantajeewarawat, E., and Akama, T. (2018b).

Side-change transformation. In Proc. 10th Inter-

national Joint Conference on Knowledge Discovery,

Knowledge Engineering and Knowledge Management

(KEOD), volume 2, pages 237–246, Seville, Spain.

Akama, K., Nantajeewarawat, E., and Akama, T. (2019).

Logical problem solving framework. Springer Inter-

national Publishing AG, part of Springer Nature 2019,

N. T. Nguyen et al. (Eds.): ACIIDS 2019, LNAI 11431,

pages 28–40.

Chang, C.-L. and Lee, R. C.-T. (1973). Academic Press.

Lloyd, J. W. (1987). Springer-Verlag, second edition.

Inventing ET Rules to Improve an MI Solver on KR-logic

281