Routing Algorithms in Connected Cars Context
Ioan Stan, Vasile Suciu and Rodica Potolea
Computer Science Department, Technical University of Cluj-Napoca, Romania
Keywords:
Connected Cars, Traffic Congestion, Routing Algorithm, Topology, Scenarios, Data Structure.
Abstract:
Most of the existing navigation solutions compute individual routes based on map topology and traffic data but,
without considering the route effect on the entire navigation ecosystem. Traffic data usage and sharing in the
context of connected cars is a key element for route planning. Such solutions require efficient implementation
and deployment in order to reduce any kind of risk. Following a smart driving methodology, we run different
route search algorithms on connected cars traffic scenarios in order to avoid traffic congestion and minimize
total driving time on the entire navigation ecosystem. The experiments in this work proved that connected cars
data usage and sharing reduce the total driving time of the navigation ecosystem and also that specific routing
algorithms are more suitable for specific connected cars scenarios in order to obtain relevant results.
1 INTRODUCTION AND
OBJECTIVES
The concept of Internet of Things (IoT) becomes
more and more a reality with the existing technolo-
gies and variety of connected gadgets. One do-
main of interest in the context of IoT is Intelli-
gent Transportation Systems. The authors in (Mar-
tinez et al., 2010) define the Intelligent Transporta-
tion System as a combination of infrastructure, com-
puting, telecommunications, wireless and transporta-
tion technologies. State of the art work on this do-
main is reviewed in (Figueiredo et al., 2001) and
(Papadimitratos et al., 2009). In terms of architec-
ture the work in (Miller, 2008) describes and analy-
ses a hierarchical architecture of the Intelligent Trans-
portation System also known as Vehicle-to-Vehicle-
to-Infrastructure (V2V2I). V2V2I architecture repre-
sents a complete solution for a safe and efficient In-
telligent Transportation System. Nowadays, just de-
veloped countries can offer reliable infrastructure for
Intelligent Transportation Systems. For less devel-
oped countries the Vehicle-to-Vehicle communication
can support and create an internet based infrastructure
where each vehicle shares information as a global ser-
vice and each vehicle can use the service to obtain
necessary data.
An Intelligent Transportation System can benefit
from connected cars data (position) usage and shar-
ing. Efficient communication and data sharing for a
Navigation System can improve different kind of ser-
vices (Martinez et al., 2010). For example, emergency
service can be one service that can benefit from this.
The Navigation System is a ket component of the In-
telligent Transportation System. Moreover, each nav-
igation system can use different route planning algo-
rithms and data structures to represent traffic informa-
tion in order to efficiently compute routes (Sanders
and Schultes, 2007).
The work in (Stan et al., 2018a) analyzes and clas-
sifies navigation system challenges in the context of
connected cars and then, proposes a smart driving
methodology for connected cars.
Several of the existing navigation systems lack the
usage and data sharing between cars. In the context
of connected cars these drawbacks doesn’t exist any-
more (e.g. in (Stan et al., 2018b) and (Stan et al.,
2018a) the authors proved that connected cars data
usage and sharing can be used to avoid traffic con-
gestion).
Although there are several works regarding con-
nected cars navigation systems and traffic avoidance,
to the best of our knowledge there is no work that
compare different connected cars traffic scenarios
considering different topologies for different routing
algorithms and different number of simulated cars.
With such traffic scenarios comparison would be pos-
sible to wider analyze and argue the benefit of con-
nected cars data usage and sharing based on the run-
ning context. Several risks for implementing and de-
ploying real traffic solutions can be avoided by inte-
grating applying such an approach on traffic simula-
290
Stan, I., Suciu, V. and Potolea, R.
Routing Algorithms in Connected Cars Context.
DOI: 10.5220/0008167302900297
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 290-297
ISBN: 978-989-758-382-7
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tion scenarios. In (RAC, 2019) is described a case that
costs the investors a lot of money because of lacking
systematic simulation.
Following the methodology proposed in (Stan
et al., 2018a) the objective of our work is to simu-
late different traffic scenarios in the connected cars
context and apply route search algorithms (Bidirec-
tional Search Routing Algorithm, Forward Oriented
Search Routing Algorithm, Dijkstra Search Routing
Algorithm) in order to avoid traffic congestion and
minimize total driving of the entire navigation ecosys-
tem.
The next section presents different route search al-
gorithms used to generate routes in several connected
cars traffic scenarios representing different urban ar-
eas topologies. The section also contains the descrip-
tion of the parameters used by the algorithms and
presents the penalization model used to simulate traf-
fic scenarios with congestion. In the third section are
discussed the measurements and results for the cho-
sen scenarios correlated with urban areas topologies
and number of simulated connected cars. The fourth
section discuss the related work in comparison with
ours. In the last section we conclude the work and
present future ideas.
2 CONNECTED CARS ROUTE
PLANNING
The route planning efficiency depends on the algo-
rithms, context parameters and calibration. There are
several routing algorithms that can run on different
contexts.
In this section we employed several route search
algorithms, their parameters and our calibration ap-
proach proposal. All of the below described route
search algorithms follow the main flows of other two
algorithms.
The first flow is used by several of the existing
navigation systems and tries to compute routes based
on predicted traffic for each individual car without
considering the influence of each computed route on
the entire navigation ecosystem. The algorithm name
is Basic Routing Algorithm and was introduced and
described in (Stan et al., 2018b).
The second flow is related to connected cars data
usage and sharing and, besides the first flow, it con-
siders all real time positions of all navigating cars.
The algorithm for this flow is named Connected
Cars Routing Algorithm and was introduced and
presented by (Stan et al., 2018b). In the Connected
Cars Routing Algorithm when a route is computed
it takes into consideration the presence of the active
navigating cars on the roads in order to avoid traffic
congestion by efficiently choosing alternative routes
if necessary.
2.1 Route Search Algorithms
Bidirectional Search Routing Algorithm is One of
the most used search routing algorithm based on A*.
(Cormen et al., 2009). The flow of the algorithm
searches a forward and a backward graph alternatively
(forward and backward cost queues). The forward
search strategy begins with the start point of the route
and the backward search strategy begins with the des-
tination point of the route. In this way two graphs are
created in parallel. We name them forward and back-
ward search graph. This strategy stops when the meet-
ing requirements of the forward search and backward
search graphs are accomplished (usually a minimal
set of edges in the two graphs are connected through
a node). The algorithm objective is to produce a set of
routes that have minimal cost, based on a cost model
(e.g. fastest routes).
The flow of the Bidirectional Search Routing Al-
gorithm is show in Algorithm 1.
Algorithm 1: Bidirectional Search Routing Algorithm.
Data: start, destination, map, connected car s data
Result: R(start, destination)
.initialize forward graph cost queue
init(forwardQueue, start)
.initialize backward graph cost queue
backwardQueue.push(destination)
while forward and backward search unmet do
forwardHead ← forwardQueue.head()
backwardHead ← backwardQueue.head()
if forwardHead ¡ backwardHead then
segmentID ← forwardQueue.pop()
end
else
segmentID ← backward.pop()
end
processSegment(segmentID)
end
Forward Oriented Search Routing Algorithm is
another approach for route search based on A* too.
The flow of this algorithm uses also two search
graphs: forward and backward. The difference
between this algorithm and the Bidirectional Search
Routing Algorithm is the fact that the number of
steps run on the backward graph are fixed (e.g. 10).
Routing Algorithms in Connected Cars Context
291

Algorithm 2: Forward Oriented Search Routing Algorithm.
Data: start, destination, map, connected car s data
Result: R(start, destination)
. initialize forward graph cost queue
init(forwardQueue, destination)
. initialize backward graph cost queue
init(backwardQueue, destination)
backwardSteps ← 10
while forward search unmet all backward processed
segments do
forwardHead ← forwardQueue.head()
backwardHead ← backwardQueue.head()
if backwardSteps == 0 OR
forwardHead ¡ backwardHead then
segmentID ← forwardQueue.pop()
end
else
segmentID ← backward.pop()
backwardSteps ← backwardSteps - 1
end
processSegment(segmentID)
end
The flow of this algorithm is presented in Algorithm
2.
To test a non-heuristic approach for route finding
we deployed Dijkstra Search Routing Algorithm.
In the Measurements and Results section we dis-
cussed and analyzed our experimented scenario that
is based on it.
2.2 Process Segment
Route Search Algorithms use several parameters dur-
ing route calculation. In table 1 are presented the
main parameters corresponding to routing algorithms
in connected cars ecosystem. A complete description
of such parameters is presented in (Stan et al., 2018a).
Figure 1: Speed Penalization in Traffic.
Algorithm 3: Process Segment processSegment(segment).
Data: segment
Result: updatedcost
foreach segmentIDinN(segment) do
if [not visited(segmentID) then
C
map
← C
map
(segmentID)
t ← predictedtimeo f cararrivalonsegment
if θ < ρ(segmentID, t) then
. try force to navigate another segment
C
cars
← C
max
end
else
C
cars
← C
cars
(ρ(segmentID,t))
end
costValue ← C
map
· C
cars
updateCost(segmentID, costValue)
end
end
All the above presented algorithms have one com-
mon part used to process a segment choosed as part
of a route. The flow of the process segment algorithm
is presented in Algorithm 3. For all the neighbours of
the segment to be processed this algorithm uses the
predicted real time traffic to compute the cost. If the
computed cost of a segment is higher than a threshold
θ the algorithm tries to suggest alternative segments
to avoid navigation on that segment in order to avoid
congestion in future.
To compute cost value of a segment it is neces-
sary to use the predicted speed of that segment which
depends on the speed limit on that segment. In this re-
gards we proposed a speed penalization model shown
in figure 1 for both Basic Routing Algorithm and Con-
nected Cars Routing Algorithm. We can observe that
Connected Cars Routing Algorithm penalize the pre-
dicted speed earlier compared to Basic Routing Algo-
rithm. This is because Connected Cars Routing Al-
gorithms tries to predict and avoid traffic congestion
happening as soon as possible.
3 ROUTING ALGORITHMS
EXPERIMENTS: SETUP,
MEASUREMENTS AND
RESULTS
The road geometry variety of the urban areas im-
pose topology classification in order to systematically
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
292

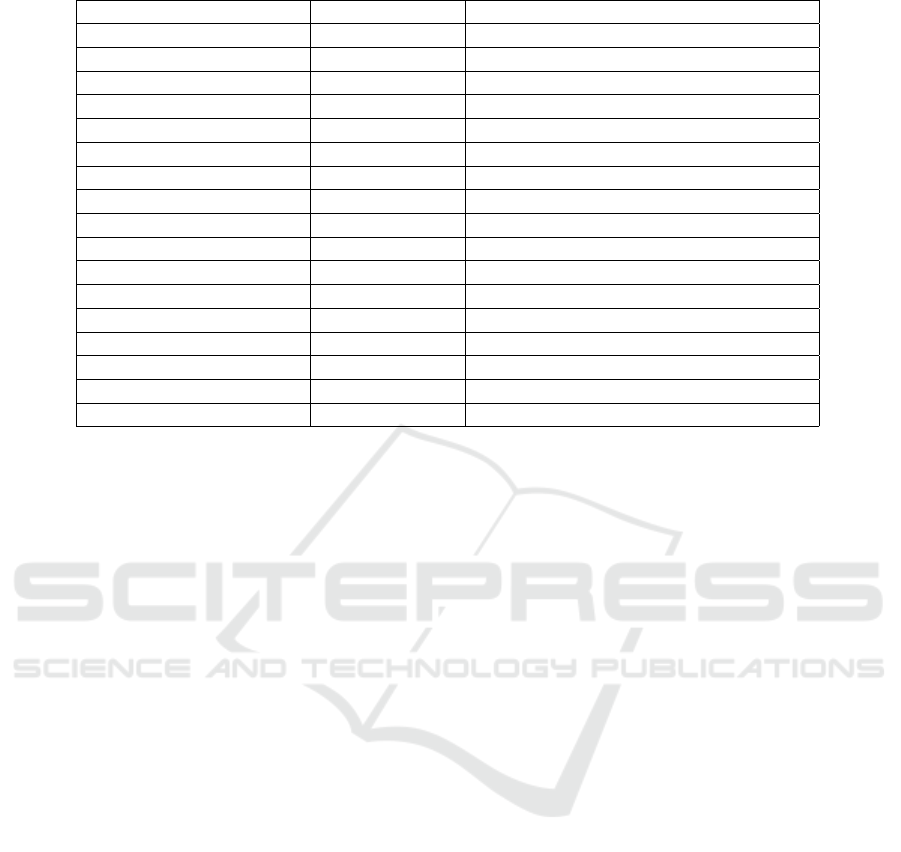
Table 1: Main Parameters used by Routing Search Algorithms.
Name Representation Description
p
s
GPS Coordinate Route starting point
p
d
GPS Coordinate Route destination point
segmentID ID Number ID of a segment from the map
N(segmentID) Set of segments Neighbours of a segment
visited(segmentID) Boolean Verifies if a segment was visited or not
C
map
(segmentID) Number Computed cost value of a segment
R(p
s
, p
d
) List of segments Fasted found route between p
s
and p
d
C
max
Number Maximum cost value
lanesCount(segmentID) Number Lanes on a segment
[t
s
, t
e
] Time Interval Predicted navigation period on a segment
carsCount(segmentID, t) Number Cars count on a segment at a time t
C
cars
(ρ(segmentID, t)) Number Cost factor
θ Number Traffic congestion threshold
length(segmentID) Meters Length of segment
carsCount(segmentID) Number Number of navigating cars on a segment
carLength Meters Average length of cars
ρ(segmentID, t) Cars/Segment Predicted car density on a segment
test and cover several traffic scenarios in urban areas.
In such an approach the segment is an atomic element
of the topology. Considering the urban areas topol-
ogy classification in (Stan et al., 2018a), our main
objective is to test and apply different route search
algorithms on several connected cars simulated traf-
fic scenarios in urban areas of different road topolo-
gies. All the tested algorithms are following the flow
of both Basic Routing Algorithm and Connected Cars
Routing Algorithm. The traffic simulation run on two
different urban areas representing different topologies
on real map data. This gains the benefit of being able
to do observations from several perspectives and to
get conclusions from a wider experience.
3.1 Infrastructure and Topology based
Scenarios
The proposed approach in this paper is tested and val-
idated by using OSMAnd open source navigation ap-
plication. OSMAnd is implemented mainly in Java
and can run on Android, iOS and desktop platforms
(Shcherb, 2019).
The Routing Algorithm that OSMAnd is using is
Bidirectional A*. We changed the implementation to
be able to use all the above presented routing algo-
rithms (Bidirectional Routing Search Algorithm, For-
ward Oriented Routing Search Algorithm, Dijkstra
Search Routing Algorithm). Also, we changed the
implementation to be able to consider traffic data dur-
ing route computation.
Based on the topology classification wedefined in
(Stan et al., 2018a) we planned to fulfill the following
topologies:
• Grid Topology)
• Mixed Topology
• Historical Topology
The test cases that covers the above mentioned
topologies were run on the following cities:
• New York
• Cluj-Napoca
• Vienna
In our test cases we simulated 10.000 and 20.000
cars. We changed from 10.000 to 20.000 in order
to simulate traffic congestion for grid topology and
also to observe the congestion evolution on historical
topology.
For New York we once simulated randomly
20.000 cars and generated their routes using Bidirec-
tional Search Routing Algorithm and Dijkstra Search
Routing Algorithm. The routes were generated by
having starting and destination points in Brooklyn
borough from New York.
In Cluj-Napoca we once simulated randomly
20.000 cars and computed their routes using Bidirec-
tional Search Routing Algorithm. Also, we simulated
randomly 10.000 cars and generated their routes us-
ing Forward Oriented Search Routing Algorithm. The
routes were generated inside the city by having start
and destination points in the 6 main districts of Cluj-
Napoca.
On the simulated scenarios we applied the routing
search algorithms that follows the flows of both Ba-
sic Routing Algorithm and Connected Cars Routing
Algorithm.
Routing Algorithms in Connected Cars Context
293

The generated routes for all topologies have
lengths between 4 kilometres to 20 kilometers.
The measurement of the route search algorithms
efficiency applied on each of the above mentioned
topologies is based on the following metrics that cov-
ers several aspects of a navigation ecosystem:
• Histogram for Lengths of the Navigated Seg-
ments - comparison based on flows of Basic Rout-
ing Algorithm and Connected Cars Routing Algo-
rithm
• Average Estimated Time of Arrival (ETA) evo-
lution during navigation - comparison based on
flows of Basic Routing Algorithm and Connected
Cars Routing Algorithm
• Average Speed of a Car - comparison based on
flows of Basic Routing Algorithm and Connected
Cars Routing Algorithm
Vienna testing proved that the complex topology
of the roads requires at least 3 times more comput-
ing time than the other two proposed topologies. Be-
cause of this, our tests regarding Vienna is in progress
because we have to better calibrate the environment
in order to provide valuable results in an acceptable
amount of time.
3.2 Grid Topology Evaluation
One of our experiment was to test, measure and val-
idate different routing algorithms that run on a real
map data grid topology. This experiment was mea-
sured using the above described metrics.
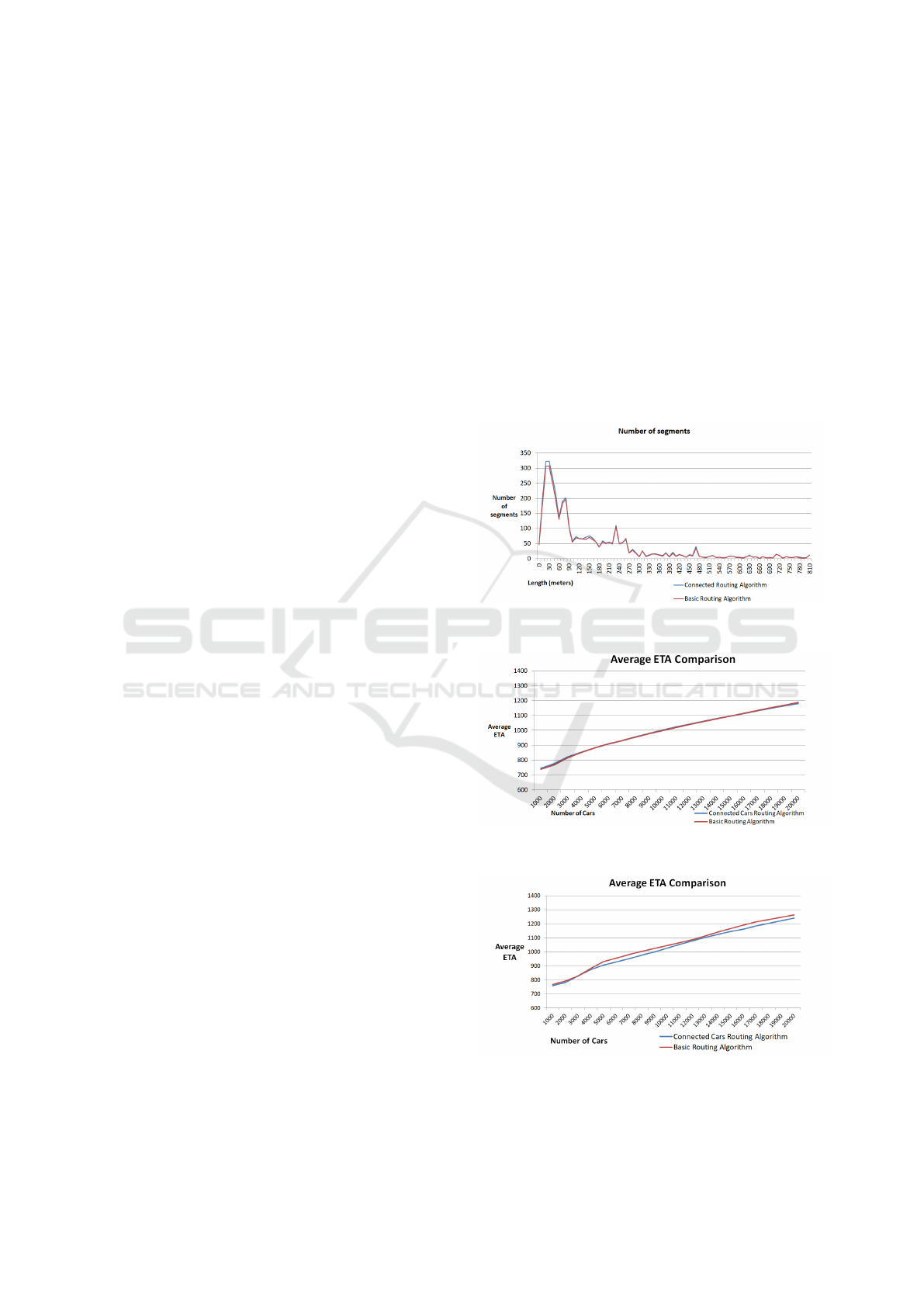
In figure 2 we see that the number of navigated
segments in case of Connected Cars Routing Algo-
rithm is higher than the number of navigated segments
in case of Basic Routing Algorithm. This proves that
Connected Cars Routing Algorithm uses more seg-
ments in order to provide route alternatives for traffic
congestion avoidance.
Also, the total number of navigated segments in
case of Connected Cars Routing Algorithm is greater
(3965 navigated segments) than the total number of
navigated segments in case of Basic Routing Algo-
rithm (3759 navigated segments).
Because the segments’ count with length greater
than 800 meters is insignificant, the chart from figure
2 contains only the segments that have length up to
800 meters.
Figure 3 represents the average ETA evolution
during cars navigation based on Bidirectional Search
Routing Algorithm for 20.000 navigating cars simu-
lation in New York. The lines representing average
ETA for Connected Cars Routing Algorithm and Ba-
sic Routing Algorithm almost overlap. Connected
Cars Routing Algorithm improves the average ETA
with 8 seconds for each car. The total time improve-
ment in this case is more than 44 hours of driving for
the entire navigation ecosystem.
In this scenario the Connected Cars Routing Algo-
rithm obtains a speed of almost 37 km/h while Basic
Routing Algorithm obtains a speed of 35 km/h.
The testing of New York traffic simulation pro-
vides better results for the approach based on Dijk-
stra Search Routing Algorithm as is shown in figure
4. In this case were simulated 20.000 navigating cars.
Starting from 5000 navigating cars the average ETA
in case of Connected Cars Routing Algorithm is vis-
ible smaller than the average ETA in case of Basic
Routing Algorithm.
Figure 2: Navigated Segments’ Lengths Histogram for New
York.
Figure 3: Bidirectional Search Routing Algorithm Average
ETA Evolution on New York Traffic Simulation.
Figure 4: Dijkstra Search Routing Algorithm Average ETA
Evolution on New York Traffic Simulation.
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
294

Comparing with Basic Routing Algorithm, the
Connected Cars Routing Algorithm improves the av-
erage ETA with 24 seconds for each car, meaning
a total driving time improvement of the navigation
ecosystem with more than 133 hours.
In this case the average speed obtained by Con-
nected Cars Routing Algorithm is 33 km/h and 31
km/h for Basic Routing Algorithm.
3.3 Historical Topology Evaluation
Many urban areas with historical topology encounter
traffic flow challenges. Therefore, an experiment we
did is trying to test, measure and validate different
routing algorithms that run on a real map data his-
torical topology. The measurements in this case are
based on the above described metrics.
The histogram in figure 5 shows that the num-
ber of navigated segments in case of Connected Cars
Routing Algorithm is higher than the number of navi-
gated segments in case of Basic Routing Algorithm.
Like for grid topology, this proves that Connected
Cars Routing Algorithm tries more segments in or-
der to provide route alternatives for traffic congestion
avoidance.
Also, number of navigated segments in case of
Connected Cars Routing Algorithm is greater (2461
navigated segments) than the total number of navi-
gated segments in case of Basic Routing Algorithm
(2381 navigated segments).
As for grid topology, because the segments’ count
with length greater than 800 meters is insignificant,
the chart from figure 2 contains only the segments that
have length up to 800 meters.
The graph in figure 3 represents the average ETA
evolution during cars navigation based on Bidirec-
tional Search Routing Algorithm for 20.000 navigat-
ing cars simulation in Cluj-Napoca. In this case, the
chart shows that only after having about 8000 navi-
gating cars that produce traffic, the Connected Cars
Routing Algorithm improves the average ETA com-
paring with Basic Routing Algorithm. The average
ETA improvement is 2 seconds for each car. The total
time improvement in this case is more than 22 hours
of driving for the entire navigation ecosystem.
In this case the Connected Cars Routing Algo-
rithm obtains a speed of almost 32 km/h while Basic
Routing Algorithm obtains a speed of 31 km/h.
The last test we considered for Cluj-Napoca was
the simulation of 10.000 navigation cars and is based
on the Forward Oriented Search Routing Algorithm.
The outcome of this test is shown in figure 7 and is
the ideal scenarios that proves the fact that Connected
Cars Routing Algorithm improves the average ETA
when the traffic congestion appears. Starting with
about 5000 navigating cars we can see on the chart
that the Connected Cars Routing Algorithm improves
the average ETA in comparison with Basic Routing
Algorithm. The average ETA improvement is 23 sec-
onds for each car and the total time improvement in
this case is more than 64 hours driving.
The average speed of a car in case of Connected
Cars Routing Algorithm is about 39 km/h while for
Basic Routing Algorithm is about 37 km/h.
From the histograms perspective we can say that
in both tested topologies (grid and historical) the short
segments are dominant over long segments. This can
be a cause of lowering cars speed.
Figure 5: Navigated Segments’ Lengths Histogram for
Cluj-Napoca.
Figure 6: Bidirectional Search Routing Algorithm Average
ETA Evolution on Cluj-Napoca Traffic Simulation.
Figure 7: Forward Oriented Search Routing Algorithm Av-
erage ETA Evolution on Cluj-Napoca Traffic Simulation.
Routing Algorithms in Connected Cars Context
295

The overall traffic time is improved by Connected
Cars Routing Algorithm comparing with Basic Rout-
ing Algorithm for all testing scenarios.
The higher improvements happened when Dijk-
stra Search Routing Algorithm and Forward Oriented
Search Routing Algorithm were used. The Forward
Oriented Search Routing Algorithm clearly confirmed
the expected behavior of the Connected Cars Routing
Algorithm in the context of connected cars.
4 RELATED WORK
The objective of improving the navigation system was
approached by many and different contextual solu-
tions were found based on several technologies. This
resulted in different strategies that combines route
planning algorithms with traffic and map data repre-
sentation. One approach that tries to improve traf-
fic flow through connected cars data is found in (Ya-
mashita et al., 2005). Also, the work in (Wang et al.,
2015) shows that by having a considerable amount
of traffic data, specific patterns can be observed and
used to predict traffic congestion. However, in case of
not having any traffic data from traffic data providers,
there are also some methods that can be used to gener-
ate and mimic the movement of cars inside a defined
area (such an approach is described in (Capela et al.,
2013)).
In both (Yamashita et al., 2005) and (Wang et al.,
2015), the common and key objective is to predict and
reduce the traffic congestion in different scenarios and
to create different reports that would underline which
are the problematic zones.
The experiments in (Yamashita et al., 2005) were
made using 25.000 simulated vehicles that are posi-
tioned on a map that simulates Tokyo city. The ap-
proach in (Wang et al., 2015) uses real map data and
a set of 12.000 real cars to find traffic patterns in Bei-
jing.
The work in (Stan et al., 2018b) uses real map
data (Open Street Map) and proposes a solution for
traffic congestion avoidance based on Segment Tree
data structure representation of the connected cars
data (GPS positions). This solution simulates 10.000
connected cars in the city of Cluj-Napoca.
In (Stan et al., 2018a) is described a methodology
proposal for smart driving in connected cars context.
Following their approach we applied route search al-
gorithms on several simulated traffic scenarios in dif-
ferent connected cars contexts in order to avoid traffic
congestion and minimize the total driving time of the
entire navigation ecosystem.
Our work simulates different numbers of con-
nected cars (10.000 and 20.0000 connected cars) in
different urban areas, representing grid and histori-
cal topologies (Brooklyn Borough in New York and
Cluj-Napoca), and applies several routing search al-
gorithms (Bidirectional Search Routing Algorithm,
Forward Oriented Search Routing Algorithm, Dijk-
stra Search Routing Algorithm) in order to obtain
routes that optimally improves the traffic flow. We run
our algorithms by using 2 different approaches: the
approach that is based on connected cars data usage
and sharing (Connected Cars Routing Algorithm) and
the approach that is based only on traffic data for each
individual route planning (Basic Routing Algorithm).
In our experiments we showed the segments’ length
histogram, measured average speed of a car and we
introduced a new metric that measures Average Esti-
mated Time of Arrival (ETA) evolution. Comparing
with other works, in this paper we proved by experi-
ments that a smart driving methodology can be used
to match specific route search algorithms with spe-
cific connected cars simulated scenarios on real map
data in order to improve traffic flow and reduce total
driving time of the entire navigation ecosystem.
5 CONCLUSIONS AND FUTURE
WORK
In this work we applied route search algorithms on
connected cars traffic scenarios in order to avoid traf-
fic congestion and improve the global driving time of
the entire navigation ecosystem.
We described three different route planning al-
gorithms (Bidirectional Search Routing Algorithm,
Forward Oriented Search Routing Algorithm, Dijk-
stra Search Routing Algorithm), their main param-
eters model and the speed penalization methods for
both Connected Cars Routing Algorithm and Basic
Routing Algorithm. In the Connected Cars Routing
Algorithm connected cars data (position) is used and
shared between cars. On the other hand, in the Basic
Routing Algorithm traffic data is used for individual
route planning.
Based on OSMAnd application and Open Street
Map data we applied the above mentioned route
search algorithms on different scenarios that simu-
lates connected cars in two urban areas (Brooklyn
from New York and Cluj-Napoca). The measure-
ments were done based on three metrics: Histogram
for Lengths of the Navigated Segments, Average Es-
timated Time of Arrival (ETA), Average Speed of a
Car. The results proved that specific route planning
algorithms are more suitable for specific connected
cars traffic scenarios in order to avoid traffic conges-
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
296

tion and improve the global driving time of the en-
tire navigation ecosystem. The ideal experiment in
terms of results was obtained by applying Forward
Oriented Search Routing Algorithm in the context of
simulated 10.000 connected cars in Cluj-Napoca (to-
tal 64 hours of driving improvement). Also, based
on the results we can say that comparing with indi-
vidual route planning, the connected cars data usage
and sharing during route planning improves always
the driving time of the entire navigation ecosystem
that encounters traffic congestion.
In the last part we compared our work with ex-
isting approaches (that uses both synthetic and real
map data) and we concluded that besides improving
the global driving time through connected cars data
usage and simulation it is suitable to apply specific
routing algorithms on specific connected cars scenar-
ios in order to obtain better traffic flow in urban areas.
For future work one aspect that we want to im-
prove is the time of connected cars simulation. This
can be approached by using more computing power
or by improving the CPU time of the route compu-
tation algorithms. The route computation algorithm
performance depends on two aspects: route search al-
gorithm and data structure that is used to represent
and query connected cars traffic data. In regards to
this will be valuable to analyze and test several data
structures for connected cars traffic data.
In terms of testing scenarios, after finishing Vi-
enna testing, we would like to add more scenarios and
also to increase the size of the tests (number of con-
nected cars and size of the areas to be tested). In the
next future will be valuable to test Forward Oriented
Search Routing Algorithm applied on New York sce-
nario with 20.000 simulated cars and Dijkstra Search
Routing Algorithm applied on Cluj-Napoca context
with 20.000 simulated cars.
Last, but not least, we would like also to research
a machine learning approach for route algorithms cal-
ibration and matching with connected cars scenarios
representing several topologies.
REFERENCES
Capela, J., Henriques Abreu, P., Castro Silva, D., Fernan-
des, G., Machado, P., and Leit
˜
ao, A. (2013). Preparing
data for urban traffic simulation using sumo.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,
C. (2009). Introduction to Algorithms, Third Edition.
The MIT Press, 3rd edition.
Figueiredo, L., Jesus, I., Machado, J. A. T., Ferreira, J. R.,
and de Carvalho, J. L. M. (2001). Towards the devel-
opment of intelligent transportation systems. In ITSC
2001. 2001 IEEE Intelligent Transportation Systems.
Proceedings (Cat. No.01TH8585), pages 1206–1211.
Martinez, F., Toh, C.-K., Cano, J.-C., Calafate, C., and
Manzoni, P. (2010). Emergency services in future
intelligent transportation systems based on vehicular
communication networks. 2:6–20.
Miller, J. (2008). Vehicle-to-vehicle-to-infrastructure
(v2v2i) intelligent transportation system architecture.
2008 IEEE Intelligent Vehicles Symposium, pages
715–720.
Papadimitratos, P., Fortelle, A. D. L., Evenssen, K., Brig-
nolo, R., and Cosenza, S. (2009). Vehicular communi-
cation systems: Enabling technologies, applications,
and future outlook on intelligent transportation. IEEE
Communications Magazine, 47(11):84–95.
RAC (2019). Report: £300m traffic jam-busting scheme
made some journeys longer. Accessed: 2019-05-13.
Sanders, P. and Schultes, D. (2007). Engineering fast route
planning algorithms. In Demetrescu, C., editor, Ex-
perimental Algorithms, pages 23–36, Berlin, Heidel-
berg. Springer Berlin Heidelberg.
Shcherb, V. (2019). Osmand. Accessed: 2019-05-14.
Stan, I., Toderici, D., and Potolea, R. (2018a). Segment
trees based traffic congestion avoidance in connected
cars context. 2018 IEEE 14th International Con-
ference on Intelligent Computer Communication and
Processing (ICCP), pages 137–143.
Stan, I., Toderici, D., and Potolea, R. (2018b). Segment
trees based traffic congestion avoidance in connected
cars context. 2018 IEEE 14th International Con-
ference on Intelligent Computer Communication and
Processing (ICCP), pages 137–143.
Wang, J., Mao, Y., Li, J., Xiong, Z., and Wang, W.-X.
(2015). Predictability of road traffic and congestion
in urban areas. PLOS ONE, 10(4):1–12.
Yamashita, T., Izumi, K., Kurumatani, K., and Nakashima,
H. (2005). Smooth traffic flow with a cooperative car
navigation system. In Proceedings of the International
Conference on Autonomous Agents, pages 478–485.
Routing Algorithms in Connected Cars Context
297