Fuzzy–rough Fuzzification in General FL Classifiers
Janusz T. Starczewski
a
, Robert K. Nowicki
b
and Katarzyna Nieszporek
Institute of Computational Intelligence, Czestochowa University of Technology, Czestochowa, Poland
Keywords:
General Type-2 Fuzzy Classifier, Fuzzy–rough Fuzzification, Triangular Fuzzification.
Abstract:
In this paper, a three-dimensional version of fuzzy-rough fuzzification is examined for classification tasks.
Similar approach based on interval fuzzy-rough fuzzification has been demonstrated to classify with three
decision labels of confidence, one of which were uncertain. The method proposed here relies on the use of
fuzzification of inputs with a triangular membership function describing the nature of imprecision in data. As a
result, we implement in fuzzy classifiers three dimensional membership functions using the calculus of general
type-2 fuzzy sets. The approach is justified when more confidence labels are expected from the decision
system, especially when the classifier is embedded in a recurrent hierarchical decision system working on
easily available economic, extended, and advanced expensive real data.
1 INTRODUCTION
An extended concept of rough sets applied to fuzzy
sets has been introduced in the form of an ap-
proximation of fuzzy sets by so-called fuzzy gran-
ules (Nakamura, 1988). In contrast to rough-fuzzy
sets, fuzzy-rough sets is based on extended equiv-
alence relations that only correspond to Zadeh’s
similarity relations, i.e. a fuzzy relation R on X
should be reflexive µ
R
(x,x) = 1 ∀x ∈ X, symmetric
µ
R
(x,y) = µ
R
(y,x) ∀x,y ∈X, and transitive µ
R
(x,z) ≥
sup
y
min(µ
R
(x,y),µ
R
(y,z)) ∀x,y,z ∈ X. This rela-
tion, as a typical fuzzy set, can be decomposed into
α-cuts in order to construct the fuzzy-rough set as an
α-composition of upper and lower rough approxima-
tions of A
µ
R
α
(A)
(x) = sup
{
µ
A
(y)|µ
R
(x,y) ≥ α
}
, (1)
µ
R
α
(A)
(x) = inf
{
µ
A
(y)|µ
R
(x,y) ≥ α
}
. (2)
The fuzzy-rough set relies on a single fuzzy relation
R. A family of fuzzy equivalence relations R
i
estab-
lishes a fuzzy partition on X by fuzzy sets F
i
which
may be complete in order to cover the whole domain,
inf
x
max
i
µ
F
i
(x) > 0. Therefore, a fuzzy-rough set A
is a family of lower and upper rough approximations
of A calculated for each i-th partition set, i.e.,
Φ
i,α
(A) = sup
{
µ
A
(x)|x ∈ [F
i
]
α
}
, (3)
Φ
i,α
(A) = inf
{
µ
A
(x)|x ∈ [F
i
]
α
}
. (4)
a
https://orcid.org/0000-0003-4694-7868
b
https://orcid.org/0000-0003-2865-2863
Exemplary fuzzy-rough sets under triangular fuzzy
partition settings are illustrated in Figures 1.
Figure 1: Construction of fuzzy-rough approximations us-
ing a triangular fuzzy set: (a,c,e) A — fuzzy set (solid
lines), F
i
— triangular fuzzy partition sets (dashed lines),
(b,d,f)

Φ
i,α
(A),Φ
i,α
(A)

— α-cuts of the fuzzy-rough set,
i = 1, 2,3.
The rough set theory is helpful when there are not
enough attributes to fully describe an object, i.e., we
have limited ability to classify particular objects since
some other objects are indiscernible to the considered
one. Considering fuzziness as a weaker form of in-
discernibility, we are able to process uncertainty for
ill-defined attributes such as measurement impreci-
sion, vague estimations, three-point approximations,
etc. The problem focuses on the use of an apriori
Starczewski, J., Nowicki, R. and Nieszporek, K.
Fuzzy–rough Fuzzification in General FL Classifiers.
DOI: 10.5220/0008168103350342
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 335-342
ISBN: 978-989-758-384-1
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
335

knowledge about the imprecision of input data in or-
der to determine an adequate shape of fuzzification.
However, usually knowledge about the nature of such
imprecisions is limited, then a three-point approxima-
tion can be considered as a satisfactory complexity
of estimation. Triangular probability distributions are
known to be successfully employed in financial anal-
ysis, management and business decision making. Tri-
angular approximations become natural, when only
its smallest, largest and the most likely values are
known in the context of expected data inaccuracies.
Such formulation lead the reasoning process to oper-
ate on three-dimensional membership functions. In
(Starczewski, 2010), we have noticed that the compo-
sition of α-cuts
S
α∈(0,1]

Φ
i,α
(A), Φ
i,α
(A)

formally
represents a fuzzy grade of type-2. Systems con-
structed on linear type-2 fuzzy sets are a point of in-
terest (Han et al., 2016; Najariyan et al., 2017).
The type-2 fuzzy set is understood as a set
˜
A
being a vague collection of elements characterized
by membership function µ
˜
A
: X → F ([0,1]), where
F ([0,1]) is a set of all classical fuzzy sets in the
unit interval [0,1]. Each x ∈ X is associated with a
secondary membership function f
x
∈ F ([0,1]) i.e. a
mapping f
x
: [0,1] → [0,1]. The fuzzy membership
grade µ
˜
A
(x) is often refered as a fuzzy truth value,
since its domain is the truth interval [0,1]. Regard-
ing bounded secondary membership functions, the
upper and lower bounds of f
x
> 0 with respect to X
will be referred as upper an lower membership func-
tions, respectively. Considering only secondary mem-
bership functions as fuzzy truth numbers, the func-
tion of x returning unique argument values of sec-
ondary functions for which f
x
= 1 will be called a
principal membership function. With this formula-
tion, we are able to construct a fuzzy-rough classifier
which outputs a four-valued confidence label associ-
ated with the category label, extending our previous
works (Starczewski, 2013; Nowicki and Starczewski,
2017; Nowicki, 2019).
2 TRIANGULAR
FUZZIFICATION USING
FUZZY-ROUGH
APPROXIMATION
Using the definition of fuzzy-rough sets directly,
fuzzy partitions F
i
reflect the uncertainty of input data.
This forms an automatic approach to perform non-
singleton fuzzification. Namely, an input vector x
should be mapped to the fuzzy-rough partition, i.e.
a membership function, in this case, triangular with a
peak value at x
0
.
In order to introduce a common notation, we may
consider non-singleton fuzzification as a generalized
membership function µ
F
(x,x
0
) = µ
F
i
(x) with implicit
parameters of left and right deviations of triangles in
our case. In the construction of triangular fuzzy-rough
sets we may use our analytical results (Starczewski,
2010; Starczewski, 2013) expressing the secondary
membership function of the antecedent A
k,n
as:
f
n

u,x
0
n

= max

µ
F
n

µ
−1
A
k,n
(u), x
0
n

,µ
F
n

µ
−1
A
k,n
(u), x
0
n

,
(5)
where k indicates a rule and n is an index for inputs.
In cases of symmetric and monotonic on slopes con-
tinuous membership functions, the secondary mem-
bership function can be expressed by cases, i.e.
f
n

u,x
0
n

=



µ
F
n

µ
−1
A
k,n
(u), x
0
n

if m
k,n
≤ x
0
n
µ
F
n

µ
−1
A
k,n
(u), x
0
n

otherwise
. (6)
2.1 Triangular Fuzzification of
Triangular MFs
In the case of triangular fuzzification, A
k,n
can be generally asymmetric, i.e. µ
A
k,n
(x
n
) =
.
x
n
−m
k,n
+δ
k,n
δ
k,n
,
m
k,n
−x
n
+γ
k,n
γ
k,n
.
, while F
n
are usually
assumed to be symmetric triangular fuzzy numbers
and µ
F
n
(x
n
) =
.
x
n
−x
0
n
+∆
n
∆
n
,
x
0
n
−x
n
+∆
n
∆
n
.
, respectively,
where δ
n
, γ
n
, ∆
k,n
denote spread values of triangular
membership functions and a boundary operator
is introduced as
/
z
/
= max(0,min (1, z)). Due to
piecewise linear shapes of both functions, the result
can be easily calculated as a composition of two
linear transformations. Therefore, the secondary
membership function of the fuzzy-valued fuzzy set
induced by the fuzzy-rough approximation can be
evaluated as follows:
f
k,n
(u) =
max


∆
n
−
|
δ
k,n
u + m
k,n
−x
0
n
−δ
k,n
|

,

∆
n
−
|
m
k,n
−x
0
n
+ γ
k,n
−γ
k,n
u
|


∆
n
.
(7)
Apparently, the obtained expression represents a
triangular function for applicable inputs x
0
n
∈
[m
k,n
−δ
k,n
,m
k,n
+ δ
k,n
]. Now we are able to return to
the primary domain, hence, the principal membership
function is described by
b
µ
A
k,n

x
0
n

= µ
A
k,n

x
0
n

, (8)
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
336

The upper membership function has a trivial ker-
nel [m
k,n
−∆
n
,m
k,n
+ ∆
n
] and is characterized by the
trapezoidal membership function alike
µ
A
k,n
(x
0
n
) =
,
x
0
n
−m
k,n
+∆
n
+δ
k,n
δ
k,n
,
m
k,n
+∆
n
−x
0
n
+γ
k,n
γ
k,n
,
, (9)
since f
k,n
(u,x
0
) = 0 for all u ∈ [0,1] whenever m
k,n
−
δ
k,n
≥ x
0
n
+ ∆
n
or m
k,n
+ γ
k,n
≤ x
0
n
−∆
n
. The lower
membership is a subnormal triangular function with
its support [m
k,n
−δ
k,n
+ ∆
n
,m
k,n
+ γ
k,n
−∆
n
] and its
peak value can be calculated as follows. Since we
search for bounds of u, i.e. limits for f
k,n
(u) > 0,
by omitting the boundary operator, we can calculate
f
k,n
(u) = 0 for the two slopes instead. Consequently,
we obtain
u
1
=
x
0
n
−m
k,n
−∆
n
+ δ
k,n
δ
k,n
, (10)
u
2
=
m
k,n
−x
0
n
−∆
n
+ γ
k,n
γ
k,n
(11)
Obviously, the lower membership function needs to
be aggregated in the following way:
µ
A
k,n
(x
0
n
) =

min(u
1
,u
2
)

. (12)
The center point of the triangle is calculated at inter-
scetion of slope lines, i.e.
c
k,n
−m
k,n
−∆
n
+ δ
k,n
δ
k,n
=
m
k,n
−c
k,n
−∆
n
+ γ
k,n
γ
k,n
c
k,n
= m
k,n
−
δ
k,n
−γ
k,n
δ
k,n
+ γ
k,n
∆
n
. (13)
and the corresponding peak value is equal to
h
k,n
=
c
k,n
−m
k,n
−∆
n
+ δ
k,n
δ
k,n
(14)
= 1 −
2∆
n
δ
k,n
+ γ
k,n
. (15)
The construction of secondary memberships func-
tions is demonstrated in Figure 2 for three exem-
plary x
0
values. To construct continuous type-2 fuzzi-
fied antecedent sets, we need to vary µ
F
(x,x
0
) in the
whole spectrum of x
0
values. Unfavorably, for x
0
n
/∈
[m
k,n
−δ
k,n
,m
k,n
+ δ
k,n
], the intersection between the
fuzzy partition set and the antecedent fuzzy set is not
sufficient, hence, secondary memberships the results
are no longer triangular. In the sequel, however, us-
ing axiomatic operations on type-2 fuzzy sets, we will
lose this non-triangularity, as we used triangular ap-
proximations for the clipped secondary membership
functions.
0 2 4 6 8 10
0
0.2
0.4
0.6
0.8
1
x
A, F
i
(a)
0
0.5
1
0
2
4
6
8
10
0
0.5
1
x
(b)
u
f
Figure 2: Construction of fuzzy-rough sets: a) A
k
—
antecedent membership function (solid line), µ
F
1
,µ
F
2
, µ
F
3
— three realizations of non-singleton premise membership
functions (dashed lines), b) f
x
0
(u) — corresponding sec-
ondary membership functions constituting f (u, x
0
).
2.2 Triangular Fuzzification of
Gaussians
The next case of triangular fuzzification involves an-
tecedents A
k,n
in the form of Gaussian fuzzy sets, i.e.
µ
A
k,n
(x
n
) = exp

−
1
2

x
n
−m
k,n
δ
k,n

2

while F
n
are trian-
gular µ
F
n
(x
n
) = min
.
x
n
−x
0
n
+∆
n
∆
n
,
x
0
n
−x
n
+∆
n
∆
n
.
, where
∆
n
and δ
k,n
denote spread values. As a result, the
secondary membership function of the type-2 fuzzy
set induced by the fuzzy-rough approximation can be
presented as follows:
f
k,n
(u,x
0
n
)
=








−
|
m
k,n
+δ
k,n
√
−2lnu−x
0
n
|
+∆
n
∆
n

if m
k,n
≤ x
0
n

−
|
m
k,n
−δ
k,n
√
−2lnu−x
0
n
|
+∆
n
∆
n

otherwise
. (16)
The obtained expression represents fragments of in-
verted Gaussian functions; however, for δ
k,n
 ∆
n
these fragments can be linearly approximated, hence,
the secondary membership function does not deviate
significantly from the triangular function.
With respect to the primary domain, the principal
membership function trivially is described by the non-
fuzzified antecedent fuzzy set
b
µ
A
k,n

x
0
n

= µ
A
k,n

x
0
n

.
The upper membership function is composed
of two Gaussians connected by a unity kernel
[m
k,n
−∆
n
,m
k,n
+ ∆
n
], i.e.
Fuzzy–rough Fuzzification in General FL Classifiers
337

µ
A
k,n
(x
0
n
) =















1 if x
0
n
∈ [m
k,n
−∆
n
,m
k,n
+ ∆
n
]
max




exp

−
1
2

x
n
−m
k,n
−∆
n
δ
k,n

2

,
exp

−
1
2

x
n
−m
k,n
+∆
n
δ
k,n

2





otherwise
.
(17)
The lower membership function is a subnormal piece-
wise Gaussian, i.e.
µ
A
k,n
(x
0
n
) = min




exp

−
1
2

x
n
−m
k,n
−∆
n
δ
k,n

2

,
exp

−
1
2

x
n
−m
k,n
+∆
n
δ
k,n

2





,
(18)
where the peak value at x
0
n
= m
k,n
is
h
k,n
= µ
A
k,n
(m
k,n
+∆
n
) = exp −
1
2

∆
n
δ
k,n

2
!
. (19)
Figure 3: Construction of fuzzy-rough sets: (a,b) µ
A
—
original Gaussian antecedent membership function (solid
lines), µ
F
i
— triangular fuzzy partitions (dashed lines);
(c,d)

Φ
i,α
(A),Φ
i,α
(A)

— α-cut representations of fuzzy-
rough sets according to the definition; (e,f) f — sec-
ondary membership functions of fuzzy-rough sets (bold
solid lines).
Note that the presented derivation gives results
which are intuitive formulations in the earliest works
on type-2 fuzzy logic systems (Karnik et al., 1999;
Mendel, 2001).
3 GENERAL FUZZY LOGIC
CLASSIFIER
Consider a type-2 fuzzy logic system of N inputs in
a vector form x, and single output y (Mendel, 2001).
The rule set is formed by K rules
e
R
k
: IF
e
A
0
is
e
A
k
THEN
e
B
0
is
e
B
k
,
where
e
A
0
is a type-2 fuzzified N-dimensional input
x,
e
B
0
is a type-2 conclusion fuzzy set,
e
A
k
is an N-
dimensional antecedent fuzzy set of type-2, and
e
B
k
is
a consequent fuzzy set, k = 1,. . .,K. We can interpret
relations
e
R
k
either as conjunctions realized in general
by type-2 t-norms, or as material implications of type-
2 (Gera and Dombi, 2008).
The conclusion of the system is that y is
e
B
0
, which
is an aggregation of all single rule conclusions cal-
culated by the compositional rule of inference
e
B
0
k
=
e
A
0
◦(
e
A
k
7→
e
B
k
), i.e.,
µ
e
B
0
k
(y) = sup
x∈X
n
e
T

µ
e
A
0
(x),
e
R

µ
e
A
k
(x), µ
e
B
k
(y)
o
,
(20)
which in its simplest form of extended sup-min com-
position was first presented by (Dubois and Prade,
1980).
Fuzzification of x
0
, which is the merits of this pa-
per, can be defined as a mapping from real input space
X ⊂ R
n
to type-2 fuzzy subsets of X. However, in
many basic cases (also examined in this paper) fuzzi-
fication functions can modify antecedent functions in-
stead of fuzzifying inputs. Therefore, input values
x
0
still may be represented by singleton type-2 fuzzy
sets, and consequently, composition (20) simplifies it-
self to the following expression
µ
e
B
0
k
(y) =
e
R

µ
e
A
k

x
0

,µ
e
B
k
(y)

. (21)
If we apply conjunction relations, we expect the
aggregated conclusion to be
e
B
0
=
S
R
k=1
e
B
0
k
, i.e.
µ
e
B
0
(y) =
K
e
S
k=1
µ
e
B
0
k
(y), (22)
where
e
S is a type-2 t-conorm. Otherwise, if we use
type-2 material implications, we expect that
e
B
0
=
T
R
k=1
e
B
0
k
, i.e.
µ
e
B
0
(y) =
K
e
T
k=1
µ
e
B
0
k
(y). (23)
3.1 Algebraic Operations on Triangular
Type-2 Fuzzy Sets
In (Starczewski, 2013), we have defined a so-called
regular t-norm on a set of triangular fuzzy truth num-
bers
µ
T
N
n=1
F
n
(u) = max(0, min (λ (u) ,ρ (u))), (24)
where
λ(u) =

u−l
m−l
if m > l
singleton(u −m) if m = l,
(25)
ρ(u) =

r−u
r−m
if r > m
singleton(u −m) if m = r,
(26)
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
338

and
l =
N
T
n=1
l
n
, (27)
m =
N
T
n=1
m
n
, (28)
r =
N
T
n=1
r
n
. (29)
This formulation allows us to use ordinary t-norms
for upper, principal and lower memberships indepen-
dently. Moreover, we have proved the function given
by (24) operating on triangular and normal fuzzy truth
values is a t-norm of type-2.
3.2 Triangular Centroid Type Redution
The first step transforming a type-2 fuzzy conclusion
into a type-1 fuzzy set is called a type reduction. In
classification, we perform only type reduction with-
out the second step of final defuzzification, which re-
lies on the extended centroid defuzzification
µ
B
(y) = sup
y=
∑
K
k=1
y
k
u
ki
∑
K
k=1
u
ki
min
k=1,...,K
f
k
(u
ki
). (30)
In (Starczewski, 2014), we have obtained exact type-
reduced sets for triangular type-2 fuzzy conclusions
as a set of ordered discrete primary values y
k
and their
secondary membership functions
f
k
(u
k
) =
,
min
u
k
−µ
k
b
µ
k
−µ
k
,
µ
k
−u
k
µ
k
−
b
µ
k
!,
(31)
for k = 1,..., K. The secondaryties are specified by
upper, principal and lower membership grades,
µ
k
>
b
µ
k
> µ
k
, k = 1,2,...,K. The well known Karnik-
Mendel algorithm (Karnik et al., 1999) is used here
to determine an interval centroid fuzzy set [y
min
,y
max
]
for the interval-valued fuzzy set constituted by the
upper and lower membership grades. There is a se-
lection of type-reduction algorithms (Greenfield and
Chiclana, 2013); however, the Karnik-Mendel algo-
rithm is chosen here becuase it results in an inter-
val. Additionally, let y
pr
be a centroid of the principal
membership grades calculated by
y
pr
=
K
∑
k=1
b
µ
k
y
k
b
µ
k
. (32)
The exact centroid of the triangular type-2 fuzzy set is
characterized by the following membership function:
µ(y) =



y−y
left
(y)
(1−q
l
(y))y+q
l
(y)y
pr
−y
left
(y)
if y ∈

y
min
,y
pr

y−y
right
(y)
(1−q
r
(y))y+q
r
(y)y
pr
−y
right
(y)
if y ∈

y
pr
,y
max

,
(33)
where the parameters are
q
l
(y) =
∑
K
k=1
b
µ
k
∑
K
k=1
←−
µ
k
(y)
, (34)
q
r
(y) =
∑
K
k=1
b
µ
k
∑
K
k=1
−→
µ
k
(y)
, (35)
and
y
left
(y) =
∑
K
k=1
←−
µ
k
(y)y
k
∑
K
k=1
←−
µ
k
(y)
,
y
right
(y) =
∑
K
k=1
−→
µ
k
(y)y
k
∑
K
k=1
−→
µ
k
(y)
,
with
←−
µ
k
(y) =
(
µ
k
if y
k
≤ y
µ
k
otherwise
,
−→
µ
k
(y) =
(
µ
k
if y
k
≥ y
µ
k
otherwise
.
An example of our type reduction algorithm is pre-
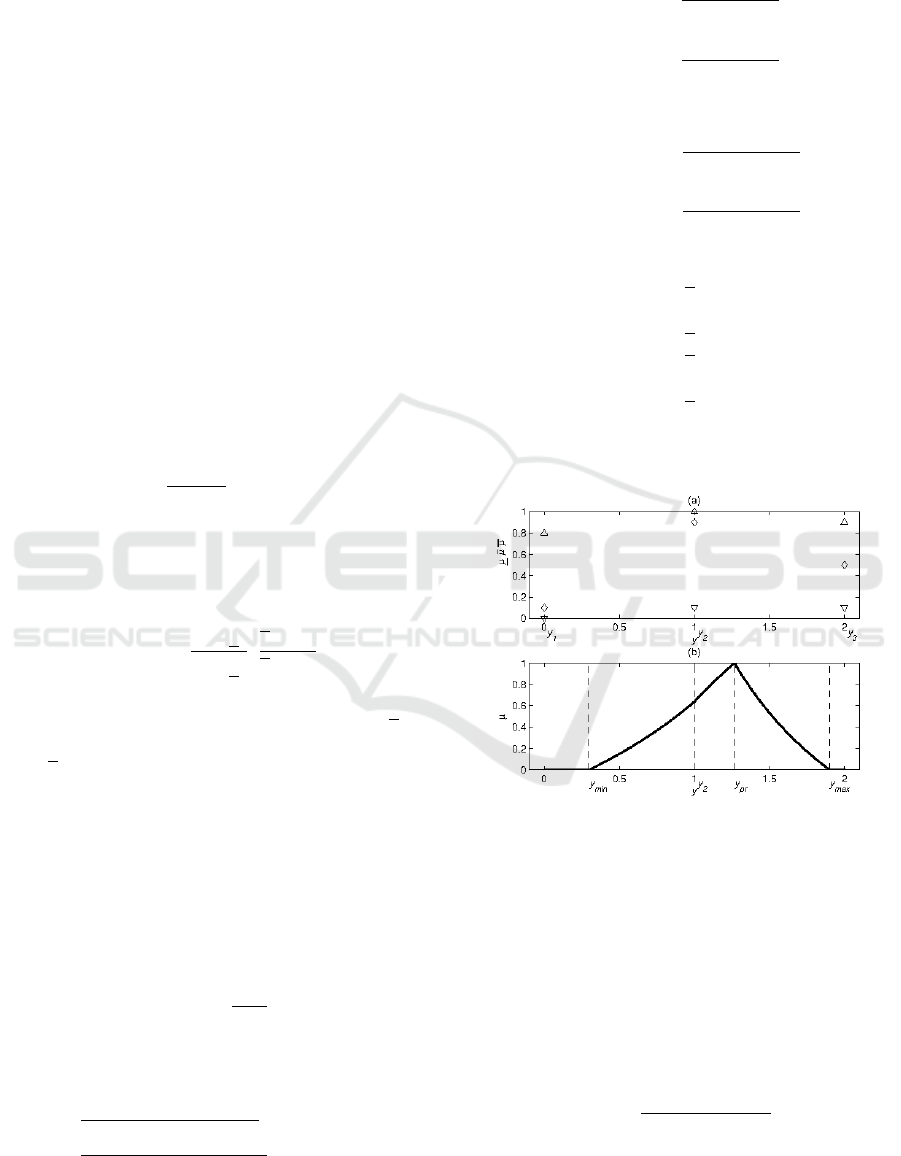
sented in Figure 4. Note that only three output values
are subject to interpretation.
Figure 4: Centroid of fuzzy-valued fuzzy sets with trian-
gular secondary membership functions: (a) 4 – upper, ♦
– principal and O – lower membership grades; (b) centroid
fuzzy set
3.3 Type Reduction in Classification
Note that in classification y
k
are either equal to 0 or
to 1. Therefore, we propose the following procedure
(Nowicki, 2009). Let us consider the fuzzy classifier
defined by the equation
y
j
=
∑
K
k=1
k : y
j,k
=1
e
µ
A
k
(x)
∑
K
k=1
e
µ
A
k
(x)
(36)
where
e
µ
A
k
(x) is a type-2 or fuzzy-rough approxima-
tion of a fuzzy set. If we limit this set with its upper
Fuzzy–rough Fuzzification in General FL Classifiers
339

and lower membership functions, µ
A
k
(x) and µ
A
k
(x),
respectively, the single-rule membership of an object
to the j-th class is binary
y
j,k
=
(
1 if x ∈C
j
0 if x /∈C
j
(37)
for all rules k = 1, . . .,K and all classes j = 1, . . . , J.
The lower and upper approximations of the member-
ship of object x to class C
j
is given by
y
min
( j) =
∑
K
k=1
k : y
j,k
=1
←−
µ
A
k
(x)
∑
K
k=1
←−
µ
A
k
(x)
(38)
and
y
min
( j) =
∑
K
k=1
k : y
j,k
=1
−→
µ
A
k
(x)
∑
K
k=1
−→
µ
A
k
(x)
(39)
where
←−
µ
A
k
(x) =
(
µ
A
k
(x) if y
j,k
= 1
µ
A
k
(x) if y
j,k
= 0
(40)
and
−→
µ
A
k
(x) =
(
µ
A
k
(x) if y
j,k
= 0
µ
A
k
(x) if y
j,k
= 1
(41)
This first-step defuzzification issue with binary mem-
berships of objects to classes, in comparison to the
standard Karnik-Mendel type reduction algorithm,
does not require any arrangement of y
j,k
.
In addition to the boundary computation, we
should have in mind, the calculation of the principal
approximation of the membership of object x to class
C
j
, i.e.,
y
pr
( j) =
∑
K
k=1
k : y
j,k
=1
b
µ
A
k
(x)
∑
K
k=1
b
µ
A
k
(x)
. (42)
The decision of the classifier is very dependent
on the interpretation of the three output variables ob-
tained, albeit linearly ordered. If we choose a thresh-
old value at
1
2
, we may enumerate four different deci-
sions:









certain classification if y
min
≥
1
2
and y
max
>
1
2
certain rejection if y
min
<
1
2
and y
max
≤
1
2
likely classification if y
min
<
1
2
and y
pr
≥
1
2
likely rejection otherwise.
(43)
4 NUMERICAL SIMULATIONS
Exemplary simulations were carried out in the follow-
ing order:
1. A fuzzy logic system with nonfuzzified inputs was
trained on exact data (laboratory training environ-
ment), with the use of Back Propagation method.
Gaussian antecedent membership functions and
binary singleton consequents (as in classification).
were applied in rules fired by the algebraic Carte-
sian product. Such system were used as a princi-
pal subsystem of the type-2 system constructed in
the next step.
2. Triangular fuzzification membership functions
were chosen with symmetric spread values ∆
i
for
all or particular singular inputs x
i
. Triangular
fuzzification was applied in the form of fuzzy-
rough sets. As a result, a triangular type-2 fuzzy
logic classifier was constructed.
3. Input data were corrupted by white additive noise
with a triangular distribution and spread values
identical to the fuzzification functions had. With
noisy data the type-2 fuzzy classifier was tested,
as it were in the real-time environment. The 10-
folds cross-validation method was applied.
The classification abilities of fuzzy-rough classifiers
were analyzed on modified datasets chosen from the
UCI repository (Dua and Graff, 2017). The Iris
flower is the standard task for classification and pat-
tern recognition studies; however, in our cases, the
dataset was corrupted with triangular additive noise.
Table 1 presents the results for the 4–rule system,
in which singular inputs were fuzzified and corre-
sponding input data were uncertain, while in Table
2, all inputs were fuzzified and all data were cor-
rupted. Correct classifications are counted whenever
a sample is either certainly classified or certainly re-
jected. Likely correct classification signifies a good
suggestion, when a likely classification is indicated
for the positive desired output or a likely rejection
is indicated for the false desired output. A confused
likely incorrect classification label is connected with
the cases of likely incorrect classification under ex-
pected classification, or likely correct classification
under expected rejection.
Even on this such elementary example, we can ob-
serve that the number of misclassifications, i.e., when
the classifier totally has made mistakes, is close to
0 in all cases. Although the standard type-1 fuzzy
logic classifier is slightly better in correct classifica-
tions (treated as certain) than the corresponding fuzzi-
fied type-2 fuzzy classifier (based on the fuzzy-rough
approach), the number of misclassifications for the
type-1 system (calculated as a complement of the cor-
rect classification) is extremely greater that the num-
ber of misclassifications made by the fuzzified sys-
tem. Obviously the number of correct classifications
is decreasing with increasing uncertainty; however,
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
340

Table 1: Iris classification with triangular fuzzy-rough
fuzzification; additional triangular noise applied to partic-
ular inputs ∆
i
, i = 1, .. ., 4.
∆
1
Type-1 FLC Triangular Fuzzification
Correct Corr./
Likely
Corr.
/
Likely
Incorr.
/Incorr.
0.2 0.974 0.966/0.011/0.006/0.017
0.5 0.965 0.897/0.079/0.020/0.004
1.0 0.941 0.673/0.296/0.026/0.005
2.0 0.863 0.428/0.512/0.055/0.005
5.0 0.548 0.419/0.442/0.130/0.009
∆
2
0.2 0.972 0.950/0.027/0.014/0.010
0.5 0.963 0.807/0.166/0.024/0.003
1.0 0.928 0.456/0.504/0.036/0.005
2.0 0.746 0.422/0.470/0.102/0.006
5.0 0.394 0.387/0.403/0.205/0.004
∆
3
0.2 0.972 0.967/0.010/0.004/0.019
0.5 0.967 0.896/0.079/0.013/0.012
1.0 0.920 0.744/0.214/0.035/0.008
2.0 0.843 0.469/0.461/0.060/0.010
5.0 0.644 0.406/0.443/0.133/0.018
∆
4
0.2 0.955 0.913/0.059/0.022/0.006
0.5 0.918 0.663/0.293/0.038/0.006
1.0 0.822 0.401/0.506/0.081/0.012
2.0 0.668 0.325/0.504/0.146/0.025
5.0 0.402 0.291/0.459/0.200/0.050
Table 2: Iris classification with triangular fuzzy-rough
fuzzification; additional triangular noise applied to all in-
puts.
∆
i
Type-1 FLC Triangular Fuzzification
Correct Corr./
Likely
Corr.
/
Likely
Incorr.
/Incorr.
0.2 0.952 0.750/0.222/0.023/0.005
0.5 0.890 0.407/0.538/0.050/0.006
1.0 0.719 0.278/0.580/0.127/0.015
2.0 0.401 0.175/0.549/0.236/0.041
5.0 0.054 0.035/0.627/0.321/0.017
the number of likely correct classifications is always
much greater than the number of likely incorrect clas-
sifications. Having only singular inputs tuned for un-
certain data, we can count on high percentages of
correct classifications (greater than 29% in the worst
case). Unfortunately high uncertainty high uncer-
tainty for all input attributes can diminish the number
of correct classifications below 4%.
The classifier for Wisconsin Breast Cancer (re-
moved instances with missing values) employed 3
rules. The results are shown in Table 3 (for partic-
ular inputs corrupted), and in Table 4 (for all inputs
corrupted). The tests carried out confirmed the gen-
eral properties of fuzzy-roughly fuzzified classifiers.
Table 3: WBC-based classification with triangular fuzzy-
rough fuzzification; additional triangular noise applied to
particular inputs ∆
i
, i = 1, .. ., 9.
∆
1
Type-1 FLC Triangular Fuzzification
Correct Corr./
Likely
Corr.
/
Likely
Incorr.
/Incorr.
2 0.955 0.918/0.060/0.011/0.011
3 0.918 0.857/0.117/0.016/0.010
5 0.847 0.791/0.172/0.026/0.011
∆
2
2 0.757 0.449/0.527/0.014/0.010
3 0.728 0.379/0.594/0.020/0.007
5 0.664 0.327/0.641/0.026/0.006
∆
3
2 0.942 0.900/0.080/0.010/0.010
3 0.871 0.849/0.129/0.013/0.009
5 0.793 0.801/0.175/0.019/0.005
∆
4
2 0.956 0.889/0.090/0.012/0.009
3 0.885 0.847/0.129/0.017/0.007
5 0.801 0.806/0.168/0.022/0.004
∆
5
2 0.969 0.894/0.085/0.010/0.011
3 0.924 0.851/0.121/0.012/0.016
5 0.840 0.798/0.167/0.014/0.021
∆
6
2 0.924 0.817/0.157/0.019/0.007
3 0.839 0.625/0.340/0.029/0.006
5 0.738 0.453/0.499/0.044/0.004
∆
7
2 0.958 0.886/0.095/0.011/0.008
3 0.918 0.844/0.136/0.014/0.006
5 0.833 0.794/0.181/0.019/0.006
∆
8
2 0.891 0.836/0.136/0.012/0.016
3 0.815 0.809/0.155/0.018/0.018
5 0.731 0.780/0.181/0.024/0.015
∆
9
2 0.925 0.859/0.114/0.022/0.005
3 0.849 0.830/0.141/0.024/0.005
5 0.742 0.808/0.158/0.028/0.006
Table 4: WBC-based classification with triangular fuzzy-
rough fuzzification; triangular noise applied to all inputs.
∆
i
Type-1 FLC Triangular Fuzzification
Correct Corr./
Likely
Corr.
/
Likely
Incorr.
/Incorr.
2 0.546 0.373/0.535/0.075/0.017
3 0.327 0.173/0.655/0.155/0.017
5 0.145 0.078/0.657/0.250/0.015
The number of incorrect is not much greater 10% in
all cases. The standard type-1 fuzzy classifier in com-
parison to the proposed type-2 classifier not always is
better in performing correct classifications (for fuzzi-
Fuzzy–rough Fuzzification in General FL Classifiers
341

fied either 3rd, or 4th, or 7th, or 8th input the percent-
age trends are even reversed). The number of type-1
approach misclassifications is much greater than the
number of type-2 approach misclassifications. made
by the fuzzified system. The number of likely correct
classifications is always much greater than the num-
ber of likely incorrect classification. Having only sin-
gular inputs fuzzified, we can count on satisfactory
percentages of correct classifications (between 33%
and 92%), while highly noised all inputs result with
the number of correct classification below 8%.
5 CONCLUSIONS
The specificity of triangular fuzzifications in fuzzy
classifiers allows us to analyze data at a deeper level
of interpretation, which comes from the simultanuous
use of principal, maximal and minimal fuzzy-rough
approximations of data processed within the system.
Instead of the standard yes-or-no classification, we
obtain groups of classified objects with the four la-
bels of confidence: certain classification, likely cer-
tain classification, likely certain rejection, definitely
certain rejection. Continuing the example of medi-
cal diagnosis, we may differentiate a support for the
four types of classifications. For the certain classifica-
tion of a medical disease, we should urgently contact
a patient with a doctor or ER care. For likely certain
classifications, we may perform expensive laboratory
tests to confirm or exclude the diagnosis. In cases of
rather certain rejections, medical laboratory test may
be more economical and can be extended over time.
For certain rejections, patients can sleep calmly until
their scheduled visits to the doctor. Similar method-
ologies can be realized by hierarchical automatic clas-
sifiers working on basic or standard, or expensive, in
particular cases, data.
ACKNOWLEDGEMENTS
The project financed under the program of the Minis-
ter of Science and Higher Education under the name
”Regional Initiative of Excellence” in the years 2019
- 2022 project number 020/RID/2018/19, the amount
of financing 12,000,000 PLN.
REFERENCES
Dua, D. and Graff, C. (2017). UCI machine learning repos.
Dubois, D. and Prade, H. (1980). Fuzzy sets and systems:
Theory and applications. Academic Press, Inc., New
York.
Gera, Z. and Dombi, J. (2008). Type-2 implications on non-
interactive fuzzy truth values. Fuzzy Sets and Systems,
159(22):3014–3032.
Greenfield, S. and Chiclana, F. (2013). Accuracy and com-
plexity evaluation of defuzzification strategies for the
discretised interval type-2 fuzzy set. International
Journal of Approximate Reasoning, 54(8):1013–1033.
Han, Z.-q., Wang, J.-q., Zhang, H.-y., and Luo, X.-x.
(2016). Group multi-criteria decision making method
with triangular type-2 fuzzy numbers. International
Journal of Fuzzy Systems, 18(4):673–684.
Karnik, N. N., Mendel, J. M., and Liang, Q. (1999). Type-
2 fuzzy logic systems. IEEE Transactions on Fuzzy
Systems, 7(6):643–658.
Mendel, J. M. (2001). Uncertain rule-based fuzzy logic sys-
tems: Introduction and new directions 2001. Prentice
Hall PTR, Upper Saddle River, NJ.
Najariyan, M., Mazandarani, M., and John, R. (2017).
Type-2 fuzzy linear systems. Granular Computing,
2(3):175–186.
Nakamura, A. (1988). Fuzzy rough sets. Note on Multiple-
Valued Logic in Japan, 9(8):1–8.
Nowicki, R. (2009). Rough-neuro-fuzzy structures for clas-
sification with missing data. IEEE Transactions on
Systems, Man, and Cybernetics B, 39.
Nowicki, R. K. (2019). Rough Set–Based Classification
Systems, volume 802 of Studies in Computational In-
telligence. Springer International Publishing, Cham.
Nowicki, R. K. and Starczewski, J. T. (2017). A new
method for classification of imprecise data using
fuzzy rough fuzzification. Information Sciences,
414:33 – 52.
Starczewski, J. T. (2010). General type-2 FLS with uncer-
tainty generated by fuzzy rough sets. In Proc. IEEE-
FUZZ 2010, pages 1790–1795, Barcelona.
Starczewski, J. T. (2013). Advanced Concepts in Fuzzy
Logic and Systems with Membership Uncertainty, vol-
ume 284 of Studies in Fuzziness and Soft Computing.
Springer.
Starczewski, J. T. (2014). Centroid of triangular and
Gaussian type-2 fuzzy sets. Information Sciences,
280:289–306.
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
342