
Multivariate Time Series Forecasting with Deep Learning Proceedings in
Energy Consumption
N
´
edra Mellouli
1 a
, Mahdjouba Akerma
2
, Minh Hoang
2
, Denis Leducq
2
and Anthony Delahaye
2
1
LIASD EA4383, IUT de Montreuil, Universit
´
e Paris 8, Vincennes Saint-Denis, France
2
Irstea, UR GPAN, Anthony, France
Keywords:
Demand Response, Deep Learning, Time Series Forecasting.
Abstract:
We propose to study the dynamic behavior of indoor temperature and energy consumption in a cold room
during demand response periods. Demand response is a method that consists of smoothing demand over time,
seeking to reduce or even stop consumption during periods of high demand in order to shift it to periods
of lower demand. Such a system can therefore be tackled as the study of a time-series, where each behav-
ioral parameter is a time-varying parameter. Different network topologies are considered, as well as existing
approaches for solving multi-step ahead prediction problems. The predictive performance of short-term pre-
dictors is also examined with regard to prediction horizon. The performance of the predictors are evaluated
using measured data from real scale buildings, showing promising results for the development of accurate
prediction tools.
1 INTRODUCTION
In France as elsewhere in the world, the balance be-
tween electricity production and consumption is a ne-
cessity that must be maintained and for which elec-
tricity suppliers are required to index electricity pro-
duction to the demand of grid users. To do this,
suppliers must regularly deploy more production re-
sources with fast response times. In addition, the Eu-
ropean Union has set itself the target of increasing the
share of renewable energy in energy consumption to
27% by 2030, from 17% in 2016. However, these new
means of production, whose productivity may vary
according to time of day, season or climate, require
a rethinking of the use of the global electricity grid
to allow more flexibility. Due to this high complex-
ity and when the main objective is the final result ob-
tained at the output of the system independently of in-
ternal operation, it may be interesting to examine the
use of Black Box models, the purpose is to predict
the output parameters according to the inputs. The
study of the dynamic behavior of such a system can
therefore be approached as the study of a time series,
where each behavioral parameter is a time-varying pa-
rameter. A time series is a sequence of real-valued
signals that are measured at successive time inter-
a
https://orcid.org/0000-0001-8858-9902
vals. Long short-term memory (LSTM)(Hochreiter
and Schmidhuber, 1997), a class of recurrent neural
networks (RNNs)(andY. Bengio and Hinton, 2015),
is particularly designed for sequential data. For time
series prediction task LSTM has particularly shown
promising results. Four deep neural network architec-
tures derived from the LSTM architecture were stud-
ied, adapted and compared. Their validation was car-
ried out using experimental data collected in a cold
room in order to evaluate their performance in pre-
dicting demand response. In this paper, we present
our methodology allows us to effectively answer the
following questions:1) Which deep learning models
are best suited to represent our specific data? 2) From
the selected models, we have sought to define and
characterize the most efficient predictive models and
to highlight all the parameters that induce them. 3) In
addition to their relevance, we are looking to evaluate
the robustness of the selected models at the last iter-
ation against the data quality (noise), data temporal
window scaling and large scaling data. The paper is
structered as following. In the next section we present
the related work, then we detail our approach. Finally
we describe the datasets used to compare four deep
leraning architectures and we discuss their results.
384
Mellouli, N., Akerma, M., Hoang, M., Leducq, D. and Delahaye, A.
Multivariate Time Series Forecasting with Deep Learning Proceedings in Energy Consumption.
DOI: 10.5220/0008168203840391
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 384-391
ISBN: 978-989-758-382-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORK
2.1 Time Series Models in Electrical
Demand Response Prediction
Time series is defined as a sequence of discrete time
data. It consists of indexed data points, measured typ-
ically at successive times, spaced at (often uniform)
time intervals. Time series analysis comprises the dif-
ferent methods for analyzing such time series in order
to understand the theory behind the data points, i.e. its
characteristics and the statistical meaning (Nataraja
et al., 2012). A time series forecasting model pre-
dicts future values based on known past events (recent
observations). Conventional time series prediction
methods commonly use a moving average model that
can be autoregressive (ARMA)(Rojo-Alvarez et al.,
2004), integrated autoregressive (ARIMA) (Hamil-
ton, 1994) or vector autoregressive (VARMA)(Rios-
Moreno et al., 2007), in order to reduce data. Such
methods must process all available data in order to
extract the model parameters that best match the new
data. These methods are useless in the face of mas-
sive data and real-time series forecasting. To ad-
dress this problem, online time learning methods have
emerged to sequentially extract representations of un-
derlying models from time series data. Unlike tradi-
tional batch learning methods, online learning meth-
ods avoid unnecessary cost retraining when process-
ing new data. Due to their effectiveness and scalabil-
ity, online learning methods, including linear model-
based methods, ensemble learning and kernels, have
been successfully applied to time series forecasting.
Each time series forecasting model could have many
forms and could be applied to many applications.
For more detailes we can see (Amjady, 2001) (Aman
et al., 2015).
In our application context, (Hagan and Behr,
1987) have been reviewed time series based models
for load forecasting. Then in 2001 (Amjady, 2001)
has studied time series modeling for short to medium
term load forecasting. To predict energy consump-
tion some authors have used time series data. For
example, (J.W et al., 2006) have concentrated their
study on the comparison of the performance of the
methods for short-term electricity demand forecast-
ing using a time series. (Simmhan et al., 2013) have
focused their study on prediction of energy consump-
tion using incremental time series clustering, (Sheng
and Duc-Sonand, 2018) have also forecasted the en-
ergy consumption time series using machine learning
techniques. In (Aman et al., 2015) the work is fo-
cused on increasing the accuracy of prediction mod-
els for dynamic demand response, this prediction is
based on a very small data granularity (15 min inter-
vals). The focus on demand response has been on
large industrial and commercial consumers (Ziekow
et al., 2013) which are expected by their high con-
tribution and adopted for the smart meters (Simmhan
et al., 2013).
2.2 Nonlinear Models
Due to the very high complexity and need for accu-
racy that the use of linear modeling, which is very
time-consuming, can imply, the transition to another
more applied type of modeling can simplify the study.
Indeed, when the main objective is the final result ob-
tained at the output of a system, regardless of internal
operation, it may be interesting to look at the use of
non-linear models, whose purpose is solely to predict
the output parameters from the inputs. This presents
in addition the advantage of being much more easily
generalizable, at least in the presence of data of suffi-
cient good quality and by finding a model correspond-
ing to our problematic, without requiring a reshaping
of the problem and adaptation of the different param-
eters when studying a new system. In particular, Arti-
ficial Neural Networks (ANN) could provide an alter-
native approach, as they are widely accepted as a very
promising technology offering a new way to solve
complex problems. ANNs ability in mapping com-
plex non-linear relationships, have succeeded in sev-
eral problems such as planning, control, analysis and
design. The literature has demonstrated their superior
capability over conventional methods, their main ad-
vantage being the high potential to model non-linear
processes, such as utility loads or energy consump-
tion in individual buildings . At present, although
studies (Hu et al., 2017)(Xue et al., 2014) have been
carried out within the wide framework of demand re-
sponse, no such method does appear to have been
applied to demand response in the field of refriger-
ation. In consideration of the energy importance of
this field which provides a panel of significant op-
portunities, the use of a pertinent modelling approach
can demonstrate (or invalidate) the use of demand re-
sponse in cold rooms and cold stores, allowing (or
not) a significant increase in the application of elec-
trical cut-off. An LSTM network, or ”Long Short
Term Memory”, is a model for retaining short-term
information (recent variations and current trends in
data) and long-term ones (periodicity, recurring or
non-recurring events). It is a matter of a deep learn-
ing model widely used for time series processing. It
is popular due to the ability of learning hidden long-
term sequential dependencies, which actually helps
in learning the underlying representations of time se-
Multivariate Time Series Forecasting with Deep Learning Proceedings in Energy Consumption
385

ries (Kuo and Huang, 2018).A convolutional LSTM
model was proposed based on the Fully Connected
LSTM model (Shi et al., 2015), particularly for its ap-
plication to predicting changes in spatial images. This
model has allowed them to obtain better results than
using a simple LSTM or Fully-Connected LSTM net-
work. The architecture of an LSTM network therefore
consists of a sequence of LSTM layers for both past
and future data, which are then processed together to
predict current data. To conclude, the modeling of a
refrigeration system being characterized by the non
linearity and the coupling of several parameters, clas-
sical physical models encounter difficulties in predict-
ing the dynamic behaviour of such systems, in par-
ticular during disturbances such as electrical cut-off
periods. Neural network methods, due to their abil-
ity to adjust and self learning, can therefore be very
promising in responding to this type of issues offering
a new way to solve complex problems. The LSTM
ability in mapping complex non-linear relationships,
have succeeded in several problems such as planning,
control, analysis and design of energy systems. The
literature has demonstrated their superior capability
over conventional methods, their main advantage be-
ing the high potential to model non-linear processes.
3 OUR APPROACH
3.1 Experimental Setup of Cold Room
A cold room or cold store ensures that the products
are kept in satisfactory conditions. This therefore re-
quires the use of a refrigeration system, which can
take the form of a regular supply of cold air, in order
to keep the air and products below a setpoint temper-
ature, generally below −18
◦
C. This phenomenon fol-
lows the refrigeration cycle, passing through its four
main stages, namely compression, condensation, ex-
pansion and evaporation. In order to avoid significant
heat leakage, it is also necessary to reduce external in-
puts, through optimal thermal insulation and to min-
imize door openings as well as human or mechanical
activities 1. The products are stored in the form of
distributed pallets to reduce the phenomenon of natu-
ral warming while facilitating access to the products
during loading and unloading. The cold room used in
this study is about 2.4m long x 2.4m width x 2m high.
For wall insulation, a 10cm layer of polyurethane with
λ = 0.023W /m.K is used. A global heat transfer co-
efficient Uc = 0.29W /m2K is obtained by measure-
ment. The room temperature is controlled using an
on/off strategy and is kept at −16.3
◦
C (within a lim-
ited range (set-point) between −15.5
◦
C and −19
◦
C).
The refrigerated unit consists of a single evaporator
with single speed fan. The measured coefficient of
performance (COP) is 1.4 at -16
◦
C. The cold room
is installed inside an external cell equipped with an
air conditioning unit to simulate the meteorological
conditions (summer, spring. . . ). To limit the infil-
tration load, the doorway is kept closed during mea-
surements. In order to measure the air and product
temperature, thermocouple sensors are used (Fig. 2).
These thermocouples are distributed as follows (cf.
Figure 1):
• 3 for cold blowing air (Ts) and 3 for return air (Tr)
• 14 for air temperature inside the cold room: 6 in
the middle of each wall, 1 near the door, 1 at one
wall surface (sample inside cold room), 6 at the
corners (2 other corners are not accessible by ther-
mocouples)
• 5 for air temperature in the external cell (Text) on
the surface of each wall
• Two wattmeters are used to measure the instanta-
neous electricity consumption of the refrigeration
system (compressor and auxiliary).
The main features of a cold room are of two cate-
gories. As a first category, we find fixed features
which take into account building geometry (as build-
ing dimensions, wall thickness), building composition
(as material conductivity, density and overall heat ex-
change coefficient), outdoor contributions (as outdoor
temperature, solar flux, air renewal), cold production
(as setpoint temperature, blowing temperature, blow-
ing rate, operation of the refrigeration machine, cool-
ing capacity) and operations on building (as Loading,
product conductivity, product density, human pres-
ence, lighting, ventilation, defrosting, etc). The sec-
ond category includes mainly temporal features like
the demand response periods (T
erasure
) including both
the demand response phase itself (switching off the
cooling system) and the recovery phase of the cool-
ing system (restoring the set temperature); The de-
frost periods, (T
de f rost
) which occur several times a
day without any decision-making power on the time
of appearance. These periods correspond to a spe-
cific temperature increasing related to the defrost-
ing of the cold room fan; The compressor on/off
periods (compressor ), which occur very regularly
and on an ad hoc basis; The time elapsed since
the last demand response period (δT
erasure
), allow-
ing the model to better predict the behavior of the
cold room in the moments following the demand re-
sponse period, while its condition is not yet restored;
And the time elapsed since the last defrost (δT
de f rost
),
also allowing better prediction of the behaviour of
the cold room in the moments following defrosting,
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
386

Figure 1: Example of a used cold room.
when the condition of the cold room is not yet stabi-
lized. According to the time parameters defined be-
low we obtain a system with three modes behavior.
The first mode (Fig.2(1))represents the steady state
where regular temperature variations according to set
points (high/low) are measured. The second mode
((Fig.2(2))is the critical state of the system refers to
electrical demand response. During this mode, the
temperature increases over a long period of time. This
period depends mainly on the demand response time
interval, typically varies between 30 minutes and 3
hours.The third mode ((Fig.2(3))is the defrost state in
which the temperature suddenly increases over a short
period of time.
3.2 Multivariate Electrical Demand
Response Data Time Series
In this section we define the list of time series data
we aim to predict. Indeed, we consider four data
classes. The first class is dedicated to measure the
Indoor Temperature (T p
In
) using 5 sensors thus we
have five T p
In
time series. Sensors are located in
five strategic positions in the cold room. The second
class is the Recovery Temperature of the Air (T p
Air
)
in the cold room and we have three sensors to mea-
sure three T p
Air
time series. The third class is focused
to measure the Product Temperature (T p
Prod
) with 8
sensors and thus we have eight T p
Prod
) time series.
The last class is to measure the Outdoor Temperature
(T p
Out
using five sensors and we obtained five out-
door temperature time series. Compressor consump-
tion (Comp
E
nergy) which is a particular data time se-
ries correlated to the previous variable classes is also
considered. To solve the problems related to the si-
multaneous occurrence of defrosting and demand re-
sponse phenomena, i.e. the confusion of their mea-
surement periods, we have chosen to recover the de-
frosting and demand response programs directly by
observing the temperature variations that occur dur-
ing demand response period and defrosting. All time
series data are measured each five seconds.
3.3 LSTM Models to Forcasting
Electrical Demand Response
We note {t p
1
,t p
2
,...,t p
n
} a time series represent-
ing any parameter T p
x
in the output set where x ∈
{Air,In,Product}. Our predictive model learns use-
ful features from a set of time series parameters to
give a prediction
ˆ
t p
t
that compares with t p
t
to update
itself, where t p
t
is the real value measured at time t
and
ˆ
t p
t
is the time series data point forecasted at the
same time. As it is proved in the literature, Long Short
Term Memory (LSTM) is required for discovering
a dependence relationships between the time series
data by using specialized gating and memory mech-
anisms. For this purpose, we are aimed to compare
four LSTM models : LSTM, Convolutionnal LSTM,
Stacked LSTM, Bidirectional LSTM. As a first model
we have used LSTM.
After a huge number of experiments following
several evaluations of the model, the parameters were
selected for this model:
• 1024 units are able to store enough information.
This choice was made balancing the learning time
and the quality of obtained prediction.
• A linear or SeLu activation function, giving us
better results than the other functions
• A cost function using the Root Mean Square Error
(RMSE),
The second model is stacked LSTM. The devel-
oped Stacked LSTM model is a modification of the
LSTM network described above, with the addition of
several layers of LSTM.
For this purpose, and after experimental tests, the
selected model consists of a stack of three layers of
LSTM, namely: A first layer of 1024 memory units,
allowing to store a large amount of information in the
short and long term; A second layer of 512 memory
units; A third layer, of 256 memory units;
Each layer of the network is separated from the
next layer by a dropout layer, allowing less overtrain-
ing and robust generalization results.
For the Bidirectional LSTM network, it consists
of a stack of two layers of LSTMs each with 512
memory units. This model thus created makes it pos-
sible to keep information related to both past and fu-
ture data.
The convolutional LSTM network was chosen
with the following parameters: 40 filters, correspond-
ing to the outputs of the convolutional part of the
model; A kernel size of 2x10, corresponding to the
dimensions of the convolution window; A normaliza-
tion layer, allowing to normalize the activations of the
convolutional LSTM layer.
Multivariate Time Series Forecasting with Deep Learning Proceedings in Energy Consumption
387

3.4 Performance Metric for Evaluation
In order to compare our different models and to se-
lect the appropriate model(s) for our study, different
criteria were implemented and computed. In the fol-
lowing, the reference values will be indicated by Y ,
the predicted values by
b
Y , the average of the refer-
ence values by
¯
Y and the number of observations by
N. The Fit criterion is needed for measuring the prox-
imity between the reference values and the predicted
values. The closer its value is to 100%, the more
it indicates a correctly predicted variable. It there-
fore corresponds to a percentage and is defined by:
Fit(Y ) = 100.(1 −
|
b
Y −Y|
|Y −
¯
Y |
).
The Mean-Squared-Error (MSE), or mean square
error, is the arithmetic mean of the squares of the dif-
ferences between the forecasts and the actual obser-
vations. The objective of a good prediction is there-
fore to obtain the lowest possible mean square error.
The advantage of squaring is to highlight high errors,
and therefore to minimize low prediction errors. This
value is therefore defined by: MSE(Y ) =
1
N
.
∑
N
i=1
(
b
Y
i
−
Y
i
)
2
. The root of this value, or Root-Mean-Squared-
Error (RMSE), is also often used, which is simply cal-
culated by: RMSE(Y ) =
p
MSE(Y ).
The Mean Absolute Error (MAE), or absolute
mean error, is the arithmetic mean of the differences
between forecasts and actual observations. Since
there is no squaring, this measure treats each dif-
ference with equal importance. The objective is
of course to minimize this value, and it is defined
over prediction horizon [t + 1,t + H] by: MAE(Y ) =
1
N
.
∑
N
i=1
|
b
Y
i
−Y
i
|.
The coefficient of variation (CV) is a little-known
measure that has been proposed by[Karatasou et al.,
2006][Amasyali et al., 2016] to evaluate the predic-
tion of models for building energy consumption. This
value is defined as a percentage, by the formula :
CV (Y ) = 100.
RMSE(Y)
¯
Y
.
As this value is only used in the field of energy
consumption, it will therefore only be evaluated on
consumption values, and not on temperatures (the lat-
ter may also be negative).
4 EXPERIMENTAL RESULTS
As mentioned above, we implemented the four LSTM
architectures described in the section 3.3. To evaluate
their performance in predicting demand response, a
set of use cases were developed based on experimen-
tal data collected in cold rooms. For the cold room,
we had access to large periods of measurement time
with acceptable accuracy where measurements were
made every five seconds. These measurements were
made in a cold room that was replicated in a con-
trolled environment to obtain data to form the models
and prove their predictive power. For these purposes,
we have proposed five use cases allowing us to an-
swer efficiently to the following questions :1) Which
deep learning models are more adapted to represent
our specific data? 2) Which model(s) is less sensitive
to the stochastic occurrence of electricity demand re-
sponse? 3) Which model(s) is more robust to the data
quality, i.e. signal noise (electrical demand response)
and horizon window? We assume that the reference
behaviour of a cold room is characterized by an ideal
”undisturbed” operation, with no phenomenon of de-
mand response or door opening and this over a long
period of time, in order to stabilize the internal tem-
perature. These data measurements are used only to
initialize the four architectures. Then we have estab-
lished five time series datasets to evaluate each LSTM
architecture. These datasets are described as follows.
We note by E
i
a dataset time series where i = 1..5
elaborated for each use case i:
• The use case 1 (train: 127975, test: 60000 )hy-
pothesis is to consider a set of measurements with
three electrical demand response periods, uni-
formly distributed over 3 days. Here we simulate
the stochastic disturbance of the system on con-
sidering a uniform distribution of the noise signal.
Hence δT
erasure
is randomly decreased and T
erasure
is fixed ;
• The use case 2 (train: 223545, test: 149030) hy-
pothesis is to consider a set of measurements with
two electrical demand response periods per day,
uniformly distributed over 5 days. In this case we
increase the frequency of occurrence of the noise
in use case 1 and increase the total number of mea-
surements. Indeed, this case allows us to study the
bias of the frequency of noise occurrence as well
as the amount of data;
• The case 3 (train: 490985, test: 294590) hypoth-
esis is to consider a set of measurements over 5
days with one electrical demand response period
randomly occured per day and with a random pe-
riod. It means both δT
erasure
and T
erasure
are ran-
dom.
• The case 4 (train: 630920, test: 420610) hypoth-
esis is to consider the union of the three previ-
ous hypothesis. It corresponds to a generalized
model of the electrical demand response problem,
i.e. We have a large amount of data, more noise
and more randomness.
• The case 5 (train: 214080, test: 142700) hypoth-
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
388
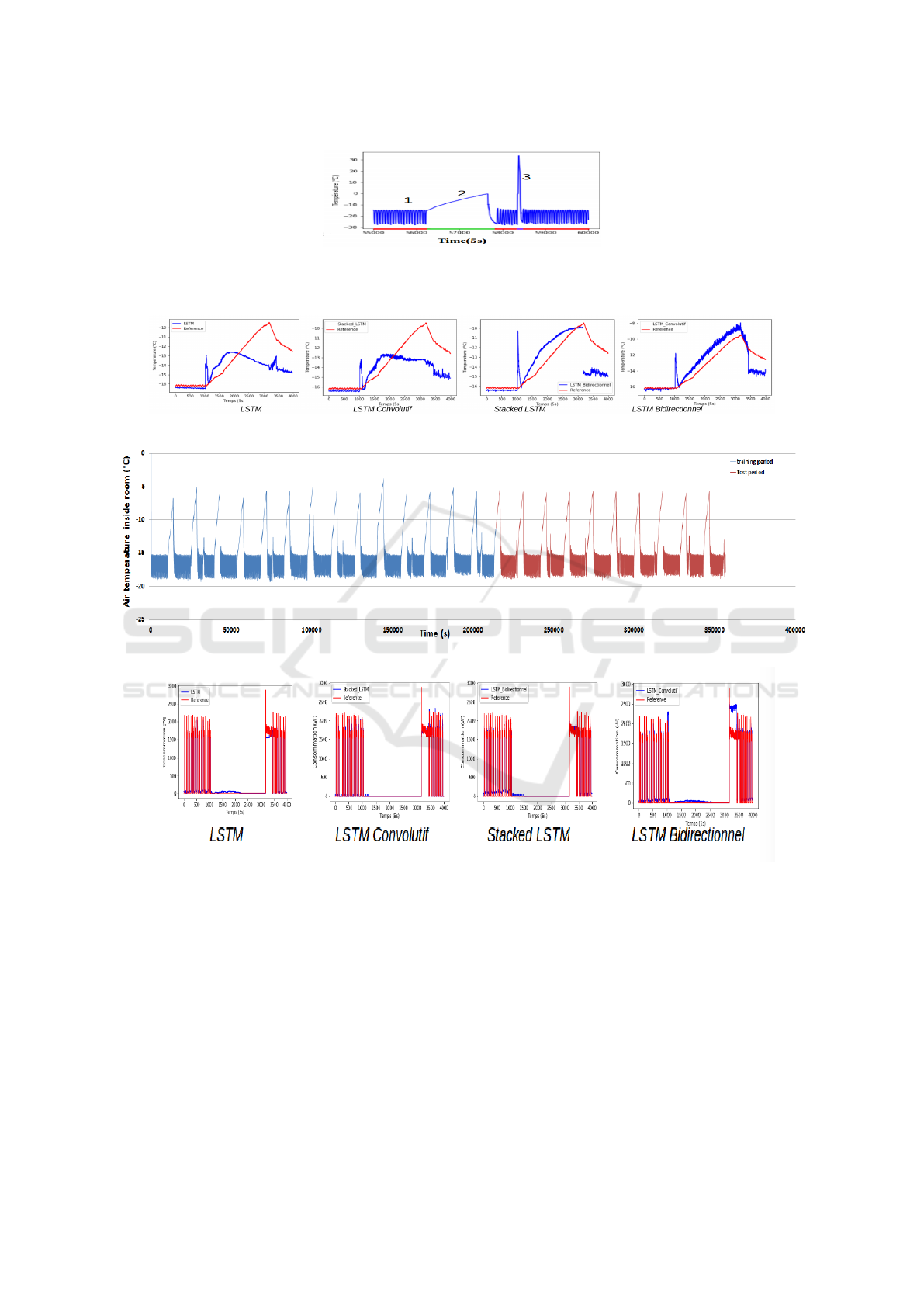
Figure 2: Three modes: (1)Steady state, regular temperature variations according to set points (high/low) ; (2)Electrical
demand response, temperature increases over a long period of time (30min-3h) ; (3)Defrosting, sudden temperature increase
for a very short time (5-10min).
Figure 3: LSTM models prediction of T p
product
in use case 1.
Figure 4: LSTM data time series prediction with E1 datasets.
Figure 5: LSTM models prediction of Compressor
Energy
in use case 1.
esis is to consider a fixed δT
erasure
, a fixed T
erasure
varing between 1 and 3 hours and we increase pre-
diction horizon H.
Each dataset E
i
is respectivly splited into 60% of data
for training (Train) and 40 for validation (Test) sets,
except the E
5
used as Test sample.
4.1 Results Analysis
As observed graphically (Figures: 4,3,5), we can
therefore see much more significant results thanks to
the use of the convolutional LSTM network using the
E
1
dataset, on all features except Compressor
Energy
,
which could be verified graphically. The other models
developed and derived from the LSTM model give us
interesting but much less significant results than those
found with the convolutional LSTM model. However,
it can be noted that the Stacked LSTM and Bidirec-
tional LSTM models obtain fairly high performance
in terms of air temperature. However, these results
are still very modest, which can easily be explained
by the small amount of data. In addition, it should
be noted that some features, such as T p
product
, are in-
sufficiently predicted by all models. These problems
Multivariate Time Series Forecasting with Deep Learning Proceedings in Energy Consumption
389

Table 1: E
i
Temperature T
p
prediction with the four derived LSTM models.
T
p
LSTM ConLSTM StackedLSTM BidirectionalLSTM
E
1
(Mae =0.38,Fit=35.8 ) (Mae=0.38, Fit=60.5 ) (Mae=0.44, Fit=42.8 ) (Mae =0.5, Fit=41.7 )
E
2
(Mae =0.16,Fit=29.7 ) (Mae=0,33, Fit=14.8 ) (Mae=0.14, Fit=30.4 ) (Mae =0.31, Fit=24.4 )
E
3
(Mae =0,27,Fit=48.0 ) (Mae=0.26, Fit=46.9 ) (Mae=0.23, Fit=50.9 ) (Mae =0.31, Fit=52.1 )
E
4
(Mae =0.27,Fit=58.2 ) (Mae=0.33, Fit=55.5 ) (Mae=0.27, Fit=61.1 ) (Mae =0.37, Fit=48.4 )
E
5
- - (Mae=0.19,Fit=69.64) -
Table 2: E
i
Compressor
Energy
prediction with the four derived LSTM models.
CV (Compressor
Energy
) LSTM ConLSTM StackedLSTM BidirectionalLSTM
E
1
18.9 23.5 18.9 20.3
E
2
15.7 13.7 47.1 20.08
E
3
15.1 13.8 54.42 22.6
E
4
16.2 15.9 16.1 16.1
E
5
- - 28.5 -
seem to be partly related to the sensors. A more de-
tailed analysis will be carried out later to check the
proper functioning of these different sensors. The re-
sults obtained with the dataset E
2
are less efficient for
predicting temperature-related features. In particular,
we note a sudden increase in the predicted tempera-
ture as soon as the electrical cut-off is triggered, fol-
lowed by an equally sudden decrease at the end of the
demand response period. As far as the energy con-
sumption is concerned, the behaviour is always repro-
duced as faithfully as ever. With this dataset Bidirec-
tional and Stacked LSTM outperform the other mod-
els. We can note that Stacked and bidirectional LSTM
are less sensible the amount of data. With the E
3
dataset, simple and Convolutional LSTM outperform
the other models. They seem to be more efficient
in the presence of random noises. Bidirectional and
Stacked LSTM are able to predict the dynamics of
time series but are sensitive to noise, especially dur-
ing the starting times of both the demand response
and the retakes. This is manifested by peaks of val-
ues predicted by the last two models. With the E
4
dataset, we recall that is the union of the three pre-
vious datasets, we obtained comparable results with
LSTM and Stacked LSTM. Their predictive accuracy
outperforms the other two models. With the dataset
E
4
we obtained comparable results with LSTM and
Stacked LSTM, their predictive accuracy outperforms
the other two models. It should be noted, however,
that four models are trained on the union of E
1
and
E
2
and they have to predict on the E
3
dataset accord-
ing to the percentages of the Train and Test samples.
What is interesting is that we expected the results in
this use case to be similar to the previous use case (use
case 3). However, learning more noise allows stacked
systems to better predict noise and random data. Also
they seem to be less sensible to the amount data. Fi-
nally the dataset E
5
is used as Test sample for the pre-
trained Stacked LSTM. Since the horizon size of E
5
is
20 minutes, four times bigger than the previous ones,
time series data are less. As long as the size of the
E
5
horizon is four times larger than the previous ones,
the data are more smoothed and less noisy. As a re-
sult, the model was able to better predict with a Gain
of approximately 10%. The Compressor
Energy
is ef-
ficiently predicted in all use cases where the fitting is
arround 90% and the MAE is arround 0.1. This is due
to its independent state from the defrosting and elec-
trical demand response and it has a stationary state.
5 CONCLUSIONS AND FUTURE
WORK
Although the results obtained in the study of series E
1
and E
4
were quite satisfactory, the results of series E
2
and E
3
remain rather moderate, as can be seen from
the graphs and values given above (Table 1, 2). In-
deed, the different models, although trained and then
tested on larger data sets, seem to encounter difficul-
ties in generalizing prediction on test values. How-
ever, some models and their predictions are encourag-
ing, suggesting that the use of deep learning methods
could lead to better results through improvements and
the use of more data. In particular, Stacked LSTM
seems to be the efficient deep learning architecture
providing acceptable predictions in the context of our
specific data. Indeed, the modeling of a refrigeration
system being characterized by the non linearity and
the coupling of several parameters, classical physi-
cal models encounter difficulties in predicting the dy-
namic behaviour of such systems, in particular dur-
ing disturbances such as electrical demand response
periods. Stacked LSTM, due to its ability to adjust
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
390

and self learning, can therefore be very promising in
responding to this type of issues. To increase its effi-
ciency, it could be a possible perspective to use weight
masks during training. Therefore, transfer learning
could be able to favour the adjustment of weights dur-
ing demand response periods, and would obtain pre-
dictions closer to the reference values.
REFERENCES
Aman, S., Frincu, M., Chelmis, C., Noor, M., Simmhan, Y.,
and Prasanna, V. K. (2015). Prediction models for dy-
namic demand response. In IEEE International Con-
ference on Smart Grid Communications (SmartGrid-
Comm).
Amjady, N. (2001). Short-term hourly load forecasting us-
ing time series modeling with peak load estimation ca-
pability. In IEEE Transactions on Power Systems.
andY. Bengio, Y. L. and Hinton, G. (2015). Deep learn-
ing. In Nature, volume 521, pages 436–444. Google
Scholar.
Hagan, M. T. and Behr, S. M. (1987). The time series ap-
proach to short term load forecasting. In IEEE Trans-
action on Power System, pages 785–791.
Hamilton, J. D. (1994). Time Series Analysis. Princeton
University Press, New Jersey, NJ, USA.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. In Neural Computation, pages 1735–1780.
Google Scholar.
Hu, M., Xiao, F., and Wang, L. (2017). Investigation of
demand response potentials of re-sidential air condi-
tioners in smart grids using grey-box room thermal
model.
J.W, T., de Menezes L.M, and P.E, M. (2006). A compar-
ison of univariate methods for forecasting electricity
demand up to a day ahead. In International Journal of
Forecasting, volume 22, pages 1–16.
Kuo, P.-H. and Huang, C. (2018). A High Precision Arti-
ficial Neural Networks Modelfor Short-Term Energy
Load Forecasting.
Nataraja, C., G.M.B, Shilpa, G., and Harsha, J. S. (2012).
Short term load forecasting using time series analysis:
A case study for karnataka. In International Journal of
Engineering Science and Innovative Technology, vol-
ume 1, India.
Rios-Moreno, G., Trejo-Perea, M., Casta
˜
neda-Miranda,
R., Hern
´
andez-Guzm
´
an, V., and Herrera-Ruiz, G.
(2007). Modelling temperature in intelligent buildings
by means of autoregressive models. In Automation in
Construction, volume 16, pages 713–722.
Rojo-Alvarez, J. L., Martınez-Ramon, M., and de Prado-
Cumplido, M. (2004). Support vector method for ro-
bust arma system identification. In IEEE Transactions
on Signal Processing, vol. 52, no. 1, pages 155–164.
Sheng, C. J. and Duc-Sonand, T. (2018). Forecasting energy
consumption time series using machine learning tech-
niques based on usage patterns of residential house-
holders. In Energy, volume 165, pages 709–726.
Shi, X., Chen, Z., Wang, H., Yeung, D.-Y., Wong, W.-K.,
and Woo, W. (2015). Convolutional LSTM Network:
A Machine Learning Approach for Precipitation Now-
casting.
Simmhan, Y., Aman, S., Kumbhare, A., Liu, R., and
Stevens, S. (2013). Cloud-based software platform
for data-driven smart grid management. In IEEE/AIP
Computing in Science and Engineering.
Xue, X., Wang, S., Yan, C., and Cui, B. (2014). A fast
chiller power demand response control strategy for
buildings connected to smart grid.
Ziekow, H., Goebel, C., Struker, J., and Jacobsen, H.
(2013). The potential of smart home sensors in for-
casting household electricity demand. In IEEE Inter-
national Conference on Smart Grid Communications
(SmartGridComm).
Multivariate Time Series Forecasting with Deep Learning Proceedings in Energy Consumption
391
