Extended Possibilistic Fuzzification for Classification
Robert K. Nowicki
a
, Janusz T. Starczewski
b
and Rafał Grycuk
c
Institute of Computational Intelligence, Czestochowa University of Technology, Czestochowa, Poland
Keywords:
Type-2 Fuzzy Classifier, Extended Possibilistic Fuzzification, 3D Possibility and Necessity of Fuzzy Events.
Abstract:
In this paper, the extended possibilistic fuzzification for classification is proposed. Similar approach with
the use of fuzzy–rough fuzzification (Nowicki and Starczewski, 2017; Nowicki, 2019) allows to obtain one
of three decisions, i.e. ”yes”, ”no”, and ”I do not know”, The last label occurs when input information is
imprecise, incomplete or in general uncertain, and consequently, determining the unequivocal decision is
impossible. We extend three-way decision (Hu et al., 2017; Liu et al., 2016; Sun et al., 2017; Yao, 2010; Yao,
2011) into four-way decision by extending possibilistic fuzzification to the three–dimensional possibility and
necessity measures of fuzzy events.
1 INTRODUCTION
Possibility distributions were introduced as an alter-
native to probability distributions. A possibility dis-
tribution on a set X is a function ϕ: X → [0,1] such
that sup
x∈X
ϕ(x) = 1. There are dual measures formed
by a degree of possibility that some event is possible
and a degree of necessity that ensures an event takes
place. Generally, we can measure possibility and ne-
cessity degrees of a fuzzy event, whenever A denotes
a fuzzy set in X , the degrees of possibility and neces-
sity of A are be defined as follows (Zadeh, 1978)
π(A) = sup
x∈X
min(ϕ(x),µ
A
(x)), (1)
ν(A) = inf
x∈X
max(1 − ϕ (x), µ
A
(x)). (2)
Note that t-norms and t-conorms may be considered
instead of min and max; however, such approach is
closer related to a concept of a rough-fuzzy set. Ex-
emplary calculations of possibility and necessity de-
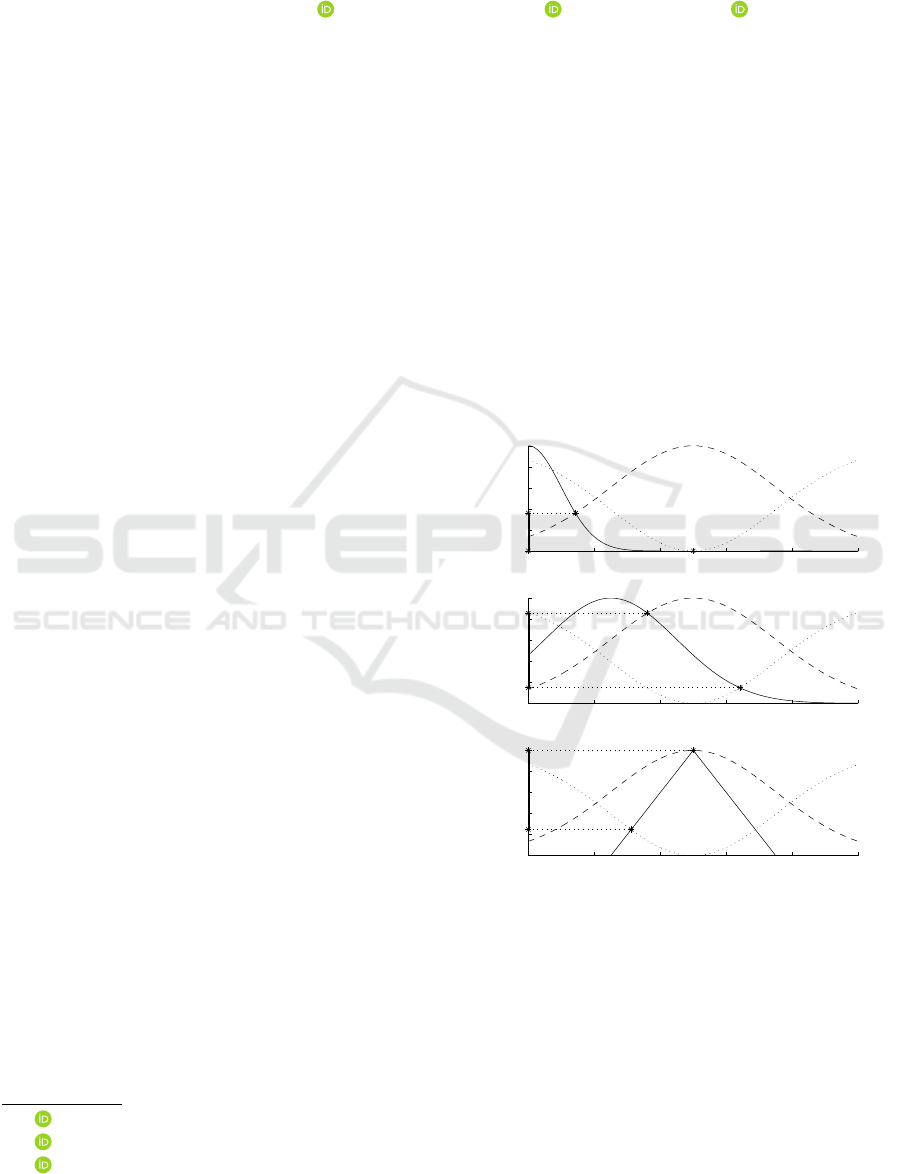
grees are presented in Fig. 1.
The possibility is related to the difficulty to de-
scribe objects by means of suitable attributes. Two
measures can independently classify events, as possi-
ble or certain, under possibility distribution describ-
ing imperfections of event’s attributes. We need to
obtain an a’priori knowledge about the imprecision
of inputs in order to determine an proper shape of
a
https://orcid.org/0000-0003-2865-2863
b
https://orcid.org/0000-0003-4694-7868
c
https://orcid.org/0000-0002-3097-985X
0 2 4 6 8 10
0
0.2
0.4
0.6
0.8
1
x
A
1
, φ
π(A
1
) →
ν(A
1
) →
(a)
0 2 4 6 8 10
0
0.2
0.4
0.6
0.8
1
x
A
2
, φ
π(A
2
) →
ν(A
2
) →
(b)
0 2 4 6 8 10
0
0.2
0.4
0.6
0.8
1
x
A
3
, φ
π(A
3
) →
ν(A
3
) →
(c)
Figure 1: Calculation of possibility and necessity degrees of
fuzzy sets: ϕ — possibility distribution (dashed lines), µ
A
i
— membership functions of fuzzy sets (solid lines), π(A
i
)
and ν(A
i
) — possibility and necessity, i = 1,2,3.
fuzzification. In many cases, knowledge about the
nature of impressions is limited, thus a three–point
estimation can be successfully applied in analogy to
the probabilistic approaches of the triangular distri-
bution in risk analysis, project management and busi-
ness decision making. Obviously, when information
about the fuzzification of an attribute is limited (e.g.
its smallest and largest values), we apply interval de-
Nowicki, R., Starczewski, J. and Grycuk, R.
Extended Possibilistic Fuzzification for Classification.
DOI: 10.5220/0008168303430350
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 343-350
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
343
scription of the membership uncertainty; however, if
the most likely value of the attribute is also known, the
fuzzification can be modelled by a triangular mem-
bership function in the truth interval [0,1] which de-
scribes a type-2 fuzzy set (Najariyan et al., 2017; Han
et al., 2016). The type-2 fuzzy subset is defined as a
set X (called also as fuzzy-valued fuzzy set), denoted
by
˜
A, which is a vague collection of elements charac-
terized by membership function µ
˜
A
: X → F ([0,1]),
where F ([0,1]) is a set of all classical fuzzy sets in
the unit interval [0, 1]. Each x ∈ X is associated with
a secondary membership function f
x
∈ F ([0, 1]) i.e.
a mapping f
x
: [0,1] → [0,1]. The fuzzy membership
grade µ
˜
A
(x) is often called a fuzzy truth value, since
its domain is the truth interval [0,1]. A type-1 mem-
bership function which is used in a type-2 set whose
secondary membership grades are equal to the unity
is called a principal membership function. The upper
and lower bounds of a secondary membership func-
tion are respectively called upper and lower member-
ship functions.
2 EXTENDED TRIANGULAR
POSSIBILITY FUZZIFICATION
Uncertainty of input data should be modeled by a non-
singleton fuzzification of system’s inputs. In several
classes of problems, we are able to assign triangular
shapes of fuzzifying functions according to an a’priori
knowledge about the uncertainty. Therefore, fuzzifi-
cation of inputs can be considered in terms of possi-
bility measures for input values x
0
, while a member-
ship function of the rule premise, µ
A
0
, can be viewed
as a possibility distribution. Consequently, the possi-
bility of A
k
forms an upper bound of fuzzified inputs
µ
A
k
x
0
= sup
x∈X
T
µ
A
0
x,x
0
,µ
A
k
(x)
, (3)
the necessity of A
k
defines a lower bound of fuzzified
inputs
µ
A
k
x
0
= inf
x∈X
S
N
µ
A
0
x,x
0
,µ
A
k
(x)
, (4)
while the original membership function of A
k
is re-
ferred as an antecedent principal membership func-
tion.
Note that the possibility expression (3) is the same
as the fuzzification in a traditional conjunction rea-
soning (Mouzouris and Mendel, 1997). On the con-
trary, the necessity expression (4) is the same as the
fuzzification in an implication reasoning. With the
use of both measures and the non-fuzzified principal
membership function. We model more information
about fuzzification.
Our method makes assumption that µ
A
0
(x,x
0
)
varies in the whole spectrum of possible values of x
0
independently of x. Thus, we are able to determine
the upper limit of a t-norm according to (3), as well
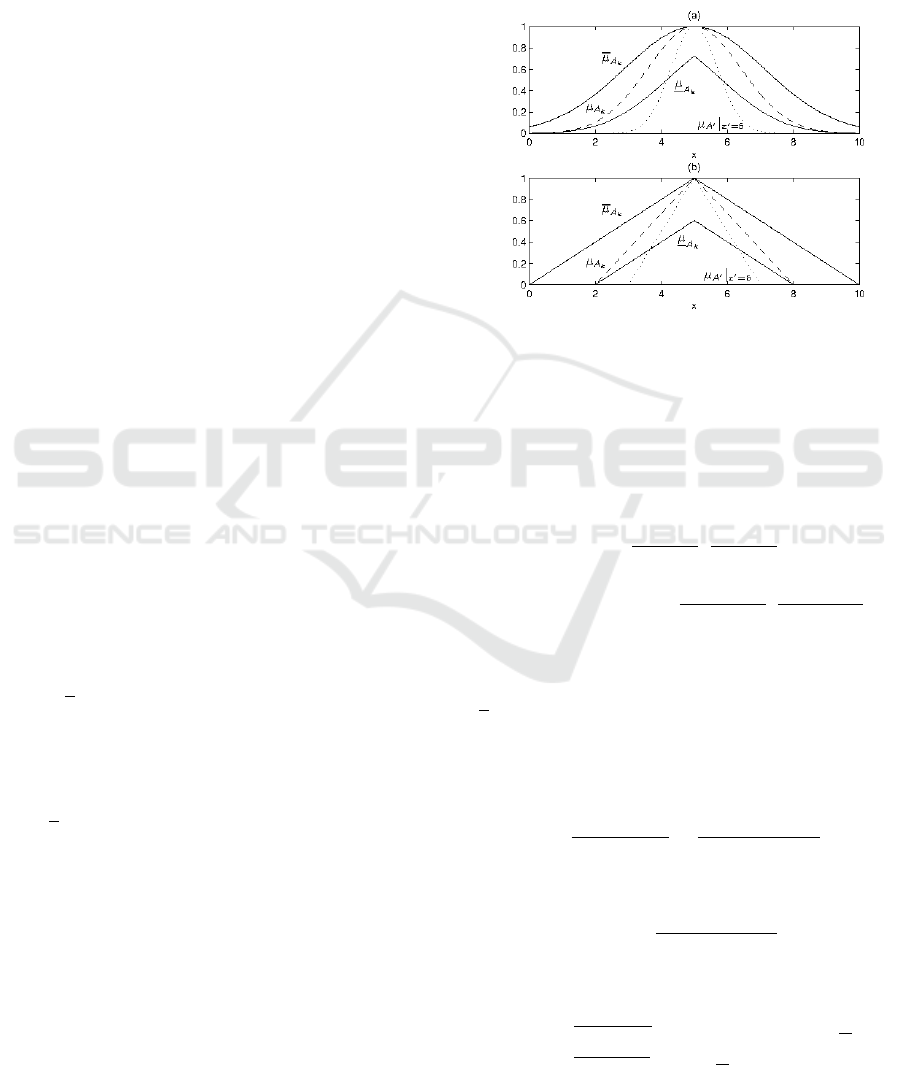
as the lower limit of an s-implication in (4). In Fig-
ure 2, the construction of possibility and necessity of
antecedent (principal) A
k
is shown.
Figure 2: Extended possibilistic triangular fuzzifications of:
(a) — Gaussian principal antecedent (dashed line), (b) —
of triangular principal antecedent (dashed line); upper and
lower membership functions (solid lines).
2.1 Triangular Fuzzification
Let two triangular membership functions be
defined as the premise membership function,
µ
A
0
n
(x
n
) =
.
min
x
n
−x
0
n
+∆
n
∆
n
,
x
0
n
+∆
n
−x
n
∆
n
.
, and the
k-th antecedent membership function, expressed
by µ
A
k,n
(x
n
) =
.
min
x
n
−m
k,n
+δ
k,n
δ
k,n
,
m
k,n
+γ
k,n
−x
n
γ
k,n
.
.
Moreover, let a t-conorm in (4) be the maximum, and
the necessity antecedent function be defined by
µ
A
k
(x
0
n
) = inf
x
n
∈X
n
max
1 − µ
A
0
n
(x
0
n
,x
n
),µ
A
k,n
(x
n
)
.
(5)
For the left slope, max
µ
A
0
n
(x
n
,x
0
n
),µ
A
k,n
(x
n
)
reaches its infimum at x
∗
n
which satisfies
1 −
x
∗
n
− x
0
n
+ ∆
n
∆
n
=
x
∗
n
− m
k,n
+ δ
k,n
δ
k,n
. (6)
Consequently,
x
∗
n
=
∆
n
m
k,n
+ δ
k,n
x
0
n
∆
n
+ δ
k,n
. (7)
Let us evaluate µ
A
k,n
(x
n
) for x
∗
n
in both slopes
µ
A
k,n
(x
∗
n
) =
x
0
n
−m
k,n
+δ
k,n
∆
n
+δ
k,n
if x
0
n
∈
m
k,n
− ∆
n
− δ
k,n
,m
k,n
m
k,n
+γ
k,n
−x
0
n
∆
n
+γ
k,n
if x
0
n
∈
m
k,n
,m
k,n
+ ∆
n
+ δ
k,n
(8)
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
344

where m
k,n
denotes a new center value.
It is profitable that the necessity being a lower
bound of triangular fuzzification remains triangular,
µ
A
k
(x
0
n
) =
,
min
x
0
n
− m
k,n
+ δ
k,n
e
δ
k,n
,
m
k,n
+ γ
k,n
− x
0
n
e
γ
k,n
!,
,
(9)
where
e
δ
k,n
= ∆
n
+ δ
k,n
and
e
γ
k,n
= ∆
n
+ γ
k,n
. A new
value of the center m
k,n
can be obtained as x
0
n
fullfill-
ing the following
x
0∗
n
− m
k,n
+ δ
k,n
∆
n
+ δ
k,n
=
m
k,n
+ γ
k,n
− x
0∗
n
∆
n
+ γ
k,n
, (10)
m
k,n
= x
0∗
n
=
∆
n
(γ
k,n
− δ
k,n
)
2∆
n
+ δ
k,n
+ γ
k,n
+ m
k,n
.
By substituting m
k,n
into (9)
h
k,n
=
γ
k,n
+ δ
k,n
2∆
n
+ δ
k,n
+ γ
k,n
. (11)
Although the possibilistic measures implement non-
singleton fuzzification using either fuzzy implications
or fuzzy conjunctions, the reasoning schema is inde-
pendent, and both implication and conjunction rea-
soning schemes can be here applied interchangeably.
3 GENERAL FL CLASSIFIER
Consider a type-2 fuzzy logic system with the un-
certainty of the general form (Mendel, 2001; Star-
czewski, 2013; Nowicki, 2019). Such system can be
adapted to classification tasks with the following form
of rules:
R
k
: IF v
1
is A
1,k
AND v
2
is A
2,k
AND. ..
THEN x ∈ ω
1
(z
1,k
),x ∈ ω
2
(z
2,k
),. ..
(12)
where observations v
i
and objects x are independent
variables, k = 1, ... ,N is the number of N rules, and
z
j,k
is a membership degree of the object x to the j–th
class ω
j
Memberships of objects are considered to be
crisp rather than fuzzy, i.e.
z
j,k
=
(
1 if x ∈ ω
j
0 if x /∈ ω
j
. (13)
Each rule of a fuzzy system can be regarded as
a certain two-place function R : [0, 1]
2
→ [0, 1]. In
the case of the conjunction-type fuzzy systems, func-
tion R is defined by any t-norm R(a, b) = T (a,b), A
logical approach use genuine fuzzy implications, i.e.
strong implication R(a,b) = S (N (a), b), residual im-
plications R(a,b) = sup
c∈[0,1]
{
c|T(a, c) ≤ b
}
, quan-
tum logic implications R(a, b) = S (N (a), T (a,b)).
Traditional t-norm T, t-conorm S, negation N, have
to be extended to operate on fuzzy values rather than
numbers from [0,1] (see eg. (Starczewski, 2013)).
The fuzzy reasoning process leads to the conclu-
sion in the form of y is B
0
, where B
0
is aggregated
from conclusions B
0
k
for k = 1,.. .,N obtained as a
result of fuzzy reasoning using separated rules R
k
.
Compositions B
0
k
= A
0
◦ R (A
k
,B
k
) are fuzzy sets with
the membership functions defined using sup−T com-
positional rule of inference, i.e.
µ
B
0
k
(y) = sup
x∈X
T
µ
A
0
(x),R
µ
A
k
(x),µ
B
k
(y)
. (14)
In the case of singleton fuzzification, equation (14)
yields the following
µ
B
0
k
(y) = R
µ
A
k
(x
0
),µ
B
k
(y)
. (15)
which allows for omitting a troublesome supremum.
In the case of conjunction reasoning, we aggregate
B
0
=
S
N
k=1
B
0
k
, consequently
µ
B
0
(y) =
N
S
k=1
µ
B
0
k
(y) (16)
while in the case of genuine implications, aggrega-
tion is performed with the use of conjunctions B
0
=
T
N
k=1
B
0
k
, i.e.,
µ
B
0
(y) =
N
T
k=1
µ
B
0
k
(y), (17)
where all operations are on type-2 fuzzy sets.
3.1 Algebraic Operations
In (Starczewski, 2013), we have defined a regular t-
norm on a set of triangular fuzzy truth numbers
µ
T
N
n=1
F
n
(u) = max (0,min (λ (u),ρ (u))), (18)
where
λ(u) =
u−l
m−l
if m > l
singleton(u − m) if m = l,
(19)
ρ(u) =
r−u
r−m
if r > m
singleton(u − m) if m = r,
(20)
and l =
T
N
n=1
l
n
, m =
T
N
n=1
m
n
, r =
T
N
n=1
r
n
. This for-
mulation allows us to use ordinary t-norms for up-
per, principal and lower memberships independently.
Moreover, we have proved the function given by (18)
operating on triangular and normal fuzzy truth values
is a t-norm on L = (F
M
([0,1]) ,v) (of type-2).
Extended Possibilistic Fuzzification for Classification
345

3.2 Triangular Centroid Type Redution
The first step transforming a type-2 fuzzy conclusion
into a type-1 fuzzy set is called a type reduction. In
classification, we perform only type reduction with-
out the second step of final defuzzification. In (Star-
czewski, 2014), we have obtained exact type-type re-
duced sets for triangular type-2 fuzzy conclusions as
a set of ordered discrete primary values y
k
and their
secondary membership functions
f
k
(u
k
) =
,
min
u
k
− µ
k
b
µ
k
− µ
k
,
µ
k
− u
k
µ
k
−
b
µ
k
!,
(21)
for k = 1,. .., K. The secondary membership func-
tions are specified by upper, principal and lower mem-
bership grades, µ
k
>
b
µ
k
> µ
k
, k = 1,2, .. .,K. Interval
type reduction gives [y
min
,y
max
] and y
pr
is a centroid
of the principal membership grades calculated by
y
pr
=
K
∑
k=1
b
µ
k
y
k
b
µ
k
. (22)
The exact centroid of the triangular type-2 fuzzy set is
characterized by the following membership function:
µ(y) =
y−y
left
(y)
(1−q
l
(y))y+q
l
(y)y
pr
−y
left
(y)
if y ∈
y
min
,y
pr
y−y
right
(y)
(1−q
r
(y))y+q
r
(y)y
pr
−y
right
(y)
if y ∈
y
pr
,y
max
,
(23)
where the parameters are
q
l
(y) =
∑
K
k=1
b
µ
k
∑
K
k=1
←−
µ
k
(y)
, q
r
(y) =
∑
K
k=1
b
µ
k
∑
K
k=1
−→
µ
k
(y)
,
y
left
(y) =
∑
K
k=1
←−
µ
k
(y)y
k
∑
K
k=1
←−
µ
k
(y)
, y
right
(y) =
∑
K
k=1
−→
µ
k
(y)y
k
∑
K
k=1
−→
µ
k
(y)
,
with
←−
µ
k
(y) =
(
µ
k
if y
k
≤ y
µ
k
otherwise
,
−→
µ
k
(y) =
(
µ
k
if y
k
≥ y
µ
k
otherwise
.
3.3 Type Reduction in Classification
In classification, y
k
are either equal to 0 or to 1. There-
fore, instead of the Karnik–Mendel iterative type re-
duction, we propose the following procedure. In the
case of conjunction (Mamdani) type of fuzzy reason-
ing, the lower and upper membership grades are ex-
pressed as follows
z
j
=
N
∑
k=1
k : z
k
j
=1
µ
A
k
L
(v)
N
∑
k=1
µ
A
k
L
(v)
z
j
=
N
∑
k=1
k : z
k
j
=1
µ
A
k
U
(v)
N
∑
k=1
µ
A
k
U
(v)
, (24)
where A
k
L
and A
k
U
are expressed as follows
A
k
L
=
(
A
k
∗
if z
k
j
= 1
A
k∗
if z
k
j
= 0
A
k
U
=
(
A
k∗
if z
k
j
= 1
A
k
∗
if z
k
j
= 0
.
(25)
Whenever the classifier is built with the use of logical-
type reasoning, we can use the following analogy
z
j
=
N
∑
k=1
k : z
k
j
=1
N
∑
r=1
r : z
r
j
=0
N
µ
A
r
L
(v)
N
∑
k=1
N
∑
r=1
r : z
r
j
6=z
k
j
N
µ
A
r
L
(v)
, (26)
z
j
=
N
∑
k=1
k : z
k
j
=1
N
∑
r=1
r : z
r
j
=0
N
µ
A
r
U
(v)
N
∑
k=1
N
∑
r=1
r : z
r
j
6=z
k
j
N
µ
A
r
U
(v)
, (27)
where A
k
L
and A
k
U
are defined as previously, by equa-
tions (25), and N is any fuzzy negation N(x) = 1 − x.
3.4 Interpretation of Type-reduced Sets
A proper interpretation of obtained is a complex prob-
lem for the extended possibilistic fuzzy classification.
If z
j
is a lower membership grade of an object x to a
class ω
j
and z
j
is its upper membership grade in the
form of equations (24) respectively, then we suggest
to fix a threshold value, e.g. 0.5 and perform a crisp
decision in the following way:
x ∈ ω
j
if z
j
≥
1
2
and z
j
>
1
2
x /∈ ω
j
if z
j
<
1
2
and z
j
≤
1
2
likely possible class. if z
j
<
1
2
and
b
z
∗
j
≥
1
2
likely impossible class. otherwise.
(28)
4 SIMULATION RESULTS
The following scheme of experiments is provided:
1. An ordinary (type-1) fuzzy system on exact data
in a laboratory environment is trained. This sys-
tem becomes a framework for a possibilistic sys-
tem. In the performed simulations the standard
Back Propagation learning method was used.
2. Real-time systems usually operate on noisy sig-
nals, and the nature of measurement noise might
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
346

Table 1: Accuracy for classification (in %) of Iris data with additional Gaussian noise to all inputs σ
i
= 0.1∆x
i
, where ∆x
i
is
a range of x
i
, i = 1,2, 3,4; σ — standard deviation of p.
System
¯
σ
i
Incorrect Unclassified Unclassified Correct
incorrect suggestion correct suggestion
lrn./test lrn./test lrn./test lrn./test
Logical-type, no noise
singleton — 18.7/24.7 — — 81.3/75.3
Logical-type, noised inputs
singleton — 37.8/36.5 — — 62.2/63.5
0,01 31,8/33,9 6,0/2,5 8,1/10,7 54,1/52, 9
0,02 27, 9/27,0 9, 9/9,5 16,7/19, 8 45,4/43, 7
0,03 23, 3/23,3 14, 5/13,1 24,0/26, 5 38,2/37, 1
fuzzy
0,10 12, 1/11,8 25, 7/24,7 54,6/56, 2 7,6/7, 3
-
0,20 7,8/8, 4 30,0/28,1 62, 0/63,1 0,2/0, 4
rough
0,30 6,1/6, 5 31,8/30,0 62, 2/63,5 0,0/0, 0
0,40 4,3/4, 5 33,5/32,0 62, 2/63,5 0,0/0, 0
0,50 3,8/2, 9 34,0/33,6 62, 2/63,5 0,0/0, 0
0,60 2,7/3, 1 35,1/33,4 62, 2/63,5 0,0/0, 0
1,00 0,5/0, 5 37,3/35,9 62, 2/63,5 0,0/0, 0
0.01 37.3/37.5 — — 62.7/62.5
0.02 37.2/36.3 — — 62.8/63.7
0.03 37.8/40.1 — — 62.2/59.9
non
0.10 40.5/41.3 — — 59.5/58.7
-
0.20 45.2/45.9 — — 54.8/54.1
singleton
0.30 46.9/49.4 — — 53.1/50.6
0.40 49.3/49.3 — — 50.7/50.7
0.50 51.8/52.1 — — 48.2/47.9
0.60 52.9/53.3 — — 47.1/46.7
1.00 58.8/59.3 — — 41.2/40.7
Conjunction-type, no noise
singleton — 0.4/7.3 — — 99.6/92.7
Conjunction-type, noised inputs
singleton — 14.3/16.1 — — 85.7/83.9
0,01 9,9/10, 4 4,4/5, 7 5,0/2, 3 80,7/81,5
0,02 6,5/7, 5 7,8/8, 6 10, 5/9,3 75, 2/74,6
0,03 4,3/4, 0 10,0/12,1 17, 1/15,5 68, 6/68,3
fuzzy
0,10 0,1/0, 2 14,2/15,9 56, 8/55,6 28, 9/28,3
-
0,20 0,0/0, 0 14,3/16,1 82, 4/80,2 3,3/3, 7
rough
0,30 0,0/0, 0 14,3/16,1 85, 7/83,9 0,0/0, 0
0,40 0,0/0, 0 14,3/16,1 85, 7/83,9 0,0/0, 0
0,50 0,0/0, 0 14,3/16,1 85, 7/83,9 0,0/0, 0
0,60 0,0/0, 0 14,3/16,1 85, 7/83,9 0,0/0, 0
1,00 0,0/0, 0 14,3/16,1 85, 7/83,9 0,0/0, 0
0.01 14.5/13.9 — — 85.5/86.1
0.02 14.0/14.9 — — 86.0/85.1
0.03 14.1/13.9 — — 85.9/86.1
non
0.10 14.5/15.6 — — 85.5/84.4
-
0.20 20.3/18.9 — — 79.7/81.1
singleton
0.30 34.6/33.7 — — 65.4/66.3
0.40 51.9/50.3 — — 48.1/49.7
0.50 63.6/63.8 — — 36.4/36.2
0.60 68.3/69.0 — — 31.7/31.0
1.00 70.3/70.5 — — 29.7/29.5
be known. Following this, a white Gaussian noise
with a standard deviation value σ
i
corresponding
to the i–th input was added.
3. The additional noise should match non-singleton
fuzzification. Consequently, non-singleton fuzzi-
fication and possibilistic fuzzification using Gaus-
sian membership functions with standard devia-
tion values
¯
σ
i
were performed.
We have decided to present a multiple output fuzzy
rough set system, in which each class was trained
against all other classes. All membership functions
were of the Gaussian type. The Cartesian product
was realized by the algebraic product t-norm. Both
Extended Possibilistic Fuzzification for Classification
347
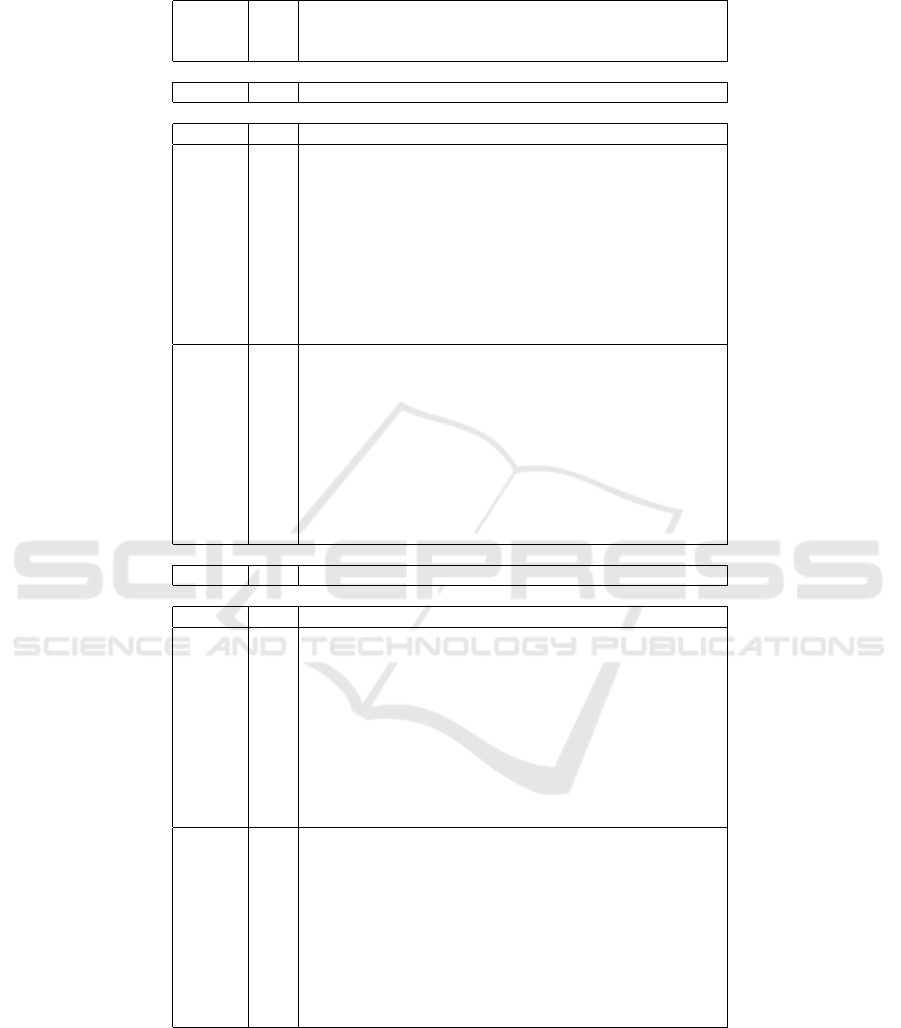
Table 2: Accuracy for classification (in %) of Wisconsin Breast Cancer data with additional Gaussian noise to all inputs
σ
i
= 0.1∆x
i
, where ∆x
i
is a range of x
i
, i = 1,2, 3,4.
System
¯
σ
i
Incorrect Unclassified Unclassified Correct
incorrect suggestion correct suggestion
lrn./test lrn./test lrn./test lrn./test
Logical-type, no noise
singleton — 2.9/5.0 — — 97.1/95.0
Logical-type, noised inputs
singleton — 23.7/25.1 — — 76.3/74.9
0,01 18, 5/18,8 5, 3/6,3 6, 0/5,6 70,3/69, 3
0,02 13, 2/13,7 10, 5/11,4 13,4/12, 0 62,9/62, 9
0,03 8,7/8, 9 15,0/16,2 20, 5/18,9 55, 8/56,0
fuzzy
0,10 0,2/0, 4 23,5/24,7 51, 5/50,7 24, 8/24,2
-
0,20 0,0/0, 1 23,7/25,0 64, 3/63,9 11, 9/11,0
rough
0,30 0,0/0, 0 23,7/25,1 71, 6/70,3 4,7/4, 6
0,40 0,0/0, 0 23,7/25,1 74, 5/72,9 1,8/2, 0
0,50 0,0/0, 0 23,7/25,1 75, 9/74,3 0,4/0, 6
0,60 0,0/0, 0 23,7/25,1 76, 3/74,9 0,0/0, 0
1,00 0,0/0, 0 23,7/25,1 76, 3/74,9 0,0/0, 0
0.01 24.0/24.8 — — 76.0/75.2
0.02 23.8/24.0 — — 76.2/76.0
0.03 23.9/23.7 — — 76.1/76.3
non
0.10 24.1/24.7 — — 75.9/75.3
-
0.20 24.9/24.9 — — 75.1/75.1
singleton
0.30 25.9/27.1 — — 74.1/72.9
0.40 27.0/27.1 — — 73.0/72.9
0.50 27.9/28.2 — — 72.1/71.8
0.60 29.3/29.6 — — 70.7/70.4
1.00 34.8/34.5 — — 65.2/65.5
Conjunction-type, no noise
singleton — 2.6/4.8 — — 97.4/95.2
Conjunction-type, noised inputs
singleton — 19.6/20.0 — — 80.4/80.0
0,01 14, 0/15,2 5, 5/4,8 6, 2/6,9 74,3/73, 0
0,02 9,0/9, 6 10,6/10,4 13, 8/14,2 66, 6/65,8
0,03 5,4/5, 9 14,1/14,1 22, 4/22,7 58, 0/57,3
fuzzy
0,10 0,1/0, 4 19,4/19,6 56, 7/56,8 23, 7/23,1
-
0,20 0,0/0, 1 19,6/19,9 69, 3/69,6 11, 2/10,4
rough
0,30 0,0/0, 0 19,6/20,0 76, 2/76,0 4,2/4, 0
0,40 0,0/0, 0 19,6/20,0 78, 9/78,3 1,6/1, 7
0,50 0,0/0, 0 19,6/20,0 80, 1/79,4 0,3/0, 6
0,60 0,0/0, 0 19,6/20,0 80, 4/80,0 0,0/0, 0
1,00 0,0/0, 0 19,6/20,0 80, 4/80,0 0,0/0, 0
0.01 18.9/19.4 — — 81.1/80.6
0.02 17.3/18.1 — — 82.7/81.9
0.03 15.3/15.7 — — 84.7/84.3
non
0.10 5.8/6.8 — — 94.2/93.2
-
0.20 3.8/4.5 — — 96.2/95.5
singleton
0.30 3.9/4.2 — — 96.1/95.8
0.40 3.9/4.1 — — 96.1/95.9
0.50 4.1/4.2 — — 95.9/95.8
0.60 4.3/4.2 — — 95.7/95.8
1.00 12.5/12.6 — — 87.5/87.4
logical-type and conjunction-type fuzzy systems were
compared in their singleton, non-singleton and pos-
sibilistic realizations. The tests were carried out us-
ing 10-fold cross validation. Tables 1-3 present a
direct comparison of average results for six classi-
fiers presented in the paper, i.e. the fuzzy classifier
with singleton fuzzification, the classifier with classic
non-singleton fuzzification and the classifier with pro-
posed extended possibilistic fuzzification, while all of
them have been realized in two versions with two dif-
ferent implication methods. The classifiers with non-
singleton and possibilistic fuzzification have been ex-
amined for various levels of assumed uncertainty of
input data. These levels are relative with respect to
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
348
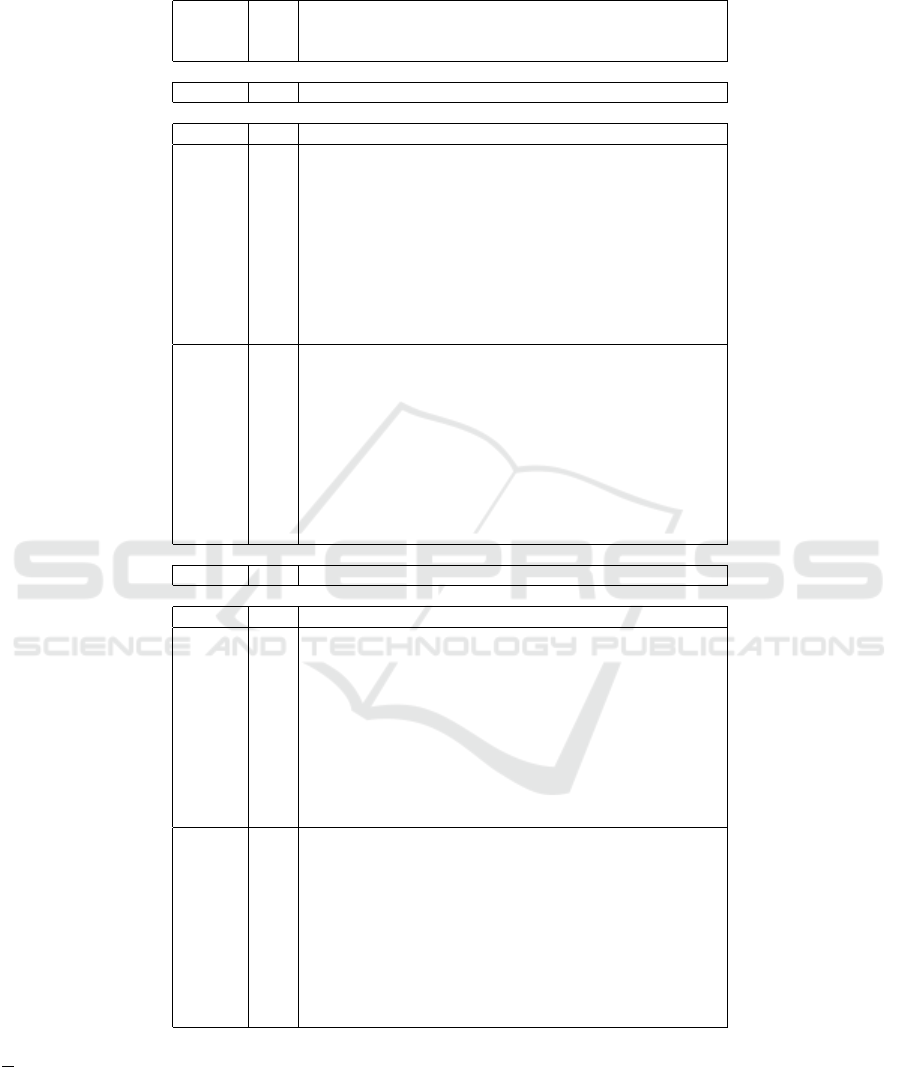
Table 3: Accuracy for classification (in %) of Pima Indians Diabetes data with additional Gaussian noise to all inputs σ
i
=
0.1∆x
i
, where ∆x
i
is a range of x
i
, i = 1,2, 3,4.
System
¯
σ
i
Incorrect Unclassified Unclassified Correct
incorrect suggestion correct suggestion
lrn./test lrn./test lrn./test lrn./test
Logical-type, no noise
singleton — 11.5/29.7 — — 88.5/70.3
Logical-type, noised inputs
singleton — 32.3/33.1 — — 67.7/66.9
0,01 16, 6/18,0 15, 7/15,1 19,4/20, 2 48,3/46, 8
0,02 7,4/7, 9 24,9/25,2 38, 2/37,7 29, 6/29,3
0,03 3,2/3, 5 29,1/29,5 51, 2/50,7 16, 6/16,3
fuzzy
0,10 0,0/0, 0 32,3/33,1 67, 6/66,8 0,1/0, 1
-
0,20 0,0/0, 0 32,3/33,1 67, 7/66,9 0,0/0, 0
rough
0,30 0,0/0, 0 32,3/33,1 67, 7/66,9 0,0/0, 0
0,40 0,0/0, 0 32,3/33,1 67, 7/66,9 0,0/0, 0
0,50 0,0/0, 0 32,3/33,1 67, 7/66,9 0,0/0, 0
0,60 0,0/0, 0 32,3/33,1 67, 7/66,9 0,0/0, 0
1,00 0,0/0, 0 32,3/33,1 67, 7/66,9 0,0/0, 0
0.01 32.3/33.2 — — 67.7/66.8
0.02 32.1/33.0 — — 67.9/67.0
0.03 32.3/33.8 — — 67.7/66.2
non
0.10 32.1/31.9 — — 67.9/68.1
-
0.20 32.2/32.7 — — 67.8/67.3
singleton
0.30 32.0/33.1 — — 68.0/66.9
0.40 31.8/33.1 — — 68.2/66.9
0.50 31.8/33.3 — — 68.2/66.7
0.60 31.7/32.2 — — 68.3/67.8
1.00 31.7/33.1 — — 68.3/66.9
Conjunction-type, no noise
singleton — 11.5/28.6 — — 88.5/71.4
Conjunction-type, noised inputs
singleton — 32.8/33.3 — — 67.2/66.7
0,01 15, 4/16,9 17, 4/16,4 22,0/22, 9 45,2/43, 8
0,02 6,0/6, 5 26,8/26,8 42, 1/42,3 25, 1/24,3
0,03 2,2/2, 6 30,6/30,8 54, 3/54,1 12, 9/12,6
fuzzy
0,10 0,0/0, 0 32,8/33,3 67, 1/66,6 0,1/0, 1
-
0,20 0,0/0, 0 32,8/33,3 67, 2/66,7 0,0/0, 0
rough
0,30 0,0/0, 0 32,8/33,3 67, 2/66,7 0,0/0, 0
0,40 0,0/0, 0 32,8/33,3 67, 2/66,7 0,0/0, 0
0,50 0,0/0, 0 32,8/33,3 67, 2/66,7 0,0/0, 0
0,60 0,0/0, 0 32,8/33,3 67, 2/66,7 0,0/0, 0
1,00 0,0/0, 0 32,8/33,3 67, 2/66,7 0,0/0, 0
0.01 32.6/33.6 — — 67.4/66.4
0.02 32.3/32.8 — — 67.7/67.2
0.03 31.7/32.7 — — 68.3/67.3
non
0.10 28.3/29.9 — — 71.7/70.1
-
0.20 28.8/29.6 — — 71.2/70.4
singleton
0.30 30.4/30.6 — — 69.6/69.4
0.40 32.0/32.4 — — 68.0/67.6
0.50 33.3/33.4 — — 66.7/66.6
0.60 33.8/33.5 — — 66.2/66.5
1.00 34.8/34.6 — — 65.2/65.4
the input domains and are expressed by parameters
σ
i
(spreads) taking values from 0 to 1. When the
value is equal to 0, the both classifiers are identical
to the corresponding singleton classifiers. The value
of the spread close to 1 means that uncertainty cov-
ers the whole range, i.e., the actual input value can
be any value in the range regardless of the actually
measured one. In such situation, a correct classifi-
cation cannot be expected. Besides, in the case of
classic non-singleton fuzzification, similar results in
the whole range of spread can be observed in Tables
1-3. The numbers of correct classifications achieve
the barely perceptible maximum. Moreover, for in-
dividual classifiers, the maximum is reached at dif-
Extended Possibilistic Fuzzification for Classification
349

ferent values of spread. This situation confirms that
classic non-singleton fuzzification does not incorpo-
rate uncertainty in input data. In contrary, the pro-
posed classifier with possibilistic fuzzification actu-
ally takes uncertainty into account. Some samples
could be unclassified if the level of uncertainty is such
high that it does not allow for an explicit classifica-
tion. When the uncertainty covers the whole range (σ
equal to 1), all samples are classified to the bound-
ary region of classes, in other words, are unclassified.
The described behavior of the classifier is desirable in
situations of the high level of uncertainty. The same
properties are observed for both examined methods of
inference.
5 CONCLUSIONS
In the presented paper the non-singleton fuzzifica-
tion have beens used to handle the imprecision of
input measurements or noisy input data. The simu-
lated classification examples have demonstrated that
possibilistic fuzzy systems (based on implications
or conjunctions) can produce no false classification
performing only certain or possible assignments. It
seems promising in such areas as medical diagno-
sis that possibilistic fuzzy systems give uncertain an-
swers rather than wrong answers. Without difficulty,
not classified cases can be redirected to a new more
particular investigation. Our future goal is to optimize
the percentage of correct classifications providing that
incorrect classification rate is equal zero.
The derived class of possibilistic fuzzy systems
is the rationally proper approach to uncertain classi-
fication, while the classical non-singleton fuzzy sys-
tems do not incorporate properly uncertainty of in-
put data, particularly, even in cases of complete un-
certainty they give. Actually, they ignore the fact of
uncertainty in data. The possibilistic fuzzy systems
work properly when there is some redundancy in in-
put data. Using such classifiers as the valuable parts
of ensemble systems is a subject of future investiga-
tions.
ACKNOWLEDGEMENTS
The project financed under the program of the Minis-
ter of Science and Higher Education under the name
”Regional Initiative of Excellence” in the years 2019
- 2022 project number 020/RID/2018/19, the amount
of financing 12,000,000 PLN.
REFERENCES
Han, Z.-q., Wang, J.-q., Zhang, H.-y., and Luo, X.-x.
(2016). Group multi-criteria decision making method
with triangular type-2 fuzzy numbers. International
Journal of Fuzzy Systems, 18(4):673–684.
Hu, B. Q., Wong, H., and fai Cedric Yiu, K. (2017). On
two novel types of three-way decisions in three-way
decision spaces. International Journal of Approximate
Reasoning, 82:285 – 306.
Liu, D., Liang, D., and Wang, C. (2016). A novel three-way
decision model based on incomplete information sys-
tem. Knowledge-Based Systems, 91:32 – 45. Three-
way Decisions and Granular Computing.
Mendel, J. M. (2001). Uncertain rule-based fuzzy logic sys-
tems: Introduction and new directions 2001. Prentice
Hall PTR, Upper Saddle River, NJ.
Mouzouris, G. C. and Mendel, J. M. (1997). Nonsingleton
fuzzy logic systems: theory and application. IEEE
Transactions on Fuzzy Systems, 5(1):56–71.
Najariyan, M., Mazandarani, M., and John, R. (2017).
Type-2 fuzzy linear systems. Granular Computing,
2(3):175–186.
Nowicki, R. K. (2019). Rough Set–Based Classification
Systems, volume 802 of Studies in Computational In-
telligence. Springer International Publishing, Cham.
Nowicki, R. K. and Starczewski, J. T. (2017). A new
method for classification of imprecise data using
fuzzy rough fuzzification. Information Sciences,
414:33 – 52.
Starczewski, J. T. (2013). Advanced Concepts in Fuzzy
Logic and Systems with Membership Uncertainty, vol-
ume 284 of Studies in Fuzziness and Soft Computing.
Springer.
Starczewski, J. T. (2014). Centroid of triangular and gaus-
sian type-2 fuzzy sets. Inf. Sci., 280:289–306.
Sun, B., Ma, W., and Xiao, X. (2017). Three-way group
decision making based on multigranulation fuzzy
decision-theoretic rough set over two universes. In-
ternational Journal of Approximate Reasoning, 81:87
– 102.
Yao, Y. (2010). Three-way decisions with probabilistic
rough sets. Information Sciences, 180(3):341 – 353.
Yao, Y. (2011). The superiority of three-way decisions in
probabilistic rough set models. Information Sciences,
181(6):1080 – 1096.
Zadeh, L. A. (1978). Fuzzy sets as a basis for a theory of
possibility. Fuzzy Sets and Systems, 1:3–28.
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
350
